表41二阶滤波器的标准传递函数
38-表41二阶滤波器的标准传递函数,零、极点分布以及幅频特性示意图
[ R ]/ 1k / 51%
10 k
12 V
74 1
10 k
12 V
图4—29 50Hz陷波器的幅频特性及输入输出波形
4—2—5
R
全通滤波器的幅频特性
是平行于频率轴的直线, 所以它对频率没有选择性。
R -
人们主要利用其相位频率 特性,作为相位校正电路
ui
+
uo
或相位均衡电路。图4—
R1
C
30所示,是一个一阶全通
滤波器或移相器,其传递 图4—30一阶全通滤波器(移相器)电路
函数为
Auf
(s)
1 1
sR1C sR1C
Auf ( j ) 1
( j ) 2 arctan RC
(4—40) (4—41a)
(4—41b)
A (ω ) 1
0 ω
(ω )
0
1 /R 1 C
R1
C4
R5
ui
-
R
C
2
3
A +
uo
Rp
(a )
图4—25带通滤波器
| A(jω) |
| A(jω) |
A(ω0) 0.707A(ω0)
R2
0
ω0
ω BW= ω0
0
ω01 ω02 ω03
ω
Q
(b)
(c)
图4—25 (a)电路;(b)幅频特性;(c)调节R2,幅频特性移动
4.3.4 带阻滤波电路(BEF)
带阻滤波器。因为
Ao s
Au
f
(s)
1
s2
Q
o s
Q
o2
二阶有源滤波器 双c 传递函数

文章标题:深度解析二阶有源滤波器的双C传递函数在现代电子领域中,滤波器是一种常用的电子设备,它可以对信号进行处理,将不需要的频率部分滤除,只留下需要的频率成分。
而有源滤波器又是一种常见的滤波器类型,它通过使用运放等有源元件来实现滤波功能。
在有源滤波器中,二阶有源滤波器尤为重要,其中的双C传递函数更是其中的核心。
1. 二阶有源滤波器的概念在深入讨论双C传递函数之前,我们首先需要了解什么是二阶有源滤波器。
二阶有源滤波器是一种可以实现二阶滤波功能的电路,它通常由运放和电容器、电感器等元件组成,能够对信号进行更为复杂的处理和滤波。
相较于一阶滤波器,二阶有源滤波器的性能更为优越,可以实现更高阶次的滤波功能。
2. 双C传递函数的定义在二阶有源滤波器中,双C传递函数是其中的重要概念。
双C传递函数是指在有源滤波器中,使用了两个电容来构成的传递函数,通过这两个电容的变化来调节滤波器的频率响应和性能。
通过合理选择电容的数值和连接方式,可以实现对滤波器性能的灵活调节,从而满足不同的工程需求。
3. 双C传递函数的特点双C传递函数具有一些独特的特点,首先是它能够实现对滤波器的频率响应进行精确调节,能够在一定范围内实现不同的频率响应曲线,这对于一些特定的应用场合非常重要。
双C传递函数还具有较高的稳定性和可靠性,能够在工程应用中发挥长期稳定的作用。
4. 我对二阶有源滤波器双C传递函数的个人理解在我的理解中,二阶有源滤波器的双C传递函数是一种非常灵活和实用的滤波器设计方案,通过调节其中的电容数值和连接方式,可以实现对滤波器性能的精确控制,从而满足不同的应用需求。
双C传递函数也提供了一种有效的手段,来解决一些频率响应要求较为苛刻的滤波器设计问题。
总结:二阶有源滤波器的双C传递函数是滤波器设计领域的重要概念,它能够实现对滤波器性能的精确调节,具有灵活性和实用性。
在工程应用中,设计人员可以通过合理利用双C传递函数,来实现对滤波器性能的优化和定制,以满足不同的应用需求。
二阶低通滤波传递函数介绍

二阶低通滤波器为了改进一阶低通滤波器的频率特性,可采用二阶低通滤波器。
一个二阶低通滤波器包含两个 如图所示为二阶低通滤波器的一般电路。
此一般电路对于二阶高通滤波器也同样适用。
图6—2-3所示的滤波器是同相 放大器。
在图6-2-3中,零频增益为気=!诗(6-2-5)在节点A 可得气打=叫(龄 + 耳 + FJ -u v Y 3-u n Y 2(6・24)在节点B 可得将式(6-2-8 )代人式(6-2-6),转变到复频域,可得一般二阶低通滤波器的传递函数为r ----- c oRC 支路,(6-2-7) (6 2呂)L;YR RATG(J )R KC仆3厲(&29)对于上图所示的二阶低通滤波器,其传递函数为在构成二阶低通滤波器时,只需选择巧,殇,蚝,%。
导纳的值即可。
例如,当选择 丫1 = 1/R 1 , 丫2 =1/R 2, Y3 = sC i Y 4=S C 2时,则构成图6 - 2 - 4所示的二阶低通滤波器门然角频率为(6-2-10)(6-242)式零频增益为粗尼系数为为了进一步简化计算,选取Q =C 2 = C.R, - = R.则式(6-2-14) ^(6-2-15)可进一步简化为1气=五f = 3 - G o采用频率归一化的方法.则上述二阶低通滤波器的传递函数为"VS 】如图6 -2 -5所示为二阶低通滤波器的幅频特性曲线,其阻带衰减特性的斜率为— 40dB / 10oct ,克服了一阶低通滤波器阻带衰减太慢的缺点。
二阶低通滤波器的各个参数,影响其滤波特性,如阻尼系数苫的大小,决定了幅频特性有无峰值,或 谐振峰的高低。
如图6 =2-6所示为苫对二阶低通滤波器幅频特性的影响。
GiwMdB) (6-243)为了简化计算■通常选G = C. = 式(6212人式(6213)可简化为1 c 7心阻(6-2-14) (6-2-15)(6-2-16) (6-2-17)(6*2-18)G(a))(dB)。
二阶振荡环节传递函数

二阶振荡环节传递函数引言二阶振荡环节传递函数是控制系统中的一种常见传递函数,用于描述振荡系统的动态特性和频率响应。
它可以被广泛应用于电子、机械和航空等领域中的控制系统设计和分析。
二阶振荡系统简介二阶振荡系统是指系统的传递函数具有二阶多项式形式的振荡系统。
它由两个一阶环节级联或串联而成,常用的结构有二阶低通滤波器、二阶带通滤波器、机械振动系统等。
在控制系统中,二阶振荡系统的传递函数通常表示为:G(s)=K(s2+2ξωn s+ωn2)其中,$ K $ 表示系统的增益,$ ξ $ 表示系统的阻尼比,$ ω_n $ 表示系统的自然频率。
二阶振荡系统的特点是具有明显的振荡行为,其频率响应曲线在某个频率处达到峰值,且在峰值附近有相位差发生。
因此,二阶振荡系统在控制系统设计中占据重要地位。
二阶振荡系统的频率响应二阶振荡系统的频率响应可以通过传递函数来分析和计算。
传递函数中的极点(Pole)对于系统的振荡特性起决定性的作用。
二阶振荡系统的极点由下式给出:s=−ξωn±ωn√1−ξ2根据极点的位置,可以将二阶振荡系统分为三种情况:1.当$ 0<ξ<1 $ 时,极点为一对复共轭极点,表示系统是过阻尼的,振荡频率较低;2.当$ ξ=1 $ 时,极点为一对重根,表示系统是临界阻尼的,振荡频率最低;3.当$ ξ>1 $ 时,极点为一对实轴上的负实数,表示系统是欠阻尼的,振荡频率较高。
根据传递函数的形式,二阶振荡系统的频率响应曲线可以分为低通、高通和带通三种类型,具体如下:1. 二阶低通滤波器当二阶振荡系统中的传递函数为低通滤波器时,频率响应曲线在截止频率附近具有较高的增益,截止频率以下的信号通过增益较大,截止频率以上的信号被抑制。
这种滤波器常用于信号处理和电子电路中。
2. 二阶高通滤波器当二阶振荡系统中的传递函数为高通滤波器时,频率响应曲线在截止频率附近具有较低的增益,截止频率以下的信号被抑制,截止频率以上的信号通过增益较大。
二阶带通滤波器中心频率和固有频率

《深入理解二阶带通滤波器:中心频率和固有频率的探讨》在探讨二阶带通滤波器的中心频率和固有频率之前,让我们先了解二阶带通滤波器的基本原理和应用。
二阶带通滤波器是一种常见的电子滤波器,它可以通过选择适当的电路元件和参数来实现对特定频率范围内信号的增强,并对其他频率的信号进行抑制。
在讨论中心频率和固有频率之前,我们需要先了解滤波器中的一些基础知识。
1. 二阶带通滤波器的基本原理二阶带通滤波器是由一个高通滤波器和一个低通滤波器级联构成的。
它的传递函数可以表示为:H(s) = k * (s^2) / (s^2 + (s/Q) + 1)其中,s是复频域变量,k是系统增益,Q是品质因数。
二阶带通滤波器可以在选择合适的参数后实现对特定频率范围内信号的增强,是一种非常常用的滤波器。
2. 中心频率的概念中心频率是指带通滤波器增益最大的频率点,也是滤波器响应曲线的中心位置。
在二阶带通滤波器中,中心频率通常由下式计算得出:fc = 1 / (2 * π * √(L * C))其中,fc表示中心频率,L表示电感值,C表示电容值。
中心频率决定了滤波器对特定频率范围内信号的响应程度,是设计带通滤波器时需要考虑的重要参数。
3. 固有频率的意义固有频率是指带通滤波器自身的振荡频率,也是在没有外部输入信号作用时,滤波器自由振荡的频率。
在二阶带通滤波器中,固有频率可以用下式表示:f0 = 1 / (2 * π * √(L * C))与中心频率类似,固有频率也与电感值和电容值有关。
固有频率可以反映出滤波器自身的特性,是分析滤波器稳定性和振荡特性的重要参数。
4. 理论与实际应用在实际应用中,中心频率和固有频率是设计二阶带通滤波器时需要重点考虑的参数。
通过合理选择电感值和电容值,可以实现对特定频率范围内信号的增强,同时保持滤波器的稳定性和响应速度。
在设计滤波器时,需要根据实际需求去调整中心频率和固有频率,以实现最佳的滤波效果。
总结回顾通过以上的讨论,我们对二阶带通滤波器的中心频率和固有频率有了更深入的了解。
二阶数字滤波器的设计-概述说明以及解释

二阶数字滤波器的设计-概述说明以及解释1.引言1.1 概述概述部分的内容可以介绍二阶数字滤波器的基本概念和作用。
可以参考以下写作思路:二阶数字滤波器是一种常用的信号处理工具,广泛应用于数字信号处理和通信系统中。
它可以对输入信号进行滤波处理,提取出我们关注的特定频率成分,抑制或消除其他频率成分。
通过控制滤波器的参数和结构,我们可以实现不同的滤波器响应和频率特性,满足不同应用需求。
二阶数字滤波器的核心原理是利用离散时间系统对输入信号进行滤波处理。
它通过将输入信号与一组预先设计好的滤波器系数相乘,并将结果累加得到输出信号。
这种基于差分方程的实现方式使得二阶数字滤波器具有较高的可调性和灵活性,可以实现不同的滤波器类型,如低通滤波器、高通滤波器、带通滤波器和带阻滤波器等。
二阶数字滤波器设计的关键在于确定滤波器的参数和结构。
参数包括滤波器的截止频率、通带增益、阻带衰减等,这些参数决定了滤波器的频率响应特性。
结构指的是选择滤波器的直接形式I、直接形式II还是级联形式等,不同结构会影响滤波器的性能和实现复杂度。
深入理解二阶数字滤波器的基本原理和设计要点,对我们正确选择和配置滤波器具有重要意义。
在接下来的正文中,我们将详细介绍二阶数字滤波器的基本原理、设计要点和实现方法,并探讨其在实际应用中的意义和未来研究方向。
通过学习和掌握二阶数字滤波器的设计,我们将能够更好地应对信号处理和通信系统中的滤波需求,提高系统性能和信号质量。
文章结构部分的内容如下:1.2 文章结构本篇文章主要以二阶数字滤波器的设计为中心,通过以下几个部分来展开讨论。
引言部分(第1节):介绍文章的背景和目的,概述二阶数字滤波器的设计,并说明本文的结构安排。
正文部分(第2节):详细阐述二阶数字滤波器的基本原理,包括数字滤波器的概念和数学模型,以及二阶滤波器的特点和性能指标。
同时,着重介绍二阶数字滤波器设计的要点,包括如何选择滤波器类型、确定滤波器参数和设计滤波器的一般步骤。
二阶有源滤波器计算器

二阶有源滤波器计算器首先,我们假设使用一个运算放大器作为有源滤波器的放大器。
运算放大器具有非常高的增益和输入阻抗,可以起到放大输入信号的作用。
H(s)=K/(s^2+βs+ω0^2)其中,H(s)表示滤波器的传递函数,s是频率的复变量,K是放大器的增益,β是阻尼系数,ω0是共振频率。
为了计算传递函数,我们需要确定放大器的增益K和阻尼系数β。
放大器的增益K可以通过选择合适的电阻和电容来设置。
例如,我们可以使用一个电阻和一个电容来构造一个低通滤波器,或使用两个电阻和一个电容来构造一个高通滤波器。
阻尼系数β可以通过调整电阻和电容来设置。
较小的β值将导致较高的共振峰,而较大的β值将导致较宽的带宽但较低的共振峰。
共振频率ω0可以通过选择合适的电阻和电容来设置。
共振频率是滤波器响应的中心频率,决定了滤波器的通带、阻带和带宽。
总的来说,设计一个二阶有源滤波器需要确定以下参数:1.放大器的增益K2.阻尼系数β3.共振频率ω0根据所需的滤波器特性,可以选择合适的电阻和电容值来设置这些参数。
一些常见的滤波器类型包括低通滤波器、高通滤波器、带通滤波器和带阻滤波器。
示例:假设我们要设计一个二阶低通滤波器,希望截止频率为1kHz,增益为10倍。
首先,我们可以选择一个适当的阻尼系数β值,例如0.707、然后,根据截止频率和阻尼系数,我们可以计算共振频率ω0。
ω0 = 2 * π * fc其中,fc是截止频率。
例如,如果fc = 1kHz,则ω0=2*π*1kHz=6.28kHz接下来,我们可以选择一个适当的放大器增益K值,例如10。
然后,我们可以使用这些参数来计算滤波器的传递函数。
H(s)=10/(s^2+0.707s+6.28^2)通过计算传递函数,我们可以了解滤波器的频率响应和幅频特性。
最后,我们可以选择适当的电阻和电容值来实现滤波器。
例如,可以选择100Ω的电阻和1μF的电容来设置滤波器的参数。
请注意,这只是一个示例,并且具体的计算取决于所需的滤波器类型和特性。
二阶RC有源滤波器的设计!!

湖南人文科技学院毕业设计二阶RC有源滤波器的设计摘要:滤波器是一种能够使有用频率信号通过,而同时抑制(或衰减)无用频率信号的电子电路或装置,在工程上常用它来进行信号处理、数据传送或抑制干扰等。
有源滤波器是由集成运放、R、C 组成,其开环电压增益和输入阻抗都很高,输出阻抗又低,构成有源滤波电路后还具有一定的电压放大和缓冲作用,但因受运算放大器频率限制,这种滤波器主要用于低频范围。
本次毕业设计主要是在所学《模拟电子技术基础》、《集成电路》等专业知识的基础上研究和设计几种典型的二阶有源滤波电路:巴特沃斯二阶有源低通滤波器、巴特沃斯二阶有源高通滤波器、二阶有源带通滤波器,研究和设计其电路结构、传递函数,并对有关参数进行计算,再利用multisim 软件进行仿真,组装和调试各种有源滤波器,探究其幅频特性。
经过仿真和调试,本次设计的二阶RC有源滤波器各测量参数均与理论计算值相符,通频带的频率响应曲线平坦,没有起伏,而在阻频带则逐渐下降为零,衰减率可达到|-40Db/10oct|,滤波效果很理想。
关键词:有源滤波器二阶 RC 频率Abstract:Filter is a kind of can make useful frequency signal through,While suppressing ( or attenuation) useless frequency signal electronic circuit or device, commonly used in engineering to signal processing, data transfer or suppression of interference. Active power filter is composed of integrated operational amplifier, R, C composition, its open loop voltage gain and input impedance is very high, and low output impedance, an active filter circuit also has a voltage amplifying and buffering effect, but due to operational amplifier frequency limit, this filter is mainly used in low frequency range.This graduation design is mainly in the" analog electronic technology"," integrated circuit" and other professional knowledge based on research and design of several typical two order active filter circuit: Butterworth two, Butterworth two step active low pass filter active high-pass filter, two step active band-pass filter, research and design of its circuit structure, transfer function, and the related parameters are calculated, then the use of Multisim software simulation, assembly and commissioning of various active filter, explore its amplitude frequency characteristic.After simulation and debugging, the design of the two order active RC filter the measurement parameters and calculation results, the pass band frequency response curve is flat, no ups and downs, and in the stop band is decreased to zero, attenuation rate can reach | - 40dB / 10oct |, filtering effect is very ideal.Key words: Active power filter Two order RC Frequency Signal第一章前言1.1 选题依据近现代,在电子工程、通信工程、自动控制、遥测控制、测量仪器、仪表和计算机等技术领域,滤波器的应用极为广泛,滤波器的优劣直接决定产品的优劣,所以,对滤波器的研究和生产历来为各国所重视。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4.3.2 二阶压控电压源高通滤波电路
频率特性: u+ uo
式中:
要求:Aup﹤3
其幅频特性曲线如图:
运放作为无限增益放大器的多重反馈有源滤波器
Y1 ui C Y2
Y4 Y3 B Rp
Y5 - A + uo
多重反馈有源滤波器
4.3.3 带通滤波电路BPF
BPF作用是使某频段内的有 用信号通过,而高于或低于 此频段的信号将被衰减。
由于开关电容滤波器属于离散时间系统,所以开关电容滤 波器的分析方法与数字滤波器类同,主要用差分方程和Z 变换
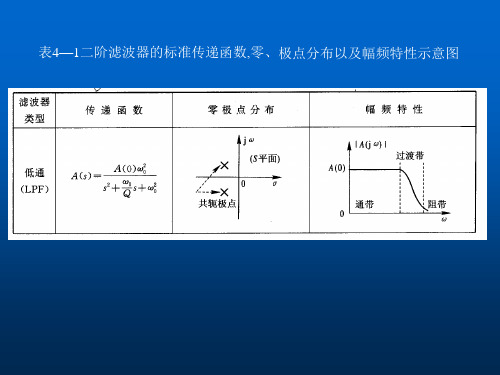
表4—1二阶滤波器的标准传递函数,零、
运放作为有限增益放大器的有源滤波器电路
Rf1 Y2 Y1 ui Y3 Y4 (a ) -
Rf2 Y2 K + Y3 uo ui Y1 C Y4 B K uo
(b )
给Y1~Y4赋予不同的阻容元件,则可构成不同 的滤波器。例如,令Y1=Y3= 1 , R Y2=Y4=sC,如图4—23所示,则传递函数
与表3—1中带通滤波器的标准传递函数
(4—32)
A( s )
A( 0 ) s2
0
Q
s
(4—33)
0
Q
2 s 0
比较,得中心角频率
1 0 C
取R2<<R1,有
1 1 1 ( ) R5 R1 R2 1 R5 R2
(4—34)
1 0 C
中心频率增益
1 R5 CR1 A(0 ) 2 2 R1 R5C -3dB带宽 2 BW Q R5C
(4—35)
0
(4—36)
画出幅频特性如图 4—25(b) 所示。调节 R2, 使中心频 率变化,但带宽不变,增益也不变。这是该电路的特 点,也是优点,如图4—25(c)所示。
R1 ui
C4 C3
R5 - A + Rp (a )
R2
uo
图4—25带通滤波器
| A(jω) | A(ω0 ) 0 .7 07 A(ω0 )
当 K > 3 时 , 分母中 s 项系数变负,极 点就会移至S平面的右半平面,从而导致 系统不稳定。一般这种电路的 Q 只能做 到10以下。
4.3.1 一阶高通滤波电路(HPF)
电路可由一阶LPF互换R C得到
传递函数为: uI u+ uo
令s=j有
-3
式中
高通截止频率 +20dB/十倍频
LPH
HPF
uo
BW
1 1 1 若令Y1 ,Y2 ,Y3 sC3 , Y4 sC4 , Y5 R1 R2 R5
则该电路为带通滤波器,如图3—25(a)所示。令
C3=C4=C,其传递函数为 1 s CR1 Auf ( s ) 2 R R2 s2 s 21 CR5 C R1R2 R5
∑
-
-
UH P (高通输出 )
图4—32 状态变量滤波器的信号流图表示法
4.4 开关电容滤波电路(SCF)
电路MOS管和小电容组成, 工作原理是 q1=C1· u1 TC
q2=C1· u2
电容C1的传输平均电流为:
电路等效于: 由此可见,开关电容滤波 电路频率特性的特征频率 仅与时钟频率和电容比值 有关。
阻 带
fH f0 fL
uo
式中 ui
LPF
HPF
用带通和相加器组成的带阻滤波器其框图如图4—27所示。 例如,采用图4—25(a)的带通滤波器和相加器组合便构成 带阻滤波器。因为
A Auf ( s ) 1 s
2
o
Q
s
(3—38)
2
o
Q
s o
BPF
+ + ∑
uo
图4—27 用带通滤波器和相加器组成带阻滤波器
4 00 k R5 - C3 0 .2 2μ A1 + 1k A(ω0 )=- 1
图4—28 50Hz陷波器电路
10k
0.22μ 200k 0.22μ
400k 741
10k 12V 10k 741
1 V/1.5 Hz /0 Deg 1 V/50 Hz /0 Deg
[R]/ 1k/ 51% 12V
图4—29 50Hz陷波器的幅频特性及输入输出波形
LPF
HPF
可以用LPF和HPF串联组成
其构成思路如图所示: fL 注意:低通截止频率fH大于 高通截止频率fL
通带
fH
fLf0 fH
二阶压控电压源BPF
电路如图: 频率特性为:
uI 等效品质因数Q等于 同相比例放大电路的放大倍数 Aup是通带电压放大倍数,有 中心频率 从特性曲线看到,Q值越大, 带宽BW越窄。
只要令A′=-1(即令图4—25(a)中的R5=2R1),则
0
Auf ( s ) 1 s2
0
Q
Q
s s 0
2
s 2 0 s2
2 2
0
Q
s 0
(4—39)
1 0k 0 .2 2μ C4 R Rf 1 0k 1 0k - R + A2 uo
2 00 k ui R1 R2
| A(jω) | R2
0
ω0 (b )
BW =
ω0 Q
ω
0
ω0 1
ω0 2 (c)
ω0 3
ω
图4—25 (a)电路;(b)幅频特性;(c)调节R2,幅频特性移动
4.3.4 带阻滤波电路(BEF)
作用是阻止某一频段内 为中心频率 的信号通过, 达到抗干扰 的目的,又名陷波器。 特性曲线是:
电路由低通和高通滤波电 由图可知,Q值越大, 阻带 路并联而成,其思路是: 宽度越窄 双T带阻滤波电路如图: 频率特性为: 低通 BW 高通
4—2—5 R 全通滤波器的幅频特性 R 是平行于频率轴的直线, - 所以它对频率没有选择性。 人们主要利用其相位频率 ui uo + 特性,作为相位校正电路 R1 或相位均衡电路。图4—ห้องสมุดไป่ตู้C 30所示,是一个一阶全通 滤波器或移相器,其传递 图4—30一阶全通滤波器(移相器)电路 函数为
1 sR1C Auf ( s ) 1 sR1C Auf ( j ) 1
(4—40) (4—41a) (4—41b)
( j ) 2 arct anRC
A(ω) 1 0 (ω) 0 -9 0° 1 /R1 C ω ω
图4—31一阶移相器的幅频特性及相频特性
-1 1 /Q A Ui Uo 1 ω0 S UBP (带通输出 ) Uo 2 ω0 S ULP (低通输出 ) Uo 3
1 K 2 2 2 K o RC Auf ( s) (4—29) 3 K 1 o 2 2 2 s s 2 2 s s o RC RC Q
与表 4—1中的标准表达式比较,该传递函数有两 个共轭复根(极点)而没有零点,可见是一个二阶低通
滤波器。其中:
Rf 2 1 1 o , K 1 ,Q RC Rf 1 3 K
