铁路缓和曲线计算
铁路三次抛物线缓和曲线的计算

次抛 物线 形 、 次 抛 物 线 余 弦 改 善 型 、 次 四项 式 三 七 型 、 波 正弦 型等 , 于三 次 抛 物 线 线 形 简 单 、 计 半 鉴 设 方便 、 立面有 效 长度 长 、 平 现场 轨道 铺设 和养 护 容易 的特 点 , 目前在 国内 外 铁路 和 高 速铁 路 中大 部 分 采
Te h o o y & Ec n m y i e s o Co c n lg o o n Ar a f mmun c to s i ain
交 通 科 技 与 经 济
2 1 年第 1 总第 6 01 期( 3期)
铁 路 三 次 抛 物 线 缓 和 曲线 的计 算
王 国栋 马 俊Байду номын сангаас海 ,
中桩 坐标计算 , 以一算例说 明 。 并
关 键 词 : 和 曲线 ; 次 抛 物 线 ; 缓 三 曲线 要 素 ; 标 坐 中 图分 类 号 : 8 . U2 4 2 文献标识码 : A 文 章 编 号 :0 85 9 (0 1 0—0 30 1 0—6 6 2 1 ) 10 1 —4
特点 , 据研究 成 果 , 和 曲线 也 有 多 种 形 式 , 根 缓 如三
…
Y一 — ・ 6 C —
L l J
式 中 : 三 次 抛 物 线 参 数 , 回旋 曲线 中 的 A 相 C为 和
似, 与抛 物 线 的长度 L 及 圆曲线 的半 径 R 有关 。 。 设 P 为抛 物线 线上 任 意一 点 , P 点处 的 转 向 则 角 或切 线偏 角 ( P点 处 的切 线 与 ZH 点 的切 线 的 夹
它 的半 径 等 于圆 曲线 的半径 R。这样 随着 半径 的减
小 , 相应 的超 高 逐 渐 增 大 , 到 了过 渡 的 作用 , 使 起 这 种 曲线 称 缓和 曲线 。 缓 和 曲线 的线 型可 以有 很多 种 , 目前 , 国公 路 我 上 广泛采 用 的缓 和 曲 线 是 回旋 曲线 , 曲线 的方 程 为 A一 ̄R ・ 。而在铁 路 路 线 设 计 中 , 虑 到 铁 路 的 / 考
第四讲3、缓和曲线

6Rl0
又 = l
3
故
b= 2 (12 22)
• 式中, 为缓和曲线上任一点的正偏角,b为该 点的反偏角。
• 同理可得, b0 20 23)
(12-
• 由 式 ( 12 - 22 ) 、 式 ( 12 - 23 ) 得 出 结 论 (a):
• 按铁路测规要求,缓和曲线应l 0 m一点,则
•
N =6
• 由式(12-21)可知
0
0 3
l0
180
6R
60 6 500
180
10845
1
0 N2
10845 62
155
• 各点偏角值计算见表12-l 7。
2.缓和曲线的测设方法
发现,它仅适用于平坦地区及支距 y 较小的曲线。长弦偏角法测设精度高、速度快、任何地区
均可适用。
• 要增加在缓和曲线任一点上测设缓和曲线的方法.
• 当l=l0时, R ,所以:
•
Rl0 C
• 式中,l0为缓和曲线总长。
•
l C 是缓和曲线的必要条
件,实用中能满足这一条件的曲
线可作为缓和曲线,如辐射螺旋
线、三次抛物线等。我国的缓和
曲线均采用辐射螺旋线。
图 12-26
二、缓和曲线方程式
• 按照 l C 为必要条件导出的缓和曲线方程为:
0
tan 0 tan 0
y0 x0
y0 x0
• 将式(12-15)代入上式,并取至二次项,
•∴
0
l0 6R
0 3
(12-18)
铁路缓和曲线坐标计算方法 (0517)
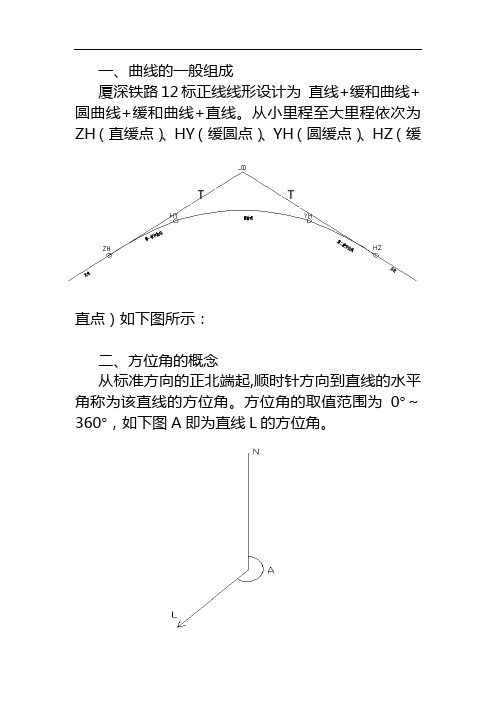
一、曲线的一般组成厦深铁路12标正线线形设计为 直线+缓和曲线+圆曲线+缓和曲线+直线。
从小里程至大里程依次为ZH (直缓点)、HY (缓圆点)、YH (圆缓点)、HZ (缓直点)如下图所示:二、方位角的概念从标准方向的正北端起,顺时针方向到直线的水平角称为该直线的方位角。
方位角的取值范围为0°~360°,如下图A 即为直线L 的方位角。
TT三、某点坐标的计算已知A 点坐标为(491548,2505452),B 点距离A 点L=125m ,直线AB 的方位角为235°,计算B 点坐标。
计算方法:Y=491548+125×SIN235=491445.606X=2505452+125×COS235=2505380.303四、曲线上任一点的坐标及切线方位角计算1 直线段上任一点的坐标及方位角直线上的坐标计算比较简单,只需要求出该点所在直线的方位角以及线路中的里程即可求得例1,求DK495+520处左中线的坐标及方位角由设计院所给的曲线要素表可知该点位于JD57 JD58的直线上,查曲线要素表JD57,JD58的坐标分别为(488809.902,2504127.029),(485660.627,2504491.226)。
通过坐标反算直线JD57 JD58的方位角:TTA=atg((485660.627-488809.902)/( 2504491.226-25 04127.029))=276.59665°注意:A的取值可根据下述条件确定ΔY>0,ΔX>0,第一象限0-90°ΔY>0,ΔX<0,第二象限90°-180°ΔY<0,ΔX<0,第三象限180°-270°ΔY<0,ΔX>0,第四象限270°-360°查曲线表,JD58切线长T= 690.303m,JD58坐标(Y58,X58)=(485660.627,2504491.226),ZH点里程为DK496+093.885。
铁路、公路线路测量公式

4)、圆曲线上任意点法线方向上任意点的大地坐标(X法,Y法),法线方位角α法,
如果转向角左偏取α法=α-3*β-3.1415/2,若α法<0,则计算结ห้องสมุดไป่ตู้加上2倍的圆周率即α法=α-3*β-l/R-3.1415/2+2*3.1415;
即α法=α-3(20Rls/(40R^2-ls^2)) -l/R-3.1415/2+2*3.1415
如果转向角右偏取
α法=α+3(20Rls/(40R^2-ls^2)) +l/R +3.1415/2;
若α法>360,
则α法=α+3(20Rls/(40R^2-ls^2)) +l/R +3.1415/2-2*3.1415;
如果转向角左偏取α法=α-3*β-3.1415/2,若α法<0,则计算结果加上2倍的圆周率即α法=α-3*β-3.1415/2+2*3.1415;
如果转向角右偏取α法=α+3*β+3.1415/2;若α法>360,则计算结果加上2倍的圆周率即α法=α+3*β+3.1415/2-2*3.1415;
法线上任意一点到切点的距离为D法,
X=l-l5/(40*R2*ls2)
Y= l3/(6*R*ls)
αi为直缓点到待求点直线的方位角(弧度);
如果转向角左偏取αi=(α-β)=(α-20R lsl2/3(40R2ls2- l4))
若(α-β)<0,则αi=(α-β)+2*3.1415,但在计算坐标中可不考虑;
如果转向角右偏取αi=(α+β)=(α+20R lsl2/3(40R2ls2- l4))
常用缓和曲线.
K
K0
l l0
ห้องสมุดไป่ตู้
①
l Rl0 C ②
由式①可见,缓和曲线长度l与其曲率K成正比。符合 这一条件的曲线称为放射螺旋线。
d dl Kdl
d
K0
l l0
dl
1 Rl0
ldl
l 0时, 0,C 0 l 2
2Rl0
d l2 D
2Rl0
l 0 时, 0 , D 0
为缓和曲线上任一点的偏角,
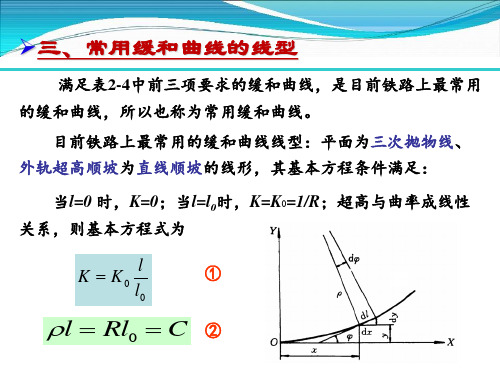
➢三、常用缓和曲线的线型
满足表2-4中前三项要求的缓和曲线,是目前铁路上最常用 的缓和曲线,所以也称为常用缓和曲线。
目前铁路上最常用的缓和曲线线型:平面为三次抛物线、 外轨超高顺坡为直线顺坡的线形,其基本方程条件满足:
当l=0 时,K=0;当l=l0时,K=K0=1/R;超高与曲率成线性 关系,则基本方程式为
在HY点,l
l0
,
0
l0 2R
l2 2Rl0
直角坐标表示的缓和曲线方程
dx dl cos, dy dl sin
0,sin
c os
cos2 2 cos 2 dx
1
2 2
dl
1
l4 8R2l02
2dl
sin 2
2
1 2sin2
1 2
2
2
1
2
2
2
dx
1
2
2
dl
1
l4 8R 2l02
dl
积分上两式,得:
dx
(1
2
)dl
(1
l4 8R 2l02
)dl
dy dl l 2 dl
2Rl0
对上两式进行积分,得
缓和曲线要素及公式介绍

为了保障车辆行驶安全,在直线与圆曲线之间加入一段半径由∞逐渐变化到R的曲线,这种曲线称为缓和曲线。
目前常用的缓和曲线多为螺旋线,它有一个特性,曲率半径ρ与曲线长度l成反比。
数学表达为:ρ∝1/l 或ρ·l = k ( k为常数)若缓和曲线长度为l0,与它相连的圆曲线半径为R,则有:ρ·l = R·l0 = k目前我国公路采用k = (V为车速,单位为km/h),铁路采用k = ,则公路缓和曲线的长度为l0 = R ,铁路缓和曲线的长度为:l0 = R 。
11.2.2 带缓和曲线的圆曲线的主点及主元素的计算带缓和曲线的圆曲线的主点有直缓点ZH、缓圆点HY、曲中点QZ、圆缓点YH、缓直点HZ 。
带缓和曲线的圆曲线的主元素及计算公式:切线长 T h = q+(R+p)·tan(α/2)曲线长 L h = 2l0+R·(α-2β0)·π/180°外矢距 E h = (R+p)·sec(α/2)-R切线加长 q = l0/2-l03/(240R2)圆曲线相对切线内移量 p = l02/(24R)切曲差 D h = 2T h -L h式中:α 为线路转向角;β0为缓和曲线角;其中q、p、β0缓和曲线参数。
11.2.3 缓和曲线参数推导dβ = dl/ρ = l/k·dl两边分别积分,得:β= l2/(2k) = l/(2ρ)当ρ = R时,则β =β0β0 = l0/(2R)若选用点为ZH原点,切线方向为X轴,垂直切线的方向为Y轴,建立坐标系,则:dx = dl·cosβ = cos[l2/(2k)]·dldy = dl·sinβ = sin[l2/(2k)]·dl考虑β很小,sinβ和cosβ即sin(l2/(2k))和cos(l2/(2k))可以用级数展开,等式两边分别积分,并把k = R·l0代入,得以曲线长度l为参数的缓和曲线方程式:X = l-l5/(40R2l02)+……Y = l3/(6Rl0)+……通常应用上式时,只取前一、二项,即:X = l-l5/(40R2l02)Y = l3/(6Rl0)另外,由图可知,q = X HY-R·sinβ0p = Y HY-R(1-cosβ0)以β0= l0/(2R)代入,并对sin[l0/(2R)]、cos[l0/(2R)]进行级数展开,取前一、二项整理可得:q = l0/2-l03/(240R2)p = l02/(24R)若仍用上述坐标系,对于圆曲线上任意一点i,则i点的坐标X i、Y i可以表示为:Xi = R·sinψi+qYi = R·(1-cosψi)+p11.2.4 带缓和曲线的圆曲线的主点桩号计算及检核ZH桩号 = JD桩号-T hHY桩号 = ZH桩号+l0QZ桩号 = HY桩号+L/2YH桩号 = QZ桩号+L/2 = HY桩号+L = ZH桩号+l0+LHZ桩号 = YH桩号+l0 = ZH桩号+L hJD桩号 = ZY桩号-T h+D h(检核)11.2.5 带缓和曲线的圆曲线的主点的测设过程:(1)在JD点安置经纬仪(对中、整平),用盘左瞄准直圆方向,将水平度盘的读数配到0°00′00″,在此方向量取T h,定出ZH点;(2)从JD沿切线方向量取T h-X HY,然后再从此点沿切线垂直方向量取Y HY , 定出HY点;(3)倒转望远镜,转动照准部到度盘读数为α,量取T h,定出HZ点;(4)从JD沿切线方向量取T h-X HY,然后再从此点沿切线垂直方向量取Y HY , 定出YH点;(5)继续转动照准部到度盘读数为(α+180°)/2,量取E h,定出QZ点。
缓和曲线半径计算公式

缓和曲线半径计算公式缓和曲线是指将两条直线或曲线段平滑地连接起来的过渡曲线。
在道路设计、铁路设计等领域中广泛应用。
计算缓和曲线半径的公式基于几何学原理和交通工程的需求。
在计算缓和曲线半径之前,首先需要了解以下几个关键参数:1.设计速度(Vd):即车辆在缓和曲线上行驶的目标速度。
2.过渡长度(L):即缓和曲线的总长度。
3.动摩擦因数(f):即车辆行驶过程中的轮胎与路面之间的摩擦系数。
4.允许超高(e):在垂直方向上,车辆离开水平线的最大允许值。
基于以上参数,可以通过以下公式计算缓和曲线半径:R=Vd^2/(127*f*e)其中,R表示缓和曲线半径。
需要注意的几点是:1.这个公式是根据欧拉公式推导得来的,适用于大多数情况。
但对于特定道路设计,如复杂弯道或高速公路等,可能需要采用更复杂的公式进行计算。
2.设计速度需要根据具体路段的要求进行选择。
一般来说,缓和曲线的设计速度应与前后道路的设计速度相匹配,以确保平稳过渡。
3.允许超高是指驶过缓和曲线过程中,车辆会偏离水平线的程度。
允许超高的值应根据实际需要进行确定。
4.确定缓和曲线总长度的计算需要根据具体情况进行。
一般来说,它被设定为车辆达到设计速度所需的时间内行驶的距离。
5.动摩擦因数是一个经验值,根据道路状况、车辆类型等因素进行选择。
一般来说,可以参考交通工程相关规范或手册中的推荐值。
需要注意的是,以上计算仅为基本公式,实际应用中还会受到其他因素的影响,如地形、道路条件、车辆特性等。
因此,在进行具体的设计和计算时,建议参考相关的交通工程规范和设计手册,确保计算结果符合实际需求。
平曲线计算公式

平曲线计算公式摘要:一、引言二、平曲线计算公式介绍1.圆曲线2.缓和曲线三、计算方法1.圆曲线计算方法2.缓和曲线计算方法四、实际应用1.在道路设计中的应用2.在铁路设计中的应用五、结论正文:一、引言平曲线计算公式是道路和铁路设计中非常重要的一个概念,它涉及到道路和铁路的曲率半径、超高缓和段长度等关键参数的计算。
本文将详细介绍平曲线计算公式及其在实际工程中的应用。
二、平曲线计算公式介绍平曲线分为圆曲线和缓和曲线两种,下面分别介绍这两种曲线的计算公式。
1.圆曲线圆曲线是最简单的平曲线形式,其计算公式如下:R = (V^2 / g) / (1 + (h / R)^2)其中,R 为曲率半径,V 为设计速度,g 为重力加速度,h 为超高缓和段长度。
2.缓和曲线缓和曲线是为了克服圆曲线在高速行驶时产生的离心力而设计的曲线形式。
缓和曲线的计算公式较为复杂,通常需要通过数值方法求解。
三、计算方法1.圆曲线计算方法根据圆曲线计算公式,可以求解出曲率半径R。
在实际应用中,需要根据设计速度V 和超高缓和段长度h 这两个已知条件,计算出合适的曲率半径R。
2.缓和曲线计算方法缓和曲线的计算方法通常采用数值方法,例如牛顿法、梯度下降法等。
在实际应用中,需要根据设计要求设定初始值,然后通过迭代计算,逐步逼近最优解。
四、实际应用1.在道路设计中的应用平曲线计算公式在道路设计中具有重要意义,它直接影响到道路的行驶安全性、舒适性和经济性。
正确使用平曲线计算公式,可以为道路设计提供科学依据,提高道路设计的质量。
2.在铁路设计中的应用与道路设计类似,平曲线计算公式在铁路设计中也具有重要意义。
在高速列车行驶过程中,平曲线的设置将直接影响到列车的运行安全、舒适性和能耗。
因此,在铁路设计中,需要根据列车设计速度和线路条件,合理设置平曲线,以满足列车运行要求。
五、结论平曲线计算公式是道路和铁路设计中的关键概念,掌握平曲线计算公式对于提高设计质量和保障工程安全具有重要意义。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
、缓和曲线的作用及其几何特征
行驶于曲线轨道的机车车辆,出现一些与直线运行显著不同的受力特征。
如曲线运行的离
心力,外轨超高不连续形成的冲击力等。
为使上述诸力不致突然产生和消失,以保持列车曲线运行的平稳性,需要在直线与圆曲线轨道之间设置一段曲率半径和外轨超高度均逐渐变化的曲线,称为缓和曲线。
当缓和曲线连接设有轨距加宽的圆曲线时,缓和曲线的轨距是呈线性变化的。
概括起来,缓和曲线具有以下几何特征:
1. 缓和曲线连接直线和半径为R的圆曲线,其曲率由零至1/R逐渐变化。
2. 缓和曲线的外轨超高,由直线上的零值逐渐增至圆曲线的超高度,与圆曲线超高相连接。
3. 缓和曲线连接半径小于350m的圆曲线时,在整个缓和曲线长度内,轨距加宽呈线性递增,由零至圆曲线加宽值。
因此,缓和曲线是一条曲率和超高均逐渐变化的空间曲线。
二、缓和曲线的几何形位条件
图2-9所示为一段缓和曲线。
其始点与终点用ZH与HY表示。
要达到设置缓和曲线的目的,根据如图所取直角坐标系,缓和曲线的线形应满足以下条件:
1.为了保持连续点的几何连续性,缓和曲线在平面上的形
状应当是:在始点处,横坐标x= 0,纵坐标y= 0,倾角φ
= 0;在终点处,横坐标x=x0,纵坐标y=y0,倾角φ=
φ0。
2.列车进入缓和曲线,车体受到离心力J的作用,为保持列车运行的平稳性,应使离心力不突然产生和消失,即在缓和曲线始点处,J=0,在缓和曲线终点处Ρ=R。
3.缓和曲线上任何一点的曲率盈余外轨超高相吻合。
在纵断面上,外轨超高顺坡的形式有两种形式。
一种形式是,如图2-10(a)所示;另一种形式是曲线形,如图2-10(b)所示。
图 2-9缓和曲线坐标图
列车经过直线顺坡的缓和曲线始点和终点时,对外轨都会产生冲击。
在行车速度不高,超高顺破相对平缓时,列车对外轨的冲击不大,可以采用直线形顺坡,即可满足曲率与超高相配合的要求。
当行车速度较高,为了消除列车对外轨的冲击,应采用曲线形超高顺坡。
其几何特征是缓和曲线始点及终点处的超高顺坡倾角r=0 ,即在始点和终点处应有:
式中h--外轨超高度,其值为:
l--曲线上任何一点至缓和曲线起点的距离。
对某一特定曲线,平均速度v p可视为常数。
令
则
可见缓和曲线上各点超高为曲率K的线性函数。
因此,在缓和曲线始、终点处应有:
4.列车在缓和曲线上运动时,其车轴与水平面倾斜角φ不断变化,亦即车体发生测滚。
要使钢轨对车体傾转的作用力不突然产生和消失,在缓和曲线始、终点处应使傾转的角加速度为零。
可见:
式中h = EK由此
图 2-10 超高顺坡
因为
所以
综上所述,缓和曲线的线形条件,可归纳如表2-5。
表 2-5 缓和曲线线形条件表
顺序符号始点终点始终至终点之间
1y0y0
连续变化
2φ0φ0
3K01/R
400
500
可以看出,表中前两项是基本的几何形位要求,而后三项则是由行车平稳性形成的力学条件推导出的几何形位要求。
在行车速度不高的线路上,满足前三项要求的缓和曲线尚能适应列车运行的需要,而在速度较高的线路上,缓和曲线的几何形位就必须考虑后两项的要求。
三、常用缓和曲线
满足表2-6中前三项要求的缓和曲线,是目前铁路上最常用的缓和曲线,所以也称为常用缓和曲线。
常用缓和曲线的外轨超高顺坡,其基本方程必须满足的条件为:
当l=0 时,K=0 ;当l=l0时,K=1/R。
由超高与曲率的线性关系可知,满足这些条件的基本方程应为:
(2-23)式中K--缓和曲线上任意一点的曲率;
l--缓和曲线上某一点离ZH点(或HZ点)的距离;
K0--缓和曲线终点HY点(或YH点)的曲率;
l0--缓和曲线长度。
由式(2-12)可见,缓和曲线长度l与其曲率K成正比。
符合这一条件的曲线称为放射螺旋线。
缓和曲线的偏角为:
(2-24)
在缓和曲线终点处,l=l0,缓和曲线偏角为:
(2-25)
由式(2-24)可见,在缓和曲线长度范围内,偏角数值较小,可取近似值:
于是可得
积分上两式得
(2-26)
(2-26)
这就是放射螺旋线得近似参变数方程式,是我国铁路常用得缓和曲线方程式。
如消去上两式得参变数l,则得
(2-28)
这是放射螺旋线得近似直角坐标方程式。
在曲线半径较小得铁路上,采用第一项作为近似式。
四、高次缓和曲线
满足表2-6中前两项或全部五项要求得缓和曲线称为高次缓和曲线。
高次缓和曲线外轨超高顺坡为曲线顺坡。
这种曲线在列车经过时,各种力得作用不突然产生和消失,适应高速行车的需要。
求缓和曲线方程的方法,可先确定一个符合条件的基本方程,在逐步推导,最后得出所需求的缓和曲线方程式。
表2-6列出可用于高速铁路的三种高次缓和曲线。
表 2-6 高次缓和曲线
缓和曲线基本方程方程式
赵氏七次式
沙氏正弦形
日本高速铁路半
波正弦形
五、缓和曲线的长度
缓和曲线长度的确定,受到许多因素影响,其中最主要的是保证行车安全和行车平稳两个条件。
1.缓和曲线要保证行车安全,使车轮不致脱轨。
机车车辆行驶在缓和曲线上,若不计轨道弹性和车辆弹簧作用,则车架一端的两轮贴着钢轨顶面;另一端的两轮,在外轨上的车轮贴着钢轨顶面,而在内轨上的车轮是悬空的。
为保证安全,应使车轮轮缘不爬越内轨顶面。
设外轨超高顺坡坡度为i,最大固定轴距为Lmax ,则车轮离开内轨顶面的高度为。
当悬空高度大于轮缘最小高度 iLmax时,车轮就有脱轨的危险。
因此必须保证:
(2-29)
式中i0-- 外轨超高顺坡坡度。
缓和曲线长度l0应为:
(2-30)
式中 h0--圆曲线超高度。
对外轨超高顺坡为曲线性的缓和曲线,外轨超高顺坡的最大坡度也要满足式(2-29)对
i0的要求。
曲线形顺坡的坡度由下式计算:
(2-31)
《铁路线路维修规则》规定:曲线超高应在整个缓和曲线内完成,顺坡坡度一般不应大于1/(9v max);困难条件下不得大于1/(7v max) 。
当1/(7v max)大于2‰时,按2‰设置。
2.缓和曲线长度要保证外轮的升高(或降低)速度不得超过限值,以满足旅客舒适度要求。
车轮在外轨上的升高速度μ由下式计算:
式中h--圆曲线外轨超高,以mm计;
v max--通过曲线的最高行车速度,以m/s计;
l0--缓和曲线长度,相当于直线形顺坡缓和曲线长度,以m计。
为保证旅客舒适度的要求,则缓和曲线长度为:
(2-32)
式中Vmax--通过曲线的最高行车速度,以km/h计;
1/换算系数。
我国根据长期运营实践,μ0在一般情况下采用32mm/s;困难地段用40mm/s 。
运营铁路以实际最高行车速度及实设超高为计算标准。
一般地段μ0=28mm/s,特别困难地段μ0=40mm/s。
则在一般地段应取:
(2-33)
计算结果取两项要求中的最大值,并取为10m的整倍数。
《铁路线路设备大修规则》规定:缓和曲线长度一般地段:
(2-34)
特别困难地段
(2-35)
式中l0--缓和曲线长,以m计;
h--超高,以m计;
Vmax--容许最高行车速度。
计算结果取10m的整倍数,长度不短于20m。
两缓和曲线间的圆曲线长度不短于20m。
缓和曲线长度应根据曲线半径,路段旅客列车设计速度和地形条件按表2-7选用。
有条件时应采用较表2-7规定的更大值。
表 2-7 缓和曲线长度(m)。
