一次回归正交设计
第七章 回归正交试验设计

个因素之间的函数关系。
因素水平编码表
自然变量xj 规范变量zj 1 -1 0 △j x1 700 300 500 200 x2 2400 1800 2100 300 x3 10 8 9 1
7.1.2一次回归方程的建立
设总的试验次数为N,其中原正交表所规定的二水平试验次数为 mc,零水平试验次数为m0,即有: N 建立回归方程
m
mc m0
ˆ a b j x j bkj xk x j,k 1,2,, m 1( j k ) y
j 1 k j
其系数的计算公式如下:
将被剔除变量的偏回归平方和、自由度并入到剩余平方和与自由度中,
然后再进行相关的方差分析计算。具体例子见书P126~129例8-1。
7.1 一次回归正交试验设计及结果分析
14
用石墨炉原子吸收分光光度计法测定食品中的铅,为提高吸光度,
对x1(灰化温度/℃)、x2(原子化温度/℃)和x3(灯电流/mA)三个
F0.05(1,6)=5.99 F0.01(1,6)=13.74
可见因素z2对指标影响高度显著,所建的回归方程高度显著:
y 0.50475 0.03375z2
7.1 一次回归正交试验设计及结果分析
N 1 SST Lyy ( yi y ) 2 yi2 ( yi ) 2 N i 1 i 1 i 1 N N
7.1 一次回归正交试验设计及结果分析
10
②一次项zj偏回归平方和
SS j m b ,j= 1 , 2, ,m
回归正交试验设计

回归正交试验设计一、概述(1)回归分析与正交试验设计的主要优缺点回归分析的主要优点是可以由试验数据求出经验公式,用于描述自变量与因变量之间的函数关系。
它的主要缺点是毫不关心试验数据如何取得,这样,不仅盲目地增加了试验次数,而且试验数据还往往不能提供充分的信息。
因此,有些工作者将经典的回归分析方法描述成:“这是撒大网,捉小鱼,有时还捉不到鱼”。
所以说,回归分析只是被动地处理试验数据,并且回归系数之间存在相关关系,若从回归方程中剔除某个不显著因素时,需重新计算回归系数,耗费大量的时间。
正交试验设计的主要优点是科学地安排试验过程,用最少的试验次数获得最全面的试验信息,并对试验结果进行科学分析(如方差分析),从而得到最佳试验条件,但是它的主要缺点是试验结果无法用一个经验公式来表达,从而不便于考察试验条件改变后,试验指标将作如何变化。
(2)回归正交试验设计回归正交试验设计,实际上就是将线性回归分析与正交试验设计两者有机地结合起来而发展出的一种试验设计方法,它利用正交试验设计法的“正交性”特点,有计划、有目的、科学合理地在正交表上安排试验,并将试验结果用一个明确的函数表达式即回归方程来表示,从而达到既减少试验次数、又能迅速地建立经验公式的目的。
根据回归模型的次数,回归正交试验设计又分为一次回归试验设计和二次回归试验设计。
二、一次回归正交试验设计(一)一次回归正交试验设计的概念一次回归设计研究的是一个因素z (或多个因素z 1,z 2,……)与试验指标y 之间的线性关系。
当只研究一个因素时,其线性回归模型:y =β0+β1z +e (1)其回归方程为:z y ∧∧∧+=10ββ (2)式中∧0β、∧1β称为回归系数,e 是随机误差,是一组相互独立、且服从正态分布N(0,σ2)的随机变量。
可以证明,∧0β、∧1β和∧y 是β0、β1和y 的无偏估计,即E(∧0β)=β0,E(∧1β)=β1,E(∧y )=y一次回归正交试验设计是通过编码公式x =f(z) −− 即变量变换,将式(2)变为:x b b y 10+=∧(3)且使试验方案具有正交性,即使得编码因素X的各水平之和为零:∑==mi ix1(4)式中m 是因素x 的水平数。
EXCEL和SPSS在回归分析正交试验设计和判别分析中的应用

EXCEL和SPSS在回归分析正交试验设计和判别分析中的应用一、回归分析回归分析是一种统计方法,通过对自变量和因变量之间关系进行建模,预测因变量的值。
EXCEL和SPSS都可以进行回归分析,并提供了丰富的功能和工具。
在EXCEL中,可以使用内置的回归分析工具实现回归分析。
首先,需要将数据输入到工作表中,然后选择“数据”选项卡的“数据分析”,再选择“回归”选项。
接下来,填写变量范围和输出范围,并选择相关的统计信息和图表。
最后,点击“确定”即可得到回归分析的结果。
在SPSS中,进行回归分析的步骤稍有不同。
首先,需要导入数据文件,并选择“回归”选项。
然后,选择因变量和自变量,并设置统计选项。
最后,点击“运行”即可得到回归分析的结果。
二、正交试验设计正交试验设计是一种多因素实验设计方法,可以用于确定影响实验结果的因素及其相互作用关系。
使用正交试验设计可以减少实验次数,提高实验效率。
EXCEL和SPSS都提供了工具支持正交试验设计。
在EXCEL中,可以使用内置的“正交表生成器”来实现正交试验设计。
首先,选择“数据”选项卡的“数据分析”,再选择“正交设计表”。
接下来,填写因素数和水平数,并选择生成正交表的方式。
最后,点击“确定”即可生成正交试验设计的表格。
在SPSS中,进行正交试验设计的步骤稍有不同。
首先,需要定义因素和水平,并选择因素的类型和因素间交互作用。
然后,可以选择“生成”选项卡的“正交表”来生成正交试验设计的表格。
三、判别分析判别分析是一种统计方法,用于确定分类变量与一组预测变量之间的关系。
它可以用于预测一个事物属于哪个类别。
EXCEL和SPSS都可以进行判别分析,并提供了相应的功能和工具。
在EXCEL中,可以使用内置的“数据分析工具包”来实现判别分析。
首先,选择“数据”选项卡的“数据分析”,再选择“判别分析”。
接下来,填写变量范围和输出范围,并选择分类变量和预测变量。
最后,点击“确定”即可得到判别分析的结果。
第8章回归正交试验设计

②二次项的中心化 对二次项的每个编码进行中心化处理 :
(二次项编码)-(二次项编码算术平均值)
z ji
'
z
j
2 i
1 n
n i 1
z
j
2 i
二元二次回归正交组合设计编码表
试验号
z1
1
1
z2
z1 z2
z12
1
1
1
2
1
-1
-1
1
3
-1
1
-1
1
4
-1
-1
1
1
5
1
0
0
1
6
-1
0
0
1
7
0
1
0
0
8
0
-1
0
1.414
1.483
3 1.147 1.353
1.471
1.547
4 1.210 1.414
1.525
1.607
5 1.267 1.471
1.575
1.664
6 1.320 1.525
1.623
1.719
7 1.369 1.575
1.668
1.771
8 1.414 1.623
1.711
1.820
9 1.457 1.668
bkj
i 1 n
(zk z j )i2
i 1
二次项偏回归系数bjj :
n
(
z
' ji
)
yi
b jj
i 1 n
(
z
' ji
)
2
i 1
⑤回归方程显著性检验
一次回归正交设计例子
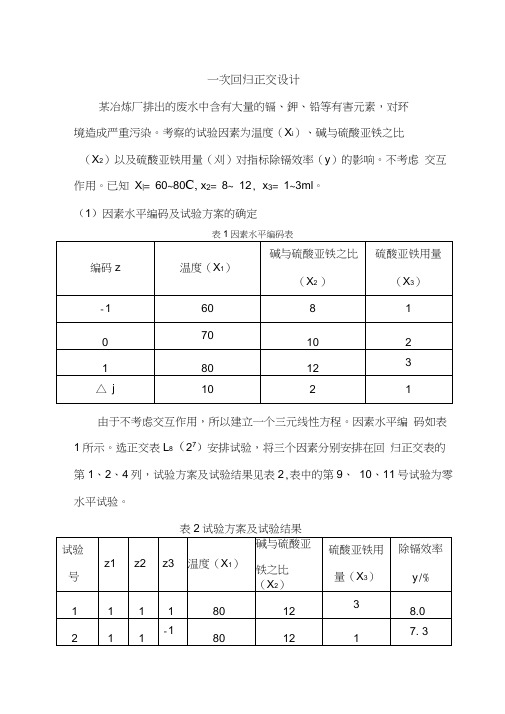
一次回归正交设计某冶炼厂排出的废水中含有大量的镉、鉀、铅等有害元素,对环境造成严重污染。
考察的试验因素为温度(X i)、碱与硫酸亚铁之比(X2)以及硫酸亚铁用量(刈)对指标除镉效率(y)的影响。
不考虑交互作用。
已知X|= 60~80C, x2= 8~ 12, x3= 1~3ml。
(1)因素水平编码及试验方案的确定由于不考虑交互作用,所以建立一个三元线性方程。
因素水平编码如表1所示。
选正交表L8(27)安排试验,将三个因素分别安排在回归正交表的第1、2、4列,试验方案及试验结果见表2,表中的第9、10、11号试验为零水平试验。
表2试验方案及试验结果⑵回归方程的建立表3试验结果及计算表由表3计算a 」皆 \ 二-72.〕6. 6 182n i.i11回归方程为y = 6.6182 0.5125/ 0.5375Z 2 0.3125Z 3由该回归方程偏回归系数绝对值的大小,可以得到各因素的主次 顺序为:X 2>X 1>X 3,即液固比 >乙醇浓度>回流次数。
又由于各偏回归 系数都为正,所以这些影响因素取上水平时,试验指标最好。
(3)回归方程显著性检验b 2b 3、Z 1i Y ii =1m c ' Z 2i%i =1i =1Z 3i Y im c41二 0.5125843二 0.537582^50. 3125 8SS = m c b 2= 8汉 0.5125 = 2.101 = m c b 荻 8 0.53752二 2.311 SQ = m j b ; = 8 0.31252 = 0.781SQ = SS + SS2 + SS3 + SS 2 + SS 厂 2.101+ 2.311+ 0.781= 5.193SS= SS-S&5. 2 9 6- 5. 1 93 0.方差分析结果见表4。
表4方差分析表差异源 SS df MS F 显著性 Z 1 2.101 1 2.101 142.9 ** Z 2 2.311 1 2.311 157.2 ** Z 3 0.781 1 0.781 53.1 ** 回归 5.193 3 1.731117.8**残差 0.103 70.0147总和5.296n — 1 = 10注:F o.o1(1, 7)= 12.25, F o.o1(3, 7) = 8.45可见,三个因素对试验指标都有非常显著的影响, 所建立的回归 方程也非常显著。
实验设计与数据处理课后答案

《试验设计与数据处理》专业:机械工程班级:机械11级专硕学号:S110805035 姓名:赵龙第三章:统计推断3-13 解:取假设H0:u1-u2≤0和假设H1:u1-u2>0用sas分析结果如下:Sample StatisticsGroup N Mean Std. Dev. Std. Error----------------------------------------------------x 8 0.231875 0.0146 0.0051y 10 0.2097 0.0097 0.0031Hypothesis TestNull hypothesis: Mean 1 - Mean 2 = 0Alternative: Mean 1 - Mean 2 ^= 0If Variances Are t statistic Df Pr > t----------------------------------------------------Equal 3.878 16 0.0013Not Equal 3.704 11.67 0.0032由此可见p值远小于0.05,可认为拒绝原假设,即认为2个作家所写的小品文中由3个字母组成的词的比例均值差异显著。
3-14 解:用sas分析如下:Hypothesis TestNull hypothesis: Variance 1 / Variance 2 = 1Alternative: Variance 1 / Variance 2 ^= 1- Degrees of Freedom -F Numer. Denom. Pr > F----------------------------------------------2.27 7 9 0.2501由p值为0.2501>0.05(显著性水平),所以接受原假设,两方差无显著差异第四章:方差分析和协方差分析4-1 解:Sas分析结果如下:Dependent Variable: ySum ofSource DF Squares Mean Square F Value Pr > FModel 4 1480.823000 370.205750 40.88 <.0001Error 15 135.822500 9.054833Corrected Total 19 1616.645500R-Square Coeff Var Root MSE y Mean0.915985 13.12023 3.009125 22.93500Source DF Anova SS Mean Square F Value Pr > Fc 4 1480.823000 370.205750 40.88 <.0001由结果可知,p值小于0.001,故可认为在水平a=0.05下,这些百分比的均值有显著差异。
试验设计与数据处理复习要点

试验设计与数据处理复习要点1、引言20世纪20年代,英国生物统计学家及数学家费歇提出了方差分析20世纪50年代,日本统计学家田口玄一将正交设计表格化。
数学家华罗庚的“优选法”。
我国数学家王元和方开泰于1978年首先提出了均匀设计。
常用的统计软件:SAS,SPSS,Origin,Excel等。
试验设计与数据处理的意义。
试验设计的目的:合理地安排试验,力求用较少的试验次数获得较好结果数据处理的目的:通过误差分析,评判试验数据的可靠性;确定影响试验结果的因素主次,抓住主要矛盾,提高试验效率;确定试验因素与试验结果之间存在的近似函数关系,并能对试验结果进行预测和优化;获得试验因素对试验结果的影响规律,为控制试验提供思路;确定最优试验方案或配方。
加权平均值:如果某组试验值用不同的方法获得,或由不同的试验人员得到的,则这组数据中不同的精度或可靠性不一致,为了突出可靠性高的数值,则可采用加权平均值。
绝对误差:试验值与真值之差误差根据其性质或产生原因分为:系统误差,随机误差,过失误差1. 随机误差:以不可预知的规律变化着的误差,绝对误差时正时负,时大时小产生的原因:偶然因素(气温的微小变2.仪器的轻微振动等)2. 系统误差:一定试验条件下,由某个或某些因素按照某一确定的规律起作用而形成的误差产生的原因:多方面(仪器不准或操作者观察终点方法不对)3.过失误差:一种显然与事实不符的误差产生的原因:实验人员粗心大意造成精密度、正确度和准确度的含义与区别。
1.精密度:反映了随机误差大小的程度,在一定的试验条件下,多次试验值的彼此符合程度2.正确度:反映系统误差的大小,精密度高并不意味着正确度也高精密度不好,但当试验次数相当多时,有时也会得到好的正确度3.准确度:反映了系统误差和随机误差的综合,表示了试验结果与真值或标准值的一致程度关于权的选择和绝对误差的选择。
权不是任意给定的,除了依据实验者的经验外,还可以按如下方法给予。
一次回归正交设计、二次回归正交设计、二次回归旋转设计说明

一次回归正交设计、二次回归正交设计、二次回归旋转设计说
明
一次回归正交设计是一种广泛应用于实验设计中的设计方式,该设计最基本的特点是每一个自变量只考虑一次。
这种设计方法可以通过排列组合的方式得到各种不同的设计方案,使得实验者可以通过设计来达到用最少的实验次数获取尽可能多的信息的目的。
一次回归正交设计在实验设计中被广泛使用,尤其在化学制药、工业生产等领域得到了广泛运用。
二次回归正交设计是一种基于一次回归正交设计的设计方式,这种设计方式可以进一步增加实验信息的获取。
在二次回归正交设计中,依然按照一次正交设计的方式来设计实验,但是在每个单独的自变量上,提高对其的测量次数,使得对这些自变量的测量更加准确。
同时,在某些需要深入探究的因素上,可以通过将这些因素的实验次数进一步提高,来获取相关信息。
二次回归旋转设计是一种在二次回归正交设计的基础上发展而来的设计方式。
在二次回归旋转设计中,实验者可以通过旋转矩阵来达到实验变量间的协方差为0的目的。
这样可以在保证基本信息获取的同时,增加获取高阶信息的可能性。
旋转设计特别适合于需要同时考虑多个变量的实验设计,可以使各个变量之间更加独立,减少不必要的干扰。
总的来说,在实验设计领域中,三种设计方法各自有着各自的优势。
对于需要更精准的信息获取的实验,应该选择更高阶的设计方法,在更基础的实验中则可以选择更为简单的设计方法。
另外,在选择设计方法的过程中,还应该根据实验具体情况灵活选择,使得实验设计更加科学合理。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
设目标性状y与z1、z2……zm等因素有关,我们可以应用回归分析的方法建立y与诸因素的回归方程,以此对y进行预测和控制,或筛选y的最优指标。z1、z2……zm构成一个因子空间,每一组z1、z2……zm值对应一个y值。如何在因子空间中选择最适当的试验点,以最少的试验点寻求y的最优区域,这就要将回归分析与正交设计结合起来应用,称为回归正交设计。按回归模型的次数,回归正交设计又分为一次回归正交设计和二次回归正交设计。
一、一次回归正交设计
一次回归正交设计主要是应用2水平正交表进行设计,其设计和分析步骤如下。
1.确定试验因素的变化范围
例如研究m个栽培因素z1、z2……zm与作物产量y的数量关系,首先需确定各个栽培因素的变化范围。设因素zj的变化区间为(z1j,z2j),则z1j和z2j分别为因素zj的下水平和上水平。那么
用二水平正交表设计的这种试验具有正交性。若以 表示在第 试验中第j个变量的编码值,于是在试验计划中有
任一列的和
任两列的内积
具有以上两个性质的设计为正交设计。
4.建立回归方程
对于3因素试验,若考虑因素间的交互作用,则回归方程为
例如用L8(27)正交表设计该试验,那么它的结构矩阵为
信息矩阵(系数矩阵)为
-1
1
-1
1
1
7
-1
1
-1
-1
1
1
-1
-1
1
-1
1
8
-1
1
-1
1
-1
-1Байду номын сангаас
-1
1
1
1
-1
9
-1
1
1
-1
-1
-1
1
-1
-1
1
1
10
-1
-1
-1
1
1
1
1
-1
-1
1
-1
11
-1
-1
1
-1
1
-1
1
1
1
-1
-1
12
-1
-1
1
1
-1
1
-1
1
-1
-1
1
如设计一个3因素试验,可选用L8(27)正交表,表中x1、x2、x3分别代表z1、z2、z3的编码值。若因素间有互作存在,在回归中可用非线性项x1x2、x1x3、x2x3等表示。每种交互作用占改造后二水平正交表的1列,该列的取值可由某两列上元素对应相乘得到。如表2L8(27)中x1x2列的元素是由x1与x2列上的对应元素相乘而得。
1
-1
1
-1
-1
y2
3
1
1
-1
1
-1
1
-1
y3
4
1
1
-1
-1
-1
-1
1
y4
5
1
-1
1
1
-1
-1
1
y5
6
1
-1
1
-1
-1
1
-1
y6
7
1
-1
-1
1
1
-1
-1
y7
8
1
-1
-1
-1
1
1
1
y8
Bj
8
8
8
8
8
8
8
B0/8
B1/8
B2/8
B3/8
B12/8
B13/8
B23/8
--
从以上计算可看出,各变量的偏回归平方和 ,与偏回归系数bj的平方成正比。bj的绝对值越大,Qj也越大。这就意味着,在利用正交表所得到的回归方程中,每一个回归系数bj的绝对值大小,反映了对应变量xj对y作用的大小。这是因为经过无量纲编码后,所以变量的取值都是1和-1,它们在所研究的区域内取值是平等的,且不受单位的影响,因此所求回归系数bj直接反映了因素zj作用的大小,回归系数的符号反映因素作用的性质。在要求不太高的情况下,一次回归正交设计可省略方差分析,直接把回归系数与零相差不大的因素从回归方程中剔除,不需重新计算其它回归系数,剔除因素对结果的影响可并入试验误差。但对精度要求较高的试验,应继续进行回归关系的显著性测验。
5.回归方程及回归系数的显著性测验
一次回归正交设计的方差分析如表4。
表4一次回归正交设计的方差分析表
变异来源
自由度
平方和
均方
F值
回归
离回归
总
x1
1
xm
1
x1x2
1
xm-1xm
1
对回归方程的显著性假设测验可通过表4中的F测验进行。但这种测验只是说明m个变量对试验结果的影响是显著的,而在研究区域内回归方程与实测值的拟合情况,即采用一次回归模型是不是最合适,从以上测验中没有得到这方面的信息。为了了解回归方程的拟合情况,需在零水平( )安排一些重复试验,如在安排p次重复试验所得试验结果为 ,其平均数为 ,则
-1
1
1
-1
-1
1
8
-1
-1
-1
1
1
1
-1
L12(211)
试验号
x1
x2
x3
x4
x5
x6
x7
x8
x9
x10
x11
1
1
1
1
1
1
1
1
1
1
1
1
2
1
1
1
1
1
-1
-1
-1
-1
-1
-1
3
1
1
-1
-1
-1
1
1
1
-1
-1
-1
4
1
-1
1
-1
-1
1
-1
-1
1
1
-1
5
1
-1
-1
1
-1
-1
1
-1
1
-1
1
6
1
-1
-1
-1
1
-1
表2常用二水平正交表L4(23)
试验号
x1
x3
x3
1
1
1
1
2
1
-1
-1
3
-1
1
-1
4
-1
-1
1
L8(27)
试验号
x1
x2
x3
x1x2
x1x3
x2x3
x1x2x3
1
1
1
1
1
1
1
1
2
1
1
-1
1
-1
-1
-1
3
1
-1
1
-1
1
-1
-1
4
1
-1
-1
-1
-1
1
1
5
-1
1
1
-1
-1
1
-1
6
-1
1
-1
-1
1
-1
1
7
-1
多个因素的编码工作可在因素水平编码表(表1)上进行。
表1因素水平编码表
zj
因素
Z1
Z2
……
Zm
下水平
Z11
Z12
……
Z1m
零水平
Z01
Z02
……
Z0m
上水平
Z21
Z22
……
Z2m
变化间距△j
△1
△2
……
△m
对因素的水平进行编码后,y对z1、z2……zm的回归问题就转化为对x1、x2……xm的回归问题。在z1、z2……zm因子空间选择试验点的问题就转化为x1、x2……xm为坐标轴的编码空间选择试验点。在二次回归设计中也要进行因素的编码工作。
3.选择合适的二水平正交表
常用的二水平正交表有L4(23)、L8(27)、L12(211)、L16(215)等。选用哪一种二水平正交表要依据因素个数及需要研究的交互作用而定。正交表确定以后,把表中的“2”改为“-1”。这样正交表中的“+1”“-1”既表示因素的不同水平,也表示xj的取值。表2列举了经代换后的几张常用二水平正交表。
相关矩阵为
常数项矩阵为
为试验结果,于是可算出回归系数矩阵
那么各类回归系数即由下式算出
回归系数的具体计算可在正交表上进行(表3).表中bj为各回归系数,Qj为偏回归平方和。从而建立回归方程。
表33因素一次回归正交设计计算表
试验号
x0
x1
x2
x3
x1x2
x1x3
x2x3
试验结果
1
1
1
1
1
1
1
1
y1
2
1
1
为因素zj的零水平。
为因素zj的变化区间。
2.对各因素的水平编码
编码就是对各个因素的取值作如下线性变换:
式中xj为编码值。如:
这样就建立了zj与xj的一一对应关系:
下水平z1jx1j(-1)
零水平z0jx0j(0 )
上水平z0jx0j(+1)
通过上面的编码可知,当zj在区间(z1j,z2j)变化时,它的编码值xj就在区间(-1,+1)内变化。
