广西蒙山县蒙山中学2020-2021学年高一上学期数学周测四缺答案
广西蒙山县一中2022-2023学年高一上数学期末质量检测试题含解析

, , , , , , , .
故排在第6的子集为 .
故答案为:
12、
【解析】直接利用两角和的正切公式计算可得;
【详解】解:
故答案为:
13、
【解析】根据对数式指数式互化公式,结合对数换底公式、对数的运算性质进行求解即可.
【详解】因为 ,所以 ,因此有:
【解析】(1)根据长方体的性质,侧棱平行且相等,利用平行四边形判定及性质,推出线线平行,再证线面平行;
(2)由(1),取平行线,即可求解异面直线所成角的平面角,再求正弦值.
【详解】(1)连结 交 于点 ,连结 ,
, ,
, .
.
又 平面 , 平面 ,
平面
(2) 与 的所成角为
在 中:
【点睛】(1)立体几何中平行关系的证明,常见方法有平行四边形对边平行,本题比较基础.
(2)借助平行线,将两条异面直线所成角转化为两条相交直线所成角,为常用方法,中等题型.
19、(1) ;(2) ;(3)存在, .
【解析】(1)根据 为 上的奇函数,得到 ,再由 时, ,设 时,则 代入求解.
(2)设 ,易知 在 上单调递减,则 ,则 , 是方程 的两个不等正根求解
(3)设 为 的一个“罗尔区间”,且 , 同号,若 ,由(2)可得,若 ,同理可求,得到 ,再根据集合 恰含有2个元素,转化为 与 的图象有两个交点,即方程 在 内恰有一个实数根,方程 ,在 内恰有一个实数根求解..
【详解】依题意 ,解得 ,故函数的定义域为 .
故答案为 .
【点睛】本小题主要考查具体函数定义域的求法,属于基础题.
三、解答题:本大题共5小题,共70分。解答时应写出文字说明、证明过程或演算步骤。
广西梧州市蒙山县蒙山中学2019-2020学年度高一上学期第二次月考数学试题
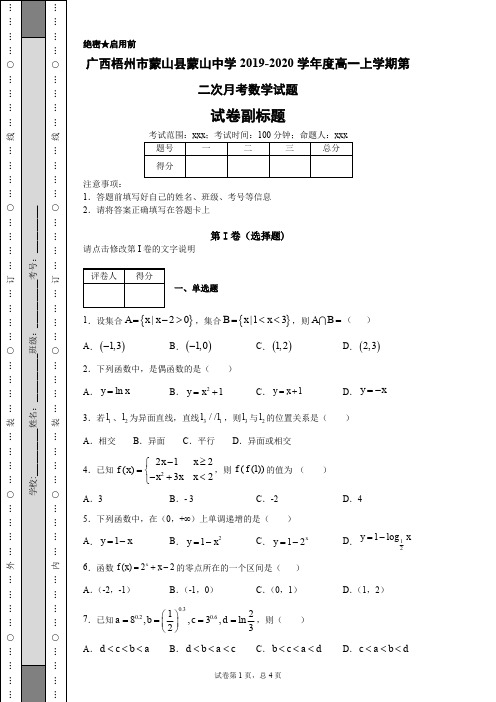
绝密★启用前广西梧州市蒙山县蒙山中学2019-2020学年度高一上学期第二次月考数学试题试卷副标题注意事项:1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)请点击修改第I 卷的文字说明 一、单选题1.设集合{}|20A x x =->,集合{}|13B x x =<<,则A B =( )A .()1,3-B .()1,0-C .()1,2D .()2,32.下列函数中,是偶函数的是( ) A .ln y x =B .21y x =+C .1y x =+D .y x =-3.若1l 、2l 为异面直线,直线31//l l ,则3l 与2l 的位置关系是( ) A .相交 B .异面 C .平行 D .异面或相交4.已知2212()32x x f x x x x -≥⎧=⎨-+<⎩,则((1))f f 的值为 ( ) A .3B .- 3C .-2D .45.下列函数中,在(0,+∞)上单调递增的是( ) A .1y x =-B .21y x =-C .12x y =-D .121log y x =-6.函数()22x f x x =+-的零点所在的一个区间是( ) A .(-2,-1)B .(-1,0)C .(0,1)D .(1,2)7.已知0.30.20.6128,,3,ln 23a b c d ⎛⎫==== ⎪⎝⎭,则( )8.已知正方体 ,则 与 所成的角为 A .B .C .D .9.设(1)23f x x +=+,()(2)g x f x =-,则g (x )等于( ) A .21x +B .21x -C .23x -D .27x +10.已知函数2()log (23)a f x x x =--+(a>0且a≠1),若f(0)<0,则此函数的单调递增区间是( ) A .(-∞,-1] B .[-1,+∞) C .[1,1)-D .(-3,-1]11.定义在R 上的偶函数()f x 满足:对任意的1x ,212[0,)()x x x ∈+∞≠,有2121()()0f x f x x x -<-,则( ).A .(3)(2)(1)f f f <-< B .(1)(2)(3)f f f <-< C .(2)(1)(3)f f f -<<D .(3)(1)(2)f f f <<-12.函数f (x )的定义域为(﹣∞,1)∪(1,+∞),且f (x+1)为奇函数,当x >1时,f (x )=2x 2﹣12x+16,则直线y=2与函数f (x )图象的所有交点的横坐标之和是( ) A .1 B .2 C .4 D .5第II 卷(非选择题)请点击修改第II 卷的文字说明 二、填空题13.已知函数25()(3)m f x m x -=-是幂函数,则1()2f =__________. 14.函数()f x =______.15.如图:在正四面体S -ABC 中,如果E ,F 分别是SC ,AB 的中点,那么异面直线EF 与SA 所成的角等于_______………○…………………○……学校:________………○…………………○……16.已知函数2()3f x x =+,()2x g x a =+,若任意1[1,4]x ∈,存在2[2,3]x ∈,使得12()()f x g x ≥,则实数a 的取值范围是____.17.某驾驶员喝了m 升酒后,血液中的酒精含量()f x (毫克/毫升)随时间x (小时)变化的规律近似满足表达式()250131() 1.53x x x f x x -⎧≤≤⎪=⎨⋅⎪⎩,,>《酒后驾车与醉酒驾车的标准及相应的处罚》规定:驾驶员血液中酒精含量不得超过0.02毫克/毫升.此驾驶员至少要过______小时后才能开车.(精确到1小时) 三、解答题18.已知集合A={x|2-a≤x≤2+a},B={x|x≤1或x≥4}. (1)当a=3时,求A∩B;(2)若a>0,且A∩B=∅,求实数a 的取值范围.19.已知:如图,P 是平行四边形ABCD 所在平面外一点,E 是PD 中点, 求证:PB ∥平面EAC .20.设集合A 是函数()f x =2()2()g x x x x A =-∈(1)求集合A ; (2)求函数()g x 的值域.21.如图,已知PA ⊥平面ABCD ,且四边形ABCD 为矩形,M 、N 分别是AB 、PC 的中点.………○……………○……(1)求证:MN ⊥CD ;(2)若∠PDA =45°,求证:MN ⊥平面PCD .22.函数()f x 对一切实数,x y 均有()()(22)f x y f y x y x +-=++成立,且(2)12f =. (1)求(0)f 的值;(2)在(1,4)上存在0x R ∈,使得00()3f x ax -=成立,求实数a 的取值范围.参考答案1.D 【解析】∵{}2A x x =,{}|13B x x =<< ∴A B ⋂= ()2,3 故选:D点睛:求集合的交、并、补时,一般先化简集合,再由交、并、补的定义求解;在进行集合的运算时要尽可能地借助Venn 图和数轴使抽象问题直观化.一般地,集合元素离散时用Venn 图表示;集合元素连续时用数轴表示,用数轴表示时要注意端点值的取舍. 2.B 【解析】 【分析】根据常见函数的性质判断奇偶性即可. 【详解】对于A ,ln y x =的定义域为(0,+∞),为非奇非偶函数; 对于B ,21y x =+的定义域为R ,为偶函数; 对于C ,1y x =+的定义域为R ,为非奇非偶函数; 对于D ,y x =-的定义域为R ,为奇函数. 故选:B 【点睛】本题考查函数奇偶性的判断,注意常见函数的奇偶性以及奇偶性的判断方法,属于基础题. 3.D【解析】解:因为12l l 、为异面直线,直线31//l l ,则3l 与2l 的位置关系是异面或相交,选D 4.A 【解析】 【分析】根据分段函数先求(1)f ,进而求()((1))2f f f =即可. 【详解】∵2212()32x x f x x x x -≥⎧=⎨-+<⎩∴(1)132f =-+=,()((1))2413f f f ==-=, 故选:A 【点睛】本题主要考 查了分段函数的函数值的求解,解题的关键是根据不同的自变量的值确定函数的解析式,属于基础试题. 5.D 【解析】 【分析】利用常见函数的图象与性质,即可作出判断. 【详解】对于A ,1y x =-在(-∞,0)上单调递减,对于B ,21y x =-开口向下的偶函数,在(0,+∞)上单调递减, 对于C ,12xy =-在(0,+∞)上单调递减, 对于D ,12log y x =在(0,+∞)上单调递减,∴121log y x =-在(0,+∞)上单调递增故选:D 【点睛】本题考查常见函数的单调性,属于基础题. 6.C 【解析】 【分析】利用函数的零点判定定理,先判断函数的单调性,然后判断端点值的符合关系. 【详解】解:∵f (x )=2x+x ﹣2在R 上单调递增 又∵f (0)=﹣1<0,f (1)=1>0由函数的零点判定定理可知,函数的零点所在的一个区间是(0,1)故选:C . 【点睛】本题主要考查函数零点区间的判断,判断的主要方法是利用根的存在性定理,判断函数在给定区间端点处的符号是否相反. 7.B 【解析】 【分析】根据指数函数的单调性以及对数函数的单调性分别判断出,,a b d 的取值范围,利用幂函数的性质比较a c 、的大小,从而可得结果. 【详解】因为0.20881a =>=;0.3110122b ⎛⎫⎛⎫<=<= ⎪⎪⎝⎭⎝⎭; 0.60.60.2328c a =>==;2lnln103d =<=, 所以d b a c <<<,故选B . 【点睛】本题主要考查对数函数的性质、指数函数的单调性及比较大小问题,属于综合题.解答比较大小问题,常见思路有两个:一是判断出各个数值所在区间(一般是看三个区间()()(),0,0,1,1,-∞+∞ );二是利用函数的单调性直接解答;数值比较多的比大小问题也可以两种方法综合应用. 8.C 【解析】 【分析】画出图形,根据两异面直线所成角的定义作出所求角,然后通过解三角形得到所求角的大小. 【详解】如图,在正方体 中,连 ,则得 ∥ ,∴ 即为异面直线 与 所成的角. 在 中,由题意得 , ∴ ,即 与 所成的角为 . 故选C . 【点睛】(1)求异面直线所成的角的步骤为:“找”、“证”、“算”。
广西蒙山县蒙山中学2020-2021学年高一上学期数学周测四

2020级高(一)上数学周测(四)班别 姓名 考号 分数:一、 选择题:(本大题共8小题,每小题6分,满分48分.给出的四个答案中,只有一个是符合题意.)1.已知A =B =R ,x ∈A ,y ∈B ,f :x →y =ax +b 是从A 到B 的映射,若1和8的原像分别是3和10,则5在f 下的像是( )A .3B .4C .5D .62.设函数f (x )=⎩⎪⎨⎪⎧ x 2+1,x ≤1,2x , x >1,则f (f (3))=( )A.15 B .3 C.23D.139 3.函数f (x )=x +3+1x +2的定义域是( )A .[-3,+∞)B .[-3,-2)C .[-3,-2)∪(-2,+∞)D .(-2,+∞)4.函数f (x )=|x |和g (x )=x (2-x )的单调递增区间分别是( )A .(-∞,0]和(-∞,1]B .(-∞,0]和[1,+∞)C .[0,+∞)和(-∞,1]D .[0,+∞)和[1,+∞)5.函数y x =+A.有最小值12,无最大值B.有最大值12,无最小值 C.有最小值12,最大值2D.无最大值,也无最小值 6.函数y =ax +1与y =ax 2+bx +1(a ≠0)的图像可能是( )7.函数f (x )=⎩⎪⎨⎪⎧ 2x -x 2,0≤x ≤3,x 2+6x ,-2≤x <0的值域是( )A .RB .[1,+∞) C.[-8,1] D .[-9,1]8.已知()f x 是定义在R 上的增函数,若()y f x =的图象过点()2,1A --和()3,1B ,则满足()111f x -<+<的x 的取值范围是( )A.(-2,3)B.(-3,2)C.(-1,4)D.(-1,1)二、 填空题(本大题共4个小题,每小题6分,满分24分)9.如果一条抛物线的形状与y =13x 2+2的图像开口形状相同,且顶点坐标为(4,-2),则它的解析式是________.10.函数f (x )=-x 2+2x ,x ∈[-1,2]的值域为11.设函数2()(2)1f x x a x =++-在区间(],2-∞上是减函数,则实数a 的最大值为.12.已知集合A =B =R ,映射f :x →x 2+2x -4,若a 在B 中且在A 中没有原像,则a 的取值范围是________.三、解答题(本题共2题,解答应写出文字说明,证明过程或演算步骤)13.(14分)(1)已知f(x)是一次函数,且满足2f(x+3)-f(x-2)=2x+21,求f(x);(2)已知f(x)满足3f(x)+2f(-x)=4x,求f(x).14.(14分)已知函数f(x)=2x-1x+1,x∈[3,5].(1)判断f(x)在区间[3,5]上的单调性并证明;(2)求f(x)在区间[3,5]上的最大值和最小值.。
广西壮族自治区梧州市蒙山县第一中学2021年高一数学文月考试题含解析

广西壮族自治区梧州市蒙山县第一中学2021年高一数学文月考试题含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. .若正数a,b满足,则的最小值为()A. B. C. 2 D.参考答案:A【分析】设,解得,又由,得,再利用基本不等式,即可求解其最小值.【详解】由题意,设,解得其中,因为,所以,整理得,又由,当且仅当,即等号成立,所以的最小值为.【点睛】本题主要考查了换元法的应用,以及利用基本不等式求最值问题,其中解答中合理利用换元法,以及准确利用基本不等式求解是解答的关键,着重考查了分析问题和解答问题的能力,属于中档试题.2. 函数的图象可由函数的图象作怎样的变换得到()A.向左平移个单位 B.向右平移个单位 C.向左平移个单位 D.向右平移个单位参考答案:C3. 若0<m<n,则下列结论正确的是()A.B.2m>2nC.D.log2m>log2n参考答案:C【考点】不等关系与不等式.【专题】函数的性质及应用.【分析】根据指数函数与对数函数的底数大于1时单调递增,底数大于0小于1时单调递减的性质进行做题.【解答】解:观察B,D两个选项,由于底数2>1,故相关的函数是增函数,由0<m<n,∴2m<2n,log2m<log2n,所以B,D不对.又观察A,C两个选项,两式底数满足0<<1,故相关的函数是一个减函数,由0<m<n,∴,所以A不对,C对.故答案为 C.【点评】指数函数与对数函数的单调性是经常被考查的对象,要注意底数大于1时单调递增,底数大于0小于1时单调递减的性质.4. 已知tanα=,则等于( )A.B.C.﹣7 D.7参考答案:A【考点】同角三角函数基本关系的运用.【专题】计算题;三角函数的求值.【分析】原式分子分母除以cosα,利用同角三角函数间基本关系化简,将tanα的值代入计算即可求出值.【解答】解:∵tanα=﹣,∴原式===,故选:A.【点评】此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.5. 已知函数f(x)=﹣x|x|,则()A.f(x)既是奇函数又是增函数B.f(x)既是偶函数又是增函数C.f(x)既是奇函数又是减函数D.f(x)既是偶函数又是减函数参考答案:C【考点】奇偶性与单调性的综合.【分析】作出函数f(x)=﹣x|x|的图象,由函数的图象可得结论.【解答】解:作出函数f(x)=﹣x|x|的图象,如图所示由函数的图象可得,f(x)既是奇函数又是减函数,故选:C.6. 函数的图象大致是参考答案:A7. 执行如图所示的程序框图,输出的结果是()A.lg97 B.lg98 C.lg99 D.2参考答案:C【考点】程序框图.【专题】计算题;图表型;数学模型法;算法和程序框图.【分析】模拟执行程序框图,依次利用对数的运算性质计算每次循环得到的b的值,计算a的值,当a=100时不满足条件a<100,退出循环,输出b的值为lg99.【解答】解:模拟执行程序框图,可得a=2,b=lg2,满足条件a<100,b=lg2+lg=lg3,a=3满足条件a<100,b=lg3+lg=lg4,a=4…满足条件a<100,b=lg98+lg=lg99,a=100不满足条件a<100,退出循环,输出b的值为lg99.故选:C.【点评】本题主要考查了循环结构的程序框图,利用对数的运算性质计算每次循环得到的b的值是解题的关键,属于基础题.8. 设平面α丄平面β,直线a.命题P:“a”命题q:“a丄α”,则命题P成立是命题q成立的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件参考答案:B略9. 函数的定义域为()A.(﹣1,2] B.(﹣1,2)C.(2,+∞)D.(﹣1,2)∪(2,+∞)参考答案:B【考点】函数的定义域及其求法.【分析】根据函数成立的条件即可求函数的定义域.【解答】解:要使函数有意义,则,即,得﹣1<x<2,即函数的定义域为(﹣1,2),故选:B【点评】本题主要考查函数的定义域的求解,要求熟练掌握常见函数成立的条件.10. 定义运算,如,已知,,则……………… …………………………(▲)A.B.C.D.参考答案:A略二、填空题:本大题共7小题,每小题4分,共28分11. 已知函数,若,则实数的值等于_________参考答案:12. 在等比数列中,已知,,则公比▲.源:学2科参考答案:2略13. 已知平面向量满足,则的最大值是_______,_____________.参考答案:4 ;2014. 如果实数满足等式,那么的最大值是()A. B. C. D.参考答案:B略15. 的最小正周期为,其中,则=_______________________.参考答案:略16. 等差数列{a n }的公差为d ,其前n 项和为S n ,当首项和d 变化时,是一个定值,则使S n 为定值的n 的最小值为_____▲______.参考答案:13根据等差数列的性质可知,所以得到是定值,从而得到为定值,故答案是13.17. 已知f (x )是定义在[(﹣2,0)∪(0,2)]上的奇函数,当x >0,f (x )的图象如图所示,那么f (x )的值域是 .参考答案:(2,3]∪[﹣3,﹣2)【考点】函数的值域;奇函数. 【专题】图表型.【分析】先根据函数的奇偶性作出函数在y 轴左侧的图象,欲求f (x )的值域,分两类讨论:①x>0;②x<0.结合图象即可解决问题.【解答】解:∵f(x )是定义在[﹣2,0∪(0,2]上的奇函数, ∴作出图象关于原点对称作出其在y 轴左侧的图象,如图. 由图可知:f (x )的值域是 (2,3]∪[﹣3,﹣2). 故答案为:(2,3]∪[﹣3,﹣2).【点评】本题考查函数的图象,考查同学们对函数基础知识的把握程度以及数形结合的思维能力.三、 解答题:本大题共5小题,共72分。
广西梧州市蒙山县蒙山中学高一上学期第二次月考数学试题(无答案)

蒙山中学2011-2012学年高一上学期第二次月考数学试题一、选择题(12×5分=60分)1、已知集合{}{}1,0,1,0,1=-=N M ,则下列各式正确的是( )A.N M ∈B.M N ∈ C 。
N M ⊆ D 。
M N ⊆2、3log 2log 66+= ( )A . 1 B. 5log 6 C.32log 6 D. 03、已知集合{}03|>+=x x A ,全集为R ,则A C R 为( )A 。
{}3|-<x x B. {}3|-≤x x C 。
{}3|->x x D 。
{}3|-≥x x4、函数y=1+x 的定义域是( )A.),+(-∞1 B 。
[)∞,+1 C 。
(]1,--∞ D. [)∞,+-1 5、不等式|x-2|>1的解集是( )A.{x|x<3} B 。
{x|-1<x<3}C 。
{x|x<1} D 。
{x|x<1或x>3}6、若函数125)(++=x x x f ,则=-)2(1f ( ) A 、37 B 、1 C 、2 D 、57、“等式log 3x 2=2成立”是“等式log 3x=1成立”的( )A 充分不必要条件B 必要不充分条件C 充要条件D 既不充分也不必要条件8、⎩⎨⎧>≤+=0,log 0,3)(2x x x x x f 则 ))1((-f f 的值是( )A 。
-1 B.0 C. 1 D. 29、函数f (x+1)的定义域为[2,3),则函数f (x+2) 的定义域是( )A 、[3,4)B 、[0,1)C 、[1,2)D 、[4,5)10、设243.03.03log 4log -===c b a ,,, 则 c b a 、、的大小关系是( )A .c b a <<B .b c a <<C .a b c <<D .c a b <<11、)(x f 是定义在]1,1[-上的的减函数,且)1()1(x f x f -<-,则x 的取值范围是( )A .(1,∞+)B .(∞-,1)C .(1,2]D .[0,1)12、函数]0,2[,12412-∈+-⎪⎭⎫ ⎝⎛=-x y x x 的值域为( )A 、[-3,-2]B 、[—2,1]C 、[1,3]D 、[-3,1]二、填空题(4×5分=20分)13、已知函数=-=)3(1)(2f xx f ,则__________。
高中广西梧州市蒙山县第一中学高一上学期第二次月考数学试题

广西梧州市蒙山县第一中学【精品】高一上学期第二次月考数学试题学校:___________姓名:___________班级:___________考号:___________一、单选题1.若集合{}{}1,0,1,3,0,1,2M N =-=,则M N =( )A .1,0,1,2B .{}1,0,1-C .{}0,12,D .{}0,1 2.下列函数是偶函数的是( )A .12y x = B .223y x =+ C .y x= D .2,[0,1]y x x =∈3.lg2lg5+=( )A .lg 7B .1C .lg32D .lg 25 4.已知直线a ,b ,c ,下列说法正确的是( )A .//a b ,//b c ,则//a cB .a 与b 异面,b 与c 异面,则a 与c 异面C .a 与b 相交,b 与c 相交,则a 与c 相交D .a 与b 所成的角与b 与c 所成的角相等,则//a c5.已知3()4f x ax bx =+-其中,a b 为常数,若(2)2f -=,则(2)f 的值等于( ) A .10- B .6- C .4- D .2- 6.如图所示是一个物体的三视图,则此三视图所描述物体的直观图是( )A .B .C .D . 7.设0.6 1.50.60.60.6 1.5a b c ===,,,则a b c ,,的大小关系是( )A .a b c <<B . a c b <<C .b a c <<D .b c a <<8.设()()132,2log 21,2x x e x f x x -⎧<⎪=⎨-≥⎪⎩,则()()2f f =( ) A .3 B .2 C .1 D .09.幂函数()()226844m m f x m m x -+=-+在()0,+∞为增函数,则m 的值为( )A .1或3B .3C .2D .1 10.如图,平面//α平面β,过平面α,β外一点P 引直线1l 分别交平面α,平面β于A 、B 两点,6PA =,2AB =,引直线2l 分别交平面α,平面β于C 、D 两点,已知12BD =,则AC 的长等于( )A .9B .10C .8D .711.设2()2x f x x =-,则在下列区间中使函数()f x 有零点的区间是( )A .(0,1)B .(1,2)C .(21)--,D .(10)-, 12.已知(3)4,1()log ,1a a x a x f x x x --<⎧=⎨≥⎩在R 上是增函数,则实数a 的取值范围是( ) A .1(0,)4B .(0,)+∞C .()1,3D .()0,1二、填空题13.函数2log (34)y x =-的定义域为________.14.函数y =log a (x −1)+1(a>0且a≠1)的图象恒过定点________.15.在正方体1111ABCD A B C D -中,1A B 与11B D 所成的角等于___________.16.如图所示是AOB ∆用斜二测画法画出的直观图,则AOB ∆的面积是________.三、解答题17.如图所示空间四边形ABCD 中,E ,F ,G ,H 分别是边AB ,AD ,CB ,CD 的中点.求证:四边形EFHG 是平行四边形.18.已知全集为R ,集合{|24}=≤<A x x ,{|3}B x x =≥,{|}C x x a =<. (1)求A B ; (2)求()R A C B ;(3)若A C ⋂=∅,求a 的取值范围.19.解关于x 的不等式22232223x x x x a a -++-> (0a >,且1a ≠).20.如图,正方体1111ABCD A B C D -中,M ,N ,E ,F 分别是棱A 1B 1,A 1D 1,B 1C 1,C 1D 1的中点,求证:平面AMN∥平面EFDB .21.已知()f x 是一次函数,且满足(1)1f -=-,(0)1f =.(1)求函数()f x 的解析式.(2)设()()g x x f x a =⋅+,求函数()g x 在区间[]1,0-上的最值.22.已知函数()21x b f x x+=+ 为奇函数. (1)求b 的值;(2)用定义证明:函数()f x 在区间()1,+∞上是减函数.参考答案1.D【解析】【分析】根据交集的概念,直接求解,即可得出结果.【详解】因为{}{}1,0,1,3,0,1,2M N =-=,所以{}0,1MN =. 故选:D【点睛】本题主要考查交集的运算,熟记概念即可,属于基础题型.2.B【分析】根据偶函数的概念,逐项判断,即可得出结果.【详解】对于A 选项,函数12y x =的定义域为[)0,+∞,不关于原点对称,因此12y x =非奇非偶,排除A ;对于B 选项,函数223y x =+的定义域为R ,关于原点对称,且222()323-+=+x x ,因此223y x =+是偶函数;B 正确; 对于C 选项,函数y x =的定义域为R ,关于原点对称,但y x =显然是奇函数,排除C ; 对于D 选项,函数2,[0,1]y x x =∈的定义域为[0,1],不关于原点对称,因此2,[0,1]y x x =∈非奇非偶,排除D.故选:B【点睛】本题主要考查判断函数的奇偶性,熟记概念即可,属于基础题型.3.B【分析】根据对数运算法则,直接求解,即可得出结果.lg 2lg5lg101+==.故选:B【点睛】本题主要考查对数的运算,熟记对数运算法则即可,属于基础题型.4.A【分析】根据平行公理,可判断A 正确,根据直线位置关系,可判断BCD 错误,进而可得出结果.【详解】A 选项,由平行公理,若//a b ,//b c ,则//a c ,故A 正确;B 选项,a 与b 异面,b 与c 异面,则a 与c 可能异面,也可能相交或平行,故B 错;C 选项,a 与b 相交,b 与c 相交,则a 与c 可能相交,也可能平行或异面,故C 错;D 选项,a 与b 所成的角与b 与c 所成的角相等,则a 与c 可能平行,也可能异面或相交,故D 错.故选:A【点睛】本题主要考查直线与直线位置关系,熟记直线间的位置关系即可,属于常考题型. 5.A【解析】()28242f a b -=---=,则826a b +=-,所以()28246410f a b =+-=--=-,故选A 。
广西梧州市蒙山县蒙山中学高一第二次月考数学试题(无答案).pdf

树立科学发展观 教学目标 初步理解科学发展观的内涵,要正确处理好人口、资源、环境之间的关系,坚持科学发展观,走可持续发展之路。
树立可持续发展的理念。
教学重点 要正确处理好人口、资源、环境之间的关系,走可持续发展之路。
教学难点 科学发展观的内涵。
教学过程 一、课程导入 展示古巴比伦图片,讨论探究: 巴比伦文明的衰亡给我们留下了什么教训?它启示我们应该坚持什么发展观? 我们应合理利用可再生性资源,决不能滥垦乱伐。
它启示我们应坚持科学发展观,实现资源的可持续利用。
自主学习提示: 1、什么是科学发展观? 2、怎样坚持科学发展观? 3、为什么说发展是第一要义?(为什么要坚持以经济建设为中心?)。
4、青少年在日常生活中应如何保护环境、节约资源? 二、教学过程 (一)知识点拨: 1、什么是科学发展观? 科学发展观就是以人为本,全面、协调、可持续的发展观。
科学发展观的第一要义是发展;其本质和核心是以人为本;基本要求是全面协调可持续发展。
发展目的就是为了满足人民群众的生存和发展的需要。
2、怎样坚持科学发展观? (1)以人为本,时时刻刻把关系人民群众切身利益的问题放在首位;不仅要增加经济建设的投入,而且要增加保护资源和环境的投入,增加社会发展的投入,使经济社会又快又好地发展,以促进人的发展与进步。
(2)节约资源,发展循环经济,保护生态环境,建设资源节约型、环境友好型社会,促进经济发展与人口、资源、环境相协调。
(3)坚持可持续发展的理念,珍惜资源,善待环境。
在生态系统可能的承载能力范围内确定自己的消耗标准,增加利用资源的科技含量,提高资源的利用率。
3、青少年在日常生活中应如何保护环境、节约资源? (请你奉献几个节能减排的小窍门) (1)少买不必要的衣服。
(2)每月手洗一次衣服。
(3)提前几分钟关空调。
(4))—地球的天更蓝,水更清,山更绿,让我们行动起来节能减排吧。
节能减排——从我做起。
从身边做起。
广西壮族自治区梧州市蒙山县新圩中学2020-2021学年高一数学理上学期期末试卷含解析

广西壮族自治区梧州市蒙山县新圩中学2020-2021学年高一数学理上学期期末试卷含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 已知=(4,3),则在=(1,0)上的投影为()A.-4 B.4 C.3 D.-3参考答案:B2. 设,函数在区间上的最大值与最小值之差为,则()A. B.2 C.D.4参考答案:D略3. 若l,m是两条不同的直线,α是一个平面,则下列命题正确的是()A.若l∥α,m∥α,则l∥m B.若l⊥m,m?α,则l⊥αC.若l∥α,m?α,则l∥m D.若l⊥α,l∥m,则m⊥α参考答案:D【考点】空间中直线与平面之间的位置关系;空间中直线与直线之间的位置关系.【分析】A.若l∥α,m∥α,则l∥m或相交或为异面直线,即可判断出真假;B.若l⊥m,m?α,则l与α相交或平行,即可判断出真假;C.若l∥α,m?α,则l∥m或为异面直线,即可判断出真假;D.由线面垂直的性质定理与判定定理可得正确.【解答】解:A.若l∥α,m∥α,则l∥m或相交或为异面直线,因此不正确;B.若l⊥m,m?α,则l与α相交或平行,因此不正确;C.若l∥α,m?α,则l∥m或为异面直线,因此不正确;D.若l⊥α,l∥m,则由线面垂直的性质定理与判定定理可得:m⊥α,正确.故选:D.【点评】本题考查了空间线面面面位置关系的判定及其性质定理,考查了推理能力与计算能力,属于中档题.4. 函数y=x2-2x , x∈ [0,3]的值域为()A.[0,3] B.[1,3] C.[-1,0] D.[-1,3]参考答案:D∵,∴函数开口向上,对称轴为,∴函数在上单调递减,单调递增,∴当时,函数值最小,最小值为;当时,函数值最大,最大值为3,即函数的值域为,故选D.5. 函数的定义域为().A.B.C.D.参考答案:B解:要使函数有意义,必须:,所以.所以函数的定义域为:.故选.6. 函数的定义域是A. B.C. D.参考答案:D略7. 已知直三棱柱的6个顶点都在球的球面上,若,,,则球的半径为().A.B.C.D.参考答案:C8. 为了了解某地参加计算机水平测试的1000名学生的成绩,从中随机抽取200名学生进行统计分析,分析的结果用右图的频率分布直方图表示,则估计在这1000名学生中成绩小于80分的人数约有()A.100人B.200人C.300人D.400人参考答案:C9. 甲、乙、丙三名射箭运动员在某次测试中各射击20次,三人的测试成绩如下表:(甲)(乙)(丙)、、分别表示甲、乙、丙三名运动员这次测试成绩的标准差,则有()A. B.C. D.参考答案:B略10. 下列集合中,只有一个子集的集合是( )A.{x|x2≤0}B.{x|x3≤0}C.{x||x|<0} D.{x|(﹣x)3≤0}参考答案:C【考点】子集与真子集.【专题】不等式的解法及应用.【分析】根据集合元素的个数与子集的个数关系,可以推出集合为空集,从而推出正确选项;【解答】解:对于A={0}的子集有两个,A不正确;对于B,{x|x3≤0}={x|x≤0},有无数个元素,子集也有无数个,所以不正确,对于C,不等式无解,是空集,只有一个子集,所以正确.对于D,{x|﹣x3≤0}={x|x≥0},与A类似,不正确.故选C.【点评】此题主要考查子集的性质,以及空集的定义,是一道基础题.二、填空题:本大题共7小题,每小题4分,共28分11. 已知点,点,若,则点的坐标是。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020级高(一)上数学周测(四)班别姓名考号分数:一、选择题:(本大题共8小题,每小题6分,满分48分.给出的四个答案中,只有一
个是符合题意.)
1.已知A =B =R ,x ∈A ,y ∈B ,f :x →y =ax +b 是从A 到B 的映射,若1和8的原像分别是3和10,则5在f 下的像是(
)A.3B.4C.5D.6
2.设函数f (x )=x 2+1,x ≤1,
2x
,x >1,则f (f (3))=()A.15B.3 C.23 D.139
3.函数f (x )=x +3+1x +2
的定义域是()A.[-3,+∞)
B.[-3,-2)C.[-3,-2)∪(-2,+∞)D.(-2,+∞)
4.函数f (x )=|x |和g (x )=x (2-x )的单调递增区间分别是(
)A.(-∞,0]和(-∞,1]
B.(-∞,0]和[1,+∞)C.[0,+∞)和(-∞,1]D.[0,+∞)和[1,+∞)
5.函数21y x x =+-()A.有最小值12,无最大值 B.有最大值12,无最小值C.有最小值12
,最大值2 D.无最大值,也无最小值6.函数y =ax +1与y =ax 2+bx +1(a ≠0)的图像可能是(
)
7.函数f (x )=2x -x 2,0≤x ≤3,
x 2+6x ,-2≤x <0的值域是()
A.R B.[1,+∞)C.[-8,1]D.[-9,1]
8.已知()f x 是定义在R 上的增函数,若()y f x =的图象过点()2,1A --和()3,1B ,则满足()111f x -<+<的x 的取值范围是(
)A.(-2,3) B.(-3,2) C.(-1,4) D.(-1,1)
题号
12345678答案
二、填空题(本大题共4个小题,每小题6分,满分24分)
9.如果一条抛物线的形状与y =1
3x 2+2的图像开口形状相同,且顶点坐标为(4,-2),则它的解析式是
________.
10.函数f (x )=-x 2
+2x ,x ∈[-1,2]的值域为11.设函数2()(2)1f x x a x =++-在区间(],2-∞上是减函数,则实数a 的最大值为.
12.已知集合A =B =R ,映射f :x →x 2
+2x -4,若a 在B 中且在A 中没有原像,则a 的取值范围是________.三、解答题(本题共2题,解答应写出文字说明,证明过程或演算步骤)
13.(14分)(1)已知f(x)是一次函数,且满足2f(x+3)-f(x-2)=2x+21,求f(x);
(2)已知f(x)满足3f(x)+2f(-x)=4x,求f(x).
14.(14分)已知函数f(x)=2x-1
,x∈[3,5].
x+1
(1)判断f(x)在区间[3,5]上的单调性并证明;
(2)求f(x)在区间[3,5]上的最大值和最小值.。
