人教版七年级数学下册《511相交线》同步练习(有答案)MnqMnP

合集下载

人教版七年级数学下册 5.1.1 相交线同步练习有答案

5.1.1 相交线一选择题1.如图所示,直线L1,L2,L3相交于一点,则下列答案中,全对的一组是( )A.∠1=90°,∠2=30°,∠3=∠4=60°;B.∠1=∠3=90°,∠2=∠4=30C.∠1=∠3=90°,∠2=∠4=60°;D.∠1=∠3=90°,∠2=60°,∠4=30°2.如图所示,直线AB和CD相交于点O,若∠AOD与∠BOC的和为236°,则∠AOC•的度数为( ) A.62° B.118° C.72° D.59°3.下列说法正确的有( )①对顶角相等;②相等的角是对顶角;③若两个角不相等,则这两个角一定不是对顶角;④若两个角不是对顶角,则这两个角不相等.A.1个B.2个C.3个D.4个4.如图所示,三条直线AB,CD,EF相交于一点O,则∠AOE+∠DOB+∠COF等于( • )A.150°B.180°C.210°D.120°5.如图所示,∠1和∠2是对顶角的图形有( )A.1个B.2个C.3个D.4个二填空题1.如图所示,直线AB,CD相交于O,若∠1=40°,则∠2•的度数为____________2.如图所示,直线AB,CD相交于点O,已知∠AOC=70°,OE把∠BOD分成两部分,•且∠BOE:∠EOD=2:3,则∠EOD=________.3.如图所示,直线AB,CD相交于点O,OE平分∠AOC,若∠AOD-∠DOB=50°,•则∠EOB=______________.4.如图所示,直线AB,CD相交于点O,若∠1-∠2=70,则∠BOD=_____,∠2=____.5.对顶角的性质是______________________.6.如图所示,已知直线AB,CD相交于O,OA平分∠EOC,∠EOC=70°,则∠BOD=•______.7.如图所示,直线AB,CD,EF相交于点O,则∠AOD的对顶角是_____,∠AOC的邻补角是_______;若∠AOC=50°,则∠BOD=______,∠COB=_______.8.如图所示,若∠1=25°,则∠2=_______,∠3=______,∠4=_______.三解答题1.如图所示,AB,CD,EF交于点O,∠1=20°,∠BOC=80°,求∠2的度数.2.如图所示,L1,L2,L3交于点O,∠1=∠2,∠3:∠1=8:1,求∠4的度数.3.如图所示,AB,CD相交于点O,OE平分∠AOD,∠AOC=120°,求∠BOD,∠AOE•的度数.4.如图所示,直线AB与CD相交于点O,∠AOC:∠AOD=2:3,求∠BOD的度数.5.如图所示,直线a,b,c两两相交,∠1=2∠3,∠2=65°,求∠4的度数.参考答案一选择题DABBA二填空题1.140°2.42°3.147.5°4 .125°55°5.对顶角相等6.35°7. 略8.155°25°155°三解答题1.∠2=60°2.∠4=36°3.∠BOD=120°,∠AOE=30°4.∠BOD=72°5.∠4=32.5°。

人教版七年级数学下册 5.1.1相交线同步练习题含答案

相交线一、单选题1.如图，对于直线A B，线段C D，射线E F，其中能相交的图是（）A．B．C．D．2.如图，已知直线AB、CD相交于点O，OA平分∠EOC，∠EOC＝110°，则∠BOD的度数是()A．25°B．35°C．45°D．55°3.如图，点O在直线A B上，射线O C平分∠D O B．若∠COB=35°，则∠A O D等于( ).A．35°B．70°C．110°D．145°4．如图，∠1=100°，∠2=145°，那么∠3=().A．55°B．65°C．75°D．85°5.如图，直线A B、C D相交于点O，且∠AOD+∠BOC=100°，则∠A O C是( )A．150°B．130°C．100°D．90°6.如图，直线AB，CD 交于O，EO⊥AB于O，∠1与∠3的关系是（）A．互余B．对顶角C．互补D．相等7．如图所示，∠1和∠2是对顶角的是（）A．B．C．D．8.下面四个图形中，∠1与∠2是邻补角的是( )A．B．C．D．9.如图，下列各组角中，互为对顶角的是（）A．∠1和∠2B．∠1和∠3C．∠2和∠4D．∠2和∠5 10．10．如图所示，下列判断正确的是( )A．图⑴中∠1和∠2是一组对顶角B．图⑵中∠1和∠2是一组对顶角C．图⑶中∠1和∠2是一对邻补角D．图⑷中∠1和∠2互为邻补角二、填空题11.如图所示，AB∥CD，EF 与AB，CD 相交，EF 与AB 交于点，EF 与CD 交于．12.两条直线相交，只有个交点．13.平面内四条直线共有三个交点，则这四条直线中最多有条平行线．14.探究题：(1)三条直线相交，最少有个交点，最多有个交点，分别画出图形，并数出图形中的对顶角和邻补角的对数；(2)四条直线相交，最少有个交点，最多有个交点，分别画出图形，并数出图形中的对顶角和邻补角的对数；(3)依次类推，n 条直线相交，最少有个交点，最多有个交点，对顶角有对，邻补角有对．三、解答题15.平面上两条直线相交于一点，三条直线俩两相交，每个交点都不经过第三条直线．（1）5 条直线的交点为个．（2）请探索n条直线的交点个数．16.如图所示，已知直线 AB 和CD 相交于点 O，OM 平分∠BOD，∠MON＝90°，∠AOC＝50°．（1）求∠AON的度数．（2）写出∠DON的余角．17.如图，直线A B与C D相交于点O，∠A O C∶∠A O D＝1∶2.求∠B O D的度数．18. 如图，三条直线 A B ，C D ，E F 交于一点，若∠1=30°，∠2=70°，求∠3 的度数．答案1．B2．D3．C4．B5．B6．A7．C8．D9．A10．D11．MN 12． 1．13．三14．(1)1，3；(2)1，6；(3)1，n (n 1) 2，n(n-1)，2n(n-1)15．（1）如图所示：我们发现：2 条直线相交有 1 个交点；3 条直线相交有 1+2=3 个交点；4 条直线相交有 1+2+3=6 个交点，则 5 条直线的交点为 1+2+3+4=10；n(n 1)（2）图（n）：1+2+3+…+n-1=．216．（1）∵∠AOC+∠AOD＝∠AOD+∠BOD＝180°，∴∠BOD＝∠AOC＝50°，∵OM 平分∠BOD，∴∠BOM＝∠DOM＝25°，又由∠MON＝90°，∴∠AON＝180°﹣（∠MON+∠BOM）＝180°﹣（90°+25°）＝65°；（2）由∠DON+∠DOM＝∠MON＝90°知∠DOM 为∠DON 的余角，∵∠AON+∠BOM＝90°，∠DOM＝∠MOB，∴∠AON+∠DOM＝90°，∴∠NO D+∠BOM＝90°，故∠DON 的余角为：∠DOM，∠BOM ．17．由邻补角的性质，得∠A OC＋∠AO D＝180°.由∠A O C∶∠A O D＝1∶2，得∠A O D＝2∠A O C，∠AOC＋2∠AOC＝180°，解得∠AOC＝60°.由对顶角相等，得∠B O D＝∠A O C＝60°.故答案为：60°.18．解：如图，∵∠4=∠2=70°（对顶角相等），∴∠3=180°-∠1-∠4=180°-30°-70°=80°．。

人教版七年级数学下册《5.1 相交线》同步练习题-附带答案

人教版七年级数学下册《5.1 相交线》同步练习题-附带答案一、选择题1．同一平面内互不重合的3条直线的交点的个数是（）A．可能是0，1，2 B．可能是0，2，3C．可能是0，1，2或3 D．可能是1，可能是32．下列图形中，∠1=∠2一定成立的是（）A．B．C．D．3．如图，要把小河里的水引到田地A处，则作AB⊥l，垂足为B，沿AB挖水沟，水沟最短．理由是（）A．两点之间，线段最短B．两点确定一条直线C．垂线段最短D．过一点作已知直线的垂线有且只有一条4．如图，将一副三角板顶点O靠在一直尺的边上，若∠AOC=50°，则∠BOD的度数（）A．30°B．40°C．50°D．60°5．如图，两只手的食指和拇指在同一平面内，在以下四种摆放方式中，它们构成的一对角可以看成内错角的是（）A．B．C．D．6．如图AD⊥BC于点D， AB=6，AC=9，AD=5 ，点P是线段BC上的一个动点，则线段AP的长度不可能是（）A．5.5 B．7 C．8 D．4.57．如图，与∠1是同旁内角的是（）A．∠2 B．∠3 C．∠4 D．∠58．如图，直线a，b被直线c所截，∠1与∠2是（）A．同位角B．内错角C．同旁内角D．对顶角二、填空题9．若∠1和∠2是对顶角，∠1＝36°，则∠2的度数是度．10．如图，若∠1+∠2=200°，则∠3=．11．如图，直线AB⊥CD于点O，EF为过点O的直线，∠1＝50°，则∠2的度数为．12．如图，给出下列结论：①∠1与∠2是同旁内角；②∠1与∠3是同位角；③∠1与∠4是内错角；④∠1与∠5是同位角；⑤∠2与∠4是对顶角．其中说法正确的是．（填序号）13．物理中有一种现象，叫折射现象，它指的是当光线从空气射入水中时，光线的传播方向会发生改变．如图，我们建立折射现象数学模型，MN表示水面，它与底面EF平行，光线AB从空气射入水里时发生了折射，变成光线BC射到水底C处，射线BD是光线AB的延长线，∠1=70°，∠2=42°，则∠DBC的度数为°．三、解答题14．如图，直线CD与EF交于点O，OC平分∠AOF，若∠AOE=40°，求∠DOE的度数．15．如图，直线AB，CD相交于点O，OM⊥AB于点O.（1）若∠BOC=4∠AOC，求∠BOD的度数.（2）若∠1=∠2，请判断ON与CD关系，并说明理由.∠COF．16．如图，已知直线EF与AB交于点M，与CD交于点O，OG平分∠DOF，若∠COM=120°，∠EMB= 12（1）求∠FOG的度数；（2）写出一个与∠FOG互为同位角的角；（3）求∠AMO的度数．参考答案1．C2．C3．C4．B5．C6．D7．D8．A9．3610．80°11．40°12．①②⑤13．2814．解：∵∠AOE=40°∴∠AOF=140°．∵OC平分∠AOF∠AOF=70°∴∠COF=12∴∠DOE=∠COF=70°15．（1）解：由邻补角的定义，得∠AOC+∠BOC＝180°∵∠BOC＝4∠AOC∴4∠AOC+∠AOC＝180°∴∠AOC＝36°由对顶角相等，得∠BOD＝∠AOC＝36°；（2）解：ON⊥CD，理由如下：∵OM⊥AB∴∠AOM＝90°∴∠1+∠AOC＝90°∵∠1＝∠2∴∠2+∠AOC＝90°即∠NOC＝90°∴ON⊥CD.16．（1）解：∵∠COM=120°∴∠DOF=120°∵OG平分∠DOF∴∠FOG=60°（2）解：与∠FOG互为同位角的角是∠BMF （3）解：∵∠COM=120°∴∠COF=60°∠COF∵∠EMB= 12∴∠EMB=30°∴∠AMO=30°。

2021年人教版七年级数学下册5.1.1《相交线》课后练习 (含答案)

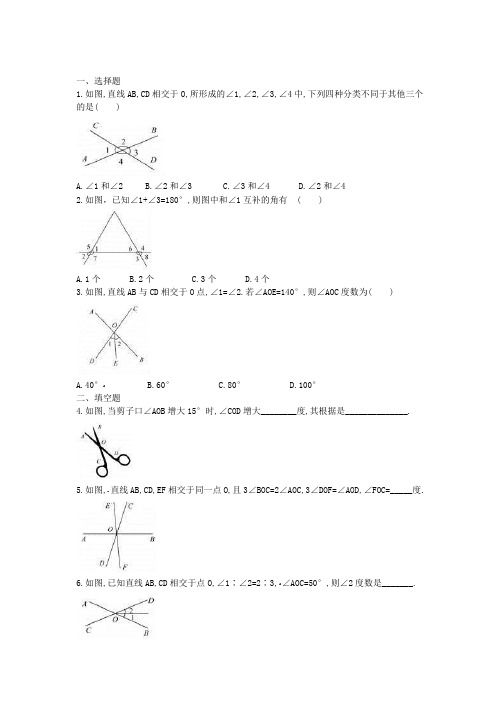
一、选择题1.如图,直线AB,CD相交于O,所形成的∠1,∠2,∠3,∠4中,下列四种分类不同于其他三个的是( )A.∠1和∠2B.∠2和∠3C.∠3和∠4D.∠2和∠42.如图，已知∠1+∠3=180°,则图中和∠1互补的角有( )A.1个B.2个C.3个D.4个3.如图,直线AB与CD相交于O点,∠1=∠2.若∠AOE=140°,则∠AOC度数为( )A.40°B.60°C.80°D.100°二、填空题4.如图,当剪子口∠AOB增大15°时,∠COD增大________度,其根据是______________.5.如图,直线AB,CD,EF相交于同一点O,且3∠BOC=2∠AOC,3∠DOF=∠AOD,∠FOC=_____度.6.如图,已知直线AB,CD相交于点O,∠1∶∠2=2∶3,∠AOC=50°,则∠2度数是_______.三、解答题7.如图,有两堵墙,要测量地面上所形成的∠AOB的度数,但人又不能进入围墙,只能站在墙外.如何运用本章知识进行测量?8.如图所示,直线AB,CD相交于点O,作∠DOE=∠BOD,OF平分∠AOE,若∠AOC=28°,求∠EOF 的度数.9.观察下列图形,寻找对顶角(不含平角):(1)两条直线相交(如图(1)),图中共有______对对顶角.(2)三条直线相交于一点(如图 (2)),图中共有________对对顶角.(3)四条直线相交于一点(如图(3)),图中共有________对对顶角.(4)研究(1)～(3)小题中直线条数与对顶角的对数之间的关系,若有n条直线相交于一点,则可构成________对对顶角.(5)若有2025条直线相交于一点,则可构成________对对顶角.参考答案1.答案为：D.2.答案为：D.3.答案为：C.4.答案为：15 对顶角相等5.答案为：1566.答案为：30°7.解：如图,延长AO与BO得到∠AOB的对顶角∠COD,测出∠COD的度数,由∠AOB=∠COD,即得∠AOB的度数.8.解：因为∠BOD=∠DOE,所以2∠DOE=∠BOE,同理2∠EOF=∠AOE,所以∠DOF=∠DOE+∠EOF=0.5∠BOE+0.5∠AOE=0.5(∠BOE+∠AOE)=0.5×180°=90°.又∠BOD和∠AOC是对顶角,所以∠BOD=∠AOC=28°,所以∠EOF=90°-28°=62°.9.解：图(1)中有两条直线,共有2对对顶角,而2=2×1;图(2)中有三条直线,共有6对对顶角,而6=3×2;图(3)中有四条直线,共有12对对顶角,而12=4×3;……当有n条直线相交于一点时,共有n(n-1)对对顶角;若有2025条直线相交于一点,则可构成2025×2024=4 098 600对对顶角.。

人教版七年级数学下册 (5.1相交线) 课时同步优化训练习题(含答案)

第五章相交线与平行线5.1 相交线5分钟训练(预习类训练，可用于课前)1.如图5-1-1所示，∠1与∠2互为对顶角的是( )图5-1-1解析:因为对顶角的角的两边互为反向延长线，所以选项A、B、C都不正确，选项D正确.答案:D2.已知∠A=40°，则∠A的补角等于( )A.50°B.90°C.140°D.180°解析:∠A的补角是180°-∠A=140°.答案:C3.如图5-1-2，一条直线c分别与直线a、b相交（也说直线a、b被直线c____________）.构成的八个角中，∠1与∠____________是同位角，∠3与∠____________是内错角，∠3与∠____________是同旁内角.图5-1-2 图5-1-3解析:同位角在截线的同旁且两条被截直线的同侧，内错角在截线的两侧且在两条被截直线的内部，同旁内角在截线的同旁且在两条被截直线内部；所以∠1与∠5是同位角，∠3与∠5是内错角，∠3与∠6是同旁内角.答案:所截 5 5 64.如图5-1-3所示，直线AB、CD、EF相交于O点，∠AOF=3∠FOB，∠AOC=90°，则∠EOC的度数为____________.解析:∠AOF=3∠FOB,又因为∠AOF+∠FOB=180°,所以∠FOB=45°.因为∠AOE=∠FOB(对顶角相等),∠AOC=90°,所以∠EOC=∠AOC-∠AOE=45°.答案:45°10分钟训练(强化类训练，可用于课中)1.下列说法中正确的是( )A.对顶角必相等B.相等的角是对顶角C.不是对顶角的角不相等D.有公共顶点的角叫做对顶角解析:因为当两个角的两边互为反向延长线时才构成对顶角，而相等的角、有公共顶点的角的两边不一定成互为反向延长线，所以选项B、D不正确；由对顶角的性质可知“对顶角相等”，但不是对顶角的两个角的大小可以相等，如等腰直角三角板中有两个角相等,所以选项A正确,选项C不正确.答案:A2.下列说法不正确的是( )A.钝角没有余角，但一定有补角B.两个角相等且互补，则它们都是直角C.锐角的补角比该锐角的余角大D.一个锐角的余角一定比这个锐角大解析:设一个角为α，则其余角为90°-α，补角为180°-α.当α为钝角时， 90°-α＜0°，所以其余角不存在，但补角一定存在,所以选项A 正确；当α=180°-α时，α=90°,所以选项B 正确；当α为锐角时，其补角为180°-α＞90°＞90°-α，所以选项C 正确；因为30°角与60°角互余，所以60°角的余角小于60°.所以选项D 错误. 答案:D3.如图5-1-4所示，∠AOC ，∠BO C ，∠DOE 都是直角，则相等的角有( )图5-1-4A.2对B.3对C.4对D.5对解析:∵∠AOD 与∠COE 都是∠DOC 的余角，∴∠AOD=∠COE. ∵∠DOC 与∠BOE 都是∠COE 的余角， ∴∠DOC=∠BOE.∵∠AOC ，∠BOC ，∠DOE 都是直角， ∴∠AOC=∠BOC=∠DOE. 答案:D4.如图5-1-5,运动会上,甲、乙两名同学测得小明的跳远成绩分别为DA=4.5米,DB=4.15米,则小明的跳远成绩应该为_____________米.图5-1-5 图5-1-6解析:根据跳远规则及直线外一点与直线上各点连结的所有线段中垂线段最短,得小明的跳远成绩应是BD 的长. 答案:4.155.如图5-1-6,∠1和∠B 是直线_____________和直线_____________被直线_____________所截得到的_____________角;∠2和∠4是直线_____________和直线_____________被直线_____________所截得到的_____________角;∠D 和∠4是直线_____________和直线_____________被直线_____________所截得到的_____________角.解析:由同位角、内错角、同旁内角的概念,进行辨析. 答案:AD BC AB 同位 AB CD AC 同位 AC AD CD 同旁内 6.一个角的余角比这个角的补角的31还小10°，求这个角的余角及补角. 解:设该角为x ，由题意得90°-x=31(180°-x)-10°,解之,得x=60°. ∴90°-x=30°，180°-x=120°，即这个角的余角与补角分别是30°、120°. 30分钟训练(巩固类训练，可用于课后) 1.下列结论不正确的是( )A.互为邻补角的两个角的平分线所成的角为90°B.互不相等的两个角不是对顶角C.两直线相交,若有一个交角为90°,则这四个角中任取两个角都互为补角D.不是对顶角的两个角互不相等解析:A 选项,如图所示,∵∠1=21∠BOD,∠2=21∠AOD,∴∠EOC=∠1+∠2=21(∠BOD+∠AOD)=90°. B 选项,由于对顶角必然相等,因此不相等的角自然不可能是对顶角,故正确. C 选项,两条直线相交形成的四个角中,如有一个为90°,则其余三个角均为90°,因此,任意两个角互为补角,故正确.D 选项,对顶角相等,但相等的角不一定是对顶角,比如等腰直角三角板的两个45°的角,故错误. 答案:D2.如图5-1-7，AB 与CD 为直线，图中共有对顶角( )图5-1-7A.1对B.2对C.3对D.4对解析:图中只有两条直线AB 与CD 相交，所以对顶角共有2对. 答案:B3.(2010广西南宁模拟，2)如图5-1-8，已知AB 、CD 相交于O 点，OE ⊥AB ，∠EOC=28°，则∠AOD=______________.图5-1-8 图5-1-9解析:利用垂直求出∠AOD 的对顶角∠COB 即可. 答案:62°4.如图5-1-9所示,直线AB 、CD 相交于O 点,∠AOD=130°,则∠BOC=______________, ∠AOC=______________,∠BOD=______________. 解析:利用对顶角相等和邻补角的关系求解. 答案:130° 50° 50°5.如图5-1-10,直线AB 、CD 相交于O,作∠DOE=∠BOD,OF 平分∠AOE,∠AOC=28°,求∠EOF 的度数.图5-1-10解:由题知∠BOD=∠AOC=28°(对顶角相等), 因为∠DOE=∠BOD,所以∠BOE=2∠BOD=56°. 因为∠AOE+∠BOE=180°,所以∠AOE=124°. 因为OF 平分∠AOE, 所以∠EOF=21∠AOE=62°. 6.A 、B 两厂在公路同侧,拟在公路边建一货场C,若由B 厂独家兴建,并考虑B 厂的利益,则要求货物离B 厂最近,请在图5-1-11中作出此时货场C 的位置,并说出这样做的道理.图5-1-11解:如图所示,过B 作公路所在直线的垂线,垂足O 就是所求货场C 的位置.理由:根据“垂线段最短”,所以BO 是点B 到公路的最短线段. 7.如图5-1-12,直线AB 、CD 、EF 相交于点O.图5-1-12(1)写出∠AOD 、∠EOC 的对顶角(2)已知∠AOC=50°,求∠BOD 、∠COB 的度数.解:(1)∠AOD 的对顶角是∠COB;∠EOC 的对顶角是∠DOF. (2)∠BOD=∠AOC=50°(对顶角相等), ∠COB=180-∠AOC=180°-50°=130°(邻补角的定义).8.图5-1-13中的∠1和∠2,∠3和∠4分别是由哪两条直线被哪一条直线所截而成的?它们各是什么角?图5-1-13解:由题图(1)知∠1和∠2的公共边所在的直线是BD,则BD 是截线,所以∠1和∠2是由直线AB,CD 被直线BD 所截而形成的内错角;∠3和∠4的公共边所在的直线是BD,则BD 是截线,所以∠3和∠4是由直线AD,BC 被直线BD 所截而形成的内错角.由题图(2)知,∠1和∠2的公共边所在的直线是BC,则B C 是截线,所以∠1和∠2是由直线AB,CD 被直线BC 所截而形成的同旁内角;∠3和∠4的公共边所在的直线是AB,则AB 是截线,所以∠3和∠4是由直线AD,BC 被直线AB 所截而形成的同位角.9.如图5-1-14,一棵小树生长时与地面成80°角，它的主根深入泥土，如果主根和小树在同一条直线上，那么∠2等于多少度？图5-1-14解:∵∠1+80°=90°，∴∠1=10°.∵∠1=∠2（对顶角相等），∴∠2=10°.10.（1）如图5-1-15（1）所示，两条直线AB与CD相交成几对对顶角？（2）如图5-1-15（2）所示,三条直线AB、CD、EF相交呢？（3）试猜想n条直线相交会成多少对对顶角？图5-1-15解:（1）两条直线AB与CD相交成2对对顶角.（2）三条直线AB、CD、EF相交有6对对顶角.（3）因为3条不同直线相交所成的对顶角有（3×2）÷2×2=6（对）；4条不同直线相交所成的对顶角有（4×3）÷2×2=12（对）；则可推测：n条直线相交所成的对顶角有n×（n-1）÷2×2=n(n-1)（对）.。

人教版七年级下册第五章相交线与平行线5.1相交线同步练习题含答案

初一数学人教版七年级下册第五章订交线与平行线5．1订交线同步练习题1. 以下说法中正确的选项是 ()A．不相等的角必定不是对顶角B．互补的两个角是邻补角C．互补且有一条公共边的两个角是邻补角D．两条直线订交所成的角是对顶角2. 以下说法正确的选项是 ()A．在同一平面内，过直线外一点向该直线画垂线，垂足必定在该直线上B．在同一平面内，过线段或射线外一点向该线段或射线画垂线，垂足必定在该线段或射线上C．过线段或射线外一点不必定能画出该线段或射线的垂线D．过直线外一点与直线上一点画的一条直线与该直线垂直3. 已知∠α和∠ β的对顶角，若∠ α＝60°，则∠ β的度数为 ()A ．30°B．60°C．70°D．150°4.如图，直线 AB ，CD 订交于点 O，由于∠ 1＋∠ 3＝180°，∠ 2＋∠ 3＝180°，因此∠ 1＝∠ 2，其推理依照是 ()A ．同角的余角相等B．对顶角相等C．同角的补角相等D．等角的补角相等5. 如图， OB⊥CD 于点 O，∠ 1＝∠ 2，则∠ 2 与∠ 3 的关系是 () A．∠2＝∠3B．∠2 与∠3 互补C．∠ 2 与∠ 3 互余D．不可以确立第1页/共4页6.如图，从地点 P 到直线公路 MN 共有四条小路，若用同样的速度行走，能最快抵达公路 MN 的小路是 ()A ．PA B．PB C．PC D．PD7.如图是一跳远运动员跳落沙坑时留下的印迹，则表示该运动员成绩的是()A ．线段 1 的长B．线段 AP2的长APC．线段 BP3的长D．线段 CP3的长8.如图，已知直线 a， b 被直线 c 所截，则∠ 1 和∠ 2 是一对 ()A ．对顶角B．同位角C．内错角D．同旁内角9.如图，已知直线 b，c 被直线 a 所截，则∠ 1 与∠ 2 是一对 ()A ．同位角B ．内错角C．同旁内角D．对顶角10.如图，直线 AB ，CD 订交于点 O，若∠ AOD ＝28°，则∠ BOC＝__________，∠AOC＝ ___________．11.如下图， OA⊥OB，∠ AOC ＝120°，则∠ BOC 等于 ______度．12.自来水企业为某小区 A 改造供水系统，如下图，沿路线 AO 铺设管道和BO主管道连接(AO⊥BO)，路线最短、工程造价最低，其依据是__________________．13. 如下图，∠ B 与 ____________是直线 _________和直线 _______被直线________所截得的同位角．14.如下图，内错角共有 ____对．15.如下图，当剪刀口∠ AOB 增大 20°时，∠ COD 增大________ ，其依据是_________________．16. 如图，已知 AB ，CD 订交于点 O，OE⊥AB ，∠EOC＝28°，则∠ AOD ＝____第2页/共4页度．17.如图， BC⊥ AC，CB＝8 cm，AC ＝6 cm，点 C 到 AB 的距离是 4.8 cm，那么点 B 到 AC 的距离是 ____ cm，点 A 到 BC 的距离是 ____ cm，A，B 两点间的距离是 ____ cm.18.如图，直线 AB ，CD，EF 订交于点 O.(1)写出∠ COE 的邻补角；(2)分别写出∠ COE 和∠ BOE 的对顶角；(3)假如∠ BOD＝60°，∠ BOF＝90°，求∠ AOF 和∠ FOC 的度数．119. 如图，O 为直线 AB 上一点，∠AOC＝3∠BOC，OC 是∠ AOD 的均分线．判断 OD 与 AB 的地点关系，并说明原因．20.如图，点 A 表示毛毛雨家，点 B 表示小樱家，点 C 表示小丽家，她们三家恰巧构成一个直角三角形，此中 AC ⊥BC，AC＝900 米，BC＝1 200 米，AB ＝1 500 米．(1)试说出毛毛雨家到街道BC 的距离以及小樱家到街道AC 的距离．(2)画出表示小丽家到街道AB 距离的线段．21.如图，直线 a，b 被直线 l 所截，已知∠ 1＝ 40°，试求∠ 2 的同位角及同旁内角的度数．参照答案：1---9AABCC BBDA10. 28°152°11.3012.垂线段最短13. ∠FAC AC BC FB第3页/共4页14.815.20°对顶角相等16.6217. 861018.解： (1)∠COE 的邻补角为∠ COF 和∠ EOD.(2)∠COE 和∠ BOE 的对顶角分别为∠ DOF 和∠ AOF.(3)由于∠ BOF＝90°，因此∠AOF＝ 180°－90°＝90°.又由于∠ AOC＝∠ BOD＝60°，因此∠ FOC＝∠ AOF＋∠A OC＝90°＋60°＝150°.19.解：OD⊥AB. 原因：由于 OC 均分∠ AOD ，因此可设∠ AOC＝∠ COD ＝x°，1而∠ AOC ＝3∠BOC ，因此∠ BOC ＝ 3∠AOC ＝ 3x° .由于∠ AOC ＋∠ BOC＝180°，因此 x＋3x＝180，因此 x＝45，因此∠ AOD ＝2∠COD＝90°，即 OD⊥AB.20.解：(1)毛毛雨家到街道 BC 的距离为 900 米，小樱家到街道 AC 的距离为 1200米．(2)过点 C 作 CD⊥AB 于点 D.线段 CD 的长表示小丽家到街道AB 的距离，图略．21.解：∵∠ 1＝40°，∴∠ 3＝∠ 1＝40°，4＝180°－∠ 1＝140°，即∠ 2的同位角是 140°，∠ 2 的同旁内角是 40°.第4页/共4页。

新人教版七年级数学下册《511相交线》同步测试题及答案.doc

新人教版七年级数学下册《5. 1. 1相交线》同步测试题及答案《相交线》同步测试题初稿：王新华（安徽省巢湖市散兵中心学校）修改：张永超（安徽省合肥市教育局教研室）审校：夏晓华（安徽省庐江县第三中学）一、选择题1 •下列4幅图中，Z1和Z2是对顶角的为（）•考查目的：考查对顶角的概念•答案：D.解析：前三个图的Z1和Z2,都只满足有公共顶点，但不具备两个角的两边分别互为反向延长线.2.如图，三条直线相交于点0 , Z AOE二Z AOC ,则与Z AOC互补的角有（）.个考查目的：考查邻补角的概念与及其性质•答案：D.解析：根据邻补角的性质，ZAOD、ZCOB与ZAOC互补，同时与ZA 0E 互补的角有ZEOB、ZAOF,因为Z AOE= Z AOC,所以ZEOB> ZA0F与ZAOC也互补・3•下列说法正确的是（）.A.邻补角一定互补B・若两个角互补,则这两个角一定是邻补角C.相等的角是对顶角D.若两个角不是对顶角，则这两个角不相等考查目的：考查对顶角和邻补角的概念及性质.答案: A.解析：邻补角是指位置具有特殊关系（一边相同另一边在一条直线上）且互补的两个角.两个角互补不一定是邻补角, 所以B错误.对顶角也是位置具有特殊关系（两边分别互为反向延长线）且相等的两个角，而相等的两个角其边不一定具有这种位置关系，因此不一定是对顶角，不是对顶角的两个角也可能相等，所以C、D错误•二、填空题4.如图，剪刀剪开纸张的过程，随着两个把手之间的夹角（ZDO C）逐渐变小，剪刀刀刃之间的夹角（Z AOB）也相•考查目的：考查对顶角的性质•答案:变小，对顶角相等•解析：由对顶角相等可知，ZAO B与ZDOC相等，所以ZAOB与ZDOC的大小变化相同.5.两条直线相交形成的四个角中，如果有一个角是90°,则另三个角的度数分别为目的：考查对顶角、邻补角的概念与性质•答案：90。

,90° , 9 0°•解析：根据对顶角相等和邻补角互补的性质可得，其它三个角都是90° ..已知直线AB与CD相交于点0,ZA0C二40。

人教版数学七年级下册5.1相交线同步练习【包含答案】

5.1相交线总分：100分班级:__________ 姓名：__________ 学号：__________ 得分：__________一、选择题（共10小题；共30分）1. 对于直线、射线、线段，在下列各图中能相交的是( )A. B.C. D.2. 如图所示，∠1与∠2是对顶角的是( )A. B.C. D.3. 如图所示，下列说法不正确的是( )A. 点B到AC的垂线段是线段ABB. 点C到AB的垂线段是线段ACC. 线段AD是点D到BC的垂线段D. 线段BD是点B到AD的垂线段4. 如图，直线AD，BC被直线BF和AC所截，则∠1的同位角和∠5的内错角分别是( )A. ∠4，∠2B. ∠2，∠6C. ∠5，∠4D. ∠2，∠45. 下面四个图形中，∠1与∠2是邻补角的是( )A. B.C. D.6. 下面四个图形中，∠1=∠2一定成立的是( )A. B.C. D.7. 过点P向线段AB所在直线画垂线，正确的是( )A. B.C. D.8. 在下面各图中，∠1与∠2是对顶角的是( )A. B.C. D.9. 如图，下列说法错误的是( )A. ∠A与∠EDC是同位角B. ∠A与∠ABF是内错角C. ∠A与∠ADC是同旁内角D. ∠A与∠C是同旁内角10. 如图，点O在直线AB上，射线OC平分∠DOB．若∠COB=35∘，则∠AOD等于( )A. 35∘B. 70∘C. 110∘D. 145∘二、填空题（共6小题；共18分）11. 当光线从空气射入水中，光的传播方向发生了改变，这就是折射现象（如图）．图中∠1与∠2是对顶角吗? （填“是”或“不是”）．12. 如图，过直线AB上一点O作射线OC，∠BOC=29∘18ʹ，则∠AOC的度数为．13. 如图，∠C与是一对内错角．14. 如图，AB与CD相交所成的四个角中，∠1的邻补角是，∠1的对顶角是．15. 如图，AH⊥BC，垂足为H．若AB=1.7cm，AC=2cm，AH=1.1cm，则点A到点B的距离是，点A到直线BC的距离是．16. 探究题：（1）如图1，两条水平的直线被一条竖直的直线所截，同位角有对，内错角有对，同旁内角有对；（2）如图2，三条水平的直线被一条竖直的直线所截，同位角有对，内错角有对，同旁内角有对；（3）根据以上探究的结果，n（n为大于1的整数）条水平直线被一条竖直直线所截，同位角有对，内错角有对，同旁内角有对．（用含n的式子表示）三、解答题（共6小题；共52分）17. 如图所示，一辆汽车在直线形的公路AB上由A向B行驶，M，N分别是位于公路AB两侧的村庄，设汽车行驶到P点位置时，离村庄M最近，行驶到Q点位置时，离村庄N最近，请你在AB上分别画出P，Q两点的位置．18. 如图，直线AB，CD相交于点O，OE把∠BOD分成两部分．（1）直接写出图中∠AOC的对顶角为，∠BOE的邻补角为；（2）若∠AOC=70∘，且∠BOE:∠EOD=2:3，求∠AOE的度数．19. 如图，直线AB，CD相交于点O，EO⊥AB，垂足为O．（1）若∠EOC=35∘，求∠EOD的度数；（2）若∠AOC+∠BOD=100∘，求∠EOD的度数．20. 直线AB和CD相交于一点O，OE，OF分别是∠AOC和∠BOD的平分线．（1）画出这个图形；（2）射线OE，OF在同一条直线上吗?（3）画∠AOD的平分线OG，OE与OG有什么位置关系?说明理由．21. 请回答下列问题：（1）指出下列各图中的∠1与∠2是同位角、内错角还是同旁内角．（2）请你归纳：辨认同位角、内错角、同旁内角的方法可以是什么?22. 已知OA⊥OB，OE平分∠AOB，过点O引射线OC，OF平分∠BOC．（1）如图1，若∠AOC=60∘，则∠EOF=；（2）如图2，若∠AOC=a(0∘<a<90∘)，则∠EOF=（用含a的式子表示）；（3）如图3，当∠AOC在∠AOB的外部时，若∠AOC=a(0∘<a<90∘)，∠EOF与a有何数量关系?试说明理由．答案第一部分1. B2. B3. C4. B5. D6. B7. C8. B9. D10. C第二部分11. 不是．12. 150∘42ʹ【解析】∵∠BOC=29∘18ʹ，∴∠AOC的度数为：180∘−29∘18ʹ=150∘42ʹ．13. ∠EBC14. ∠2和∠4，∠315. 1.7cm，1.1cm16. 4，2，2，12，6，6，2n(n−1)，n(n−1)，n(n−1)第三部分17.18. （1）∠BOD；∠AOE（2）因为∠DOB=∠AOC=70∘，∠DOB=∠BOE+∠EOD，∠BOE:∠EOD=2:3，∠BOE，所以得∠EOD=32∠BOE=70∘，所以∠BOE+32所以∠BOE=28∘，所以∠AOE=180∘−∠BOE=152∘．19. （1）∵∠COD是平角，∴∠COD=180∘．∵∠COE=35∘，∴∠EOD=180∘−∠COE=145∘．（2）∵∠AOC+∠BOD=100∘，又∠AOC=∠BOD，∴∠BOD=50∘．∵OE⊥AB，∴∠EOB=90∘，∴∠EOD=∠EOB+∠BOD=140∘．20. （1）（2）射线OE，OF在同一条直线上．∵直线AB和CD相交于一点O，∴∠AOC=∠BOD .∵OE，OF分别是∠AOC和∠BOD的平分线，∴∠AOE=∠COE，∠DOF=∠BOF .∴∠AOE=∠BOF .∴射线OE，OF在同一条直线上．（3）OE⊥OG .∵直线AB和CD相交于一点O，∴∠AOC+∠AOD=180∘ .∵OE，OG分别是∠AOC和∠AOD的平分线，∴∠AOE=12∠AOC，∠AOG=12∠AOD .∴∠EOG=12(∠AOC+∠AOD)=90∘ .【解析】提示：说明∠EOG=90∘或∠FOG=90∘．21. （1）①内错角②同旁内角③同位角④同位角（2）在截线的同旁找同位角和同旁内角，在截线的不同旁找内错角，因此在“三线八角”的图形中主线是截线，抓住了截线，再利用图形结构特征（F形为同位角，Z形为内错角，U形为同旁内角）判断．22. （1）30∘（2）12a（3）∠EOF=12a．。

人教版七年级数学下册《5.1相交线》同步练习(含答案)

人教版七年级数学下册第五章相交线与平行线 5.1 相交线同步练习一、单选题（共10题；共30分）1.如图所示，∠1和∠2是对顶角的图形有( )A. 1个B. 2个C. 3个D. 4个2.如图，下列说法不正确的是（）A. ∠1和∠2是同旁内角B. ∠1和∠3是对顶角C. ∠3和∠4是同位角D. ∠1和∠4是内错角3.如图所示，∠1和∠2是对顶角的是（）A. B. C. D.4.下列说法中正确的个数为（）①两条直线相交成四个角，如果有两个角相等，那么这两条直线垂直；②两条直线相交成四个角，如果有一个角是直角，那么这两条直线垂直；③一条直线的垂线可以画无数条；④在同一平面内，经过一个已知点能画一条且只能画一条直线和已知直线垂直．A. 1B. 2C. 3D. 45.如图，∠1=15°，∠AOC=90°，点B，O，D在同一直线上，则∠2的度数为（）A. 75°B. 15°C. 105°D. 165°6.如图所示，下列说法错误的是（）A. ∠A和∠B是同旁内角B. ∠A和∠3是内错角C. ∠1和∠3是内错角D. ∠C和∠3是同位角7.如图，三条直线相交于点O．若CO⊥AB，∠1=56°，则∠2等于（）A. 30°B. 34°C. 45°D. 56°8.在下列语句中，正确的是（）．A. 在平面上，一条直线只有一条垂线;B. 过直线上一点的直线只有一条;C. 过直线上一点且垂直于这条直线的直线有且只有一条;D. 垂线段就是点到直线的距离9.如图，下列6种说法：①∠1与∠4是内错角；②∠1与∠2是同位角；③∠2与∠4是内错角；④∠4与∠5是同旁内角；⑤∠2与∠4是同位角；⑥∠2与∠5是内错角．其中正确的有( )A. 1个B. 2个C. 3个D. 4个10.如图所示，OA⊥OC，OB⊥OD，下面结论中，其中说法正确的是（）①∠AOB＝∠COD；②∠AOB＋∠COD＝90°；③∠BOC＋∠AOD＝180°；④∠AOC－∠COD＝∠BOC.A. ①②③B. ①②④C. ①③④D. ②③④二、填空题（共10题；共30分）11.如图，直线AB，CD相交于点O，EO⊥AB，垂足为点O，若∠AOD=132°，则∠EOC=________12.如图，已知直线AB与CD相交于点O，OA平分∠COE，若∠DOE=70°，则∠BOD=________．13.如图，∠1和∠2是________角，∠2和∠3 是________角。

人教版数学七年级下册《5.1相交线》同步练习(含答案)

第1页共7页七年级（下）《相交线》同步测试考试范围：第五章第一节《相交线》；考试时间：100分钟；命题人：王通学校：姓名：班级：考号：一、选择题被直线所截，那么的同位角是( )A. B. C. D.2. 已知和是对顶角，若，则的度数为( )A. B. C. D.3. 如图，直线AB ，CD 相交于点O ，且，则 ( )A. B. C. D.4. 如图，，，，，则图中其长度能表示点到直线的距离的线段有( )A. 4条B. 6条C. 7条D. 8条5. 如图，直线与相交于点O ，，若，则等于( )A. B. C. D.6. 如图，在所标识的角中，互为同位角的两个角是( )A. 和B. 和C. 和D. 和7. 有下列说法:①两条直线互相垂直,则所成的任意相邻两角均相等;②同一平面内,一条直线不可能与两条相交直线都垂直;③两条直线相交所成的四个角中,如果有三个角相等,那么这两条直线互相垂直;④直线外一点与直线上的一点间的线段的长度是这一点到这条直线的距离.其中正确的有()A. 1个B. 2个C. 3个D. 4个8. 在下列各图形中，线段PQ的长表示点P到直线MN的距离的是( )A. B.C. D.二、填空题CD相交于点O，，若，则的度数是________.第3页共7页10. 如图，中，，，则点到的距离是线段________的长度，点到的距离是线段________的长度，点到的距离是线段________的长度.11. 如图，，则 ________°， ________°.12.如图所示,AC ⊥BC ,C 为垂足,CD ⊥AB ,D 为垂足,BC =8,CD =4.8,BD =6.4,AD =3.6,AC =6,那么点C 到AB的距离是,点A 到BC 的距离是 ,点B 到CD 的距离是 ,A ,B 两点间的距离是 .13. 如图，两条直线相交只有1个交点，.三条直线相交最多有3个交点，四条直线相交最多有6个交点，……，二十条直线相交最多有________个交点.…两条直线三条直线四条直线 14. 将两块相同的直角三角尺的直角顶点重合为如图所示的位置,若∠AOD =120°,则∠BOC = .三、解答题15. 如图，直线,相交于点，平分，，，求的度数.16. 如图，当光线从空气中射入水中时，光线的传播方向会发生变化，在物理学中这种现象叫做光的折射，在图中，，问光的传播方向改变了多少度？17. 如图所示的是明明自制的对顶角“小仪器”示意图.先将直角三角尺的边固定且延长；再将另一直角三角尺的直角顶点与前一个三角尺的直角顶点重合；最后延长，与就是一对对顶角.已知，则的度数是多少？18. 如图，两直线AB，CD相交于点O，已知OE平分，且.(1)求的度数；(2)若，求的度数.第5页共7页19. 如图，直线AB 与CD 相交于点O ，， .(1)图中的余角有________.(把符合条件的角都填出来)(2)图中除直角相等外，还有相等的角，请写出三对：①________，②________，③________.(3)(i)如果，那么根据________可得 ________；(ii)如果，求的度数.20. 如图,直线AB ,CD 相交于点O ,过O 点画射线OE ,OF ,使OE ⊥CD ,OD 平分∠BOF .如果∠BOE =50°,求∠AOC ,∠EOF 和∠AOF 的度数.四、作图题的的垂线.22. 如图所示.(1)过点A 作射线CB 的垂线l ;(2)过点A 作线段AC 的垂线m.参考答案1--8 AADD BCCA9.10. ；；11. 60；12012. 4.8;6;6.4;1013. 19014. 60°15. 根据对顶角的性质，得.因为平分，所以，所以可得.16. 根据对顶角的性质，得，则，所以光的传播方向改变了.17. 因为，所以.又因为，所以可得.18.(1) 因为两直线AB，CD相交于点O，，所以.所以.又因为OE平分，所以.(2) 因为，，所以，所以.19.(1) 的余角有，，.(2) 答案不唯一，如，，(提示：同角的余角相等).(3) (i)对顶角相等；.(ii)因为，，且，所以，所以.20. 因为OE⊥CD,所以∠DOE=90°.因为∠BOE=50°,所以∠AOC=180°-90°-50°=40°.因为∠AOC和∠BOD是对顶角,所以∠BOD=40°,因为OD平分∠BOF,所以∠DOF=∠BOD =40°.所以∠EOF=∠EOD+∠DOF=90°+40°=130°,∠AOF=∠AOB-∠BOF=180°-2×40°=100°.21. 所画垂线如图所示.22.(1) 如图所示,直线l即为所求;(2) 如图所示,直线m即为所求.第7页共7页。

人教版数学七年级下册5.1相交线同步练习【含答案】

人教版七年级数学下册同步练习附答案5.1相交线第2课时

人教版七下数学 5.1 订交线第 2 课时一、选择题（共 3 小题；共9 分）1. 过点画线段所在直线的垂线段，此中正确的选项是A. B.C. D.2. 如图，，若，则的度数是A. B. C. D.3.如图，，，，则等于A. B. C. D.二、填空题（共10 小题；共38 分）4. 如图，直线，订交于点，若，则．6.点到直线的距离是指．7.如图，直线与订交于点．（）若，则；（）若于点，则．8. 如图，直线，订交于点，，垂足是点，，则．9. 已知两条直线订交，有一组邻补角相等，则这两条直线的地点关系是．10. 如图，想在河的两岸搭建一座桥，搭建方式最短的是（用字母表示）．11. 如图，立定跳远竞赛时，小明从点起跳落在沙坑内点处，跳远成绩是米，则小明从起跳点到落脚点的距离米．（填“大于”“小于”或“等于”）12. 如图，，垂足为，，，，那么点到的距离是；点到的距离是；，两点间的距离是．13. 同一平面内，与的两边相互垂直，比的倍少，则的度数为．三、解答题（共 5 小题；共53 分）14. 如图，过点，分别画，的垂线．15. 如图，火车站，码头分别位于，两点，直线和分别表示河流与铁路．（）从火车站到码头如何走近来，绘图并说明原因；（）从码头到铁路如何走近来，绘图并说明原因；（）从火车站到河流如何走近来，绘图并说明原因．16. 如图，两直线，订交于点，均分，．（ 1）求的度数；（ 2）若，求的度数，17. 如图，直线，订交于点，，均分．（ 1）判断与的地点关系；并说明原因；（ 2）若，求的度数．18. 如图，直线，交于点，，均分．（ 1）若，求的度数；（ 2）求的值．答案第一部分1. D2. B3. A第二部分4.5.6.直线外一点到这条直线的垂线段的长度7.，，，8.9.相互垂直10.11.大于12.，，13.或第三部分14. 画线段或射线的垂线，就是画这条线段或射线所在直线的垂线，此题中的垂足分别在的反向延伸线上和的延伸线上．15.如图，（）沿走，两点之间线段最短；（）沿走，垂线段最短；（）沿走，垂线段最短．16. （ 1）易求，，又由于均分，因此，因此．（2）由于，因此，因此，因此．17. （ 1），即．．（2）设，．，．．又，．18.（1）；（2）设，则，，．。

2019-2020年人教版七年级数学下册 5.1 相交线同步训练(解析版)

2019-2020学年人教版七年级数学下册5.1 相交线同步训练一．选择题（共8小题）1．平面上4条直线两两相交，交点的个数是（）A．1个或4个B．3个或4个C．1个、4个或6个D．1个、3个、4个或6个2．如图，直线a，b相交于点O，若∠1等于30°，则∠2等于（）A．60°B．70°C．150°D．170°3．下列各图中，∠1＝∠2一定成立的是（）A．B．C．D．4．如图，OA⊥OB，若∠1＝55°30′，则∠2的度数是（）A．34°B．34°30′C．35°D．35°30′5．能解释：“用两个钉子就可以把木条固定在墙上”，这实际问题的数学知识是（）A．两点之间线段最短B．两点确定一条直线C．垂线段最短D．在同一平面内，过一点有且只有一条直线与已知直线垂直6．若直线l上一点P和直线l外一点Q的距离为8cm，则点Q到直线l的距离是（）A．等于8cm B．小于或等于8cmC．大于8cm D．以上三种都有可能7．如图，下列说法正确的是（）A．∠A与∠B是同旁内角B．∠1与∠2是对顶角C．∠2与∠A是内错角D．∠2与∠3是同位角8．如图，与∠B互为同旁内角的角有（）个A．2B．3C．4D．5二．填空题（共6小题）9．观察图形，并阅读相关的文字，回答：如有9条直线相交，最多有交点．10．如图，直线AB、CD相交于点O，OE平分∠BOD；OF平分∠COE，若∠AOC＝82°，则∠BOF ＝°．11．如图，已知直线AB和CD相交于点O，射线OE在∠COB内部，OE⊥OC，OF平分∠AOE，若∠BOD＝40°，则∠COF＝度．12．如图所示，想在河的两岸搭建一座桥，搭建方式最短的是（用字母表示）．13．如图，AH⊥BC，若AB＝3cm、AC＝4.5cm、AH＝2cm，则点A到直线BC的距离为．14．如图，图中，∠B的同旁内角除了∠A还有．三．解答题（共4小题）15．如图，直线AB，CD相交于点O，OA平分∠EOC；（1）请你数一数，图中有个小于平角的角；（2）若∠EOC＝80°，求∠BOD的度数．16．如图，直线AB与CD相交于点O，OE是∠COB的平分线，OE⊥OF．（1）图中∠BOE的补角是；（2）若∠COF＝2∠COE，求∠BOE的度数；（3）试判断OF是否平分∠AOC，并说明理由；请说明理由．17．如图，AB、CD、NE相交于点O，OM平分∠BOD，∠MON＝90°，∠AOC＝50°（1）线段的长度表示点M到NE的距离；（2）比较MN与MO的大小（用“＜”号连接）：，并说明理由：；（3）求∠AON的度数．18．如图所示，把一根筷子一端放在水里，一端露出水面，筷子变弯了，它真的弯了吗？其实没有，这是光的折射现象，光从空气中射入水中，光的传播方向发生了改变．（1）请指出与∠1是同旁内角的有哪些角？请指出与∠2是内错角的有哪些角？（2）若∠1＝115°，测得∠BOM＝145°，从水面上看斜插入水中的筷子，水下部分向上折弯了多少度？请说明理由．2019-2020学年人教版七年级数学下册5.1 相交线同步训练参考答案与试题解析一．选择题（共8小题）1．平面上4条直线两两相交，交点的个数是（）A．1个或4个B．3个或4个C．1个、4个或6个D．1个、3个、4个或6个【分析】4条直线相交，有3种位置关系，画出图形，进行解答．【解答】解：若4条直线相交，其位置关系有3种，如图所示：则交点的个数有1个，或4个，或6个．故选：C．【点评】本题主要考查了直线相交时交点的情况，关键是画出图形．2．如图，直线a，b相交于点O，若∠1等于30°，则∠2等于（）A．60°B．70°C．150°D．170°【分析】因∠1和∠2是邻补角，且∠1＝30°，由邻补角的定义可得∠2＝180°﹣∠1＝180°﹣30°＝150°．【解答】解：∵∠1+∠2＝180°，且∠1＝30°，∴∠2＝150°．故选：C．【点评】此题主要考查了对顶角和邻补角的特征和应用，要熟练掌握，解答此题的关键是要明确：①有一个公共顶点，并且一个角的两边分别是另一个角的两边的反向延长线，具有这种位置关系的两个角，互为对顶角．②邻补角互补，即和为180°．3．下列各图中，∠1＝∠2一定成立的是（）A．B．C．D．【分析】根据对顶角相等，判断C组中的两个角是对顶角，前提均不是对顶角，而D只有两直线平行同位角相等，当两条直线不平行时，这两个不相等．【解答】解：根据对顶角相等可知，C选项是正确的，故选：C．【点评】考查对顶角的意义及性质，正确判断对顶角是判断的关键．4．如图，OA⊥OB，若∠1＝55°30′，则∠2的度数是（）A．34°B．34°30′C．35°D．35°30′【分析】由图象可知，∠1与∠2互余，根据∠1的度数，可求出∠2得度数，做出选择．【解答】解：∵OA⊥OB，∴∠AOB＝90°∵∠1＝55°30′，∴∠2＝90°﹣55°30′＝34°30′，故选：B．【点评】考查互相垂直、互为余角的意义以及角度的计算，掌握互余的意义是前提．5．能解释：“用两个钉子就可以把木条固定在墙上”，这实际问题的数学知识是（）A．两点之间线段最短B．两点确定一条直线C．垂线段最短D．在同一平面内，过一点有且只有一条直线与已知直线垂直【分析】根据直线的性质解答即可．【解答】解：用两个钉子就可以把木条固定在墙上”，这实际问题的数学知识是两点确定一条直线，故选：B．【点评】此题主要考查了直线的性质，关键是掌握两点确定一条直线．6．若直线l上一点P和直线l外一点Q的距离为8cm，则点Q到直线l的距离是（）A．等于8cm B．小于或等于8cmC．大于8cm D．以上三种都有可能【分析】根据点到直线的距离的定义与垂线段最短的性质，易得答案．【解答】解：根据题意，点P到l的距离为P到直线l的垂线段的长度，其垂足是P到直线l上所有点中距离最小的点；而不能明确PQ与l是否垂直，则点P到l的距离应小于等于PQ的长度，即不大于8cm．故选：B．【点评】本题考查了点到直线的距离，关键是根据点到直线的距离的定义及垂线段最短的性质解答．7．如图，下列说法正确的是（）A．∠A与∠B是同旁内角B．∠1与∠2是对顶角C．∠2与∠A是内错角D．∠2与∠3是同位角【分析】根据同位角、内错角以及同旁内角的定义进行解答．【解答】解：A、∠A与∠B是同旁内角，故说法正确；B、∠2与∠1是邻补角，故说法错误；C、∠A与∠2是同位角，故说法错误；D、∠2与∠3是内错角，故说法错误；故选：A．【点评】本题考查了同位角、内错角以及同旁内角的定义．同位角的边构成“F“形，内错角的边构成“Z“形，同旁内角的边构成“U”形．8．如图，与∠B互为同旁内角的角有（）个A．2B．3C．4D．5【分析】根据同旁内角的定义，结合图形进行寻找即可．【解答】解：与∠B互为同旁内角的角有∠AOB，∠BAO，∠BCD，∠BAD共4个．故选：C．【点评】此题考查了同旁内角的定义，属于基础题，关键是掌握互为同旁内角的两个角的位置特点．二．填空题（共6小题）9．观察图形，并阅读相关的文字，回答：如有9条直线相交，最多有交点36．【分析】根据题意，结合图形可猜想，n条直线相交，最多有1+2+3+…+（n﹣1）＝n（n﹣1）个交点．【解答】解：∵3条直线相交最多有3个交点，4条直线相交最多有6个交点，5条直线相交最多有10个交点，而3＝×2×3，6＝×3×4，10＝1+2+3+4＝×4×5，∴n条直线相交，最多有1+2+3+…+（n﹣1）＝n（n﹣1）个交点，∴当n＝9时，n（n﹣1）＝×8×9＝36．故答案为：36．【点评】此题主要考查了相交线，着重培养学生的观察、实验和猜想、归纳能力，掌握从特殊向一般猜想的方法．10．如图，直线AB、CD相交于点O，OE平分∠BOD；OF平分∠COE，若∠AOC＝82°，则∠BOF ＝28.5°．【分析】根据对顶角相等求得∠BOD的度数，然后根据角的平分线的定义求得∠EOD的度数，则∠COE即可求得，再根据角平分线的定义求得∠EOF，最后根据∠BOF＝∠EOF﹣∠BOF求解．【解答】解：∵∠BOD＝∠AOC＝82°，又∵OE平分∠BOD，∴∠DOE＝∠BOD＝×82°＝41°．∴∠COE＝180°﹣∠DOE＝180°﹣41°＝139°，∵OF平分∠COE，∴∠EOF＝∠COE＝×139°＝69.5°，∴∠BOF＝∠EOF﹣∠BOF＝69.5°﹣41°＝28.5°．故答案是：28.5．【点评】本题考查了角平分线的定义，以及对顶角的性质，理解角平分线的定义是关键．11．如图，已知直线AB和CD相交于点O，射线OE在∠COB内部，OE⊥OC，OF平分∠AOE，若∠BOD＝40°，则∠COF＝25度．【分析】根据对顶角相等的性质可得∠AOC＝∠BOD＝40°，根据垂直的定义可得∠COE＝90°，根据角的和差关系得出∠AOE的度数，再根据角平分线的定义求出∠AOF的度数，再根据角的和差关系计算即可．【解答】解：∠AOC＝∠BOD＝40°，∵OE⊥OC，∴∠COE＝90°，∴∠AOE＝∠AOC+∠COE＝130°，∵OF平分∠AOE，∴∠AOF＝，∴∠COF＝∠AOF﹣∠AOC＝65°﹣40°＝25°．故答案为：25【点评】此题主要考查了对顶角的性质，角平分线的性质以及垂直的定义，正确利用角平分线的性质分析是解题关键．12．如图所示，想在河的两岸搭建一座桥，搭建方式最短的是PM（用字母表示）．【分析】根据垂线段最短的性质填写即可．【解答】解：∵PM⊥MN，∴由垂线段最短可知PM是最短的，故答案为：PM．【点评】本题主要考查垂线段的性质，掌握垂线段最短是解题的关键．13．如图，AH⊥BC，若AB＝3cm、AC＝4.5cm、AH＝2cm，则点A到直线BC的距离为2cm．【分析】根据点到直线的距离的定义解答即可．【解答】解：点A到直线BC的距离是线段AH的长度，AH＝2，∴点A到直线BC的距离为2cm．故答案为：2cm【点评】此题考查点到直线的距离，关键是根据点到直线的距离的概念解答．14．如图，图中，∠B的同旁内角除了∠A还有∠ACB，∠ECB．【分析】直接利用同旁内角的定义化简得出答案．【解答】解：∠B的同旁内角除了∠A还有：∠ACB，∠ECB．故答案为：∠ACB，∠ECB．【点评】此题主要考查了同旁内角的定义，正确掌握定义是解题关键．三．解答题（共4小题）15．如图，直线AB，CD相交于点O，OA平分∠EOC；（1）请你数一数，图中有8个小于平角的角；（2）若∠EOC＝80°，求∠BOD的度数．【分析】（1）根据角的定义，平角的定义得到；（2）根据角平分线定义得到∠AOC＝∠EOC＝×80°＝40°，然后根据对顶角相等得到∠BOD＝∠AOC＝40°．【解答】解：（1）小于平角的角有：∠AOC，∠AOE，∠EOD，∠BOD，∠BOC，∠EOC，∠AOD，∠EOB，共有8个，故答案为：8；（2）∵OA平分∠EOC，∴∠AOC＝∠EOC＝×80°＝40°，∴∠BOD＝∠AOC＝40°．【点评】考查了角的计算，角平分线的定义和对顶角的性质．解题的关键是明确角平分线的定义和对顶角的性质，1直角＝90°；1平角＝180°．16．如图，直线AB与CD相交于点O，OE是∠COB的平分线，OE⊥OF．（1）图中∠BOE的补角是∠AOE；（2）若∠COF＝2∠COE，求∠BOE的度数；（3）试判断OF是否平分∠AOC，并说明理由；请说明理由．【分析】（1）根据平角的意义，依据图形可直接得出答案；（2）根据互余和∠COF＝2∠COE，可求出∠COF、∠COE，再根据角平分线的意义可求答案；（3）根据互余，互补、角平分线的意义，证明∠FOA＝∠COF即可．【解答】解：（1）∵∠AOE+∠BOE＝∠AOB＝180°，∴∠BOE的补角是∠AOE，故答案为：∠AOE；（2）∵OE⊥OF．∠COF＝2∠COE，∴∠COF＝×90°＝60°，∠COE＝×90°＝30°，∵OE是∠COB的平分线，∴∠BOE＝∠COE＝30°；（3）OF平分∠AOC，∵OE是∠COB的平分线，OE⊥OF．∴∠BOE＝∠COE，∠COE+∠COF＝90°，∵∠BOE+∠EOC+∠COF+∠FOA＝180°，∴∠COE+∠FOA＝90°，∴∠FOA＝∠COF，即，OF平分∠AOC．【点评】考查互为余角、互为补角、角平分线的意义，通过图形直观，得到各个角之间的关系式解决问题的关键．17．如图，AB、CD、NE相交于点O，OM平分∠BOD，∠MON＝90°，∠AOC＝50°（1）线段MO的长度表示点M到NE的距离；（2）比较MN与MO的大小（用“＜”号连接）：MO＜MN，并说明理由：垂线段最短；（3）求∠AON的度数．【分析】（1）根据点到直线的距离解答即可；（2）根据垂线段最短解答即可；（3）根据垂直的定义和角之间的关系解答即可．【解答】解：（1）线段MO的长度表示点M到NE的距离；（2）比较MN与MO的大小为：MO＜MN，是因为垂线段最短；（3）∵∠BOD＝∠AOC＝50°，OM平分∠BOD，∴∠BOM＝25°，∴∠AON＝180°﹣∠BOM﹣∠MON＝180°﹣25°﹣90°＝65°．故答案为：MO；MO＜MN；垂线段最短．【点评】本题考查的是点到直线的距离，掌握点到直线的距离是解题的关键18．如图所示，把一根筷子一端放在水里，一端露出水面，筷子变弯了，它真的弯了吗？其实没有，这是光的折射现象，光从空气中射入水中，光的传播方向发生了改变．（1）请指出与∠1是同旁内角的有哪些角？请指出与∠2是内错角的有哪些角？（2）若∠1＝115°，测得∠BOM＝145°，从水面上看斜插入水中的筷子，水下部分向上折弯了多少度？请说明理由．【分析】（1）根据同位角、内错角的定义（两条直线被第三条直线所截，处于两条直线的同旁，位于第三条直线的一侧的两个角叫同位角，处于两条直线之间，处于第三条直线两侧的两个角叫内错角）逐个判断即可．（2）根据平行线的性质解答即可．【解答】解：（1）与∠1是同旁内角的有∠AOE，∠MOE，∠ADE；与∠2是内错角的有∠MOE，∠AOE；（2）∵AB∥CD，∴∠BOE＝∠1＝115°，∵∠BOM＝145°，∴∠MOE＝∠BOM﹣∠BOE＝145°﹣115°＝30°，∴向上折弯了30°．【点评】本题考查了对同位角定义，内错角定义的应用，主要考查学生的理解能力，题目是一道比较好的题目，难度适中．。

人教版七年级数学下册《511相交线》同步测试含答案初一数学考点要点试卷.docx

5.1.1 相交线姓名年级分数B有公共顶点且互补的两个角D有公共顶点且有一条公共边，另一边互为反向延长3•如图，直线AB与CD相交于点O ,若ZAOC+ZBOD=90° ,则ZBOC ()5•如果一个角比它的邻补角小30°,则这个角的度数为______ ° o6.如图，AB交CD于O点，OE是端点为O的一条射线，图中的对顶角有____ 对邻补角各有______ 对一、选择题1 •如图所示，Z1和Z2是对顶角的图形冇(A 135°B 120°C 100°D 145°4题图训是-----A和为180°的两个角C有一条公共边相等的两个角线的两个角ZAOC=80° , Zl=30°,求Z2 的度数 )&如图，直线AB、CD相交于点O,解：因为ZDOB=Z ______ ((己知)所以，ZDOB二__ ° (等量代换)=80°又因为ZI=30°( )所以Z2=Z ___ - Z _____ = ______ - ______ =____ °三、解答题：9.如图，直线AB, CD相交于点O , OE平分ZBOD, OF平分ZCOE, ZAOD： ZAOF的度数。

ZBOE=4:L 求F10.如图所示是某城市古建筑群中一座古塔底部的建筑平面图，请你利用学过的知识设计如何测量出古塔外墙底部的ZABC的大小的方案，并说明理由。

参考答案：1. A2.D3.A4.2 个ZACD ZB5.75°6. 2； 57.35°8. ZAOC,对顶角相等，ZAOC,8()° ,已知ZBOD, Z1, 80° , 30° , 50°9 解：由已知设ZAOD=4x° , ZBOE=x°VOE 平分ZBOD,・*. ZBOD=2ZBOE=2x°VZAOD+ZBOD=180°・\6x=180°x=30°・°・ ZBOE=30° ,・\ZAOD=120°ZBOD=60° ZCOE=150°VOF 平分ZCOE ・•・ ZEOF=- ZCOE=75°2・・・ Z BOF= ZEOF- ZBOE=450ZAOF=ZAOB-ZBOF=135°10.方法一：作AB的延长线，如图1所示，量出ZCBD的度数，ZABC=180° -ZCBD 方法二：作AB和CB的延长线，如图2所示，量I1IZDBE的度数，ZABC=ZDBE我的写字心得体会从小开始练习写字，几年来我认认真真地按老师的要求去练习写字。

人教版初一数学七年级下册第5章相交线与平行线5.1相交线同步训练题含答案

人教版初一数学七年级下册第5章相交线与平行线5．1相交线同步训练题含答案1. 以下说法正确的选项是( )A．垂线最短B．对顶角相等C．两点之间直线最短D．过一点有且只要一条直线垂直于直线2. 如图，直线AB，CD相交于点O，假定∠1＋∠2＝100°，那么∠BOC等于( )A．130° B．140° C．150° D．160°3. 如图，能表示点到直线的距离的线段共有( )A．2条 B．3条 C．4条 D．5条4. 如图，直线a，b被直线c所截，那么以下说法中错误的选项是( ) A．∠1与∠2是邻补角 B．∠1与∠3是对顶角C．∠2与∠4是同位角 D．∠3与∠4是内错角5. 如图，直线AB，CD相交于点O，以下条件中，不能说明AB⊥CD的是( ) A．∠AOD＝90° B．∠AOC＝∠BOCC．∠BOC＋∠BOD＝180° D．∠AOC＋∠BOD＝180°6. 如图，∠F的内错角有_____________．7. 如下图，AB交CD于点O，∠AOC＝60°，那么∠AOD的度数为_______．8. 如图，直线l1，l2被直线l3所截，那么图中同位角有_____对．9. 图所示，一个破损的扇形零件，应用图中的量角器可以量出这个扇形零件的圆心角的度数，测量的依据是_________．10. 如图，要把小河里的水引到田地A处，那么作AB⊥l，垂足为点B，沿AB 挖水沟，水沟最短，理由是______________．11. 如图，直线AB，CD相交于点O，OE平分∠BOC，∠COE＝65°，那么∠BOD ＝________°.12. 两条直线都与第三条直线相交，∠1和∠2是内错角，∠3和∠2是邻补角．(1)依据上述条件，画出契合题意的图形；(2)假定∠1∶∠2∶∠3＝1∶2∶3，求∠1，∠2，∠3的度数．13. 如图，直线AB，CD相交于点O，过点O作两条射线OM，ON，且∠AOM＝∠CON＝90°.(1)假定OC平分∠AOM，求∠AOD的度数；(2)假定∠1＝∠BOC，求∠AOC和∠MOD.参考答案：1---11 BADDC6. ∠AEF和∠ADF7. 120°8. 49. 对顶角相等10. 垂线段最短11. 5012. 解：(1)如图：(2)由∠1∶∠2∶∠3＝1∶2∶3，设∠1＝x°，∠2＝2x°，∠3＝3x°.由∠2与∠3是邻补角，得∠2＋∠3＝2x°＋3x°＝180°，解得x＝36，2x＝72，3x＝108.所以∠1＝36°，∠2＝72°，∠3＝108°.13. 解：(1)由于∠AOM＝∠CON＝90°，OC平分∠AOM，所以∠1＝∠AOC＝45°，所以∠AOD＝180°－∠AOC＝180°－45°＝135°.(2)由于∠AOM＝90°，所以∠BOM＝180°－90°＝90°.由于∠1＝∠BOC，所以∠1＝∠BOM＝30°，所以∠AOC＝90°－30°＝60°，∠MOD＝180°－30°＝150°.。

人教版初中数学七年级下册第五章第一节《5.1相交线》同步练习题(含答案)

人教版初中数学七年级下册第五章第一节《 5.1相交线》同步练习题（含答案）5.1《相交线》同步练习题、选择题（每小题只有一个正确答案） 1 •如图所示，/ 1与/2不是同位角的是（）A.2 .在同一平面内，下列说法中，错误的是 A. 过两点有且只有一条直线B. 过一点有无数条直线与已知直线平行C. 过直线外一点有且只有一条直线与已知直线平行D. 过一点有且只有一条直线与已知直线垂直3 .已知：0A 丄 0C , / AOB :/ AOC , 2 : 3,则/ BOC 的度数为（），A. 30 °B.60 °C. 150 °D.30。

或 150 °4.如图，点A 到线段BC 所在直线的距离是线段（）A. / 1和/ 3是同位角B. / 1和/ 5是同位角C. / 1和/ 2是同旁内角D. / 5和/6是内错角6 .两条直线相交所构成的四个角中：①有三个角都相等；②有一对对顶角互补；③有一个角是直角；④有一对邻补角相等.其中能判定这两条直线垂直的有（） A. 1个 B. 2个 C. 3个 D. 4个7 .平面上三条直线两两相交最多能构成对顶角的对数是（ A. 7 B. 6 C. 5 D. 4二、填空题8.如图，直线a 与b 相交于点 0,直线c 丄b ,且垂足为0,若/仁35 °,则/2= ______________D.A. AC 的长度B. AD 的长度C. AE 的长度5. 如图所示，下列说法错误的是（）D. AB 的长度9 .如图，计划把河水引到水池 A 中，先作AB 丄CD ，垂足为B ，然后沿AB 开渠，能使所开的渠道最短，这样设计的依据是 _______________10 .两条直线相交所成的四个角中，有两个角分别是(2x -10)°和(110-x) °，则 x= _________11 .如图，在平面内，两条直线 l i , 12相交于点0,对于平面内任意一点 M ，若p , q 分别是点M 到直线11，12的距离，则称(p, q)为点M 的距离坐标”.根据上述规定，距离坐标”是(2，1的点共有 _____________________ 个.三、解答题13 .如图，直线 AB, CD 相交于点 0, / BOE=90°，OF 平分/ AOD / COE=20°，求/ BOD 与/ DOF 的度数.BC D(1)/ 1和/ 3是直线被直线所截得的 (2)/ 1和/ 4是直线被直线所截得的 (3)/ B 和/2是直线被直线所截得的 (4)/ B 和/4是直线被直线所截得的12 .看图填空:人教版初中数学七年级下册第五章第一节《 5.1相交线》同步练习题（含答案）14 .在同一平面内三条直线交点有多少个？甲：同一平面三直线相交交点的个数为 0个，因为a , b ,c 如图（1）所示.乙：同一平面内三条直线交点个数只有 1个，因为a , b,c 交于同一点0,如图（2）所示.以上说法谁对谁错？为什么？15 .已知，如图，直线AB 和CD 相交于点 0, / C0E 是直角，0F 平分/ AOE, / COF=34°, 求/ A0C和/ BOD 的度数.16 .探究题：(I)(1) 三条直线相交，最少有____ 个交点；最多有 _____ 个交点，画出图形，并数出图形中的对顶角和邻补角的对数；(2) 四条直线相交，最少有____ 个交点；最多有 _______ 个交点，画出图形，并数出图形中的对顶角和邻补角的对数；(3) 依次类推，n条直线相交，最少有________ 个交点；最多有_______ 个交点，对顶角有对，邻补角有__________ 对.参考答案I. B2. B3. D4. B5. B6. D7. B8. 55°9•垂线段最短10. 40 或80II. 4,12. 解析：根据同旁内角、同位角及内错角的概念可得：(1) / 1和/3是直线AB、BC被直线AC所截得的同旁内角；(2) / 1和/ 4是直线AB, BC被直线AC所截得的同位角；(3) / B和/ 2是直线AB, AC被直线BC所截得的同位角；(4) / B和/4是直线AC, BC被直线AB所截得的内错角•13. / BOD=70°, / DOF=55°解：•••/ COE=20°,Z BOE=90°,•••/ BOD=180°, 20°, 90° =70°,•••/ AOD—180°, 70° =110°,•/ OF 平分/ AOD ,1• / DOF=-/AOD=55°,•••/ BOD=70°,Z DOF=55°.14. 甲，乙说法都不对，各自少了三种情况，具体见解析解析：甲、乙说法都不对，都少了三种情况.a// b,c与a,b相交如图(1);a,b,c两两相交如图(2),所以三条直线互不重合，交点有0个或1个或2个或3个，共四种情况15. / AOC=22 , / BOD=22 .解析：，，COE=90 , , COF=34 ,,,EOF= COE , COF=56°,,OF是，AOE的平分线,,,AOE=2, EOF=112°,,,AOC=112°, 90 ° =22 ° ,,,BOD和，AOC是对顶角，,,BOD=22°,16. (1)1,3,画图见解析，对顶角有6对，邻补角有12对;(2)1,6, 画图见解析，对顶角有12对,邻补角有24对;(3)1, n n 1,n(n —1),2 n(n —1).2分析：当直线同交于一点时，只有一个交点；当直线两两相交，且不过同一点时，交点个数2最多；根据对顶角与邻补角的定义找出即可.;1三条直线相交，最少有 1个交点，最多有3个交点，如图:对顶角：6对，邻补角：12对；；2四条直线相交，最少有 1个交点，最多有6个交点，如图:对顶角：12对，邻补角：24对；n n 1(3) n 条直线相交，最少有 1个交点，最多有个交点，对顶角有 n (n - 1)对,2邻补角有2n (n - 1)对. 丄,“宀,n n 1故答案为：(1) 1, 3 ； (2) 1, 6； (3) 1, , n ( n- 1), 2n (n - 1).2。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第五章相交线与平行线5．1相交线5.1.1相交线关键问答①邻补角的特征是什么？②对顶角的特征是什么？③在两直线相交的图中，常用的求角的推理依据是什么？1．①下列选项中，∠1与∠2是邻补角的是()5－1－12．②下列图形中，∠1与∠2是对顶角的是()5－1－23．③如图5－1－3，直线AB与CD相交于点O，∠AOC∶∠AOD＝1∶2.求∠BOD的度数．图5－1－3命题点1邻补角的识别与计算[热度：86%]4．④如图5－1－4所示，∠1的邻补角是()A．∠BOC B．∠BOE或∠AOFC．∠AOF D．∠BOE或∠AOF或∠DOF＋∠BOC易错警示④邻补角是有一定位置关系和数量关系的两个角．5．⑤下列说法正确的是()A．直角没有邻补角B．互补的两个角一定是邻补角C．一个角的邻补角大于这个角D．一个角的邻补角可能是锐角、钝角或直角易错警示⑤互为邻补角的两个角一定互补，而互补的两个角不一定是邻补角．6．⑥若∠AOB和∠BOC互为邻补角，且∠AOB比∠BOC大18°，则∠AOB的度数是() A．54°B．81°C．99°D．162°方法点拨⑥本题可以通过列一元一次方程解决．7.如图5－1－5，直线AB，CD相交于点O，若∠1＝27∠2，则∠2＝________°.命题点2对顶角的识别与计算[热度：88%]8.⑦如图5－1－6，直线AB，CD，EF2＋∠3的度数等于()A．90°B．150°C．180°D．210°解题突破⑦本题利用“对顶角相等”把三个角的和转化成一个平角．9．⑧如图5－1－7，直线AB，CD相交于点O，∠BOC＝2x°＋40°，则∠BOC＝________°.易错警示⑧解出x后，还需求2x＋40.10．图5－1－8．命题点3邻补角与对顶角的综合[热度：90%]11.⑨如图5－1－9，直线AB，CD相交于点O，OE是∠AOC的平分线，∠BOC＝130°，∠BOF＝140°，则∠EOF的度数为()A．95°B．65°C．50°D．40°解题突破⑨求∠EOF的度数可以转化成求两个角的和或差，再利用对顶角相等或邻补角互补进行求解.12．如图5－1－10，∠AOC和∠BOC互为邻补角，OD，OE分别是∠AOC，∠BOC的平分线，则∠DOE＝________°.13.⑩如图5－1－11，直线AB，CD相交于点O，作∠DOE＝∠BOD，OF平分∠AOE.若∠AOC＝28°，则∠EOF＝__________°.图5－1－11模型建立⑩互为邻补角的两个角的平分线的夹角是直角.14．如图5－1－12，直线AB，CD相交于点O，∠EOB＝90°，OC平分∠AOF，∠AOF＝40°，求∠EOD 的度数．15.⑪已知：如图5－1－13，直线AB，CD相交于点O，∠1＝40°，∠BOE与∠BOC互补，OM平分∠BOE，且∠CON∶∠NOM＝2∶3.求∠COM和∠NOE的度数．方法点拨⑪求角时，常用到：1．将未知角转化成两个已知角的和或差；2．对顶角相等或邻补角互补；3．等角(或同角)的余角(或补角)相等；4．角平分线的性质；5．有关比例问题常用方程解决.16．图5－1－14是某墙角的示意图，为了测量底面内角∠ABC的大小，采用了在院外画线，测量后得到其大小的方法．请你设计两种测量方案．17.⑫观察图5－1－15中的图形，寻找对顶角(不含平角)：(1)两条直线相交(如图①)，图中共有________对对顶角；(2)三条直线相交于一点(如图②)，图中共有________对对顶角；(3)四条直线相交于一点(如图③)，图中共有________对对顶角；(4)研究(1)～(3)小题中直线条数与对顶角的对数之间的关系，若有n条直线相交于一点，则可构成________对对顶角；(5)若有2019条直线相交于一点，则可构成________1－15解题突破⑫本题可通过平移的方法，把n条直线相交于一点构成的对顶角问题转化为n条直线相交最多有多少个交点的问题(即n条直线两两相交)．因为每个交点处有两对对顶角，所以对顶角的对数是交点个数的2倍.18.⑬两条直线相交，四个交角中的一个锐角或一个直角称为这两条直线的“夹角”(如图5－1－16)．现在平面上有若干条直线，它们两两相交并且“夹角”只能是30°，60°或90°，问：平面上最多有多少条直线？当直线条数最多时，所有的“夹角”的和是多少？解题突破⑬将若干条直线两两相交的图形先转化成若干条直线交于一点的图形，按“夹角”定义看能画出多少条直线.典题讲评与答案详析1．D 2.C3．解：由邻补角的性质，得∠AOC ＋∠AOD ＝180°.由∠AOC ∶∠AOD ＝1∶2，得∠AOD ＝2∠AOC ，∠AOC ＋2∠AOC ＝180°，解得∠AOC ＝60°.由对顶角相等，得∠BOD ＝∠AOC ＝60°.4．B [解析]∠1是直线AB ，EF 相交于点O 形成的角，所以它的邻补角与直线CD 无关，即它的邻补角是∠BOE 或∠AOF .5．D [解析] 把直角的一边反向延长，可得这个直角的邻补角．互补的两个角不一定是邻补角，但邻补角一定互补．若一个角是锐角，则它的邻补角是钝角且大于这个锐角；若一个角是直角，则它的邻补角等于它本身；若一个角是钝角，则它的邻补角是锐角且小于这个钝角．6．C [解析] 设∠AOB ＝x °，则∠BOC ＝180°－x °.又因为∠AOB 比∠BOC 大18°，所以∠AOB －∠BOC ＝18°，即x °－(180°－x °)＝18°，解得x ＝99.7．140 [解析] 由题意，得∠2＋27∠2＝180°，解得∠2＝140°.8．C [解析] 由对顶角相等，可知∠1＋∠2＋∠3正好是一个平角的度数．9．120 [解析] 由对顶角相等，可得2x ＋40＝3x ，解得x ＝40，所以∠BOC ＝120°. 10．对顶角相等11．B [解析] 因为∠BOF ＝140°，所以∠AOF ＝180°－140°＝40°. 因为∠BOC ＝130°，所以∠AOC ＝50°. 因为OE 是∠AOC 的平分线，所以∠AOE ＝∠EOC ＝25°，所以∠EOF ＝∠AOE ＋∠AOF ＝65°.12．90 [解析] 因为OD ，OE 分别是∠AOC ，∠BOC 的平分线，所以∠COD ＝12∠AOC ，∠COE ＝12∠BOC .因为∠BOC ＋∠AOC ＝180°，所以∠COE ＋∠COD ＝12(∠BOC ＋∠AOC )＝90°.13．62 [解析] 由∠AOE ＋∠BOE ＝180°，OF 平分∠AOE ，∠DOE ＝∠BOD ，可得∠DOF ＝∠COF ＝90°.又因为∠AOC ＝28°，所以∠BOD ＝∠DOE ＝∠AOC ＝28°，所以∠EOF ＝∠AOF ＝62°.14．解：因为OC 平分∠AOF ，∠AOF ＝40°，所以∠AOC ＝12∠AOF ＝20°，所以∠BOD ＝90°.因为∠EOB ＝90°，所以∠EOD ＝∠EOB －∠BOD ＝70°.6＝40°. 因为∠6＋∠BOC ＝180°，∠BOE 与∠BOC 互补，所以∠6＝∠BOE ＝40°，所以∠BOC ＝140°，所以∠COE ＝100°.因为OM 平分∠BOE ，所以∠2＝∠3＝20°，所以∠COM ＝120°.因为∠CON ∶∠NOM ＝2∶3，所以∠NOM ＝120°×35＝72°，所以∠NOE ＝72°－20°＝52°.16．解：方案一：如图①所示，延长AB ，量出∠CBD 的度数．由邻补角的定义，可得∠ABC ＝180°－∠CBD (也可延长CB )．方案二：如图②所示，分别延长AB ，CB ，量出∠DBE 的度数，由对顶角相等，可得∠ABC ＝∠DBE .17．(1)2 (2)6 (3)12 (4)n (n －1)[解析] 图①中有两条直线，共有2图，三条直线相交最多有3个交点，故共有6对对顶角；以此类推，图③中有四条直线相交，最多有3×42＝6(个)交点，故共有12对对顶角……n 条直线相交，最多有n （n －1）2个交点，故共有n (n －1)对对顶角．故若有2019条直线相交于一点，则可构成2019×2018＝4074342(对)对顶角．18．解：因为“夹角”只能是30°，60°或90°，其均为30°的倍数，所以每画一条直线后，逆时针旋转30°画下一条直线，这样就能够保证每两条直线的“夹角”为30°的倍数，即为30°，60°或90°.因为该平面上的直线两两相交，也就是说不会出现两条直线平行的情况，在画出6条直线时，直线旋转了5次，5×30°＝150°，若再画出第7条直线，则旋转6次，6×30°＝180°，这样第7条直线就与第1条直线平行或重合．如图：所以平面上最多有六条直线．第2条至第6条直线与第1条直线的“夹角”的和是30°＋60°＋90°＋60°＋30°＝270°，第3条至第6条直线与第2条直线的“夹角”的和是270°－30°＝240°；第4条至第6条直线与第3条直线的“夹角”的和是270°－30°－60°＝180°；第5条和第6条直线与第4条直线的“夹角”的和是60°＋30°＝90°；第6条直线与第5条直线的“夹角”的和是30°，则270°＋240°＋180°＋90°＋30°＝810°. 即当直线条数最多时，所有的“夹角”的和是810°. 【关键问答】①(1)有公共顶点；(2)其中一边为公共边，另一边互为反向延长线；(3)两个邻补角的和为180°. ②(1)有公共顶点；(2)角的两边分别互为反向延长线；(3)对顶角相等． ③(1)互为邻补角的两个角的和为180°；(2)对顶角相等．。

人教版七年级数学下册《511相交线》同步练习(有答案)MnqMnP