2019年12月06日四川省宜宾市高2020届高2017级一诊考试文科综合试题地理试题
2019年12月05日四川省宜宾市高2020届高2017级一诊考试理科综合试题语文试题参考答案

宜宾市普通高中2017级一诊语文试题参考答案1 D (A原文有限定语,“观看知识类短视频”;B项把原文中的“通常“替换为“都想”。
C. 因果倒置,是受众整体的文化水平以及生活格调的提高改变了以往的审美观念,并追求“美而不同”的新境界。
)2.C(C项“比喻论证”有误。
)3.B (B项“传统文化在互联网传播的快速性和跨时空性特质”是引发关注的客观因素。
)4 B (B项“5G的三大特性解决了人工智能的核心要素在实际运用中面临的困境”一句有误,原文只提及5G的三大特性解决了“数据”“算力”问题,未包括“算法”。
)5 C(原文说“5G网络已在全国主要城市城区实现连片覆盖”,而C项“大、中城市”的说法扩大了5G网络覆盖范围。
)6 (1)开启万物互联新时代,催生各领域各行业不断创新发展;(2)为中国社会发展带来生产方式与生产力的巨大革新;(3)人们日常生活将变得更加智能、高效与便捷;(3)支撑经济数字化网络化智能化发展,促进中国经济新增长;(4)实现与国际社会的合作交流,提升中国国际影响力;(5)带来网络安全等新风险。
(每点2分,答到三点满分)7 D(全文用的是倒叙的顺序,插叙应是文章中间内容的补充与解释)8、答案:①是女卫生兵们工作的责任与智慧的体现。
②是女兵与兵哥哥的真情所在。
③是高原士兵们崇高精神与坚守使命的情怀。
(以下答案也给分①女兵们把士兵们都当哥哥,避免了在医疗救护中的种种尴尬和羞涩。
②在没有亲人地地方,把所有的战士当哥哥,结成没有血缘胜似血缘的战友之情,在条件艰苦的高原成了最温暖的慰藉。
③把每一个士兵当哥哥当亲人,年轻的生命紧紧连在一起,共同保卫国家的边界,铸成最坚硬的共和国界碑。
)9.答案:①承接上文,是兵哥哥对“我”的话语的回答,蕴含着不言而喻的答案。
②是对曾经艰苦生活的总结和战友之情的怀念③深化主题,抒发士兵们戍守边陲保家卫国的自豪感。
10 C11 A(敕,中国古代帝王诏令文书的文种名称之一,不能用于“肱股之臣”。
2019-2020年高三第一次综合练习(一模)文科综合试题 含答案
2019-2020年高三第一次综合练习(一模)文科综合试题含答案第一部分(选择题,满分140分)本部分共35小题,每小题4分,共140分。
开普勒452b(Kepler 452b)位于距离地球1400光年的天鹅座,是迄今为止发现的首个围绕着与太阳同类型恒星旋转,且与地球大小相近的“宜居”行星。
回答第1题。
1.开普勒452bA.属于太阳系中的类地行星B.可能拥有大气层和液态水C.组成物质与地球类似D.自身可以发光发热下表为我国四个城市某月连续一周的天气预报。
回答2、32.此时段A. 锋面雨带正在自南向北移动B.寒潮的影响范围遍及四城市C.东部地区自北向南依次出现冷锋天气过程D.用于预报天气的卫星云图依靠GIS获取3.四城市的天气与相关诗句的描写最吻合的是A.北京周四的天气——忽如一夜春风来,千树万树梨花开B.杭州周一的天气——沾衣欲湿杏花雨,吹面不寒杨柳风C.广州周三的天气——黄梅时节家家雨,青草池塘处处蛙D.昆明周日的天气——接天莲叶无穷碧,映日荷花别样红图1中虚线表示北极地区7月份10℃等温线。
读图,回答4、5题。
4.图中10℃等温线A.以北地区的盛行风为西北风B.自西向东经过亚洲、欧洲、北美洲C.在甲地外凸主要受洋流影响D.在乙地附近经过板块消亡边界5.北极冰盖面积的变化会对环境产生较大影响。
若冰盖持续萎缩,北极地区A.太阳辐射强度将变大B.出现极昼的范围将变小C.陆地面积将扩大D.通航能力将提高韩国济州岛由120万年前的火山活动形成,是中国游客境外旅游的主要目的地之一。
图2为岛上旅游景点分布图;图3为南部海岸柱状节理带景观照片。
回答6、7题。
6.济州岛A.成为中国游客境外旅游主要目的地是受市场距离影响B.以古代艺术、风土民情等人文旅游资源为主C.旅游活动突出探险、购物特色D.自然环境特征与海南岛类似7.图3所示景观A.岩石中含有海洋生物化石B.形成受流水堆积作用影响C.适合在夏季选择特定位置观赏D.位置适合在冬季观看海上日出2016年3月9日—3月12日中国家电及消费电子博览会(AWE)在上海开幕,展示包括传统家电、视听、数码、通讯、智能家居等消费电子和智能应用产品。
四川省宜宾市高中2020届高三数学第一次诊断测试试题文(含解析)

四川省宜宾市高中2020届高三数学第一次诊断测试试题文(含解析)1.已知集合U={1,3,4,5,7,9},A={1,4,5},则∁U A=()A. {3,9}B. {7,9}C. {5,7,9}D. {3,7,9} 【答案】D【解析】【分析】利用补集的运算,直接求出A在U中的补集即可.【详解】解:因为集合U={1,3,4,5,7,9},A={1,4,5},A =.所以{3,7,9}U故选:D.【点睛】本题考查了补集的运算,属基础题.2.已知i是虚数单位,复数m+1+(2﹣m)i在复平面内对应的点在第二象限,则实数m的取值范围是()A. (﹣∞,﹣1)B. (﹣1,2)C.(2,+∞)D. (﹣∞,﹣1)∪(2,+∞)【答案】A 【解析】【分析】根据复数对应的点在第二象限,可得1020m m+⎧⎨-⎩<>,然后解不等式组得到m的取值范围. 【详解】解:因为复数m+1+(2﹣m)i在复平面内对应的点在第二象限, 所以1020m m+⎧⎨-⎩<>,解得m<﹣1. 所以实数m的取值范围为(﹣∞,﹣1). 故选:A. 【点睛】本题考查了复数的几何意义和一元一次不等式组的解法,属基础题. 3.已知向量a=()1m,,()2,1b=-且()a b b-⊥,则实数m=()A. 3B.12C. 12-D. ﹣3【答案】D 【解析】 【分析】根据平面向量的坐标运算和数量积运算法则,列出关于m 的方程,然后解方程求出m 的值. 【详解】解:由(1,),(2,1)a m b ==-,得(1,1)a b m -=-+, 因为()a b b -⊥,所以()0a b b -=, 所以121(1)0m -⨯-⨯+=,所以3m =-. 故选:D .【点睛】本题考查了平面向量的坐标运算和数量积,属基础题.4.某车间生产A ,B ,C 三种不同型号的产品,产量之比分别为5:k :3,为检验产品的质量,现用分层抽样的方法抽取一个容量为120的样本进行检验,已知B 种型号的产品共抽取了24件,则C 种型号的产品抽取的件数为( ) A. 12 B. 24C. 36D. 60【答案】C 【解析】 【分析】 根据题意可得2412053kk =++,解方程求出k 的值,再根据C 种型号的产品所占的比例,求出C 种型号的产品应抽取的数量.【详解】解:由题意,得2412053kk =++,所以k =2, 所以C 种型号的产品抽取的件数为1203523⨯=++36. 故选:C .【点睛】本题考查了分层抽样的定义和特点,属基础题. 5.要得到函数24y cos x π⎛⎫=+ ⎪⎝⎭的图象,只需要将函数y =cos x 的图象( ) A. 向左平行移动8π个单位长度,横坐标缩短为原来的12倍,纵坐标不变.B. 向左平行移动4π个单位长度,横坐标缩短为原来的12倍,纵坐标不变. C. 向右平行移动8π个单位长度,横坐标伸长为原来的2倍,纵坐标不变.D. 向右平行移动4π个单位长度,横坐标伸长为原来的2倍,纵坐标不变.【答案】B 【解析】 【分析】直接利用三角函数图象的平移和伸缩变换,得到由y =cosx 变换为24y cos x π⎛⎫=+⎪⎝⎭的方式. 【详解】解:要得到函数24y cos x π⎛⎫=+ ⎪⎝⎭的图象,只需要将函数y =cosx 的图象向左平移4π个单位, 得到y =cos (x 4π+),再把横坐标缩短为原来的12,纵坐标不变即可. 故选:B .【点睛】本题考查了三角函数图象的平移和伸缩变换,属基础题.6.设直线m ,n 是两条不同的直线,α,β是两个不同的平面,下列命题中正确的是( ) A. m ∥n ,m ∥α⇒n ∥α B. m ⊥n ,m ⊥α,n ⊥β⇒α⊥β C. m ∥α,m ∥β⇒α∥β D. α⊥β,m ∥α⇒m ⊥β【答案】B 【解析】 【分析】在A 中,n 与α平行或n ⊂α;在B 中,由线面垂直的性质定理得αβ⊥;在C 中,α与β相交或平行;在D 中,//m α,m αβ⊥⇒与β相交、平行或m β⊂. 【详解】解:因为m ,n 是两条不同的直线,α,β是两个不同的平面, 所以在A 中,m ∥n ,m ∥α⇒n ⊂α或n ∥α,故A 错误;在B 中,m ⊥n ,m ⊥α,n ⊥β,由线面垂直的性质定理得α⊥β,故B 正确; 在C 中,m ∥α,m ∥β⇒α与β相交或平行,故C 错误; 在D 中,m ∥α,α⊥β⇒m 与β相交、平行或m ⊂β,故D 错误. 故选:B .【点睛】本题考查了命题真假的判断和空间中线线、线面、面面间的位置关系,属基础题. 7.已知412ln33332e 3a b c ===,,,则( )A. b <c <aB. c <b <aC. c <a <bD. b <a <c【答案】A 【解析】 【分析】将,,a b c 都化为13x 的形式,根据幂函数的单调性判断出三者的大小关系. 【详解】依题意13111ln333316,3,9a b e c ====,而13y x =为R 上的增函数,故b c a <<.故选:A.【点睛】本小题主要考查指数运算,考查幂函数的单调性,考查指数幂比较大小,属于基础题.8.执行如图所示的程序框图,输出的k 值为( )A. 4B. 5C. 6D. 7【答案】B 【解析】执行程序框图,可知:第一次循环:2,2a k ==;第二次循环:4,3a k ==; 第三次循环:8,4a k ==;第四次循环:16,5a k ==, 此时满足判断条件,终止循环,输出5k =,故选B.9.函数f (x )1lnxx =+的图象大致是( )A. B. C. D.【答案】C 【解析】 【分析】求出f (x )的导函数,利用导数研究函数的单调性,然后结合图象得到答案.【详解】解:由f (x )1lnxx =+,得f ′(x )211(0)(1)lnx x x x +-=>+, 令g (x )=11lnx x +-,则g ′(x )22111xx x x+=--=-<0, 所以g (x )在(0,+∞)上单调递减,又g (e )1e=>0,g (e 2)2221111lne e e =+-=-<0, 所以存在x 0∈(e ,e 2),使得g (x 0)=0, 所以当x ∈(0,x 0)时,g (x )>0,f ′(x )>0; 当x ∈(x 0,+∞)时,g (x )<0,f ′(x )<0,所以f (x )在(0,x 0)上单调递增,在(x 0,+∞)上单调递减. 故选:C .【点睛】本题考查了利用导数研究函数的单调性和零点存在定理,属中档题.10.已知02πα⎛⎫∈ ⎪⎝⎭,,且3sin 2α﹣5cos 2α+sin2α=0,则sin2α+cos2α=( )A. 1B. 2317-C. 2317-或1 D. ﹣1【答案】A 【解析】【分析】利用同角三角函数基本关系式化弦为切,求出tan α,再求出α的值,进一步求出sin 2α+cos 2α.【详解】解:由3sin 2α﹣5cos 2α+sin 2α=0,得22223520sin cos sin cos sin cos αααααα-+=+, 所以2232501tan tan tan ααα+-=+,即3tan 2α+2tanα﹣5=0,解得tanα=1或tan 53α=-. 因为0,2πα⎛⎫∈ ⎪⎝⎭,所以tanα=1,所以4πα=,所以sin 2α+cos 2α=sin 2π+cos 12π=. 故选:A .【点睛】本题考查了三角函数的化简求值和同角三角函数基本关系式,考查了转化思想和计算能力,属基础题.11.如图,在Rt △ABC 中,2C π∠=,6B π∠=,AC =4,D 在AC 上且AD :DC =3:1,当∠AED最大时,△AED 的面积为( )A.32B. 2C. 3D. 33【答案】C 【解析】 【分析】根据条件得到AED AEC DEC ∠=∠-∠,然后设∠AED =θ,∠AEC =α,∠DEC =β,用两角差的正切公式求出tanθ,再用基本不等式求出tanθ最大值,从而得到当∠AED 最大时,△AED 的面积.【详解】解:因为AD :DC =3:1,所以DC 14=AC =1, 所以S △AED =S △ACE ﹣S △DEC 12=AC •CE 12-DC •EC12=AC •CE 12-•14AC •CE =AC •CE (113)288-=AC •EC . 因为AC =4,CE ≤CB ,而在Rt △ABC 中,,26C B ππ∠=∠=,AC =4,所以CB =AED =∠AEC ﹣∠DEC . 设∠AED =θ,∠AEC =α,∠DEC =β,则tanθ=tan (α﹣β)()211AC DCAC DC EC tan tan EC EC AC DC tan tan EC AC DCEC ECαβαβ--⋅-===-⋅+⋅+⋅2333444EC EC EC EC ==≤=++,当且仅当EC 4EC=,即EC =2时,取等号, 所以tanθ的最大值为34,此时∠AED 最大, 所以当∠AED 最大时,△AED 的面积AEDS =38•4•2=3. 故选:C .【点睛】本题考查了三角形的面积公式和利用基本不等式求最值,考查了转化思想和计算能力,属中档题.12.已知函数f (x )=4alnx ﹣3x ,且不等式f (x +1)≥4ax ﹣3e x ,在(0,+∞)上恒成立,则实数a 的取值范围( ) A. 34⎛⎫-∞ ⎪⎝⎭, B. 34⎛⎤-∞ ⎥⎝⎦,C. (﹣∞,0)D. (﹣∞,0] 【答案】B 【解析】 【分析】不等式f (x +1)≥4ax ﹣3e x ,在(0,+∞)上恒成立等价于(1)()x f x f e +>在(0,)+∞上恒成立,然后利用函数f (x )单调性进一步求出a 的范围.【详解】解:f (e x )=4ax ﹣3e x ,所以f (x +1)≥4ax ﹣3e x 在(0,+∞)上恒成立,等价于f (x +1)≥f (e x)在(0,+∞)上恒成立,因为x ∈(0,+∞)时,1<x +1<e x,所以f (x )在(1,+∞)上递减, 所以当x >1时,f ′(x )≤0恒成立,即x >1时,430ax-≤恒成立, 所以a 34≤x ,所以a 34≤, 所以a 的取值范围为3,4∞⎛⎤- ⎥⎝⎦. 故选:B .【点睛】本题考查了函数恒成立问题和利用函数的单调性求参数范围,考查了转化思想和计算能力,属中档题.13.书架上有6本不同的数学书,4本不同的英语书,从中任意取出1本,取出的书恰好是数学书的概率是_____. 【答案】35【解析】 【分析】先算出“任意取出1本书”的基本事件总数,再算出事件“取出的书恰好是数学书”包含的基本事件个数,然后利用概率公式求出概率.【详解】解:从6本不同的数学书,4本不同的英语书中任意取出1本的基本事件总数为10, 取出的书恰好是数学书包含的基本事件个数为6, 则取出的书恰好是数学书的概率P =63105=, 故答案为:35. 【点睛】本题考查了古典概型的概率计算,关键属熟悉古典概型的概率计算步骤,属基础题. 14.已知函数f (x )=2x 3﹣ax 2+2在x =2处取得极值,则实数a =_____. 【答案】6 【解析】 【分析】先求出()f x ',再根据2x =是()f x 的一个极值点,得到f '(2)0=,然后求出a 的值.【详解】解:由f (x )=2x 3﹣ax 2+2,得f '(x )=6x 2﹣2ax . 因为在x =2处取得极值,所以f '(2)=24﹣4a =0,所以a =6.经检验a =6时x =2是f (x )的一个极值点,所以a =6. 故答案为:6.【点睛】本题考查了函数极值点的定义,考查了方程思想,属基础题.15.若△ABC 的内角A 、B 、C 的对边分别为a 、b 、c ,其面积为S ,484b BA AC S =⋅==,,,则a =_____.【答案】【解析】 【分析】根据8BA AC =,b =4得到cos 2c A =-①,再根据4S =得到sin 2c A =②,联立①②解出A 和c ,然后在△ABC 中利用余弦定理求出a .【详解】解:因为8BA AC ⋅=,4b =,所以48AB AC bccosA ccosA ⋅===-,所以ccosA =﹣2①. 因为1442S csinA ==,所以csinA =2②.联立①②,得tanA =﹣1,所以34A π=,所以cosA =,所以2c cosA =-=,在△ABC 中,由余弦定理,得2222168402a b c bccosA ⎛⎫=+-=+--= ⎪ ⎪⎝⎭,所以a =故答案:【点睛】本题考查了平面向量的数量积、三角形的面积公式和余弦定理,考查了方程思想和计算能力,属基础题.16.同学们有如下解题经验:在某些数列求和中,可把其中一项分裂为两项之差,使某些项可以抵消,从而实现化简求和.如:已知数列{a n }的通项()11n a n n =+,则将其通项化为111n a n n =-+,故数列{a n }的前n 项的和11111111223111n n S n n n n ⎛⎫⎛⎫⎛⎫=-+-++-=-= ⎪ ⎪ ⎪+++⎝⎭⎝⎭⎝⎭.斐波那契数列是数学史上一个著名数列,在斐波那契数列{a n }中,a 1=1,a 2=1,()*21n n n a a a n N ++=+∈,若a2021=a ,那么S 2019=_____. 【答案】a ﹣1 【解析】 【分析】根据题意可得21n n n a a a ++=-,然后类比数列的裂项相消法求出S 2019. 【详解】解:由题意,得a n =a n +2﹣a n +1,则S 2019=a 1+a 2+a 3+…+a 2019=a 3﹣a 2+a 4﹣a 3+a 5﹣a 4+…+a 2021﹣a 2010 =a 2021﹣a 2=a ﹣1. 故答案为:a ﹣1.【点睛】本题考查了数列的裂项相消法求和,考查了类比推理能力,属基础题. (一)必考题:共60分.17.已知数列{a n }的前n 项和为S n ,满足122n n S +=-.(1)求数列{a n }的通项公式;(2)设b n =(2n ﹣1)a n ,求数列{b n }的前n 项和T n .【答案】(1)2nn a =;(2)()12326n n T n +=-+【解析】 【分析】(1)根据数列的递推式可知,当1n =时,11S a =,当2n 时,1n n n a S S -=-,进一步求出通项公式;(2)先求出{}n b 的通项公式,再利用错位相减法求出{b n }的前n 项和T n .【详解】解:(1)因为122n n S +=-,所以当1n =时,112S a ==,当2n 时,1122222n n n n n n a S S +-=-=--+=,上式对1n =也成立,所以2nn a =.(2)由(1)知(21)(21)2n n n b n a n =-=-, 所以23123252(21)2n n T n =+++⋯+-,23412123252(21)2n n T n +=+++⋯+-,两式相减,得23122(222)(21)2n n n T n +-=+++⋯+--114(12)22(21)212n n n -+-=+---,所以16(23)2n n T n +=+-.【点睛】本题考查了利用递推公式求通项公式和错位相减法求数列的前n 项和,考查了分类讨论思想和计算能力,属中档题.数列前n 项和的求法有公式法、倒序相加法、裂项相消法、错位相减法、并项求和法和分组求和法.18.在△ABC 中,a ,b ,c 分别为内角A ,B ,C 的对边,且满足53acosC b c cosA ⎛⎫=- ⎪⎝⎭. (1)若15sinC =,a +c =10,求c ;(2)若a =4,c =ABC 的面积S .【答案】(1)2c =;(2)225【解析】 【分析】(1)利用正弦定理,将边化为角,然后求出sin A ,进一步求出c ;(2)利用余弦定理,得到关于b 的一元二次方程,并求出b ,然后代入面积公式中求出S .【详解】解:(1)因为5cos ()cos 3a C b c A =-,所以5sin cos (sin sin )cos 3A CBC A =-,所以5sin cos sin cos cos sin sin()sin 3B A A C A C A C B =++=+=,因为sin 0B ≠,所以3cos 5A =,4sin 5A =,由正弦定理,知sin :sin 4:1:A C a c ==,所以4a c =, 又10a c +=,所以2c =. (2)由(1)知3cos 5A =,4sin 5A =,所以由余弦定理,得222cos2b c a A bc+-=,所以235=,即25550b --=,所以b ,所以△ABC 的面积122sin 25S bc A ==.【点睛】本题考查了正余弦定理在解三角形中的应用和三角形的面积公式,考查了转化思想和方程思想,属中档题.19.手机运动计步已经成为一种新时尚.某单位统计了职工一天行走步数(单位:百步),绘制出如下频率分布直方图:(1)求直方图中a 的值,并由频率分布直方图估计该单位职工一天步行数的中位数; (2)若该单位有职工200人,试估计职工一天行走步数不大于13000的人数;(3)在(2)的条件下,该单位从行走步数大于15000的3组职工中用分层抽样的方法选取6人参加远足拉练活动,再从6人中选取2人担任领队,求这两人均来自区间(150,170]的概率.【答案】(1)125;(2)112;(3)25【解析】 【分析】(1)由频率和为1,列出关于a 的方程,然后求出a 的值,再利用中位数两边频率相等,求出中位数的值;(2)根据一天行走步数不大于13000频率⨯样本容量,求出频数;(3)根据分层抽样原理抽取6人,利用列举法求出基本事件数,计算所求的概率值.【详解】解:(1)由题意,得(0.0020.0060.0080.0100.0080.0020.002)201a +++++++⨯=, 所以0.012a =.设中位数为110x +,则0.002200.006200.008200.0120.5x ⨯+⨯+⨯+=, 所以15x =,所以中位数为125.(2)由200(0.002200.006200.008200.01220)112⨯⨯+⨯+⨯+⨯=, 所以估计职工一天步行数不大于13000步的人数为112人.(3)在区间(150,170]中有2000.0082032⨯⨯=人, 在区间(170,190]中有2000.002208⨯⨯=人, 在区间(190,210]中有2000.002208⨯⨯=人,按分层抽样抽取6人,则从(150,170]中抽取4人,(170,190]中抽取1人,(190,210]中抽取1人;设从(150,170]中抽取职工为a 、b 、c 、d ,从(170,190]中抽取职工为E ,从(190,210]中抽取职工为F ,则从6人中抽取2人的情况有ab 、ac 、ad 、aE 、aF 、bc 、bd 、bE 、bF 、cd 、cE 、cF 、dE 、dF 、EF 共15种情况,它们是等可能的,其中满足两人均来自区间(150,170]的有ab 、ac 、ad 、bc 、bd 、cd 共有6种情况, 所以两人均来自区间(150,170]的概率62155P ==; 【点睛】本题考查了利用频率分布直方图求中位数和古典概型的概率计算问题,属基础题. 20.如图,正方形ABCD 的边长为2,点E 是边CD 的中点,将△ADE 沿AE 翻折得到△ASE ,且平面ASE ⊥平面ABCE .(1)求三棱锥B ﹣CES 的体积; (2)设线段SC 上一点G 满足2SGGC=,在BE 上是否存在点H 使GH ∥平面SAE ?若存在,求出EH 的长度;若不存在,说明理由. 【答案】(125;(25【解析】 【分析】(1)过S 作SO AE ⊥于O ,从而得到SO ⊥平面ABCE ,进一步得到B CES S BCE V V --=,由此求出三棱锥B CES -的体积.(2)连接AC ,交BE 于H ,连接GH ,推导出//GH SA ,由此能求出结果.【详解】解:(1)过S 作SO AE ⊥于O ,因为平面ASE ⊥平面ABCE 交线为AE ,所以SO ⊥平面ABCE .在Rt ASE ∆中由1,2SE SA ==,得25SO =, 因为112122BCE S ∆=⨯⨯=,所以11225133155B CES S BCE BCE V V S SO --∆==⋅=⨯⨯=. 所以三棱锥B CES -的体积为2515.(2)连接AC ,交BE 于H ,连接GH , 因为//CE AB ,12CE AB =, 所以ABH CEH ∆∆∽,所以12CH EH CE HA HB AB ===, 又因为2SG GC =,所以12CG GS =,所以CG CHGS HA=,所以//GH SA . 又因为GH ⊂/平面SAE ,SA ⊂平面SAE ,所以//GH 平面SAE ,此时153EH BE ==.【点睛】本题考查了折叠问题、三棱锥体积的求法和线面平行的判定定理,考查了转化思想和运算求解能力,属中档题. 21.已知函数f (x )=lnx ()12a x x --+.(1)若a =4,求函数f (x )的单调区间;(2)若函数f (x )在区间(0,1]内单调递增,求实数a 的取值范围; (3)若x 1、x 2∈R +,且x 1≤x 2,求证:(lnx 1﹣lnx 2)(x 1+2x 2)≤3(x 1﹣x 2). 【答案】(1)见解析;(2)3a ≤;(3)见解析【解析】 【分析】(1)将a =4代入f (x )求出f (x )的导函数,然后根据导函数的符号,得到函数的单调区间; (2)根据条件将问题转化为434ax x++在(0,1]上恒成立问题,然后根据函数的单调性求出a 的范围;(3)根据条件将问题转化为1122123()2x x x lnx x x -+成立问题,令12(0,1)x t x =∈,即3(1)02t lnt t --+成立,再利用函数的单调性证明即可.【详解】解:(1)()f x 的定义域是(0,)+∞,22213(43)4()(2)(2)a x a x f x x x x x +-+'=-=++, 所以4a =时,2284()(2)x x f x x x -+'=+,由()0f x '>,解得04x <<-4x >+由()0f x '<,解得44x -<+故()f x 在(0,4-和(4+,)+∞上单调递增,在(4-4+上单调递减. (2)由(1)得22(43)4()(2)x a x f x x x +-+'=+,若函数()f x 在区间(0,1]递增,则有2(43)40x a x +-+在(0,1]上恒成立,即434ax x ++在(0,1]上恒成立成立,所以只需min434a x x ⎛⎫++ ⎪⎝⎭, 因为函数44y x x =++在1x =时取得最小值9,所以min 4349a x x ⎛⎫++= ⎪⎝⎭,所以a 的取值范围为](,3-∞. (3)当12x x =时,不等式显然成立,当12x x ≠时,因为1x ,2x R +∈,所以要原不等式成立,只需11122121223(1)3()22x x x x x lnx x x x x --=++成立即可, 令12(0,1)x t x =∈,则3(1)02t lnt t --+,由(2)可知函数()f x 在(0,1]递增,所以()(1)0f x f ≤=, 所以3(1)02t lnt t --+成立,所以(lnx 1﹣lnx 2)(x 1+2x 2)≤3(x 1﹣x 2).【点睛】本题考查了利用导数研究函数的单调性,函数恒成立问题和不等式的证明,考查了转化思想和分类讨论思想,属难题. (二)选考题:共10分.22.如图所示,“8”是在极坐标系Ox 中分别以112C π⎛⎫ ⎪⎝⎭,和2322C π⎛⎫ ⎪⎝⎭,为圆心,外切于点O 的两个圆.过O 作两条夹角为3π的射线分别交⊙C 1于O 、A 两点,交⊙C 2于O 、B 两点.(1)写出⊙C 1与⊙C 2的极坐标方程; (2)求△OAB 面积最大值. 【答案】(1)1:2sin C ρθ=;2:4sin C ρθ=-;(23【解析】 【分析】 (1)直接由条件求出1C 与2C 的极坐标方程即可;(2)由(1)得(2sin ,)A θθ,(4sin()3B πθ--,)3πθ-,代入三角形面积公式,再利用三角函数求出△OAB 面积的最大值.【详解】解:(1)因为在极坐标系中圆1C 和圆2C 的圆心分别为11,2C π⎛⎫ ⎪⎝⎭和232,2C π⎛⎫⎪⎝⎭, 所以圆1C 和圆2C 的极坐标方程分别为2sin ρθ=和4sin ρθ=-. (2)由(1)得(2sin ,)A θθ,(4sin()3B πθ--,)3πθ-,则12sin [4sin()]sin 233ABC S ππθθ∆=--(sin cos cos sin )33ππθθθ=--23sin cos θθθ=+)6πθ=+.所以当sin(2)16πθ+=时,OAB ∆【点睛】本题考查简单曲线的极坐标方程、三角形的面积公式和三角函数求最值,考查了转化思想和函数思想,属中档题.23.已知函数f (x )=|x ﹣2|﹣t ,t ∈R,g (x )=|x +3|. (1)x ∈R,有f (x )≥g (x ),求实数t 的取值范围;(2)若不等式f (x )≤0的解集为[1,3],正数a 、b 满足ab ﹣2a ﹣b =2t ﹣2,求a +2b 的最小值.【答案】(1)(],5-∞-;(2)min (2)9a b += 【解析】 【分析】(1)由条件可知,当x ∈R 时,|2||3|t x x --+恒成立,因此只需()min |2||3|t x x --+,然后利用绝对值三角不等式可求出|2||3|x x --+的小值即可.(2)根据不等式f (x )≤0的解集为[1,3],求出t 的值,然后将t 代入222ab a b t --=-中,得到关于a ,b 的方程,再利用基本不等式求出2+a b 的最小值即可.【详解】解:(1)因为x ∈R ,有f (x )≥g (x ),所以|2||3|x t x --+在x ∈R 时恒成立, 即|2||3|t x x --+在x ∈R 时恒成立,所以只需()min |2||3|t x x --+因为||2||3|||23|5x x x x --+---=,所以5|2||3|5x x ---+,所以()min |2||3|5tx x --+=-,所以t 的取值范围为(,5]-∞-. (2)由|2|x t -,得22t x t -+, 因为不等式()0f x 的解集为[1,3],所以2123t t -=⎧⎨+=⎩,解得1t =.将1t =带入222ab a b t --=-中,得20ab a b --=,所以211b a+=,所以21222(2)()559a b a b a b b a b a +=++=++≥=,当且仅当3a b ==时取等号, 所以2+a b 的最小值为9.【点睛】本题考查了不等式恒成立问题、不等式的解集与方程根的关系、绝对值三角不等式和利用基本不等式求最值,考查了转化思想和方程思想,属中档题.。
2019年12月05日四川省宜宾市高2020届高2017级一诊考试理科综合试题文科数学试题参考答案

宜宾市高2017级第一次诊断测试(文史类)数学试题参考答案说明:一、本解答给出了一种解法供参考,如果考生的解法与本解答不同,可比照评分意见制订相应的评分细则.二、对计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应得分数的一半,如果后继部分的解答有较严重的错误,就不再给分.三、解答右端所注分数,表示考生正确做到这一步应得的累加分数.四、只给整数分数,选择题和填空题不给中间分. 一、选择题 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案DADCBBDCCACB二、填空题13.35 14.6 15. 210 16. 1a -三、解答题17.解:(1)∵122n n S +=-,当1=n 时,112S a ==当2≥n 时 122n n S +=-,122n n S -=-两式相减得 1(22)(22)2n n n n a +=---= (2)n ≥ 当1=n 时,满足通项. ∴{}n a 是以首项为2,公比为2的等比数列n n a 2=(n *∈N ) ..........6分(2)由(1)知n n n b 2)12(-=n n n n n T 2)12(2)32(252321132⋅-+⋅-++⋅+⋅+⋅=- 14322)12(2)32(2523212+⋅-+⋅-+⋅+⋅+⋅=n n n n n T两式相减得nn n n T 2)12(22222132⋅--+++⨯+=--)(62)32(2)12(622)12(21)21(22112113---=⋅---=⋅----⋅+=-++++-n n n n n n n n n T62)32(1+-=+n n n T ....................12分18.解:(1)55cos ()cos ,sin cos (sin sin )cos 33a C b c A A C B C A =-∴=-5sin cos cos sin sin cos 3A C A C B A ∴+=,5sin cos sin()sin 3B A A C B ∴=+=3sin 0,cos 5B A ≠∴=,则4sin 5A =, 由正弦定理得,sin 4sin a Ac C==,即4a c =,联立10a c +=,得2c = …………………………………………………………………6分 (2)由余弦定理可得,222cos 2b c a A bc +-=,即223516,565550525b b b b+-=--= 得1155b =,则122sin 25S bc A == …………………………………………12分 19.解:(1)由题意得120002.020002.020008.020010.02020008.020006.020002.0=⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯a解得012.0=a 设中位数为x +110,则5.0012.020008.020006.020002.0=⋅+⨯+⨯+⨯x解得15=x ∴中位数是125 ........................................... 4分 (2)由112)20012.020008.020006.020002.0(200=⨯+⨯+⨯+⨯⨯∴估计职工一天步行数不大于13000步的人数为112人 ........................................... 6分 (3) 在区间(]170,150中有3220008.0200=⨯⨯人在区间(]190,170中有820002.0200=⨯⨯人 在区间(]210,190中有820002.0200=⨯⨯人按分层抽样抽取6人,则从(]170,150抽取4人,(]190,170抽取1人(]210,190抽取1人. ...... 8分 设从(]150,170抽取职工为1234,,,A A A A ,从(]170,190抽取职工为B ,从(]190,210抽取职工为C ,则从6人中抽取2人的情况有,,,,,,,,,,,,,,,44334322423211413121BC C A B A C A B A A A C A B A A A A A C A B A A A A A A A 共15种情况,它们是等可能的,其中满足两人均来自区间(]170,150的有,,,,,,434232413121A A A A A A A A A A A A 共有6种情况,O52156==∴P ∴两人均来自区间(]170,150的概率为52. ...... 12分 20.解:(1)过S 作AE SO ⊥于O ∵平面⊥ASE 平面ABCE 交线为AE ∴⊥SO 平面ABCE .在ASE Rt ∆中 由2,1==SA SE 得52=SO211221=⨯⨯=∆BCE S 15525213131=⨯⨯=⋅==∴∆--SO S V V BCE BCE S CES B . ∴三棱锥CES B -的体积1552..........6分 (2)连接AC 交BE 于H ,连接GH ∵AB CE AB CE 21,//=∴ABH ∆∽CEH ∆21===∴AB CE HB EH HA CH 又∵2=GCSG21=∴GS CG HACHGS CG =∴.SA GH //∴. 又⊄GH 平面SAE ⊂SA 平面SAE//GH ∴平面SAE 此时3531==BE EH ...............................12分21.解:(1)()f x 的定义域是(0,)+∞,22213(43)4()(2)(2)a x a x f x x x x x +-+'=-=++ ,若函数()f x 在区间(0,1]递增, 则有2(43)40x a x +-+≥在(0,1]内恒成立, 即434a x x≤++恒成立, 又函数44y x x=++在1x =时取得最小值9,故3a ≤; ..................6分 (2)要原不等式成立, 只要11122121223(1)3()ln (2)(2)x x x x x x x x x x --≤=++成立即可, 令12(0,1]x t x =∈,故只要3(1)ln 0(2)t t t --≤+即可, 由(1)可知函数()f x 在(0,1]递增, 故()(1)0f x f ≤=, 故3(1)ln 0(2)t t t --≤+成立. ..................12分 22.解:(1)1:2sin C ρθ=;2:4sin C ρθ=-;(2)由(I)得(2sin ,)A θθ,(4sin(),)33B ππθθ---12sin [4sin()]23ABC S πθθ∆∴=⋅⋅--33sin(2)62πθ=+-32≤23.解(1)解:(1)由)()(x g x f ≥,得32+≥--x t x 恒成立 t x x ≥+--∴32,在R ∈x 时恒成立()t x x ≥+--∴min 32()()53232=+--≤+--x x x x5325≤+--≤-∴x x ()532min -=+--∴x x5-≤∴tt ∴的取值范围是(]5,-∞-......................................................................................5分方法二:根据函数32+--=x x y 的图像,找出32+--x x 的最小值5-(2)由02)(≤--=t x x f 得t x ≤-2 解得t x t +≤≤-22⎩⎨⎧=+=-∴3212t t 解得1=t 将1=t 带入222-=--t b a ab ,整理得02=--b a ab112=+∴ab 9542522)12()2(2=+≥++=+⋅+=+∴a b b a a b b a b a 当且仅当a bb a 22=,即b a =时取等号 9)2(min =+∴b a ...................................................................................................10分。
2019年12月06日四川省宜宾市高2020届高2017级一诊考试文科综合试题地理试题
2020级诊断性考试《地理》“夜间经济”是20世纪70年代英国为改善城市中心区夜晚“空巢”现象提出的经济学名词,指发生在18:00到次日清晨6:00,以当地居民、工作人群及游客为消费主体,以购物、餐饮、旅游、娱乐、文化、影视、健身、休闲等为主要形式的现代城市消费经济。
目前,我国“夜间经济”,在空间上具有围绕城市商务中心、自然或文化遗产、城市中心“边缘地带”分布的规律。
据此回答 1 题。
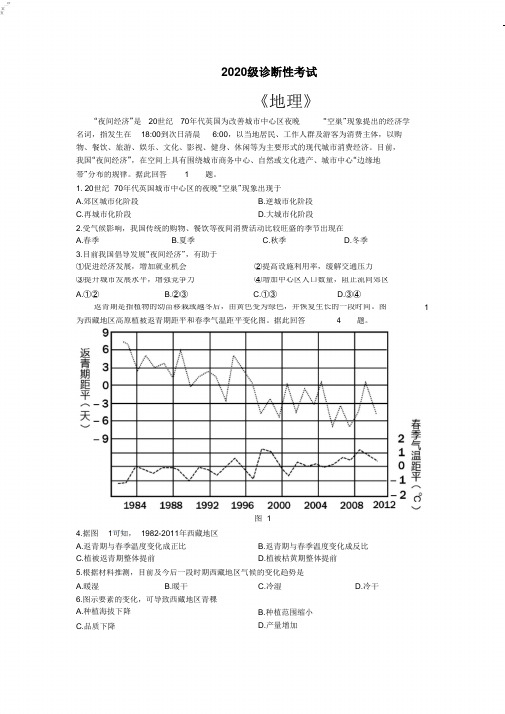
1. 20世纪70年代英国城市中心区的夜晚“空巢”现象出现于A.郊区城市化阶段C.再城市化阶段B.逆城市化阶段D.大城市化阶段2.受气候影响,我国传统的购物、餐饮等夜间消费活动比较旺盛的季节出现在A.春季B.夏季C.秋季D.冬季3.目前我国倡导发展“夜间经济”,有助于①促进经济发展,增加就业机会②提高设施利用率,缓解交通压力③提升城市发展水平,增强竞争力④增加中心区人口数量,阻止流向郊区A.①②B.②③C.①③D.③④返青期是指植物的幼苗移栽或越冬后,由黄色变为绿色,并恢复生长的一段时间。
图 1 为西藏地区高原植被返青期距平和春季气温距平变化图。
据此回答 4 题。
图 14.据图1可知,1982-2011年西藏地区A.返青期与春季温度变化成正比C.植被返青期整体提前B.返青期与春季温度变化成反比D.植被枯黄期整体提前5.根据材料推测,目前及今后一段时期西藏地区气候的变化趋势是A.暖湿B.暖干C.冷湿D.冷干6.图示要素的变化,可导致西藏地区青稞A.种植海拔下降B.种植范围缩小D.产量增加C.品质下降建于1960年的瓦依昂水库,横跨意大利东北部的深山峡谷,当地为石灰岩和粘土相互层叠的岩层结构。
1963年8-10月,该区域经历多次大雨。
1963年10月9日晚大雨滂沱,2为瓦依昂水库滑坡体区22时41分,瓦依昂水库南岸发生大规模滑坡,造成重大损失。
图南北向剖面图。
据此回答7 题。
图 27.相对原冰川谷底,形成现在峡谷形态的主要原因是A.冰川侵蚀B.海水侵蚀C.风力侵蚀8.导致此次瓦依昂水库滑坡的直接诱因是A.水位上升B.植被稀少C.岩体破碎9.从地质角度分析,瓦依昂水库坝址区存在的危险因素D.流水侵蚀D.库岸陡峭A.地处峡谷,坝体抗压能力低C.向斜构造,岩体向谷底倾斜B.坡度太陡,汇水速度快D.断层发育,泉水涌出多我国是海水养殖大国。
宜宾市普通高中2017级高三第一次诊断试题(文史类)数学参考答案

宜宾市高2017级第一次诊断测试 (文史类)数学试题参考答案说明:一、本解答给出了一种解法供参考,如果考生的解法与本解答不同,可比照评分意见制订相应的评分细则.二、对计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应得分数的一半,如果后继部分的解答有较严重的错误,就不再给分.三、解答右端所注分数,表示考生正确做到这一步应得的累加分数.四、只给整数分数,选择题和填空题不给中间分. 一、选择题 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案DADCBBDCCACB二、填空题13.3514.6 15. 210 16. 1a - 三、解答题17.解:(1)∵122n n S +=-,当1=n 时,112S a ==当2≥n 时 122n n S +=-,122n n S -=-两式相减得 1(22)(22)2n n n n a +=---= (2)n ≥ 当1=n 时,满足通项. ∴{}n a 是以首项为2,公比为2的等比数列n n a 2=(n *∈N ) ..........6分(2)由(1)知n n n b 2)12(-=n n n n n T 2)12(2)32(252321132⋅-+⋅-++⋅+⋅+⋅=- 14322)12(2)32(2523212+⋅-+⋅-+⋅+⋅+⋅=n n n n n T两式相减得nn n n T 2)12(22222132⋅--+++⨯+=--)(62)32(2)12(622)12(21)21(22112113---=⋅---=⋅----⋅+=-++++-n n n n n n n n n T62)32(1+-=+n n n T (12)分18.解:(1)55cos ()cos ,sin cos (sin sin )cos 33a Cbc A A C B C A =-∴=-5sin cos cos sin sin cos 3A C A C B A ∴+=,5sin cos sin()sin 3B A A C B ∴=+=3sin 0,cos 5B A ≠∴=,则4sin 5A =, 由正弦定理得,sin 4sin a Ac C==,即4a c =,联立10a c +=,得2c =…………………………………………………………………6分(2)由余弦定理可得,222cos 2b c a A bc +-=,即223516,565550525b b b b+-=--= 得1155b = ,则122sin 25S bc A == …………………………………………12分19.解:(1)由题意得120002.020002.020008.020010.02020008.020006.020002.0=⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯a解得012.0=a 设中位数为x +110,则5.0012.020008.020006.020002.0=⋅+⨯+⨯+⨯x解得15=x∴中位数是125........................................... 4分(2)由112)20012.020008.020006.020002.0(200=⨯+⨯+⨯+⨯⨯ ∴估计职工一天步行数不大于13000步的人数为112人........................................... 6分(3) 在区间(]170,150中有3220008.0200=⨯⨯人在区间(]190,170中有820002.0200=⨯⨯人 在区间(]210,190中有820002.0200=⨯⨯人。
(审核版)四川省宜宾市2020届高三第一次诊断性测试语文试卷(含答案解析).doc

宜宾市2020届高三第一次诊断性测试题语文1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.作答时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
4.选择题答案一律..用2B铅笔填涂在“机读部分”处。
第一部分阅读(70分)―、现代文阅读(35分)(一)论述类文本(9分)阅读下面的文字,完成1~3题。
西方自上世纪60年代以来的自由派文化主流,在过去一些年对维护西方文化优势发挥了极大作用。
比如,过去西方的资本家贪婪吃相难看,巨贾富翁大腹便便,但现在财富浪漫化,新大亨如盖茨、扎克伯格都是关爱慈善的典范,谁想骂都难找着力点。
比如资本主义过去只赚钱不环保,但现在西方却以“最环保,最关心人类”的形象呈现在世人面前。
再比如原来同性恋等边缘群体都受轻视,但现在他们中的很多人已经成为精英,这促进了劳动力多样化,精英多样化,对非西方反西方的文化冲击很大。
可以说,自由派文化是主导这一波全球化的文化力量。
中国许多“文艺青年”深受这些观念影响。
随着中国中产化的大进程,文艺青年越来越普泛化,物质生活的细腻精致和精神生活的超越性一起被想象。
而文艺青年在中国语境中的话语权和自信都很强,他们否定中产普通生活,追求诗意浪漫,于是新话语几乎无往而不利。
最近的鲍勃·迪伦获得诺贝尔文学奖和特朗普当选,都与西方60年代的这股潮流有关,前者是它已经完全主流化,被社会充分承认,后者却是它受到冲击的标志。
特朗普胜选或英国脱欧的震撼就在于这是西方内部传统中产掀起的“颜色革命”。
在这套话语中,这些西方传统中产没得到好处,反而经济地位下降,生活受到冲击。
而西方在中东等地做大事,反而遭遇大的难民潮,这就是“反噬”。
西方那一套文化优势变成经济社会的拖累,内部的社会基础不答应了,就用选票说话。
这和全球化这些年的变化有关,也和西方国家内部人口和社会状况的变化有关。
这让自信满满,觉得自己非常正确的那些“文艺青年”也感到震撼。
四川省宜宾市2022-2023学年高三上学期第一次诊断测试文科综合试题

宜宾市普通高中2020级第一次诊断性测试文科综合能力测试本试卷共14页,45题,全卷满分300分。
考试时间150分钟。
注意事项:1、答题前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上。
2.回答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,请将答题卡交回。
一、选择题:本题共35道小题,每道小题4分,共140分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
图1为湖南省2010年和2020年GDP排名前五位的城市常住人口占全省人口比重示意图。
据此完成1~3题。
1.据图可知,五城市A.人口均以自然增长为主C.产业发展方向趋于相同B.常住人口数量均减少D.经济发展水平差异大2.长沙市常住人口变化可能带来的影响是A.出现再城市化C.加剧人地矛盾B.增加社会失业率D.加速人口老龄化3.衡阳市应对常住人口变化,可采取的最有效措施是A.发展交通运输C.发展假日旅游B.承接产业转移D.改善环境质量美国中部平原某地冬春季多大风,当地农田传统做法是在秋季翻耕,但长期翻耕会对土壤及生态环境造成破坏。
后来,免耕法得到推广。
免耕法是指不翻动或少翻动表土,并全年在土壤表面留下足以保护土壤的作物残茬的耕作方式。
多年免耕后会使耕作层上层养分富化、下层贫化,农作物产量受到影响。
据此完成4~6题。
4.传统的秋季翻耕可能给当地环境带来的影响是A.土壤病虫害增多 C.沙尘天气增多5.秋季免耕后可使土壤A.含水量增加C.孔隙度增大B.温室气体排放减少D.河流含沙量减少B.保温性变差D.有机质减少6.多年免耕后,为进一步提高农作物产量,当地可以①改良作物品种②提高复种指数③实行轮作休耕④适时翻耕土地A.①②B.②③C.③④D.①④川藏铁路东起四川盆地成都平原,东西横穿横断山区,西达西藏拉萨,全长1629千米,设计时速200千米(限制区段时速160千米),将建设数十个长达10公里以上的超长隧道,堪称人类铁路建设史上难度最大的超级工程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
宜宾市2017级第一次诊断性考试
地理
“夜间经济”是20世纪70年代英国为改善城市中心区夜晚“空巢”现象提出的经济学名词,指发生在18:00到次日清晨6:00,以当地居民、工作人群及游客为消费主体,以购物、餐饮、旅游、娱乐、文化、影视、健身、休闲等为主要形式的现代城市消费经济。
目前,我国“夜间经济”,在空间上具有围绕城市商务中心、自然或文化遗产、城市中心“边缘地带”分布的规律。
据此回答1~3题。
1.20世纪70年代英国城市中心区的夜晚“空巢”现象出现于
A.郊区城市化阶段
B.逆城市化阶段
C.再城市化阶段
D.大城市化阶段
2.受气候影响,我国传统的购物、餐饮等夜间消费活动比较旺盛的季节出现在
A.春季
B.夏季
C.秋季
D.冬季
3.目前我国倡导发展“夜间经济”,有助于
①促进经济发展,增加就业机会②提高设施利用率,缓解交通压力
③提升城市发展水平,增强竞争力④增加中心区人口数量,阻止流向郊区
A.①②
B.②③
C.①③
D.③④
返青期是指植物的幼苗移栽或越冬后,由黄色变为绿色,并恢复生长的一段时间。
图1为西藏地区高原植被返青期距平和春季气温距平变化图。
据此回答4~6题。
图1
4.据图1可知,1982-2011年西藏地区
A.返青期与春季温度变化成正比
B.返青期与春季温度变化成反比
C.植被返青期整体提前
D.植被枯黄期整体提前
5.根据材料推测,目前及今后一段时期西藏地区气候的变化趋势是
A.暖湿
B.暖干
C.冷湿
D.冷干
6.图示要素的变化,可导致西藏地区青稞
A.种植海拔下降
B.种植范围缩小
C.品质下降
D.产量增加
建于1960年的瓦依昂水库,横跨意大利东北部的深山峡谷,当地为石灰岩和粘土相互层叠的岩层结构。
1963年8-10月,该区域经历多次大雨。
1963年10月9日晚大雨滂沱,22时41分,瓦依昂水库南岸发生大规模滑坡,造成重大损失。
图2为瓦依昂水库滑坡体区南北向剖面图。
据此回答7~9题。
图2
7.相对原冰川谷底,形成现在峡谷形态的主要原因是
A.冰川侵蚀
B.海水侵蚀
C.风力侵蚀
D.流水侵蚀
8.导致此次瓦依昂水库滑坡的直接诱因是
A.水位上升
B.植被稀少
C.岩体破碎
D.库岸陡峭
9.从地质角度分析,瓦依昂水库坝址区存在的危险因素
A.地处峡谷,坝体抗压能力低
B.坡度太陡,汇水速度快
C.向斜构造,岩体向谷底倾斜
D.断层发育,泉水涌出多
我国是海水养殖大国。
海水养殖对水体盐度、溶氧量、水质等要求较高。
对海水养殖而言,盐度的稳定性极其重要。
若盐度短时间的快速降低,可能会造成养殖的鱼虾等大量死亡。
溶氧量是水域中所含氧气的溶解量,主要来源是水生植物(特别是浮游植物)光合作用产生的氧气,其次是空气中氧气的溶解。
表1为溶解氧与气压、水温的关系。
据此回答10~11题。
表1溶解氧与气压、水温的关系
温度℃
大气压力(hPa)11151013912811709608507
氧的溶解度(mg/l)
514.0612.7711.4810.208.917.62 6.34 1511.1010.089.058.037.01 5.98 4.96 259.128.267.40 6.56 5.70 4.84 4.00 357.69 6.95 6.22 5.47 4.75 4.01 3.28 10.从水温、气压和光合作用(不考虑水生植物数量差异)角度分析,易导致水体溶氧量变小的天气(系统)是
A.寒潮
B.台风
C.伏旱
D.沙尘暴
11.福建是我国南方最大的海水养殖省份,该省沿岸海水盐度快速降低的情况易出现在
A.2月
B.5月
C.8月
D.11月
36.阅读图文材料,完成下列要求。
(24分)
材料一莼菜有“植物锌王、水中人参”的美称,是国家一级保护野生植物。
常食莼菜具有药食两用的保健作用。
材料二莼菜适宜生长的环境气温在13.3~27.0℃、水温在22~25℃、水质清洁、底土肥沃、水深20~60cm的池塘湖沼中。
重庆石柱县多年平均气温为16.4℃,有水库33座、大小溪河75条,常年流水不断,非常适宜莼菜生长。
材料三浙江杭州的西湖、四川雷波县的马湖、湖北省利川市、重庆石柱县是我国莼菜主要生产地。
石柱县人工种植莼菜始于1991年,目前占全球种植面积的2/3,已成为世界规模最大的莼菜生产区,并建成国家级出口莼菜质量安全示范区。
石柱莼菜已获得农业部地理标志农产品认证。
当地正发挥“莼菜+”效应,打造“康养石柱”。
图3示意莼菜景观,图4示意石柱县位置和地形
图3图4
(1)简析莼菜被列为国家一级保护野生植物的原因。
(6分)
(2)与杭州西湖相比,分析石柱县莼菜有利的水环境生长条件。
(6分)
(3)简述石柱县成为世界规模最大莼菜生产区的社会经济条件。
(6分)
(4)为充分发挥“莼菜+”效应,请给当地康养产业发展提出你的建议。
(6分)
37.阅读图文材料,完成下列要求。
(22分)
材料一越南,位于亚洲中南半岛东部,人口近一亿,领土面积32.9万平方千米,近年来经济发展较快。
龙江工业园是中国在越南建立的第一个独资工业园,其在“一带一路”沿线国家和地区的45个中国海外工业园中发展排名第一。
龙江工业园所依托的胡志明市是越南的经济中心。
材料二园区为入园企业提供系列优惠政策、基础配套设施,园区投资企业分为五类,分别为:电子机械类、木制品建材类、原材料加工类、医药食品加工类和轻纺新材料加工类,投资企业数最多的为轻纺新材料加工类行业,目前入园的企业有40家,其中中企达30家(包括港、台),还有来自韩国、日本等国家投资的企业。
图5示意龙江工业园的位置
图5
(1)指出该工业园选址的合理性。
(6分)
(2)从经济效益角度,说明该工业园区内目前轻纺新材料加工类企业最多的原因。
(8分)
(3)为促进“一带一路”建设,我国有学者提出大规模扩大海外园区的数量和规模,你是否赞同并说出理由。
(8分)
43.阅读图文材料,完成下列要求。
(10分)
融雪性洪水是指由积雪(季节性、永久性)融化而形成的洪水,也称雪洪,一般在春、夏两季发生在中高纬地区和高山地区。
新疆是雪洪多发地区,南、北疆习惯上以天山为界,图6示意2001—2012年南、北疆年内各月雪洪发生的次数。
图7示意新疆地形图。
图6图7
指出南、北疆雪洪发生的季节差异,并解释导致这种差异的原因。
(10分)。
