第七章土的强度理论
合集下载
土体破坏与强度理论培训讲义PPT95页

27
§5.2 抗剪强度测定试验 一、三轴试验 1、试样应力特点与试验方法 2、强度包线 3、试验类型 4、试验条件与现场条件对应关系 有机玻璃罩
橡皮膜 压力水
轴向加压杆
顶帽
压力室
试
样
透水石
排水管 阀门
量测体变或孔压
28
§5.2 抗剪强度测定试验 一、三轴试验
1、试样应力特点与试验方法
特点:
试样处于轴对称应力状态。竖向应力z一般 是大主应力;径向与周向应力总是相等r=, 亦即1=z;2=3=r=const
§5.1 土体破坏与强度理论 §5.2 抗剪强度测定试验 §5.3 应力路径与破坏主应力线 §5.4 抗剪强度指标
1
§5.1 土体破坏与强度理论
一、土的强度特点 二、土的强度机理 三、莫尔-库仑强度理论
2
§5.1 土体破坏与强度理论
一、土的强度特点
材料的强度是材料抵抗外荷载的能力, 其数值等于作用在其上的极限应力。
z 1
大主应力: 1 p r
σz按顺时针方向旋转α
小主应力: 3 p r
σx按顺时针方向旋转α
圆心: p ( x z ) / 2
半径:
r
(
x
z
)
/
2 2
2 xz
莫 尔 圆:代表一个单元的应力状态; 圆上一点:代表一个面上的一对应力与
p ( 1 3 ) / 2
q ( 1 3 ) / 2 r
❖ 绘制各围压下破坏状态的应力莫尔 圆,画出它们的公切线—强度包线, 得到强度指标 c 与
寻找破坏偏差应力(σ1-σ3)f的方法
❖ 取峰值对应的偏差应力
❖ 规定的轴向应变值(通常取
c
§5.2 抗剪强度测定试验 一、三轴试验 1、试样应力特点与试验方法 2、强度包线 3、试验类型 4、试验条件与现场条件对应关系 有机玻璃罩
橡皮膜 压力水
轴向加压杆
顶帽
压力室
试
样
透水石
排水管 阀门
量测体变或孔压
28
§5.2 抗剪强度测定试验 一、三轴试验
1、试样应力特点与试验方法
特点:
试样处于轴对称应力状态。竖向应力z一般 是大主应力;径向与周向应力总是相等r=, 亦即1=z;2=3=r=const
§5.1 土体破坏与强度理论 §5.2 抗剪强度测定试验 §5.3 应力路径与破坏主应力线 §5.4 抗剪强度指标
1
§5.1 土体破坏与强度理论
一、土的强度特点 二、土的强度机理 三、莫尔-库仑强度理论
2
§5.1 土体破坏与强度理论
一、土的强度特点
材料的强度是材料抵抗外荷载的能力, 其数值等于作用在其上的极限应力。
z 1
大主应力: 1 p r
σz按顺时针方向旋转α
小主应力: 3 p r
σx按顺时针方向旋转α
圆心: p ( x z ) / 2
半径:
r
(
x
z
)
/
2 2
2 xz
莫 尔 圆:代表一个单元的应力状态; 圆上一点:代表一个面上的一对应力与
p ( 1 3 ) / 2
q ( 1 3 ) / 2 r
❖ 绘制各围压下破坏状态的应力莫尔 圆,画出它们的公切线—强度包线, 得到强度指标 c 与
寻找破坏偏差应力(σ1-σ3)f的方法
❖ 取峰值对应的偏差应力
❖ 规定的轴向应变值(通常取
c
土的强度理论--影响土强度的内部因素

例如,粗砂和细砂,孔隙比 相同,两者强度相同;相对 密度相同,粗砂强度高
(2)表面糙度,针、片状形状及棱角颗粒
①在其他条件相同时,颗粒表面糙度增加将会增加砂
土的内摩擦角。
②粗粒土的针、片状形状及棱角的影响较复杂:
(a)加强了颗粒间的咬合作用:。 (b)针片状颗粒更易于折断,棱角易于折损:。
室内粘土压缩实验,三轴试验
正常固结土
历史上最大固结应力=当前受到的有效固结应力
室内制备正常固 结重塑土试样
历史上最大固结应力=实验时施加的围压
A
B
C
D
f tan '
c' 0
不同围压下固结压缩
没有施加任何有效应力的泥 浆,不具有任何强度。即正 常固结土强度包线过原点
但是,强度包线是通过若干个初始状态不同的试验得到的
围压下,三轴试验时也不发 生剪胀而是体积剪缩
围压等于临界围压
•
破坏的体变为零
试样固结后达到临界孔隙比
围压低于临界围压
•
破坏时试样发生剪胀 破坏时试样发生剪缩
围压高于临界围压
•
砂土孔隙比与抗剪强度
M--粉土 S--砂土 G--砾石
L--低塑限 H--高塑限
W--级配良好 P--级配不良
孔隙比与粘性土强度
不同孔隙比下真强度包线
破坏时不同孔隙比的试样
e: 基本是常数
ce :是孔隙比的函数。由于正常固结土强度包线 过原点,所以ce 应与固结应力成正比
f tan e +ce
ce为真粘聚力,e为真摩擦角
优点:在一定程度上反映了粘土的粘聚力和摩擦力的强度机理 不足:尽管试样破坏时的孔隙比是相同的,但是未能反映出它们的应 力历史上造成的细观结构的不同,所以与真正的粘聚力和摩擦力还是 有一定的区别
7-2强度理论-土木

考虑安全系数后:
E3O3 O1O3 D3O3 D1O1 OO1 OO3 E2O2 O1O2 D2O2 D1O1 OO1 OO3
1 3 tu 3 D3O3 , D1O1 , OO3 1 2 2 2 u tu cu D O c , OO1 , OO2 2 2 2 2 2
3.强度条件:
1 [ ]
4.应用情况:符合脆性材料的拉断试验,如铸铁 单向拉伸、扭转中的脆断
第一强度理论
实验表明:脆性材料在二向或三向拉伸断裂时,此
理论与试验结果相当接近;当存在压应力时,只要 最大压应力不超过拉应力或超过不多,理论与试验 结果也大致相符。
但是该理论:
①未考虑其余两个主应力影响; ②不能用于无拉应力的应力状态,如单向、三向 压缩等。 该理论与均质的脆性材料的实验结果吻合较好.
畸变能密度理论(第四强度理论)
1.屈服原因:畸变能vd(与应力状态无关)
2 2 2 2 2.屈服条件: (1 2 ) ( 2 3 ) ( 3 1 ) 2 s
3.强度条件:
1 [( 1 2 ) 2 ( 2 3 ) 2 ( 3 1 ) 2 ] [ ] 2
强度理论概述
由于:复杂应力状态下的强度准则不能由 实验确定(不可能针对每一种应力状态做无 数次实验) 强 度 理 论: ——材料失效原因的假说 (假说—实践—理论) 通过强度理论,利用单向拉伸实验结果建 立各种应力状态下的失效判据和相应的设计准 则。
§7.6.2 四种常用强度理论及其相当应力
1、第一类强度理论(以 脆性断裂破坏为标志)
在一定范围与实际相符合,上升为理论。
为了建立复杂应力状态下的强度条件,而提出 的关于材料破坏原因的假设及计算方法。
土力学1-第6章-抗剪强度

极限平衡状态 (破坏) 安全状态 不可能状态 (破坏)
O
c
3f
1
土单元是否破坏的判别
39
§7.2 土的抗剪强度理论 – 莫尔-库仑强度理论
方法三: 由1 , 3 m ,比较 和m
sinφm σ1 σ σ1 σ c cot φ
f = c + tan
方法一: 由3 1f,比较1和1f
φ φ σ1f σ tan ( ) c tan( ) 2 2
f = c + tan
1 = 1f 1 < 1f 1 > 1f
极限平衡状态 (破坏) 安全状态 不可能状态 (破坏)
2
1f
切破坏:
σ 1, 3 σx σz σ σz 2 2 ( x ) τ xz 2 2
• 由3 1f,比较1和1f • 由1 3f,比较3和3f
• 由1 , 3 m,比较 和 m
土单元是否破坏的判别
37
§7.2 土的抗剪强度理论 – 莫尔-库仑强度理论
T tg N
T
N
W
天然休止角,也是最
松状态下的砂内摩擦角
土的强度及其特点
6
§7.1 概述 - 土体强度及其特点
天然状态下的沙丘
30~35 静止砂丘 移动砂丘
固定沙丘背风坡角度接近天然休止角,一般
为 =30-35,大于矿物滑动摩擦角 颗粒间存在一定的咬合作用
土的强度及其特点
• 当采用总应力时,称为总应力抗剪强度指标 • 当采用有效应力时,称为有效应力抗剪强度指标
对无黏性土通常认为,黏聚力c =0
第七章 土的强度理论

c ´ —— 土的有效粘聚力(内聚力),kPa
´—— 土的有效内摩擦角,度。
与剪切速率、应力状态和应力历史等许多因素有关。
土的抗剪强度的两种表示方法
三、莫尔—库伦强度理论
1910年莫尔(Mohr)提出材料的破坏是剪切破坏,当任一平面上的剪 应力等于材料的抗剪强度时该点就发生破坏,并提出在破坏面上的剪应
1
3
3
将抗剪强度包线与应力状
态(采用莫尔应力圆表示)画
在同一张坐标图上。它们之间
的关系有以下三种情况:
Ⅰ稳定状态
Ⅱ极限平衡状态 Ⅲ不可能状态
c
1
强度线
极限应力圆
ⅠⅡ Ⅲ
3
1 1 1
1、任意一点的某一平面的 法向应力和剪应力
dlsin
1
3
3
3
1
【解答】
已知1=430kPa,3=200kPa,c=15kPa, =20o
1.计算法A
1f
3
tan
2
45o
2c tan 45o
2
450.8kPa
2
计算结果表明:1f大于该单元土体实际大主应力1,实
际应力圆半径小于极限应力圆半径,所以,该单元土体 处于弹性平衡状态
第七章 土的抗剪强度
抗剪强度的理论问题 破坏准则(极限平衡条件) 抗剪强度测定问题(抗剪强度参数的确定)
土的抗剪强度的工程意义
以土作为建造材料的土工构筑物的 稳定性问题,如土坝、路堤等填方边坡 以及天然土坡等的稳定性问题。
土作为建筑物地基的承载力问
题,如果基础下的地基土体产生整 体滑动或因局部剪切破坏而导致过 大的地基变形,将会造成上部结构 的破坏或影响其正常使用功能 。
´—— 土的有效内摩擦角,度。
与剪切速率、应力状态和应力历史等许多因素有关。
土的抗剪强度的两种表示方法
三、莫尔—库伦强度理论
1910年莫尔(Mohr)提出材料的破坏是剪切破坏,当任一平面上的剪 应力等于材料的抗剪强度时该点就发生破坏,并提出在破坏面上的剪应
1
3
3
将抗剪强度包线与应力状
态(采用莫尔应力圆表示)画
在同一张坐标图上。它们之间
的关系有以下三种情况:
Ⅰ稳定状态
Ⅱ极限平衡状态 Ⅲ不可能状态
c
1
强度线
极限应力圆
ⅠⅡ Ⅲ
3
1 1 1
1、任意一点的某一平面的 法向应力和剪应力
dlsin
1
3
3
3
1
【解答】
已知1=430kPa,3=200kPa,c=15kPa, =20o
1.计算法A
1f
3
tan
2
45o
2c tan 45o
2
450.8kPa
2
计算结果表明:1f大于该单元土体实际大主应力1,实
际应力圆半径小于极限应力圆半径,所以,该单元土体 处于弹性平衡状态
第七章 土的抗剪强度
抗剪强度的理论问题 破坏准则(极限平衡条件) 抗剪强度测定问题(抗剪强度参数的确定)
土的抗剪强度的工程意义
以土作为建造材料的土工构筑物的 稳定性问题,如土坝、路堤等填方边坡 以及天然土坡等的稳定性问题。
土作为建筑物地基的承载力问
题,如果基础下的地基土体产生整 体滑动或因局部剪切破坏而导致过 大的地基变形,将会造成上部结构 的破坏或影响其正常使用功能 。
土力学-第七章土的抗剪强度
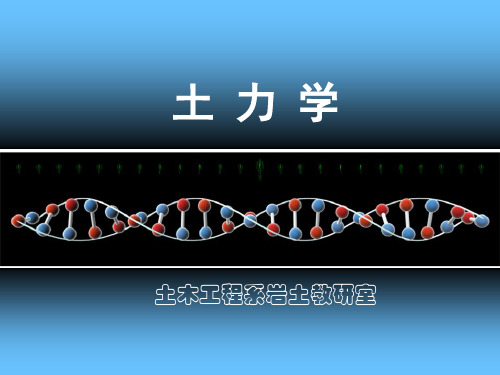
7.3.2 三轴压缩试验
土力学
天津城市建设学院土木系岩土教研室
7.3 土的抗剪强度试验
7.3.2 三轴压缩试验 抗剪强度包线
土力学
分别在不同的周围压力3作用下进行剪切,得到3~4 个 不同的破坏应力圆,绘出各应力圆的公切线即为土的抗剪 强度包线
抗剪强度包线
c
天津城市建设学院土木系岩土教研室
2 2
土力学
圆心坐标[1/2(1 +3 ),0]
应力圆半径r=1/2(1-3 )
A(, )
O
3
2 1/2(1 +3 )
1
土中某点的应 力状态可用莫 尔应力圆描述
天津城市建设学院土木系岩土教研室
7.2 土的抗剪强度理论
7.2.2 莫尔—库伦强度理论及极限平衡条件 土的极限平衡条件
f
f f ( )
f f ( )
这是一条曲线,称为莫尔包络线,简 称莫尔包线(破坏包线、抗剪强度包 线)。 理论和实践证明,土的莫尔包线通常 可用直线代替,该直线方程就是库伦公 式表达的方程。
c
莫尔—库伦强度理论:由库伦公式表示莫尔包线的强度理论。
天津城市建设学院土木系岩土教研室
天津城市建设学院土木系岩土教研室
7.3 土的抗剪强度试验
7.3.3 无侧限抗压强度试验 量表 量力环
qu
土力学
升降 螺杆
试 样
加压 框架
qu
无侧限压缩仪
无侧限抗压强度试验是三轴剪切试验的特例,对试样不施加周围压力, 即3=0,只施加轴向压力直至发生破坏,试样在无侧限压力条件下,剪切破 坏时试样承受的最大轴向压力qu,称为无侧限抗压强度
土力学
天津城市建设学院土木系岩土教研室
7.3 土的抗剪强度试验
7.3.2 三轴压缩试验 抗剪强度包线
土力学
分别在不同的周围压力3作用下进行剪切,得到3~4 个 不同的破坏应力圆,绘出各应力圆的公切线即为土的抗剪 强度包线
抗剪强度包线
c
天津城市建设学院土木系岩土教研室
2 2
土力学
圆心坐标[1/2(1 +3 ),0]
应力圆半径r=1/2(1-3 )
A(, )
O
3
2 1/2(1 +3 )
1
土中某点的应 力状态可用莫 尔应力圆描述
天津城市建设学院土木系岩土教研室
7.2 土的抗剪强度理论
7.2.2 莫尔—库伦强度理论及极限平衡条件 土的极限平衡条件
f
f f ( )
f f ( )
这是一条曲线,称为莫尔包络线,简 称莫尔包线(破坏包线、抗剪强度包 线)。 理论和实践证明,土的莫尔包线通常 可用直线代替,该直线方程就是库伦公 式表达的方程。
c
莫尔—库伦强度理论:由库伦公式表示莫尔包线的强度理论。
天津城市建设学院土木系岩土教研室
天津城市建设学院土木系岩土教研室
7.3 土的抗剪强度试验
7.3.3 无侧限抗压强度试验 量表 量力环
qu
土力学
升降 螺杆
试 样
加压 框架
qu
无侧限压缩仪
无侧限抗压强度试验是三轴剪切试验的特例,对试样不施加周围压力, 即3=0,只施加轴向压力直至发生破坏,试样在无侧限压力条件下,剪切破 坏时试样承受的最大轴向压力qu,称为无侧限抗压强度
第七章 强度理论

莫尔强度理论
其中:
O3 N O3 K O1L 1 1 1 3 t 2 2 O2 P O2 M O1 L 1 1 c t 2 2 O3O1 O1O O3O
注意:以上各式中[c]是指 绝对值, 1,3是指代数值。 (b)
可得
r3 4 , r4 3
12
§ 7-2
四种常用的强度理论
例题7-2-1 试全面校核图a,b,c所示焊接工字梁的强度,
梁的自重不计。已知:梁的横截面对于中性轴的惯性矩为
Iz = 88×106 mm4;半个横截面对于中性轴的静矩为S*zmax = 338×103 mm3;梁的材料Q235钢的许用应力为 [ ]=170 MPa,[ ]=100 MPa。
2
u
s
2
强度条件:
1 3
实践证明该理论对塑性材料比较符合,理论表达的强度条件形 式简明。在对用塑性材料制成的构件进行强度计算时,经常采用这 个理论。但是该理论忽略了中间应力2的影响,势必将要产生误差。 且该理论只适用拉、压许用应力相同的材料。
8
§ 7-2
四种常用的强度理论
塑性材料和脆性材料
}
塑性 材料
t rM 1 3 c
rM:称为莫尔相当应力。
10
§ 7-2
四种常用的强度理论
五、利用强度理论解题的步骤
1、分析计算结构危险点处的应力; 2、确定主应力1 、 2 、 3 ; 3、选择适当的强度理论,计算相当应力r ; 4、进行强度校核r ≤[]或其它计算。
§ 7-1
概述
2.复杂应力情况
1
P
2
p
P
土的抗剪强度理论
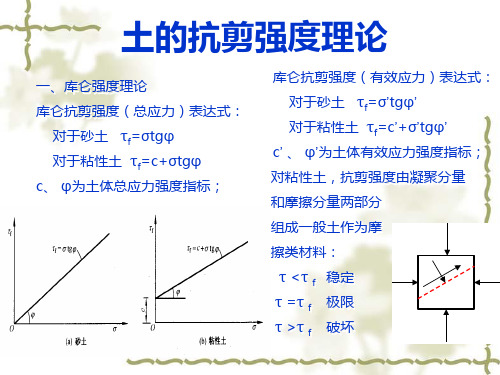
莫尔应力圆
可以证明:D点对应的正应力和剪应力刚好等于面上等于 正应力和剪应力。
莫尔应力圆圆周上的任意点,都代表着单元土体中相应面上的应力状 态。
θ
3
1
土的极限平衡条件 根据这一准则,当土处于极限平衡状态即应理解为破坏状 态,此时的莫尔应力圆即称为极限应力圆或破坏应力圆, 相应的一对平面即称为剪切破坏面(简称剪破面)。
下面将根据莫尔-库仑破坏准则来研究某一土体单元处于 极限平衡状态时的应力条件及其大、小主应力之间关系, 该关系称为土的极限平衡条件。
根据莫尔-库仑破坏准则,当单元土体达到极限平衡状态 时,莫尔应力圆恰好与库仑抗剪强度线相切。
根据图中的几何关系并经过三角公式的变换,可得
1 3
s cot
2
上式即为土的极限平衡条件。当土的强度指标c,φ 为已知,若土中某点的大小 主应力σ1和σ3满足上列关系式时,则该土体正好处于极限平衡或破坏状态。 上式也可适用于有效应力,相应c,φ应该用c’,φ’。
上式也可适用于有效应力,相应c,φ应该用c’,φ’
3f
1f
tg
2
(45
2
)
2c
•
tg(45
2
)
1f
τ <τ f 稳定 τ =τ f 极限 τ >τ f 破坏
二、莫尔-库仑强度理论及土的极限平衡条件
τ=τf 时的极限平衡状态作为土的破坏准则:土体中 某点任意面上剪应力满足该式,该点破坏。
可以把莫尔应力圆与库仑抗剪强度定律互相结合起 来。通过两者之间的对照来对土所处的状态进行判 别。把莫尔应力圆与库仑抗剪强度线相切时的应力 状态,破坏状态—称为莫尔-库仑破坏准则,它是 目前判别土体(土体单元)所处状态的最常用或最基本 的准则。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第七章 土的抗剪强度
?抗剪强度的理论问题 ?破坏准则(极限平衡条件 ) ?抗剪强度测定问题(抗剪强度参数的确定)
土的抗剪强度的工程意义
以土作为建造材料的土工构筑物的 稳定性问题,如土坝、路堤等填方边坡 以及天然土坡等的稳定性问题。
土作为建筑物地基的承载力问 题,如果基础下的地基土体产生整 体滑动或因局部剪切破坏而导致过 大的地基变形,将会造成上部结构 的破坏或影响其正常使用功能 。
?
2
特别指出:剪破面并不产生于最大剪应力面,而与最大剪应力面成? / 2
的夹角,可知,土的剪切破坏并不是由最大剪应力τ max 所控制
五、例题分析
? 【例】地基中某一单元土体上的大主应力为430kPa,小
主应力为200kPa。通过试验测得土的抗剪强度指标c=15 kPa,? =20o。试问①该单元土体处于何种状态?②单元
际应力圆半径小于极限应力圆半径,所以,该单元土体 处于弹性平衡状态
?
3f
?
?
1
tan
2
?? ?
45
o
?
? ?? ?
2?
2c tan ??45 o ?
?
?
2
?? ? 189 .8kPa ?
计算结果表明:? 3f小于该单元土体实际小主应力? 3,
?1
3、莫尔-库仑破坏准则
?
A ?max
? c ? f 2? f
cctg? ? 3
?1 ?
(? 1 +? 3 ) /2
?1 ?3
?f ?1
sin ? ?
1 2
??
1
??
3?
c cot ?
?
1 2
??
1
??
3?
? 3 无粘性土:c=0
?
1
?
?
3
tan 2 ?? 45 o ?
?
?
2
?? ?
?
3
?
?
1 tan 2 ?? 45 o ?
土体最大剪应力出现在哪个面上,是否会沿剪应力最大的
面发生剪破?
【解答】
已知? 1=430kPa,? 3=200kPa,c=15kPa,? =20o
1.计算法A
?
1f
?
?
3
tan 2 ?? 45 o ?
?
?
2
?? ? ?
2c tan ?? 45 o ?
?
?
2
?? ? ?
450 .8kPa
计算结果表明:? 1f大于该单元土体实际大主应力? 1,实
土作为工程构筑物环境的安全性问题,即 土压力问题,如挡土墙、地下结构等的周围土 体,它的强度破坏将造成对墙体过大的侧向土 压力,以至可能导致这些工程构筑物发生滑动、 倾覆等破坏事故 。
路堤塌方
挡土结构物破坏
地基失稳
§7.1概述
土的抗剪强度 土体对于外荷载所产生的剪应力的极限抵抗能力。
土的剪切破坏: 在外荷载作用下,土体中将产
? 将抗剪强度包线与应力状
态(采用莫尔应力圆表示)画
在同一张坐标图上。它们之间
的关系有以下三种情况:
Ⅰ稳定状态 Ⅱ极限平衡状态 Ⅲ不可能状态
?
c
?3
?1
? ?3
? ?
?1
强度线
?3
极限应力圆
ⅠⅡ Ⅲ
? ? 1 ? 1 ? 1
1、任意一点的某一平面的 法向应力和剪应力
?1
?3
?3
?
?
? ?
? 3 ?dlsin
?
砂土
?
?
?
后来,根据 粘性土剪切试验,又提出更普遍的表达式:
?f
? f ? ? tan ? ? c
抗剪强度指标
?
c
粘土
?
c:土的粘聚力
? :土的内摩擦角
二、土体抗剪强度影响因素
?与土的性质有关:
无粘性土的抗剪强度与剪切面上的法向应力成正比,其本质是由于土粒之 间的滑动摩擦以及凹凸面间的镶嵌作用所产生的摩阻力,其大小决定于土粒表 面的粗糙度、密实度、土颗粒的大小以及颗粒级配等因素。
c ′—— 土的有效粘聚力(内聚力),kPa
? ′—— 土的有效内摩擦角,度。
?与剪切速率、应力状态和应力历史等许多因素有关。
土的抗剪强度的两种表示方法
三、莫尔—库伦强度理论
1910年莫尔(Mohr)提出材料的破坏是剪切破坏,当任一平面上的剪
应力等于材料的抗剪强度时该点就发生破坏,并提出在破坏面上的剪应
粘性土的抗剪强度由两部分组成,一部分是摩擦力(与法向应力成正比), 另—部分是土粒之间的粘结力,它是由于粘性土颗粒之间的胶结作用和静电引 力效应等因素引起的。
?与排水条件有关: 根据有效应力概念,土体内的剪应力仅能由土的骨架
承担.库伦公式应修改为:τf =? ′tan? ′或τf = c′+? ′tan? ′ 式中 ? ′—— 剪切滑动面上的法向有效应力,kPa
生剪应力和剪切变形,当土中某 点由外力所产生的剪应力达到土 的抗剪强度时,土就沿着剪应力 作用方向产生相对滑动,该点便 发生剪切破坏。
土的强度问题实质上就是土的抗剪强度问题。
§7.2土的抗剪强度与极限平衡条件
一、库仑公式及抗剪强度指标
1776年,库仑根据 砂土剪切试验,提出:
?
?f
? f ? ? tan ?
?
?
2
?? ?
?
1
?
?
3 tan 2 ?? 45 o ?
?
?
2
?? ? ?
2c tan ?? 45 o ?
?
?
2
?? ?
?
3
?
?
1 tan 2 ?? 45 o ?
?
?
2
?? ? ?
2c tan ?? 45 o ?
?
?
2
?? ?
破坏面与大主应力
作用面的夹角为? f
?
f
?
1?90?? ? ??
2
45? ?
力τf 是该面上法向应力? 的函数,即τf =f (? )。莫尔理论对土比较合
适,土的莫尔包线通常近似地用直线代替,该直线方程就是库伦公式。 由库伦公式表示莫尔包线的强度理论称为莫尔—库伦强度理论。
四、莫尔—库伦破坏准则 —— 土的极限平衡条件
极限平衡条件: 当土体中任意一点在某一平面
上的剪应力达到土的抗剪强度时,就 发生剪切破坏。此时,土体处于极限 平衡状态。此状态下,大、小主应力 之间的关系,称为莫尔—库伦破坏准 则。
?1
?1
dlcos?
楔体静 ? 3dl sin ? ? ? dl sin ? ? ?dl cos ? ? 0
力平衡 ? 1dl cos ? ? ? dl cos ? ? ?dl sin ? ? 0
?
?
1 ??
2
1
?
?
3 ??
1 2
??
1
?
?
3 ?cos 2?
?
?
1 2
??
1
?
?
3
?sin
2?
2、一点的应力状态( 莫尔应力圆表示法)
?
A(? , ? )
?
2?
?
O ? 3 (? 1 +? 3 ) /2 ? 1
圆心坐标 [(? 1 +? 3 ) /2 ,0] 应力圆半径 r =(? 1-? 3 ) /2
莫尔应力圆方程
?1
? ?3
? ?
??ቤተ መጻሕፍቲ ባይዱ?
?
1 2
??
1
?
?
3
2
????
?
?
2
?
?1 ?? 2
??
1
?
?
2
3 ????
?3
A点的应力
?抗剪强度的理论问题 ?破坏准则(极限平衡条件 ) ?抗剪强度测定问题(抗剪强度参数的确定)
土的抗剪强度的工程意义
以土作为建造材料的土工构筑物的 稳定性问题,如土坝、路堤等填方边坡 以及天然土坡等的稳定性问题。
土作为建筑物地基的承载力问 题,如果基础下的地基土体产生整 体滑动或因局部剪切破坏而导致过 大的地基变形,将会造成上部结构 的破坏或影响其正常使用功能 。
?
2
特别指出:剪破面并不产生于最大剪应力面,而与最大剪应力面成? / 2
的夹角,可知,土的剪切破坏并不是由最大剪应力τ max 所控制
五、例题分析
? 【例】地基中某一单元土体上的大主应力为430kPa,小
主应力为200kPa。通过试验测得土的抗剪强度指标c=15 kPa,? =20o。试问①该单元土体处于何种状态?②单元
际应力圆半径小于极限应力圆半径,所以,该单元土体 处于弹性平衡状态
?
3f
?
?
1
tan
2
?? ?
45
o
?
? ?? ?
2?
2c tan ??45 o ?
?
?
2
?? ? 189 .8kPa ?
计算结果表明:? 3f小于该单元土体实际小主应力? 3,
?1
3、莫尔-库仑破坏准则
?
A ?max
? c ? f 2? f
cctg? ? 3
?1 ?
(? 1 +? 3 ) /2
?1 ?3
?f ?1
sin ? ?
1 2
??
1
??
3?
c cot ?
?
1 2
??
1
??
3?
? 3 无粘性土:c=0
?
1
?
?
3
tan 2 ?? 45 o ?
?
?
2
?? ?
?
3
?
?
1 tan 2 ?? 45 o ?
土体最大剪应力出现在哪个面上,是否会沿剪应力最大的
面发生剪破?
【解答】
已知? 1=430kPa,? 3=200kPa,c=15kPa,? =20o
1.计算法A
?
1f
?
?
3
tan 2 ?? 45 o ?
?
?
2
?? ? ?
2c tan ?? 45 o ?
?
?
2
?? ? ?
450 .8kPa
计算结果表明:? 1f大于该单元土体实际大主应力? 1,实
土作为工程构筑物环境的安全性问题,即 土压力问题,如挡土墙、地下结构等的周围土 体,它的强度破坏将造成对墙体过大的侧向土 压力,以至可能导致这些工程构筑物发生滑动、 倾覆等破坏事故 。
路堤塌方
挡土结构物破坏
地基失稳
§7.1概述
土的抗剪强度 土体对于外荷载所产生的剪应力的极限抵抗能力。
土的剪切破坏: 在外荷载作用下,土体中将产
? 将抗剪强度包线与应力状
态(采用莫尔应力圆表示)画
在同一张坐标图上。它们之间
的关系有以下三种情况:
Ⅰ稳定状态 Ⅱ极限平衡状态 Ⅲ不可能状态
?
c
?3
?1
? ?3
? ?
?1
强度线
?3
极限应力圆
ⅠⅡ Ⅲ
? ? 1 ? 1 ? 1
1、任意一点的某一平面的 法向应力和剪应力
?1
?3
?3
?
?
? ?
? 3 ?dlsin
?
砂土
?
?
?
后来,根据 粘性土剪切试验,又提出更普遍的表达式:
?f
? f ? ? tan ? ? c
抗剪强度指标
?
c
粘土
?
c:土的粘聚力
? :土的内摩擦角
二、土体抗剪强度影响因素
?与土的性质有关:
无粘性土的抗剪强度与剪切面上的法向应力成正比,其本质是由于土粒之 间的滑动摩擦以及凹凸面间的镶嵌作用所产生的摩阻力,其大小决定于土粒表 面的粗糙度、密实度、土颗粒的大小以及颗粒级配等因素。
c ′—— 土的有效粘聚力(内聚力),kPa
? ′—— 土的有效内摩擦角,度。
?与剪切速率、应力状态和应力历史等许多因素有关。
土的抗剪强度的两种表示方法
三、莫尔—库伦强度理论
1910年莫尔(Mohr)提出材料的破坏是剪切破坏,当任一平面上的剪
应力等于材料的抗剪强度时该点就发生破坏,并提出在破坏面上的剪应
粘性土的抗剪强度由两部分组成,一部分是摩擦力(与法向应力成正比), 另—部分是土粒之间的粘结力,它是由于粘性土颗粒之间的胶结作用和静电引 力效应等因素引起的。
?与排水条件有关: 根据有效应力概念,土体内的剪应力仅能由土的骨架
承担.库伦公式应修改为:τf =? ′tan? ′或τf = c′+? ′tan? ′ 式中 ? ′—— 剪切滑动面上的法向有效应力,kPa
生剪应力和剪切变形,当土中某 点由外力所产生的剪应力达到土 的抗剪强度时,土就沿着剪应力 作用方向产生相对滑动,该点便 发生剪切破坏。
土的强度问题实质上就是土的抗剪强度问题。
§7.2土的抗剪强度与极限平衡条件
一、库仑公式及抗剪强度指标
1776年,库仑根据 砂土剪切试验,提出:
?
?f
? f ? ? tan ?
?
?
2
?? ?
?
1
?
?
3 tan 2 ?? 45 o ?
?
?
2
?? ? ?
2c tan ?? 45 o ?
?
?
2
?? ?
?
3
?
?
1 tan 2 ?? 45 o ?
?
?
2
?? ? ?
2c tan ?? 45 o ?
?
?
2
?? ?
破坏面与大主应力
作用面的夹角为? f
?
f
?
1?90?? ? ??
2
45? ?
力τf 是该面上法向应力? 的函数,即τf =f (? )。莫尔理论对土比较合
适,土的莫尔包线通常近似地用直线代替,该直线方程就是库伦公式。 由库伦公式表示莫尔包线的强度理论称为莫尔—库伦强度理论。
四、莫尔—库伦破坏准则 —— 土的极限平衡条件
极限平衡条件: 当土体中任意一点在某一平面
上的剪应力达到土的抗剪强度时,就 发生剪切破坏。此时,土体处于极限 平衡状态。此状态下,大、小主应力 之间的关系,称为莫尔—库伦破坏准 则。
?1
?1
dlcos?
楔体静 ? 3dl sin ? ? ? dl sin ? ? ?dl cos ? ? 0
力平衡 ? 1dl cos ? ? ? dl cos ? ? ?dl sin ? ? 0
?
?
1 ??
2
1
?
?
3 ??
1 2
??
1
?
?
3 ?cos 2?
?
?
1 2
??
1
?
?
3
?sin
2?
2、一点的应力状态( 莫尔应力圆表示法)
?
A(? , ? )
?
2?
?
O ? 3 (? 1 +? 3 ) /2 ? 1
圆心坐标 [(? 1 +? 3 ) /2 ,0] 应力圆半径 r =(? 1-? 3 ) /2
莫尔应力圆方程
?1
? ?3
? ?
??ቤተ መጻሕፍቲ ባይዱ?
?
1 2
??
1
?
?
3
2
????
?
?
2
?
?1 ?? 2
??
1
?
?
2
3 ????
?3
A点的应力
