自动控制原理电子教案新 (2)优秀课件
合集下载
【精编】自动控制原理第2章PPT课件

隙磁通的乘积成正比,又因磁通恒定,有Md Kmia,
联立求解,整理后得
w ww K L e a K J m d d 2 t2 K R e a K J m d d t K 1 eu a K R e K a m M L K L e K a m d M d tL
自动控制原理
6
(续上页)
w ww K L e a K J m d d 2 t2 K R e a K J m d d t K 1 eu a K R e K a m M L K L e K a m d M d tL
自动控制原理
15
2.3.1 传递函数的性质
(1)传递函数是复变量s的有理真分式函数,分子的阶数m一 般低于或等于分母的阶数n, 即m≤n ,且所有系数均为 实数。
(2)传递函数只取决于系统和元件的结构和参数,与外作用 及初始条件无关。
(3)一定的传递函数有一定的零、极点分布图与之对应,因
此传递函数的零、极点分布图也表征了系统的动态性能。
的中间变量无法反映出来。
(6)一个传递函数只能表示一个输入对一个输出的函数关系。
自动控制原理
16
2.3.1 典型环节及其传递函数
(1)比例环节 G(s)= K
(2)惯性环节 G(s) 1 Ts 1
T ——惯性环节时间常 数
(3)积分环节 G(s) 1 Ts
当积分环节的输入信号为单位阶跃 函数时,则输出为t/T,它随着时间直线 增长。
或
w ww T a T m d d 2 t2 T m d d t K 1 eu a T J m M L T a J T m d M d tL
Tm
Ra J K eKm
——机电时间常数(秒)
Ta
联立求解,整理后得
w ww K L e a K J m d d 2 t2 K R e a K J m d d t K 1 eu a K R e K a m M L K L e K a m d M d tL
自动控制原理
6
(续上页)
w ww K L e a K J m d d 2 t2 K R e a K J m d d t K 1 eu a K R e K a m M L K L e K a m d M d tL
自动控制原理
15
2.3.1 传递函数的性质
(1)传递函数是复变量s的有理真分式函数,分子的阶数m一 般低于或等于分母的阶数n, 即m≤n ,且所有系数均为 实数。
(2)传递函数只取决于系统和元件的结构和参数,与外作用 及初始条件无关。
(3)一定的传递函数有一定的零、极点分布图与之对应,因
此传递函数的零、极点分布图也表征了系统的动态性能。
的中间变量无法反映出来。
(6)一个传递函数只能表示一个输入对一个输出的函数关系。
自动控制原理
16
2.3.1 典型环节及其传递函数
(1)比例环节 G(s)= K
(2)惯性环节 G(s) 1 Ts 1
T ——惯性环节时间常 数
(3)积分环节 G(s) 1 Ts
当积分环节的输入信号为单位阶跃 函数时,则输出为t/T,它随着时间直线 增长。
或
w ww T a T m d d 2 t2 T m d d t K 1 eu a T J m M L T a J T m d M d tL
Tm
Ra J K eKm
——机电时间常数(秒)
Ta
自动控制原理-绪论、第2章新 114页PPT文档

5.5 用频率法分析控制系统的稳定性
5.6 系统暂态特性和开环闭环特性的关系
第六章 控制系统的校正及综合
6学时
6.1 控制系统校正的一般概念
6.2 串联校正
6.3 反馈校正
注:实验6学时依课程进度安排;另在期中、期末各安排2学时
习题课。
三、学习方法和要求
1、自动控制理论发展的不同阶段 自动控制的飞速发展是在20世纪,主要阶段为: 20世纪30 ~ 50年代,形成经典控制理论 主要成就:
3学时 (2)
(1)
第二章 自动控制系统的数学模型
10~12学时
2.1 动态微分方程式的编写
(3)
2.2 非线性数学模型线性化
(1)
2.3 传递函数
(3)
2.4 系统动态结构图
(3)
2.5 系统传递函数和结构图的等效变换 (2)
第三章 自动控制系统的时域分析 时
3.1 自动控制系统的时域指标 3.2 一阶系统的阶跃响应 3.3 二阶系统的阶跃响应 3.4 高阶系统的暂态响应 3.5 自动控制系统的代数稳定判据 3.6 稳态误差
(2)现代控制理论 — 采用状态空间法,研究多输入— 多输出(MIMO)、时变、非线性、高精度、高效能 等控制系统 的分析与设计问题。
(3)智能控制 — 以人工智能、控制理论和计算机科学为 基础的新型控制技术。
3、学习方法和要求
(1)熟练掌握各章节基本概念、基本理论和分析方法; (2)了解时域法、频域法和根轨迹法的内在联系,以便
特点: 不满足叠加原理;暂态特性与初始条件有关。
3、典型的非线性环节特性 4、两者的关系(参考教材Page6)
二、 连续数据系统和离散数据系统
1 、连续数据系统—— 信号为模拟的连续函数。
自动控制原理教学ppt

前馈校正
在系统的输入端引入一个前馈环节, 根据输入信号的特性对系统进行补 偿,以提高系统的跟踪精度和抗干 扰能力。
复合校正方法
串联复合校正
将串联超前、串联滞后和串联滞 后-超前等校正方法结合起来, 设计一个复合的串联校正环节, 以实现更复杂的系统性能要求。
反馈复合校正
将局部反馈、全局反馈和前馈等 校正方法结合起来,设计一个复 合的反馈校正环节,以实现更全
自适应控制系统概述
简要介绍自适应控制系统的基本原理、结构和特点,为后续内容 做铺垫。
自适应控制方法
详细介绍自适应控制方法,如模型参考自适应控制、自校正控制等, 及其在自动控制领域中的应用实例。
自适应控制算法
阐述自适应控制算法的实现过程,包括参数估计、控制器设计等关 键技术。
鲁棒控制理论应用
鲁棒控制系统概述
自动控制应用领域
工业领域
自动控制广泛应用于工业领域,如自 动化生产线、工业机器人、智能制造 等。
01
02
航空航天领域
自动控制是航空航天技术的重要组成 部分,如飞行器的自动驾驶仪、导弹 的制导系统等。
03
交通运输领域
自动控制也应用于交通运输领域,如 智能交通系统、自动驾驶汽车等。
其他领域
此外,自动控制还应用于农业、医疗、 环保等领域,如农业自动化、医疗机 器人、环境监测与治理等。
提高系统的稳态精度。
串联滞后-超前校正
03
结合超前和滞后校正的优点,设计一个既有超前又有滞后的校
正环节,以同时改善系统的动态性能和稳态精度。
反馈校正方法
局部反馈校正
在系统的某个局部引入反馈环节, 以改善该局部的性能,而不影响 系统的其他部分。
全局反馈校正
在系统的输入端引入一个前馈环节, 根据输入信号的特性对系统进行补 偿,以提高系统的跟踪精度和抗干 扰能力。
复合校正方法
串联复合校正
将串联超前、串联滞后和串联滞 后-超前等校正方法结合起来, 设计一个复合的串联校正环节, 以实现更复杂的系统性能要求。
反馈复合校正
将局部反馈、全局反馈和前馈等 校正方法结合起来,设计一个复 合的反馈校正环节,以实现更全
自适应控制系统概述
简要介绍自适应控制系统的基本原理、结构和特点,为后续内容 做铺垫。
自适应控制方法
详细介绍自适应控制方法,如模型参考自适应控制、自校正控制等, 及其在自动控制领域中的应用实例。
自适应控制算法
阐述自适应控制算法的实现过程,包括参数估计、控制器设计等关 键技术。
鲁棒控制理论应用
鲁棒控制系统概述
自动控制应用领域
工业领域
自动控制广泛应用于工业领域,如自 动化生产线、工业机器人、智能制造 等。
01
02
航空航天领域
自动控制是航空航天技术的重要组成 部分,如飞行器的自动驾驶仪、导弹 的制导系统等。
03
交通运输领域
自动控制也应用于交通运输领域,如 智能交通系统、自动驾驶汽车等。
其他领域
此外,自动控制还应用于农业、医疗、 环保等领域,如农业自动化、医疗机 器人、环境监测与治理等。
提高系统的稳态精度。
串联滞后-超前校正
03
结合超前和滞后校正的优点,设计一个既有超前又有滞后的校
正环节,以同时改善系统的动态性能和稳态精度。
反馈校正方法
局部反馈校正
在系统的某个局部引入反馈环节, 以改善该局部的性能,而不影响 系统的其他部分。
全局反馈校正
《自动控制原理》课件第二章

Cen idRd
Ld
d id dt
ud
(2-4)
当略去电动机的负载力矩和粘性摩擦力矩时,机械运动
微分方程式为
M GD2 d n 375 d t
(2-5)
式中,M为电动机的转矩(N·m); GD2为电动机的飞轮矩
(N·m2)。当电动机的励磁不变时,电动机的转矩与电枢电
流成正比,即电动机转矩为
M=Cmid
称为相似量。如式(2-1)中的变量ui、uo分别与式(2-3)中的变
量f(t)、y(t)为对应的相似量。
2.1.2 线性定常微分方程求解及系统运动的模态 当系统微分方程列写出来后,只要给定输入量和初始条
件,便可对微分方程求解,并由此了解系统输出量随时间变 化的特性。
若线性定常连续系统的微分方程模型的一般表示形式为 y(n)(t)+a1y(n-1)(t)+···+any(t)=b0u(m)(t)+b1u(m-1)(t)+…+bmu(t)
x0
( x x0 )2
当增量x-x0很小时,略去其高次幂项,则有
y
y0
f (x)
f (x0)
d f (x) dx
x0
(x x0)
令Δy=y-y0=f(x)-f(x0),Δx=x-x0,K=(df(x)/dx)|x0,则线性
化方程可简记为Δy=KΔx。这样,便得到函数y=f(x)在工作
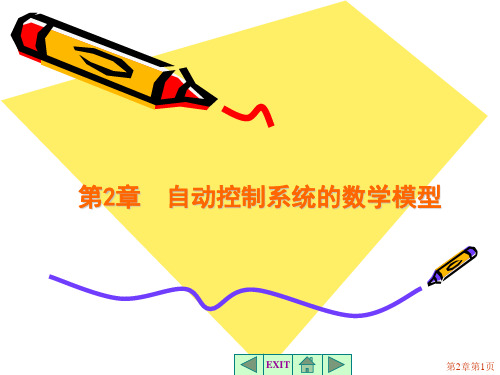
点A附近的线性化方程为y=Kx。
图2-4 小偏差线性化示意图
对于有两个自变量x1、x2的非线性函数f(x1,x2),同样 可在某工作点(x10,x20)附近用泰勒级数展开为
y
f (x1 ,x2 )
f
自动控制原理第2章ppt课件
1 2 f 2! r12
(r1 r10)2
2 f r22
(r2
r20)2
yK1r1K2r2
函数变化与自变量变化成线性比例关系。
EXIT
第2章第21页
2.2.3 系统线性化的条件及步骤 1.条件 ① 系统工作在正常的工作状态,有一个稳定的工作 点; ② 在运行过程中偏离且满足小偏差条件; ③ 在工作点处,非线性函数各阶导数均存在,即函 数属于单值、连续、光滑的非本质非线性函数。
EXIT
第2章第14页
2.1.3 机电系统
图示为一他激直流电动机。 +
图中,ω为电动机角速度
〔rad/s ) ,Mc 为折 算到电
ua _
动机轴上的总负载力矩 +
〔N·m ) , ua 为 电 枢 电 压 〔V)。设激磁电流恒定, _
并忽略电枢反应。
ia La
ea Ra
Mc
负载
取ua为给定输入量, ω为输出量,Mc为扰动量,忽略电枢电感, 得:
因而,对于不太严重的非线性系统,可以在一定的工 作范围内线性化处理。工程上常用的方法是将非线性函数 在平衡点附近展开成泰勒级数,去掉高次项以得到线性函 数。
EXIT
第2章第19页
2.2.2 举例
y
① 一个自变量 y=f(r)
y0+△y
y0
r—元件的输入信号,y—元件的输出
AB
设信原号运行于某平衡点〔静态工作点)
频率特性
同一个系统,可以选用不同的数学模型, 如研究时域响应时可以用传递函数, 研究频域响应时则要用频率特性。
EXIT
第2章第5页
4.建立方法
a.分析计算法
分析计算法是根据支配系统的内在运动规律以 及系统的结构和参数,推导出输入量和输出量之间 的数学表达式,从而建立数学模型——适用于简单 的系统。
《自动控制原理》课件

集成化:智能控制技术将更加集 成化,能够实现多种控制技术的 融合和应用。
添加标题
添加标题
添加标题
添加标题
网络化:智能控制技术将更加网 络化,能够实现远程控制和信息 共享。
绿色化:智能控制技术将更加绿 色化,能够实现节能减排和环保 要求。
控制系统的网络化与信息化融合
网络化控制:通过互联网实现远程控制和监控
现代控制理论设计方法
状态空间法:通过建立状态空间模型,进行系统分析和设计 频率响应法:通过分析系统的频率响应特性,进行系统分析和设计 极点配置法:通过配置系统的极点,进行系统分析和设计 线性矩阵不等式法:通过求解线性矩阵不等式,进行系统分析和设计
最优控制理论设计方法
基本概念:最优控制、状态方程、控制方程等 设计步骤:建立模型、求解最优控制问题、设计控制器等 控制策略:线性二次型最优控制、非线性最优控制等 应用领域:航空航天、机器人、汽车电子等
动态性能指标
稳定性:系统在受到扰动后能否恢复到平衡状态 快速性:系统在受到扰动后恢复到平衡状态的速度 准确性:系统在受到扰动后恢复到平衡状态的精度 稳定性:系统在受到扰动后能否保持稳定状态
抗干扰性能指标
稳定性:系统在受到干扰后能够 恢复到原来的状态
准确性:系统在受到干扰后能够 保持原有的精度和准确性
信息化控制:利用大数据、云计算等技术实现智能化控制
融合趋势:网络化与信息化的融合将成为未来控制系统的发展方向 应用领域:工业自动化、智能家居、智能交通等领域都将受益于网络化与 信息化的融合
控制系统的模块化与集成化发展
模块化:将复杂的控制系统分解为多个模块,每个模块负责特定的功能,便于设计和维护 集成化:将多个模块集成为一个整体,提高系统的性能和可靠性 发展趋势:模块化和集成化是未来控制系统发展的重要方向 应用领域:广泛应用于工业自动化、智能家居、智能交通等领域
自动控制原理02PPT课件

第30页/共32页
第31页/共32页
感谢您的观看!
第32页/共32页
第29页/共32页
微分方程式的解
a、 A、B、
指数函数 Aeat 正弦函数 Bsin(t+)
微分方程式的各系数
外部条件
起始条件
✓应用拉氏变换法求解微分方程时,由于初始条件已自动地 包含在微分方程的拉氏变换式中,因此,不需要根据初始 条件求积分常数的值就可得到微分方程的全解。
✓如果所有的初始条件为零,微分方程的拉氏变换可以简单 地用sn代替dn/dtn得到。
正弦函数是控制系统中常用的一种典型外作用,很多实 际
的随动系统就是常工作在此外作用下。 更为重要的是系统在正弦函数作用下的响应,即频率
响应是自动控制理论中研究系统性能的重要依据。
4
第4页/共32页
Part 2.2 拉氏变换及其反变换
2.2.1 拉氏变换的定义 2.2.2 拉氏变换的计算 2.2.3 拉氏变换求解方程
2
第2页/共32页
(3)、脉冲函数
A
为强脉度冲为函A数的定脉义冲为函:。数在f可(tt表)0时示tl0im刻0 f出(t(0tt[)现1(tt的0)A)单1((tt)位 t脉0 )]冲
函数为
。
注意:脉冲函数仅用于分析研究,现实中并 不存在。
3
第3页/共32页
(4)、正弦函
正弦数函数的数学表达式为: f (t) Asin( t )
.... bm1s .... an1s
bm bn
,m
n
L-1[F(s)] = L-1[F1(s)]+L-1[F2(s)]+…+L-1[Fn(s)] = f1(t) + f2(t) + … + fn(t)
第31页/共32页
感谢您的观看!
第32页/共32页
第29页/共32页
微分方程式的解
a、 A、B、
指数函数 Aeat 正弦函数 Bsin(t+)
微分方程式的各系数
外部条件
起始条件
✓应用拉氏变换法求解微分方程时,由于初始条件已自动地 包含在微分方程的拉氏变换式中,因此,不需要根据初始 条件求积分常数的值就可得到微分方程的全解。
✓如果所有的初始条件为零,微分方程的拉氏变换可以简单 地用sn代替dn/dtn得到。
正弦函数是控制系统中常用的一种典型外作用,很多实 际
的随动系统就是常工作在此外作用下。 更为重要的是系统在正弦函数作用下的响应,即频率
响应是自动控制理论中研究系统性能的重要依据。
4
第4页/共32页
Part 2.2 拉氏变换及其反变换
2.2.1 拉氏变换的定义 2.2.2 拉氏变换的计算 2.2.3 拉氏变换求解方程
2
第2页/共32页
(3)、脉冲函数
A
为强脉度冲为函A数的定脉义冲为函:。数在f可(tt表)0时示tl0im刻0 f出(t(0tt[)现1(tt的0)A)单1((tt)位 t脉0 )]冲
函数为
。
注意:脉冲函数仅用于分析研究,现实中并 不存在。
3
第3页/共32页
(4)、正弦函
正弦数函数的数学表达式为: f (t) Asin( t )
.... bm1s .... an1s
bm bn
,m
n
L-1[F(s)] = L-1[F1(s)]+L-1[F2(s)]+…+L-1[Fn(s)] = f1(t) + f2(t) + … + fn(t)
自动控制原理课件ppt

控制目标。
传感器
检测系统的状态或参数,并将 检测结果转换为电信号传输给
控制器。
调节机构
根据控制器的指令调整系统的 参数或结构,以实现系统的稳
定和性能优化。
02
控制系统基本概念
系统稳定性
01Biblioteka 0203稳定性的定义
一个控制系统在受到扰动 后能够回到原始状态的能 力。
稳定性的分类
根据系统响应的不同,可 以分为渐近稳定、指数稳 定和不稳定三种类型。
闭环控制系统
系统的输出反馈到输入端,通过反馈 控制提高控制精度。
03
控制系统的数学模型
传递函数
定义
传递函数是描述线性定常系统动 态特性的数学模型,它反映了系 统输出与输入之间的函数关系。
形式
传递函数通常表示为有理分式的 形式,即 G(s) = num(s)/den(s) ,其中 s 是复变量,num(s) 是 分子多项式,den(s) 是分母多项
参数优化
根据系统性能指标,调整控制器的参数,以实现更好的控制效果 。
结构优化
对控制系统结构进行调整,以提高系统的稳定性和动态性能。
鲁棒性优化
提高系统对不确定性和干扰的抵抗能力,保证系统在各种情况下 都能稳定运行。
控制系统的调试与测试
硬件调试
对控制系统的硬件部分进行调试,确保硬件设备正常工作 。
软件调试
自动控制的应用
工业自动化
航空航天
交通运输
智能家居
自动化生产线、机器人 、自动化仪表等。
飞行器控制、卫星轨道 控制等。
自动驾驶车辆、列车控 制等。
智能家电、智能照明等 。
自动控制系统的组成
01
02
03
传感器
检测系统的状态或参数,并将 检测结果转换为电信号传输给
控制器。
调节机构
根据控制器的指令调整系统的 参数或结构,以实现系统的稳
定和性能优化。
02
控制系统基本概念
系统稳定性
01Biblioteka 0203稳定性的定义
一个控制系统在受到扰动 后能够回到原始状态的能 力。
稳定性的分类
根据系统响应的不同,可 以分为渐近稳定、指数稳 定和不稳定三种类型。
闭环控制系统
系统的输出反馈到输入端,通过反馈 控制提高控制精度。
03
控制系统的数学模型
传递函数
定义
传递函数是描述线性定常系统动 态特性的数学模型,它反映了系 统输出与输入之间的函数关系。
形式
传递函数通常表示为有理分式的 形式,即 G(s) = num(s)/den(s) ,其中 s 是复变量,num(s) 是 分子多项式,den(s) 是分母多项
参数优化
根据系统性能指标,调整控制器的参数,以实现更好的控制效果 。
结构优化
对控制系统结构进行调整,以提高系统的稳定性和动态性能。
鲁棒性优化
提高系统对不确定性和干扰的抵抗能力,保证系统在各种情况下 都能稳定运行。
控制系统的调试与测试
硬件调试
对控制系统的硬件部分进行调试,确保硬件设备正常工作 。
软件调试
自动控制的应用
工业自动化
航空航天
交通运输
智能家居
自动化生产线、机器人 、自动化仪表等。
飞行器控制、卫星轨道 控制等。
自动驾驶车辆、列车控 制等。
智能家电、智能照明等 。
自动控制系统的组成
01
02
03
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x 2 ( t) A 0 (A kck o t s B ksk itn ) k 1
分析:因斜对称性 A0=0 据付立叶分析
Ak
2
0x2(t)cosktd(t)
Bk
2
0x2(t)sinktd(t)
1.非线性系统的描述函数定义
分析:因低通滤斜波特性,k>1, Ak=Bk=0
于是有
x 2 ( t ) A 1 ct o B 1 st s i C 1 s n t i1 ) n
2K[2sin1a Aa A1(a A)2]
A>a
0
A<a
2. 典型非线性元件的描述函数
(3)滞环特性的描述函数
2
2 jtg1A1
A B e 1
1
B1
A>a
N(A)=
A
0
A<a
A14K[AaA2aA] B14K[A 2sin112Aa212Aa aAaA2]
3.用描述函数法研究非线性控制系统
(1) 非线性控制系统
N(A,)=N(A)
2. 典型非线性元件的描述函数
(1)饱和特性的描述函数法
x2
x2
K
-a
a x1
-
t
Hale Waihona Puke x1- t
2. 典型非线性元件的描述函数
(1)饱和特性的描述函数法 当A<a , x2(t) = KA sin t, N(A)=X2(A)/X1(A)=K 当A>a,
KA sin t
0 t
x2(t) = Ka KA sin t
-1/N(A). Ⅰ)稳定系统
(3)滞环特性 K(x-a sign x ) |x |0
y=
不变
x =0
y
对系统性能的影响
x
• 增大稳态误差
• 使波形失真
• 稳定裕量减小,振荡加剧,动态特性变坏
5.典型非线性元件及对系统性能的影响
(4)继电特性 ym
y=
-ym
x0+ x0-
y ym
对系统性能的影响
x
• 增大稳态误差
-ym
• 造成自振荡
1.非线性系统的描述函数定义
系统框图
x1
x2
N
假设条件
(1) 正弦输入 x1(t)=Asint (2)非储能元件
无动态特性,无惯性,不是时间的函数 (3)特性斜对称
f(-x1)=-f(x1) (4) 其线性部分具有较好的低通滤波性能
x2 x1
1.非线性系统的描述函数定义
描述函数推导
输入: x1(t)=Asint 稳态输出(付立叶级数表示):
R
N(A)
G0(s)
Y
(2) 闭环频率特性
G (j)Y R ((jj ))1 N N (A ()A G )G 0(0j( j ))
(3) 闭环特征方程
1 N (A )G 0 (j) 0
3.用描述函数法研究非线性控制系统
(4) 稳定性分析
当G(j)=-1/N(A) 时,产生临界振荡. 线性系统的临 界点为(-1,j0), 而在非线性系统中有一条临界曲线为
K(x - a sign x) x>0 x<0
|x|a |x|>a
5.典型非线性元件及对系统性能的影响
特性曲线
y K
a
x
对系统性能的影响
• 直接造成稳态误差
• 会使振荡减弱,因处于死区时,相当于信号断开。 • 滤去小幅干扰,提高系统抗干扰能力。 • 跟踪斜坡信号时有时间滞后。
5.典型非线性元件及对系统性能的影响
• 稳定性减弱
6.非线性控制系统的分析方法
以上为粗略定性分析. 由于非线性系统建模困 难,解方程更难,所以至今 没有精确和统一的分析方法. 下面介绍的三种常用方 法也不完善的. (1)描述函数法
用一次谐波代替非正弦波, 只是近似分析 适用于周期信号,不适用非周期信号 (2)相平面法 用相平面图研究非线性系统的动态特性,只适 用于二阶系统. (3)李雅普诺夫第二方法(直接法)
t - - t
∵ A sin =a
∴ = sin-1(a/A)
A1 20x2(t)costd(t) 0
B1 20x2(t)sintd(t)
2. 典型非线性元件的描述函数
(1)饱和特性的描述函数法
B1
2
0 KA
(sin
t ) 2 d ( t )
2
Ka
sin
td ( t )
2
3.线性系统与非线性系统的关系
实际系统总含非线性环节,所以是非线性系统。 但在小信号范围内可线性化为线性系统来分析。
4.非线性系统的特征
(1)输出响应与输入信号大小和系统初态有关
4.非线性系统的特征
(2)系统稳定性与输入信号大小和系统初态有关
(3)会产生自激振荡
4.非线性系统的特征
(4)可能产生跳跃谐振
KA
(sin
t ) 2 d ( t )
2 KA [sin 1 a a 1 ( a ) 2 ]
AA
A
C 1 A12 B12 B1
1 0
2. 典型非线性元件的描述函数
(1)饱和特性的描述函数
2K[sin1aa 1(a)2]
A>a
N(A)=
AA A
K
A<a
(2) 死区特性的描述函数
N(A)=
振幅 频率
(5)会产生波形畸变
非线性系统
5.典型非线性元件及对系统性能的影响
(1)饱和特性 Kx
y = Ka -Ka
|x|a x>a x<-a
y x
在饱和区,增益减小,振荡减弱,稳态误差增大。 在线性区发散振荡的系统,到饱和区将转为等幅振荡。
(2)死区特性
数学表达式
sign x = 1 -1
0 y=
用李雅普诺夫函数V(x)来研究, 但V(x)难确定.
第二节 描述函数法
本节内容
1。描述函数定义 2。典型非线性元件的描述函数 3。用描述函数法研究非线性系统 描述函数法是线性系统理论中频率法在 非线性系统中的应用。主要用来分析非 线性系统的稳定性及正弦输入下的输出 特性。适用于任意阶非线性系统。
C 1 A12 B12
1
tg
1
A1 B1
用正弦量的矢量表示法有
X1(A,)=A
X2(A,)=C1e
j 1
1.非线性系统的描述函数定义
描述函数定义式:
N(A ,)X X1 2((A A ,, ))C A 1ej1
描述函数定义陈述:
非线性系统的描述函数为输出基波分量 与输入信号之比
由于假设非线性系统是非储能元件,所以可只考虑 A, 不顾, 于是
自动控制原理电子教案新
第一节 非线性系统概述
1. 何谓线性系统?
y
静态特性:输入和输出成比例
动态特性:可应用叠加原理
x
y=f1(x1)+f2(x2)+f3(x3)
y=f(kx)=kf(x)
2. 何谓非线性系统?
y
静态特性:输入和输出不成比例
动态特性:不可应用叠加原理
x
y (t) (y 2 (t) 1 y (t) ) y 3 (t) A sitn
