2020届河南省名校联盟高三2月质量检测巩固卷数学(文)试题解析
【精准解析】河南省普通高中2020届高三质量测评(二)数学(文)试题

大象联考 2020年河南省普通高中高考质量测评(二)数学(文科)注意事项:1.答题前,考生务必将自己的姓名、准考证号填写在答题卡上相应的位置.2.全部答案在答题卡上完成,答丰本试题上无效3.回答选择题时,选出每小题答案后,用3B 铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案用0.5毫米及以上黑色笔迹签字笔写在答题卡上.4.考试结束后,将本试题和答题卡一并交回. 参考公式锥体的体积公式:13V Sh =(其中为S 为锥体的底面积,h 为锥体的高). 第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知全集U =R ,集合{}2|log 1A x x =<,{}2|0B x x x =->,则AB =( )A. {|12x x <<}B. {|2x x <}C. {|12x x ≤≤}D.{|14x x ≤<} 【答案】A 【解析】 【分析】求出不等式2log 1x <和20x x ->的解,然后根据集合的交集运算,即可得到本题答案. 【详解】由2log 1x <,得02x <<,故{|02}A x x =<<, 由20x x ->,得1x >或0x <,故{|1B x x =>或0}x <, 所以,{|12}A B x x =<<.故选:A【点睛】本题主要考查集合的交集运算,其中涉及对数不等式和一元二次不等式的求解. 2. 已知复数z 满足21iz i-=+,则z =( )A. 13 2i+B.132i-C.32i+D.32i-【答案】B【解析】【分析】利用复数的除法运算,即可得答案.【详解】∵2(2)(1)131(1)(1)2i i i i z i i i----===++-. 故选:B. 【点睛】本题考查复数的除法运算,考查基本运算求解能力,属于基础题. 3. 由我国引领的5G时代已经到来,5G的发展将直接带动包括运营、制造、服务在内的通信行业整体的快速发展,进而对GDP增长产生直接贡献,并通过产业间的关联效应和波及效应,间接带动国民经济各行业的发展,创造岀更多的经济增加值.如图是某单位结合近年数据,对今后几年的5G经济产出所做的预测.结合下图,下列说法正确的是()A. 5G的发展带动今后几年的总经济产出逐年增加B. 设备制造商的经济产出前期增长较快,后期放缓C. 设备制造商在各年的总经济产出中一直处于领先地位D. 信息服务商与运营商的经济产出的差距有逐步拉大的趋势【答案】ABD【解析】【分析】本题结合图形即可得出结果.【详解】由图可知设备制造商在各年的总经济产出中在前期处于领先地位,而后期是信息服务商处于领先地位,故C项表达错误.故选:ABD.【点睛】本题主要考查数学文字及图形的阅读理解能力.本题属基础题. 4. 已知角θ的终边过点()3,4-,则()cos πθ-=( ) A. 45-B.45C.35D.35【答案】D 【解析】 【分析】根据三角函数的定义及诱导公式即可求解. 【详解】因为角θ的终边过点()3,4-, 所以3cos 5θ=-,3cos()cos 5πθθ-=-=. 故选:D.【点睛】本题主要考查了三角函数定义,诱导公式,属于容易题.5. 若椭圆221(0)2x y p p p+=>的一个焦点与抛物线22(0)y px p =>的焦点重合,则p =( ) A. 2 B. 3C. 4D. 8【答案】C 【解析】 【分析】由椭圆方程,抛物线方程写出焦点,根据焦点重合即可求解. 【详解】椭圆的焦点坐标为()),,抛物线的焦点坐标为,02p ⎛⎫⎪⎝⎭, 2p=,解得4p =, 故选:C.【点睛】本题主要考查了椭圆的简单几何性质,抛物线的简单几何性质,属于容易题.6. 已知函数()xf x ae x b =++,若函数()f x 在(0,(0))f 处的切线方程为23y x =+,则ab的值为( ) A. 1 B. 2 C. 3 D. 4【答案】B 【解析】 【分析】对函数求导得(0)2f '=,求得a 的值,再根据切点既在切线上又在曲线上,可求得b 的值,即可得答案.【详解】∵()1xf x ae '=+,∴(0)12f a '=+=,解得1,(0)13a f a b b ==+=+=,∴2b =, ∴2ab =. 故选:B.【点睛】本题考查导数的几何意义,考查函数与方程思想,考查逻辑推理能力和运算求解能力,求解时注意切点既在切线上又在曲线上的应用. 7. 函数2sin ()1x xf x x +=+在[,]-ππ的图象大致为( ) A. B.C. D.【答案】D 【解析】 【分析】根据函数为奇函数及()0f π>,再结合排除法,即可得答案. 【详解】∵函数的定义域为R ,关于原点对称,且2sin()()()()()1x x f x f x x -+--==--+,∴()f x是奇函数,故排除A ;22sin ()011f ππππππ+==>++,排除B ,C.故选:D.【点睛】本题考查根据函数的解析式选择函数的图象,考查数形结合思想,求解时注意充分利用函数的性质及特殊点的函数值进行求解.8. 如图,在四棱锥P ABCD -中,//AD BC ,2AD =,3BC =,E 是PD 的中点,F 在PC 上且13PF PC =,G 在PB 上且23PG PB =,则( )A. 3AG EF =,且AG 与EF 平行B. 3AG EF =,且AG 与EF 相交C. 2AG EF =,且AG 与EF 异面D. 2AG EF =,且AG 与EF 平行 【答案】D 【解析】 【分析】取CF 的中点H ,连接,DH GH ,通过证明四边形ADHG 为平行四边形,可得AG DH //且AG DH =,由在PHD ∆中,,E F 分别为PD 和PH 的中点,可得EF DH //且12EF DH =,综上,即可得到本题答案.【详解】取CF 的中点H ,连接,DH GH ,则在PBC ∆中,23PG PH PB PC ==,所以GH BC //,223GH BC ==,又因为AD BC //且2AD =,所以GH AD //,且GH AD =,所以四边形ADHG 为平行四边形,所以AG DH //,且AG DH =.在PHD ∆中,,E F 分别为PD 和PH的中点,所以EF DH //,且12EF DH =,所以EF AG //,且12EF AG =,即2AG EF =. 故选:D【点睛】本题主要考查空间中两直线的位置关系及大小关系,数形结合思想的应用是解决此题的关键.9. 已知等差数列{}n a 的前n 项和为n S ,22a =,728S =,则数列11n n a a +⎧⎫⎨⎬⎩⎭的前2020项和为( )A. 20202021 B.20182020 C. 20182019D. 20212020【答案】A 【解析】 【分析】根据等差数列前n 项和公式及728S =,可得4a 的值.代入22a =由等差数列通项公式,即可求得首项与公差,进而得数列{}n a 的通项公式.结合裂项求和法即得数列11n n a a +⎧⎫⎨⎬⎩⎭的前2020项和.【详解】等差数列{}n a 的前n 项和为n S ,728S =, 由等差数列前n 项和公式可得74728S a == 所以44a =,结合22a =,由等差数列通项公式可得4121342a a d a a d =+=⎧⎨=+=⎩,解得111a d =⎧⎨=⎩,由等差数列通项公式可得()111n a n n =+-⨯=, 则()1111n n a a n n +=+.所以122334202020211111a a a a a a a a +++⋅⋅⋅+ 111112233420202021=+++⋅⋅⋅+⨯⨯⨯⨯ 111111112233420202021=-+-+-+⋅⋅⋅+-20202021=. 故选:A.【点睛】本题考查了等差数列前n 项和的性质应用,等差数列通项公式的求法,裂项求和的应用,属于基础题.10. “角谷定理”的内容为对于每一个正整数,如果它是奇数,则对它乘3再加1;如果它是偶数,则对它除以2.如此循环,最终都能够得到1.如图为研究角谷定理的一个程序框图.若输入n 的值为10,则输出i 的值为()A. 5B. 6C. 7D. 8【答案】B 【解析】 【分析】根据流程逐步分析,直到1n =时,计算出i 的值即可.【详解】(1)10,0n i ==;(2)5,1n i ==;(3)16,2n i ==;(4)8,3n i ==;(5)4,4n i ==;(6)2,5n i ==;(7)1,6n i ==. 故选B .【点睛】本题考查根据程序框图计算输出值,难度较易.程序框图问题,多数可以采用列举法的方式解答问题.11. 现有一副斜边长相等的直角三角板.若将它们的斜边AB 重合,其中一个三角板沿斜边折起形成三棱锥A BCD -,如图所示,已知,64DAB BAC ππ∠=∠=,三棱锥的外接球的表面积为4π,该三棱锥的体积的最大值为( )A.33B.36C.324D.348【答案】B 【解析】 【分析】设三棱锥A BCD -的外接球的半径为r ,由球的体积得球的半径,当平面ABC ⊥平面ABD 时,三棱锥的体积达到最大,利用体积公式计算,即可得答案.【详解】设三棱锥A BCD -的外接球的半径为r ,因为244r ππ=⇒1r =, 因为90ADB ACB ︒∠=∠=,所以AB 为外接球的直径, 所以2AB =,且3,1,2AD BD AC BC ====当点C 到平面ABD 距离最大时,三枝锥A BCD -的体积最大, 此时平面ABC ⊥平面ABD ,且点C 到平面ABD 的距离1d =, 所以1113311332A BCD C ABD ABD V V S d --==⋅=⨯⨯=△. 故选:B.【点睛】本题考查三棱锥与球的内接问题、三棱锥体积的最大值、球的体积公式,考查函数与方程思想、转化与化归思想,考查空间想象能力和运算求解能力,求解时注意球心位置的确定.12. 设函数()sin()f x x ωϕ=+,其中0,,43ππωϕ⎡⎤>∈⎢⎥⎣⎦,已知()f x 在[0,2]π上有且仅有4个零点,则下列ω的值中满足条件的是( ) A. 136ω=B. 116ω=C. 74ω=D. 34ω=【答案】A 【解析】 【分析】设t x ωϕ=+,则2t ϕπωϕ+,从而将问题转化为sin y t =在[,2]ϕπωϕ+上有4个零点,从而得到425ππωϕπ+<,再利用不等式恒成立问题求得ω的范围,即可得答案. 【详解】设t x ωϕ=+,则2t ϕπωϕ+, 所以sin y t =在[,2]ϕπωϕ+上有4个零点, 因为,43ππϕ⎡⎤∈⎢⎥⎣⎦,所以425ππωϕπ+<, 所以52222ϕϕωππ-<-, 所以5342222ππωππ-<-,即15783ω<,满足的只有A. 故选:A.【点睛】本题考查根据三角函数的零点个数求参数值,考查函数与方程思想、转化与化归思想,考查逻辑推理能力和运算求解能力,求解时注意换元法的应用.第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13. 若||3a =,||2b =,237a b +=,则a 与 b 的夹角为______________. 【答案】3π 【解析】【分析】由222|2|44a b a a b b +=+⋅+及||||cos a b a b θ⋅=⋅,即可得到本题答案. 【详解】设a与b的夹角为θ,则222|2|449432cos 4437a b a a b b θ+=+⋅+=+⨯⨯⨯+⨯=,得1cos 2θ=,所以3πθ=.故答案为:3π【点睛】本题主要考查利用向量的模的计算公式求向量的夹角,属基础题. 14. 记S n 为等比数列{a n }的前n 项和,若数列{S n ﹣2a 1}也为等比数列,则43S S =_____ 【答案】1514【解析】 【分析】设等比数列{a n }的公比为q ,根据数列{S n ﹣2a 1}为等比数列得到﹣(q 2+q ﹣1)=(q ﹣1)2,解得q 12=,再计算43S S 得到答案.【详解】根据题意,设等比数列{a n }的公比为q ,对于等比数列{S n ﹣2a 1},其前三项为:﹣a 1,a 2﹣a 1,a 3+a 2﹣a 1,则有(﹣a 1)(a 3+a 2﹣a 1)=(a 2﹣a 1)2,变形可得:﹣(q 2+q ﹣1)=(q ﹣1)2,解可得:q 12=或0(舍),则q 12=,则()()414433311115111411a q S q q S q a q q---===---; 故答案为:1514. 【点睛】本题考查了等比数列的相关计算,意在考查学生的计算能力.15. 某工厂生产的产品中分正品与次品,正品重100克,次品重110 克.现有5袋产品(每袋装有10个产品),已知其中有且只有一袋次品(10个产品均为次品),如果将5袋产品以1-5编号,第i 袋取出i 个产品(i =1,2,3,4,5),并将取出的产品一起用秤(可以称出物体重量的工具)称出其重量y ,若次品所在的袋子的编号是2,此时的重量y =__________克;若次品所在袋子的编号是n ,此时的重量y =_________克.【答案】 (1). 1520 (2). 150010n +,{}1,2,3,4,5n ∈【解析】 【分析】按照题意,可得从5个袋子中取得的总个数及第2个袋子中取的个数,进而确定总质量;再写出次品是第n 个时的个数及对应解析式即可.【详解】第1袋中取1个,第2袋取2个,第3袋取3个,第4袋取4个,第5袋取5个,共15个.若次品从第2袋中取,则共有13个正品,2个次品,所以总质量为1001311021520y =⨯+⨯=;若次品是第n 袋中取,则15个产品中共有次品n 个,正品15n -, 则()10015110150010y n n n =⨯-+⨯=+,{}1,2,3,4,5n ∈故答案为:1520;150010n +,{}1,2,3,4,5n ∈【点睛】本题考查了实际问题中函数的应用,属于基础题.16. 已知点P 是双曲线2213y x -=右支上一动点,12,F F 是双曲线的左、右焦点,动点Q 满足下列条件:①12212||0||PF PF QF PF PF ⎛⎫+= ⎪⎝⎭⋅,②12120||||PF PF QP PF PF λ⎛⎫++= ⎪⎝⎭,则点Q 的轨迹方程为________________. 【答案】221(0)x y y +=≠ 【解析】 【分析】设动点Q 的坐标为(,)x y ,延长2F Q 交1PF 于点A ,根据向量的加法法则及数量积为0,可得2QF PQ ⊥,利用双曲线的定义可得11||12OQ AF ==,即可得答案. 【详解】设动点Q 的坐标为(,)x y ,延长2F Q 交1PF 于点A , 由条件②知点Q 在12F PF ∠的角平分线上, 结合条件①知2QF PQ ⊥,所以在2PF A △中,2PQ F A ⊥.又PQ 平分2APF ∠, 所以2PF A △为等腰三角形,即2||PA PF =,2||AQ QF =.因为点P 为双曲线上的点,所以122PF PF -=,即12||2PA AF PF +-=, 所以12AF =.又在12F AF 中,Q 为2AF 的中点,O 为12F F 的中点, 所以11||12OQ AF ==, 所以点Q 的轨迹是以O 为圆心,半径为1的圆, 所以点Q 的轨迹方程为221(0)x y y +=≠.故答案为:221(0)x y y +=≠.【点睛】本题考查单位向量、向量的数量积、向量的加法法则的几何意义、双曲线的定义、轨迹方程的求解,考查函数与方程思想、转化与化归思想、数形结合思想,考查逻辑推理能力和运算求解能力,求解时注意平面几何知识的应用.三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答. (一)必考题:共60分.17. 在ABC ∆中,角A ,B ,C 所对的边分别是a ,b ,c ,且sin 2sin()0c B b A B -+= (1)求角B 的大小;(2)设4a =,6c =,求sin C 的值. 【答案】(1)3B π=(2)32114【解析】【分析】(1)由已知结合正弦定理化简可求cos B ,进而可求B ;(2)由余弦定理可得,2221cos 22a c b B ac +-==,代入可求b ,由正弦定理可得,sin sin c B C b =可求.【详解】解:(1)由正弦定理得sin sin 2sin sin()0C B B A B -+=, 化简得2sin sin cos sin sin 0C B B B C -=. 因为在三角形中,sin 0B ≠,sin 0C ≠, 可得1cos 2B =. 又因为(0,)B π∈,所以3B π=(2)由余弦定理可得,2221cos 22a cb B ac +-==,2163612462b +-=⨯⨯,所以27b =,由正弦定理可得,sin 321sin c B C b ==. 【点睛】本题主要考查了两角和及二倍角的公式,正弦定理,余弦定理的综合应用,属于中等试题.18. “不忘初心、牢记使命”主题教育活动正在全国开展,某区政府为统计全区党员干部一周参与主题教育活动的时间,从全区的党员干部中随机抽取n 名,获得了他们一周参加主题教育活动的时间(单位:时)的频率分布直方图,如图所示,已知参加主题教育活动的时间在(]12,16内的人数为92.(1)估计这些党员干部一周参与主题教育活动的时间的平均值;(2)用频率估计概率,如果计划对全区一周参与主题教育活动的时间在(]16,24内的党员干部给予奖励,且参与时间在(]16,20,(]20,24内的分别获二等奖和一等奖,通过分层抽样方法从这些获奖人中随机抽取5人,再从这5人中任意选取3人,求3人均获二等奖的概率. 【答案】(1)13.64(2)25【解析】 【分析】(1)根据频率分布直方图以每个小矩形的中值为估值计算即可求出;(2)用分层抽样抽取的人数:在(]16,20内为4人,设为a b c d ,,,;在(]20,24内为1人,设为A ,列出基本事件,根据古典概型计算概率即可.【详解】(1)由已知可得,()140.02500.04750.05000.01250.1150a =÷-+++=, 所以这些党员干部一周参加主题教育活动的时间的平均值为()60.0250100.0475140.1150180.0500220.0125413.64⨯+⨯+⨯+⨯+⨯⨯=.(2)因为0.1150492n ⨯⨯=,所以922000.11504n ==⨯.故参与主题教育活动的时间在(]16,20的人数为0.0500420040⨯⨯=, 参与主题教育活动的时间在(]20,24的人数为0.0125420010⨯⨯=.则利用分层抽样抽取的人数:在(]16,20内为4人,设为a b c d ,,,;在(]20,24内为1人,设为A.从这5人中选取3人的事件空间为:{}(,,),(,,),(,,),(,,),(,,),(,,),(,,),(,,),(,,),(,,)a b c a b d a b A a c d a c A a d A b c d b c A b d A c d A ,共10种情况,其中全是二等奖的有4种情况. 故42105P ==. 【点睛】本题主要考查了频率分布直方图,均值,分层抽样你,古典概型,属于中档题. 19. 如图,圆柱的轴截面ABCD 是边长为2的正方形,点P 是圆弧CD 上的一动点(不与,C D重合),点Q 是圆弧AB 的中点,且点,P Q 在平面ABCD 的两侧.(1)证明:平面PAD ⊥平面PBC ;(2)设点P 在平面ABQ 上的射影为点O ,点,E F 分别是PQB ∆和POA ∆的重心,当三棱锥P ABC -体积最大时,回答下列问题.(i )证明://EF 平面PAQ ; (ii )求三棱锥A OEF -的体积.【答案】(1)证明见解析(2)(i )证明见解析(ii )427【解析】 【分析】(1)由PC PD ⊥,AD PC ⊥可得PC ⊥平面PAD ,即可证明;(2)(i )连接PE 并延长交BQ 于点M ,连接PF 并延长交OA 于点N ,连接MN ,利用平行线分线段成比例可得//EF MN ,即可得//EF AQ 得证; (ii )根据A EOF E AOF V V --=即可求解. 【详解】(1)证明:因为ABCD 是轴截面, 所以AD ⊥平面PCD ,所以AD PC ⊥,又点P 是圆弧CD 上的一动点(不与,C D 重合),且CD 为直径, 所以PC PD ⊥, 又ADPD D =,PD ⊂平面PAD ,AD ⊂平面PAD ,所以PC ⊥平面PAD ,PC ⊂平面PBC , 故平面PAD ⊥平面PBC(2)当三棱锥P ABC -体积最大时,点P 为圆弧CD 的中点.所以点O 为圆弧AB 的中点,所以四边形AQBO 为正方形,且PO ⊥平面ABO .(i )证明:连接PE 并延长交BQ 于点M ,连接PF 并延长交OA 于点N ,连接MN ,则//MN AQ ,因为,E F 分别为三角形的重心,所以23PE PF PM PN ==, 所以//EF MN , 所以//EF AQ ,又AQ ⊂平面PAQ ,EF ⊄平面PAQ , 所以//EF 平面PAQ . (ii )因为PO ⊥平面ABO , 所以PO BO ⊥, 又AO BO ⊥,AOPO O =,所以BO ⊥平面PAO , 因为////EF AQ BO ,所以EF ⊥平面PAO ,即EF ⊥平面FAO ,即EF 是三棱锥E AOF -的高. 又22233EF BO ==1112223323AOF APO S S ∆∆==⨯⨯=, 所以112224||3327A EOF E AOF AOF V V S EF --∆==⋅==. 【点睛】本题主要考查了线面垂直、面面垂直的判定,线面平行,等体积法求棱锥体积,属于中档题.20. 已知椭圆2222:1(0)x y C a b a b+=>>的左、右焦点分别为12,F F ,长轴长为4,且过点31,2P ⎛⎫⎪⎝⎭. (1)求椭圆C 的方程;(2)过2F 的直线l 交椭圆C 于,A B 两点,过A 作x 轴的垂线交椭圆C 与另一点Q (Q 不与,A B 重合).设ABQ ∆的外心为G ,求证2ABGF 为定值. 【答案】(1)22143x y +=(2)证明见解析【解析】 【分析】(1)根据长轴及椭圆过点即可求出;(2)由题意设直线AB 为1x my =+,联立椭圆方程可求||AB ,求出ABQ ∆外接圆圆心21,034G m ⎛⎫⎪+⎝⎭,计算2GF ,化简即可证明2AB GF 为定值.【详解】(1)由题意知2a =,将P 点坐标代入椭圆方程22221x y a b+=得291414b+=,解得b =所以椭圆方程为22143x y +=.(2)由题意知,直线AB 的斜率存在,且不为0,设直线AB 为1x my =+, 代入椭圆方程得()2234690m y my ++-=. 设()()1122,,,A x y B x y ,则12122269,3434m y y y y m m --+==++, 所以AB 的中点坐标为2243,3434m m m -⎛⎫⎪++⎝⎭,所以()212212134m AB y y m +=-=-+.因为G 是ABQ ∆的外心,所以G 是线段AB 的垂直平分线与线段AQ 的垂直平分线的交点,AB 的垂直平分线方程为22343434m y m x m m ⎛⎫+=-- ⎪++⎝⎭, 令0y =,得2134x m =+,即21,034G m ⎛⎫⎪+⎝⎭,所以222213313434m GF m m +=-=++, 所以()22222121||1234433334m AB m m GF m ++===++,所以2||AB GF 为定值,定值为4. 【点睛】本题主要考查了椭圆的标准方程,直线与椭圆的位置关系,定值问题,属于难题. 21. 已知函数()2(12)ln a f x x a x x=+-+. (1)讨论()f x 的单调性;(2)如果方程()f x m =有两个不相等的解12,x x ,且12x x <,证明:1202x x f +⎛⎫'> ⎪⎝⎭. 【答案】(1)见解析(2)见解析 【解析】 【分析】(1)对函数()f x 进行求导得2()(21)()(0)x a x f x x x-+'=>,再对a 进行分类讨论,解不等式,即可得答案;(2)当0a 时,()f x 在(0,)+∞单调递增,()f x m =至多一个根,不符合题意;当0a >时,()f x 在(0,)a 单调递减,在(,)a +∞单调递增,则()0f a '=.不妨设120x a x <<<,只要证122x x a +>212x a x >-⇔,再利用函数的单调性,即可证得结论. 【详解】(1)2222122(12)()(21)()2(0)a a x a x a x a x f x x x x x x -+---+'=+-==>.①当0a 时,(0,),()0,()x f x f x '∈+∞>单调递增;②当0a >时,(0,),()0,()x a f x f x '∈<单调递减;(,),()0,()x a f x f x '∈+∞>单调递增.综上:当0a 时,()f x 在(0,)+∞单调递增;当0a >时,()f x 在(0,)a 单调递减,在(,)a +∞单调递增. (2)由(1)知,当0a 时,()f x 在(0,)+∞单调递增,()f x m =至多一个根,不符合题意;当0a >时,()f x 在(0,)a 单调递减,在(,)a +∞单调递增,则()0f a '=.不妨设120x a x <<<, 要证1202x x f +⎛⎫'>⎪⎝⎭,即证122x x a +>,即证122x x a +>,即证212x a x >-. 因为()f x 在(,)a +∞单调递增,即证()()212f x f a x >-,因为()()21f x f x =,所以即证()()112f x f a x >-,即证()()f a x f a x +<-. 令()()()g x f a x f a x =+--2()(12)ln()2()(12)ln()a a a x a a x a x a a x a x a x ⎡⎤⎡⎤=++-++--+--+⎢⎥⎢⎥+-⎣⎦⎣⎦4(12)ln()(12)ln()a ax a a x a a x a x a x=+-+---+-+-, 221212()4()()a a a ag x a x a x a x a x --'=++--+-+- ()()22222222222242(12)4()()()()a a x x x a a a a a x a x a x a x a x +---=+-=-+-+-. 当(0,)x a ∈时,()0,()g x g x '<单调递减,又(0)(0)(0)0g f a f a =+--=, 所以(0,)x a ∈时,()(0)0g x g <=,即()()f a x f a x +<-, 即()(2)f x f a x >-.又1(0,)x a ∈,所以()()112f x f a x >-,所以1202x x f +⎛⎫'>⎪⎝⎭.【点睛】本题考查利用导数研究函数的单调性、证明不等式,考查函数与方程思想、转化与化归思想、分类讨论思想,考查逻辑推理能力和运算求解能力,求解时注意将所证不等式转化为利用函数的单调性进行证明.(二)选考题:共10分,请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分22. 在直角坐标系xOy 中,曲线C的参数方程为21,2x s y ⎧=⎪⎨⎪=⎩(s 为参数),以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系,直线l 的极坐标方程为cos 2sin 90ρθρθ++=. (1)求C 和l 的直角坐标方程;(2)设P 为曲线C 上的动点,求点P 到直线l 的距离的最小值. 【答案】(1)24y x =,290x y ++=(2【解析】 【分析】(1)直接利用消参法可得曲线C 的直角坐标方程;将cos ,sin x y ρθρθ==代入l 的极坐标方程得l 的直角坐标方程;(2)设212P s ⎛⎫⎪⎝⎭,利用点到直线的距离公式,结合二次函数的性质求最值,即可得答案.【详解】(1)C 的直角坐标方程为:24y x =,将cos ,sin x y ρθρθ==代入l 的极坐标方程得l 的直角坐标方程为:290x y ++=. (2)设212P s ⎛⎫⎪⎝⎭, 则点P 到直线l的距离21|9s d ++==,当s =-d ==【点睛】本题考查极坐标方程、参数方程、普通方程的互化、点到直线的距离公式,考查逻辑推理能力和运算求解能力,求解时注意点的参数设法. 23. 已知函数()|1||24|f x x x =++-.(1)求不等式()6f x ≤的解集;(2)若函数()y f x =的图象最低点为(),m n ,正数,a b 满足6ma nb +=,求23a b +的取值范围.【答案】(1)[]13,x ∈-(2)2325,6a b ⎡⎫+∈+∞⎪⎢⎣⎭【解析】【分析】(1)分类讨论去掉绝对值得分段函数求解即可;(2)由分段函数求出最低点,得236a b +=,构造1,利用均值不等式求解即可. 【详解】(1)33,2()5,1233,1x x f x x x x x -≥⎧⎪=-+-<<⎨⎪-+≤-⎩,所以由()6f x ≤可得2336x x ≥⎧⎨-≤⎩,或1256x x -<<⎧⎨-+≤⎩,或1336x x ≤-⎧⎨-+≤⎩, 解得:[]2,3x ∈或()1,2x ∈-或1x =-.综上,[]13,x ∈-. (2)因为33,2()5,1233,1x x f x x x x x -≥⎧⎪=-+-<<⎨⎪-+≤-⎩,所以当2x =时,()min 3f x =,最低点为()2,3,即236a b +=,所以132a b +=. 23232313252323266a b b a a b a b a b ⎛⎫⎛⎫+=++=+++≥+= ⎪⎪⎝⎭⎝⎭, 当且仅当65a b ==时等号成立, 所以2325,6a b ⎡⎫+∈+∞⎪⎢⎣⎭【点睛】本题主要考查了含绝对值不等式的解法,分段函数的最值,均值不等式,属于中档题.。
河南省2020届高三第二次模拟考试卷 文科数学(二)(PDF版,答案解析)

成立.
(1)求实数 k 的值;
(2)若 m 1 , n 1 且求证 f (m) f (n) 10 ,求证: 9 1 16 .
2
2
mn 3
二模测试卷 第 7 页(共 8 页)
二模测试卷 第 8 页(共 8 页)
高三第二次模拟考试卷
文科数学(二)答 案
一、选择题:本大题共 12 小题,每小题 5 分,在每小题给出的四个选项中,只有一项是符 合题目要求的. 1.【答案】C
B.若 1 x 1,则 x2 1
C.若 x 1或 x 1,则 x2 1
D.若 x 1或 x 1,则 x2 1
4焦点分别为 F1 ,F2 ,过 F2 且垂直于长轴的直线交椭圆于 A, B 两点,
则 △ABF1的周长为( )
A. 4
B. 6
C. 8
D.16
为
cos2
2asin (a
0)
,过点
P(1, 2)
的直线 l
的参数方程为
x
1
2t 2 ( t 为参数),l
y
2
2t 2
与 C 交于 A , B 两点.
(1)求 C 的直角坐标方程和 l 的普通方程;
(2)若 PA , AB , PB 成等比数列,求 a 的值.
23.(12 分)已知定义在 R 上的函数 f (x) 2x k 2 x , k N* .存在实数 x0 使 f (x0 ) 2
∴△ABF1的周长为| AF1 | | BF1 | | AB | (| AF1 | | AF2 |) (| BF1 | | BF2 |) 8 ,
故选 C. 5.【答案】A
【解析】因为平面向量 a (1, 3) , b (2, 0) ,
2020届全国大联考高三2月联考文科数学试题(带答案解析)
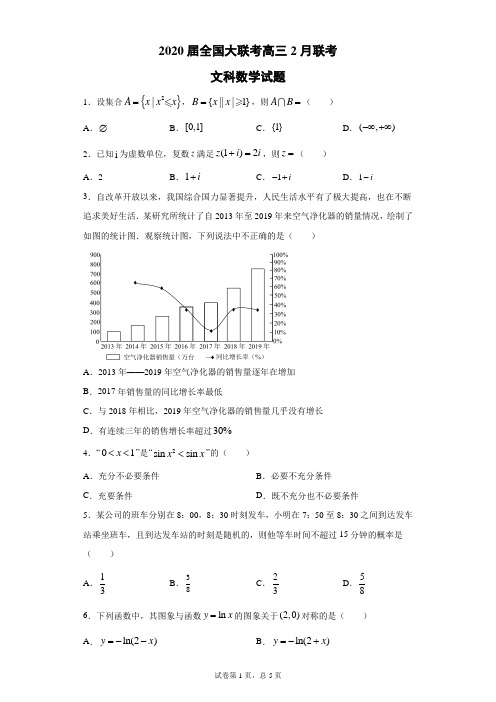
6.下列函数中,其图象与函数 的图象关于 对称的是()
A. B.
C. D.
7.我国古代木匠精于钻研,技艺精湛,常常设计出巧夺天工的建筑.在一座宫殿中,有一件特别的“柱脚”的三视图如图所示,则其体积为()
A. B. C. D.
8.将函数 的图象向右平移 个单位,再向上平移1个单位,所得图象经过点 ,则 的最小值为()
(1)请求出 点轨迹 的直角坐标方程;
(2)设点 的极坐标为 若直线 经过点 且与曲线 交于点 ,弦 的中点为 ,求 的取值范围.
23.已知 , .
(1)若关于 的不等式 对任意实数 都成立,求实数 的最小值;
(2)求证: .
参考答案
1.C
【解析】
【分析】
将集合 , 化简,利用交集的定义域,即可得到答案.
(1)求椭圆的方程;
(2)求证: 点在直线 上.
20.如图,在四棱锥 中,底面 为直角梯形, ,平面 底面 , 为 的中点, 是棱 的的中点 .
(1)求证:平面 平面 ;
(2)求四面体 的体积.
21.已知函数 在定义域上满足 恒成立.
(1)求实数 的值;
(2)令 在 上的最小值为 ,求证: .
22.在平面直角坐标系 , .以坐标原点为极点, 轴正半轴为极轴建立极坐标系,已知曲线 的极坐标方程为 ,点 为 上的动点, 为 的中点.
4.A
【解析】
【分析】
首先将 化简可得 ,然后根据充分条件和必要条件即可得到答案
【详解】
由 得 ,
因为 在 上单调递增,所以 ,而 ,所以 ,
故充分性成立;
而当 时, 且 ,
故必要性不成立.
故选:A.
2020高三文科数学2月份特供卷二(河南省名校联盟)(解析版)

2020高三文科数学2月份特供卷二(河南省名校联盟)(解析版)第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合{}|51xA y y ==+,B x y ⎧⎪==⎨⎪⎩,则A B =I ( ) A .()1,2 B .()1,-+∞ C .(]1,2 D .[]1,2 【答案】C【解析】因为()1,A =+∞,201xx -≥+,解得(]1,2x ∈-,(]1,2B =-, 所以(]1,2A B =I ,故选C .2.复数()()23i z a a =+-∈R 在复平面内对应的点位于第四象限,且20z z ⋅=,则z =( ) A .23i - B .23i + C .24i - D .24i + 【答案】D【解析】因为z 在复平面内对应的点位于第四象限,所以30a -<, 由20z z ⋅=,可得()24320a +-=,解得7a =,所以24i z =-,24i z =+,故选D .3.已知2log 3a =, 1.30.2b =,2log 0.3c =,则( ) A .c b a << B .c a b << C .a b c << D .b c a << 【答案】A【解析】因为2log 31a =>,()1.30.20,1b =∈,2log 0.30c =<,所以c b a <<,故选A .4.学校按年级采用分层抽样的方法从高中三个年级的学生中抽取135人进行问卷调查,已知该校高一、高二、高三的学生分别有450人、400人、500人,则从高一年级的学生中应抽取的人数为( ) A .40 B .45 C .50 D .54【答案】B【解析】由题意知,该校共有高中生4504005001350++=人, 则从高一年级的学生中应抽取135450451350⨯=人,故选B . 5.函数()2cos xxx xf x e e --=+的大致图象为( ) A . B .C .D .【答案】C【解析】因为()()2cos x xx xf x f x e e--==+-,所以()f x 为偶函数,排除A ; 因为()102f =-,所以排除B ; 因为()()210,1f ee π-π+∈+π=π,所以排除D , 故选C .6.我国古代数学家对圆周率π的近似值做出过杰出的贡献,魏晋时期的数学家刘徽首创用圆的内接正多边形的面积来逼近圆面积的方法,称为“割圆术”.在割圆术求π的方法中,若使用正三十二边形,则圆周率的近似值( )(附:sincos 0.09753232ππ≈) A .3.13 B .3.12 C .3.064 D .3.182 【答案】B【解析】设正三十二边形的外接圆半径为r ,三十二个小等腰三角形顶角为16π, sin2sin cos 0.195163232≈ππ=π, 圆的内接正多边形的面来逼近圆面积由2221232sin16sin 23216r r r ππ≈π⨯=,得16sin 3.1216ππ=≈,故选B . 7.已知双曲线C 的一个焦点为()0,5,且与双曲线2214x y -=的渐近线相同,则双曲线C 的标准方程为( )A .2214y x -= B .221520y x -= C .221205x y -= D .2214x y -= 【答案】B【解析】∵双曲线C 与2214x y -=的渐近线相同,且焦点在y 轴上,∴可设双曲线C 的方程为2214y x k k-=,一个焦点为()0,5,∴425k k +=,∴5k =,故C 的标准方程为221520y x -=,故选B . 8.在空间四边形ABCD 中,已知2AD =,22BC =,E ,F 分别是AB ,CD 的中点,5EF =,则异面直线AD 与BC 所成角的大小为( )A .6πB .3πC .4πD .34π【答案】C【解析】取AC 的中点G ,连接EG ,FG ,则EGF ∠即异面直线AD 和BC 所成的角或补角, 因为122EG BC ==,112FG AD ==,5EF =,EGF △中,结合余弦定理可得,所以1252cos 2212EGF +-∠==⨯⨯, 则异面直线AD 与BC 所成角的大小为45︒,故选C .9.已知抛物线()2:20C x py p =>上一点(),3P m 到焦点F 的距离为4,直线l 过()0,3M 且与C 交于A ,B 两点,5BF =,若AM BM λ=,则λ=( )A .23 B .35 C .25 D .34【答案】D【解析】由题可知342p +=,得12p=,故抛物线C 的方程为24x y =,∵5BF =,∴B 点的坐标为()4,4±,当B 点的坐标为()4,4时,直线l 的方程为134y x =+,与24x y =联立可得2120x x --=,解得4x =或3x =-,∴A 点的坐标为93,4⎛⎫- ⎪⎝⎭,∴34A B AM x BM x ==,∴34λ=; 同理,当B 点的坐标为()4,4-时,34λ=,故选D . 10.执行如图所示的程序框图,若输出的49S =,则输入的P 的取值范围是( )A .(]15,16B .(]16,17C .(]17,18D .(]18,19 【答案】B【解析】由图知()()111233412n S n n =++⋅⋅⋅+⨯⨯+⨯+1122n =-+,当16n =时,49S =,故(]16,17P ∈,故选B . 11.在ABC Rt △中,6AC =,斜边10AB =,点M ,N 在其内切圆上运动,且MN 是一条直径,点P 在ABC △的三条边上运动,则PM PN ⋅u u u u r u u u r的最大值是( )A .36B .24C .16D .12 【答案】A【解析】由题可知ABC △的内切圆的半径4222BC AC AB r +-===.设ABC △内切圆的圆心为O ,由2PM PN PO +=u u u u r u u u r u u u r,得()224PM PNPO +=u u u u r u u u r u u u r ,即22224PM PN PM PN PO ++⋅=u u u u r u u u r u u u u r u u u r u u u r ,①由PM PN NM -=u u u u r u u u r u u u u r,得()22PM PNMN -=u u u u r u u u r u u u u r ,即22216PM PN PM PN +-⋅=u u u u r u u u r u u u u r u u u r,②①-②得24416PM PN PO ⋅=-u u u u r u u u r u u u r ,即24PM PN PO ⋅=-u u u u r u u u r u u u r .当P 在点B 时,()22822210PO BO =-+==,所以PM PN ⋅u u u u r u u u r 的最大值为2440436PO -=-=.12.函数()()23x f x x e =-,关于x 的方程()()210f x mf x -+=恰有四个不同实数根,则正数m 的取值范围为( )A .()0,2B .()2,+∞C .3360,6e e ⎛⎫+ ⎪⎝⎭D .336,6e e ⎛⎫++∞ ⎪⎝⎭【答案】D【解析】()()()()22331xxx x e x f e x x =+-=+-',令()0f x '=,得3x =-或1x =,当3x <-时,()0f x '>,函数()f x 在(),3-∞-上单调递增,且()0f x >; 当31x -<<时,()0f x '<,函数()f x 在()3,1-上单调递减; 当1x >时,()0f x '>,函数()f x 在()1,+∞上单调递增. 所以极大值()363f e -=,极小值()12f e =-,作出大致图象:令()f x t =,则方程210t mt -+=有两个不同的实数根, 且一个根在360,e ⎛⎫ ⎪⎝⎭内,另一个根在36,e ⎛⎫+∞ ⎪⎝⎭内或者两个根都在()2,0e -内.因为两根之和m 为正数,所以两个根不可能在()2,0e -内. 令()21g x x mx =-+,因为()010g =>,所以只需360g e ⎛⎫<⎪⎝⎭, 即6336610m e e -+<,得3366e m e >+,即m 的取值范围为336,6e e ⎛⎫++∞ ⎪⎝⎭,故选D .第Ⅱ卷二、填空题:本大题共4小题,每小题5分.13.在ABC △中,角A ,B ,C 所对的边分别为a ,b ,c ,已知a =4b =,120A =︒,则c =______.【答案】2【解析】由余弦定理2222cos a b c bc A =+-,可得2c =,6c =-(舍), 故答案为2.14.从三双不同的袜子中随机抽取2只,则这2只恰好是同一双的概率为______. 【答案】15【解析】将三双不同的袜子标记为(),A a ,(),B b ,(),C c ,则从这三双的袜子中随机抽取3只的情况有(),A a ,(),B b ,(),C c ,(),a b ,(),a c ,(),b c ,(),a B ,(),a C ,(),b A ,(),b C ,(),c A ,(),c B ,(),A B ,(),A C ,(),B C ,共15种情况,其中2只恰好是同一双的情况有(),A a ,(),B b ,(),C c ,共3种, 即概率为31155=,故答案为15. 15.把函数()3sin 23f x x π⎛⎫=+ ⎪⎝⎭的图象向右平移12π个单位长度后得到函数()g x 的图象.若函数()g x在,12θ⎡π⎤-⎢⎥⎣⎦上的值域是⎡⎤⎢⎥⎣⎦,则θ=______. 【答案】712π【解析】由题知()3sin 23sin 21236x x g x ⎡⎤⎛⎫⎛⎫=-+=+ ⎪ ⎪⎢⎥⎝ππ⎭⎝⎭⎣⎦π, 作出函数大致图象函数()3sin 26g x x ⎛⎫=+ ⎝π⎪⎭在,12θ⎡π⎤-⎢⎥⎣⎦上先增后减,且012g π⎛⎫⎪⎝⎭-=, 若函数()3sin 26g x x ⎛⎫=+ ⎝π⎪⎭在,12θ⎡π⎤-⎢⎥⎣⎦上的值域是33,32⎡⎤-⎢⎥⎣⎦, 必()332g θ=-,结合图象:则4263θπ+=π,712θ=π. 故答案为712π.16.在三棱锥P ABC -中,8AB BC ==,120ABC ∠=︒,D 为AC 的中点,PD ⊥平面ABC ,且8PD =,则三棱锥P ABC -的外接球的表面积为______.【答案】260π【解析】在ABC △中,8AB BC ==,120ABC ∠=︒, 所以ABC △的外接圆的半径18382sin120r ⨯︒==, 结合图形分析:圆心到D 点的距离为4,另设三棱锥P ABC -的外接球球心到平面ABC 的距离为d ,设外接球的半径为R ,则1O OB △中,2228d R +=,直角梯形1O ODP 中,()222248PD d R =+-=,解得1d =,265R =,所以24260S R =π=π,故答案为260π.三、解答题:本大题共6个大题,共70分.解答应写出文字说明、证明过程或演算步骤.17.(12分)已知数列{}n a 的前n 项和n S 满足310n n S a +-=. (1)求{}n a 的通项公式; (2)设16log n n b a =,求数列11n n b b +⎧⎫⎨⎬⋅⎩⎭的前n 项和n T .【答案】(1)14nn a ⎛⎫= ⎪⎝⎭;(2)41n n +.【解析】(1)由11310S a +-=,得114a =. 310n n S a +-=,当2n ≥时,11310n n S a --+-=,两式相减得14n n a a -=,所以数列{}n a 是以14为首项,14为公比的等比数列,则1111444n nn a -⎛⎫⎛⎫=⋅= ⎪ ⎪⎝⎭⎝⎭.(2)因为16log 2n n nb a ==-, 所以()11411411n n b b n n n n +⎛⎫==- ⎪⋅++⎝⎭,所以1111111141223341n T n n ⎛⎫=-+-+-++- ⎪+⎝⎭L 144111n n n ⎛⎫=-= ⎪++⎝⎭. 18.(12分)某地区实施“光盘行动”以后,某自助啤酒吧也制定了自己的行动计划,进店的每一位客人需预交50元,啤酒根据需要自己用量杯量取.结账时,剩余酒量不足1升的,按0升计算(如剩余1.7升,记为剩余1升).统计表明饮酒量与人数有很强的线性相关关系,下面是随机采集的5组数据(),x y (其中x 表示饮酒人数,y (升)表示饮酒量):()1,0.8,()2,1.5,()3,2.5,()4,3.2,()5,4.5. (1)求由这5组数据得到的y 关于x 的回归直线方程;(2)小王约了5位朋友一同来饮酒,小王及朋友用量杯共量取了8升啤酒,这时,酒吧服务生对小王说,根据他的经验,小王和朋友量取的啤酒可能喝不完,可以考虑再邀请一个或两个朋友一起来饮酒,会更划算.试问小王是否该接受服务生的建议. 参考数据:回归直线的方程是y bx a =+$$$,其中()()()1221121niii nnin i i ii i i x y nx y b n x x x x y x x y ====-=---=-∑∑∑∑$,$ay bx =-$. 【答案】(1)$0.910.23y x =-;(2)应该接受建议,且再邀请1位朋友更划算. 【解析】(1)1234535x ++++==,0.8 1.5 2.5 3.2 4.52.55y ++++==,515221546.637.50.9155455i ii i i x y x ybx x=---===--∑∑$,$ 2.50.9130.23a y bx =⨯=---=$, 所求回归直线方程为$0.910.23y x =-.(2)小王和5位朋友共6人大约需要饮酒0.9160.23 5.23⨯-=升, 若不再邀请人,则剩余酒量8 5.23 2.77-=升,酒吧记为剩余2升, 预计需要支付506120%360⨯⨯=元;若再邀请1人,大约需饮酒0.9170.23 6.14⨯-=升,剩余酒量8 6.14 1.86-=升, 酒吧记为剩余1升,预计支付5071350⨯⨯=元;若再邀请2人,大约需饮酒0.9180.237.05⨯-=升,剩余酒量87.050.95-=升, 酒吧记为剩余0升,预计支付50890%360⨯⨯=元.所以应该接受建议,且再邀请1位朋友更划算.19.(12分)如图,在四棱锥P ABCD -中,四边形ABCD 是边长为2的正方形,17PA PD ==,E 为PA 的中点,点F 在PD 上,EF ⊥平面PCD ,M 在DC 的延长线上,且215MC CD =.(1)证明:EF P 平面PBM ;(2)过点C 作BD 的平行线,与直线AB 相交于点G ,点Q 为CG 的中点,求E 到平面PDQ 的 距离.【答案】(1)证明见解析;(2)1213. 【解析】(1)证明:记PB 的中点为H ,连接EH ,过F 作//FK DM 交PM 于K ,连接HK , 则//EH AB ,且112EH AB ==. 因为EF ⊥平面PCD ,所以EF PD ⊥.在PAD △中,17PA PD ==2AD =,易求17EF =,217PF =, 又215MC CD =,则3415MD =, 因为PF KF PD MD=,所以1KF =, 因为EH FK =,且//////AB EH CD FK ,所以四边形EFKH 是平行四边形,所以//EF HK ,又HK ⊂平面PBM ,EF ⊄平面PBM ,所以//EF 平面PBM .(2)因为EF ⊥平面PCD ,所以EF CD ⊥,而ABCD 是正方形,所以CD AD ⊥. 因为EF 与AD 显然是相交直线,所以CD ⊥平面PAD ,所以平面PAD ⊥平面ABCD .记AD 的中点为O ,连接OP ,OQ ,则PO ⊥平面ABCD ,且1714PO =-=. 因为点Q 为CG 的中点,所以3OQ =,5PQ =,10QD =在PQD △中,5PQ =,10QD =17PD = 所以cos 510PQD ∠=sin 510PQD ∠=, 所以11351022510PQD S =⨯=△, 而三棱锥P ADQ -的体积11234432V ⎛⎫=⨯⨯⨯⨯= ⎪⎝⎭. 记A 到平面PDQ 的距离为d ,则143PQD S d ⨯⨯=△,所以2413d =. 因为E 到平面PDQ 的距离是A 到平面PDQ 的距离的一半,所以E 到平面PDQ 的距离为1213. 20.(12分)已知()11x x f x e x+=-,()()1g x a x =+. (1)求曲线()y f x =在点()()0,0f 处的切线方程;(2)当0a >时,若关于x 的方程()()0f x g x +=存在两个正实数根,证明:2a e >.【答案】(1)310x y -+=;(2)证明见解析.【解析】(1)∵()()2231x x e f x x '-=-,∴()01f =,()03f '=, ∴曲线()y f x =在点()()0,0f 处的切线方程为310x y -+=.(2)证明:由()()0f x g x +=存在两个正实数根,整理得方程()()11x e a x x =-≠存在两个正实数根,记这两个正实数根为()1212,x x x x <,由0a >,知211x x >>,令()x h x e ax a =-+,则()xh x e a '=-, 当ln x a >时,()0h x '>,()h x 在()ln ,a +∞上单调递增;当ln x a <时,()0h x '<,()h x 在()0,ln a 上单调递减.所以()()min ln 2ln h x h a a a a ==-,因为()xh x e ax a =-+有两个零点,即2ln 0a a a -<, 所以2ln 0a -<,解得2a e >.21.(12分)已知椭圆2222:1x y W a b +=(0a b >>)的左、右焦点分别是1F ,2F ,点P 为W 的上顶点,点Q 在W 上,227PF F Q =u u u u r u u u u r ,且1167PF PQ ⋅=-u u u r u u u r . (1)求W 的方程;(2)已知过原点的直线1l 与椭圆W 交于C ,D 两点,垂直于1l 的直线2l 过1F 且与椭圆W 交于M ,N 两点,若26CD MN =,求2F CD S △. 【答案】(1)2214x y +=;(2. 【解析】(1)设椭圆W 的焦距为2c ,∵227PF F Q =u u u u r u u u u r ,∴Q 的坐标为8,77c b ⎛⎫- ⎪⎝⎭, ∵Q 在W 上,将8,77Q c b ⎛⎫- ⎪⎝⎭代人22221x y a b+=,得2234c a =, 又∵1167PF PQ ⋅=-u u u r u u u r ,∴()8816,777,c b c b ⎛⎫⋅-=- ⎪⎝⎭--,∴222c b -=.又∵222a b c =+,∴24a =,21b =,W 的方程为2214x y +=. (2)当直线2l 的斜率不存在时,||2CD =,||4MN =,不符合题意; 当直线2l 的斜率为0时,||4CD =,||1MN =,也不符合题意.∴可设直线2l的方程为(()0y k x k =≠,联立(2214y k x x y ⎧=+⎪⎨⎪+=⎩,得()2222411240k x x k +++-=,则12x x +=,212212441k x x k -=+.()2241||41k MN k +==+.由22114y x k x y ⎧=-⋅⎪⎪⎨⎪+=⎪⎩,得x y ⎧=⎪⎪⎨⎪=⎪⎩或x y ⎧=⎪⎪⎨⎪=⎪⎩, ∴()222161||4k CD k +=+. 又∵26||||MN CD =,∴()()2222241161444k k k k ++=++,∴22k =,∴||CD = ∵2F到直线CD的距离1d ==,∴2112F CD S =⨯⨯=△.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分 22.(10分)【选修4-4:坐标系与参数方程】在直角坐标系xOy 中,曲线1C 的参数方程为3cos 3sin x y ββ=⎧⎨=⎩(β为参数),将曲线1C 上的所有点的横 坐标缩短为原来的232C ,以坐标原点为极点,x 轴的正半轴 为极轴建立极坐标系,直线l的极坐标方程为sin 4ρθ=π⎛⎫+ ⎪⎝⎭. (1)求2C 的极坐标方程和l 的直角坐标方程;(2)在极坐标系中,射线4θπ=与l ,2C 分别交于A ,B 两点(异于极点),定点()14,0M ,求MAB △的面积.【答案】(1)22123sin ρθ=+,60x y +-=;(2)21- 【解析】(1)将曲线13c 3s n :os i x y C ββ=⎧⎨=⎩(β为参数),消去β得229x y +=,经过伸缩变换23x x y y ⎧'=⎪⎪⎨⎪'=⎪⎩后得曲线222143:x C y +=, 化为极坐标方程为22123sin ρθ=+. 直线l的极坐标方程为sin 4ρθ=+ ⎪⎝⎭,即cos sin 60ρθρθ+-=, 所以l 的直角坐标方程为60x y +-=.(2)M 到射线4θπ=的距离14sin 4d =π=.因为A ρ=,7B ρ=,所以7A B AB ρρ=-=,112122MABS AB d⎛=⋅=⨯⨯=-⎝⎭△23.(10分)【选修4-5:不等式选讲】已知函数()212f x x x=-++.(1)解不等式()6f x<;(2)若()f x的最小值为m,2223522a b c m++=,求64ab bc+的最大值.【答案】(1)7533x x⎧⎫-<<⎨⎬⎩⎭;(2)5.【解析】(1)()31,213,22131,2x xf x x xx x⎧⎪--≤-⎪⎪=--<<⎨⎪⎪+≥⎪⎩,当2x≤-时,由316x--<,得73x>-,所以723x-<≤-;当122x-<<时,由36x-<,得3x>-,所以122x-<<;当12x≥时,由316x+<,得53x<,所以1523x≤<,综上,不等式()6f x<的解集为7533x x⎧⎫-<<⎨⎬⎩⎭.(2)由(1)知()f x的最小值52m=,所以22252352m a b c==++()()22223264a b c b ab bc=+++≥+,所以64ab bc+的最大值为5,当且仅当a b c==时取等号.。
2020届河南省洛阳市普通高中高三下学期第二次统一考试(二模)数学(文)试题(解析版)

绝密★启用前河南省洛阳市普通高中2020届高三毕业班下学期第二次统一考试(二模)数学(文)试题(解析版)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分.考试时间120分钟.第Ⅰ卷(选择题,共60分)注意事项:1.答卷前,考生务必将自己的姓名、考号填写在答题卡上.2.考试结束,将答题卡交回.一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合{|0}A x x =>,{}2|log (31)2B x x =-<,则( ). A. 50,3A B ⎛⎫= ⎪⎝⎭B. 10,3A B ⎛⎤= ⎥⎝⎦C. 1,3A B ⎛⎫⋃=+∞ ⎪⎝⎭D. (0,)A B =+∞【答案】D【解析】【分析】根据题意,求出集合A,进而求出集合A B 和A B ,分析选项即可得到答案.【详解】根据题意,{}215|log (31)2|33B x x x x ⎧⎫=-<=<<⎨⎬⎩⎭ 则15(0,),,33A B A B ⎛⎫⋃=+∞⋂= ⎪⎝⎭故选:D【点睛】此题考查集合的交并集运算,属于简单题目,2.已知复数z 满足(1)2z i -=,其中i 为虚数单位,则1z -=( ).A. iB. i -C. 1i +D. 1i - 【答案】A【解析】【分析】先化简求出z ,即可求得答案.【详解】因(1)2z i -=, 所以()()()()2121211112i i z i i i i ++====+--+ 所以111z i i -=+-=故选:A【点睛】此题考查复数的基本运算,注意计算的准确度,属于简单题目.3.已知角α的顶点为坐标原点,始边与x 轴的非负半轴重合,终边上有一点(3,4)P -,则sin 2α=( ). A. 1225- B. 2425- C. 165 D. 85【答案】B【解析】【分析】根据角终边上的点坐标,求得sin ,cos αα,代入二倍角公式即可求得sin 2α的值.【详解】因为终边上有一点(3,4)P -,所以43sin ,cos 55αα==-, 4324sin 22sin cos 25525ααα⎛⎫∴==⨯⨯-=- ⎪⎝⎭ 故选:B【点睛】此题考查二倍角公式,熟练记忆公式即可解决,属于简单题目.。
2020年河南省高三联考文科数学试卷答案

2020年河南省六市高三第二次联合教学质量监测参考答案1-5 CBABC 6-10 BDCCA 11-12 DA 13. 2 14. 3 15. )(6,1- 16. 2317解:(Ⅰ)∵.①∴当n=1时,可得a 1=4,……........................................................…1分 当n ≥2时,.②….................……2分①—②可得: =(2n ﹣1)+1=2n ,……................................…4分∴.n=1时也满足…….....................................................…5分 ∴.…………................................................................….…6分(Ⅱ)=…..............................................…..…8分∴S n ,……..........................…10分又4019>n S ,可得n>19,….............................................................……11分 可得最小正整数n 为20.……....................................................………12分 18解:(Ⅰ)证明:因为G 为AE 中点,2AD DE == 所以DG AE ⊥.............................................................…1分因为平面ADE ⊥平面ABCE ,平面ADE I 平面ABCE AE =,DG ⊂平面ADE , 所以DG ⊥平面ABCE ............................................................................…3分 在直角三角形ADE 中,易求22AE =则2AD DEDG AE⋅==.............…4分 所以四棱锥D ABCE -的体积为1(15)222232D ABCE V -+⨯=⨯=…………6分(Ⅱ)在BD 上存在点P ,使得//CP 平面ADE 且45BP BD =……...................…7分过点C 作//CF AE 交AB 于点F ,过点F 作//FP AD 交DB 于点P ,连接PC 因为CF//A E ,AE ⊂平面,ADE CF ⊄平面ADE ,所以CF //平面ADE ,同理//FP 平面ADE ,又因为CF PF F ⋂=,所以平面CFP //平面ADE .…......................................................................……9分因为CP ⊂平面CFP , 所以//CP 平面ADE .所以在BD 上存在点P ,使得//CP 平面ADE .…….............................…10分 因为四边形AECF 为平行四边形,所以1==CE AF ,即4=BF 故45BP BF BD AB ==所以在BD 上存在点P ,使得//CP 平面ADE 且45BP BD =…..........………12分19(Ⅰ)0.4;(Ⅱ)107.(Ⅲ)选择方案(1) 解:(Ⅰ)设事件A 为“随机选取一天,这一天该快递公司的骑手的人均日快递业务量不少于65单”依题意,快递公司的人均日快递业务量不少于65单的频率分别为:0.20.150.05,,因为0.20.150.050.4++=所以()P A 估计为0.4. ……4分(Ⅱ)设事件B 为“从五名骑手中随机选取2人,至少有1名骑手选择方案(2)” 从五名骑手中随机选取2名骑手,有10种情况,即{甲,乙} ,{甲,丙},{甲,丁},{甲,戊},{乙,丙},{乙,丁},{乙,戊},{丙,丁} {丙,戊} {丁,戊}..........................................................................................…6分 其中至少有1名骑手选择方案(2)的情况为{甲,丁},{甲,戊} ,{乙,丁},{乙,戊},{丙,丁}, {丙,戊} ,{丁,戊}共7种情况, 所以7()10P B =.……...................................................................................…8分 (Ⅲ)方法1:快递公司人均日快递量的平均数是:300.05400.05500.2600.3700.2800.15900.0562⨯+⨯+⨯+⨯+⨯+⨯+⨯=因此,方案(1)日工资约为50623236+⨯= …............................….…10分 方案(2)日工资约为()10062445190 236+-⨯=<故骑手应选择方案(1) ...................................................................…12分 方法2: 设骑手每日完成快递业务量为n 单方案(1)的日工资*1503()y n n =+∈N ,方案(2)的日工资*2*100,44,1005(44),44,n n y n n n ⎧≤∈⎪=⎨+->∈⎪⎩NN当17n <时,12y y <依题意,可以知道25n ≥,所以这种情况不予考虑 当25n ≥时 令()503100544n n +>+- 则85n < ……..................…10分 即若骑手每日完成快递业务量在85单以下,则方案(1)日工资大于方案(2)日工资,而依题中数据,每日完成快递业务量超过85单的频率是0.05 ,较低, 故建议骑手应选择方案(1)……................................................…......12分 方法3:设骑手每日完成快递业务量为n 单,方案(1)的日工资*1503()y n n =+∈N ,方案(2)的日工资*2*100,44,1005(44),44,n n y n n n ⎧≤∈⎪=⎨+->∈⎪⎩NN所以方案(1)日工资约为1400.051700.052000.22300.32600.22900.153200.05⨯+⨯+⨯+⨯+⨯+⨯+⨯ 236= ……......................................................................................…10分方案(2)日工资约为1000.051000.051300.21800.32300.22800.153300.05⨯+⨯+⨯+⨯+⨯+⨯+⨯ 194.5=因为236194.5>,所以建议骑手选择方案(1).…….....…12分20(Ⅰ)()()21212,0x ax f x x a x x x-+'=-+=> ………………1分1x =Q 时,()f x 取得极值.()0,31f a ∴'==. ……………………………2分 .()()()2211231 x x x x f x x x---+'∴==解()0f x '>得102x <<或1x > 解()0f x '<得112x <<……………4分()f x ∴的单调增区间为10,,(1,)2⎛⎫+∞ ⎪⎝⎭,单调减区间为1,12⎛⎫⎪⎝⎭. …………5分(Ⅱ)()()221,0x ax f x x x-+'=>()f x Q 存在两个极值点∴方程()0f x '=即2210x ax -+=在(0,)+∞上有两个不等实根∴212180,02a x x ∆=->=>,1202ax x +=> ……………………………………………………………………………6分 ()()22212221112121ln ln f x f x x ax x x ax x x x x x -+-+--=--2121212121ln ln ln ln 2x x x x a x x a x x x x --=+-+=-+--……………………………7分∴所证不等式()()212142f x f x ax x a >---等价于2121ln ln 4x x x x a ->-……………………8分 即212121ln ln 2x x x x x x ->-+……………………………………………………………………9分不妨设210x x >>,即证2212111ln 21x x xx x x ->+ (10)分令211x t x =>,()()21ln 1t h t t t -=-+,()()()()222114011t h t t t t t -'=-=>++, ()h t ∴在(1,)+∞上递增.()()10h t h ∴>=. …………………………………………………………………………11分2212111ln 21x x x x x x -∴>+成立.()()212142f x f x a x x a ∴>---成立. ……………………………12分 21解:(Ⅰ)由题知点Q 到F 的距离||QF 等于Q 到y 轴的距离加2 所以||QF 等于Q 到直线2x =-的距离……..............................…2分 由抛物线的定义可知:点Q 的轨迹W 是以F 为焦点,以2-=x 为准线的抛物线…….............................…….......................................................…3分所以动点Q 的轨迹W 的方程为x y 82=…......................................……4分 (Ⅱ)设直线AM 的方程为2)4(+-=y m x )(0>m ,与x y 82=联立,得0163282=-+-m my y ,则0)1632(4642>-⨯-=∆m m ,1100><<∴>m m m 或Θ, .........................................................……6分 设 ),(),,(2211y x N y x M ,则m y 841=+,即481-=m y ,以m 1-代替m ,得482--=my , 则向量NM →在y 轴正方向上的投影为)1(821m m y y +=-............................................................................……9分设函数)1(8)(mm m f +=,则)(m f 在)(1,0上单调递减,在),(∞+1上单调递增,从而16)1()(=>f m f ............................................................…...................…11分 故向量NM 在y 轴正方向上的投影的取值范围为),(∞+16.............……12分22.解:(Ⅰ)由曲线1C的参数方程为112x y t ⎧=-⎪⎪⎨⎪=⎪⎩(t为参数)消去参数得40x +-= cos ,sin x y ρθρθ==由得,cos sin 4ρθθ= 即cos sinsin cos266ππρθρθ+=即曲线1C 的极坐标方程为sin()26πρθ+= ……………3分由222y x +=ρ,22222(12sin )3,23x y y ρθ+=++= 即2213x y +=…...................................5分 (Ⅱ)设1(,)A ρθ,2(,)2B πρθ+,3(,)D ρθ,4(,)2C πρθ+故2221222222113391912sin 12cos 4412sin 12cos 416()2AOB S ρρθθθθ∆==≥=+++++,即AOB ∆面积的最小值为34 当且仅当12ρρ=(即4πθ=)时取“=” …...................................8分(法2::222211cos sin 13ρθρθ+=,222222sin cos 13ρθρθ+=,故22121143ρρ+=22121221143ρρρρ∴≤+=,当且仅当12ρρ=(即4πθ=)时取“=” 121324AOB S ρρ∆=≥ ................................8分) 此时34112222sin()cos()4646COD S ρρππππ∆==++g 48cos 3π== 故所求四边形的面积为329844-= …...................................10分23. 证明:(Ⅰ),,0a b c >Q ,∴222111()4f x x x a c b =+++-222111()4x x c b a ≥+--+2221114a b c =++ ∴2221114a b c ++1= …...................................3分 由柯西不等式得222(4)a b c ++222111()4a b c++2(111)9≥++=当且仅当2a b c ====”∴22249a b c ++≥ …...................................5分(Ⅱ) 22112,a b ab +≥Q22111,4b c bc +≥221114a c ac+≥(以上三式当且仅当2a b c ====”)…...................................…...................................7分将以上三式相加得211ab bc ac ++≤2221112()24a b c++= 即111122ab bc ac++≤ …...................................10分。
河南省TOP二十名校2023-2024学年高三下学期质检二 数学试题(含解析)
2024届高三年级TOP 二十名校质检二数学全卷满分150分,考试时间120分钟注意事项:1.答卷前,考生务必将自己的姓名,准考证号填写在答题卡上,并将条形码粘贴在答题卡上的指定位置.2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效.3.考试结束后,将本试卷和答题卡一并收回.一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{12}A x x =-<<,){}3log 3B y y ==,则A B = ()A .()2,1-B .()1,1-C .[)1,2D .()1,+∞2.已知复数z 满足()12i 2i z -=+,则z =()A .3B .2C .1D3.已知向量()()3,3,,3a b x ==-,则“()a b b +⊥r r r ”是“3x =-”的()A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件4.中国传统文化博大精深,源远流长,其中我国古代建筑文化更是传统文化中一颗璀璨之星,在古代建筑中台基是指建筑物底部高出室外地面的部分,通常由台阶,月台,栏杆,台明四部分组成,某地的国家二级文化保护遗址一玉皇阁,其台基可近似看作上、下底面边长分别为2m,4m ,侧棱长为3m 的正四棱台,则该四棱台的体积约为()A 3B .3C .313mD .325m 5.在直角坐标系xOy 中,椭圆2222:1x y C a b+=的右焦点为(),0(0),F c c A >是C 上一点,且AF x ⊥轴,若直线OA 的斜率为2,则C 的离心率为()A 1B1C .3D .126.已知数列{}n a 的前n 项和为n S ,且()()111,11n n a nS n S n n +==+++,则1314a =()A .1056B .1123C .1315D .26277.若某公司一共有3个食堂,现调研发现员工小王周一去知味餐厅的概率为35,周二去知味餐厅的概率为310,且小王周一不去知味餐厅的条件下周二去知味餐厅的概率是周一去知味餐厅的条件下周二去知味餐厅的概率的2倍,则员工小王周一、周二都去知味餐厅的概率为()A .970B .910C .35D .13158.已知0,2a b c <<>,且12212,e (1),2ln2bab c c a==+=,则()A .b a c <-<B .a b c -<<C .c a b<-<D .b c a<<-二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.2023年10月份诺贝尔奖获奖名单已经全部揭晓,某校为调研同学们对诺贝尔奖获奖科学家的了解程度,随机调查了该校不同年级的8名同学所知道的获得过诺贝尔奖的科学家人数,得到一组样本数据:1,1,2,4,1,4,1,2,则()A .这组数据的众数为1B .这组数据的极差为2C .这组数据的平均数为2D .这组数据的40%分位数为110.已知位于第一象限的点(),a b 在曲线111x y+=上,则()A .()()111a b --=-B .4ab ≥C .49a b +≤D .221223a b +≥11.定义函数()y f x =的曲率函数()()()3221y K x y ''='+(y ''是y '的导函数),函数()y f x =在0x x =处的曲率半径为该点处曲率()0K x 的倒数,曲率半径是函数图象在该点处曲率圆的半径,则下列说法正确的是()A .若曲线在各点处的曲率均不为0,则曲率越大,曲率圆越小B .函数sin y x =在π2x =处的曲率半径为1C .若圆C 为函数ln y x =的一个曲率圆,则圆C 半径的最小值为2D .若曲线ln y x =在()1212,x x x x ≠处的弯曲程度相同,则1212x x <三、填空题:本题共3小题,每小题5分,共15分.12.在1121x ⎫⎪⎭的展开式中,3x 的系数为.(填数字)13.已知函数()π2sin (0)6f x x ωω⎛⎫=+> ⎪⎝⎭,若关于x 的方程()10f x -=在区间()0,π上恰有两个实数根,则ω的取值范围为.14.已知,A B 为抛物线24y x =上两点,π,4AOB F ∠=为焦点,O 为坐标原点,A 在第一象限,且点A 的纵坐标大于点B 的纵坐标,若1914AF BF -=-,则点A 的坐标为.四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.在ABC 中,,,a b c分别为角,,A B C 的对边,且sin sin sin sin cos B C A C A C ++.(1)求tan2A;(2)若a b c +=+,求ABC 面积的最小值.16.近日,欧冠拉开帷幕,引得无数球迷的纷纷关注,成了体育竞技赛事的又一热点,为此某中学组织人员对在校学生“是否热爱踢足球”做了一次随机调查.共随机调查了18名男生和12名女生,调查发现,男、女生中分别有12人和6人喜爱该项运动,其余不喜爱.(1)根据以上数据完成以下22⨯列联表.喜欢踢足球不喜欢踢足球合计男女合计依据小概率值0.01α=的独立性检验,分析性别与喜欢踢足球是否有关?(2)从被调查的女生中随机抽取3人,若其中喜爱踢足球的人数为ξ,求ξ的分布列及数学期望.附:()()()()22()n ad bc a b c d a c b d χ-=++++,其中n a b c d =+++.α0.150.100.050.0250.0100.0050.001ax 2.072 2.706 3.841 5.024 6.6357.87910.82817.如图,在直三棱柱111ABC A B C -中,18,6,AC AA BC BC AC ===⊥,点D 在线段AB 上.(1)当12AD AB =时,证明:1//AC 平面1B CD ;(2)当3BA BD =时,求直线1B B 与平面1CDB 所成角的正弦值.18.已知双曲线22:13y C x -=的左、右焦点分别为12,F F ,点A 在C 的右支上,12AF F △为等腰三角形且周长为10.(1)求点A 的坐标;(2)若点P 满足2cos APF ∠=2AF P △面积的最大值.19.已知函数()()(]2sin cos 1,0,f x x x x a x x π=+-+∈.(1)若0a =,求()f x 的最大值;(2)若关于x 的不等式()0f x ≥有解,求实数a 的取值范围.1.C【分析】借助对数函数的性质可解出集合B ,利用交集定义运算即可得.33≥,故)3log 31y =+≥,故{}1B y y =≥,即{12}A B x x ⋂=≤<.故选:C.2.C【分析】由复数四则运算以及模的运算公式即可求解.【详解】因为()12i 2i z -=+,所以()()()()2i 12i 5i i12i 12i 5z ++===-+,所以1z=.故选:C.3.B【分析】由()a b b +⊥r r r列方程求得x 的值,结合必要不充分条件的定义即可得解.【详解】由题意()()3,3,,3a b x ==-,则()3,0a b x +=+r r ,而()()()300a b b a b b x x x +⊥⇔+⋅=+=⇔=r r r r r r或3x =-,所以“()a b b +⊥r r r”是“3x =-”的必要不充分条件.故选:B.4.A【分析】借助正四棱台的性质可得其高,结合体积公式即可得解.【详解】该正四棱台上、下底面的对角线分别为=则(221282433V =++⨯.故选:A.5.B【分析】根据给定条件,求出点A 的坐标,借助斜率坐标公式列式计算即得.【详解】依题意,点A 在第一象限,设00(,)(0)A c y y >,则220221y c a b +=,解得20b y a=,由直线OA 的斜率为2,得2y c=,即22b ac =,于是2220c ac a +-=,即2()210c c a a+⋅-=,又01c a <<,解得1ca =,所以C 1.故选:B 6.D【分析】将已知变形得到n S n ⎧⎫⎨⎬⎩⎭为等差数列,进而求得n S n n =,然后得到2n S n =,用2n ≥时,1n n n a S S -=-求解.【详解】因为()()111,11n n a nS n S n n +==+++,所以111,11n nS S S n n+=-=+,所以数列n S n ⎧⎫⎨⎬⎩⎭是首项为1公差为1的等差数列,所以n S n n =,所以2n S n =,所以22131413141313131413132627a S S =-=-=.故选:D 7.A【分析】借助全概率公式与条件概率公式计算即可得.【详解】设“小王周一去知味餐厅”为事件A ,“小王周二去知味餐厅”为事件B ,则有()35P A =,()()215P A P A =-=,()310P B =,由题意可得()()2P B A P B A =,()()()()()310P B P A P B A P A P B A =⋅+⋅=,即有()()32325510P B A P B A +⨯=,解得()314P B A =,则()()()33951470P AB P A P B A ==⨯=.故选:A.8.B 【分析】令1t a=,构造()22,0t f t t t =-<,求导得到单调性,求出()1,2a -∈;令()()2e 1x g x x =-+,0x >,二次求导得到单调性,结合隐零点和零点存在性定理得到()2,3b ∈;令()2ln 2,2h x x x x =->,求导得到其单调性,结合零点存在性定理得到()4,5c ∈,比较出大小.【详解】令1t a=,则22t t =,令()22,0t f t t t =-<,则()2ln 220tf t t '=->在(),0t ∈-∞上恒成立,故()22t f t t =-在(),0t ∈-∞上单调递增,且()11102f -=-<,11024f ⎛⎫--> ⎪⎝⎭,故112t -<<-,故()1,2a -∈,令()()2e 1x g x x =-+,0x >,则()()e 21xg x x '=-+,令()()e 21xq x x =-+,则()e 2x q x '=-,令()0q x '>得ln 2x >,令()0q x '<得0ln 2x <<,故()()e 21xq x x =-+在()0,ln 2上单调递减,在()ln 2,+∞上单调递增,则()()ln 222ln 210q =-+<,()22e 60q =->,由零点存在性定理可得,存在()0ln 2,2x ∈,使得()00q x =,且()()2e 1x g x x =-+在()00,x 上单调递减,在()0,x +∞上单调递增,又()00g =,故()()000g x g <=,又()22e 90g =-<,()33e 160g =->,故()2,3b ∈,令()2ln 2,2h x x x x =->,则()21h x x'=-,当2x >时,()0h x '>,故()2ln 2h x x x =-在()2,+∞上单调递增,又因为()446ln 20h =-<,()552ln100h =->,故()4,5c ∈,综上,a b c -<<.故选:B【点睛】方法点睛:构造函数比较大小是高考热点和难点,结合代数式的特点,选择适当的函数,通过导函数研究出函数的单调性,从而比较出代数式的大小,本题中,分别构造三个函数,结合函数单调性和零点存在性定理比较出大小.9.ACD【分析】根据众数的定义可判断A 的正误,根据极差公式或均值公式或p 百分位数计算方法可判断BCD 的正误,故可得正确的选项.【详解】数据从小到大排列为1,1,1,1,2,2,4,4.对于A ,该组数据的众数为1,故A 正确;对于B ,极差为413-=,故B 错误;对于C ,平均数为14224228⨯+⨯+⨯=,故C 正确;对于D ,840% 3.2⨯= ,∴这组数据的40%分位数为第4个数1,故D 正确.故选:ACD.10.BD【分析】对A :计算后代换即可得;对B 、C :借助基本不等式即可得;对D :借助消元法用b 表示a 后,借助二次函数的性质即可得.【详解】由题意可得111a b+=,且0a >,0b >,对A :由111a b+=,即a b ab +=,故()()()1111a b ab a b --=-++=,故A 错误;对B :111a b =+≥2a b ==时,等号成立,即224ab ≥=,故B 正确;对C :()1144414529b a a b a b a b a b ⎛⎫+=+=+++≥+ ⎪⎝⎭,当且仅当4b aa b=时,等号成立,故C 错误;对D :由111a b +=,故1110a b =->,故101b<<,2222221212321122113,2333a b b b b b b ⎛⎫⎛⎫⎡⎫+=-+=-+=-+∈ ⎪ ⎪⎪⎢⎝⎭⎝⎭⎣⎭,故D 正确.故选:BD.11.ABD【分析】直接根据倒数的性质即知A 正确;直接根据曲率半径的定义计算函数sin y x =在π2x =处的曲率,再取倒数得到曲率半径即可判断B 正确;使用三元均值不等式可以证明函数ln y x =的曲率圆的半径一定大于2,从而C 错误;设21x a =,22x b =,然后将条件转化为关于,a b 的等式,再使用基本不等式进行处理,即可证明D 正确.【详解】对于A ,若曲线在各点处的曲率均不为0,显然()0K x ≥,由()0K x ≠知()0K x >,由于曲线在0x x =处的曲率为()0K x ,曲率圆的半径为()01K x ,所以曲率圆的半径等于曲率的倒数.而曲率大于0,所以曲率越大,曲率圆越小,A 正确;对于B ,若sin y x =,直接计算知()()()()()()333222222sin sin 1cos 11cos y xx K x xy x '-===+'++',所以322πsinπ12121π1cos 2K ⎛⎫=== ⎪⎝⎭⎛⎫+ ⎪⎝⎭,从而函数sin y x =在π2x =处的曲率为1,从而函数sin y x =在π2x =处的曲率半径为1的倒数,即1,B 正确;对于C ,若ln y x =,直接计算知()()()()2233332222222211111111y x x x K x xy x x '-====⎛⎫⎛⎫++⎛⎫+ ⎪+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭'',这里0x >.所以x 处的曲率圆半径()()()32211x R x K x x+==,从而我们有()()()332232221111222x x R x K x xx x ⎛⎫⎛⎫ ⎪++ ⎪+⎝⎭⎝⎭===≥>,所以圆C 的半径一定大于2,不可能以2为最小值,C 错误;对于D ,若ln y x =,在C 选项的过程中已经计算得知()()3221xK x x=+,现在如果曲线ln y x =在()1212,x x x x ≠处的弯曲程度相同,则()()12K x K x =,故()()123322221211x x xx =++,所以()()221233221211x x xx=++,即()()332212221211x x xx++=.设21x a =,22x b =,则a b ¹,,0a b >,()()3311a b ab++=,将()()3311a b ab++=两边展开,得到22113333a a b b a b +++=+++,从而()()221130a b a b a b ⎛⎫-+-+-= ⎪⎝⎭.故()()()()()()()221110333b a a b a b a b a b a b a b a b a b ab ab -⎛⎫⎛⎫=-+-+-=-++-+=-++- ⎪ ⎪⎝⎭⎝⎭,而a b ¹,故()130a b ab ++-=,这意味着133a b ab=++>+,从而3232112312322⎛⎫⎛⎫+<=+ ⎪ ⎪⎝⎭⎝⎭.定义函数()3223g x x x =+,则12gg ⎛⎫< ⎪⎝⎭,0>,函数()3223g x x x =+在()0,∞+上递增,12<,所以1212x x =,D 正确.故选:ABD.【点睛】关键点点睛:在适当的时候使用均值不等式是解决本题C ,D 选项的关键.12.11【分析】借助二项展开式的通项公式赋值计算即可得.【详解】对1121x ⎫+⎪⎭,有1151121111121C C kkkkk k T x x --+⎛⎫== ⎪⎝⎭,{}0,1,2,,11k ∈⋯,令11532k -=,可得1k =,即有133211C 11T x x ==,故3x 的系数为11.故答案为:11.13.823ω≤<【分析】由题意可得π1sin 62x ω⎛⎫+= ⎪⎝⎭在()0,π上恰有两个实数根,即有6π2π6π5ππ2π6ω++≤<+,解出即可得.【详解】令()π12sin 106f x x ω⎛⎫-=+-= ⎪⎝⎭,即π1sin 62x ω⎛⎫+= ⎪⎝⎭,当()0,πx ∈时,πππ,π666x ωω⎛+∈⎫+ ⎪⎝⎭,即有6π2π6π5ππ2π6ω++≤<+,解得823ω≤<.故答案为:823ω≤<.14.()36,12【分析】设2(,2)A a a ,2(,2)B b b ,当,A B 位于x 轴同侧时无解;当,A B 位于x 轴的不同侧时,211AF a BF b -⎛⎫= ⎪-⎝⎭,tan tan()11OA OB OA OB k k AOB AOx BOx k k -∠=∠+∠==+⋅,联立求解即可.【详解】设2(,2)A a a ,2(,2)B b b ,0a >,则2OA k a=,2OB k b =,结合抛物线定义,211AF a BF b -⎛⎫= ⎪-⎝⎭,当,A B 位于x 轴的不同侧时,tan ,tan (0)OA OB AOx k BOx k b ∠=∠=-<,由tan tan()11OA OB OA OBk k AOB AOx BOx k k -∠=∠+∠==+⋅,整理可得2122221a a b a a--==++,所以22042a a a b a -=<+,221291424AF a a BF a -⎛⎫-== ⎪-+⎝⎭,所以223422a a a -=-+,解得6a =(负值舍),此时A 的坐标为()36,12;当,A B 位于x 轴同侧时,223422a a a -=+,此时无解.故答案为:()36,12【点睛】思路点睛:设出2(,2)A a a ,2(,2)Bb b ,0a >,则2OA k a=,2OB k b =,由AOB AOx BOx ∠=∠+∠,将其转化为直线OA 与OB 的斜率,建立关于a 的方程求解即可.15.(2)【分析】(1)借助两角和的正弦公式及辅助角公式对所给式子化简即可得;(2)借助余弦定理与基本不等式计算即可得.【详解】(1)由()()sin sin πsin sin cos sin cos B A C A C A C C A =--=+=+,故有sin cos sin cos sin sin sin cos A C C A C A C A C ++=+,即sin cos sin sin C A C A C +=,又sin 0C ≠,故cos 1A A +=,即π1sin 62A ⎛⎫-= ⎪⎝⎭,由()0,πA ∈,故ππ66A -=,即π3A =,故tan tan 23π6A ==;(2)由余弦定理可得222222cos a b c bc A b c bc =+-=+-,由a b c +=+,故(())22212a b c b c b c =+-=+-++,即())22212b c b c b bc c -+-+++=,整理可得)312b c bc +=+,故b c =+≥当且仅当b c =时,等号成立,即3120bc -+≥,即)3120260bc -=-≥,即43bc ≤或12bc ≥,当43bc ≤时,)31216b c bc =++≤,即3b c +≤,与a b c +=+矛盾,故舍去,故12bc ≥,则11sin 1222ABC S bc A =炒即ABC 面积的最小值为16.(1)22⨯列联表见解析,(2)分布列见解析,()32E ξ=【分析】(1)由题意可列出22⨯列联表,计算出卡方后与6.635比较即可得;(2)ξ的可能取值为0、1、2、3,借助超几何分布的概率公式计算即可得其分布列,即可得其期望.【详解】(1)22⨯列联表如下:喜欢踢足球不喜欢踢足球合计男12618女6612合计181230零假设0H 为:性别与喜欢踢足球无关,225181230(12666)50.83361812.636χ⨯⨯⨯-⨯==≈⨯⨯<,故依据小概率值0.01α=的独立性检验,可得性别与喜欢踢足球无关;(2)ξ的可能取值为0、1、2、3,则()36312C 1C 110P ξ===,()2166312C C 9C 221P ξ===,()1266312C C 9C 222P ξ===,()36312C 1C 113P ξ===,故其分布列为:ξ0123P 111922922111其期望为:()199********2222112E ξ=⨯+⨯+⨯+⨯=.17.(1)证明过程见解析【分析】(1)连接1BC 交1B C 于点E ,连接DE ,利用中位线定理证明1//ED AC ,结合线面平行线的判定定理即可得证;(2)建立适当的空间直角坐标系,求出直线1B B 与平面1CDB 的方向向量、法向量,由向量夹角的坐标公式即可求解.【详解】(1)连接1BC 交1B C 于点E ,连接DE ,如图,因为四边形11BCC B 为平行四边形,所以E 为1BC 中点,若12AD AB = ,则D 为AB 中点,从而ED 为三角形1ABC 的中位线,所以1//ED AC ,又ED ⊂平面1B CD ,1AC ⊄平面1B CD ,所以1//AC 平面1B CD ;(2)由题意1CC ⊥面ABC ,又,CA CB ⊂面ABC ,所以11,CC CA CC CB ⊥⊥,而BC AC ⊥,从而1,,CB CA CC 两两互相垂直,所以以C 为原点,1,,CB CA CC 所在直线分别为,,x y z轴建立如图所示的空间直角坐标系,则(0,0,0)C ,(6,0,0)B ,()16,0,8B ,(0,8,0)A ,设(,,0)D a b ,由3BA BD = 得(6,8,0)3(6,,0)a b -=-,解得84,3a b ==,即84,,03D ⎛⎫ ⎪⎝⎭,84,,03CD ⎛⎫∴= ⎪⎝⎭,()16,0,8CB = ,设平面1B CD 的法向量为(),,n x y z = ,则18403680CD n x y CB n x z ⎧⋅=+=⎪⎨⎪⋅=+=⎩,令6y =,解得4,3x z =-=,所以()4,6,3n =- ,又()10,0,8BB = ,所以直线1B B 与平面1CDB所成角的正弦值为111cos ,61n BB n BB n BB ⋅===⋅ .18.(1)322⎛⎫ ⎪ ⎪⎝⎭或3,22⎛⎫- ⎪ ⎪⎝⎭(2)4【分析】(1)直接根据双曲线的定义和12AF F △的周长即可解出1AF 和2AF ,进而确定A 的坐标.值得注意的是,尽管我们不需要使用12AF F △为等腰三角形的条件就能求出A 的坐标,但我们在求出后必须验证所求的A 的坐标满足该条件,以保证所求的A 的坐标的确符合题意,从逻辑上排除无解的可能;(2)通过余弦定理研究PA 和2PF 之间的关系,然后通过等式的变形证明2AF P △的面积不超过44的例子即可得到最大值为4.【详解】(1)如图所示:由双曲线的方程知双曲线半长轴长1a =,半短轴长b =,故半焦距2c ==,这表明()12,0F -,()22,0F .然后由12AF F △的周长为10,知121212121024AF AF F F AF AF c AF AF =++=++=++,所以126AF AF +=.再由双曲线的定义及点A 在双曲线C 的右支上,知1222AF AF a -==,故()()112121131422AF AF AF AF AF =++-=+=,()()212121131222AF AF AF AF AF =+--=-=.设点A 的坐标是(),x y ,则()22222116244AF x y x y x ==++=+++,()2222224244AF x y x y x ==-+=+-+,两式相减,知812x =,所以32x =.而22444x y x =+-+,故229154644y x x =-=-=,所以y ==y 当点A的坐标是3,22⎛ ⎝⎭或3,22⎛⎫- ⎪ ⎪⎝⎭时,由302>,2239512344⎛⎫⎝⎭-=-= ⎪⎝⎭知A 在双曲线右支上.此时有:14AF ====,22AF ====,故11242AF c F F ===,121242410AF AF F F ++=++=,所以12AF F △为等腰三角形,且周长为10.综上,点A的坐标是32⎛ ⎝⎭或3,2⎛ ⎝⎭.(2)设PA p =,2PF q =,2AF P △的面积为S .在2AF P △中使用余弦定理,得22222222242cos 2AF PA PF PA PF APF p q pq ==+-∠=+-,所以2242p q pq +=.从而我们有()222422222p q pq p q pq pq ⎛⎫⎛=+-=-+-≥- ⎪ ⎪ ⎝⎭⎝⎭,故(84pq ≤=+.而21111sin 2228S pq APF pq =∠===,这就表明148S pq =≤.最后,由于22242AF +=>=,从而我们一定能够选取一个合适的点P,使得22PA PF ==.在这种条件下,我们有:()2222222222444cos 28PA PF AF APF PA PF ++-+-∠==⋅()22181118842-=-=-=-=,故条件满足.此时,我们有2p q ==,故(2111484882S pq ==⋅=+=.综上,2AF P△的面积的最大值是4.19.(1)2π(2)(,1)-∞【分析】(1)利用导数判断函数的单调性,求解函数最值;(2)含参数的不等式衡等问题,分类讨论,利用函数的导数判断单调性,进而分析函数的范围,求得参数范围;【详解】(1)当0a =时,()sin cos f x x x x =+,所以()cos f x x x '=,当π(0,)2x ∈时,()0,()f x f x '>单调递增;当π(,π]2x ∈时,()0,()f x f x '<单调递减;故()f x 的最大值为ππ()22f =.(2)()(cos 2),f x x x a '=-当21a ≤-,即12a ≤-时,()0,()f x f x '≥在(]0,πx ∈单调递增,所以()()2π11π0f a =--+≥即可,故211a ≤-+π,此时12a ≤-;当21a ≥,即12a ≥时,()0,()f x f x '≤在(]0,πx ∈单调递减,所以()010f a =->即可,故1a <,此时112a ≤<;当1122a -<<时,(]00,πx ∃∈使0cos 2x a =;当0(0,)x x ∈,则cos 2,x a >()0,()f x f x '>单调递增,当0(,π)x x ∈,则cos 2,x a <()0,()f x f x '<单调递减,所以()()2200000000001sin cos 1sin cos cos 22x f x x x x a x x x x x =+-+=+-,令()21sin cos cos ,(0,π]22x h x x x x x x =+-∈,则()21sin sin 022x h x x x '=+>,所以()h x 在(0,π]x ∈上单调递增,故()1(0)2h x h >=,即()0f x ≥成立.综上,实数a 的取值范围(,1)-∞【点睛】关键点点睛:本题第二问的关键是对a 进行合理的分类讨论,当当1122a -<<时,采取隐零点法得到()0f x ,最后设()h x ,利用导数即可得到范围.。
2020届河南省普通高中高考质量测评(二)数学(文)试题(解析版)
2020届河南省普通高中高考质量测评(二)数学(文)试题一、单选题1.已知全集U =R ,集合{}{}22|log 1,|0A x x B x x x =<=->,则A B =I ( )A .{|12}x x <<B .{|2}x x <C .{|12}x x <„D .{|14}x x <„【答案】A【解析】解对数不等式和一元二次不等式化简集合,A B ,再进行交运算,即可得答案. 【详解】由题意得{}2|log 1{|02},{|(1)0}{|0A x x x x B x x x x x =<=<<=->=<或1}x >,∴{|12}A B x x =<<I . 故选:A. 【点睛】本题考查数不等式和一元二次不等式的求解、集合的交运算,考查运算求解能力,属于基础题.2.已知复数z 满足21iz i -=+,则z =( ) A .132i+ B .132i - C .32i +D .32i- 【答案】B【解析】利用复数的除法运算,即可得答案. 【详解】 ∵2(2)(1)131(1)(1)2i i i iz i i i ----===++-. 故选:B. 【点睛】本题考查复数的除法运算,考查基本运算求解能力,属于基础题. 3.已知角θ的终边过点()3,4-,则()cos πθ-=( ) A .45-B .45C .35-D .35【答案】D【解析】根据三角函数的定义及诱导公式即可求解. 【详解】因为角θ的终边过点()3,4-,所以3cos 5θ=-,3cos()cos 5πθθ-=-=. 故选:D. 【点睛】本题主要考查了三角函数的定义,诱导公式,属于容易题.4.若椭圆221(0)2x y p p p+=>的一个焦点与抛物线22(0)y px p =>的焦点重合,则p =( )A .2B .3C .4D .8【答案】C【解析】由椭圆方程,抛物线方程写出焦点,根据焦点重合即可求解. 【详解】椭圆的焦点坐标为()),,抛物线的焦点坐标为,02p ⎛⎫⎪⎝⎭,2p=,解得4p =, 故选:C. 【点睛】本题主要考查了椭圆的简单几何性质,抛物线的简单几何性质,属于容易题.5.已知函数()xf x ae x b =++,若函数()f x 在(0,(0))f 处的切线方程为23y x =+,则ab 的值为( ) A .1 B .2C .3D .4【答案】B【解析】对函数求导得(0)2f '=,求得a 的值,再根据切点既在切线上又在曲线上,可求得b 的值,即可得答案. 【详解】∵()1x f x ae '=+,∴(0)12f a '=+=,解得1,(0)13a f a b b ==+=+=,∴2b =, ∴2ab =. 故选:B. 【点睛】本题考查导数的几何意义,考查函数与方程思想,考查逻辑推理能力和运算求解能力,求解时注意切点既在切线上又在曲线上的应用. 6.函数2sin ()1x xf x x +=+在[,]-ππ的图象大致为( ) A . B .C .D .【答案】D【解析】根据函数为奇函数及()0f π>,再结合排除法,即可得答案. 【详解】∵函数的定义域为R ,关于原点对称,且2sin()()()()()1x x f x f x x -+--==--+,∴()f x 是奇函数,故排除A ;22sin ()011f ππππππ+==>++,排除B ,C.故选:D. 【点睛】本题考查根据函数的解析式选择函数的图象,考查数形结合思想,求解时注意充分利用函数的性质及特殊点的函数值进行求解.7.如图,在四棱锥P ABCD -中,//,2,3AD BC AD BC ==,E 是PD 的中点,F 在PC 上且13PF PC =,G 在PB 上且23PG PB =,则( )A .3AG EF =,且AG 与EF 平行B .3AG EF =,且AG 与EF 相交C .2AG EF =,且AG 与EF 异面D .2AG EF =,且AG 与EF 平行【答案】D【解析】取CF 的中点H ,连接,DH GH ,证明//AG DH ,且AG DH =,即可得答案. 【详解】取CF 的中点H ,连接,DH GH ,则在三角形PBC 中23PG PH PB PC ==, 所以//GH BC ,且223GH BC ==, 又因为//AD BC 且2AD =,所以//GH AD ,且GH AD =, 所以四边形ADHG 为平行四边形, 所以//AG DH ,且AG DH =.在PDH △中,,E F 分别为PD 和PH 的中点,所以//EF DH ,且12EF DH =, 所以//EF AG ,且12EF AG =,即2AG EF =,故选:D.【点睛】本题考查空间中直线、平面的平行关系,考查转化与化归思想,考查空间想象能力,求解时注意利用线段的比例关系,证明平行.8.已知等差数列{}n a 的前n 项和为n S ,22a =,728S =,则数列11n n a a +⎧⎫⎨⎬⎩⎭的前2020项和为( )A .20202021 B .20182020 C .20182019D .20212020【答案】A【解析】根据等差数列前n 项和公式及728S =,可得4a 的值.代入22a =由等差数列通项公式,即可求得首项与公差,进而得数列{}n a 的通项公式.结合裂项求和法即得数列11n n a a +⎧⎫⎨⎬⎩⎭的前2020项和. 【详解】等差数列{}n a 的前n 项和为n S ,728S =, 由等差数列前n 项和公式可得74728S a == 所以44a =,结合22a =,由等差数列通项公式可得4121342a a d a a d =+=⎧⎨=+=⎩,解得111a d =⎧⎨=⎩,由等差数列通项公式可得()111n a n n =+-⨯=,则()1111n n a a n n +=+. 所以122334202020211111a a a a a a a a +++⋅⋅⋅+ 111112233420202021=+++⋅⋅⋅+⨯⨯⨯⨯ 111111112233420202021=-+-+-+⋅⋅⋅+-20202021=. 故选:A. 【点睛】本题考查了等差数列前n 项和的性质应用,等差数列通项公式的求法,裂项求和的应用,属于基础题.9.“角谷定理”的内容为对于每一个正整数,如果它是奇数,则对它乘3再加1;如果它是偶数,则对它除以2.如此循环,最终都能够得到1.如图为研究角谷定理的一个程序框图.若输入n 的值为10,则输出i 的值为()A .5B .6C .7D .8【答案】B【解析】根据流程逐步分析,直到1n =时,计算出i 的值即可. 【详解】(1)10,0n i ==;(2)5,1n i ==;(3)16,2n i ==;(4)8,3n i ==;(5)4,4n i ==;(6)2,5n i ==;(7)1,6n i ==. 故选B . 【点睛】本题考查根据程序框图计算输出值,难度较易.程序框图问题,多数可以采用列举法的方式解答问题.10.现有一副斜边长相等的直角三角板.若将它们的斜边AB 重合,其中一个三角板沿斜边折起形成三棱锥A BCD -,如图所示,已知,64DAB BAC ππ∠=∠=,三棱锥的外接球的表面积为4π,该三棱锥的体积的最大值为( )A .33B 3C .324D .348【答案】B【解析】设三棱锥A BCD -的外接球的半径为r ,由球的体积得球的半径,当平面ABC ⊥平面ABD 时,三棱锥的体积达到最大,利用体积公式计算,即可得答案.【详解】设三棱锥A BCD -的外接球的半径为r ,因为244r ππ=⇒1r =, 因为90ADB ACB ︒∠=∠=,所以AB 为外接球的直径,所以2AB =,且1,AD BD AC BC ====当点C 到平面ABD 距离最大时,三枝锥A BCD -的体积最大, 此时平面ABC ⊥平面ABD ,且点C 到平面ABD 的距离1d =,所以11111332A BCD C ABD ABD V V S d --==⋅=⨯⨯=△. 故选:B. 【点睛】本题考查三棱锥与球的内接问题、三棱锥体积的最大值、球的体积公式,考查函数与方程思想、转化与化归思想,考查空间想象能力和运算求解能力,求解时注意球心位置的确定.11.设函数()sin()f x x ωϕ=+,其中0,,43ππωϕ⎡⎤>∈⎢⎥⎣⎦,已知()f x 在[0,2]π上有且仅有4个零点,则下列ω的值中满足条件的是( ) A .136ω=B .116ω=C .74ω=D .34ω=【答案】A【解析】设t x ωϕ=+,则2t ϕπωϕ+剟,从而将问题转化为sin y t =在[,2]ϕπωϕ+上有4个零点,从而得到425ππωϕπ+<„,再利用不等式恒成立问题求得ω的范围,即可得答案. 【详解】设t x ωϕ=+,则2t ϕπωϕ+剟, 所以sin y t =在[,2]ϕπωϕ+上有4个零点, 因为,43ππϕ⎡⎤∈⎢⎥⎣⎦,所以425ππωϕπ+<„,所以52222ϕϕωππ-<-„,所以5342222ππωππ-<-„,即15783ω<„,满足的只有A.故选:A.【点睛】本题考查根据三角函数的零点个数求参数值,考查函数与方程思想、转化与化归思想,考查逻辑推理能力和运算求解能力,求解时注意换元法的应用.二、多选题12.由我国引领的5G时代已经到来,5G的发展将直接带动包括运营、制造、服务在内的通信行业整体的快速发展,进而对GDP增长产生直接贡献,并通过产业间的关联效应和波及效应,间接带动国民经济各行业的发展,创造岀更多的经济增加值.如图是某单位结合近年数据,对今后几年的5G经济产出所做的预测.结合下图,下列说法正确的是()A.5G的发展带动今后几年的总经济产出逐年增加B.设备制造商的经济产出前期增长较快,后期放缓C.设备制造商在各年的总经济产出中一直处于领先地位D.信息服务商与运营商的经济产出的差距有逐步拉大的趋势【答案】ABD【解析】本题结合图形即可得出结果.【详解】由图可知设备制造商在各年的总经济产出中在前期处于领先地位,而后期是信息服务商处于领先地位,故C项表达错误.故选:ABD.【点睛】本题主要考查数学文字及图形的阅读理解能力.本题属基础题.三、填空题13.若||3a =r ,||2b =r,2a b +=r r ,则a r 与 b r的夹角为______________. 【答案】3π 【解析】由222|2|44a b a a b b +=+⋅+r rr r r r 及||||cos a b a b θ⋅=⋅r r r r ,即可得到本题答案.【详解】设a r 与 b r的夹角为θ,则222|2|449432cos 4437a b a a b b θ+=+⋅+=+⨯⨯⨯+⨯=r rr r r r ,得1cos 2θ=,所以3πθ=.故答案为:3π 【点睛】本题主要考查利用向量的模的计算公式求向量的夹角,属基础题.14.记n S 为等比数列{}n a 的前n 项和,若数列{}12n S a -也为等比数列,则43S S =________. 【答案】1514【解析】设等比数列{}n a 的公比为q ,利用等比数列{}12n S a -的等比中项性质可得公比q ,再代入等比数列的前n 项和公式中,即可得答案. 【详解】设等比数列{}n a 的公比为q , ∵数列{}12n S a -为等比数列,∴()()2211231a a a a a a -=-+-,解得:12q =, ∴4211231241332315(1)1587(1)144Sa q q q S a q a a a a a a q a +++====+++++++. 故答案为:1514.【点睛】本题考查等比数列中的基本量法运算、等比数列的通项公式和前n 项和公式,考查函数与方程思想、转化与化归思想,考查逻辑推理能力和运算求解能力.15.某工厂生产的产品中分正品与次品,正品重100克,次品重110 克.现有5袋产品(每袋装有10个产品),已知其中有且只有一袋次品(10个产品均为次品),如果将5袋产品以1-5编号,第i 袋取出i 个产品(i =1,2,3,4,5),并将取出的产品一起用秤(可以称出物体重量的工具)称出其重量y ,若次品所在的袋子的编号是2,此时的重量y =__________克;若次品所在袋子的编号是n ,此时的重量y =_________克. 【答案】1520 150010n +,{}1,2,3,4,5n ∈【解析】按照题意,可得从5个袋子中取得的总个数及第2个袋子中取的个数,进而确定总质量;再写出次品是第n 个时的个数及对应解析式即可. 【详解】第1袋中取1个,第2袋取2个,第3袋取3个,第4袋取4个,第5袋取5个,共15个.若次品从第2袋中取,则共有13个正品,2个次品,所以总质量为1001311021520y =⨯+⨯=;若次品是第n 袋中取,则15个产品中共有次品n 个,正品15n -, 则()10015110150010y n n n =⨯-+⨯=+,{}1,2,3,4,5n ∈故答案为:1520;150010n +,{}1,2,3,4,5n ∈【点睛】本题考查了实际问题中函数的应用,属于基础题.16.已知点P 是双曲线2213y x -=右支上一动点,12,F F 是双曲线的左、右焦点,动点Q 满足下列条件:①12212||0||PF PF QF PF PF ⎛⎫+=⎪⎝⎭⋅u u u u u u u r u u r u u u u r u u r r u ,②12120||||PF PF QP PF PF λ⎛⎫++= ⎪⎝⎭u u u r u u u ru u u r u u u r u u u r ,则点Q 的轨迹方程为________________. 【答案】221(0)x y y +=≠【解析】设动点Q 的坐标为(,)x y ,延长2F Q 交1PF 于点A ,根据向量的加法法则及数量积为0,可得2QF PQ ⊥,利用双曲线的定义可得11||12OQ AF ==,即可得答案. 【详解】设动点Q 的坐标为(,)x y ,延长2F Q 交1PF 于点A ,由条件②知点Q 在12F PF ∠的角平分线上, 结合条件①知2QF PQ ⊥,所以在2PF A △中,2PQ F A ⊥.又PQ 平分2APF ∠, 所以2PF A △为等腰三角形,即2||PA PF =,2||AQ QF =.因为点P 为双曲线上的点,所以122PF PF -=,即12||2PA AF PF +-=, 所以12AF =.又在12F AF V 中,Q 为2AF 的中点,O 为12F F 的中点, 所以11||12OQ AF ==, 所以点Q 的轨迹是以O 为圆心,半径为1的圆, 所以点Q 的轨迹方程为221(0)x y y +=≠.故答案为:221(0)x y y +=≠. 【点睛】本题考查单位向量、向量的数量积、向量的加法法则的几何意义、双曲线的定义、轨迹方程的求解,考查函数与方程思想、转化与化归思想、数形结合思想,考查逻辑推理能力和运算求解能力,求解时注意平面几何知识的应用.四、解答题17.在ABC ∆中,角A ,B ,C 所对的边分别是a ,b ,c ,且sin 2sin()0c B b A B -+= (1)求角B 的大小;(2)设4a =,6c =,求sin C 的值. 【答案】(1)3B π=(2321【解析】(1)由已知结合正弦定理化简可求cos B ,进而可求B ;(2)由余弦定理可得,2221cos 22a cb B ac +-==,代入可求b ,由正弦定理可得,sin sin c BC b=可求. 【详解】解:(1)由正弦定理得sin sin 2sin sin()0C B B A B -+=, 化简得2sin sin cos sin sin 0C B B B C -=. 因为在三角形中,sin 0B ≠,sin 0C ≠, 可得1cos 2B =. 又因为(0,)B π∈,所以3B π=(2)由余弦定理可得,2221cos 22a cb B ac +-==,2163612462b +-=⨯⨯,所以27b =,由正弦定理可得,sin 321sin c B C b ==. 【点睛】本题主要考查了两角和及二倍角的公式,正弦定理,余弦定理的综合应用,属于中等试题.18.“不忘初心、牢记使命”主题教育活动正在全国开展,某区政府为统计全区党员干部一周参与主题教育活动的时间,从全区的党员干部中随机抽取n 名,获得了他们一周参加主题教育活动的时间(单位:时)的频率分布直方图,如图所示,已知参加主题教育活动的时间在(]12,16内的人数为92.(1)估计这些党员干部一周参与主题教育活动的时间的平均值;(2)用频率估计概率,如果计划对全区一周参与主题教育活动的时间在(]16,24内的党员干部给予奖励,且参与时间在(]16,20,(]20,24内的分别获二等奖和一等奖,通过分层抽样方法从这些获奖人中随机抽取5人,再从这5人中任意选取3人,求3人均获二等奖的概率. 【答案】(1)13.64(2)25【解析】(1)根据频率分布直方图以每个小矩形的中值为估值计算即可求出;(2)用分层抽样抽取的人数:在(]16,20内为4人,设为a b c d ,,,;在(]20,24内为1人,设为A ,列出基本事件,根据古典概型计算概率即可. 【详解】(1)由已知可得,()140.02500.04750.05000.01250.1150a =÷-+++=, 所以这些党员干部一周参加主题教育活动的时间的平均值为()60.0250100.0475140.1150180.0500220.0125413.64⨯+⨯+⨯+⨯+⨯⨯=.(2)因为0.1150492n ⨯⨯=,所以922000.11504n ==⨯.故参与主题教育活动的时间在(]16,20的人数为0.0500420040⨯⨯=, 参与主题教育活动的时间在(]20,24的人数为0.0125420010⨯⨯=.则利用分层抽样抽取的人数:在(]16,20内为4人,设为a b c d ,,,;在(]20,24内为1人,设为A.从这5人中选取3人的事件空间为:{}(,,),(,,),(,,),(,,),(,,),(,,),(,,),(,,),(,,),(,,)a b c a b d a b A a c d a c A a d A b c d b c A b d A c d A ,共10种情况,其中全是二等奖的有4种情况. 故42105P ==. 【点睛】本题主要考查了频率分布直方图,均值,分层抽样你,古典概型,属于中档题. 19.如图,圆柱的轴截面ABCD 是边长为2的正方形,点P 是圆弧CD 上的一动点(不与,C D 重合),点Q 是圆弧AB 的中点,且点,P Q 在平面ABCD 的两侧.(1)证明:平面PAD ⊥平面PBC ;(2)设点P 在平面ABQ 上的射影为点O ,点,E F 分别是PQB ∆和POA ∆的重心,当三棱锥P ABC -体积最大时,回答下列问题. (i )证明://EF 平面PAQ ; (ii )求三棱锥A OEF -的体积.【答案】(1)证明见解析(2)(i )证明见解析(ii )427【解析】(1)由PC PD ⊥,AD PC ⊥可得PC ⊥平面PAD ,即可证明;(2)(i )连接PE 并延长交BQ 于点M ,连接PF 并延长交OA 于点N ,连接MN ,利用平行线分线段成比例可得//EF MN ,即可得//EF AQ 得证; (ii )根据A EOF E AOF V V --=即可求解. 【详解】(1)证明:因为ABCD 是轴截面, 所以AD ⊥平面PCD ,所以AD PC ⊥,又点P 是圆弧CD 上的一动点(不与,C D 重合),且CD 为直径, 所以PC PD ⊥,又AD PD D =I ,PD ⊂平面PAD ,AD ⊂平面PAD , 所以PC ⊥平面PAD ,PC ⊂平面PBC , 故平面PAD ⊥平面PBC .(2)当三棱锥P ABC -体积最大时,点P 为圆弧CD 的中点.所以点O 为圆弧AB 的中点,所以四边形AQBO 为正方形,且PO ⊥平面ABO .(i )证明:连接PE 并延长交BQ 于点M ,连接PF 并延长交OA 于点N ,连接MN ,则//MN AQ ,因为,E F 分别为三角形的重心,所以23PE PF PM PN ==, 所以//EF MN , 所以//EF AQ ,又AQ ⊂平面PAQ ,EF ⊄平面PAQ , 所以//EF 平面PAQ . (ii )因为PO ⊥平面ABO , 所以PO BO ⊥,又AO BO ⊥,AO PO O =I , 所以BO ⊥平面PAO , 因为////EF AQ BO ,所以EF ⊥平面PAO ,即EF ⊥平面FAO ,即EF 是三棱锥E AOF -的高. 又2233EF BO ==,1112223323AOF APO S S ∆∆==⨯⨯=, 所以112224||333327A EOF E AOF AOF V V S EF --∆==⋅=⨯⨯=. 【点睛】本题主要考查了线面垂直、面面垂直的判定,线面平行,等体积法求棱锥体积,属于中档题.20.已知椭圆2222:1(0)x y C a b a b+=>>的左、右焦点分别为12,F F ,长轴长为4,且过点31,2P ⎛⎫ ⎪⎝⎭. (1)求椭圆C 的方程;(2)过2F 的直线l 交椭圆C 于,A B 两点,过A 作x 轴的垂线交椭圆C 与另一点Q (Q 不与,A B 重合).设ABQ ∆的外心为G ,求证2ABGF 为定值. 【答案】(1)22143x y +=(2)证明见解析【解析】(1)根据长轴及椭圆过点即可求出;(2)由题意设直线AB 为1x my =+,联立椭圆方程可求||AB ,求出ABQ ∆外接圆圆心21,034G m ⎛⎫⎪+⎝⎭,计算2GF ,化简即可证明2AB GF 为定值. 【详解】(1)由题意知2a =,将P 点坐标代入椭圆方程22221x y a b+=得291414b +=,解得b =所以椭圆方程为22143x y +=.(2)由题意知,直线AB 的斜率存在,且不为0,设直线AB 为1x my =+, 代入椭圆方程得()2234690m y my ++-=. 设()()1122,,,A x y B x y ,则12122269,3434m y y y y m m --+==++, 所以AB 的中点坐标为2243,3434m m m -⎛⎫⎪++⎝⎭,所以()212212134m AB y y m +=-=-+. 因为G 是ABQ ∆的外心,所以G 是线段AB 的垂直平分线与线段AQ 的垂直平分线的交点,AB 的垂直平分线方程为22343434m y m x m m ⎛⎫+=-- ⎪++⎝⎭,令0y =,得2134x m =+,即21,034G m ⎛⎫⎪+⎝⎭,所以222213313434m GF m m +=-=++,所以()22222121||1234433334m AB m m GF m ++===++,所以2||AB GF 为定值,定值为4. 【点睛】本题主要考查了椭圆的标准方程,直线与椭圆的位置关系,定值问题,属于难题. 21.已知函数()2(12)ln af x x a x x=+-+. (1)讨论()f x 的单调性;(2)如果方程()f x m =有两个不相等的解12,x x ,且12x x <,证明:1202x x f +⎛⎫'> ⎪⎝⎭. 【答案】(1)见解析(2)见解析【解析】(1)对函数()f x 进行求导得2()(21)()(0)x a x f x x x-+'=>,再对a 进行分类讨论,解不等式,即可得答案;(2)当0a „时,()f x 在(0,)+∞单调递增,()f x m =至多一个根,不符合题意;当0a >时,()f x 在(0,)a 单调递减,在(,)a +∞单调递增,则()0f a '=.不妨设120x a x <<<,只要证122x x a +>212x a x >-⇔,再利用函数的单调性,即可证得结论. 【详解】(1)2222122(12)()(21)()2(0)a a x a x a x a x f x x x x x x-+---+'=+-==>. ①当0a „时,(0,),()0,()x f x f x '∈+∞>单调递增; ②当0a >时,(0,),()0,()x a f x f x '∈<单调递减;(,),()0,()x a f x f x '∈+∞>单调递增.综上:当0a „时,()f x 在(0,)+∞单调递增;当0a >时,()f x 在(0,)a 单调递减,在(,)a +∞单调递增. (2)由(1)知,当0a „时,()f x 在(0,)+∞单调递增,()f x m =至多一个根,不符合题意;当0a >时,()f x 在(0,)a 单调递减,在(,)a +∞单调递增,则()0f a '=.不妨设120x a x <<<,要证1202x x f +⎛⎫'> ⎪⎝⎭,即证122x x a +>,即证122x x a +>,即证212x a x >-. 因为()f x 在(,)a +∞单调递增,即证()()212f x f a x >-,因为()()21f x f x =,所以即证()()112f x f a x >-,即证()()f a x f a x +<-. 令()()()g x f a x f a x =+--2()(12)ln()2()(12)ln()a a a x a a x a x a a x a x a x ⎡⎤⎡⎤=++-++--+--+⎢⎥⎢⎥+-⎣⎦⎣⎦4(12)ln()(12)ln()a ax a a x a a x a x a x=+-+---+-+-, 221212()4()()a a a ag x a x a x a x a x --'=++--+-+- ()()22222222222242(12)4()()()()a a x x x a a a a a x a x a x a x a x +---=+-=-+-+-. 当(0,)x a ∈时,()0,()g x g x '<单调递减,又(0)(0)(0)0g f a f a =+--=, 所以(0,)x a ∈时,()(0)0g x g <=,即()()f a x f a x +<-, 即()(2)f x f a x >-.又1(0,)x a ∈,所以()()112f x f a x >-,所以1202x x f +⎛⎫'> ⎪⎝⎭.【点睛】本题考查利用导数研究函数的单调性、证明不等式,考查函数与方程思想、转化与化归思想、分类讨论思想,考查逻辑推理能力和运算求解能力,求解时注意将所证不等式转化为利用函数的单调性进行证明.22.在直角坐标系xOy 中,曲线C的参数方程为21,2x s y ⎧=⎪⎨⎪=⎩(s为参数),以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系,直线l 的极坐标方程为cos 2sin 90ρθρθ++=.(1)求C 和l 的直角坐标方程;(2)设P 为曲线C 上的动点,求点P 到直线l 的距离的最小值. 【答案】(1)24y x =,290x y ++=(2【解析】(1)直接利用消参法可得曲线C 的直角坐标方程;将cos ,sin x y ρθρθ==代入l 的极坐标方程得l 的直角坐标方程; (2)设212P s ⎛⎫⎪⎝⎭,利用点到直线的距离公式,结合二次函数的性质求最值,即可得答案. 【详解】(1)C 的直角坐标方程为:24y x =,将cos ,sin x y ρθρθ==代入l 的极坐标方程得l 的直角坐标方程为:290x y ++=. (2)设212P s ⎛⎫⎪⎝⎭, 则点P 到直线l的距离21|9s d ++==,当s =-d ==. 【点睛】本题考查极坐标方程、参数方程、普通方程的互化、点到直线的距离公式,考查逻辑推理能力和运算求解能力,求解时注意点的参数设法. 23.已知函数()|1||24|f x x x =++-. (1)求不等式()6f x ≤的解集;(2)若函数()y f x =的图象最低点为(),m n ,正数,a b 满足6ma mb +=,求23a b+的取值范围.【答案】(1)[]13,x ∈-(2)2325,6a b ⎡⎫+∈+∞⎪⎢⎣⎭【解析】(1)分类讨论去掉绝对值得分段函数求解即可;(2)由分段函数求出最低点,得236a b +=,构造1,利用均值不等式求解即可. 【详解】(1)33,2()5,1233,1x x f x x x x x -≥⎧⎪=-+-<<⎨⎪-+≤-⎩,所以由()6f x ≤可得2336x x ≥⎧⎨-≤⎩,或1256x x -<<⎧⎨-+≤⎩,或1336x x ≤-⎧⎨-+≤⎩,解得:[]2,3x ∈或()1,2x ∈-或1x =-. 综上,[]13,x ∈-.(2)因为33,2()5,1233,1x x f x x x x x -≥⎧⎪=-+-<<⎨⎪-+≤-⎩,所以当2x =时,()min 3f x =,最低点为()2,3,即236a b +=,所以132a b +=. 23232313252323266a b b a a b a b a b ⎛⎫⎛⎫+=++=+++≥+= ⎪⎪⎝⎭⎝⎭, 当且仅当65a b ==时等号成立, 所以2325,6a b ⎡⎫+∈+∞⎪⎢⎣⎭【点睛】本题主要考查了含绝对值不等式的解法,分段函数的最值,均值不等式,属于中档题.。
2020年河南省郑州市高考(文科)数学二模试卷 (word版含解析)
2020年河南省郑州市高考(文科)数学二模试卷一、选择题(共12小题).1.设函数y=的定义域为A,函数y=ln(3﹣x)的定义域为B,则A∩B=()A.(﹣∞,3)B.(一8,﹣3)C.{3} D.[﹣3,3)2.已知复数z=a﹣i(a∈R),若z+=8,则复数z=()A.4+i B.4﹣i C.﹣4+i D.﹣4﹣i3.已知命题p:∀x>0,则3x>1;命题q:若a<b,则a2<b2,下列命题为真命题的是()A.p∧q B.p∧¬q C.¬p∧q D.¬p∧¬q4.若m,n是两条不同的直线,α,β,γ是三个不同的平面,则下列命题中的真命题是()A.若m⊂β,α⊥β,则m⊥αB.若m⊥β,m∥α,则α⊥βC.若α⊥γ,α⊥β,则β⊥γD.若α∩γ=m,β∩γ=n,m∥n,则α∥β5.郑州市2019年各月的平均气温(°C)数据的茎叶图如图:则这组数据的中位数是()A.20 B.21 C.20.5 D.236.在如图所示的程序框图中,若输出的值是4,则输入的x的取值范围是()A.(2,十∞)B.(2,4] C.(4,10] D.(4,+∞)7.已知△ABC是边长为1的等边三角形,点D、E分别是边AB、BC的中点,连接DE并延长到点F,使得DE=2EF,则•的值为()A.﹣B.C.D.8.已知双曲线的一条渐近线与直线3x﹣y+5=0垂直,则双曲线C的离心率等于()A.B.C.D.9.函数f(x)=的图象大致为()A.B.C.D.10.为了研究国民收入在国民之间的分配,避免贫富过分悬殊,美国统计学家劳伦茨提出了著名的劳伦茨曲线,如图所示.劳伦茨曲线为直线OL时,表示收人完全平等.劳伦茨曲线为折线OKL时,表示收人完全不平等.记区域A为不平等区域,a表示其面积;S为△OKL的面积.将Gini=,称为基尼系数.对于下列说法:①Gini越小,则国民分配越公平;②设劳伦茨曲线对应的函数为y=f(x),则对∀x∈(0,1),均有>1;③若某国家某年的劳伦茨曲线近似为y=1﹣(x∈[0,1]),则Gini=﹣1;其中正确的是()A.①②B.①③C.②③D.①②③11.在正方体ABCD﹣A1B1C1D1中,三棱锥A1﹣BC1D内切球的表面积为4π,则正方体外接球的体积为A.B.36πC.D.12.已知函数f(x)=﹣,g(x)=x•cos x﹣sin x,当x∈[﹣4π,4π],且x≠0时,方程f(x)=g(x)根的个数是()A.5 B.6 C.7 D.8二、填空题:共4小题,每小题5分,共20分.13.幂函数f(x)=(m2﹣3m+3)x m的图象关于y轴对称,则实数m=.14.将一颗骰子先后投掷两次分别得到点数a、b,则直线ax+by=0与圆(x﹣2)2+y2=2有公共点的概率为.15.在△ABC中,内角A,B,C所对的边分别为a,b,c,且b=,c=(sin A+cos A)b,则△ABC 的面积的最大值为.16.据国家统计局发布的数据,2019年11月全国CPI(居民消费价格指数),同比上涨4.5%,CPI上涨的主要因素是猪肉价格的上涨,猪肉加上其他畜肉影响CPI上涨3.27个百分点.如图是2019年11月CPI一篮子商品权重,根据该图,下列四个结论正确的有.①CPI一篮子商品中权重最大的是居住;②CPI一篮子商品中吃穿住所占权重超过50%③猪肉在CPI一篮子商品中权重为2.5%;④猪肉与其他禽肉在CPI一篮子商品中权重约为0.18%三、解答题:共70分.18.在改革开放40年成就展上有某地区某衣产品近几年的产扯统计如表:年份2014 2015 2016 2017 2018 2019 年份代码x 1 2 3 4 5 6 年产量(万吨) 6.6 6.7 7 7.1 7.2 7.4(I)根据表中数据,建立y关于x的线性回归方程=x+a;(II)根据线性回归方程预测2020年该地区该农产品的年产量.附:对于一组数据(x1,y1),(x2,y2),…,(x n,y n),其回归直线=x+a的斜率和截距的最小二乘估计分别为=,=﹣.(参考数据:(x i﹣)(y i﹣)=2.8,计算结果保留到小数点后两位)17.巳知数列{a n}的前n项和为S n,且S n=n2+2n﹣1.(Ⅰ)求数列{a n}的通项公式;(Ⅱ)若数列{b n}满足,求数列{b n}的前n项和T n.19.如图,三棱柱ABC﹣A1B1C1中,平面AA1B1B⊥平面ABC,D是AC的中点.(Ⅰ)求证:B1C∥平面A1BD;(Ⅱ)若∠A1AB=∠ACB=60°,AB=BB1,AC=2,BC=1,求三棱锥C﹣AA1B的体积.20.已知椭圆C:的短轴长为2,离心率为.(Ⅰ)求椭圆C的标准方程;(Ⅱ)直线l平行于直线y=x,且与椭圆C交于A,B两个不同的点,若∠AOB为钝角,求直线l在x 轴上的截距m的取值范围.21.已知函数f(x)=,曲线y=f(x)在点(e,f(e))处的切线方程为y=.(Ⅰ)求实数a的值,并求f(x)的单调区间;(Ⅱ)求证:当x>0时,f(x)≤x﹣1.(二)选考题:共10分.请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题记分.[选修4-4:坐标系与参数方程]22.在极坐标系中,圆C的方程为ρ=2a sinθ (a>0).以极点为坐标原点,极轴为x轴的正半轴建立平面直角坐标系,设直线l的参数方程为(t为参数).(Ⅰ)求圆C的标准方程和直线l的普通方程;(Ⅱ)若直线l与圆C交于A,B两点,且.求实数a的取值范围?[选修4-5:不等式选讲]23.已知函数f(x)=|x+1|﹣a|x﹣l|.(Ⅰ)当a=﹣2时,解不等式f(x)>5;(Ⅱ)若(x)≤a|x+3|,求a的最小值.参考答案一、选择题:共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设函数y=的定义域为A,函数y=ln(3﹣x)的定义域为B,则A∩B=()A.(﹣∞,3)B.(一8,﹣3)C.{3} D.[﹣3,3)【分析】由根式内部的代数式大于等于0求解x的范围化简A,由对数式的真数大于0求解x的范围化简B,再由交集运算得答案.解:由9﹣x2≥0,得﹣3≤x≤3,∴A=[﹣3,3],由3﹣x>0,得x<3,∴B=(﹣∞,﹣3).∴A∩B=[﹣3,3).故选:D.2.已知复数z=a﹣i(a∈R),若z+=8,则复数z=()A.4+i B.4﹣i C.﹣4+i D.﹣4﹣i【分析】利用复数的运算法则、共轭复数的定义即可得出.解:复数z=a﹣i(a∈R),若z+=8,∴a﹣i+a+i=8,解得a=4.则复数z=4﹣i.故选:B.3.已知命题p:∀x>0,则3x>1;命题q:若a<b,则a2<b2,下列命题为真命题的是()A.p∧q B.p∧¬q C.¬p∧q D.¬p∧¬q【分析】根据条件判断命题p,q的真假,结合复合命题真假关系进行判断即可.解:∀x>0,则3x>1为真命题,即命题p是真命题,当a=﹣3,b=0时,满足a<b,但a2<b2,不成立,即命题q是假命题,则p∧¬q是真命题,其余是假命题,故选:B.4.若m,n是两条不同的直线,α,β,γ是三个不同的平面,则下列命题中的真命题是()A.若m⊂β,α⊥β,则m⊥αB.若m⊥β,m∥α,则α⊥βC.若α⊥γ,α⊥β,则β⊥γD.若α∩γ=m,β∩γ=n,m∥n,则α∥β【分析】可以通过空间想象的方法,想象每个选项中的图形,并通过图形判断是否能得到每个选项中的结论,即可找出正确选项.解:A.错误,由β⊥α,得不出β内的直线垂直于α;B.正确,m∥α,根据线面平行的性质定理知,α内存在直线n∥m,∵m⊥β,∴n⊥β,n⊂α,∴α⊥β;C.错误,若两个平面同时和一个平面垂直,可以想象这两个平面可能平行,即不一定得到β⊥γ;D.错误,可以想象两个平面α、β都和γ相交,交线平行,这两个平面不一定平行.故选:B.5.郑州市2019年各月的平均气温(°C)数据的茎叶图如图:则这组数据的中位数是()A.20 B.21 C.20.5 D.23【分析】根据茎叶图中的数据,计算这组数据的中位数即可.解:由茎叶图知,这组数据从小到大排列为:1,2,15,16,18,20,21,23,23,28,32,34,所以中位数是×(20+21)=20.5.故选:C.6.在如图所示的程序框图中,若输出的值是4,则输入的x的取值范围是()A.(2,十∞)B.(2,4] C.(4,10] D.(4,+∞)【分析】根据题意i=3,循环三次,可通过循环三次解出x.解:根据结果,3[3(3x﹣2)﹣2]﹣2≤82,且3{3[3(3x﹣2)﹣2]﹣2}﹣2>82,解之得2<x≤4,故选:B.7.已知△ABC是边长为1的等边三角形,点D、E分别是边AB、BC的中点,连接DE并延长到点F,使得DE=2EF,则•的值为()A.﹣B.C.D.【分析】由题意画出图形,把、都用表示,然后代入数量积公式得答案.解:如图,∵D、E分别是边AB、BC的中点,且DE=2EF,∴•========.故选:C.8.已知双曲线的一条渐近线与直线3x﹣y+5=0垂直,则双曲线C的离心率等于()A.B.C.D.【分析】由题意可判断出直线3x﹣y+5=0与渐近线y=﹣x垂直,利用相互垂直的直线的斜率之间的关系和离心率的计算公式即可得出.解:∵双曲线的渐近线方程为y=±x.又直线3x﹣y+5=0可化为y=3x+5,可得斜率为3.∵双曲线的一条渐近线与直线3x﹣y+5=0垂直,∴=,=∴双曲的离心率e==.故选:B.9.函数f(x)=的图象大致为()A.B.C.D.【分析】利用偶函数可排除A,B,再根据x>时,函数值恒大于0,排除C.解:因为f(﹣x)===f(x),所以f(x)为偶函数,其图象关于y轴对称,所以排除A、B,又x>2时,f(x)>0,所以排除C.故选:D.10.为了研究国民收入在国民之间的分配,避免贫富过分悬殊,美国统计学家劳伦茨提出了著名的劳伦茨曲线,如图所示.劳伦茨曲线为直线OL时,表示收人完全平等.劳伦茨曲线为折线OKL时,表示收人完全不平等.记区域A为不平等区域,a表示其面积;S为△OKL的面积.将Gini=,称为基尼系数.对于下列说法:①Gini越小,则国民分配越公平;②设劳伦茨曲线对应的函数为y=f(x),则对∀x∈(0,1),均有>1;③若某国家某年的劳伦茨曲线近似为y=1﹣(x∈[0,1]),则Gini=﹣1;其中正确的是()A.①②B.①③C.②③D.①②③【分析】由基尼系数的计算公式入手,借助于图象及定积分解决问题.解:对于①,根据基尼系数公式Gini=,可得基尼系数越小,不平等区域的面积a越小,国民分配越公平,所以①正确;对于②,根据劳伦茨曲线为一条凹向横轴的曲线,由图得∀x∈(0,1),均有f(x)<x,可得<1,所以②错误;对于③,因为a=∫[x﹣(1﹣)]dx=∫(x﹣1)dx+∫dx=(x2﹣x)|+π×12=﹣+π,S=,所以Gini===,所以③正确.故①③正确.故选:B.11.在正方体ABCD﹣A1B1C1D1中,三棱锥A1﹣BC1D内切球的表面积为4π,则正方体外接球的体积为()A.B.36πC.D.【分析】根据三棱锥的内切球进一步求出正方体的棱长,最后求出正方体的外接球的半径,进一步求出结果.解:设正方体的棱长为a,则BD=a,由于三棱锥A1﹣BC1D内切球的表面积为4π,所以球的半径为1,根据球与正四面体的体积的关系式,利用体积相等及关系式的应用,所以1=,解得a=2.所以正方体的外接球的半径为,所以正方体的外接球的体积为故选:B.12.已知函数f(x)=﹣,g(x)=x•cos x﹣sin x,当x∈[﹣4π,4π],且x≠0时,方程f(x)=g(x)根的个数是()A.5 B.6 C.7 D.8【分析】先对两个函数分析可知,函数f(x)与g(x)都是奇函数,且f(x)是反比例函数,g(x)在[0,π]上是减函数,在[π,2π]上是增函数,在[2π,3π]上是减函数,在[3π,4π]上是增函数,且g(0)=0,g(π)=﹣π,g(2π)=2π,g(3π)=﹣3π,g(4π)=4π;从而作出函数的图象,由图象求方程的根的个数即可.解:g′(x)=cos x﹣x sin x﹣cos x=﹣x sin x;令g′(x)=0得x=kπ,k∈Z.∴g(x)在[0,π]上是减函数,在[π,2π]上是增函数,在[2π,3π]上是减函数,在[3π,4π]上增.且g(0)=0,g(π)=﹣π,g(2π)=2π,g(3π)=﹣3π,g(4π)=4π;故作函数f(x)与g(x)在[0,4π]上的图象如下,结合图象可知,两图象在[0,4π]上共有4个交点;又f(x),g(x)都是奇函数,且f(x)不经过原点,∴f(x)与g(x)在[﹣4π,4π]上共有8个交点,故方程f(x)=g(x)根的个数是8个.故选:D.二、填空题:共4小题,每小题5分,共20分.13.幂函数f(x)=(m2﹣3m+3)x m的图象关于y轴对称,则实数m=2.【分析】根据幂函数的定义与性质,列方程求出m的值,再验证即可.解:函数f(x)=(m2﹣3m+3)x m是幂函数,∴m2﹣3m+3=1,解得m=1或m=2;当m=1时,函数y=x的图象不关于y轴对称,舍去;当m=2时,函数y=x2的图象关于y轴对称;∴实数m=2.故答案为:2.14.将一颗骰子先后投掷两次分别得到点数a、b,则直线ax+by=0与圆(x﹣2)2+y2=2有公共点的概率为.【分析】根据题意,将一颗骰子先后投掷两次,所有的点数所形成的数组(a,b)有36种情况.若直线ax+by=0与圆(x﹣2)2+y2=2有公共点,则圆心到直线的距离小于半径,利用点到直线的距离公式建立不等式解出a≤b,列举出满足条件的(a,b)有21种.再利用古典概型公式加以计算,即可得到所求的概率.解:根据题意,将一颗骰子先后投掷两次,得到的点数所形成的数组(a,b)有(1,1)、(1,2)、(1,3)、…、(6,6),共36种,其中满足直线ax+by=0与圆(x﹣2)2+y2=2有公共点,即圆心(2,0)到直线的距离小于或等于半径r,可得,化简得a≤b,满足条件的(a,b)有数组情况如下:①a=1时,b=1、2、…、6,共6种情况;②a=2时,b=2、3、…、6,共5种情况;③a=3时,b=3、4、…、6,共4种情况;④a=4时,b=4、5、6,共3种情况;⑤a=5时,b=5、6,共2种情况;⑥a=6时b=6,1种情况.总共有6+5+4+3+2+1=21种.因此,所求的概率P==.故答案为:15.在△ABC中,内角A,B,C所对的边分别为a,b,c,且b=,c=(sin A+cos A)b,则△ABC 的面积的最大值为.【分析】将b=代入第二个等式,即可约去b,可得c=,然后代入面积公式,就可以将三角形的面积转化为A的三角函数,则最大值可求.解:∵b=,c=(sin A+cos A)b,.∴,∴===,当时,,.故答案为:.16.据国家统计局发布的数据,2019年11月全国CPI(居民消费价格指数),同比上涨4.5%,CPI上涨的主要因素是猪肉价格的上涨,猪肉加上其他畜肉影响CPI上涨3.27个百分点.如图是2019年11月CPI一篮子商品权重,根据该图,下列四个结论正确的有①②③.①CPI一篮子商品中权重最大的是居住②CPI一篮子商品中吃穿住所占权重超过50%③猪肉在CPI一篮子商品中权重为2.5%④猪肉与其他禽肉在CPI一篮子商品中权重约为0.18%【分析】根据2019年11月全国CPI(居民消费价格指数),即可判断出正误.解:①CPI一篮子商品中权重最大的是居住为23%,正确;②CPI一篮子商品中吃穿住所占权重为23%+8.0%+10.3%+19.9%=61.2%>50%,正确;③猪肉在CPI一篮子商品中权重为2.5%,正确;④猪肉与其他禽肉在CPI一篮子商品中权重约为2.1%+2.5%=4.6%,因此不正确.故答案为:①②③.三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:共60分17.巳知数列{a n}的前n项和为S n,且S n=n2+2n﹣1.(Ⅰ)求数列{a n}的通项公式;(Ⅱ)若数列{b n}满足,求数列{b n}的前n项和T n.【分析】本题第(Ⅰ)题先将n=1代入表达式得到a1的值,当n≥2时,利用公式a n=S n﹣S n﹣1可计算出a n的表达式,然后将a1的值代入验证,即可得到数列{a n}的通项公式;第(Ⅱ)题先根据第(Ⅰ)题的结果计算出数列{b n}的通项公式,然后运用裂项相消法计算前n项和T n,本题注意要验证n=1的情况.解:(Ⅰ)由题意,当n=1时,a1=S1=2.当n≥2时,.而当n=1时,a1=2不满足上式,故数列{a n}的通项公式为a n=.(Ⅱ)由(Ⅰ)知,当n=1时,,当n≥2时,,∴b n=.故当n=1时,,当n≥2时,T n=b1+b2+b3+…+b n==.又适合,∴.18.在改革开放40年成就展上有某地区某衣产品近几年的产扯统计如表:年份2014 2015 2016 2017 2018 2019 年份代码x 1 2 3 4 5 6 年产量(万吨) 6.6 6.7 7 7.1 7.2 7.4(I)根据表中数据,建立y关于x的线性回归方程=x+a(II)根据线性回归方程预测2020年该地区该农产品的年产量.附:对于一组数据(x1,y1),(x2,y2),…,(x n,y n),其回归直线=x+a的斜率和截距的最小二乘估计分别为=,=﹣.(参考数据:(x i﹣)(y i﹣)=2.8,计算结果保留到小数点后两位)【分析】(Ⅰ)求得样本中心点和回归系数,利用最小二乘法即可求得线性回归方程;(Ⅱ)由(Ⅰ)回归方程,计算x=7时得2020年该地区农产品的年产量.解:(1)由题意可知:,,,所以,又,故y关于x的线性回归方程为.(2)由(1)可得,当年份为2020年时,年份代码x=7,此时.所以可预测2020年该地区该农产品的年产量约为7.56万吨.19.如图,三棱柱ABC﹣A1B1C1中,平面AA1B1B⊥平面ABC,D是AC的中点.(Ⅰ)求证:B1C∥平面A1BD;(Ⅱ)若∠A1AB=∠ACB=60°,AB=BB1,AC=2,BC=1,求三棱锥C﹣AA1B的体积.【分析】(Ⅰ)连结AB1交A1B于点O,则O为AB1的中点,可得OD∥B1C,再由直线与平面平行的判定可得B1C∥平面A1BD;(Ⅱ)求解三角形求得得AB⊥BC.再证明BC⊥平面AA1B1B.求出三角形A1AB的面积,由棱锥体积公式可得三棱锥C﹣AA1B的体积.【解答】(Ⅰ)证明:连结AB1交A1B于点O,则O为AB1的中点,∵D是AC的中点,∴OD∥B1C,又OD⊂平面A1BD,B1C⊄平面A1BD,∴B1C∥平面A1BD;(Ⅱ)解:∵AC=2,BC=1,∠ACB=60°,∴AB2=AC2+BC2﹣2AC•BC•COS∠ACB=3,得.∴AC2=AB2+BC2,得AB⊥BC.又∵平面AA1B1B⊥平面ABC,平面AA1B1B∩平面ABC=AB,∴BC⊥平面AA1B1B.∵∠A1AB=60°,AB=BB1=AA1,∴.∴.∴.20.已知椭圆C:的短轴长为2,离心率为.(Ⅰ)求椭圆C的标准方程;(Ⅱ)直线l平行于直线y=x,且与椭圆C交于A,B两个不同的点,若∠AOB为钝角,求直线l 在x轴上的截距m的取值范围.【分析】(Ⅰ)由题意可得,所以,通过离心率求出a,然后求解椭圆方程.(Ⅱ)由于直线l平行于直线,即,所以l的方程为.联立直线与椭圆方程,利用韦达定理,结合∠AOB为钝角,向量的数量积的符号,求出n的范围,然后求解即可.解:(Ⅰ)由题意可得,所以,,解得,所以椭圆C的标准方程为.(Ⅱ)由于直线l平行于直线,即,所以l的方程为.由得x2+2nx+2n2﹣4=0,因为直线l与椭圆C交两个不同的点,所以△=(2n)2﹣4(2n2﹣4)>0,解得﹣2<n<2.设A(x1,y1),B(x2,y2),则x1+x2=﹣2n,.∠AOB为钝角等价于,且n≠0,由=,即n2<2,且n≠0,所以直线l在x轴上的截距m的取值范围.21.已知函数f(x)=,曲线y=f(x)在点(e,f(e))处的切线方程为y=.(Ⅰ)求实数a的值,并求f(x)的单调区间;(Ⅱ)求证:当x>0时,f(x)≤x﹣1.【分析】(•I)先对函数求导,然后结合已知切线方程及导数的几何意义即可求解;(II)当x>0时,要证f(x)≤x﹣1,即证lnx﹣x2+x≤0,构造函数g(x)=lnx﹣x2+x(x>0),然后结合导数可求解单调性,进而可求函数g(x)的范围,可求.解:(I)∵,∴,∴,又曲线y=f(x)在点(e,f(e))处的切线方程为,f'(e)=0,即a=0.∵,∴,令f'(x)>0,得1﹣lnx>0,即0<x<e;令f'(x)<0,得1﹣lnx<0,即x>e,所以f(x)的单调增区间是(0,e),单调减区间是(e,+∞).(II)证明:当x>0时,要证f(x)≤x﹣1,即证lnx﹣x2+x≤0,令g(x)=lnx﹣x2+x(x>0),则,当0<x<1时,g'(x)>0,g(x)单调递增;当x>1时,g'(x)<0,g(x)单调递减,所以g(x)≤g(1)=0,即当x>0时,f(x)≤x﹣1.(二)选考题:共10分.请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题记分.[选修4-4:坐标系与参数方程]22.在极坐标系中,圆C的方程为ρ=2a sinθ (a>0).以极点为坐标原点,极轴为x轴的正半轴建立平面直角坐标系,设直线l的参数方程为(t为参数).(Ⅰ)求圆C的标准方程和直线l的普通方程;(Ⅱ)若直线l与圆C交于A,B两点,且.求实数a的取值范围?【分析】(Ⅰ)利用极坐标方程进行转化即可求圆C的标准方程,消去参数即可求直线l的普通方程;(Ⅱ)利用直线和圆相交的弦长公式进行转化求解即可.解:(Ⅰ)∵ρ=2a sinθ (a>0).∴ρ2=2aρsinθ,即x2+y2=2ay,即x2+(y﹣a)2=a2,(a>0).则圆C的标准方程为x2+(y﹣a)2=a2,(a>0).由,消去参数t得4x﹣3y+5=0,即直线l的普通方程为4x﹣3y+5=0;(Ⅱ)由圆的方程得圆心C(0,a),半径R=a,则圆心到直线的距离d=,∵.∴2≥a,即a2﹣d2≥a2,则d2≤,即d≤,则≤,则﹣≤≤,由得得≤a≤10.即实数a的取值范围是≤a≤10.[选修4-5:不等式选讲]23.已知函数f(x)=|x+1|﹣a|x﹣l|.(Ⅰ)当a=﹣2时,解不等式f(x)>5;(Ⅱ)若(x)≤a|x+3|,求a的最小值.【分析】(Ⅰ)将a=2代入f(x),表示出f(x)的分段形式,结合函数的单调性求出不等式的解集即可;(Ⅱ)问题转化为≤,求出a的最小值即可.解:(Ⅰ)当a=﹣2时,f(x)=,由f(x)的单调性及f(﹣)=f(2)=5,得f(x)>5的解集为{x|x<﹣,或x>2}.…(Ⅱ)由f(x)≤a|x+3|得a≥,由|x﹣1|+|x+3|≥2|x+1|得≤,得a≥.(当且仅当x≥1或x≤﹣3时等号成立)故a的最小值为.…。
2020年河南省普通高中高考质量测评(二)数学文科试题(带答案解析)
绝密★启用前2020年河南省普通高中高考质量测评(二)数学文科试题试卷副标题注意事项:1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)请点击修改第I 卷的文字说明 一、单选题1.已知全集U =R ,集合{}{}22|log 1,|0A x x B x x x =<=->,则A B =I ( )A .{|12}x x <<B .{|2}x x <C .{|12}x x <„D .{|14}x x <„2.已知复数z 满足21iz i -=+,则z =( ) A .132i+ B .132i - C .32i +D .32i- 3.已知角θ的终边过点()3,4-,则()cos πθ-=( ) A .45-B .45C .35-D .354.若椭圆221(0)2x y p p p+=>的一个焦点与抛物线22(0)y px p =>的焦点重合,则p =( )A .2B .3C .4D .85.已知函数()xf x ae x b =++,若函数()f x 在(0,(0))f 处的切线方程为23y x =+,则ab 的值为( ) A .1B .2C .3D .46.函数2sin ()1x xf x x +=+在[,]-ππ的图象大致为( )…………○…………订………………线…………○……※※在※※装※※订※※线※※内※※答※※题…………○…………订………………线…………○……A . B .C .D .7.如图,在四棱锥P ABCD -中,//,2,3AD BC AD BC ==,E 是PD 的中点,F 在PC 上且13PF PC =,G 在PB 上且23PG PB =,则( )A .3AG EF =,且AG 与EF 平行B .3AG EF =,且AG 与EF 相交C .2AG EF =,且AG 与EF 异面D .2AG EF =,且AG 与EF 平行8.已知等差数列{}n a 的前n 项和为n S ,22a =,728S =,则数列11n n a a +⎧⎫⎨⎬⎩⎭的前2020项和为( )A .20202021 B .20182020 C .20182019D .202120209.“角谷定理”的内容为对于每一个正整数,如果它是奇数,则对它乘3再加1;如果它是偶数,则对它除以2.如此循环,最终都能够得到1.如图为研究角谷定理的一个程序框图.若输入n 的值为10,则输出i 的值为()………○…………订…………线…………○……__________班级:___________考号:………○…………订…………线…………○……A .5B .6C .7D .810.现有一副斜边长相等的直角三角板.若将它们的斜边AB 重合,其中一个三角板沿斜边折起形成三棱锥A BCD -,如图所示,已知,64DAB BAC ππ∠=∠=,三棱锥的外接球的表面积为4π,该三棱锥的体积的最大值为( )A B C D 11.设函数()sin()f x x ωϕ=+,其中0,,43ππωϕ⎡⎤>∈⎢⎥⎣⎦,已知()f x 在[0,2]π上有且仅有4个零点,则下列ω的值中满足条件的是( ) A .136ω= B .116ω=C .74ω=D .34ω=二、多选题12.由我国引领的5G 时代已经到来,5G 的发展将直接带动包括运营、制造、服务在内的通信行业整体的快速发展,进而对GDP 增长产生直接贡献,并通过产业间的关联效应和波及效应,间接带动国民经济各行业的发展,创造岀更多的经济增加值.如图是某单位结合近年数据,对今后几年的5G 经济产出所做的预测.结合下图,下列说法正确的…线…………○……线…………○…是()A.5G的发展带动今后几年的总经济产出逐年增加B.设备制造商的经济产出前期增长较快,后期放缓C.设备制造商在各年的总经济产出中一直处于领先地位D.信息服务商与运营商的经济产出的差距有逐步拉大的趋势第II卷(非选择题)请点击修改第II卷的文字说明三、填空题13.若||3a=,||2b=,2a b+=r r,则ar与br的夹角为______________.14.记n S为等比数列{}n a的前n项和,若数列{}12nS a-也为等比数列,则43SS=________.15.某工厂生产的产品中分正品与次品,正品重100克,次品重110 克.现有5袋产品(每袋装有10个产品),已知其中有且只有一袋次品(10个产品均为次品),如果将5袋产品以1-5编号,第i袋取出i个产品(i=1,2,3,4,5),并将取出的产品一起用秤(可以称出物体重量的工具)称出其重量y,若次品所在的袋子的编号是2,此时的重量y=__________克;若次品所在袋子的编号是n,此时的重量y=_________克.16.已知点P是双曲线2213yx-=右支上一动点,12,F F是双曲线的左、右焦点,动点Q满足下列条件:①12212||||PF PFQFPF PF⎛⎫+=⎪⎝⎭⋅u u u uu u u r u uru u uu ru u rr u,②1212||||PF PFQPPF PFλ⎛⎫++=⎪⎝⎭u u u r u u u ru u u ru u u r u u u r,则点Q的轨迹方程为________________.四、解答题…外…………○…………订…………○…学校:____________考号:___________…内…………○…………订…………○…17.在ABC ∆中,角A ,B ,C 所对的边分别是a ,b ,c ,且sin 2sin()0c B b A B -+= (1)求角B 的大小;(2)设4a =,6c =,求sin C 的值.18.“不忘初心、牢记使命”主题教育活动正在全国开展,某区政府为统计全区党员干部一周参与主题教育活动的时间,从全区的党员干部中随机抽取n 名,获得了他们一周参加主题教育活动的时间(单位:时)的频率分布直方图,如图所示,已知参加主题教育活动的时间在(]12,16内的人数为92.(1)估计这些党员干部一周参与主题教育活动的时间的平均值;(2)用频率估计概率,如果计划对全区一周参与主题教育活动的时间在(]16,24内的党员干部给予奖励,且参与时间在(]16,20,(]20,24内的分别获二等奖和一等奖,通过分层抽样方法从这些获奖人中随机抽取5人,再从这5人中任意选取3人,求3人均获二等奖的概率.19.如图,圆柱的轴截面ABCD 是边长为2的正方形,点P 是圆弧CD 上的一动点(不与,C D 重合),点Q 是圆弧AB 的中点,且点,P Q 在平面ABCD 的两侧.(1)证明:平面PAD ⊥平面PBC ;(2)设点P 在平面ABQ 上的射影为点O ,点,E F 分别是PQB ∆和POA ∆的重心,当三棱锥P ABC -体积最大时,回答下列问题.(ii )求三棱锥A OEF -的体积.20.已知椭圆2222:1(0)x y C a b a b+=>>的左、右焦点分别为12,F F ,长轴长为4,且过点31,2P⎛⎫ ⎪⎝⎭. (1)求椭圆C 的方程;(2)过2F 的直线l 交椭圆C 于,A B 两点,过A 作x 轴的垂线交椭圆C 与另一点Q (Q不与,A B 重合).设ABQ ∆的外心为G ,求证2ABGF 为定值.21.已知函数()2(12)ln af x x a x x=+-+. (1)讨论()f x 的单调性;(2)如果方程()f x m =有两个不相等的解12,x x ,且12x x <,证明:1202x x f +⎛⎫'> ⎪⎝⎭. 22.在直角坐标系xOy 中,曲线C 的参数方程为21,2x s y ⎧=⎪⎨⎪=⎩(s 为参数),以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系,直线l 的极坐标方程为cos 2sin 90ρθρθ++=.(1)求C 和l 的直角坐标方程;(2)设P 为曲线C 上的动点,求点P 到直线l 的距离的最小值. 23.已知函数()|1||24|f x x x =++-. (1)求不等式()6f x ≤的解集;(2)若函数()y f x =的图象最低点为(),m n ,正数,a b 满足6ma mb +=,求23a b+的取值范围.参考答案1.A 【解析】 【分析】解对数不等式和一元二次不等式化简集合,A B ,再进行交运算,即可得答案. 【详解】由题意得{}2|log 1{|02},{|(1)0}{|0A x x x x B x x x x x =<=<<=->=<或1}x >, ∴{|12}A B x x =<<I . 故选:A. 【点睛】本题考查数不等式和一元二次不等式的求解、集合的交运算,考查运算求解能力,属于基础题. 2.B 【解析】 【分析】利用复数的除法运算,即可得答案. 【详解】 ∵2(2)(1)131(1)(1)2i i i iz i i i ----===++-. 故选:B. 【点睛】本题考查复数的除法运算,考查基本运算求解能力,属于基础题. 3.D 【解析】 【分析】根据三角函数的定义及诱导公式即可求解. 【详解】因为角θ的终边过点()3,4-,所以3cos 5θ=-,3cos()cos 5πθθ-=-=. 故选:D. 【点睛】本题主要考查了三角函数的定义,诱导公式,属于容易题. 4.C 【解析】 【分析】由椭圆方程,抛物线方程写出焦点,根据焦点重合即可求解. 【详解】椭圆的焦点坐标为()),,抛物线的焦点坐标为,02p ⎛⎫⎪⎝⎭,2p=,解得4p =, 故选:C. 【点睛】本题主要考查了椭圆的简单几何性质,抛物线的简单几何性质,属于容易题. 5.B 【解析】 【分析】对函数求导得(0)2f '=,求得a 的值,再根据切点既在切线上又在曲线上,可求得b 的值,即可得答案. 【详解】∵()1xf x ae '=+,∴(0)12f a '=+=,解得1,(0)13a f a b b ==+=+=,∴2b =, ∴2ab =. 故选:B. 【点睛】本题考查导数的几何意义,考查函数与方程思想,考查逻辑推理能力和运算求解能力,求解时注意切点既在切线上又在曲线上的应用. 6.D 【解析】 【分析】根据函数为奇函数及()0f π>,再结合排除法,即可得答案. 【详解】∵函数的定义域为R ,关于原点对称,且2sin()()()()()1x x f x f x x -+--==--+,∴()f x 是奇函数,故排除A ;22sin ()011f ππππππ+==>++,排除B ,C.故选:D. 【点睛】本题考查根据函数的解析式选择函数的图象,考查数形结合思想,求解时注意充分利用函数的性质及特殊点的函数值进行求解. 7.D 【解析】 【分析】取CF 的中点H ,连接,DH GH ,证明//AG DH ,且AG DH =,即可得答案. 【详解】取CF 的中点H ,连接,DH GH ,则在三角形PBC 中23PG PH PB PC ==, 所以//GH BC ,且223GH BC ==, 又因为//AD BC 且2AD =,所以//GH AD ,且GH AD =, 所以四边形ADHG 为平行四边形, 所以//AG DH ,且AG DH =.在PDH △中,,E F 分别为PD 和PH 的中点,所以//EF DH ,且12EF DH =, 所以//EF AG ,且12EF AG =,即2AG EF =,故选:D.【点睛】本题考查空间中直线、平面的平行关系,考查转化与化归思想,考查空间想象能力,求解时注意利用线段的比例关系,证明平行. 8.A 【解析】 【分析】根据等差数列前n 项和公式及728S =,可得4a 的值.代入22a =由等差数列通项公式,即可求得首项与公差,进而得数列{}n a 的通项公式.结合裂项求和法即得数列11n n a a +⎧⎫⎨⎬⎩⎭的前2020项和. 【详解】等差数列{}n a 的前n 项和为n S ,728S =, 由等差数列前n 项和公式可得74728S a == 所以44a =,结合22a =, 由等差数列通项公式可得4121342a a d a a d =+=⎧⎨=+=⎩,解得111a d =⎧⎨=⎩,由等差数列通项公式可得()111n a n n =+-⨯=,则()1111n n a a n n +=+. 所以122334202020211111a a a a a a a a +++⋅⋅⋅+ 111112233420202021=+++⋅⋅⋅+⨯⨯⨯⨯ 111111112233420202021=-+-+-+⋅⋅⋅+-20202021=. 故选:A. 【点睛】本题考查了等差数列前n 项和的性质应用,等差数列通项公式的求法,裂项求和的应用,属于基础题. 9.B 【解析】 【分析】根据流程逐步分析,直到1n =时,计算出i 的值即可. 【详解】(1)10,0n i ==;(2)5,1n i ==;(3)16,2n i ==;(4)8,3n i ==;(5)4,4n i ==;(6)2,5n i ==;(7)1,6n i ==. 故选B . 【点睛】本题考查根据程序框图计算输出值,难度较易.程序框图问题,多数可以采用列举法的方式解答问题. 10.B 【解析】 【分析】设三棱锥A BCD -的外接球的半径为r ,由球的体积得球的半径,当平面ABC ⊥平面ABD 时,三棱锥的体积达到最大,利用体积公式计算,即可得答案. 【详解】设三棱锥A BCD -的外接球的半径为r ,因为244r ππ=⇒1r =, 因为90ADB ACB ︒∠=∠=,所以AB 为外接球的直径,所以2AB =,且1,AD BD AC BC ====当点C 到平面ABD 距离最大时,三枝锥A BCD -的体积最大, 此时平面ABC ⊥平面ABD ,且点C 到平面ABD 的距离1d =,所以11111332A BCD C ABD ABD V V S d --==⋅=⨯⨯=△.故选:B. 【点睛】本题考查三棱锥与球的内接问题、三棱锥体积的最大值、球的体积公式,考查函数与方程思想、转化与化归思想,考查空间想象能力和运算求解能力,求解时注意球心位置的确定. 11.A 【解析】 【分析】设t x ωϕ=+,则2t ϕπωϕ+剟,从而将问题转化为sin y t =在[,2]ϕπωϕ+上有4个零点,从而得到425ππωϕπ+<„,再利用不等式恒成立问题求得ω的范围,即可得答案. 【详解】设t x ωϕ=+,则2t ϕπωϕ+剟, 所以sin y t =在[,2]ϕπωϕ+上有4个零点, 因为,43ππϕ⎡⎤∈⎢⎥⎣⎦,所以425ππωϕπ+<„, 所以52222ϕϕωππ-<-„, 所以5342222ππωππ-<-„,即15783ω<„,满足的只有A.故选:A. 【点睛】本题考查根据三角函数的零点个数求参数值,考查函数与方程思想、转化与化归思想,考查逻辑推理能力和运算求解能力,求解时注意换元法的应用. 12.ABD 【解析】 【分析】本题结合图形即可得出结果. 【详解】由图可知设备制造商在各年的总经济产出中在前期处于领先地位, 而后期是信息服务商处于领先地位,故C 项表达错误.故选:ABD . 【点睛】本题主要考查数学文字及图形的阅读理解能力.本题属基础题. 13.3π 【解析】 【分析】由222|2|44a b a a b b +=+⋅+rrrrrr 及||||cos a b a b θ⋅=⋅rrr r,即可得到本题答案. 【详解】设a r 与 b r 的夹角为θ,则222|2|449432cos 4437a b a a b b θ+=+⋅+=+⨯⨯⨯+⨯=r rr r r r ,得1cos 2θ=,所以3πθ=.故答案为:3π【点睛】本题主要考查利用向量的模的计算公式求向量的夹角,属基础题. 14.1514【解析】 【分析】设等比数列{}n a 的公比为q ,利用等比数列{}12n S a -的等比中项性质可得公比q ,再代入等比数列的前n 项和公式中,即可得答案. 【详解】设等比数列{}n a 的公比为q , ∵数列{}12n S a -为等比数列,∴()()2211231a a a a a a -=-+-,解得:12q =, ∴4211231241332315(1)1587(1)144Sa q q q S a q a a a a a a q a +++====+++++++.故答案为:1514. 【点睛】本题考查等比数列中的基本量法运算、等比数列的通项公式和前n 项和公式,考查函数与方程思想、转化与化归思想,考查逻辑推理能力和运算求解能力. 15.1520 150010n +,{}1,2,3,4,5n ∈【解析】 【分析】按照题意,可得从5个袋子中取得的总个数及第2个袋子中取的个数,进而确定总质量;再写出次品是第n 个时的个数及对应解析式即可. 【详解】第1袋中取1个,第2袋取2个,第3袋取3个,第4袋取4个,第5袋取5个,共15个. 若次品从第2袋中取,则共有13个正品,2个次品,所以总质量为1001311021520y =⨯+⨯=;若次品是第n 袋中取,则15个产品中共有次品n 个,正品15n -, 则()10015110150010y n n n =⨯-+⨯=+,{}1,2,3,4,5n ∈故答案为:1520;150010n +,{}1,2,3,4,5n ∈【点睛】本题考查了实际问题中函数的应用,属于基础题. 16.221(0)x y y +=≠ 【解析】 【分析】设动点Q 的坐标为(,)x y ,延长2F Q 交1PF 于点A ,根据向量的加法法则及数量积为0,可得2QF PQ ⊥,利用双曲线的定义可得11||12OQ AF ==,即可得答案. 【详解】设动点Q 的坐标为(,)x y ,延长2F Q 交1PF 于点A , 由条件②知点Q 在12F PF ∠的角平分线上,结合条件①知2QF PQ ⊥,所以在2PF A △中,2PQ F A ⊥.又PQ 平分2APF ∠, 所以2PF A △为等腰三角形,即2||PA PF =,2||AQ QF =.因为点P 为双曲线上的点,所以122PF PF -=,即12||2PA AF PF +-=, 所以12AF =.又在12F AF V 中,Q 为2AF 的中点,O 为12F F 的中点, 所以11||12OQ AF ==, 所以点Q 的轨迹是以O 为圆心,半径为1的圆, 所以点Q 的轨迹方程为221(0)x y y +=≠.故答案为:221(0)x y y +=≠. 【点睛】本题考查单位向量、向量的数量积、向量的加法法则的几何意义、双曲线的定义、轨迹方程的求解,考查函数与方程思想、转化与化归思想、数形结合思想,考查逻辑推理能力和运算求解能力,求解时注意平面几何知识的应用.17.(1)3B π=(2 【解析】 【分析】(1)由已知结合正弦定理化简可求cos B ,进而可求B ;(2)由余弦定理可得,2221cos 22a cb B ac +-==,代入可求b ,由正弦定理可得,sin sin c BC b=可求. 【详解】解:(1)由正弦定理得sin sin 2sin sin()0C B B A B -+=, 化简得2sin sin cos sin sin 0C B B B C -=. 因为在三角形中,sin 0B ≠,sin 0C ≠, 可得1cos 2B =. 又因为(0,)B π∈,所以3B π=(2)由余弦定理可得,2221cos 22a cb B ac +-==,2163612462b +-=⨯⨯,所以b =由正弦定理可得,sin sin 14c B C b ==. 【点睛】本题主要考查了两角和及二倍角的公式,正弦定理,余弦定理的综合应用,属于中等试题. 18.(1)13.64(2)25【解析】 【分析】(1)根据频率分布直方图以每个小矩形的中值为估值计算即可求出;(2)用分层抽样抽取的人数:在(]16,20内为4人,设为a b c d ,,,;在(]20,24内为1人,设为A ,列出基本事件,根据古典概型计算概率即可. 【详解】(1)由已知可得,()140.02500.04750.05000.01250.1150a =÷-+++=, 所以这些党员干部一周参加主题教育活动的时间的平均值为()60.0250100.0475140.1150180.0500220.0125413.64⨯+⨯+⨯+⨯+⨯⨯=.(2)因为0.1150492n ⨯⨯=,所以922000.11504n ==⨯.故参与主题教育活动的时间在(]16,20的人数为0.0500420040⨯⨯=, 参与主题教育活动的时间在(]20,24的人数为0.0125420010⨯⨯=.则利用分层抽样抽取的人数:在(]16,20内为4人,设为a b c d ,,,;在(]20,24内为1人,设为A.从这5人中选取3人的事件空间为:{}(,,),(,,),(,,),(,,),(,,),(,,),(,,),(,,),(,,),(,,)a b c a b d a b A a c d a c A a d A b c d b c A b d A c d A ,共10种情况,其中全是二等奖的有4种情况. 故42105P ==. 【点睛】本题主要考查了频率分布直方图,均值,分层抽样你,古典概型,属于中档题. 19.(1)证明见解析(2)(i )证明见解析(ii )427【解析】 【分析】(1)由PC PD ⊥,AD PC ⊥可得PC ⊥平面PAD ,即可证明;(2)(i )连接PE 并延长交BQ 于点M ,连接PF 并延长交OA 于点N ,连接MN ,利用平行线分线段成比例可得//EF MN ,即可得//EF AQ 得证; (ii )根据A EOF E AOF V V --=即可求解. 【详解】(1)证明:因为ABCD 是轴截面, 所以AD ⊥平面PCD ,所以AD PC ⊥,又点P 是圆弧CD 上的一动点(不与,C D 重合),且CD 为直径, 所以PC PD ⊥,又AD PD D =I ,PD ⊂平面PAD ,AD ⊂平面PAD ,所以PC ⊥平面PAD ,PC ⊂平面PBC , 故平面PAD ⊥平面PBC .(2)当三棱锥P ABC -体积最大时,点P 为圆弧CD 的中点.所以点O 为圆弧AB 的中点, 所以四边形AQBO 为正方形,且PO ⊥平面ABO .(i )证明:连接PE 并延长交BQ 于点M ,连接PF 并延长交OA 于点N ,连接MN ,则//MN AQ ,因为,E F 分别为三角形的重心,所以23PE PF PM PN ==, 所以//EF MN , 所以//EF AQ ,又AQ ⊂平面PAQ ,EF ⊄平面PAQ , 所以//EF 平面PAQ . (ii )因为PO ⊥平面ABO , 所以PO BO ⊥,又AO BO ⊥,AO PO O =I , 所以BO ⊥平面PAO , 因为////EF AQ BO ,所以EF ⊥平面PAO ,即EF ⊥平面FAO ,即EF 是三棱锥E AOF -的高.又23EF BO ==,1112332AOF APO S S ∆∆==⨯⨯=,所以114||3327A EOF E AOF AOF V V S EF --∆==⋅==.【点睛】本题主要考查了线面垂直、面面垂直的判定,线面平行,等体积法求棱锥体积,属于中档题.20.(1)22143x y +=(2)证明见解析【解析】 【分析】(1)根据长轴及椭圆过点即可求出;(2)由题意设直线AB 为1x my =+,联立椭圆方程可求||AB ,求出ABQ ∆外接圆圆心21,034G m ⎛⎫⎪+⎝⎭,计算2GF ,化简即可证明2AB GF 为定值.【详解】(1)由题意知2a =,将P 点坐标代入椭圆方程22221x y a b+=得291414b +=,解得b =所以椭圆方程为22143x y +=.(2)由题意知,直线AB 的斜率存在,且不为0,设直线AB 为1x my =+, 代入椭圆方程得()2234690m y my ++-=. 设()()1122,,,A x y B x y ,则12122269,3434m y y y y m m --+==++, 所以AB 的中点坐标为2243,3434m m m -⎛⎫⎪++⎝⎭,所以()212221213434m AB y y m m +=-=-++. 因为G 是ABQ ∆的外心,所以G 是线段AB 的垂直平分线与线段AQ 的垂直平分线的交点,AB 的垂直平分线方程为22343434m y m x m m ⎛⎫+=-- ⎪++⎝⎭,令0y =,得2134x m =+,即21,034G m ⎛⎫⎪+⎝⎭,所以222213313434m GF m m +=-=++,所以()22222121||1234433334m AB m m GF m ++===++,所以2||AB GF 为定值,定值为4. 【点睛】本题主要考查了椭圆的标准方程,直线与椭圆的位置关系,定值问题,属于难题. 21.(1)见解析(2)见解析 【解析】 【分析】(1)对函数()f x 进行求导得2()(21)()(0)x a x f x x x-+'=>,再对a 进行分类讨论,解不等式,即可得答案;(2)当0a „时,()f x 在(0,)+∞单调递增,()f x m =至多一个根,不符合题意;当0a >时,()f x 在(0,)a 单调递减,在(,)a +∞单调递增,则()0f a '=.不妨设120x a x <<<,只要证122x x a +>212x a x >-⇔,再利用函数的单调性,即可证得结论. 【详解】(1)2222122(12)()(21)()2(0)a a x a x a x a x f x x x x x x-+---+'=+-==>. ①当0a „时,(0,),()0,()x f x f x '∈+∞>单调递增; ②当0a >时,(0,),()0,()x a f x f x '∈<单调递减;(,),()0,()x a f x f x '∈+∞>单调递增.综上:当0a „时,()f x 在(0,)+∞单调递增;当0a >时,()f x 在(0,)a 单调递减,在(,)a +∞单调递增. (2)由(1)知,当0a „时,()f x 在(0,)+∞单调递增,()f x m =至多一个根,不符合题意;当0a >时,()f x 在(0,)a 单调递减,在(,)a +∞单调递增,则()0f a '=.不妨设120x a x <<<,要证1202x x f +⎛⎫'> ⎪⎝⎭,即证122x x a +>,即证122x x a +>,即证212x a x >-. 因为()f x 在(,)a +∞单调递增,即证()()212f x f a x >-,因为()()21f x f x =,所以即证()()112f x f a x >-,即证()()f a x f a x +<-. 令()()()g x f a x f a x =+--2()(12)ln()2()(12)ln()a a a x a a x a x a a x a x a x ⎡⎤⎡⎤=++-++--+--+⎢⎥⎢⎥+-⎣⎦⎣⎦ 4(12)ln()(12)ln()a a x a a x a a x a x a x=+-+---+-+-, 221212()4()()a a a a g x a x a x a x a x --'=++--+-+- ()()22222222222242(12)4()()()()a a x x x a a a a a x a x a x a x a x +---=+-=-+-+-. 当(0,)x a ∈时,()0,()g x g x '<单调递减,又(0)(0)(0)0g f a f a =+--=, 所以(0,)x a ∈时,()(0)0g x g <=,即()()f a x f a x +<-,即()(2)f x f a x >-.又1(0,)x a ∈,所以()()112f x f a x >-,所以1202x x f +⎛⎫'>⎪⎝⎭. 【点睛】本题考查利用导数研究函数的单调性、证明不等式,考查函数与方程思想、转化与化归思想、分类讨论思想,考查逻辑推理能力和运算求解能力,求解时注意将所证不等式转化为利用函数的单调性进行证明.22.(1)24y x =,290x y ++=(2【解析】【分析】(1)直接利用消参法可得曲线C 的直角坐标方程;将cos ,sin x y ρθρθ==代入l 的极坐标方程得l 的直角坐标方程;(2)设212P s ⎛⎫⎪⎝⎭,利用点到直线的距离公式,结合二次函数的性质求最值,即可得答案.【详解】 (1)C 的直角坐标方程为:24y x =,将cos ,sin x y ρθρθ==代入l 的极坐标方程得l 的直角坐标方程为:290x y ++=. (2)设212P s ⎛⎫ ⎪⎝⎭, 则点P 到直线l的距离21|9s d ++==,当s =-d ==. 【点睛】本题考查极坐标方程、参数方程、普通方程的互化、点到直线的距离公式,考查逻辑推理能力和运算求解能力,求解时注意点的参数设法.23.(1)[]13,x ∈-(2)2325,6a b ⎡⎫+∈+∞⎪⎢⎣⎭【解析】【分析】(1)分类讨论去掉绝对值得分段函数求解即可;(2)由分段函数求出最低点,得236a b +=,构造1,利用均值不等式求解即可.【详解】 (1)33,2()5,1233,1x x f x x x x x -≥⎧⎪=-+-<<⎨⎪-+≤-⎩,所以由()6f x ≤可得2336x x ≥⎧⎨-≤⎩,或1256x x -<<⎧⎨-+≤⎩,或1336x x ≤-⎧⎨-+≤⎩, 解得:[]2,3x ∈或()1,2x ∈-或1x =-.综上,[]13,x ∈-. (2)因为33,2()5,1233,1x x f x x x x x -≥⎧⎪=-+-<<⎨⎪-+≤-⎩,所以当2x =时,()min 3f x =,最低点为()2,3,即236a b +=,所以132a b +=. 23232313252323266a b b a a b a b a b ⎛⎫⎛⎫+=++=+++≥+= ⎪⎪⎝⎭⎝⎭, 当且仅当65a b ==时等号成立, 所以2325,6a b ⎡⎫+∈+∞⎪⎢⎣⎭【点睛】本题主要考查了含绝对值不等式的解法,分段函数的最值,均值不等式,属于中档题.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020届河南省名校联盟高三2月质量检测巩固卷数学(文)试题一、单选题1.已知集合{}|36M x N x =∈-<<,{}2,0,2,4,6N =-,则M N =I ( ) A .{}0,2,4 B .{}2,0,2,4- C .{}0,2,4,6 D .{}2,4答案:A将集合M 化简可得{}0,1,2,3,4,5M =,再由交集的定义即可求出答案. 解:依题意,{}{}|360,1,2,3,4,5M x N x =∈-<<=,故{}0,2,4M N =I . 故选:A. 点评:本题主要考查交集的运算,属于基础题.2.已知a ,b 均为实数,若(1)(1)2a i b i ++-=,则a ib i+=-( ) A .1 B .iC .-iD .1-答案:B根据两个复数相等的充要条件可求得1a b ==,再由复数的乘除运算即可得到答案. 解:由已知,得()+() 2+-=a b a b i ,则2a b a b +=⎧⎨-=⎩,解得1a b ==,所以21(1)21(1)(1)2a i i i ii b i i i i +++====---+. 故选:B. 点评:本题主要考查两个复数相等的充要条件,复数代数形式的乘除运算,属于基础题. 3.已知等差数列{}n a 的前n 项和为n S ,若19380S =,则( ) A .510a = B .920a = C .1010a =D .1020a =答案:D由等差数列的前n 项和公式可得()11919193802a a S +==,再由等差数列的性质可得119102a a a +=,代入即可的到答案.解: 依题意,()11919193802a a S +==,因为119102a a a +=,所以1020a =.故选:D. 点评:本题主要考查等差数列前n 项和公式的应用,等差数列的性质,属于基础题. 4.曲线3sin y x x =-在点()0,0处的切线方程为( ) A .10x y +-= B .0x y += C .10x y -+= D .0x y -=答案:B根据导数的几何意义求出在点()0,0处的切线的斜率,再由点斜式即可得到答案. 解:因为3sin y x x =-,所以23cos y x x '=-,则0x =时,1y '=-, 所以曲线3sin y x x =-在点()0,0处的切线的斜率1k =-, 所以切线方程为()00y x -=--,即0x y +=. 故选:B. 点评:本题主要考查在一点处的切线方程,同时考查直线的点斜式方程,属于基础题 5.已知命题p :若1a >,则0.2log 0.21a a<<;命题q :若函数22()1f x mx m x =--在(1,)+∞上单调递增,则实数m 的取值范围为(](),00,2-∞U .下列说法正确的是( )A .p q ∧为真命题B .q 为真命题C .p 为假命题D .()p q ⌝∧为假命题 答案:D根据指数函数和对数函数的单调性可判断命题p 是真命题,根据函数()f x 在(1,)+∞上单调递增,求出实数m 的取值范围可判断命题q 是假命题. 解:若1a >,则函数log ay x =与函数x y a =在(0,)+∞上单调递增,所以log 0.2log 10a a <=,00.21a a >=, 所以0.2log 0.21a a<<,所以命题p 是真命题;若函数22()1f x mx m x =--在(1,)+∞上单调递增,则2012m m m>⎧⎪⎨--≤⎪⎩,解得02m <≤,所以命题q 是假命题.故选:D. 点评:本题主要考查命题真假的判断,同时考查复合命题真假的判断,属于基础题. 6.函数()221x x x f x =+-的图象大致为( ) A . B .C .D .答案:C由()f x 是偶函数可排除A 、B ;再由,0x >有()0f x >可排除D. 解:由已知,()()()2111221221x x xx f x x +⎛⎫=+= ⎪--⎝⎭, 则()()()()()()()2121221221xx xxx x f x f x --+-+-===--,所以()f x 为偶函数,故可排除A 和B ; 当0x >时,()0f x >,故可排除D. 故选:C. 点评:本题考查已知函数解析式确定函数图象的问题,在处理这类问题时,通常利用函数的性质,如单调性、奇偶性、特殊点的函数值来处理,是一道容易题.7.2013年华人数学家张益唐证明了孪生素数猜想的一个弱化形式,此事引起了国际数学界的轰动许多专家认为这是数论研究中的一项重大突破世界主流媒体都对这项重要成果作了报道并给予了高度评价,印度媒体甚至称赞张益唐为“中国的拉马努金”.孪生素数猜想是希尔伯特在1900年提出的23个问题之一,可以这样描述:存在无穷多个素数p ,使得2p +是素数,素数对(),2p p +称为孪生素数.在不超过20的素数中,随机选取两个不同的数,其中能够组成孪生素数的概率是( ) A .445B .115C .328D .17答案:D根据已知条件可求出不超过20的素数有8个,从中随机选取两个共有28种不同的情况,而不超过20的素数组成的孪生素数对有4个,根据古典概型计算公式即可得到答案. 解:不超过20的素数有2,3,5,7,11,13,17,19共计8个, 从中随机选取两个共有28种不同的情况, 根据素数对(),+2p p 为孪生素数,所以不超过20的素数组成的孪生素数对为()()()()3,55,711,1317,19,,,共有4个, 故能够组成的字孪生素数的概率41287P ==. 故选:D. 点评:本题主要考查古典概型概率的计算,属于基础题.8.已知双曲线2222:1(0,0)x y E a b a b-=>>的右焦点为(),0F c ,虚轴的一个端点为A ,若原点O 到直线AF 的距离为12c ,则双曲线E 的渐近线方程为( )A .y x =B .y =C .12y x =±D .2y x =±答案:A在直角OFH V 中,12OH OF =,故30OFH ∠=o ,从而在直角OAF △中,可得=c ,再结合222c a b =+,即可得到答案.解:设原点O 到直线AF 的投影为H . 在直角OFH V 中,1122OH c OF ==,则30OFH ∠=o ,所以OF OA =,即=c ,所以222+3=a b b ,解得2b a =,所以双曲线E 的渐近线方程为2y x =±. 故选:A. 点评:本题主要考查双曲线的渐近线方程,属于基础题.本题关键是找出a 与b 等量关系.9.若1cos 0332ππαα⎛⎫⎛⎫+=-<< ⎪ ⎪⎝⎭⎝⎭,则5sin 212⎛⎫+ ⎪⎝⎭πα的值为( )A B C . D 答案:B 设3πβα=+,则1cos 3β=-,3παβ=-,从而将已知的角转化为单角,而5sin 212⎛⎫+ ⎪⎝⎭πα可化为sin 24⎛⎫- ⎪⎝⎭πβ,再利用两角差的正弦公式展开,利用二倍角公式求出sin 2β和cos 2β,代入即可得到答案. 解:设3πβα=+,则1cos 3β=-,3παβ=-,因为02πα<<,所以536ππβ<<,所以sin 3β===,所以1sin 22sin cos 23⎛⎫==-= ⎪⎝⎭βββ 2271cos 22cos 12139⎛⎫=-=⨯--=- ⎪⎝⎭ββ,所以55sin 2sin 2sin 2123124⎡⎤⎛⎫⎛⎫⎛⎫+=-+=- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦πππαβπβ7sin 2coscos 2sin449ππββ⎛⎛⎫=-=--= ⎪ ⎝⎭⎝⎭故选:B. 点评:本题主要考查二倍角公式,两角差的正弦公式,关键是将未知角用已知角来表示,若未知角直接已知角表示较为困难,可对已知角换元.10.已知函数()f x 对任意的R x ∈都有()()()21f x f x f +-=.若函数()2y f x =+的图象关于2x =-对称,且()08f =,则()()99100f f +=( ) A .0 B .4C .5D .8答案:D由函数()2y f x =+的图象关于2x =-对称,可得()f x 为偶函数,再对()()()21f x f x f +-=赋值1x =-可得()10f =,从而可得()()+2f x f x =,即()f x 的最小正周期为2,从而可得()()()()9910010f f f f +=+. 解:因为()+2=y f x 的图象关于直线2x =-对称,所以()y f x =的图象关于直线0x =对称,即()f x 为偶函数.因为()()()+21-=f x f x f ,所以()()()1211f f f -+--=,又()()11f f -=, 所以()10f =,可得()()+2f x f x =,所以()f x 的最小正周期为2, 所以(99)(1)0f f ==,(100)(0)8f f ==, 所以(99)(100)8f f +=. 故选:D. 点评:本题主要考查利用函数的奇偶性及周期性,求抽象函数的值,同时考查函数的图象的平移变换,属于中档题.11.已知四棱锥S ABCD -所有的棱都相等,过BD 与SC 平行的平面与SA 交于点E ,则BE 与CD 所成角的大小是( )A .30°B .45︒C .60︒D .90︒答案:A要求异面直线BE 与CD 所成角,又//AB CD ,根据异面直线所成的角的定义可知ABE ∠就是BE 与CD 所成角,而//SC 平面BDE ,由线面平行的性质定理可得//SC OE ,再结合O 是BD 的中点,可得E 是SA 的中点,在正SAB V 中即可求出ABE∠的大小. 解:设AC BD O =I ,连接OE ,由//SC 平面BDE ,SC ⊂平面SAC ,平面SAC I 平面BDE OE =, 所以//SC OE ,由O 是BD 的中点,得E 是SA 的中点, 因为//AB CD ,所以ABE ∠就是BE 与CD 所成角, 因为SAB V 为正三角形,所以30ABE ∠=︒. 故选:A. 点评:本题主要考查求异面直线所成的角,同时考查线面平行的性质定理,属于中档题.12.已知椭圆()2222:10x y C a b a b +=>>的左、右焦点分别为12,,F F P 是C 上一点,且2PF x ⊥轴,直线1PF 与C 的另一个交点为Q ,若114PF FQ =,则C 的离心率为( ) A 25B 2C 15D 21 答案:D由题可设2,b P c a ⎛⎫⎪⎝⎭,再根据线段比例关系求得Q 的坐标,代入椭圆化简求解即可.解:由2PF x ⊥轴,得22b PF a =,不妨设2,b P c a ⎛⎫ ⎪⎝⎭;设00(,)Q x y ,由114PF FQ =, 得2003,24c b x y a =-=-代入椭圆方程,得222291416c b a a+=.结合222b a c =-,解得c e a ==故选:D 点评:本题主要考查了椭圆中的基本量求解方法,同时也考查了根据比例求解点的坐标,进而代入点入椭圆的方程求解的方法,属于中等题型.二、填空题13.已知向量()3,2m =-u r ,()1,n λ=r ,若m n ⊥u r r,则n =r ______.答案:2根据m n ⊥u r r得到320m n λ⋅=-=u r r ,得到31,2n ⎛⎫= ⎪⎝⎭r ,计算模长得到答案.解:根据题意,向量()3,2m =-u r ,()1,n λ=r ,m n ⊥u r r ,则320m n λ⋅=-=u r r ,解得32λ=,则31,2n ⎛⎫= ⎪⎝⎭r,则n ==r. 点评:本题考查了根据向量垂直求参数,向量的模,意在考查学生的计算能力.14.设实数x ,y 满足不等式组123x y x y x +≥⎧⎪+≥⎨⎪≥⎩,则2z x y =-的最小值为_____________.答案:2作出不等式组表示的平面区域,将目标函数化为2y x z =-,通过平移可知当直线2y x z =-过点()3,4时,此时截距-z 最大,从而可得z 的最小值.解:作出不等式组所表示的平面区域如下图阴影部分所示,将目标函数2z x y=-变形为2y x z=-,由图可知当直线经过点(3,4)A时,截距z-最大,即z最小.所以此时2z x y=-取得最小值为2.故答案为:2点评:本题主要考查简单线性规划,解决线性规划问题的关键是正确地作出可行域,准确地理解目标函数的几何意义.15.已知各项为正的等比数列{}n a满足()*14nn na a n+=∈N,则1a=_____________.2根据已知分别取1n=,2n=可得124a a=,2234a a=,联立方程即可求出1a.解:设{}n a的公比为()0q q>.由题意,得2231244a aa a⎧=⎨=⎩①②,①÷②,得24q=,结合0q>,解得2q=.将2q=代人②,解得12a=2点评:本题主要考查等比数列的通项公式,属于基础题.16.在四棱锥S ABCD-中,底面四边形ABCD为矩形,SA⊥平面ABCD,P,Q分别是线段BS AD ,的中点,点R 在线段SD 上,若4AS =,2AD =,AR PQ ⊥,则AR =____________.答案:45取SA 的中点E ,连接,PE QE ,则//PE AB ,可证AB ⊥平面SAD ,从而可得PE ⊥平面SAD ,即可得PE AR ⊥,进而可证AR ⊥平面PEQ ,可得AR EQ ⊥,在直角ASD V 中,利用等面积法即可求出AR 的长. 解:取SA 的中点E ,连接,PE QE ,则//PE AB因为SA ⊥平面ABCD ,AB Ì平面ABCD ,所以SA AB ⊥, 又AB AD ⊥,AD SA A =I ,所以AB ⊥平面SAD , 所以PE ⊥平面SAD ,又AR ⊂平面SAD ,所以PE AR ⊥. 又AR PQ ⊥,PE PQ P =I ,,PQ PE ⊂平面PEQ ,所以AR ⊥平面PEQ ,因为EQ ⊂平面PEQ ,所以AR EQ ⊥. 因为E Q ,分别为SA AD ,的中点,所以//EQ SD ,所以AR SD ⊥, 在直角ASD V 中,42AS AD ==,,所以2216425SD AS AD =+=+=所以4525AD AS AR SD ⋅==. 45点评:本题主要考查线面垂直的判定定理,等面积法,属于中档题.三、解答题17.某学校高中三个年级共有4000人,为了了解各年级学周末在家的学习情况,现通过分层抽样的方法获得相关数据如下(单位:小时),其中高一学生周末的平均学习时间记为x .高一:14 15 15.5 16.5 17 17 18 19 高二:15 16 16 16 17 17 18.5 高三:16 17 18 21.5 24 (1)求每个年级的学生人数;(2)从高三被抽查的同学中随机抽取2人,求2人学习时间均超过x 的概率. 答案:(1)高一年级1600人;高二年级1400人;高三年级1000人;(2)35(1)根据已知求出三个年级被抽查的人数,再利用分层抽样求解即可;(2)根据已知求出x ,用列举法列出在高三被抽查的同学中,随机抽取2人的所有可能的情况,再列出2人学习时间均超过x 的所有可能情况,根据古典概型计算公式即可求出答案. 解:(1)由于三个年级被抽查的人数分别是8,7,5, 故高一年级的学生人数为840001600875⨯=++;高二年级的学生人数为740001400875⨯=++;高三年级的学生人数为540001000875⨯=++.(2)1(141515.516.517171819)16.58x =+++++++=.在高三被抽查的同学中随机抽取2人,所有可能的情况为 (16,17),(16,18),(16,21.5),(16,24),(17,18),(17,21.5),(17,24),(18,21.5),(18,24),(21.5,24),共10种,其中满足条件的为(17,18),(17,18),(17,21.5),(17,24),(18,21.5),(18,24),(21.5,24),共6种,故所求概率63105P ==. 点评:本题主要考查分层抽样的应用、古典概型概率的计算,考查运算求解能力,属于基础题.18.在四边形ABCD 中,1AB =,BC =AC CD =,90ACD ∠=o ,135ABC ∠=o .(1)求sin ACB ∠的值; (2)求BD 的长.答案:(1)10;(2)3. (1)在ABC V 中,由余弦定理可求得AC ,再在ABC V 中,由正弦定理,即可求出sin ACB ∠的值;(2) 由(1)得AC CD ==BCD V 中,由余弦定理,即可求出BD 的长.解:(1)在ABC V 中,由余弦定理,得AC ==在ABC V 中,由正弦定理,得sin sin AC ABABC ACB=∠∠,所以sin sin AB A C AC A B CB ⋅∠===∠(2)由(1),得AC CD ==()cos cos 90sin ACB ACB BCD ︒∠==-=∠+∠ 在BCD V 中,由余弦定理,得3BD ==.点评:本题主要考查正弦定理、余弦定理在解三角形中的应用,属于基础题.19.如图,在三棱柱111ABC A B C -中,1AA ⊥平面ABC ,D ,E ,F 分别是1BC ,AB ,1AA 的中点,点G 在线段BC 上,A ABC CB =∠∠.(1)求证://EF 平面1A BC ;(2)若平面//EFG 平面1A BD ,90BAC ∠=o ,14AB AA ==,求点1B 到平面FEG 的距离.答案:(1)证明见解析;(2)23(1)由E ,F 分别是AB ,1AA 的中点,可得1//EF A B ,再由线面平行的判定定理即可证出;(2)根据平面//EFG 平面1A BD ,可得点G 是线段BC 上靠近B 的四等分点,从而可求得12三棱锥G B EF V -=,利用等体积法即可求出点1B 到平面FEG 的距离. 解:(1)因为在1A AB V 中,E ,F 分别是AB ,1AA 的中点, 所以1//EF A B ,又1A B ⊂平面1A BC ,EF ⊄平面1A BC , 所以//EF 平面1A BC .(2)设点1B 到平面EFG 的距离为2h ,点G 到平面1B EF 的距离为1h ,则122h BG =取BC 的中点H 连结AH ,DH ,则//1AH A D ,又1⊂A D 平面1A BD ,AH ⊄平面1A BD ,所以//AH 平面1A BD , 又平面//EFG 平面1A BD ,而AH ⊄平面EFG ,所以//AH 平面EFG ,又AH ⊂平面ABC ,所以//AH EG , 又E 为AB 的中点,所以G 为BH 的中点, 所以点G 是线段BC 上靠近B 的四等分点,所以2BG =,所以1111116233△三棱锥E E B F F B G V h S -=⋅⋅=⨯⨯=,22EF =在ABG V 中,由余弦定理,得 2222cos 162242102=+-⋅⋅∠=+-⨯⨯⨯=AG AB BG AB BG ABG 所以2241014FG AF AG =++ 在EFG V 中,由余弦定理,得22257cos 222214EF FG EG EFG EF FG +-∠===⋅⨯⨯所以221sin 1cos 14EFG EFG ∠-∠=, 所以1221112122142332△三棱锥GEF B GEF V h S h -=⋅⋅=⋅⋅⋅=,解得223h =1B 到平面FEG 的距离3点评:本题主要考查线面平行的判定定理,等体积法求点到面的距离,属于中档题. 20.在平面直角坐标系xOy 中,抛物线2:2(0)C x py p =>的焦点为F ,(2,)A m (其中1m >)是C 上的一点,且5||2AF =.(1)求抛物线C 的方程;(2)已知P 为抛物线C 上除顶点O 之外的任意一点,在点P 处的切线与y 轴交于点Q ,过Q 点的直线z 交抛物线于M ,N 两点,设OM ,ON ,OP 的斜率分别为1k ,2k ,3k ,求证:1k ,3k ,2k 成等比数列.答案:(1)22x y =;(2)证明见解析. (1)根据抛物线的定义可得5||22+==p AF m ,由(2,)A m 在抛物线C 列出方程,联立解方程组即可求出p ;(2) 设点20,2x P x ⎛⎫ ⎪⎝⎭,利用导数的几何意义求出点P 处切线的斜率,再由点斜式可求出切线的方程()2002x y x x x -=-,令0x =,可得200,2x Q ⎛⎫- ⎪⎝⎭,从而可设直线l 的方程为20(0)2x y kx k =-≠,与22x y =联立方程组消去y 可得22020x kx x --=,设()()1122,,,M x y N x y ,利用根与系数关系可得2120x x x =,再将12k k 用1x ,2x 表示并化简可得2124x k k =,而032x k =,从而可证出1k ,3k ,2k 成等比数列.解:(1)由题意,得222522pm p m ⎧=⎪⎨+=⎪⎩,解得12p m =⎧⎨=⎩,或412p m =⎧⎪⎨=⎪⎩, 又1m >,所以1p =,所以抛物线C 的方程为22x y =. (2)由题意,得直线l 的斜率存在,且不为0.由22x y =,得22x y =,则y x '=,设点200,2x P x ⎛⎫ ⎪⎝⎭,则切线的斜率为0x ,于是切线的方程为()20002x y x x x -=-,即202x y x x =-,所以200,2x Q ⎛⎫- ⎪⎝⎭.设直线l 的方程为20(0)2x y kx k =-≠,代入22x y =,消去y 并整理,得2220-+=x kx x , 由直线l 交抛物线于M N ,两点,得()2222004440k x k x ∆=-=->.设()()1122,,,M x y N x y ,所以2120x x x =,又2112x y =,2222x y =,所以21112y x =,22212y x =, 所以22201212121212122244x y y x x x x k k x x x x =⋅=⋅==,又200300202x xk x -==-, 所以2123k k k =,故132, , k k k 成等比数列. 点评:本题主要考查抛物线的标准方程,抛物线的定义及直线与抛物线的位置关系,同时考查导数的几何意义和根与系数关系,属于中档题.证明1k ,3k ,2k 成等比数列的关键是将12k k 和3k 用0x 其来表示. 21.已知函数()ln (1)f x x m x =--. (1)若3m =,求函数()f x 的极值;(2)当[1,)x ∈+∞时,()xe ef x e +≥,求实数m 的取值范围.答案:(1)详见解析;(2)(,2]-∞(1)当3m =时,()ln 3(1)f x x x =--,先求定义域,再求导并判断单调性,即可求出函数()f x 的极值;(2)将()f x 代入得[ln (1)]x e e x m x e +--≥,即1ln (1)1x e x m x -+--≥,令1()ln (1)x g x e x m x -=--+,只需求出min ()1g x ≥即可,11()x g x e m x-'=+-,令11()e x F x m x-=+-,利用导数研究其单调性可得所以()F x 在[1,)+∞上单调递增,且()()121F m g '=-=,对m 分2m ≤和2m >,即可求出答案. 解:(1)当3m =时,()ln 3(1)f x x x =--,函数()f x 的定义域为(0,)+∞, 所以113()3x f x x x-'=-=. 当10,3x ⎛⎫∈ ⎪⎝⎭,()0f x '>,所以函数()f x 在10,3⎛⎫ ⎪⎝⎭上单调递增;当1,3x ⎛⎫∈+∞ ⎪⎝⎭时,()0f x '<,函数()f x 在1,3⎛+∞⎫ ⎪⎝⎭上单调递减. 所以当13x =时,函数()f x 有极大值111ln 312ln 3333f ⎛⎫⎛⎫=--=- ⎪ ⎪⎝⎭⎝⎭,无极小值.(2)依题意,得[ln (1)]xe e x m x e +--≥,即1ln (1)1x e x m x -+--≥,令1()ln (1)x g x e x m x -=--+, 所以11()x g x em x -'=+-,令11()e x F x m x-=+-,则121()x F x e x -'=-. 令121()()(0)x x F x e x x ϕ-'==->,所以132()0x x e x ϕ-'=+>, 所以()F x '在[)1,+∞上单调递增,又(1)0F '=,当[)1,x ∈+∞时,()0F x '≥,所以()F x 在[1,)+∞上单调递增,且()()121F m g '=-=.当2m ≤时,[1,)x ∈+∞,()0g x '≥,()g x 在[)1,+∞上单调递增,()()11g x g ≥=,满足条件;当2m >时,()120-g m '=<. 又因为ln 11(ln 1)e0ln 1ln 1'+=-+=>++mg m m m m ,所以0(1,ln 1)x m ∃∈-,使得()00g x '=,当()01,,()0x x g x '∈<,当()0,ln 1,()0x x m g x ∈->,所以()g x 在()01,x 上单调递减,()01,x x ∈,都有()()11g x g <=,不符合题意. 综上所述,实数m 的取值范围为(,2]-∞. 点评:本题主要考查利用导数求函数的极值,由恒成立求参数取值范围,属于中档题.对于第(2)问进行一次求导运算后,很难判断出一阶导数的正负,也就很难对原函数的单调性作出判断,若对一阶导数继续求导,往往可以收到很好的效果,使得我们能通过二阶导数的正负,判断出一阶导数的正负,进而判断出原函数的单调性,使问题得以解决.22.在平面直角坐标系xOy 中,直线l的参数方程为3x y t ⎧=⎪⎨=⎪⎩t 为参数),以坐标原点为极点,x 轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线C 的极坐标方程为2223sin 12ρρθ+=.(1)求直线l 的极坐标方程和曲线C 的参数方程;(2)若()1,0P ,直线l 与曲线C 交于,M N 两点,求PM PN +的值.答案:(1)2cos 6πρθ⎛⎫-= ⎪⎝⎭2cos x y αα=⎧⎪⎨=⎪⎩(α为参数);(2)165(1)先将直线l 的参数方程消去参数t 化为普通方程,再直角坐标方程与极坐标方程的互化公式,即求出直线l 的极坐标方程;同样由直角坐标方程与极坐标方程的互化公式,先将曲线C 的极坐标方程化为直角坐标方程,进而可求出曲线C 的参数方程; (2)求出直线l 的参数方程的标准形式,然后利用参数t 的几何意义,即可求出PM PN +的值.解:(1)依题意,得直线0l y -=cos sin 0θρθ--=, 所以直线l的极坐标方程为2cos 6πρθ⎛⎫+= ⎪⎝⎭因为2223sin 12ρρθ+=,则223412x y +=,即22143x y +=.所以曲线C的参数方程为2cos x y αα=⎧⎪⎨=⎪⎩(α为参数).(2)因为直线0l y --=经过点()1,0P ,故直线l的参数方程的标准形式为112x t y ⎧=+⎪⎪⎨⎪=⎪⎩,代入22143x y +=,可得254120t t +-=,所以1245t t +=-,12125t t =-,所以1216||||||5PM PN t t +=-==.点评:本题主要考查参数方程化为极坐标方程的互化,关键是掌握互化方法,同时考查直线参数方程中参数t 的几何意义,属于中档题. 23.已知函数()|2 ||2 2|f x x m x =-++. (1)若3m =,求不等式()8f x <的解集;(2)若12,(0,)x x ∀∈∃∈+∞R ,使得()212232f x x x -≥-,求实数m 的取值范围.答案:(1)79,44⎛⎫- ⎪⎝⎭;(2)(,4][0,)-∞-+∞U(1) 若3m =,则()|2 3||2 2|f x x x =-++,然后对()f x 分为1x <-,312x -≤≤,32x >三种情况讨论去掉绝对值,解不等式即可;(2)问题转为1()3f x -的最小值大于等于2222x x -最小值,利用绝对值不等式可求出1()f x 的最小值,利用二次函数的性质可求出2222x x -最小值,从而问题转化为|2|31m +-≥-,解此不等式即可.解:(1)当3m =时,|2 3|+|2 2|8x x -+<,若1x <-,则32228x x ---<,得74x >-,所以714x -<<-;若312x -≤≤,则322258x x -++=<,所以312x -≤≤; 若32x >,则2 3 2 28x x -++<,得94x <,所以3924x <<,综上所述,不等式的解集为79,44⎛⎫- ⎪⎝⎭.(2)()11132223|2|3f x x m x m -=-++-≥+-,而当2(0,)x ∈+∞时,()222222111x x x -=--≥-, 所以()212232f x x x -≥-,等价于|2|31m +-≥-,解得0m ≥或4m ≤-,即实数m 的取值范围为(,4][0,)-∞-+∞U . 点评:本题主要考查绝对值不等式的解法,绝对值不等式的应用,同时考查双变量不等式恒成立的处理方法,属于中档题.。
