用“小范围搜索法”求“线性规划问题”的最优整数解
线性规划中的最优整数解
线性规划中的最优整数解线性规划中的最优解,就是在线性约束条件下使目标函数取得最大值或最小值的可行解,而求最优整数解,是同学们的棘手问题,下面以例题的形式讲讲如何求最优解。
例. 某人承揽了一项业务:需做文字标牌6个,绘画标牌5个。
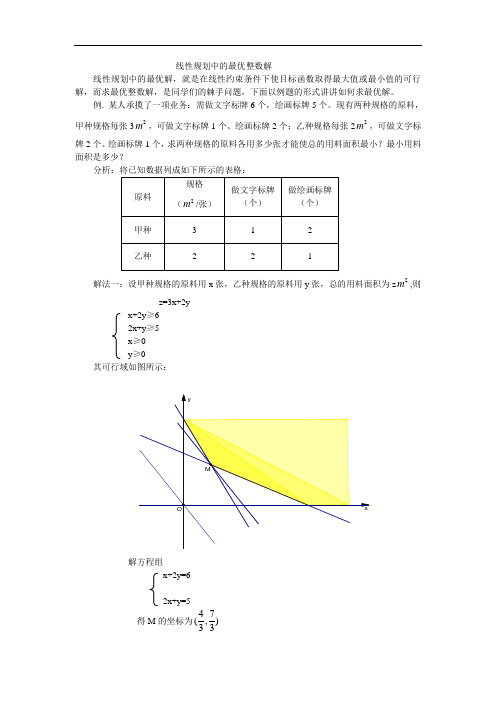
现有两种规格的原料,甲种规格每张32m ,可做文字标牌1个、绘画标牌2个;乙种规格每张22m ,可做文字标牌2个、绘画标牌1个,求两种规格的原料各用多少张才能使总的用料面积最小?最小用料面积是多少?分析:将已知数据列成如下所示的表格:解法一:设甲种规格的原料用x 张,乙种规格的原料用y 张,总的用料面积为z 2m ,则z=3x+2yx+2y ≥62x+y ≥5x ≥0y ≥0其可行域如图所示:解方程组x+2y=62x+y=5得M 的坐标为47(,)33当直线z=3x+2y过点M47(,)33时z最小,此时472632333z=⨯+⨯=由题意可知,点M47(,)33不是最优解,因为此问题最优解(x,y)中x,y应都是非负整数,所以目标函数z的最小值一定是大于263的整数,且x,y都是非负整数。
取z=9,得3x+2y=9,其非负整数解是(1,3)和(3,0),但点(3,0)不在可行域内,舍去,所以点(1,3)是最优解,min 9z=解法二:由解法一可知,点M47(,)33不是最优解,这时可求出可行域内左下侧靠近边界的整点,依次为A(0,5),B(1,3),C(2,2),D(3,2),E(4,1),F(5,1),G(6,0),将这些点的坐标分别代入目标函数z=3x+2y,求出z的各对应值,经检验可知,在整点B(1,3)处z取得最小值9。
答:甲种规格的原料用1张,乙种规格的原料用3张时,总的用料面积最小,其最小用料面积为92m。
对于线性规划中的最优整数解问题,当解方程组得到的解不是整数解时,可采用如下的方法:1.调整优值法:先求“非整点最优解”及“最优值”,根据题意调整“最优值”,再求目标函数中的整数解,便可得出最优整数解。
求线性规划问题的最优整数解的方法

求线性规划问题的最优整数解的方法作者:陈树礼来源:《中学教学参考·理科版》2010年第01期线性规划是新教材新增内容,在近几年高考中都以较易题目出现,要学好本节内容,应注意以下三点.一、判定最优解求线性目标函数z=ax+by(a≠0、b≠0)在线性约束条件下的最优解问题,可转化为求直线y=-abx+zb在y轴上的截距的最大值和最小值.易知在b>0时,当zb最大时,z取得最大值,当zb最小时,z取得最小值;在b二、求出最优解依据边界直线的斜率(或倾斜角)计算出最优解.三、修正最优解,得到最优整数解现改编人教版高二(上例3的问题,以求达到抛砖引玉的目的.【例】某工厂生产甲、乙两种产品.已恬生产甲种产品1t需耗A种矿石10t、B种矿石5t、煤4t;生产乙种产品1t需耗A种矿石4t、B种矿石4t、煤9t.每1t甲种产品的利润是600元,每1t乙种产品的利润是1000元.工厂在生产这两种产品的计划中要求消耗A种矿石不超过300t、B种矿石不超过200t、煤不超过360t.求:(1)甲、乙两种产品各生产多少吨(精确到1吨)才能使利润最大?(2)若甲种产品每吨利润600元,乙产品每吨利润200元.甲、乙两种产品各生产多少吨(精确到1吨)才能使利润最大?(3)若甲种产品每吨利润400元,乙产品每吨利润200元.甲、乙两种产品各生产多少吨(精确到1吨)才能使利润最大?(4)若甲种产品每吨利润200元,乙产品每吨利润600元.甲、乙两种产品各生产多少吨(精确到1吨)才能使利润最大?(5)若甲种产品每吨利润1000元,乙产品每吨利润800元.甲、乙两种产品各生产多少吨(精确到1吨)才能使利润最大?解:(1)设生产甲、乙两种产品分别为x吨,y吨.利润为z元.则10x+4y≤300,5x+4y≤200,4x+9y≤360,x≥0,y≥0,z=600x+1000y.作出以上不等式组表示的平面区域,即可行域.作直线:600x+1000y=0,即直线:3x+5y=0,则z=200(3x+5y).设u=3x+5y,则当u最大时,z最大.易知直线NQ、MN、PM的斜率分别为-52,-54,-49,直线l的斜率为-53.平移直线∵M点为最优解点.由方程组5x+4y=200,4x+9y=360得M点的坐标为(36029,100029).∵x,y都是正整数,∴u=3x+5y=608029也应为正整数.∴u=3x+5y≤209.于是整点(11,35)为所求.当生产甲产品11吨,乙产品35吨时,能使利润总额最大.(2)此时目标函数为z=600x+200y.作直线平移直线∵直线经过点Q(30,0)时,z取得最大值.即只生产甲产品30吨时,获得利润最大.(3)此时目标函数为z=400x+200y.作直线平移直线∵-类似(1)可求解.(4)此时目标函数为z=200x+600y.作直线平移直线∵--49.∴当直线经过点P(0,40)时,5x+4y=0,即只生产乙产品40吨时,获得利润最大.(5)此时目标函数为z=1000x+800y.作直线平移直线∵-∴当直线与直线5x+4y=0重合时,z取得最大值.∴当点位于线段MN上任意一点时,都能使z取得最大值.总之,在本部分内容的学习中,要做到“一定、二算、三修正”.(责任编辑金铃)。
3.3.2简单的线性规划问题

变式:求利润z=x+3y的最大值. y
x2y 8
44
x y
16 12
x
0
y 0
4 N(2,3) 3
0
4
8x
y 1 x4
2
y1x z
33
zmax 2 3 3 11
名称 约束条件 线性约束条件 目标函数 线性目标函数
(3)掌握对一些实际优化问题建立线性规划数学 模型并运用图解法进行求解的基本方法和步骤 .
学习重点:线性规划的图解法
学习难点:寻求线性规划问题的最优解
一、导学提示,自主学习
2.本节主要题型 题型一 求线性目标函数的最值 题型二 线性规划的实际应用 3.自主学习教材P87-P91 3. 3.2简单的线性规划问题
经理,问各截这两种钢板多少张既能满足顾客要求又使所用钢板张
数最少。
分 析
解:设需截第一种钢板x张,第二种钢板y张,
2x+y≥15,
钢板总张数为Z则,
问
x+2y≥18,
题
x+3y≥27, x≥0
:
y≥0
标目函数: z=x+y (x,y N)
约束条件:
{ 2x+y≥15, x+2y≥18, x+3y≥27, x≥0,
33
3
在y轴上的截距为 z 的直线, 3
当点P在可允许的取值范围变化时,
求截距 z 的最值,即可得z的最值. 3
问题:求利润z=2x+3y的最大值. y
x2y 8
44
x y
16 12
数学建模线性规划与整数规划

数学建模线性规划与整数规划数学建模是一门将实际问题转化为数学问题,并利用数学方法解决的学科。
线性规划和整数规划是数学建模中常用的两种模型,它们在实际问题中有着广泛的应用。
本文将重点介绍线性规划和整数规划的概念、模型形式以及求解方法。
一、线性规划(Linear Programming)线性规划是一种在约束条件下求解线性目标函数最优解的数学模型,它的基本形式可以表示为:Min(或Max):C₁X₁ + C₂X₂ + ... + CₙXₙSubject to:A₁₁X₁ + A₁₂X₂ + ... + A₁ₙXₙ ≤ b₁A₂₁X₁ + A₂₂X₂ + ... + A₂ₙXₙ ≤ b₂...Aₙ₁X₁ + Aₙ₂X₂ + ... + AₙₙXₙ ≤ bₙX₁, X₂, ... , Xₙ ≥ 0在上述模型中,C₁,C₂,...,Cₙ为目标函数的系数,Aᵢₙ为不等式约束条件的系数,bᵢ为不等式约束条件的右端常数,X₁,X₂,...,Xₙ为决策变量。
线性规划的求解可以通过单纯形法或内点法等算法实现。
通过逐步优化决策变量的取值,可以得到满足约束条件并使目标函数达到最优的解。
二、整数规划(Integer Programming)整数规划是在线性规划基础上增加了决策变量必须取整的要求,其模型形式为:Min(或Max):C₁X₁ + C₂X₂ + ... + CₙXₙSubject to:A₁₁X₁ + A₁₂X₂ + ... + A₁ₙXₙ ≤ b₁A₂₁X₁ + A₂₂X₂ + ... + A₂ₙXₙ ≤ b₂...Aₙ₁X₁ + Aₙ₂X₂ + ... + AₙₙXₙ ≤ bₙX₁, X₂, ... , Xₙ ≥ 0X₁,X₂,...,Xₙ为整数整数规划在实际问题中常用于需要求解离散决策问题的情况,如装配线平衡、旅行商问题等。
然而,由于整数规划问题的整数约束,其求解难度大大增加。
求解整数规划问题的方法主要有分支定界法、割平面法、遗传算法等。
线性规划问题的解法

线性规划问题的解法线性规划(Linear Programming,LP)是一种数学优化方法,用于求解线性约束条件下的最大化或最小化目标函数的问题。
线性规划问题在经济学、管理学、工程学等领域都具有广泛的应用,其求解方法也十分成熟。
本文将介绍线性规划问题的常用解法,包括单纯形法和内点法。
一、单纯形法单纯形法是解决线性规划问题最常用的方法之一。
它通过在可行解空间中不断移动,直到找到目标函数的最优解。
单纯形法的基本步骤如下:1. 标准化问题:将线性规划问题转化为标准形式,即将目标函数转化为最小化形式,所有约束条件均为等式形式,且变量的取值范围为非负数。
2. 初始可行解:选择一个初始可行解,可以通过人工选取或者其他启发式算法得到。
3. 进行迭代:通过不断移动至更优解来逼近最优解。
首先选择一个非基变量进行入基操作,然后选取一个基变量进行出基操作,使目标函数值更小。
通过迭代进行入基和出基操作,直到无法找到更优解为止。
4. 结束条件:判断迭代是否结束,即目标函数是否达到最小值或最大值,以及约束条件是否满足。
单纯形法的优点是易于理解和实现,而且在实际应用中通常具有较好的性能。
但是,对于某些问题,单纯形法可能会陷入循环或者运算效率较低。
二、内点法内点法是一种相对较新的线性规划求解方法,它通过在可行解空间的内部搜索来逼近最优解。
与单纯形法相比,内点法具有更好的数值稳定性和运算效率。
内点法的基本思想是通过将问题转化为求解一系列等价的非线性方程组来求解最优解。
首先,将线性规划问题转化为等价的非线性优化问题,然后通过迭代求解非线性方程组。
每次迭代时,内点法通过在可行解空间的内部搜索来逼近最优解,直到找到满足停止条件的解。
内点法的优点是在计算过程中不需要基变量和非基变量的切换,因此可以避免单纯形法中可能出现的循环问题。
此外,内点法还可以求解非线性约束条件下的最优解,具有更广泛的适用性。
三、其他方法除了单纯形法和内点法,还有一些其他的线性规划求解方法,如对偶方法、割平面法等。
如何寻找_线性规划问题_的整点最优解

- 2 0 1 2 3 4 5 6 7 8 9 10 11 12
x
图1
作出一组平行的直线 200x + 150y = t. 当 t= 0 时, 即 200x + 150y = 0 也就是直线
l0: 4x + 3y = 0. 将直线 l0 向上平移至 l1 的位置时, 直线 l1 经
过可行域上的点A , 且与原点的距离最大, 此时 z = 200x + 150y 取最大值Ζ
= 1, 2, 3, 4, 如图 4, 打出网格, 这时网格在可行域
内的交点, 即可行域内的整点Ζ
将直线 l1 向上平移到 l2 的位置时, 直线 l2 最
先经过可行域内的整点B (5, 2) , 且使 z = 160x +
252y 取最小值, 此时
z 最小= 160×5+ 252×2= 1304.
2000 年 第 3 期 数学通报
19
如何寻找《线性规划问题》的整点最优解
安培录 (山西省代县中学校 034200)
试验教材高二数学 (上) 增加了《简单的线性
规划》的内容, 利用图解法解答线性规划的两类问 题Ζ 对此, 大纲要求“会简单的应用”Ζ
学生对线性规划的基本概念、基本方法在两
类实际问题中的应用, 基本可以达纲, 但对寻找 《线性规划问题》的整点最优解的问题, 感到不好 入手, 完成作业困难较大Ζ 在这个问题上, 试验教 材安排了一个例题 (P 76 页例 4) , 两个习题 (P 79 页第 3、4 题) , 一个复习题 (P 107 页第 17 题) Ζ 针 对学生从认知到应用这一过程存在的问题, 笔者 在教学实践中归纳整理了三种基本方法, 现举例 说明如下:
线性规划与最优化问题的解法

稻壳学院
感谢观看
汇报人:XX
求解方法:使用 单纯形法、椭球 法等算法求解线 性规划问题
线性规划的几何解释
添加 标题
线性规划问题可以看作是在多维空间中寻找一条直 线,使得该直线在满足一系列约束条件下,最大化 或最小化某个目标函数。
添加 标题
线性规划的基本概念包括决策变量、目标函数 和约束条件。决策变量是问题中需要求解的未 知数,目标函数是希望最大化或最小化的函数, 约束条件是限制决策变量取值的条件。
解决方案:运输问题的解决方案通常包括 确定最优的运输路线和数量,以最小化运 输成本或最大化运输效益。
分配问题
简介:线性规划与最优化问题的实际应用之一是解决分配问题,通过合理分配资源,实 现最大化效益。
实例:如将有限的生产任务分配给不同的生产部门,以最小化生产成本或最大化总产量。
解决方法:利用线性规划模型描述问题,通过求解得到最优解,实现资源的最优分配。
添加 标题
在几何解释中,决策变量可以看作是坐标轴上 的点,目标函数可以看作是该点所在的高或低。 通过移动坐标轴上的点,可以找到使目标函数 取得最大值或最小值的点,即最优解。
添加 标题
线性规划的几何解释有助于直观地理解问题,并快 速找到最优解。在实际应用中,线性规划可以用于 资源分配、生产计划、运输问题等领域。
数。
线性规划问题 在现实生活中 应用广泛,如 生产计划、资 源分配和运输
问题等。
线性规划的基 本概念包括变 量、约束条件 和目标函数。
线性规划问题 通常在凸集上 进行,这使得 问题具有全局
最优解。
线性规划的数学模型
目标函数:要求 最大或最小化的 线性函数
约束条件:决策 变量的限制条件
用“小范围搜索法”求“线性规划问题”的最优整数解

对的. 之 , 于教科书 的要求 , 马虎虎 , 反 低 马 一 带 而 过 , 是 不 对 的. 师 应 该 认 真 钻 研 教 也 教 材 , 教 学 过 程 中把 教 科 书 的 内容 落 实 好 , 在 使
学 生 学 懂 教 科 书 上 的 知 识, 会 做 教 科 书 上 学
使 搜 索 范 围缩 到 最 小 , 算 的工 作 量 减 到 最 计 小 . 面 以教 科 书 中 的 题 目为 例 , 明 “ 范 下 说 小 围搜 索 法 ” 运 用 . 的
例 1 教科 书第 6 5页 习 题 7 4题 , 目 . 题
略.
能 , 到 大 纲 要 求 的“ 单 会 用 ” 目的 . 达 简 的 笔 者 对 教 科 书 中 的 全 部 7个 线 性 规 划 的 实 际 应 用 问 题 进 行 了 研 究 和 分 类 。 中 1个 其 问题 ( 科书 第 6 教 1页 例 3 的 最 优 解 不 是 整 ) 数 解 , 优 解 有 且 只有 一 个 , 优 解 显 然 在 边 最 最
数 , 不是最优解. 故 由于 要 使 目标 函数 取 最 大 值 , 此 要 寻 找 可 行 域 右 上 侧 靠 近 边 界 或 边 因 界 上 的 整 点 . 点 邻 近 的 整 点 共 有 4个 与
( ,) ( ,) ( ,) ( ,) 显 然 点 ( ,) 28 ,2 9 ,3 8 与 3 9 , 2 8 是 可 行 域 内 的 整 点 , ( , ) 是可 行 域 内 的整 点 39不
去 寻 找 , 生 不 容 易掌 握 , 习 困难 比较 大 . 学 学 为 了解决 这类 寻 找最 优 整数 解 的困难 , 笔 者 采 用 “ 范 围 搜 索 法 ” 行 教 学 . 方 法 小 进 该
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
用“小范围搜索法”求“线性规划问题”的最优整数解
笔者对教科书中的全部7个线性规划的实际应用问题进行了研究和分类。
其中1个问题(教科书第61页例3)的最优解不是整数解,最优解有且只有一个,最优解显然在边界折线的顶点处,此为第一类问题;有3个问题(教科书第64页练习第2题、第65页习题第3题,第66页研究课题与实习作业)的最优解为整数解,最优整数解有且只有一个,最优解整点显然在边界折线的顶点处,此为第二类问题;另有3个问题(教科书第63页例4、第65页习题第4题、第87页复习参考题七A组第16题)的最优解为整数解,最优整数解可能不止一个,最优解整点不在边界折线的顶点处,或虽在边界折线的顶点处但并不显然,此为第三类问题。
第一、第二类问题的最优解可以通过解一个二元一次方程组直接得到,学生比较容易掌握。
第三类问题的最优解不能通过解一个二元一次方程组直接得到,必须通过观察图形或计算检验去寻找,学生不容易掌握,学习困难比较大。
为了解决这类寻找最优整数解的困难,笔者采用“小范围搜索法”进行教学。
该方法的优点在于,把在大范围同寻找最优整数解转化为在小范围内寻找最优整数解,而且在通过观察图形作出准确判断有困难的情况下,通过计算检验作出准确判断的工作量比较小。
其步骤为(1)在边界折线顶点附近的小范围内搜索一个可行域内的年整点;(2)过该点作一条斜率为-(其中A,B分别为目标函数中变量x,y的系数)的直线,与可行域边界折线相交得到一个小范围的区域;(3)在这个小范围区域内继续搜索全部最优整数解。
用“小范围搜索法”成功解题的关键是分析,要把分析贯彻于解题的全过程,观察图形要分析,计算检验也要分析,通过分析充分发掘线性约束条件和线性目标函数的特殊性,使搜索范围缩到最小,计算的工作量减到最小。
下面以教科书中的题目为例,说明“小范围搜索法”的运用。
例1教科书第65页习题题,题目略。
本题的线性约束条件
线性目标函数z=200x+150y,其中x,y分别为大房间与小房间的间数。
作出可行域如图1。
(1)搜索一个可行域内邻近边界折线顶点的整点。
解方程组
得到点A(,),由于点A的坐标不是整数,故不是最优解。
由于要使目标函数取最大值,因此要寻找可行域右上侧靠近边界或边界上的整点。
与点A邻近的整点共有4个(2,8),(2,9),(3,8)与(3,9),显然点(2,8)是可行域内的整点,点(3,9)不是可行域内的整点。
记点(a,b)处的目标函数的值为z(2,8),所以还应检验点(2,9)与(3,8)是否在可行域内。
注意到目标函数z=200x+150y=150(x+y)+50x,而2+9=3+8,所以必有z (3,8)>z(2,9),所以应先检验点(3,8)是否在可行域内。
观察与计算都表明该点在可行域内。
记点(3,8)为B,B即为搜索到的可行域内邻近边界折线顶点的整点。
(2)作出可行域内的小范围搜索区域。
算出z(3,8)=1800,过B作直线200x+150y=18004x+3y=36.
得到点C(0,12),C为整点。
解方程组
得到点D(4,),△ACD即是新的搜索区域,在S△ACD(包括边)内可以搜索到全部最优解整点,该搜索区域比可行域大大缩小,如图2。
(3)在△ACD(包括边)内整点只有B(3,8)与C(0,12),由于B,C在一直线上,所以z(0,12)= z(3,8)=1800,B,C均为最优解整点,1800为目标函数的最大值。
若要通过计算检验在△ACD(包括边)内搜索,由于x∈[0,4),y∈(,12],所以选择x的整数值检验可使计算量小些,令x=0,1,2,3,即可得到△ACD(包括边)内的全部整点只有B(3,8)与C(0,12)。
显然,“小范围搜索法”的计算量要比把可行域内的整点逐一代入计算检验大大减少。
至此用“小范围搜索法”解题已全部完成,但在此解题过程中还可以有新的发现。
注意到点C(0,12)即为直线6x+5y=50与y轴的交点,直线5x+3y=40与x轴的交点为(8,0),这两个点都在可行域内,且都是可行域边界折线的顶点,又z(8,0)=1600<z(0,12),所以在以实施“小范围搜索法”的第一步操作时,即可选定点C,再过点C 作直线200x+150y=18004x+3y=36,同样可以得到△ACD。
这就是第二种搜索方法。
显然第二种搜索方法比前面的第一种搜索方法更简便。
只是第二种搜索方法在观察图形时不易发现,因为观察图1总让人觉得应该在点A(,)附近找一个整点比较好。
这正是观察的局限性。
观察是认识事物的开端和基础,其重要性是不容忽视的。
但观察不容易深入事物的本质,总不如思维的深刻严密,也不如计算的准确可靠。
例2教科书第85页复习参考题七A组第16题,题目略。
本题的线性约束条件
线性目标函数z=160x+252y,其中x,y分别为A型车和B型车的辆数。
作出可行域如图3。
(1)搜索一个可行域内邻近边界折线顶点的整点。
解方程组
得到点A(7,).
得到点A(,4).
A,B两点都是可行域边界折线的顶点,但它们都不是整点,所以不是最优解。
由于要使目标函数取最小值,因此要寻找可行域左下侧靠近边界上的整点。
显然点(7,1)与(3,4)都是可行域内的整点,又z(7,1)=160×7+252×1=1372,z(3,4)=160×3+252×4=1488,z(7,1)<z(3,4),故点(7,1)优于点(3,4)。
记点(7,1)为C,点C即为搜索到的可行域内邻近边界折线顶点的整点。
(2)作出可行域内的小范围搜索区域。
过C点直线160x+252y=137240x+63y=343.
解方程组
得到
设点(,)为D,得到△ACD,在△ACD(包括边)内可以搜索到全部最优解整点,该搜索范围比可行域大大缩小,如图4。
(3)在△ACD(包括边)内,整点只有(7,1)与(5,2),由于点(5,2)在线段CD的下方,故必有z(5,2)<z(7,1),记点(5,2)为E,E即为最优解整点。
z(5,2)=160×5+252×2=1304即为目标函数的最小值。
若要通过计算检验在△ACD(包括边)内搜索,由于x∈,7],y∈[1,,所以选择y的整数值检验可以使计算量小些,令y=1,2,3,即可得到△ACD(包括边)内的全部整点只有C(7,1)与E(5,2)。
显然,“小范围搜索法”的计算量比将可行域内的整点逐一代入计算检验大大减少。
从上面的两个例子中可以看到,用“小范围搜索法”解线性规划应用问题,目标明确,思路清晰,步骤简明,操作性强,计算量小,准确可靠,既不会增解也不会失解,且不怕作图和观察的误差。
笔者在用此法进行“简单线性规则”教学时,收到了较好的效果,学生感到容易理解接受,操作运用也方便。
事实上,这种逐步缩小目标范围的搜索法是一种具有普遍意义的方法,对培养学生的探索精神,进行思维训练,提高分析问题、解决问题的能力很有好处。
