原子中学物理学——单电子辐射跃迁选择定则
原子物理学总复习

段正路
2014年
1
第一章 原子的基本状况
重点: 1,原子的核式结构 2,α粒子散射实验的意义
2
1、卢瑟福的原子核式模型
原子中的全部正电荷和几乎全部质量都集中在原子中央一 个很小的体积内,称为原子核。原子中的电子在核的周围 绕核运动。
2. α粒子的散射实验:
α粒子被静止核的库仑场散射的角度θ由下式决定
• Z:质子数 • A: 质量数
C4 0
20
a
原子核的角动量
P 核 LnSnLpSp
P核 I(I1)h
原子核的磁矩
I g
I(I1) he 2M
38
原子核的统计性:A为奇数的原子核属于费米子;A为偶 数的原子核属于玻色子。
原子核的结合能
E [Z m p (A Z )m n m 核 ]C 2 或 E [Z m H (A Z )m n m 原 子 ]C 2
r rr 总角动量 JLS JLS,LS 1 ,......,LS
L LS耦合下的原子态符号表示:
2S 1
s=0,单重态
J s=1,三重态
能级排布规则
洪特定则 朗德间隔定则
17
j-j 耦合
rjrj21 rrll12srsr12 rr r Jj1j2
j1 l1 s 1 ,l1 s 1 1 ,....,l1 s 1 j2 l2 s 2 ,l2 s 2 1 ,....,l2 s 2 Jj1j2,j1j2 1 ,....,j1j2
% 1R (m 12n 1 2)Tm Tn
R — 里德堡常数;T(m) —光谱项。
光谱线系 m = 1,n = 2、3、4…,赖曼系(紫外) m = 2,n = 3、4、5…,巴尔末系(可见光) m = 3,n = 4、5、6…,帕邢系(红外) m = 4,n = 5、6、7…,布喇开系(远红外)
原子物理学褚圣麟第四、五章复习

第四章:碱金属原子和电子自旋锂、钠、钾、铷、铯、钫化学性质相仿、都是一价、电离电势都比较小,容易被电离,具有金属的一般性质。
一、碱金属原子的光谱1、四个线系(锂为例):其他碱金属光谱系相仿,只是波长不同主线系:波长范围最广,第一条线是红色的,其余在紫外,系限2299.7埃;第一辅线系(漫线系):在可见部分;第二辅线系(锐线系):第一条线在红外,其余在可见部分;伯格漫线系(基线系):全在红外。
2、巴尔末氢原子光谱规律: ,5,4,3),1-21(1~22===n nR v H λ 碱金属原子光谱:2*∞-~~nR v v n = R 为里德伯常数,当,所以∞v ~是线系限的波数,且有效量子数*n 不是整数,Δ==-*n TR n 3、碱金属原子的光谱项:22*Δ)-(n R n R T == 4、同一线系的有效量子数与主量子数差别不大;与某一量子数对应不同线系的有效量子数差别明显,引进角量子数加以区分:5、每一线系线系限波数恰好是另一线系第二谱项值中最大的那个。
共振线:主线系第一条。
6、碱金属原子氢原子能级的比较n 很大时,碱金属原子能级 很接近氢原子能级;n 较小时,碱金属原子能级 与氢原子能级相差大; 且n 相同,l 不同的能级高低差别很大。
二、原子实极化和轨道贯穿:原子=原子实+价电子1、原子实:碱金属原子中的电子具有规则组合,共同点是在一个完整的结构之外,多余一个电子,这个完整而稳固的结构称为原子实。
由于原子实的存在,发生原子实的极化和轨道在原子实中的贯穿。
2、价电子:原子实外的那个电子称作价电子。
价电子在较大的轨道上运动,与原子实结合不是很强,容易脱离。
它决定元素的化学性质,在较大的轨道上运动。
3、原子实的极化:由于价电子的电场的作用,原子实中带正电的原子核和带负电的电子的中心发生微小相对位移,于是负电的中心不再在原子核上,形成一个电偶极子。
① 角量子数l 小:轨道偏心率大(椭圆),极化强,能量影响大;② 角量子数l 大:轨道偏心率小(接近圆),极化弱,能量影响小。
7跃迁和选择定则电偶极跃迁
F
=
−∇U
=
−
i
∂U ∂x
+
j ∂U ∂y
+ k ∂U ∂z
其直角坐标分量
Fx
= − ∂U ∂x
= µx ∂∂Bxx
+ µy
∂By ∂x
+ µz
∂Bz ∂x
Fy
= − ∂U ∂y
= µx ∂∂Byx
+ µy
∂By ∂y
+ µz
∂Bz ∂y
Fz
= − ∂U ∂z
= µx ∂∂Bzx
+ µy
f
= exp −
ω kBT
exp
−
ω kBT
= Bif I (ω) Afi + Bfi I (ω)
I (ω) = Afi
1
Bif
ω
exp
kBT
−
B fi Bif
§2.7 跃迁和选择定则—Einstein辐射唯象理论
Planck黑体辐射公式
I (ω)
=
ω3 π 2c3
exp
∂By ∂z
+ µz
∂Bz ∂z
如果磁场是均匀的,梯度为零,则磁矩所受力为零。
§3.1 轨道磁矩和Stern-Gerlach实验—磁矩与磁场相互作用
磁矩受到的力矩: τ= µ × B
B
力矩的作用将引起角动量的变化
τ= dL= µ × B
dt
在均匀磁场中磁矩虽然不受净平移力的作用,但仍要受 到一个力矩作用
原子分子的低激发态的能级寿命一般在10-8 ~ 10-9 s,相 应的能级宽度为Γ = 10-8 ~ 10-7 eV。
对于稳定的基态,τ=∞,相应的 Γ = 0。
第5节 辐射跃迁的普用选择定则

l
不允许出现跃迁
i
1 2 3 (奇数)
同理,同一组态中不同原子组态间的跃迁也是不允许的。
除了满足奇偶性条件外,还要满足如下关系: L-S耦合选择定则: S 0、L 1、J 0, 1(0 0除外) 碱金属的只有一个电子,如果满足了 l 1 ,自然也 就满足了奇偶性的变化以及 L 1 的要求;同时S总 是1/2,所以 S 0 自然满足。 在有些较重的原子中,由于L-S 耦合遭到部分破坏,会产 生例外的跃迁。如汞原子的一个波长2537埃的强谱线,是 由6s6p3P1 6s6s1S0跃迁产生的,违反了 S 0 。 J-J耦合选择定则: J p 0 或对换 j 0, 1
J 0,பைடு நூலகம்1(0 0除外)
P165有错
§ 5.5 辐射跃迁的普用选择定则
对于多个电子的辐射跃迁,也存在着一个选择定则 原子中电子的空间分布分为偶性和奇性两类,这性质称作 “宇称”。原子中各电子的 l 量子数相加,如果得到偶数, 则原子为偶性,如果得到奇数,则原子为奇性。跃迁只发生 在不同宇称的状态之间.
偶性态( li 偶数) 奇性态( li 奇数) (必要条件)
高二物理竞赛单电子辐射跃迁的选择定则课件

•只考虑自旋轨道耦合时,
Els 0, j l 1 /2; 3p(n=3,l=1)
Els 0, j l 1 / 2; •相对论效应与自旋轨道耦合都考虑后,
Er Els 0
3p(n=3,l=1)
32P3/2 32P1/2
32P3/2 32P1/2
11
Balmer系第一条谱线Hα 7种跃迁,5条谱线
单电子辐射跃迁的选择定则
一、选择定则: 单电子,电偶极辐射跃迁(吸收或发射光子)只能在
下列条件下发生,
l 1 j 0, 1
• 主量子数n的改变不受限制; • 跃迁对角动量有选择性; •选择性既是由光谱线实验测量规律总结,在量子力学中也 有理论推导.
1
4.5 单电子辐射跃迁的选择定则
二、碱金属光谱的解释
n,j相同、l不同的能级简并
氢原子精细结构能级图 •主量子数n的改变不受限制,但是由于跃迁几率与辐射频 率立方成正比,同一n值的不同能级间跃迁的几率很小.
12
例题: 氢原子考虑精细结构之后有状态32D3/2, 32P3/2和 22P1/2, 22S1/2。试问这两组状态之间能否产生跃迁, 有几种可能,实际对应几条谱线?
A. 不能跃迁; B. 二种可能,一条谱线; C. 四种可能,四条谱线; D. 二种可能,两条谱线。
13
氢 原 子 光 谱 的 精 细 结 构
E
S L =0
p
d
L =1
L =2
f L =3
Hn
…
32
12
12
52 32
72
4
32
12
12
52 32
3
32
2
12
12
跃迁类型和选择定则
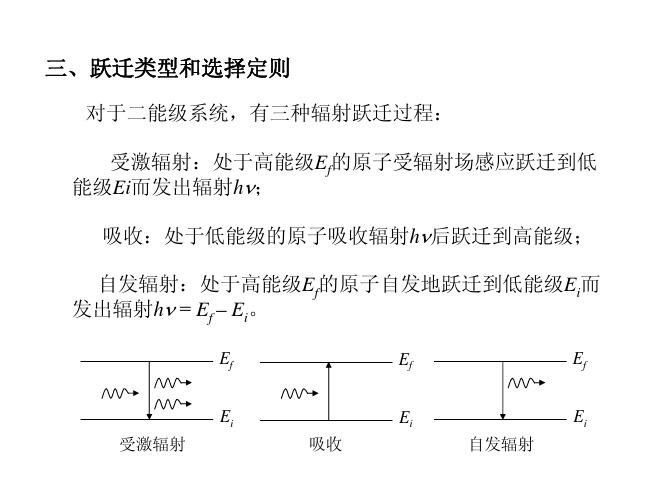
将原子和电偶极辐射场作为一个整体系统处理,用k表示 辐射的波矢,ε表示偏振态,-er是电偶极矩。 如果系统处在有nk,ε个量子的初始态(用i标记)中,则单 位时间内系统跃迁到有nk,ε+1个量子的终态(用f标记)的跃迁 速率为
λif =
( Ei − E f
3πε 0 c
)
3
4 3
∫ψ
* f
(-er )ψ i dτ (nk,ε + 1)
M ˆ M ba1E2 = ψ b (ik ⋅ r )(ε ⋅∇) ψ a M E = M ba1 + M ba2
其中
M
M1 ba
=−
ωba
2 c
ψ b ly ψ a
E M ba2
2 imωba =− ψ b xi zi ψ a 2 c
原子序数为Z的类氢离子的磁偶极跃迁的跃迁速率与电 偶极跃迁速率之比为:
三、跃迁类型和选择定则
对于二能级系统,有三种辐射跃迁过程: 受激辐射:处于高能级Ef的原子受辐射场感应跃迁到低 能级Ei而发出辐射hν; 吸收:处于低能级的原子吸收辐射hν后跃迁到高能级; 自发辐射:处于高能级Ef的原子自发地跃迁到低能级Ei而 发出辐射hν = Ef – Ei。
Ef Ei 受激辐射 吸收 Ef Ei 自发辐射 Ef Ei
2
电偶极矩-er在空间反演下变号,宇称为奇,P = -1。由于 宇称守恒,初态和末态波函数的宇称必须改变。
e
− ik ⋅r
1 = 1 − (ik ⋅ r ) + (ik ⋅ r ) 2 − 2!
磁偶极和电四极辐射由展开式第二项贡献,要多乘一项 k·r。因而磁偶极和电四极辐射作用算符是偶宇称的,P = 1, 由于宇称守恒,初态和末态波函数的宇称应不变。 由此可以得到电多极辐射和磁多极辐射的宇称,以及原 子分子初态和末态宇称Pf和Pi与光子角动量有如下关系:
原子物理学复习资料

解释:光谱,氢原子线系,类氢离子,电离电势,激发电势,原子空间取向量子化,原子实极化,轨道贯穿,有效电荷数,电子自旋,磁矩,旋磁比,拉莫尔进动,拉莫尔频率,朗德g因子,电子态,原子态,塞曼效应,电子组态,LS耦合,jj耦合,泡利原理,同科电子,元素周期表,壳层,原子基态,洪特定则,朗德间隔定则数据记忆:电子电量,质量,普朗克常量,玻尔半径,氢原子基态能量,里德堡常量,hc,ħc,玻尔磁子,精细结构常数,拉莫尔进动频率著名实验的内容、现象及解释:α粒子散射实验,光电效应实验,夫兰克—赫兹实验,施特恩—盖拉赫实验,碱金属光谱的精细结构,塞曼效应,反常塞曼效应,理论解释:(汤姆逊原子模型的不合理性),卢瑟福核式模型的建立、意义及不足,玻尔氢原子光谱理论的建立、意义及不足,元素周期表计算公式:氢原子光谱线系,玻尔理论能级公式、波数公式,角动量表达式及量子数取值(l,s,j),LS耦合原子态,jj耦合原子态,朗德间隔定则,g因子,塞曼效应,原子基态谱线跃迁图:精细结构,塞曼效应;电子态及组态、原子态表示,选择定则1.同位素:一些元素在元素周期表中处于同一地位,有相同原子序数,这些元素别称为同位素。
2.类氢离子:原子核外只有一个电子的离子,这类离子与氢原子类似,叫类氢离子。
3.电离电势:把电子在电场中加速,如使它与原子碰撞刚足以使原子电离,则加速时跨过的电势差称为电离电势。
4.激发电势:将初速很小的自由电子通过电场加速后与处于基态的某种原子进行碰撞,当电场电压升到一定值时,发生非弹性碰撞,加速电子的动能转变成原子内部的运动能量,使原子从基态激发到第一激发态,电场这一定值的电压称为该种原子的第一激发电势5.原子空间取向量子化:在磁场或电场中原子的电子轨道只能取一定的几个方向,不能任意取向,一般的说,在磁场或电场中,原子的角动量的取向也是量子化的。
6.原子实极化:当价电子在它外边运动时,好像是处在一个单位正电荷的库伦场中,当由于价电子的电场的作用,原子实中带正电的原子核和带负电的电子的中心会发生微小的相对位移,于是负电的中心不再在原子核上,形成一个电偶极子,这就是原子实的极化。
张东海原子物理学考点总结

原子物理学考点总结第一章 原子的基本状况(总结)一、 原子的大小和质量1、 原子的大小各种原子有不同的半径,其数量级均为10-10m.2、 原子的质量在化学和物理学上原子的质量通常用它们的相对质量来表示,质量单位为12C 的质量的1/12。
二、 原子的组成1、E. Rutherford 原子核式结构模型原子是由原子核和核外电子组成:原子核处于原子的中心位置,其半径在10-15m 到10-14m 之间,原子核带正电荷,其数值为原子序数乘单位电荷数值;电子分布在原子核外,分布半径为10-10m 。
2、E. Rutherford 原子核式结构模型的验证1)、库仑散射公式(1)式中:M 为α粒子的质量,v 为α粒子的速度,Z 为原子核的电荷数,θ为散射角,b 为碰撞参数。
公式(1)无法直接和实验进行比较。
2)、E. Rutherford 散射公式2sin )()41(422220θπεσΩ=d Mv Ze d (2)式中:d σ称为微分散射截面,其物理意义是α粒子散射到θ-θ+d θ之间立体角为d Ω内每个原子的有效散射截面。
公式的实用范围θ=450-1500.3、 原子核的大小估计利用E. Rutherrford 散射理论可以估计出原子核的大小,即α粒子距原子核的最近距离:))2s i n (11(241220θπε+=Mv Ze r m 由于E. Rutherford 散射公式在θ=1500时仍有效,所以取θ=1500。
第二章、原子的能级和辐射(玻尔氢原子理论)一、 玻尔理论1、玻尔理论的基础1)、氢原子光谱的经验规律氢原子光谱的波数的一般规律:)11(~22nm R v H -= (1) 式中:m=1,2,3,…;对每一个m,n=m+1,m+2,m+3,….4354) 、原子的核式结构模型2、玻尔理论电子绕原子核运动体系的总能量:r Ze E 24120πε-= (2) 考虑到光谱的一般规律,(1)式两边同乘hc 则有:)()11(~2222m hcR n hcR n m hcR h v hc H H H ---=-==ν (3) 如果原子辐射前的能量E 2,辐射后的能量为E 1(E 1<E 2),辐射放出的能量为:12E E h -=ν (4)比较(3),(4)式,原子的能量取负数,则有:2nhcR E H -= (5) 考虑到原子的结构,玻尔提出下列假定:假定1:原子中能够实现的电子轨道必须符合下列条件6.131-=E eV由氢原子波数公式,可以得出氢原子的里德伯常数:ch me R H 32042)4(2πεπ= 考虑到原子核的质量不是无限大的,原子核也是运动的,则里德伯常数变为:M m R Mm c h me R A +=+=∞1111)4(232042πεπ 10973731=∞R m -13、玻尔理论的验证1)氢原子的第一玻尔半径的理论值为a 1=0.529×10-10m ,这与原子的大小的数量级是一致的。
