椭球面的几何特征与测量计算
椭球面参数方程

椭球面参数方程
椭球面参数方程是一种描述椭球面的数学表达式,这种方程通常用于工程和测量科学中,也应用于地理学、天文学、航海科学等科学领域中。
椭球面参数方程同样可以用于地图制作。
椭球面参数方程一般以如下形式给出:
\begin{equation}F(X,Y,Z)={X^2 \over a^2}+{Y^2 \over b^2}+{Z^2 \over c^2}-1\end{equation}
其中,a,b,c分别指椭球半长轴,半短轴,半高轴。
椭球面参数方程可以用来描述椭球面几何形状。
通常情况下,椭球面的半长轴比半短轴长,而半高轴比半短轴短,故椭球面参数方程可以表示出椭球面的高程变化,从而更精确地描述出椭球面的几何特征。
使用椭球面参数方程的主要好处是,它能够更精确地反映出一个零维空间中的经纬度变化,因此可以用于地图制图工具中,例如 ArcGIS 和谷歌地图。
椭球面参数方程还用于地球拉伸模型,模拟地球表面变形过程。
此外,椭球面参数方程还可用于测量科学中,特别是在航海科学中。
它用于确定船舶行进的位置和航线,以及根据船只的航行路程构建航海图。
椭球面参数方程还可以用于地图制作,例如进行地形测量以制作地形图和地形模型。
椭球面参数方程是一种高精度的空间几何表达式,它对于工程和测量科学具有重要意义,可用于确定两个位置之间的距离,有助于更精准地制图和模拟地球表面变形,从而更好地理解地球的地形特征。
椭球面的几何特征与测量计算课件

椭球面的离散化方法
椭球面的离散化方法是将椭球面分割成 若干个小的离散单元,以便于进行数值
计算和分析。
常见的离散化方法包括网格法、元胞自 动机法、粒子群优化算法等。
离散化方法需要考虑离散单元的大小和 形状,以及离散单元之间的连接关系等 因素。离散化方法的精度和效率直接影 响到数值计算和分析的准确性和可靠性
数据处理方法
在空间数据处理过程中,椭球面可以作为基础数据结构,用于建立各种地理信息要素的空 间关系,如点、线、面等要素的相互关系。
椭球面在空间信息分析中的应用
信息分析方法
空间信息分析是地理信息系统的核心功能之一,包括空间查询、空间分析、空间统计等。椭球面作为一种几何模型, 可以为空间信息分析提供重要的方法和手段。
椭球面的几何特 征与测量计算课 件
目录
• 椭球面的基本几何特征 • 椭球面的测量计算方法 • 椭球面在地理信息系统中的应用 • 椭球面在大地测量学中的应用 • 椭球面的数学模型与计算方法 • 椭球面在地球科学领域的应用前
景
01
椭球面的基本几何特征
椭球面的定义与方程
Hale Waihona Puke 椭球面定义椭球面是一种二次曲面,由椭圆 围绕其主轴旋转形成。
椭球面方程
对于一个椭球面,其一般方程可 写为 x^2 / a^2 + y^2 / b^2 + z^2 / c^2 = 1,其中a、b、c是 椭球的长半轴、中半轴和高半轴 。
椭球面的主轴与极点
主轴
椭球面的主轴是椭圆的主轴,也是椭 球面的旋转轴。
极点
在椭球面上,与主轴等距离的点形成 的曲线称为极曲线,极曲线的交点称 为极点。
椭球面的基本性质
封闭性
参考椭球体的概念

参考椭球体的概念参考椭球体是地球形状的一种理想化模型,用于描述地球形状的基本特征,由它的椭率、长半轴和短半轴等参数来定义。
参考椭球体的概念是基于观测数据和测量技术而建立的。
地球的形状是不规则的,而参考椭球体是一种在整个地球表面都近似成立的假设模型。
它可以通过大量观测数据和数学计算得到。
参考椭球体的参数包括:- 长半轴(a):参考椭球体的赤道半径,即椭球体的最长轴。
- 短半轴(b):参考椭球体极半径,即椭球体的最短轴。
- 扁率(f):椭球体的扁平程度,定义为 (a-b)/a,即赤道半径和极半径的差值与赤道半径的比值。
- 椭率(e):椭球体离心率,定义为√(a^2-b^2)/a,即长半轴和短半轴的差值与长半轴的比值。
参考椭球体的使用方便了地球测量和地图制图的工作,因为它可以作为一个统一的基准来描述地球的形状。
其中常用的参考椭球体包括WGS84、GRS80等。
不同的参考椭球体会在形状和大小上有所差异,所以在地理坐标系统的定义中需要指定使用的参考椭球体。
椭球体是一种几何体,它由一个椭圆围绕其短轴旋转形成。
椭球体具有三个主要参数:长轴(a),短轴(b)和极半径(c)。
每个椭球体都可以通过这些参数来描述。
椭球体在地理学中被广泛应用,特别是在描述地球形状和测量地球表面上。
根据椭球体的参数,可以确定地球的大小和形状。
这些参数是根据测量数据和观测结果得出的。
椭球体的概念也应用于地理信息系统(GIS)和全球定位系统(GPS)等技术中。
这些技术使用椭球体模型来计算地球上的位置和测量距离。
不同的椭球体模型适用于不同的地区和特定的应用。
总之,椭球体是用来描述地球形状的几何体,它在地理学和地理信息系统中具有重要的应用。
椭球参数方程

椭球参数方程椭球参数方程是一种应用广泛的几何方程。
它可以表示一个椭球,借此可以描述椭球的各个特征,如长轴、短轴、扁率、位置参数等。
椭球参数方程的应用非常广泛,可以用来描述宇宙的形状,计算所有已知星体的距离,改变物体的相位等。
椭球参数方程可以使用以下公式表示,给出椭球的空间坐标(x,y,z)$frac{x^2}{a^2} + frac{y^2}{b^2} + frac{z^2}{c^2} = 1$ 其中,a,b,c分别为椭球长轴、短轴和扁率,其中长轴a一般大于短轴b,而扁率c一般小于a。
由于椭球参数方程可以表示复杂的几何形状,可以用于许多不同的应用,如天文、地球物理学、航空航天、机械设计等。
在天文学中,椭球参数方程可以用来描述宇宙的形状,提供宇宙中的行星距离和其他物体的位置信息。
在地球物理学中,它可以用来直接测量地球的形状及表面的强度,从而确定磁力场的分布情况。
在航空航天技术中,它可以用来改变物体的相位,进行高精度的航迹计算,地球轨道解算,以及预测地球环境要素,如气温、湿度、大气压等。
在机械设计领域,它可以用来设计和制造椭球形的零件,即圆柱形的零件加上一个椭球形的轴承,可以增加零件的稳定性和耐久性。
此外,椭球参数方程还可以用于测量地球空间,如测量地球上某物体离地球中心的距离,计算某地空间围成实体的表面积,将坐标转换为空间坐标,以及测算行星等其他天体的位置等等。
椭球参数方程有多种变体,但主要变体是以上述方程为基础,在此基础上添加椭球的位置参数。
下面的公式是其最常用的变体:$(frac{x-x_0}{a})^2 + (frac{y-y_0}{b})^2 +(frac{z-z_0}{c})^2 = 1$其中,(x0,y0,z0)代表椭球的中心点,a,b,c分别为椭球的长轴、短轴和扁率,其中长轴a一般大于短轴b,而扁率c一般小于a。
总之,椭球参数方程是一个重要的几何方程,它可以描述椭球空间中任何一个点的位置。
《测绘学概论》课程笔记

《测绘学概论》课程笔记第一章:测绘学总论1.1 测绘学的基本概念测绘学是一门研究地球形状、大小、重力场、表面形态及其空间位置的科学。
它的主要任务是对地球表面进行测量,获取地球表面的空间信息,并对其进行处理、分析和应用。
测绘学的研究对象包括地球的形状、大小、重力场、表面形态等自然属性,以及人类活动产生的各种地理现象和空间信息。
1.2 测绘学的研究内容测绘学的研究内容主要包括以下几个方面:(1)大地测量学:研究地球的形状、大小和重力场,建立地球的数学模型,为各种测量提供基准。
(2)摄影测量学:利用航空或卫星摄影技术,获取地球表面的空间信息,并通过图像处理技术对其进行解析和应用。
(3)全球卫星导航定位技术:利用卫星导航系统,如GPS、GLONASS、北斗等,进行地球表面空间位置的测量和定位。
(4)遥感科学与技术:利用遥感技术,如卫星遥感、航空遥感等,获取地球表面和大气的物理、化学和生物信息,并进行处理和应用。
(5)地理信息系统:利用计算机技术,对地理空间信息进行采集、存储、管理、分析和可视化,为地理研究和决策提供支持。
1.3 测绘学的现代发展随着科技的发展,测绘学进入了一个新的发展阶段。
现代测绘技术主要包括卫星大地测量、数字摄影测量、激光扫描、遥感技术、地理信息系统等。
这些技术的发展,使得测绘工作更加高效、精确和全面,为地球科学、资源调查、环境保护、城市规划等领域提供了强大的支持。
1.4 测绘学的科学地位和作用测绘学在科学体系中占有重要地位,它是地球科学的基础学科之一,为其他学科提供了重要的数据支持。
同时,测绘学在国民经济和国防建设中发挥着重要作用,如土地管理、城市规划、环境监测、资源调查、灾害预警等,都离不开测绘学的支持。
第二章:大地测量学2.1 概述大地测量学是测绘学的一个重要分支,主要研究地球的形状、大小、重力场及其变化,建立地球的数学模型,为各种测量提供基准。
大地测量学具有广泛的应用,如地球科学研究、资源调查、环境保护、城市规划等。
参考椭球实例贝塞尔椭球1841年,克拉克椭球1866-
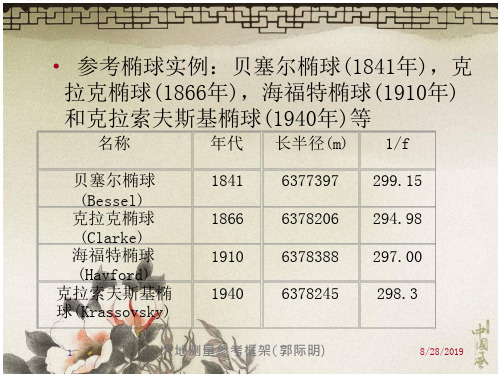
6
大地测量参考框架( 郭际明)
8/28/2019
总地球椭球实例:WGS84, GRS80
WGS84(GPS)
GRS80(ITRS)
a
6378137
6378137
f
1/298.257223563
1262.999·10-8
108263·10-8
ω(rad/s) 7292115·10-11
·1996年,WGS84坐标框架再次进行更新, 得到了WGS84(G873)
25
大地测量参考框架( 郭际明)
8/28/2019
3.7 地方坐标系
1 目的
➢ 减小图上距离或坐标反算距离与实测距离的 差值;
➢ 工程建设的急需;
➢ 满足特定工程的精度要求;
➢ 满足工程特定的使用习惯。
2)依据:长度归化从观测表面到投影面,当投 影面低于观测表面时变短,反之变长;高斯 投影的长度比大于1,并且离中央子午线越远, 长度比越大。在城市或工程建设地区要求归 化变形和投影变形的代数和不超过1:40000(相 当于每公里2.5cm)
地原点)
2
大地测量参考框架( 郭际明)
8/28/2019
椭球定向
3
大地测量参考框架( 郭际明)
8/28/2019
大地原点和大地起算数据
大地原点也叫大地基准点或大地起算点, 参考椭球参数和大地原点上的起算数据构 成经典大地测量基准。
4
大地测量参考框架( 郭际明)
8/28/2019
· 现代大地测量基准/卫星大地测量基准
高斯投影长度改化
y(km)
11.6 1:600000
36.8 1:60000
当观测点位离中央子午线小 45.0
(椭球、投影、变形)PPT课件
在地图制作中,椭球变换用于将地球的椭球体模型转换为更便于分析的数学模型。这涉及 到对地球的形状、大小和赤道半径等参数的精确测量和计算,以确保地图的准确性和可靠 性。
遥感影像处理中的椭球、投影、变形应用
遥感影像校正
遥感影像在获取过程中会受到多种因素的影响,如地球曲率、大气折射等,导致影像产生畸变和失真。遥感影像校正 的目的是消除这些影响,提高影像质量和精度。
缺点
投影需要使用特定的设备和材料,成本较高;投影的精度和稳定性可能受到环 境因素的影响;投影的图像质量可能会受到投影角度、距离和光线等因素的影 响。
03 变形的基本概念
变形的原因
地球是一个近似于椭球的旋转体,由于地球自转、公转和地球内部物质 分布不均匀等因素的影响,地球表面各点的位置会发生微小的变化。
投影方法是将球面上的点投影到平面上的方法,由于投影方法的不同, 会导致投影结果与实际地形存在一定的差异,从而产生变形。
不同的地图用途和比例尺要求也会对地图的变形产生影响,例如在大比 例尺地图中,为了更好地反映地形细节,需要进行地图的局部放大,这 也会导致地图的变形。
变形的分类
按变形性质可分为几何变形和投影变形。几何变形是由于地图制作过程中几何图形的变化而 引起的变形,如地图投影时产生的变形;投影变形是由于投影方法不同而引起的变形,如将 地球表面投影到平面时产生的变形。
投影方法
在地理信息系统中,投影是将地球表面上的点映射到二维平面上的方法。 不同的投影方法适用于不同的应用场景,如地图制作、遥感影像处理等。
03
变形处理
在地理信息系统中,由于地球的椭球体模型与实际地球形状存在差异,
因此需要进行变形处理以减小误差。变形处理的方法包括地图投影、地
5-椭球面的几何特征与测量计算解析
2
0
1
MN
2
M NtgA
M1 N co2sAdA
设 t M tgA N
则
dt
M N
1 cos2
dA A
大地测量学基础
第二节 椭球面上法截线曲率半径
四、平均曲率半径
此时积分限要作相应变更:当A=0时,t=0;A
2
时,t 。
照此换元后,经积分得到下式,
R2
MN
dt
2
0 1t2
MNarctg 0 t
第三节 椭球面上弧长计算 大地测量学基础
一、子午圈弧长公式
(用于高斯投影计算,椭球面上大地问题解算)
1、计算B=0到B的子午圈弧长X
由M=dX/dB得X:
B
dX
B
MdB
0
0
将
代入上式,从0到B积分,可得X。 可知,X是B的函数。
大地测量学基础
第三节 椭球面上弧长计算
一、子午圈弧长公式
(用于高斯投影计算,椭球面上大地问题解算)
11 (11)(2 s A ic n2 o A )s 11
RR A 90 MN
MN
大地测量学基础
第二节 椭球面上法截线曲率半径
四、平均曲率半径
1 n
R ni1
RAi
(n)
R 2 10 2 R A d A 2 10 2 N c o s 2A M N M s in 2A d A
R2
dyta9 n0 (B)coBt dx
yx(1e2)tanB
x
a
coBs
1e2sinB2
N a c WV
VW1e2 WV1e2bVaV,ca2 ac b
W1e2si2nB V1e'2co2B s12
椭球型体积计算公式
椭球型体积计算公式椭球是一种形状介于球和椭圆之间的几何体,其体积的计算公式可以通过计算椭球的长半轴、短半轴和极轴之间的关系得到。
椭球的公式如下:V = (4/3)πabc其中,V表示椭球的体积,a、b和c分别表示椭球的三个轴的长度。
为了理解这个公式,我们可以先来看一下椭圆的定义。
椭圆是平面上到两个定点的距离之和等于常数的点的轨迹。
如果我们把一个椭圆绕其长轴旋转一周,就可以得到一个椭球。
椭球的体积可以通过先将其切割为无数个薄的圆盘,然后对这些圆盘的体积进行求和来计算。
每个圆盘都可以看作是一个半径不断变小的圆柱体,其体积可以通过将其底面积乘以高度来计算。
因为椭球是由无数个这样的圆柱体组成的,所以我们可以通过对所有这些圆柱体的体积进行求和,来获得椭球的体积。
为了计算椭球的体积,我们需要先确定椭球的三个轴的长度:a、b和c。
其中,a和b分别代表椭圆的两个半轴的长度,c则代表椭圆的极轴的长度。
通过上述的计算公式,我们可以得到一个椭球的体积,而如果我们已知椭球的体积,也可以根据这个公式来计算椭球的长半轴、短半轴和极轴的长度。
椭球的体积计算公式在数学和物理等领域有着广泛的应用。
在工程上,通过计算椭球的体积可以帮助我们确定椭球的尺寸和容量,从而进行设计和建模。
在天文学中,椭球体积的计算可以用来推算行星、卫星和恒星的质量和密度。
在地理学和地球科学中,椭球的体积计算可以帮助我们研究地球的形状和内部结构。
总之,椭球的体积计算公式是一种重要的数学工具,通过它我们可以计算椭球的体积,进而研究和应用椭球的属性和特征。
计算椭球面积公式
计算椭球面积公式椭球是几何学中的一个重要概念,它是一个具有两个焦点的闭合曲面。
椭球的形状在数学上由两个参数确定,即长半轴和短半轴的长度。
椭球的面积计算公式可以通过积分来推导,这是一个常见的数学问题。
为了计算椭球的面积,首先需要了解椭球的基本形状特征。
椭球与球体有些相似,但其形状更为扁平。
想象一个绕着短半轴旋转的椭圆,其形成的曲面即为椭球。
这个几何体在许多领域中都有广泛应用,例如天文学、地质学和工程学等。
为了计算椭球的面积,我们可以使用曲面面积元素的定积分方法。
假设椭球的长半轴为a,短半轴为b。
为了推导出椭球的面积公式,我们对椭球进行切割,将其分为许多小块。
然后,通过计算每个小块的面积并将其相加,就可以得到整个椭球的表面积。
如果我们将椭球放在坐标系中,其长轴沿着x轴,短轴沿着y轴,那么我们可以用参数方程来描述椭球的形状。
对于一个椭球面上的点P,其位置可以用参数u和v来表示,其中u的取值范围为[0, 2π],v的取值范围为[0, π]。
椭球的参数方程可以写为:x = a * cos(u) * sin(v)y = b * sin(u) * sin(v)z = c * cos(v)接下来,我们可以计算参数方程对应的椭球面积元素。
通过对参数u和v的微小变化,椭球面积元素可以表示为:dS = |(∂r/∂u) × (∂r/∂v)|其中∂r/∂u和∂r/∂v是对参数u和v的偏导数。
对椭球参数方程进行求导,并进行一些简化后,可以得到:dS = ab * cos(v) dudv然后,我们对整个曲面进行积分,范围为u从0到2π,v从0到π。
这样,我们就可以得到椭球的表面积公式:S = ∫∫ ab * cos(v) dudv计算这个二重积分可以得到椭球的表面积。
当然,这可能需要使用一些数值计算方法,或者借助计算机进行处理。
不过,通过这样的计算,我们可以准确地获得椭球的表面积。
了解椭球的面积计算公式对于许多应用场景都是十分有用的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6356752.3142
e2 0.00669342162297 0.00669438499959
0.00669437999013
e′2 0.0067385254468
0.00673950181947
0.00673949674227
f 1:298.3
1:298.257
1:298.257223563
我国所采用的的1954年北京坐标系应用的是克拉索夫
a2 b2
并得:
(1 e2 )(1 e'2 ) 1
推得:
e2
e'2 1 e'2
e'2
1 e2
e
'2
e2 1 e2
e2 1 e'2
同理 可得:
a b 1 e 2 ,b a 1 e2 c a 1 e 2 ,a c 1 e2
V W 1 e 2 ,W V 1 e2 b V a V ,c a2
ac
b
W 1 e2 sin2 B,V 1 e'2 cos2 B 1 2
第一节 地球椭球及其定位 大地测量学基础
一、椭球的几何参数及其关系
几种椭球几何参数
kpaCOBCKuu
1980国家大地坐标系 WGS-84
a 6378245
6378140
6378137
b 6356863.01877
6356755.28816
大地测量学基础
第一节 地球椭球及其定位
和三个旋转角度 X ,Y。, Z
经典大地测量难以获得这六个参数,椭球定位一般都是通过大 地原地的天文观测来实现的。
大地测量学基础
第一节 地球椭球及其定位
三、椭球的定位 椭球的定位一般满足一下三个条件:
⑴椭球的短轴与某一指定历元的地球自转轴相平行; ⑵起始大地子午面与起始天文子午面相平行; ⑶在一定区域范围内,椭球面与大地水准面(或似大地水准面) 最为密和。 前两个条件为定向条件,
第一偏心率: e 第二偏心率:e′
e和e反映椭球体的扁平程 度,偏心率越大,椭球愈
扁
第一节 地球椭球及其定位 大地测量学基础
一、椭球的几何参数及其关系
关系:
第一偏心率: e
a2 b2 a
,e2
1
b2 a2
b a 1 e2
a b 1 e '2
第二偏心率: e
a2 b2 b
, e2
a2 b2
大地测量学基础
第一节 地球椭球及其定位
一、椭球的几何参数及其关系
椭 圆——NESW 旋转轴——NS 子午圈——NRS 平行圈——C-C′
第一节 地球椭球及其定位 大地测量学基础
一、椭球的几何参数及其关系
椭圆的长半轴: a 椭圆的短半轴: b
a、b称为长度元素
F1
F2
椭圆的扁率:f
扁率反映了椭球体 的扁平程度
第一节 地球椭球及其定位 大地测量学基础
B
Lcos
B L sec
第一节 地球椭球及其定位 大地测量学基础
Z P
90°-B
S Q1
BO90°-B
P1
N
z Mq
Z R A
z1
θ ε Z2
μ
η
Z1 90°-ψ
R1 θ1
m
u
λ-L P
O
O1
P2
Q2
R1 R
Q
OZ1为过O的铅垂线,Z1为天文天顶,∠ZOZ1=u,即为O点垂
第一节 地球椭球及其定位
三、椭球的定位
椭球定位——将一定参数的椭球与大地体的相关位置固定下 来,确定测量计算基准面的具体位置和大地测量起算数据。
椭球定位包括定位和定向两个方面,定位指确定椭球中心的位 置,定向则指椭球坐标轴的指向。
从ห้องสมุดไป่ตู้学上讲,椭球的定位和定向就是确定大地直角坐标系相对
于地心坐标系的平移量和旋转角,即三个平移参数 X 0,Y0, Z0
斯基椭球参数;以后采用的1980国家大地坐标系应用
的是1975国际椭球参数;而GPS应用的是WGS-84系
椭球参数。
第一节 地球椭球及其定位 大地测量学基础
二、垂线偏差及其基本公式
垂线偏差——地面一点上,铅垂线方向和相应的椭球面法线方 向之间的夹角。 垂线偏差μ 的分量—— 子午圈分量ξ 和卯酉圈分量η
大地测量学基础
第五章 地球椭球及 椭球面上的计算
山东科技大学测绘学院大地测量系
大地测量学基础
地球椭球面作为计算的基准面
问题:
1、地球椭球要素(点,线、面等)的几何特征及其数学性质 地球椭球及其定位 椭球面的法截线及其曲率半径 椭球面上的弧长计算
2、观测元素由地面化算至椭球面
3、椭球面上的三角形解算和大地坐标计算
线偏差。弧Z1P=90°-φ。 ∠ZPZ1=λ-L。
cos L tan900 B cot900 cotB tan
sin L sin sin sin 900 cos
第一节 地球椭球及其定位 大地测量学基础
cos L 1 sin L L sin
B
Lcos
1
扁率: f a b 1 b 1 1 e2
a
a
1 e2 1 e'2 1
e' e 1 e' 2 e e' 1 e2
偏心距: OF1(或OF2 ) a2 b2
e2 2 f f 2
第一节 地球椭球及其定位 大地测量学基础 由前面式子得:
地球椭球参数间的相互关系
1 e2
b2 a2
1 e2
B L sec
第一节 地球椭球及其定位
天文方位角与大地方位角之间的关系
大地测量学基础
1 R1, A R
1 ( L)sin
A (1 ) (R1 R)
A ( L) sin
tan
R1 R ( sin A cos A) cot z1
大地测量学基础
P1P2为椭球短轴,Q1Q2为赤 道面,在椭球面上有一测站O, 将O点法线O1O向上延伸得到 大 地 天 顶 Z , 令 OP 平 行 于 O1P1,则弧ZP=90°-B。
第一节 地球椭球及其定位 大地测量学基础
二、垂线偏差及其基本公式
垂线偏差——地面一点上,铅垂线方向和相应的椭球面法线方 向之间的夹角。 垂线偏差μ 的分量—— 子午圈分量ξ 和卯酉圈分量η ξ=φ-B η=(λ-L)cosφ A=α-(λ-L)sinφ=α-η·tanφ
第一节 地球椭球及其定位 大地测量学基础
测量的外业工作------地球表面(对地球表面进行观测) 无法进行严密的测量计算
地球椭球------在其表面完成测量计算工作 一个大小和形状最接近于地球的规则形体
用椭球来表示地球必须解决2个问题: 一是椭球参数的选择; 二是确定椭球与地球的相关位置,即椭球的定位。
