七年级数学希望工程义演
5应用一元一次方程—“希望工程”义演-北师大版七年级数学上册教案

5 应用一元一次方程—“希望工程”义演-北师大版七年级数学上册教案一、教学目标1.通过了解“希望工程”义演活动,拓宽学生的视野,引导学生体验做公益的快乐;2.理解一元一次方程的概念,能够解决简单的一元一次方程问题;3.获得一些实际应用问题的解题经验,特别是在义演活动中的应用;4.养成良好的思维习惯和解题方法,培养学生的数学逻辑思维能力。
二、教学重难点1.难点:学生对于实际应用问题的理解和解题;2.重点:培养学生讲解解题思路和训练逻辑思维。
三、教学准备1.提前准备好义演活动的介绍,包括活动的意义、支持的对象和实现的方式等;2.准备足够的黑板粉笔和教学用具,如计算器、直尺和圆规等;四、教学过程1. 引入通过介绍“希望工程”义演活动,让学生了解公益活动的重要性,引导学生从小学会奉献和助人为乐,体验做公益的快乐。
2. 讲解一元一次方程1.引出一元一次方程的概念,引导学生从公式的意义上了解概念;2.指导学生掌握解一元一次方程的基本步骤和方法;3.给学生提供一些简单的练习题,在解决问题的过程中深化对一元一次方程的理解和应用。
3. 应用一元一次方程——“希望工程”义演活动1.教师讲解义演活动的背景和意义;2.将义演活动中遇到的一些问题抽象出来,转化成一元一次方程;3.引导学生通过解一元一次方程解决义演活动中实际应用的问题。
4. 总结与归纳1.结合义演活动,对学生进行总结展示;2.让学生讲解自己的解题思路,培养学生训练逻辑思维的能力;3.教师对学生的解题思路和方法做出评价和提出建议。
五、课堂作业1.答完课本上的相关习题,提交练习册;2.围绕“希望工程”义演活动,自己编写一些应用问题,并用一元一次方程解决。
六、教学反思通过本次教学,学生们对“希望工程”义演活动有了更深刻的理解和认识,掌握了一元一次方程的基本概念和解题方法。
在应用一元一次方程解决实际问题的过程中,学生们逐步养成了良好的思维习惯和解题方法,并培养了数学逻辑思维能力。
北师大版七年级数学上册:应用一元一次方程——“希望工程”义演课件

3
票不可能出现分数,所以不可能 结论:在实际问题中,方程的解是有实际意义的,
因此应将解带入原方程看是否符合题意。
例2:某工厂三个车间共有180人,第二车间人 数是第一车间 人数的3倍还多1人,第三车间人 数是第一车间人数的 一半还少1人,三个车间 各有多少人?
解:设第一车间有x人,则第二车间有3(x+1)人,
解: 设三个水管同时开放x小时可注满水池,
由题意得:
解得:
x =4
答:三个水管同时开放4小时可注满水池.
(2)若甲管先开放1小时,而后同时开放乙、丙两个水管,则共需 几小时可注满水池?
解:设共需y小时可注满水池,
由题意得: 解得: y =
答:共需 小时可注满水池
(3)若甲管先开放1小时后关闭,而后同时开放乙、丙两个水管, 能注满水池吗?并说明理由.
分析:果冻个数+巧克力=40个
果冻的钱+买巧克力的钱=115元
解: 设买了x个果冻,则买了(40-x)块巧克力,
由题意得:Biblioteka x×5+(40 2
x)
3=115
解得:
x = 10
当x=10时,40-x=40-10=30
答:他买了10个果冻,30块巧克力.
第三车间有(0.5x-1)人.
据题意得 x+3(x+1)+(0.5x-1)=180.
解得
x=40.
此时,
3(x+1)= 3(40+1)=121
0.5x-1=0.5×40-1=19
答:第一、二、三车间分别有40人,121人,19人.
练1:在甲处工作的有22人,在乙处工作的有 12人.现在调来18人,分别派往甲、乙两处,使 甲处工作的人数是乙处工作人数的2倍. 问:应派往甲、乙两处各多少人?
七年级数学北师大版上册课时练第5章《应用一元一次方程——“希望工程”义演》(含答案解析)(1)

答卷时应注意事项1、拿到试卷,要认真仔细的先填好自己的考生信息。
2、拿到试卷不要提笔就写,先大致的浏览一遍,有多少大题,每个大题里有几个小题,有什么题型,哪些容易,哪些难,做到心里有底;3、审题,每个题目都要多读几遍,不仅要读大题,还要读小题,不放过每一个字,遇到暂时弄不懂题意的题目,手指点读,多读几遍题目,就能理解题意了;容易混乱的地方也应该多读几遍,比如从小到大,从左到右这样的题;4、每个题目做完了以后,把自己的手从试卷上完全移开,好好的看看有没有被自己的手臂挡住而遗漏的题;试卷第1页和第2页上下衔接的地方一定要注意,仔细看看有没有遗漏的小题;5、中途遇到真的解决不了的难题,注意安排好时间,先把后面会做的做完,再来重新读题,结合平时课堂上所学的知识,解答难题;一定要镇定,不能因此慌了手脚,影响下面的答题;6、卷面要清洁,字迹要清工整,非常重要;7、做完的试卷要检查,这样可以发现刚才可能留下的错误或是可以检查是否有漏题,检查的时候,用手指点读题目,不要管自己的答案,重新分析题意,所有计算题重新计算,判断题重新判断,填空题重新填空,之后把检查的结果与先前做的结果进行对比分析。
亲爱的小朋友,你们好!经过两个月的学习,你们一定有不小的收获吧,用你的自信和智慧,认真答题,相信你一定会闯关成功。
相信你是最棒的!课时练应用一元一次方程——“希望工程”义演一、选择题1.北流市某风景区的门票价格在2019年国庆期间有如下优惠:购票人数为1~50人时,每人票价格为50元;购票人数为51~100人时,每人门票价格45元;购票人数为100人以上时,每人门票价格为40元.某初中初一有两班共103人去该风景区,如果两班都以班为单位分别购票,一共需付4860元,则两班人数分别为()A.56,47B.57,48C.58,45D.59,442.已知甲组有28人,乙组有20人,则下列调配方法中,能使一组人数为另一组人数的一半的是()A.从甲组调12人去乙组B.从乙组调4人去甲组C.从乙组调12人去甲组D.从甲组调12人去乙组,或从乙组调4人去甲组3.江陵县青少年活动中心组织实验中学七年级第一批学生前往宜昌参加研学旅行,需要与旅行社联系车辆.如果每辆旅游大巴坐45人,则有28人没有座位,如果每辆坐50人,只有一辆车空12个座位无人坐,其余车辆全部坐满,设有x 辆旅游大巴,则可列方程()A.45x+28=50x﹣12B.45x﹣28=50x+12C.45x﹣28=50x﹣12D.45x+28=50x+124.某超市在“元旦”活动期间,推出如下购物优惠方案:①一次性购物在100元(不含100元)以内,不享受优惠;②一次性购物在100元(含100元)以上,350元(不含350元)以内,一律享受九折优惠;③一次性购物在350元(含350元)以上,一律享受八折优惠;小敏在该超市两次购物分别付了85元和270元,如果小敏把这两次购物改为一次性购物,则小敏至少需付款()元A.284B.308C.312D.3205.某班同学一起去看电影,票价每张50元,20张以上(不含20张)打八折,他们一共花了1000元,则共买了()张电影票.A.20B.25C.20或25D.25或306.某车间有26名工人,每人每天能生产螺栓12个或螺母18个.若要使每天生产的螺栓和螺母按1:2配套,则分配几人生产螺栓?设分配x 名工人生产螺栓,其他工人生产螺母,所列方程正确的是()A.()121826x x =-B.()181226x x =-C.()2181226x x ´=-D.()2121826x x ´=-7.41人参加运土劳动,有30根扁担,要安排多少人抬,多少人挑,可以使扁担和人数相配不多不少?若设有x 人挑土,则可列出的方程是()A.2(30)41x x --=B.(41)302xx +-=C.41302x x -+=D.3041x x-=-8.甲、乙、丙三人共捐611元支援山区建设,甲比乙多25元,比丙少36元,则丙捐款()A.200元B.175元C.236元D.218元9.阳光书店推出售书优惠方案:①一次性购书不超过100元,不享受优惠;②一次性购书超过100元,但不超过200元,一律打九折;③一次性购书超过200元,一律打八折.如果小明同学一次性购书付款171元,那么他所购书的原价为()A.190元或213.75元B.213.75元C.200元D.190元或200元10.某超市推出如下优惠方案:(1)一次性购物不超过100元不享受优惠;(2)一次性购物超过100元,但不超过300元一律九折;(3)一次性购物超过300元一律八折;兰兰两次购物分别付款80元,252元.如果兰兰一次性购买和上两次相同的物品应付款()A.288元B.288元和332元C.332元D.288元和316元11.甲、乙两店以同样价格出售一种商品,并推出不同的优惠方案在甲店累计购物超过100元后,超出100元的部分打9折;在乙店累计购物超过50元后,超出50元的部分打9.5折,则顾客到州两店购物花费一样时为()A.累计购物不超过50元B.累计购物超过50元不超过100元C.累计购物超过100元D.累计购物不超过50元或刚好为150元12.王芳和李丽同时采摘樱桃,王芳平均每小时采摘8kg ,李丽平均每小时采摘7kg .采摘结束后,王芳从她采摘的樱桃中取出0.25kg 给了李丽,这时两人的樱桃一样多.她们采摘用了多长时间?设她们采摘所用时间为t 小时,下列方程正确的是()A.80.257t t -=B.()80.257t t-=C.()()80.2570.25t t-=+D.80.2570.25t t -=+13.在2016年“手拉手”活动中,新泰安实验小学向山区一所农村学校赠送了20个日记本和20支钢笔,价值共70元.已知每个日记本比每支钢笔少0.5元,则每个日记本和每支钢笔的价格分别为()A.1元,1.5元B.2元,2.5元C.1.5元,2元D.2元,1.5元14.《九章算术》是中国古代数学最重要的著作,奠定了中国古代数学的基本框架.其中,方程术是《九章算术》最高的数学成就.《九章算术》中记载:“今有共买羊,人出五,不足四十五;人出七,不足三.问人数,羊价各几何?”译文:“假设有若干人共同出钱买羊,如果每人出5钱,那么还差45钱;如果每人出7钱,那么仍旧差3钱,求买羊的人数和羊的价钱.”设羊是x 钱,则可列方程为()A.45375x x --=B.45357x x ++=C.45357x x --=D.45375x x ++=15.某班参加“3.12”植树活动,若每人植2棵树,则余21棵树;若每人植3棵树,则差24棵树,求该班有多少名学生?若设该班有x 名学生,则可列方程是()A.224321x x +=+B.224321x x -=-C.221324x x -=+D.221324x x +=-二、填空题16.一个大人一餐能吃四个面包,两个幼儿一餐共吃一个,大人和幼儿共7人,14个面包,则大人有____个,幼儿有____个.17.某人走进一家商店,进门付l角钱,然后在店里购物花掉当时他手中钱的一半,走出商店付1角钱;之后,他走进第二家商店付1角钱,在店里花掉当时他手中钱的一半,走出商店付1角钱;他又进第三家商店付l角钱,在店里花掉当时他手中钱的一半,出店付1角钱;最后他走进第四家商店付l角钱,在店里花掉当时他手中钱的一半,出店付1角钱,这时他一分钱也没有了.该人原有钱的数目是________角.18.甲、乙两人练习赛跑,若甲让乙先跑10米,则甲跑5秒种就能追上乙.若甲让乙先跑2秒钟,则甲跑4秒种就能追上乙,则甲每秒跑____米,乙每秒跑____米.19.小明、小华、小敏三人分别拿出相同数量的钱,合伙订购某种笔记本若干本,笔记本买来后,小明、小华分别比小敏多拿了5本和7本,最后结算时,三人要求按所得笔记本的实际数量付钱,多退少补,结果小明要付给小敏3元,那么,小华应付给小敏_____元.20.一群学生参加夏令营活动,男生戴白色帽子,女生戴红色帽子,休息时他们坐在一起,大家发现了一个有趣的现象:每位男生看到的白色与红色的帽子一样多,而每位女生看到的白色帽子数量是红色的2倍.根据信息,这群学生共有______人.21.校团委组织65名新团员为学校建花坛搬砖,女同学每人每次搬6块,男同学每人每次搬8块,每人搬了4次,共搬了1800块,则这些新团员中有______名男同学.三、解答题22.为拓宽学生视野,某中学决定组织部分师生去庐山西海开展研学旅行活动,在参加此次活动的师生中,若每位老师带19个学生,还剩11个学生没人带;若每位老师带20个学生,就有一位老师少带7个学生,为了安全,既要保证所有师生都有车坐,又要保证每辆客车上至少要有2名老师.现有甲、乙两种大客车,它们的载客量和租金如表所示.甲种客车乙种客车载客量/(人/辆)3050租金/(元辆)300400(1)参加此次研学旅行活动的老师和学生各有多少人?(2)这次活动全部租甲种客车行吗?如果行,怎样安排;如果不行,请说明理由.(3)学校计划此次研学旅行活动的租车总费用不超过4100元,租用乙种客车不少于7辆,你能得出哪几种不同的租车方案?其中哪种租车方案最省钱?请说明理由.23.明德中学某班需要购买20本笔记本和x(x>40)支圆珠笔作为期末考试的奖品,笔记本每本8元,圆珠笔每支0.8元.现有甲、乙两家文具店可供选择,甲文具店优惠方法:买1本笔记本赠送2支圆珠笔;乙文具店优惠方法:全部商品按九折出售.(1)求单独到甲,乙文具店购买奖品,应各付多少元?(2)圆珠笔买多少支时,单独到甲文具店和单独到乙文具店购买所花的总钱数一样多?(3)若该班需要购买60支圆珠笔,则怎么样购买最省钱?写出购买方案.24.临近春节,上海到扬州的单程汽车票价为80元/人,为了给春节回家的旅客提供优惠,汽车客运站给出了如下优惠方案:乘客优惠方案学生凭学生证票价一律打6折非学生10人以下(含10人)没有优惠;团购:超过10人,其中10人按原价售票,超出部分每张票打8折.(1)若有15名非学生乘客团购买票,则共需购票款多少元?(2)已知一辆汽车共有乘客60名,非学生乘客若达到团购人数则按团购方式缴款,这一车总购票款为3680元,则车上有学生和非学生乘客各多少名?25.某种同样品牌的乒乓球和乒乓球拍.乒乓球拍每副定价30元,乒乓球每盒定价5元,经洽谈后,甲店每买一副球拍赠一盒乒乓球,乙店全部按定价的九折优惠.该班需球拍5副,乒乓球若干盒(不小于5盒).问:(1)当购买乒乓球多少盒时,两种优惠办法付款一样?(2)购买15盒、30盒乒乓球时,请你去办这件事,你打算去哪家商店购买?为什么?参考答案1-5:CDABC6-10:DCCAD 11-15:DDCCD 16.3417.4518.6419.9.20.721.3022.解:(1)设有x 个老师,依题意,得:19x +11=20x -7,解得:x =18,∴19x +11=353.(2)(18+353)÷30=12(辆)……11(人),12+1=13(辆),13×2=26(人),∵18<26,∴老师数不足以每辆车分2人,∴这次活动不能全部租甲种客车.(3)18+353-50×7=21(人),21<30<50,∴有两种租车方案,方案1:租用1辆甲种客车,7辆乙种客车;方案2:租用8辆乙种客车.方案1所需费用为300+400×7=3100(元);方案2所需费用为400×8=3200(元).∵3100<3200,∴方案1最省钱,即:租用1辆甲种客车,7辆乙种客车.23.解:(1)甲:2080.8(40)0.8128x x ´+-=+乙:(2080.8)0.90.72144x x ´+´=+(2)令0.81280.72144x x +=+200x =(3)(方案一)单独去甲店:0.8x 1280.860128176+=´+=(元)(方案二)单独去乙店:0.72x 1440.7260144187.2+=´+=(元)(方案三)208160´=0.80.9(6040)14.4´´-=(元)16014.4174.4+=由此方案三最省钱,即去甲店买20本笔记本,去乙店买20支圆珠笔.24.解:(1)由题意得:10×80+(15-10)×80×0.8=1120(元);(2)解:设车上有非学生x 人,则有学生(60-x )人,①若0≤x ≤10,由题意得:80x +80×0.6(60-x )=3680,x =25不符合题意,舍去,②若10<x ≤60,由题意得:80×10+80×0.8(x -10)+80×0.6(60-x )=3680,x =40符合题意,综上所述,x =40,25.解:(1)设购买x 盒乒乓球时,两种优惠办法付款一样.根据题意:()()3055530550.9x x ´+-´=´+´,解得20x =.所以,购买20盒乒乓球时,两种优惠办法付款一样.(2)当购买15盒时:甲店需付款()3051555200´+-´=(元),乙店需付款()3051550.9202.5´+´´=(元).因为200202.5<,所以,购买15盒乒乓球时,去甲店较合算.当购买30盒时:甲店需付款()3053055275´+-´=(元);乙店需付款()3053050.9270´+´´=(元).因为275270>,所以购买30盒乒乓球时,去乙店较合算.。
北师大版七年级上册数学《应用一元一次方程―“希望工程”义演》一元一次方程PPT课件
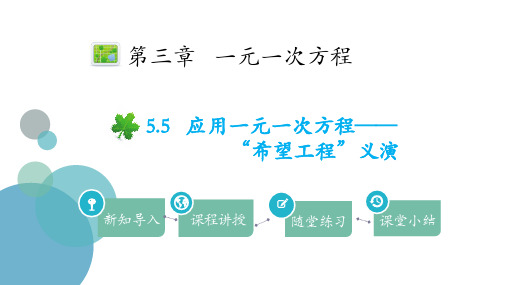
22-x=12 答:应安排10名工人生产螺钉,12名工人生产螺母.
课程讲授
1 分配问题
分配问题解题思路: 1.利用分配问题中物品之间具有的数量关系作为列方程的依据; 2.利用分配问题中的套数不变作为列方程的依据.
课程讲授
1 分配问题
练一练:学校购买40套课桌椅(一把椅子配一张桌子),
总价为2800元,若每把椅子20元,则每张桌子多少元?设
x+0.25 x=60.
解方程,得
x=48.
设亏损25%的衣服进价是 y元, 依题意得
y-0.25y=60.
解方程,得
y=80.
课程讲授
1 销售问题
两件衣服总成本:
x+y=48+80=128 (元).
因为120-128=-8(元) 所以卖这两件衣服共亏损了8元.
60元
60元
课程讲授
1 销售问题
销售问题解题思路: 1.销售问题中的常见数量关系:(1)利润=售价-成本(进价); (2)利润率=利润成本×100%;(3)利润=成本×利润率;(4) 售价=标价×折扣数10;(5)售价=成本+利润=成本×(1+利润 率). 2.折扣数表示现价是原价的十分之几.
随堂练习
解:设用x张白铁皮制盒身,根据题意有: 16x×2=(150-x)×43, 解得x=86, 所以150-x=64.
答:用86张白铁皮制作盒身,64张制作盒底, 做出的盒身与盒底正好配套.
随堂练习
4.一项工作,甲队单独做要12天完成,乙队单独做要8天完成. 现甲队先做3天后,乙队来支援,那么两队合做几天后完成 这项工作的三分之二?
A.不赚不赔 B.赔了100元 C.赚了100元 D.赚了360元
北师大数学七年级上册《5.5“希望工程”义演》课件6
练一练
一个书架宽88厘米,某一层上摆满了 第一册的数学书和语文书,共90本.小 明量得一本数学书厚0.8厘米,一本语 文书厚1.2厘米.你知道这层书架上数 学书和语文书各有多少本吗?
等量关系:
1. 数学书册数+语文书册数=90本
2.数学书总厚度+语文书总厚度 =书架宽88厘米
“组织了一场义 演,共售出1000 张票,筹得票款 6950元.成人票 与学生票各售出 多少张?
某文艺团体为“希望工程”募捐 组织了一场义演,共售出1000张票, 筹得票款6950元.成人票与学生 票各售出多少张?
该问题中包含了哪些等量关系? 成人票数+学生票数=售出的票数 1000张 成人票款+学生票款=所得票款 6950元
解得x=__3_5_6__23_____
不符合题意,所以 售出1000张票所得
票款不可能是6930元.
b
设售出的学生票为x张,
根据等量关系2,可列出方程:
B _5_x_+_8__×__(_1_0_0_0_-_x_)_=__6_9_3__2__
解得x=_3_5__6__ 因此,售出成人票__6_4_4___张,学生票
成人票数+学生票数=售出的票数 1000张
成人票款+学生票款=所得票款 6950元
设售出的学生票为x张,
学生
成人
票数(张)
x
1000-x
票款(元)
5x
8×(1000-x)
根据等量关系2,可列出方程:
_5__x_+_8__×__(_1_0_0_0__-x__)=__6__9_5_0_
解得x=__3_5_0__
因此,售出成人票__6_5_0___张,学生票_3__5_0__张.
北师大版七年级数学上册:5.5应用一元一次方程-“希望工程”义演教案

(三)实践活动(用时10分钟)
1.分组讨论:学生们将分成若干小组,每组讨论一个与一元一次方程相关的实际问题。
2.实验操作:为了加深理解,我们将进行一个简单的实验操作,通过实际操作演示一元一次方程的求解过程。
a.通过“希望工程”义演案例,让学生体会数学在实际生活中的应用
b.运用一元一次方程解决义演中的票价、观众人数等问题
3.教学内容列举:
a.义演门票价格问题
b.观众人数与总收入的关系
c.通过一元一次方程解决实际问题,培养学生的逻辑思维能力和解决问题的能力
二、核心素养目标
1.培养学生运用数学知识解决实际问题的能力,提升数学应用素养。
北师大版七年级数学上册:5.5应用一元一次方程-“希望工程”义演教案
一、教学内容
北师大版七年级数学上册:5.5应用一元一次方程-“希望工程”义演教案
1.知识点:一元一次方程的应用
a.理解一元一次方程在实际问题中的运用
b.学会列出与实际问题相关的一元一次方程
c.掌握解一元一次方程的方法
2.教材案例:“希望工程”义演
2.通过小组讨论和实验操作,学生们在实践中掌握了一元一次方程的求解方法,这有助于提高他们解决实际问题的能力。
3.教学过程中,我注意到学生们在方程求解时容易出现的错误,并及时进行了纠正和指导,使得他们在理解上更加深入。
需要改进的地方:
1.在导入新课环节,我发现有些学生对于问题的理解不够深入,可能是因为问题与他们的生活实际联系不够紧密。在今后的教学中,我需要更加注重问题的选择,使之更贴近学生的生活。
初中数学七年级上册《56“希望工程”义演》-5页精选文档

观察内容的选择,我本着先静后动,由近及远的原则,有目的、有计划的先安排与幼儿生活接近的,能理解的观察内容。随机观察也是不可少的,是相当有趣的,如蜻蜓、蚯蚓、毛毛虫等,孩子一边观察,一边提问,兴趣很浓。我提供的观察对象,注意形象逼真,色彩鲜明,大小适中,引导幼儿多角度多层面地进行观察,保证每个幼儿看得到,看得清。看得清才能说得正确。在观察过程中指导。我注意帮助幼儿学习正确的观察方法,即按顺序观察和抓住事物的不同特征重点观察,观察与说话相结合,在观察中积累词汇,理解词汇,如一次我抓住时机,引导幼儿观察雷雨,雷雨前天空急剧变化,乌云密布,我问幼儿乌云是什么样子的,有的孩子说:乌云像大海的波浪。有的孩子说“乌云跑得飞快。”我加以肯定说“这是乌云滚滚。”当幼儿看到闪电时,我告诉他“这叫电光闪闪。”接着幼儿听到雷声惊叫起来,我抓住时机说:“这就是雷声隆隆。”一会儿下起了大雨,我问:“雨下得怎样?”幼儿说大极了,我就舀一盆水往下一倒,作比较观察,让幼儿掌握“倾盆大雨”这个词。雨后,我又带幼儿观察晴朗的天空,朗诵自编的一首儿歌:“蓝天高,白云飘,鸟儿飞,树儿摇,太阳公公咪咪笑。”这样抓住特征见景生情,幼儿不仅印象深刻,对雷雨前后气象变化的词语学得快,记得牢,而且会应用。我还在观察的基础上,引导幼儿联想,让他们与以往学的词语、生活经验联系起来,在发展想象力中发展语言。如啄木鸟的嘴是长长的,尖尖的,硬硬的,像医生用的手术刀―样,给大树开刀治病。通过联想,幼儿能够生动形象地描述观察对象。课型:新授
家庭是幼儿语言活动的重要环境,为了与家长配合做好幼儿阅读训练工作,孩子一入园就召开家长会,给家长提出早期抓好幼儿阅读的要求。我把幼儿在园里的阅读活动及阅读情况及时传递给家长,要求孩子回家向家长朗诵儿歌,表演故事。我和家长共同配合,一道训练,幼儿的阅读能力提高很快。
七年级数学上册 “希望工程”义演教案 北师大版

“希望工程”义演教学设计教学设计思想本节课以“希望工程”义演为例引入课题,通过学生自主探索、协作交流,教师点拨相结合的方式,引导学生借助列表的方法分析问题,体会用图表语言分析复杂问题表达思维方法的优点,从而抓住等量关系“部分量之和等于总量”展开教学活动。
对“想一想”由学生独立完成,并通过这个问题,使学生进一步明确必须检验方程的解是否符合实际。
教学目标知识与技能1.用列表格分析实际问题中的等量关系.2.用不同的设未知数的方法列方程.过程与方法情感态度价值观(二)能力训练要求1.借助表格分析复杂问题中的数量关系,从而建立方程解决实际问题,发展分析问题、解决问题的能力,进一步体会方程模型的作用.2.体会不同的设未知数的方法,通过比较,选择最优.(三)情感与价值观要求1.通过体会方程模型的实际价值,提高学习数学的兴趣.2.提高遇到较复杂数学问题的良好心理素质以及面对复杂问题时克服困难的勇气.教学重点1.借助表格分析复杂问题的数量关系.2.选择比较恰当的设未知数的方法.教学难点面对若干个等量关系,如何恰当地应用它们设出未知数并列出方程.教学方法引导—自主探索相结合方法.学生在教师的引导下,找出若干个较直接的等量关系,然后用不同的设未知数的方法让学生通过列表格自主探索根据等量关系,列出方程,从中体会设未知数方法的不同,方程的复杂程度也不同.教具准备投影片一张:(记作§)“希望工程”义演.教学过程Ⅰ创设情境,引入新课[师]上一节课,我们讨论过了用一元一次方程解决实际问题的一般步骤谁来给大家简单的陈述一下.[生]当用一元一次方程解决实际问题时,首先要从实际问题中抽象出数学问题;然后分析数学问题中的等量关系,并由此列出方程;求出所列方程的解;检验解的合理性,合理就用以解决实际问题,不合理需重新开始讨论.[师]应用一元一次方程解决实际问题的关键步骤是什么[生]根据题意,首先寻找“等量关系”同时,解出方程后应注意检验求出的值是不是方程的解,是否符合实际.[师]接下来,我们就用一元一次方程解决生活中一个献爱心的问题——“希望工程”义演.Ⅱ讲授新课[师]在我们的生活中,还有不少贫困地区的孩子因为贫穷而上不起学,也有不少有爱心的好人为了他们而献出自己的一片“爱心”下面我们就来看投影:“希望工程”义演.出示投影片(§)分析:售出的票包括成人票和学生票,所得票款包括成人票款和学生票款由第(1)问和第(2)问可知:票款=票数×价格/张因此上述问题存在两个等量关系.成人票数学生票数=总票数,①成人票款学生票款=总票款②解:(1)填写下表:由上表可知共得票款:600×5300×8=30002400=5400(元).(2)填写下表:由上表可知共卖出学生和成人票为:2500÷56400÷8=500800=1300(张).(3)解法一:设售出的学生票为张,填写下表:根据等量关系②,可列出方程:58(1000-)=6950解,得=350.1000-350=650(张)答:售出的成人票650张,学生票350张.解法二:设所得学生票款元,填写下表根据等量关系①可得869505y y =1000解,得=17501750÷5=3501000-350=650答:售出的学生票数为350张,成人票650张.讨论:从上述(3)的两种设未知数方法,同时根据自己的亲身体验,相互交流各自的意见.[生]我认为第二种方法比第一种方法复杂.[师]在以前,我们列方程时,通常找一个等量关系即可列出方程,为什么在这个题中寻找到了两个等量关系,它们各有何用途.[生]我们在填表的时候就可以看出:如果设售出的学生票数为张,根据等量关系①就可设成人票数为(1000-)张这时,等量关系②元,则根据等量关系②就可设成人票款为(6950-)元,此时,等量关系①就用来列方程.[生]我认为这个问题中有两个未知量:售出的学生票和成人票,可我们现在只设一个未知数,而另一个未知数就需要题意中的等量关系用含有第一个未知数的代数式来表示.[师]同学们的分析很好现在我们遇到的这个问题比前面的问题要复杂,含有两个未知量,而只设一个未知数表示一个量,另一个量就需用题中的等量关系,用含有第一个未知数的代数式来表示,而另一个等量关系则用来列方程.[师]在这个较为复杂的实际问题中,为了搞清楚各个量之间的关系,我们采用了一个非常清楚明了的方法——列表格希望同学们慢慢地学着用它来分析较复杂的问题.想一想:如果票价不变,那么售出1000张票所得的票款可能是6930元吗我们也列表来完成(由两个学生板演)解:可设售出的学生票为元,填写下表:根据题意,可得方程:58(1000-)=6930解,得=35632显然,=35632是不符合题意的因此如果票价不变,售出1000张票所得票款不可能是6930元.[师]因此,我们用方程这样的数学模型解决实际问题时,一定要注意检验方程的解是否符合实际.Ⅲ课堂练习、1课本P171解:单价为18元的本买了本,单价为10元的本买了(10-)本,列表如下:根据题意,得1810(10-)=172解,得=9.10-9=1答:单价为18元、10元的本各买9本、1本.Ⅳ课时小结这节课我们通过列表的方式分析实际问题中的等量关系,使题中的已知条件与未知条件的关系清晰明了同时我们还尝试着用多种方法去解决问题.Ⅴ课后作业1.课本P习题1712.到网上收集有关方程史的资料.Ⅵ活动与探究小张在商店中买了14瓶汽水,又知每3个空汽水瓶可换1瓶汽水,问小张最多能够喝到多少瓶汽水过程:乍看题目觉得甚为简单,有同学就认为是18瓶汽水,原因是14瓶水喝完后可换4瓶,故可喝18瓶那么4瓶喝完后呢应该是4瓶喝完后,总共还有6个空瓶可换2瓶汽水,总共可喝20瓶其实这还不是最多,最后2个空瓶虽不能换一瓶汽水,但我可以用“先借后还”的方法多喝一瓶汽水,即先借商店一瓶汽水喝完,还三个瓶,换一瓶汽水,再将那一瓶汽水还掉.结果:通过分析,我们会发现最后的14个空瓶,通过先借后还,实际总共可换七瓶汽水即平均2个空瓶换1瓶汽水.板书设计三、课时小结:(由学生先来完成)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
下列对滤过除菌法的说法错误的是A.只能滤除活的微生物B.适用于不耐热的低黏度药物溶液C.采用孔径为0.2μm的微孔薄膜可有效地阻挡微生物及芽孢的通过D.本法需要在无菌条件下进行E.在滤除细菌的同时可以除去一些微粒杂质 应用顺序标号,来保证系统每笔日记账都是唯一的,并且系统不会接受相同编号,能达到的信息处理目标是。A.完整性B.准确性C.授权D.访问限制 怎样理解党在过渡时期总路线? 病毒感染细胞的主要形态为()A.核增大,大小不等B.核染色质粗糙且深染C.核仁增大,数目增多D.核畸形E.核内可见嗜酸性包涵体 TEE用于心功能监测时哪项不正确()A.可同时测定CO、EF和EDV等参数B.有二尖瓣返流时,CO测定值比实际CO值小C.不规则心律可致时间、流速积分发生变化D.只要二尖瓣口舒张期保持恒定,及瓣口必须呈环形才能测定COE.可代替漂浮导管,耗费较漂浮导管低 牙拔除后,牙槽窝内的血凝块有、和的功能。 不能鉴别Broca失语、完全性失语、混合性失语的要点是()A.听理解的水平B.口语表达C.言语的流利度D.阅读能力E.书写能力 矿业工程进度控制必须要优选施工方案,下列优选施工方案的具体措施不正确的是。A.根据实际情况,综合分析、全面衡量,缩短井巷工程关键线路的工程量B.在制定各单位工程施工技术方案时,必须充分考虑自然条件C.井巷工程关键路线贯通掘进,以主、副井方向开拓为主,风井为辅D.采用的 下面哪种情况不适合机械通气治疗A.吉兰-巴雷综合征B.ARDSC.未行闭式引流的气胸D.多发肋骨骨折致连枷胸E.脑干出血 “身之本”是指A.心B.气C.脾D.肾E.精 Berg平衡量表评定无支持闭目站立评分为1提示A.能够安全地站10sB.监护下能够安全地站10sC.能站3sD.闭眼不能达3s,但站立稳定E.为了不摔倒而需要2个人的帮助 “慎独”出自于哪本著作A.《大医精诚》B.《礼记》C.《物理论》D.《黄帝内经》E.《本草纲目》 “棕色瘤”见于A.骨囊肿B.动脉瘤样骨囊肿C.甲状旁腺功能亢进D.血友病性关节炎E.痛风性关节炎 根据《海关对保税仓库及所存货物的管理办法》规定,保税仓库允许存放的货物有.A.转口货物B.供维修外国产品所进口寄售的零配件C.未办结海关手续的一般贸易货物D.针对外贸企业使用的进口货物 人禽流感患者发病初期尚未产生抗体,用于确诊的方法是A、微量中和试验B、蛋白免疫印迹C、病毒核酸检测D、胶体金免疫层析分析E、血凝抑制试验 运输投资的实质是()A.改变投资结构B.转变增长方式C.追加生产要素,形成直接或间接的运输生产能力D.提高运输业投资在国民经济总投资中的比例,逐步解决其比例偏低问题E.建立符合我国国情、适应社会经济发展需要的,技术先进、结构合理、效率高的全国综合运输体系 刑法第78条规定应当予以减刑的条件是A、一般立功B、自首C、重大立功D、坦白 感染人的禽流感病毒亚型主要为A.H5Nl、H9N2和H7N7B.H5Nl、H9N2和H3N8C.H2N8、H9N2和H7N7D.H5Nl、HIN1和H2N2E.H5Nl、H2N2和H7N7 功效有某种共性的药物配合应用,辅药能增强主药的疗效。这种配伍关系是。A.相反B.相恶C.相杀D.相畏E.相使 进度计划执行中,判断某项工程进度偏差对后续工作、总工期的影响程度,不属于重点分析的是。A.此项工作是否位于关键线路上B.此项工作的进度偏差与质量的关系C.此项工作的进度偏差是否大于总时差D.此项工作的进度偏差是否大于自由时差 公民的生育权包含哪几个方面的内容 某煤矿所穿过的岩层比较复杂,设计石门支护结构主要采用锚杆和喷射素混凝土支护;对于巷道支护,喷射素混凝土的设计强度等级不应低于。A.Cl0B.C15C20D.C25 按照《中国药典》2010年版要求,施于眼部的散剂粒度应为A.粗粉B.中粉C.细粉D.最细粉E.极细粉 棘轮齿数的选择与有关。A、倾斜角B、转速C、齿形角D、转角 下面不属于SI基本单位的是。A.米;B.安培;C.摩(尔);D.欧(姆)。 下列哪一项不是理财规划建议书的前言应该包括的。A.致谢B.理财规划建议书的由来C.姓名D.客户义务 通信网按其所能实现的业务种类来分有。A、电话通信网B、数据通信网C、广播电视网D、传输网 路面各结构层的持续时间的考虑因素有。A.水泥稳定碎石的延迟时间B.沥青材料的拌合能力C.沥青混合料的温度要求D.无机稳定类材料的养护时间E.最大工作面的要求 关于散剂叙述不正确的是A.散剂应为干燥、疏松的粉末B.液体药物不能制成散剂C.眼用散应为极细粉,并要求无菌D.单味化学毒剧药应制成倍散E.儿科及外用散应为最细粉 飞机降落前,提前分钟吊车放回支架或摆到内安全区域待命。A.5B.10C.15D.20 GB8978-1996《污水综合排放标准》规定,废水的PH值为。A、5-8;B、6-9;C、4-9。 房屋租赁行为合法有效的凭证是。A.房屋所有权证B.验收合格证C.登记备案证D.房屋租赁证 中胚叶造血期首先形成血岛的是以下哪个组织A.骨髓B.胸腺C.卵黄囊D.肝E.脾 20世纪中后期,由于微生物学的、等技术的渗透和应用的拓宽及发展,动、植物细胞也可以像微生物一样在平板或三角瓶中分离、培养和在发酵罐中进行生产。 注册建造师签章文件按照管理程序可分类为。A.报审类B.核准类C.内部管理类D.报告备案类E.对外履行责任类
