常用气体的基本物理化学参数
SF6气体

当SF6气体中含有水分时会对电气设备造成 以下危害: (1)在水分存在下,SF6分解产物发生水解反 应,阻碍了SF6分解产物的复合,降低了SF6的介质 恢复强度,从而降低设备的绝缘特性; (2)加剧了低氟化物水解和金属氟化物的分 解。生成的氟化亚硫酸剧毒,对人体有很大的危害, HF还会腐蚀电极和绝缘材料; (3)在设备内结露。由于气体中的水分以水 蒸气的形式存在,当温度降低时,可能在设备内部 结露,附着在设备表面如电极、绝缘子表面等,容 易产生沿面放电(闪络)而引起事故。
SF6电器设备现场水分检测时注意事项: 选合适的管材:测量管路材质应采用不锈钢、厚壁 聚四氟乙烯管,不得使用乳胶管和橡胶管。 管路尽量短、接头少、密封严格; 正确使用各类仪器; 认真准确记录; 尽量在20℃,101325Pa下测定,环境湿度不可 太大; 使用的仪器必须在检定期内。
SF6电器设备现场水分检测测试误差产生 的原因及控制方法
温度的影响
由于露点仪是通过冷却镜面使水蒸气凝露来测量气体湿度的,环境温度 的高低必然影响到制冷的效果。对于大多数测量下限为-60℃的露点仪,如 DP9、DP19,在炎热的夏季环境温度很高时测量湿度较低的气体,有可能出 现仪器的制冷量达不到要求的情况,即镜面温度已无法再下降,但却始终没 有结露。这种情况下,根据理论分析和DP系列说明书的推荐,可采用提高测 量室内的气体压力,从而升高露点,最后再进行换算的方法。但实践证明, 该法并不总是可行,大多数情况下仪器示值反复振荡,不能得到稳定值。其 原因可能是因为升高压力后,SF6气体液化温度随之上升,测量过程中SF6气 体在镜面上液化从而干扰测定。 在露点仪受高温影响无法正常工作的情况下,目前最好的办法是避开高温天 气,如趁早晚较凉爽时进行测试,或换用其它类型的测试仪器。
标准气体常数

标准气体常数标准气体常数是描述气体物理性质的一个重要物理常数,通常用符号R表示。
在理想气体状态方程中,标准气体常数R是一个关键参数,它与气体的摩尔质量和摩尔体积有关。
本文将对标准气体常数的定义、计算方法以及在物理学和化学中的应用进行详细介绍。
1. 标准气体常数的定义。
标准气体常数R是指在标准状态下,1摩尔理想气体的压强与体积之比,通常用J/(mol·K)或cal/(mol·K)作为单位。
在国际单位制中,标准气体常数的数值约为8.314 J/(mol·K)。
在化学反应中,标准气体常数R可以用来计算气体的压强、体积和温度之间的关系,是气体物理性质研究的重要基础参数。
2. 标准气体常数的计算方法。
标准气体常数R的数值可以通过测定气体的压强、体积和温度,并应用理想气体状态方程进行计算。
理想气体状态方程可以表示为PV=nRT,其中P为气体的压强,V为气体的体积,n为气体的摩尔数,T为气体的温度,R为标准气体常数。
通过测定实验数据,可以利用理想气体状态方程计算得到标准气体常数R的数值。
3. 标准气体常数的应用。
标准气体常数R在物理学和化学中有着广泛的应用。
在热力学和动力学的研究中,标准气体常数R可以用来描述气体的热力学性质,如内能、焓、熵等。
在化学反应动力学中,标准气体常数R可以用来计算气体反应速率常数,从而推导出反应速率方程。
此外,在工程领域中,标准气体常数R也被广泛应用于气体的工艺设计和控制中。
4. 结语。
标准气体常数是描述气体物理性质的重要物理常数,它在理想气体状态方程中起着关键作用。
本文对标准气体常数的定义、计算方法以及在物理学和化学中的应用进行了简要介绍,希望能够对读者有所帮助。
在今后的学习和工作中,我们应该深入理解标准气体常数的概念和意义,进一步探索其在科学研究和工程实践中的应用价值。
烟气空气参数
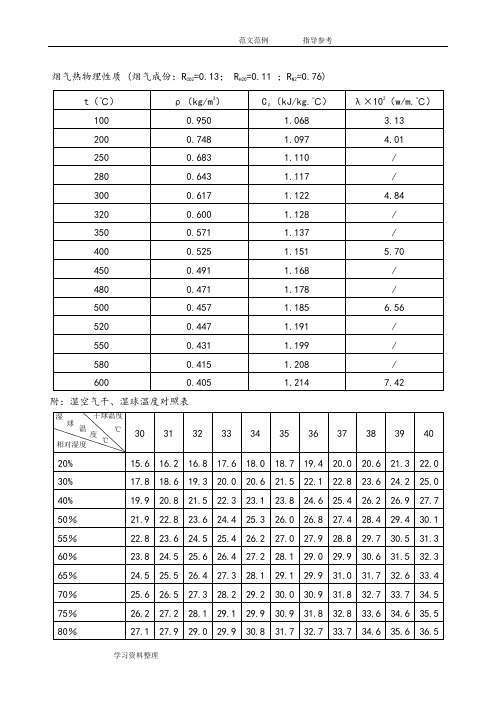
烟气热物理性质 (烟气成份:RCO2=0.13; RH2O=0.11 ;RN2=0.76)附:湿空气干、湿球温度对照表水的汽化热为40.8千焦/摩尔,相当于2260千焦/千克天然气是一种无毒无色无味的气体,其主要成份是甲烷,天然气的低热值为34.91MJ/Nm3。
天然气(甲烷)的密度在0℃,101.352Kpa时为0.7174Kg/Nm3,相对密度(设空气的密度为1)为0.5548,天然气约比空气轻一半,完全燃烧时,需要大量的空气助燃。
1立方米天然气完全燃烧大约需要9.52立方米空气。
如果燃烧不完全,会产生有毒气体一氧化碳,因而在燃气器具使用场所,必须保持空气流通。
在封闭空间内,天然气与空气混合后易燃、易爆、当空气中的天然气浓度达到5-15%时,遇到明火就会爆炸,因而一定要防止泄漏。
天然气的密度定义为单位体积气体的质量。
在标准状况(101325Pa,15.55℃)下,天然气中主要烃类成分的密度为0.6773Kg/m3(甲烷)-3.0454Kg/m3(戊烷)。
天然气混合物的密度一般为0.7-0.75Kg/m3,其中石油伴生气特别是油溶气的密度最高可达1.5Kg/m3甚至更大些。
天然气的密度随重烃含量尤其是高碳数的重烃气含量增加而增大,亦随CO2和H2S的含量增加而增大。
天然气的相对密度是指在相同温度、压力条件下天然气密度与空气密度的比值,或者说在相同温度、压力下同体积天然气与空气质量之比。
天然气烃类主要成分的相对密度为0.5539(甲烷)-2.4911(戊烷),天然气混合物一般在0.56-1.0之间,亦随重烃及CO2和H2S的含量增加而增大。
在标准状况下,天然气的比重与密度、相对比重与相对密度在数值上完全相同。
天然气中常见组分的密度和相对密度值如表所示。
天然气在地下的密度随温度的增加而减小,随压力的增加而加大。
但鉴于天然气的压缩性极强,在气藏中,天然气的体积可缩小到地表体积的1/200-1/300,压力效应远大于温度效应,因此地下天然气的密度远大于地表温压下的密度,一般可达150-250Kg/m3;凝析气的密度最大可达225-450Kg/m3。
LNG的物理化学特性

LNG的物理化学特性LLNG 的基本性质的基本性质1.LNG的物理性质主要成分:甲烷,临界温度:190.58K在常温下,不能通过加压将其液化,而是经过预处理,脱除重烃、硫化物、二氧化碳和水等杂质后,深冷到-162 O C,实现液化。
主要物理性质如表1-1所示:无色透明41.5~45.3 430~460 约-162°C 0.60~0.70 颜色高热值(MJ/m 3 )液体密度(g/l)(沸点下)沸点/°C (常压)气体相对密度表1-1 4 4 . LNG . LNG 的基本性质的基本性质2. 典型的LNG组成(摩尔分数)/% N 2 CH 4 C 2 H 6 C 3 H 8 I-C 4 H 10 N-C 4 H 10 C 5 H 12 摩尔质量/(kg/mol)泡点温度/ o C 密度/(kg/m 3 )LNG 的基本性质的基本性质3. LNG的性质特点温度低在大气压力下,LNG沸点都在-162°C左右。
液态与气态密度比大1体积液化天然气的密度大约是1体积气态天然气的600倍,即1体积LNG大致转化为600体积的气体。
可燃性一般环境条件下,天然气和空气混合的云团中,天然气含量在5%~15%(体积)范围内可以引起着火,其最低可燃下限(LEL)为4%LNG 的基本性质4. LNG的安全特性1)燃烧特性燃烧范围:5%~15%,即体积分数低于5%和高于15%都不会燃烧;自燃温度:可燃气体与空气混合物,在没有火源的情况下,达到某一温度后,能够自动点燃着火的最低温度称为自燃温度。
甲烷性质比较稳定,在大气压力条件下,纯甲烷的平均自燃温度为650°C。
以甲烷为主要成分的天然气自燃温度较高,LNG的自燃温度随着组份的变化而变化。
燃烧速度:是火焰在空气-燃气的混合物中的传递速度。
天然气的燃烧速度较低,其最高燃烧速度只有0.3m/s。
LNG 的基本性质的基本性质低温特性隔热保冷:LNG系统的保冷隔热材料应满足导热系数低,密度低,吸湿率和吸水率小,抗冻性强,并在低温下不开裂,耐火性好,无气味,不易霉烂,对人体无害,机械强度高,经久耐用,价格低廉,方便施工等。
物理化学第一章气体

17
18
第一章 气体的pVT关系
1.了解理想气体的微观模型,能熟练使用理 想气体的状态方程 2.理解气体的液化和临界参数 3.了解真实气体的状态方程及对应状态原理 与压缩因子图 重点: 理想气体的状态方程、微观模型、 临界参数。 难点:对应状态原理与压缩因子图。
1
问题:1.理想气体的状态方程式主要有哪些 应用? 2.何为理想气体混合物?在理想气体混合物中 某组分的分压是如何定义的?其物理意义如何,如 何计算? 3.何为纯液体的饱和蒸气压?它与哪些因素
有关?
2
3
1.分子之间无相互作用力 2.分子本身不占有体积
状态方程 理想气体 分压及分体积定律 气体 液化及临界现象 实际气体 对应状态原理及压缩因子图 状态方程
如何变成理 想气体?
4
1.1 理想气体的状态方程
pV nRT
导出公式:
M mRT / pV
pM / RT
例:六氟化铀UF6是密度很大的一种气体,求在
适合条件:理想气体或低压下的真实气体
6
1.分子之间无相互作用力 2.分子本身不占有体积
状态方程 理想气体 分压及分体积定律 气体
液化及临界现象
实际气体 状态方程 对应状态原理及压缩因子图
7
1.3 气体的液化及临界参数
饱和蒸气压:指定温度下,密闭系统中某物质处 于气液平衡共存时其蒸气的压力。
临界参数:
9
b.求真实气体的压缩因子Z
真实气体的pVT关系: 对比参数: 对比压力: pr =p/pc
pVm ZRT
对比温度: Tr =T/Tc
对比体积: Vr =Vm/ Vm,c
第一章 气体pTV的关系 物理化学资料

现
nA=1
kmol,故得:
nB
pB pA
nA
3.167 101 .198
1000
31.30mol
(2) 设所求初始体积为V
V nRT nART nBRT 24.65m3
p pA pB
15
4. 阿马加定律
•数学表达式: V VB*
B
证: V nRT / p ( nB )RT / p
He CH4
2500
2000
15 100000 2 4 60 80 1001
3000K下N0 2,He,CH4的pVm2 –p等温2线5
N2
H2 问题:
CH4
CO2
N2、H2、 CH4、CO2何者
1.000
TB最高、最低?
p/MPa
26
2. 范德华方程
Van der Waals J D,1837—1923 27
( p a Vm2 )(Vm b) RT
范德华方程
29
内压:
压力修正项a Vm2
p内
1
Vm2
1 r6
pi.g. p a Vm2
p内 a Vm2
分子间引力愈大,a 愈大,愈易液化
• 体积修正项
30
例.试写出实际气体的范德华方程
。
2020/7/5
31
(2)范德华常数与临界参数的关系
p V TC 0, 2 p V 2 TC 0
水蒸气H2O(g),在平衡条件下,缓慢的压缩到压力
p=(
)kPa时,才可能有水滴H2O(l)出现。
2020/7/5
24
第四节 真实气体状态方程
1.真实气体的pVm – p图及波义尔温度
物理化学01气体

,
§1-1 理想气体的状态方程
气体理论的三位奠基者:
• 玻义尔 (1627 — 1691) Born in Ireland
00-7-22
•盖· 吕萨克 (1778 — 1850) Frenchman
• 阿伏加德罗 (1776 —1856) an Italian
3
1. 理想气体状态方程
波义尔定律 pV = 常数 (n, T 恒定)
pV (实际) nRT
Z def pV pVm (实) Vm (实) nRT RT Vm (理)
压缩因子Z:
Z 的大小描述了实际气体的关系偏离理想行为的情况:
Z 1, 理想气体; Z 1, Vm (实) Vm (理), 易压缩实际气体;
00-7-22
Z 1, Vm (实) Vm (理), 难压缩实际气体.
13
0.0323 y( Ar) 0.0094 3.452 2.694 y( N 2 ) 0.7804 3.452
00-7-22
(2)各组分气体的分压为
p( N 2 ) y( N 2 ) p 0.7804101.3 79.05kPa
p(O2 ) y(O2 ) p 0.2099101.3 21.26kPa
VB / V nB / n yB
而对非理想气体, 此二式不能成立. 应注意分压力和分体积的定义上的不同.
00-7-22 12
例:若有一空气样品,组成(质量%)如下:N275.47%,O223.19%, Ar1.29%,CO20.05%。(1)试用体积分数表示此空气的组成;(2) 计算25℃及101.325kPa下,此空气各组分气体的分压。设空气可看成理 想气体的混合物。 解:(1)体积分数即各气体的摩尔分数。设有100g空气,则
理想气体(物理化学)

将这三个定律相结合,经过一定的数据处理 参看第三版 参看第三版), 将这三个定律相结合,经过一定的数据处理(参看第三版 ,可 得到理想气体状态方程: 得到理想气体状态方程 pV=nRT 或 pVm=RT 或
m pV = RT M
(R为摩尔气体常数 为摩尔气体常数) 为摩尔气体常数 为气体的摩尔体积) (Vm为气体的摩尔体积) 为气体的相对摩尔质量) (M为气体的相对摩尔质量) 为气体的相对摩尔质量
即混合气的平均摩尔质量是其中所有各组分的摩尔分数与 其摩尔质量乘积之和。
2. 道尔顿定律与分压力 道尔顿定律与分压力(part pressure) 气体的压力是分子对容器器壁碰撞的结果,混合气的压力是 构成该混合气的各组分对压力所作贡献之和, 因此在热力学计 算中,人们提出了一个分压力的概念: 分压力pB:混合气中任一组分对压力所作贡献。 p = ∑ pB 混合气总压力 B 且有 pB = y B p 或 y B =
物理量 ,如上图及下表 如上图及下表: 如上图及下表 单位
p/MPa
…………
………… pVm/J . mol-1 ↑ ↑ 表头中物理量的表示: 物理量 表中均为纯数
单位
低压气体可近似视作为理想气体。 ⑶ 低压气体可近似视作为理想气体。 即低压气体可近似使用理想气体状态方程计算p、T、V 关系。
理想气体的微观模型( ) 二 理想气体的微观模型(p9)
按照分子运动论,理想气体微观模型应该是: 1. 分子间无作用力; 分子间无作用力; 2. 分子本身没有体积 3. 分子不停顿地作无规则的热运动 分子不停顿地作无规则的热运动。 低压气体,气体密度小,分子间距离大,分子间作用 力及分子本身的体积均可忽略,故可当作理想气体处 理。
低压混合气(理想气体混合物) 三 低压混合气(理想气体混合物)(ideal gas mixture)(p11) ( ) 在工业生产中所遇到的气体在很多情况下为混合气体,实 验表明,低压混合气也服从理想气体状态方程,即低压混合气 可视为理想混合气处理
