高中数学必修三模块综合测试卷
高中数学必修3综合测试及答案

必修3综合测试用最小二乘法求线性回归方程系数公式:一、选择题:本题共有10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1、程序框图符号可用于( )A、输出a=10 B 、赋值a=10 C 、判断a=10 D 、输入a=102、将两个数a=8,b=17交换,使a=17,b=8,下面语句正确一组是 ( )3、右边程序输出的结果是 ( ) A .5 B . x +5 C .10 D .14、在下列各数中,最大的数是( ) A 、)9(85 B 、)6(210 C 、)4(1000 D 、)2(111115、为了在运行下面的程序之后得到输出16,键盘输入x 应该是( ) INPUT xIF x<0 THEN y=(x+1)*(x+1) ELSEy=(x-1)*(x-1) END IF PRINT y ENDA 、 3或-3B 、 -5C 、5或-3D 、 5或-56.工人月工资y (元)与劳动生产率x (千元)变化的回归方程x y 8050^+=,x =5 y =1 x =x +5 y =x PRINT y END下列判断正确的是 ( )①劳动生产率为1千元时,工资为130元 ②劳动生产率提高1千元时,月工资提高80元 ③劳动生产率提高1千元时,月工资提高130元 ④当月工资为210元时,劳动生产率2千元A .① ②B .① ② ④C .② ④D .① ② ③ ④7、200辆汽车经过某一雷达地区,时速频率分布直方图如右图所示,则时速超过70km/h 的汽车数量为( ) A 、2辆 B 、10辆 C 、20辆 D 、70辆8、如果数据n x x x ,,,21 的平均数是 x , 方差是2S ,则32,,32,3221+++n x x x 的平均数和 方差分别是 ( )A.x 与2SB.2 x +3 和2SC. 2 x +3 和 42SD. 2x +3 和 42S +12S +99、某公司在甲、乙、丙、丁四个地区分别有150个、120个、180个、150个销售点,公司为了调查产品销售的情况,需从这600个销售点中抽取一个容量为100的样本,记这项调查为(1);在丙地区中有20个特大型销售点,要从中抽取7个调查其销售收入和售后服务情况,记这项调查为(2)。
高中数学必修3综合测试题
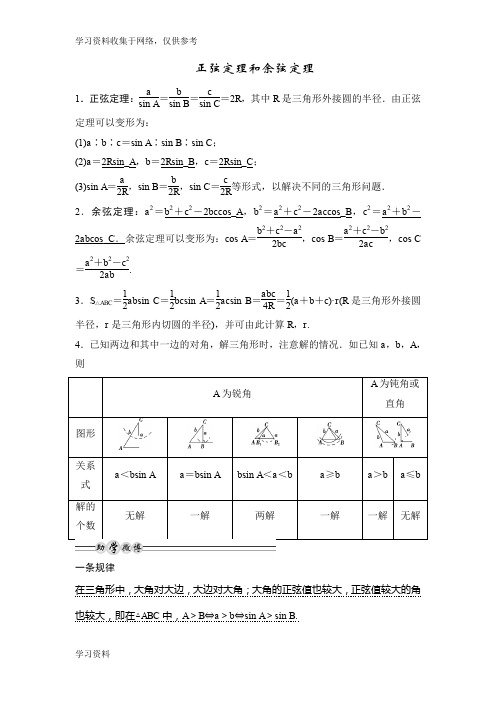
正弦定理和余弦定理1.正弦定理:a sin A =b sin B =csin C =2R ,其中R 是三角形外接圆的半径.由正弦定理可以变形为:(1)a ∶b ∶c =sin A ∶sin B ∶sin C ;(2)a =2R sin_A ,b =2R sin_B ,c =2R sin_C ;(3)sin A =a 2R ,sin B =b 2R ,sin C =c2R 等形式,以解决不同的三角形问题. 2.余弦定理:a 2=b 2+c 2-2bc cos_A ,b 2=a 2+c 2-2ac cos_B ,c 2=a 2+b 2-2ab cos_C .余弦定理可以变形为:cos A =b 2+c 2-a 22bc ,cos B =a 2+c 2-b 22ac ,cos C =a 2+b 2-c 22ab .3.S △ABC =12ab sin C =12bc sin A =12ac sin B =abc 4R =12(a +b +c )·r (R 是三角形外接圆半径,r 是三角形内切圆的半径),并可由此计算R ,r .4.已知两边和其中一边的对角,解三角形时,注意解的情况.如已知a ,b ,A ,则一条规律在三角形中,大角对大边,大边对大角;大角的正弦值也较大,正弦值较大的角也较大,即在△ABC 中,A >B ⇔a >b ⇔sin A >sin B .两类问题在解三角形时,正弦定理可解决两类问题:(1)已知两角及任一边,求其它边或角;(2)已知两边及一边的对角,求其它边或角.情况(2)中结果可能有一解、两解、无解,应注意区分.余弦定理可解决两类问题:(1)已知两边及夹角求第三边和其他两角;(2)已知三边,求各角. 两种途径根据所给条件确定三角形的形状,主要有两种途径:(1)化边为角;(2)化角为边,并常用正弦(余弦)定理实施边、角转换.双基自测1.在△ABC 中,A =60°,B =75°,a =10,则c 等于( ). A .5 2 B .10 2 C.1063D .5 6解析 由A +B +C =180°,知C =45°, 由正弦定理得:a sin A =csin C , 即1032=c 22.∴c =1063.答案 C 2.在△ABC 中,若sin A a =cos Bb ,则B 的值为( ). A .30° B .45° C .60° D .90° 解析 由正弦定理知:sin A sin A =cos Bsin B ,∴sin B =cos B ,∴B =45°.答案 B3.在△ABC 中,a =3,b =1,c =2,则A 等于( ). A .30° B .45° C .60° D .75° 解析 由余弦定理得:cos A =b 2+c 2-a 22bc =1+4-32×1×2=12,∵0<A <π,∴A =60°.答案 C4.在△ABC 中,a =32,b =23,cos C =13,则△ABC 的面积为( ). A .3 3 B .2 3 C .4 3 D. 3 解析 ∵cos C =13,0<C <π,∴sin C =223, ∴S △ABC =12ab sin C =12×32×23×223=4 3. 答案 C5.已知△ABC 三边满足a 2+b 2=c 2-3ab ,则此三角形的最大内角为________. 解析 ∵a 2+b 2-c 2=-3ab , ∴cos C =a 2+b 2-c 22ab =-32,故C =150°为三角形的最大内角.答案 150°考向一 利用正弦定理解三角形【例1】►在△ABC 中,a =3,b =2,B =45°.求角A ,C 和边c . 解 由正弦定理得a sin A =b sin B ,3sin A =2sin 45°, ∴sin A =32.∵a >b ,∴A =60°或A =120°.当A =60°时,C =180°-45°-60°=75°, c =b sin Csin B =6+22;当A =120°时,C =180°-45°-120°=15°, c =b sin Csin B =6-22.(1)已知两角一边可求第三角,解这样的三角形只需直接用正弦定理代入求解即可.(2)已知两边和一边对角,解三角形时,利用正弦定理求另一边的对角时要注意讨论该角,这是解题的难点,应引起注意.【训练1】 在△ABC 中,若b =5,∠B =π4,tan A =2,则sin A =______a =________. 解析 因为△ABC 中,tan A =2,所以A 是锐角, 且sin Acos A =2,sin 2A +cos 2A =1,联立解得sin A =255,再由正弦定理得a sin A =bsin B , 代入数据解得a =210.答案255 210考向二 利用余弦定理解三角形【例2】►在△ABC 中,a 、b 、c 分别是角A 、B 、C 的对边,且cos B cos C =-b2a +c .(1)求角B 的大小;(2)若b =13,a +c =4,求△ABC 的面积.[审题视点] 由cos B cos C =-b2a +c ,利用余弦定理转化为边的关系求解.解 (1)由余弦定理知:cos B =a 2+c 2-b 22ac , cos C =a 2+b 2-c 22ab .将上式代入cos B cos C =-b2a +c 得:a 2+c 2-b 22ac ·2ab a 2+b 2-c 2=-b2a +c , 整理得:a 2+c 2-b 2=-ac .∴cos B =a 2+c 2-b 22ac =-ac 2ac =-12.∵B 为三角形的内角,∴B =23π. (2)将b =13,a +c =4,B =23π代入b 2=a 2+c 2-2ac cos B , 得b 2=(a +c )2-2ac -2ac cos B ,∴13=16-2ac ⎝ ⎛⎭⎪⎫1-12,∴ac =3.∴S △ABC =12ac sin B =334.【训练2】 已知A ,B ,C 为△ABC 的三个内角,其所对的边分别为a ,b ,c ,且2cos 2 A2+cos A =0. (1)求角A 的值;(2)若a =23,b +c =4,求△ABC 的面积. 解 (1)由2cos 2 A2+cos A =0, 得1+cos A +cos A =0,即cos A =-12,∵0<A <π,∴A =2π3. (2)由余弦定理得,a 2=b 2+c 2-2bc cos A ,A =2π3, 则a 2=(b +c )2-bc , 又a =23,b +c =4, 有12=42-bc ,则bc =4, 故△ABC =12bc sin A = 3.考向三 利用正、余弦定理判断三角形形状【例3】►在△ABC 中,若(a 2+b 2)sin(A -B )=(a 2-b 2)sin C ,试判断△ABC 的形状.[审题视点] 首先边化角或角化边,再整理化简即可判断. 解 由已知(a 2+b 2)sin(A -B )=(a 2-b 2)sin C , 得b 2[sin(A -B )+sin C ]=a 2[sin C -sin(A -B )], 即b 2sin A cos B =a 2cos A sin B ,即sin 2B sin A cos B =sin 2A cos B sin B ,所以sin 2B =sin 2A , 由于A ,B 是三角形的内角. 故0<2A <2π,0<2B <2π. 故只可能2A =2B 或2A =π-2B ,即A =B 或A +B =π2.故△ABC 为等腰三角形或直角三角形.判断三角形的形状的基本思想是;利用正、余弦定理进行边角的统一.即将条件化为只含角的三角函数关系式,然后利用三角恒等变换得出内角之间的关系式;或将条件化为只含有边的关系式,然后利用常见的化简变形得出三边的关系.【训练3】 在△ABC 中,若a cos A =b cos B =ccos C ;则△ABC 是( ). A .直角三角形 B .等边三角形 C .钝角三角形D .等腰直角三角形解析 由正弦定理得a =2R sin A ,b =2R sin B ,c =2R sin C (R 为△ABC 外接圆半径). ∴sin A cos A =sin B cos B =sin C cos C .即tan A =tan B =tan C ,∴A =B =C . 答案 B考向三 正、余弦定理的综合应用【例3】►在△ABC 中,内角A ,B ,C 对边的边长分别是a ,b ,c ,已知c =2,C =π3.(1)若△ABC 的面积等于3,求a ,b ;(2)若sin C +sin(B -A )=2sin 2A ,求△ABC 的面积. 解 (1)由余弦定理及已知条件,得a 2+b 2-ab =4.又因为△ABC 的面积等于3,所以12ab sin C =3,得ab =4,联立方程组⎩⎨⎧ a 2+b 2-ab =4,ab =4,解得⎩⎨⎧a =2,b =2.(2)由题意,得sin(B +A )+sin(B -A )=4sin A cos A , 即sin B cos A =2sin A cos A .当cos A =0,即A =π2时,B =π6, a =433,b =233;当cos A ≠0时,得sin B =2sin A , 由正弦定理,得b =2a .联立方程组⎩⎨⎧a 2+b 2-ab =4,b =2a ,解得⎩⎪⎨⎪⎧a =233,b =433.所以△ABC 的面积S =12a b sin C =233.【训练3】 (2011·北京西城一模)设△ABC 的内角A ,B ,C 所对的边长分别为a ,b ,c ,且cos B =45,b =2. (1)当A =30°时,求a 的值;(2)当△ABC 的面积为3时,求a +c 的值. 解 (1)因为cos B =45,所以sin B =35. 由正弦定理a sin A =b sin B ,可得a sin 30°=103, 所以a =53.(2)因为△ABC 的面积S =12ac ·sin B ,sin B =35, 所以310ac =3,ac =10.由余弦定理得b 2=a 2+c 2-2ac cos B ,得4=a 2+c 2-85ac =a 2+c 2-16,即a 2+c 2=20. 所以(a +c )2-2ac =20,(a +c )2=40. 所以a +c =210.【示例】►在△ABC中,a,b,c分别为内角A,B,C所对的边长,a=3,b =2,1+2cos(B+C)=0,求边BC上的高.正解∵在△ABC中,cos(B+C)=-cos A,∴1+2cos(B+C)=1-2cos A=0,∴A=π3.在△ABC中,根据正弦定理asin A=bsin B,∴sin B=b sin Aa=22.∵a>b,∴B=π4,∴C=π-(A+B)=5 12π.∴sin C=sin(B+A)=sin B cos A+cos B sin A=22×12+22×32=6+24.∴BC边上的高为b sin C=2×6+24=3+12.【试一试】△ABC的三个内角A,B,C所对的边分别为a,b,c,a sin A sin B +b cos2A=2a.(1)求b a;(2)若c2=b2+3a2,求B.[尝试解答](1)由正弦定理得,sin2A sin B+sin B cos2A=2sin A,即sin B(sin2A+cos2A)=2sin A.故sin B=2sin A,所以ba= 2.(2)由余弦定理和c2=b2+3a2,得cos B=(1+3)a2c.由(1)知b2=2a2,故c2=(2+3)a2.可得cos2B=12,又cos B>0,故cos B=22,所以B=45°.高中数学必修3综合测试题一、选择题1、已知一组数据为20、30、40、50、60、60、70,则这组数据的众数、中位数、平均数的大小关系为()A、中位数 >平均数 >众数B、众数 >中位数 >平均数C、众数 >平均数 >中位数D、平均数 >众数 >中位数2、某影院有60排座位,每排70个座号,一次报告会坐满了听众,会后留下座号为15的所有听众60人进行座谈,这是运用了()A、抽签法B、随机数法C、系统抽样法D、分层抽样法3、某大学中文系共有本科生5000人,其中一、二、三、四年级的学生比为5:4:3:1,要用分层抽样的方法从该系所有本科生中抽取一个容量为260的样本,则应抽二年级的学生()A、100人B、60人C、80人D、20人4、一个均匀的正方体,把其中相对的面分别涂上红色、黄色、蓝色,随机向上抛出,正方体落地时“向上面为红色”的概率是()A、1/6B、1/3C、1/2 D 5/65、下列两个变量之间的关系哪个不是函数关系()A、角度和它的正切值B、人的右手一柞长和身高C、正方体的棱长和表面积D、真空中自由落体运动物体的下落距离和下落时间6、为了解A、B两种轮胎的性能,某汽车制造厂分别从这两种轮胎中随机抽取8个进行测试,下面列出了每一种轮胎行驶的最远里程数(单位:1000km)轮胎A:108、101、94、105、96、93、97、106轮胎B:96、112、97、108、100、103、86、98你认为哪种型号的轮胎性能更加稳定()A、轮胎AB、轮胎BC、都一样稳定D、无法比较7、我们对那大中学高二(1)班50名学生的身高进行了调查,按区间145--150,150--155,…,180—185(单位:cm)进行分组,得到的分布情况如下图所示,由图可知样本身高在165--170的频率为()A、0.24B、0.16C、0.12D、0.208、一个射手进行一次射击,则事件“命中环数小于6环”的对立事件是()A、命中环数为7、8、9、10环B、命中环数为1、2、3、4、5、6环C、命中环数至少为6环D、命中环数至多为6环9、从一副标准的52张的扑克牌中随机地抽取一张,则事件“这张牌是梅花”的概率为()A、1/26B、13/54C、1/13D、1/410、从一箱产品中随机地抽取一件,设事件A=“抽到一等品”,事件B = “抽到二等品”,事件C =“抽到三等品”,且已知 P(A)= 0.65 ,P(B)=0.2 ,P(C)=0.1。
高中数学模块综合检测新人教A版选择性必修第三册

模块综合检测(时间:120分钟,满分150分)一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合A ={5},B ={1,2},C ={1,3,4},若从这三个集合中各取一个元素构成空间直角坐标系中点的坐标,则确定的不同点的个数为( )A .36B .35C .34D .33【答案】D 【解析】不考虑限定条件确定的不同点的个数为C 12C 13A 33=36,但集合B ,C 中有相同元素1,由5,1,1三个数确定的不同点的个数只有三个,故所求的个数为36-3=33.2.在4次独立重复试验中,事件A 出现的概率相同,若事件A 至少发生一次的概率是6581,则事件A 在一次试验中出现的概率是( )A .13B .25C .56D .23【答案】A 【解析】设事件A 在一次试验中出现的概率是p .由事件A 至少发生1次的概率为6581,可知事件A 一次都不发生的概率为1-6581=1681,所以(1-p )4=1681,则p =13.3.已知随机变量X 的分布列为P (X =k )=12k ,k =1,2,…,则P (2<X ≤4)等于( )A .516B .316C .116D .14【答案】B 【解析】P (2<X ≤4)=P (X =3)+P (X =4)=123+124=316.4.抛掷一枚质地均匀的硬币两次,在第一次正面向上的条件下,第二次反面向上的概率为( )A .14B .13C .12D .23【答案】C 【解析】记事件A 表示“第一次正面向上”,事件B 表示“第二次反面向上”,则P (AB )=14,P (A )=12,∴P (B |A )=P AB P A =12.5.已知二项式⎝ ⎛⎭⎪⎫x +12x 2n 的展开式的二项式系数之和为64,则展开式中含x 3项的系数是( )A .1B .32C .52D .3【答案】D 【解析】由2n=64得n =6,T r +1=C r 6x 6-r·⎝⎛⎭⎪⎫12x 2r =12rC r 6x 6-3r ,令6-3r =3,得r=1,故含x 3项的系数为121C 16=3.6.为了考察某种中成药预防流感的效果,抽样调查40人,得到如下数据:项目 患流感 未患流感 服用药 2 18 未服用药812下表是χ2独立性检验中几个常用的小概率值和相应的临界值:α 0.1 0.05 0.01 0.005 x α2.7063.8416.6357.579根据表中数据,计算χ2=n ad -bc 2a +bc +d a +cb +d,若由此认为“该药物有效”,则该结论出错的概率不超过( )A .0.05B .0.1C .0.01D .0.005【答案】A 【解析】完成2×2列联表项目 患流感 未患流感 合计 服用药 2 18 20 未服用药 8 12 20 合计103040χ2=40×2×12-8×18210×30×20×20=4.8>3.841=x 0.05.7.某机构对儿童记忆能力x 和识图能力y 进行统计分析,得到如下数据:记忆能力x 4 6 8 10 识图能力y3568由表中数据,求得经验回归方程为y =0.8x +a ,若某儿童记忆能力为12,则预测他的识图能力为( )A .9.5B .9.8C .9.2D .10【答案】A 【解析】∵x =14×(4+6+8+10)=7,y =14×(3+5+6+8)=5.5,∴样本点的中心为(7,5.5),代入回归方程得5.5=0.8×7+a ^,∴a ^=-0.1,∴y =0.8x -0.1,当x =12时,y =0.8×12-0.1=9.5.8.甲、乙、丙3位志愿者安排在周一至周五5天中参加某项志愿者活动,要求每人参加一天且每天至多安排一人,并要求甲安排在另外两位前面,则不同的安排方法共有( )A .40种B .30种C .20种D .60种【答案】C 【解析】分类解决.甲排周一,乙,丙只能是周二至周五4天中选两天进行安排,有A 24=12(种)方法;甲排周二,乙,丙只能是周三至周五选两天安排,有A 23=6(种)方法;甲排周三,乙,丙只能安排在周四和周五,有A 22=2(种)方法.由分类加法计数原理可知,共有12+6+2=20(种)方法.二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9.若(3x -1)7=a 7x 7+a 6x 6+…+a 1x +a 0,则( ) A .a 0=1B .a 1+a 2+…+a 7=129C .a 1+a 3+a 5+a 7=8 256D .a 0+a 2+a 4+a 6=8 128【答案】BC 【解析】令x =0,则a 0=-1,A 错误;令x =1,得a 7+a 6+…+a 1+a 0=27=128①,所以a 1+a 2+…+a 7=129,B 正确;令x =-1,得-a 7+a 6-a 5+a 4-a 3+a 2-a 1+a 0=(-4)7②,①-②,得2(a 1+a 3+a 5+a 7)=128-(-4)7,∴a 1+a 3+a 5+a 7=8 256,C 正确;①+②,得2(a 0+a 2+a 4+a 6)=128+(-4)7,∴a 0+a 2+a 4+a 6=-8 128,D 错误.10.设离散型随机变量X 的分布列为若离散型随机变量Y )A .E (X )=2B .D (X )=1.4C .E (Y )=5D .D (Y )=7.2【答案】ACD 【解析】由离散型随机变量X 的分布列的性质得q =1-0.4-0.1-0.2-0.2=0.1,E (X )=0×0.1+1×0.4+2×0.1+3×0.2+4×0.2=2,D (X )=(0-2)2×0.1+(1-2)2×0.4+(2-2)2×0.1+(3-2)2×0.2+(4-2)2×0.2=1.8,∵离散型随机变量Y 满足Y =2X +1,∴E (Y )=2E (X )+1=5,D (Y )=4D (X )=7.2.故选ACD .11.某学生想在物理、化学、生物、政治、历史、地理、技术这七门课程中选三门作为选考科目,下列说法错误的是( )A .若任意选择三门课程,选法总数为A 37 B .若物理和化学至少选一门,选法总数为C 12C 26 C .若物理和历史不能同时选,选法总数为C 37-C 15D .若物理和化学至少选一门,且物理和历史不同时选,选法总数为C 12C 25-C 15【答案】ABD 【解析】对于A,若任意选择三门课程,选法总数为C 37,错误;对于B,若物理和化学选一门,有C 12种方法,其余两门从剩余的5门中选,有C 25种选法,选法为C 12C 25;若物理和化学选两门,有C 22种选法,剩下一门从剩余的5门中选,有C 15种选法,有C 22C 15种,由分类加法计数原理知,总数为C 12C 25+C 22C 15,错误;对于C,若物理和历史不能同时选,选法总数为C 37-C 22C 15=(C 37-C 15)种,正确;对于D,有3种情况:①只选物理且物理和历史不同时选,有C 11C 24种选法;②选化学,不选物理,有C 11C 25种选法;③物理与化学都选,有C 22C 14种选法,故总数为C 11C 24+C 11C 25+C 22C 14=6+10+4=20(种),错误.故选ABD .12.为研究需要,统计了两个变量x ,y 的数据情况如下表:其中数据x 1,x 2,x 3,…,x n 和数据y 1,y 2,y 3,…,y n 的平均数分别为x 和y ,并且计算相关系数r =-0.8,经验回归方程为y ^=b ^x +a ^,则下列结论正确的为( )A .点(x ,y )必在回归直线上,即y =b ^ x +a ^B .变量x ,y 的相关性强C .当x =x 1,则必有y =y 1D .b ^<0【答案】ABD 【解析】A .回归直线y ^=b ^x +a ^过样本点中心(x ,y ),即y =b ^ x +a ^,所以A 正确;B .相关系数r =-0.8,|r |>0.75,变量x ,y 的相关性强,所以B 正确;C .当x =x 1时,不一定有y =y 1,因此C 错误;D .因为r =-0.8<0,是负相关,所以b ^<0,D 正确;故选ABD .三、填空题:本大题共4小题,每小题5分,共20分.13.一射击测试中,每人射击3次,每击中目标一次记10分,没有击中目标记0分,某人每次击中目标的概率为23,则此人得分的均值是________,得分的方差是________.【答案】202003 【解析】记此人3次射击击中目标η次,得分为ξ分,则η~B ⎝ ⎛⎭⎪⎫3,23,ξ=10η,所以E (ξ)=10E (η)=10×3×23=20,D (ξ)=100D (η)=100×3×23×13=2003. 14.在二项式(2+x )9的展开式中,常数项是________.【答案】16 2 【解析】由二项展开式的通项公式可知T r +1=C r 9·(2)9-r·x r,令r =0,得常数项为C 09·(2)9·x 0=(2)9=16 2.15.某城市新修建的一条道路上有12盏路灯,为了节省用电而又不能影响正常的照明,可以熄灭其中的3盏灯,但两端的灯不能熄灭,也不能熄灭相邻的两盏灯,则熄灯的方法有________种(填数字).【答案】56 【解析】由题意可知,最终剩余的亮着的灯共有9盏,且两端的必须亮着,所以可用插空的方法,共有8个空可选,所以应为C 38=56(种).四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤. 16.某校高三年级有6个班,现要从中选出10人组成高三女子篮球队参加高中篮球比赛,且规定每班至少要选1人参加.求这10个名额有多少种不同的分配方法.解:除每班1个名额以外,其余4个名额也需要分配.这4个名额的分配方案可以分为以下几类:(1)4个名额全部分给某一个班,有C 16种分法; (2)4个名额分给两个班,每班2个,有C 26种分法;(3)4个名额分给两个班,其中一个班1个,一个班3个,共有A 26种分法;(4)4个名额分给三个班,其中一个班2个,其余两个班每班1个,共有C 16·C 25种分法; (5)4个名额分给四个班,每班1个,共有C 46种分法. 故共有C 16+C 26+A 26+C 16·C 25+C 46=126(种)分配方法.17.已知(a 2+1)n 展开式中的各项系数之和等于⎝⎛⎭⎪⎫165x 2+1x 5的展开式的常数项,而(a 2+1)n的展开式的系数最大的项等于54,求a 的值.解:⎝ ⎛⎭⎪⎫165x 2+1x 5的展开式的通项为T r +1=C r 5⎝ ⎛⎭⎪⎫165x 25-r·⎝ ⎛⎭⎪⎫1x r =⎝ ⎛⎭⎪⎫1655-r C r 5x 20-5r 2,令20-5r =0,得r =4,故常数项T 5=165×C 45=16.又(a 2+1)4展开式的各项系数之和等于2n, 由题意知2n=16,得n =4,由二项式系数的性质知,(a 2+1)4展开式中系数最大的项是中间项T 3, 故有C 24a 4=54,解得a =± 3.18.某饮料公司招聘了一名员工,现对其进行一项测试,以便确定工资级别.公司准备了两种不同的饮料共8杯,其颜色完全相同,并且其中4杯为A 饮料,另外4杯为B 饮料,公司要求此员工一一品尝后,从8杯饮料中选出4杯A 饮料.若4杯都选对,则月工资定为3 500元;若4杯选对3杯,则月工资定为2 800元,否则月工资定为2 100元.令X 表示此人选对A 饮料的杯数,假设此人对A 和B 两种饮料没有鉴别能力.(1)求X 的分布列; (2)求此员工月工资的均值.解:(1)依题意知X 所有可能取值为0,1,2,3,4, P (X =0)=C 04C 44C 48=170,P (X =1)=C 14C 34C 48=835,P (X =2)=C 24C 24C 48=1835,P (X =3)=C 34C 14C 48=835,P (X =4)=C 44C 04C 48=170.所以X 的分布列为X 0 1 2 3 4 P1708351835835170(2)令Y 表示此员工的月工资,则Y 的所有可能取值为2 100,2 800,3 500, 则P (Y =3 500)=P (X =4)=170, P (Y =2 800)=P (X =3)=835,P (Y =2 100)=P (X ≤2)=1835+835+170=5370.所以E (Y )=170×3 500+835×2 800+5370×2 100=2 280(元).所以此员工月工资的均值为2 280元.19.“中国式过马路”存在很大的交通安全隐患.某调查机构为了解路人对“中国式过马路”的态度是否与性别有关,从马路旁随机抽取30名路人进行了问卷调查,得到了如下列联表:态度 性别合计 男性 女性反感 10不反感 8总计30已知在这30人中随机抽取1人,抽到反感“中国式过马路”的路人的概率是815.(1)请将上面的列联表补充完整(直接写结果,不需要写求解过程),并据此资料分析是否有90%的把握认为反感“中国式过马路”与性别是否有关?(2)若从这30人中的女性路人中随机抽取2人参加一活动,记反感“中国式过马路”的人数为X ,求X 的分布列和均值.附:χ2=n ad -bc 2a +bc +d a +c b +d. α 0.10 0.05 0.010 0.005 x α2.7063.8416.6357.879解:(1)态度 性别合计 男性 女性 反感 10 6 16 不反感6814合计1614 30由已知数据得χ2=30×10×8-6×6216×14×16×14≈1.158<2.706=x 0.1.所以,没有90%的把握认为反感“中国式过马路”与性别有关.(2)X 的可能取值为0,1,2,P (X =0)=C 28C 214=413,P (X =1)=C 16C 18C 214=4891,P (X =2)=C 26C 214=1591.所以X 的分布列为X 0 1 2 P41348911591X 的均值为E (X )=0×413+1×4891+2×1591=67.20.近年来,随着以煤炭为主的能源消耗大幅攀升、机动车持有量急剧增加,某市空气中的PM2.5(直径小于等于2.5微米的颗粒物)的含量呈逐年上升的趋势,如图是根据该市环保部门提供的2016年至2020年该市PM2.5年均浓度值画成的散点图(为便于计算,把2016年编号为1,2017年编号为2,…,2020年编号为5).(1)以PM2.5年均浓度值为因变量,年份的编号为自变量,利用散点图提供的数据,用最小二乘法求出该市PM2.5年均浓度值与年份编号之间的经验回归方程y ^=b ^x +a ^;(2)按世界卫生组织(WHO)过渡期-1的标准,空气中的PM2.5的年均浓度限值为35微克/立方米,该市若不采取措施,试预测到哪一年该市空气中PM2.5的年均浓度值将超过世界卫生组织(WHO)过渡期-1设定的限值.解:(1)由散点图可得,变量x i ,y i 组成的几组数据为(1,13),(2,15),(3,20),(4,22),(5,25),则x =3,y =19,所以b ^=-2×-6+-1×-4+0×1+1×3+2×6-22+-12+02+12+22=3.1.a ^=y -b ^x =19-3.1×3=9.7.所以所求经验回归方程为y ^=3.1x +9.7.(2)由3.1x +9.7>35,得x >8.16,因为x ∈N ,所以x =9.故可预测到2024年该市空气中PM2.5的年均浓度值将超过世界卫生组织(WHO)过渡期-1设定的限值.21.某品牌专卖店准备在国庆期间举行促销活动.根据市场调查,该店决定从2种不同型号的洗衣机、2种不同型号的电视机和3种不同型号的空调中(不同种商品的型号不同),选出4种不同型号的商品进行促销,该店对选出的商品采用的促销方案是有奖销售,即在该商品现价的基础上将价格提高150元,同时,若顾客购买任何一种型号的商品,则允许有3次抽奖的机会,若中奖,则每次中奖都获得m (m >0)元奖金.假设顾客每次抽奖时获奖的概率都是12.(1)求选出的4种不同型号商品中,洗衣机、电视机、空调都至少有1种型号的概率; (2)设顾客在3次抽奖中所获得的奖金总额(单位:元)为随机变量X ,请写出X 的分布列,并求X 的均值;(3)该店若想采用此促销方案获利,则每次中奖奖金要低于多少元?解:(1)设“选出的4种不同型号商品中,洗衣机、电视机、空调都至少有1种型号”为事件A ,则P (A )=2C 12C 13+C 12C 12C 23C 47=2435. (2)X 的所有可能的取值为0,m,2m,3m .P (X =0)=C 03⎝ ⎛⎭⎪⎫120×⎝ ⎛⎭⎪⎫123=18, P (X =m )=C 13⎝ ⎛⎭⎪⎫121×⎝ ⎛⎭⎪⎫122=38, P (X =2m )=C 23⎝ ⎛⎭⎪⎫122×⎝ ⎛⎭⎪⎫121=38,P (X =3m )=C 33⎝ ⎛⎭⎪⎫123×⎝ ⎛⎭⎪⎫12=18,所以顾客在3次抽奖中所获得的奖金总额X 的分布列为于是顾客在3E (X )=0×18+m ×38+2m ×38+3m ×18=1.5m .(3)要使促销方案对商场有利,应使顾客获得的奖金总额的均值低于商场的提价数额,因此应有1.5m <150,所以m <100.故每次中奖奖金要低于100元,才能使促销方案对商场有利.。
2021新教材人教版高中数学A版选择性必修第三册模块练习题--6.3.1 二项式定理

6.3二项式定理6.3.1二项式定理基础过关练题组一二项式定理的正用与逆用1.(a+b)2n,n∈N*的展开式的项数是( )A.2nB.2n+1C.2n-1D.2(n+1)2.设S=(x-1)3+3(x-1)2+3(x-1)+1,则S等于( )A.(x-1)3B.(x-2)3C.x3D.(x+1)33.设A=37+C72×35+C74×33+C76×3,B=C71×36+C73×34+C75×32+1,则A-B的值为( )A.128B.129C.47D.04.用二项式定理展开(1+1x )4= .5.(2019海南海口实验中学高三上月考)3C n1+9C n2+27C n3+…+3n C n n= (n∈N*).题组二二项展开式的特定项、项的系数及二项式系数6.(2020河北石家庄高二下阶段测试)(3x3-√x )7的展开式中x7的系数是( )A.5 103B.21C.-945D.9457.(2020湖南岳阳高二上期末)若(x-√ax2)6的展开式的常数项为60,则实数a的值为( )A.4B.2C.8D.68.(2020四川绵阳中学高三4月线上学习评估)(2x+a)5(其中a≠0)的展开式中,x2的系数与x3的系数相同,则实数a的值为( )A.±12B.12C.-2D.29.(2020四川成都双流中学高三月考)若(1-√x)n(n∈N*)的展开式的第2、3、4项的二项式系数成等差数列,则sin(nπ-π3)=( )A.12B.12或-12C.√32D.√32或-√3210.(2020辽宁本溪高三下线上模拟)若(x6+x√x )n(n∈N*)的展开式中含有常数项,则n的最小值等于( ) A.3 B.4 C.5 D.611.(2020辽宁大连高三第一次模拟)(12x+2y)6的展开式中x2y4的系数为.12.(2020山东枣庄高三上期末)(√x+1x )6的展开式中的常数项等于,有理项共有项.13.已知(2x√x )n(n∈N*)的展开式的第2项与第3项的二项式系数之比是2∶5.(1)求n的值;(2)求展开式的常数项.题组三 赋值法求系数和14.(2020山东济宁高二下质量检测)若(x -12)n(n∈N *)的展开式的第3项的二项式系数是15,则展开式的所有项系数之和为( ) A.132B.164C.-164D.112815.(2020山东烟台栖霞一中高二下月考)设(1-3x)9=a 0+a 1x+a 2x 2+…+a 9x 9,则|a 0|+|a 1|+|a 2|+…+|a 9|的值为( ) A.29 B.49 C.39 D.5916.(2020陕西宝鸡高考模拟检测)若(5x -3√x)n(n∈N *)的展开式的各项系数之和为32,则展开式中x 的系数为 .17.(2020山东枣庄滕州一中高二下月考)已知(1+mx)10=a 0+a 1x+a 2x 2+…+a 10x 10,其中m≠0,且a 6+14a 3=0. (1)求实数m 的值; (2)求a 2+a 4+a 6+a 8+a 10.能力提升练题组一 多项式展开式中的特定项及项的系数 1.(2020山东济宁高二下质量检测,)(1-2x )7x的展开式中x 2的系数为( )A.-84 B .84C.-280D.2802.(2020广东珠海高三教学质量检测,)(x+1)·(2x-1x )5的展开式的常数项为( )A.-40B.40C.-80D.803.(2020山东枣庄第三中学高二下月考,)在(1+x+1x2020)10的展开式中,x2的系数为( ) A.30 B.45 C.60 D.904.(2020陕西榆林二中高三月考,)若(√x+12x )8(ax-1)的展开式中含x12的项的系数为21,则实数a的值为( )A.3B.-3C.2D.-25.(2020辽宁沈阳二中高二下月考,)已知x(x-2)8=a0+a1(x-1)+a2(x-1)2+…+a9(x-1)9,则a6=( )A.-28B.-448C.112D.4486.(2019河北邯郸第一中学高三期中,)(x+2y)·(x-y)5的展开式中x3y3的系数为.7.(2020天津杨村第一中学高三上一模,)(a+x)(1+x)4的展开式中,若x的奇数次幂的项的系数之和为32,则a= .题组二赋值法求系数和8.(2020山东济南一中高二下第二次月考,)已知(1+x)(a-x)6=a0+a1x+…+a7x7,若a0+a1+…+a7=0,则a3=( )A.-5B.-20C.15D.359.(2020浙江杭州高级中学高三下模拟,)已知(x+2)5(2x-5)=a0+a1x+…+a6x6,则a0= ,a5= .10.(2020湖南长沙长郡中学高三月考,)设(x2+1)·(4x-2)8=a0+a1(2x-1)+a2(2x-1)2+…+a10(2x-1)10,则a1+a2+…+a10= .11.(2019浙江杭州高考模拟,)若(x-3)3(2x+1)5=a0+a1x+a2x2+…+a8x8,则a0= ,a0+a2+…+a8= .12.()在(2x-3y+1)5的展开式中,不含y的所有项的系数和为(用数值作答).13.()已知(1+2x)4=a0+a1x+a2x2+a3x3+a4x4,则a1-2a2+3a3-4a4= .14.()已知A n5=56C n7,且(1-2x)n=a0+a1x+a2x2+a3x3+…+a n x n.(1)求n的值;(2)求a12+a222+…+a n2n的值.题组三二项式定理的应用15.(2020湖南衡阳高二期末,)1.957的计算结果精确到个位的近似值为( )A.106B.107C.108D.10916.(2019江西九江高二期末,)1-90C101+902C102-903C103+…+9010C1010除以88的余数是( )A.2B.1C.86D.8717.(2020辽宁阜新高二调研,)设a∈Z,且0≤a≤13,若512 020+a能被13整除,则a=( )A.0B.1C.11D.1218.(2020山东青岛莱西一中高二下期中,)求302 020被7除的余数.答案全解全析6.3.1 二项式定理基础过关练1.B 根据二项式定理可知,展开式共有2n+1项.2.C S=(x-1)3+3(x-1)2+3(x-1)+1=C30(x-1)3+C31(x-1)2+C32(x-1)+C33=[(x-1)+1]3=x3.3.A A-B=C70×37-C71×36+C72×35-C73×34+C74×33-C75×32+C76×31-C77×30 =(3-1)7=27=128.4.答案 1+4x +6x2+4x3+1x4解析解法一:(1+1x )4=C40(1x)+C41(1x)1+C42(1x)2+C43(1x)3+C44(1x)4=1+4x+6x2+4x3+1x4.解法二:(1+1x )4=(1x)4(x+1)4=(1 x )4(C40x4+C41x3+C42x2+C43x+C44x0)=1+4x +6x2+4x3+1x4.5.答案4n-1解析3C n1+9C n2+27C n3+…+3n C n n=C n0+3C n1+9C n2+27C n3+…+3n C n n-1=(1+3)n-1=4n-1.6.D (3x3√x )7的展开式的通项是T r+1=C7r(3x3)7-r(√x )r=(-1)r37-r C7r x21-7r2,令21-7r2=7,解得r=4,所以展开式中x7的系数是(-1)437-4C74=945.故选D.7.A (x-√ax2)6的展开式的通项为T r+1=C6r x6-r(-√ax2)r=(-1)r a r2C6r x6-3r,令6-3r=0,解得r=2,则常数项为(-1)2a C62=60,解得a=4.故选A.8.D (2x+a)5的展开式的通项为T r+1=C5r(2x)5-r a r=25-r a r C5r x5-r,因为x 2的系数与x 3的系数相同,所以22a 3C 53=23a 2C 52,即4a 3=8a 2,又a≠0,所以a=2.故选D.9.C ∵(1-√x )n (n∈N *)的展开式的第2、3、4项的二项式系数成等差数列,∴2C n 2=C n 1+C n 3(n≥3),解得n=7,∴sin (nπ-π3)=sin (7π-π3)=sin 2π3=√32.故选C.10.C (x 6+x √x)n的展开式的通项为T r+1=C n r (x 6)n-r (x √x)r =C n r x 6n -6r -32r =C n r x 6n -152r,令6n-152r=0 ,得n=54r.又n∈N *,所以当r=4 时,n 取得最小值5. 故选C. 11.答案 60解析 (12x +2y)6的展开式的通项为T r+1=C 6r(12x)6-r(2y)r =22r-6C 6r x 6-r y r.令r=4,得T 5=60x 2y 4. 故x 2y 4的系数为60. 12.答案 15;4解析 (√x +1x )6的展开式的通项为T r+1=C 6r (√x )6-r (1x)r=C 6rx 6-3r 2.当6-3r 2=0时,r=2,此时常数项为C 62=15.当6-3r 2为整数时,对应的项为有理项,因为r∈N 且r≤6,所以r 可取0,2,4,6,故共有4项为有理项. 13.解析 (2x √x)n的展开式的通项为T r+1=C n r(2x)n-r (√x)r =(-1)r 2n-r C n r x n -32r .(1)由展开式的第2项与第3项的二项式系数之比是2∶5,可得C n 1∶C n 2=2∶5,解得n=6.(2)由(1)知T r+1=(-1)r26-rC 6r x 6-32r,令6-32r=0,解得r=4,所以展开式的常数项为(-1)4×26-4×C 64=60.14.B由题意知C n 2=n (n -1)2=15,解得n=6或n=-5(舍去),故(x -12)n =(x -12)6,令x=1,得所有项系数之和为(12)6=164.15.B 易得(1-3x)9的展开式的通项为T r+1=C 9r(-3)r x r ,∴a 0,a 2,a 4,a 6,a 8为正数,a 1,a 3,a 5,a 7,a 9为负数, ∴|a 0|+|a 1|+|a 2|+…+|a 9| =a 0-a 1+a 2-a 3+…+a 8-a 9,令x=-1,得(1+3)9=a 0-a 1+a 2-a 3+…+a 8-a 9=49, ∴|a 0|+|a 1|+…+|a 9|=49. 16.答案 2 025解析 依题意,令x=1,得(5-3)n=32,解得n=5,则该式为(5x-3√x)5,其展开式的通项为T r+1=C 5r (5x)5-r(-3x 12)r=55-r ·(-3)r·C 5r x 3r2-5,令32r-5=1,得r=4,所以x 的系数为55-4×(-3)4×C 54=2 025.故答案为2 025.17.解析 (1)(1+mx)10的展开式的通项为T r+1=C 10r (mx)r =C 10r m r x r ,所以a 3=C 103m 3,a 6=C 106m 6,依题意得C 106m 6+14C 103m 3=0,即210m 6+14×120m 3=0,整理得m 3(m 3+8)=0,因为m≠0,所以m 3=-8,所以m=-2.(2)由(1)得m=-2,所以(1-2x)10=a 0+a 1x+a 2x 2+…+a 10x 10. 令x=1,得a 0+a 1+a 2+a 3+a 4+a 5+a 6+a 7+a 8+a 9+a 10=(1-2)10=1.① 令x=-1,得a 0-a 1+a 2-a 3+a 4-a 5+a 6-a 7+a 8-a 9+a 10=(1+2)10=310.② ①+②得2(a 0+a 2+a 4+a 6+a 8+a 10)=1+310,即a 0+a 2+a 4+a 6+a 8+a 10=1+3102.又a 0=C 100(-2)0=1,所以a 2+a 4+a 6+a 8+a 10=1+3102-1=310-12=29 524. 能力提升练1.C 易得(1-2x)7的展开式的通项为T k+1=(-2)kC 7k x k,则(1-2x )7x的展开式的通项为(-2)k C 7k x k-1,令k-1=2,得k=3,所以x 2的系数为(-2)3C 73=-280.故选C. 2.A (2x -1x)5的展开式的通项为T r+1=C 5r (2x)5-r (-1x)r =(-1)r 25-r C 5r x 5-2r,令5-2r=-1,得r=3, 令5-2r=0,得r=52(舍去),所以(x+1)(2x -1x)5的展开式的常数项为(-1)3×22×C 53=-40.故选A.3.B (1+x +1x2 020)10的展开式的通项为T r+1=C 10r(x +1x 2 020)r,r≤10,r∈N.(x +1x 2 020)r的展开式的通项为T k+1=C rk x r-2 021k ,k≤r,k∈N, 令r-2 021k=2,可得r=2+2 021k, 只有k=0,r=2满足题意,故x 2的系数为C 102×C 20=45,故选B.4.A (√x +12x )8的展开式的通项为T r+1=C 8r(√x )8-r (12x )r =(12)rC 8r x 8-3r2,令8-3r 2=-12,得r=3,此时(√x +12x )8(ax-1)的展开式中含x 12的项的系数为(12)3C 83a=7a,令8-3r 2=12,得r=73∉N,舍去,所以(√x +12x )8(ax-1)的展开式中含x 12的项的系数为7a,所以7a=21,得a=3.故选A.5.A 由x(x-2)8=[(x-1)+1][(x-1)-1]8知,当第一个因式取(x-1)时,第二个因式取C 83(x-1)5(-1)3,其系数为-56,当第一个因式取1时,第二个因式取C 82(x-1)6(-1)2,其系数为28,故a 6=-56+28=-28.故选A.6.答案 10解析 (x+2y)(x-y)5=(x+2y)(C 50x 5-C 51x 4y+C 52x 3y 2-C 53x 2y 3+C 54x 1y 4-C 55y 5),故它的展开式中x 3y 3的系数为-C 53+2C 52=10,故答案为10.7.答案 3解析 因为(1+x)4=1+4x+6x 2+4x 3+x 4,所以(a+x)(1+x)4的展开式中含x 的奇数次幂的项分别为4ax,4ax 3,x,6x 3,x 5,其系数之和为4a+4a+1+6+1=32,解得a=3.8.A 由题意,令x=1,可得a 0+a 1+…+a 7=(1+1)(a-1)6=2×(a -1)6=0,解得a=1,∴(1+x)(a -x)6=(1+x)(1-x)6=(1-x)6+x×(1-x)6,∴展开式中x 3的系数为C 63(-1)3+C 62(-1)2=-20+15=-5,故选A.9.答案 -160;15解析 令x=0,得25×(-5)=a 0,即a 0=-160.a 5为x 5的系数,由(x+2)5(2x-5)=2x(x+2)5-5(x+2)5可知,x 5的系数为C 51×21×2+C 50×(-5)=15,即a 5=15.10.答案 512解析 ∵(x 2+1)(4x-2)8=a 0+a 1(2x-1)+a 2(2x-1)2+…+a 10(2x-1)10,∴令x=1,得(1+1)×(4×1-2)8=a 0+a 1+a 2+…+a 10=29,令x=12,得(14+1)×(4×12-2)8=a 0=0,∴a1+a2+…+a10=29-0=512.故答案为512.11.答案-27;-940解析令x=0,得(-3)3=a0,所以a0=-27.令x=1,得(-2)3×35=a0+a1+a2+…+a8,①令x=-1,得(-4)3×(-1)5=a0-a1+a2-…+a8,②①+②得2(a0+a2+…+a8)=-1 880,∴a0+a2+…+a8=-940.12.答案243解析要求(2x-3y+1)5的展开式中不含y的项,只需令y=0,所以(2x-3y+1)5的展开式中不含y的所有项的系数和为(2x+1)5的展开式中各项的系数和,令x=1,得35=243.故答案为243.13.答案-8解析等式两边同时对x求导,可得8(1+2x)3=a1+2a2x+3a3x2+4a4x3,令x=-1,得a1-2a2+3a3-4a4=-8.14.解析(1)易知n≥7,n∈N.∵A n5=56C n7,∴n(n-1)(n-2)(n-3)(n-4)=56×n(n-1)(n-2)(n-3)(n-4)(n-5)(n-6),7×6×5×4×3×2×1=1,整理可得(n-5)(n-6)90即n2-11n-60=0,解得n=15或n=-4(舍去).故n的值为15.(2)由(1)得n=15,∴(1-2x)n =(1-2x)15=a 0+a 1x+a 2x 2+a 3x 3+…+a 15x 15,令x=0,可得a 0=1,令x=12,可得(1-2×12)15=a 0+a 12+a 222+a 323+…+a 15215=0, ∴a 12+a222+…+a 15215=-1.15.B ∵1.957=(2-0.05)7=27-C 71×26×0.05+C 72×25×0.052-…-0.057≈107.21,∴1.957≈107.故选B.16.B 1-90C 101+902C 102-903C 103+…+9010C 1010=(1-90)10=(1+88)10=1+88C 101+882C 102+883C 103+…+8810C 1010=1+88(C 101+88C 102+882C 103+…+889C 1010),所以1-90C 101+902C 102-903C 103+…+9010C 1010除以88的余数是1,故选B.17.D 因为51=52-1,所以512 020=(52-1)2 020=C 2 0200522 020-C 2 0201522 019+…-C 2 0202 019521+1,又因为52能被13整除,所以只需1+a 能被13整除,因为a∈Z,0≤a≤13,所以a=12,故选D.18.解析 302 020=(28+2)2 020=282 020+C 2 0201×282 019×2+…+C 2 0202 019×28×22 019+22 020=28×(282 019+C 2 0201×282 018×2+…+C 2 0202 019×22 019)+22 020, 故只需求出22 020被7除的余数即可,因为22020=2×8673=2×(7+1)673=2×(7673+C 6731×7672+C 6732×7671+…+C 673672×7+1)=2×7×(7672+C 6731×7671+C 6732×7670+…+C 673672)+2,所以余数为2.。
北师大版高中数学必修三单元测评:第一章统计(A卷)(含解析)

高中数学学习材料(灿若寒星精心整理制作)单元测评统计(A卷)(时间:90分钟满分:120分)第Ⅰ卷(选择题,共50分)一、选择题:本大题共10小题,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的,将答案填在指定答题栏内.1.下列调查方式合适的是()A.要了解一批灯泡的使用寿命,采用普查方式B.要了解收看中央电视台的“法制报道”栏目的情况,采用普查方式C.为了保证“天宫一号”太空舱发射成功,对重要零件采取抽查方式D.要了解外国人对“上海世博会”的关注度,可采用抽查方式答案:D2.某班的78名同学已编号1,2,3,…,78,为了解该班同学的作业情况,老师收取了学号能被5整除的15名同学的作业本,这里运用的抽样方法是()A.简单随机抽样法B.系统抽样法C.分层抽样法D.抽签法答案:B3.容量为100的样本数据按从小到大的顺序分为8组,如下表:组号12345678频数 10 13 x 14 15 13 12 9第3组的频数与频率分别是( ) A .14和0.14 B .0.14和14 C.114和0.14D.13和114解析:频数为100-(10+13+14+15+13+12+9)=14,频率为14100=0.14.答案:A4.一次选拔运动员,测得7名选手的身高(单位:cm)分布茎叶图如图,记录的平均身高为177 cm ,有一名候选人的身高记录不清楚,其末位数为x ,那么x 的值是( )A .5B .6C .7D .8解析:设这名候选人的身高为m ,则180+181+170+173+178+179+m 7=177. 解得m =178.∴x =8. 答案:D5. 如图是某学校抽取的学生体重的频率分布直方图,已知图中从左到右的前3个小组的频率之比为1∶2∶3,第2小组的频数为10,则抽取的学生人数为( )A .20B .30C .40D .50解析:前3组的频率之和等于1-(0.012 5+0.037 5)×5=0.75,第2小组的频率是0.75×21+2+3=0.25,设样本容量为n ,则10n =0.25,即n =40.答案:C6.已知两个变量x ,y 之间具有线性相关关系,试验测得(x ,y )的四组值分别为(1,2),(2,4),(3,5),(4,7),则y 与x 之间的回归直线方程为( )A .y =0.8x +3B .y =-1.2x +7.5C .y =1.6x +0.5D .y =1.3x +1.2解析:利用排除法.∵x =14(1+2+3+4)=2.5,y =14(2+4+5+7)=4.5, 由于回归直线y =bx +a 必过定点(2.5,4.5),故排除A ,D. 又由四组数值知y 随x 的增大而增大,知b >0,排除B. 答案:C7.某同学使用计算器求30个数据的平均数时,错将其中一个数据105输入为15,那么由此求出的平均数与实际平均数的差是( )A .3.5B .-3C .3D .-0.5解析:少输入90,9030=3,平均数少3,求出的平均数减去实际的平均数等于-3.答案:B8.为了稳定市场,确保农民增收,某农产品3月以后的每月市场收购价格与其前三个月的市场收购价格有关,并使其与前三个月的市场收购价格之差的平方和最小,下表列出的是该产品今年前六个月的市场收购价格:( )月份 1 2 3 4 5 6 7 价格(元/担)687867717270则前七个月该产品的市场收购价格的方差为 A.757 B.767 C .11D.787解析:设7月份该产品的市场收购价格为a ,由题意得(a -71)2+(a -72)2+(a -70)2值最小时a =71+72+703=71,前七个月该产品的市场收购价格先各减去71后得:-3,7,-4,0,1,-1,0.所得数据的平均数恰好为0,方差为s 2=17[(-3)2+72+(-4)2+0+1+1+0-7×02]=767.答案:B9.已知数据x 1,x 2,x 3的中位数为k ,众数为m ,平均数为n ,方差为p ,则下列说法中,错误的是( )A .数据2x 1,2x 2,2x 3的中位数为2kB .数据2x 1,2x 2,2x 3的众数为2mC .数据2x 1,2x 2,2x 3的平均数为2nD.数据2x1,2x2,2x3的方差为2p解析:当数据由x1,x2,x3变为2x1,2x2,2x3时,其中位数、众数、平均数也变为原来的2倍,但是其方差应变为原来的4倍.故数据2x1,2x2,2x3的方差为4p.答案:D10.为了调查利群超市的营业情况,下表是利群超市五月份一周的利润情况记录.日期14日15日16日17日18日19日20日当日利润0.200.170.230.210.230.180.25 (万元)根据上表你估计利群超市今年五月份的总利润是()A.6.51万元B.6.4万元C.1.47万元D.5.88万元解析:根据这一周的记录可以求得每天的平均利润为:0.20+0.17+0.23+0.21+0.23+0.18+0.257=0.21(万元),故五月份的总利润为:0.21×31=6.51(万元).答案:A第Ⅱ卷(非选择题,共70分)二、填空题:本大题共4小题,每小题5分,共20分.将答案填在题中横线上.11.某公司生产三种型号的轿车,产量分别为1 200辆,6 000辆和2 000辆,现用分层抽样的方法抽取46辆进行检验.这三种型号的轿车依次抽取__________辆,__________辆,__________辆.解析:各种型号的轿车差别较大,可用分层抽样法抽取,抽取比例为46∶(1 200+2 000+6 000)=1∶200.所以这三种型号的轿车依次应抽取6辆,30辆,10辆.答案:6 30 1012.为了解某校教师使用多媒体进行教学的情况,采用简单随机抽样的方法,从该校200名授课教师中抽取20名教师,调查了他们上学期使用多媒体进行教学的次数,结果用茎叶图表示如图,据此可估计该校上学期200名教师中,使用多媒体进行教学的次数在[15,25)内的人数为__________.解析:由茎叶图知,抽取的20名教师中使用多媒体进行教学的次数在[15,25)内的人数为6,频率为620,故200名教师中使用多媒体进行教学的次数在[15,25)内的人数为620×200=60.答案:6013.某市高三数学抽样考试中,对90分以上(含90分)的成绩进行统计,其频率分布图如图所示,若130~140分数段的人数为90,则90~100分数段的人数为__________.解析:设总人数为n ,则90n =0.05,故n =1 800,故90~100分数段的人数为1 800×0.45=810.答案:81014.调查了某地若干户家庭的年收入x (单位:万元)和年饮食支出y (单位:万元),调查显示年收入x 与年饮食支出y 具有线性相关关系,并由调查数据得到y 对x 的回归直线方程:y =0.254x +0.321.由回归直线方程可知,家庭年收入每增加1万元,年饮食支出平均增加__________万元.解析:本题考查了对线性回归知识的理解和应用.回归直线方程中的斜率就是平均增长率.答案:0.254三、解答题:本大题共4小题,满分50分.解答应写出文字说明、证明过程或演算步骤.15.(12分)某化肥厂甲、乙两个车间包装肥料,在自动包装传送带上每隔30分钟抽取一包产品,称其重量(单位:kg),分别记录,抽查数据如下:甲:102,101,99,98,103,98,99;乙:110,115,90,85,75,115,110. (1)这种抽样方法是哪一种?(2)估计甲、乙两车间包装的肥料重量的平均值与方差,并说明哪个车间产品较稳定?解:(1)这种抽样方法是系统抽样;(2分)(2)x 甲=102+101+99+98+103+98+997=100(kg), s 2甲=17[(102-100)2+(101-100)2+(99-100)2+(98-100)2+(103-100)2+(98-100)2+(99-100)2]≈3.428 6(kg 2),(6分)x 乙=110+115+90+85+75+115+1107=100(kg), s 2乙≈228.57(kg 2),因为x 甲=x 乙,s 2甲<s 2乙,所以甲车间产品较稳定.(12分)16.(12分)一汽车厂生产A ,B ,C 三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):轿车A 轿车B 轿车C 舒适型 100 150 x 标准型300450600按类用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A 类轿车10辆.(1)求z 的值;(2)用分层抽样的方法在C 类轿车中抽取一个容量为5的样本,应如何抽取?解:(1)设该厂本月生产轿车n 辆, 由题意,得50n =10100+300,所以n =2 000,则z =2 000-100-300-150-450-600=400.(6分) (2)设所抽样本中有m 辆舒适型轿车,因为要用分层抽样的方法在C 类轿车中抽取一个容量为5的样本,所以4001 000=m5,解得m =2,即在C 类轿车中抽取2辆舒适型轿车,3辆标准型轿车.(12分) 17.(12分)某零售店近五个月的销售额和利润额资料如下表:商店名称 A B C D E 销售额x /千万 3 5 6 7 9 利润额y /百万元23345(1)画出散点图.观察散点图,说明两个变量有怎样的相关关系; (2)用最小二乘法计算利润额y 关于销售额x 的回归直线方程;(3)当销售额为4(千万元)时,利用(2)的结论估计该零售店的利润额(百万元).⎣⎢⎢⎢⎡⎦⎥⎥⎥⎤参考公式:b =∑i =1n(x i-x )(y i-y )∑i =1n(x i-x )2,a =y -b x 解:(1)散点图如下. 两个变量呈线性相关关系.(4分)(2)设回归直线的方程是y =bx +a . 由题中的数据可知y =3.4,x =6.所以b =∑i =1n(x i -x )(y i -y )∑i =1n(x i -x )2=-3×(-1.4)+(-1)×(-0.4)+1×0.6+3×1.69+1+1+9=1020=12.a =y -b x =3.4-12×6=0.4.所以利润额y 关于销售额x 的回归直线方程为y =0.5x +0.4.(8分) (3)由(2)知,当x =4时,y =0.5×4+0.4=2.4,所以当销售额为4千万元时,可以估计该店的利润额为2.4百万元.(12分)18.(14分)在某中学举行的信息知识竞赛中,将高二年级两个班的参赛学生成绩(得分均为整数)进行整理后分成五组,绘制出如图所示的频率分布直方图.已知图中从左到右的第一、第三、第四、第五小组的频率分别是0.30,0.15,0.10,0.05,第二小组的频数是40.(1)求第二小组的频率,并补全这个频率分布直方图;(2)求这两个班参赛的学生人数是多少?(3)这两个班参赛学生的成绩的中位数应落在第几小组内?(不必说明理由)解:(1)因为各小组的频率之和为1.00,第一、三、四、五小组的频率分别是0.30,0.15,0.10,0.05,所以第二小组的频率为1.00-(0.30+0.15+0.10+0.05)=0.40.(3分)因为第二小组的频率为0.40,所以落在59.5~69.5内的第二小组的小长方形的高=频率组距=0.4010=0.04,由此可补全频率分布直方图(如图阴影部分所示).(6分)(2)设高二年级两个班参赛的学生人数为x 人,因为第二小组的频数为40,频率为0.40,所以40x =0.40.解得x =100(人).所以高二年级两个班参赛的学生人数为100.(12分)(3)高二年级两个班参赛学生的成绩的中位数应落在第二小组内.(14分)。
高中数学必修三综合检测试题

综合检测试题(时间:120分钟满分:150分)一、选择题(每小题5分,共60分)1.总体容量为203,若采用系统抽样法进行抽样,当抽样间距为多少时不需要剔除个体( D )(A)4 (B)5 (C)6 (D)7解析:由于203=7×29,即203在四个选项中只能被7整除,故间隔为7时不需剔除个体.2.在线段[0,3]上任取一点,则此点坐标大于1的概率是( B )(A)(B)(C)(D)解析:根据几何概型可知,在线段[0,3]上任取一点,则此点坐标大于1就是1<x≤3,所以所求的概率为,故选B.3.一个射手进行射击,记事件E1:“脱靶”,E2:“中靶”,E3:“中靶环数大于4”,E4:“中靶环数不小于5”,则在上述事件中,互斥而不对立的事件共有( B )(A)1对(B)2对(C)3对(D)4对解析:E1,E2互斥且对立,E1与E3,E1与E4均为互斥而不对立的事件.E2与E3,E2与E4包含关系,E3与E4有同时发生的情况,故选B.4.某产品共有三个等级,分别为一等品、二等品和不合格品.从一箱产品中随机抽取1件进行检测,设“抽到一等品”的概率为0.65,“抽到二等品”的概率为0.3,则“抽到不合格品”的概率为( D )(A)0.95 (B)0.7 (C)0.35 (D)0.05解析:“抽到一等品”与“抽到二等品”是互斥事件,所以“抽到一等品或二等品”的概率为0.65+0.3=0.95,“抽到不合格品”与“抽到一等品或二等品”是对立事件,故其概率为1-0.95=0.05.5.用秦九韶算法求多项式f(x)=0.5x5+4x4-3x2+x-1,当x=3的值时,先算的是( C )(A)3×3=9(B)0.5×35=121.5(C)0.5×3+4=5.5(D)(0.5×3+4)×3=16.5解析:由题f(x)=(((0.5x+4)x-3)x+1)x-1.从里到外先算0.5x+4的值,即先计算0.5×3+4=5.5.故选C.6.若某校高一年级8个班参加合唱比赛的得分如茎叶图所示,则这组数据的中位数和平均数分别是( A )(A)91.5和91.5 (B)91.5和92(C)91和91.5 (D)92和92解析:这组数据从小到大排列后可得其中位数为=91.5,平均数为=91.5.故选A.7.如图所示是计算函数y=的值的程序框图,则在①,②,③处应分别填入的是( B )(A)y=-x,y=0,y=x2(B)y=-x,y=x2,y=0(C)y=0,y=x2,y=-x (D)y=0,y=-x,y=x2解析:框图为求分段函数的函数值,当x≤-1时,y=-x,故①为y=-x,当-1<x≤2时,y=0,故③为y=0,那么②为y=x2.故选B.8.已知Ω={(x,y)|x+y≤6,x≥0,y≥0},A={(x,y)|x≤4,y≥0,x-2y≥0},若向区域Ω上随机投一点P,则点P落入区域A的概率为( A ) (A)(B)(C)(D)解析:如图所示,由几何概型概率公式,得P===.故选A.9.某中学号召学生在暑假期间至少参加一次社会公益活动(以下简称活动).该校文学社共有100名学生,他们参加活动的次数统计如图所示,则从文学社中任意选1名学生,他参加活动次数为3的概率是( B )(A)(B)(C)(D)解析:从中任意选1名学生,他参加活动次数为3的概率是=.故选B.10.三个数390,455,546的最大公约数是( D )(A)65 (B)91 (C)26 (D)13解析:用辗转相除法.因为546=390×1+156,390=156×2+78,156=78×2,所以546与390的最大公约数为78.又因为455=78×5+65, 78=65+13,65=13×5,所以455与78的最大公约数为13,故390,455, 546的最大公约数为13.故选D.11.某程序框图如图所示,若输出的结果是126,则判断框中可以是( A )(A)i>6? (B)i>7? (C)i≥6? (D)i≥5?解析:根据题意可知该程序运行情况如下:第1次:S=0+21=2,i=1+1=2;第2次:S=2+22=6,i=3;第3次:S=6+23=14,i=4;第4次:S=14+24=30,i=5;第5次:S=30+25=62,i=6;第6次:S=62+26=126,i=7;此时S=126,结束循环,因此判断框应该是“i>6?”.故选A.12.有2个人从一座10层大楼的底层进入电梯,设他们中的每一个人自第二层开始在每一层离开是等可能的,则2个人在不同层离开的概率为( D )(A)(B)(C)(D)解析:设2个人分别在x层、y层离开,则记为(x,y).基本事件构成集合Ω={(2,2),(2,3),(2,4),…,(2,10),(3,2),(3,3),(3,4),…, (3,10),…,(10,2),(10,3),(10,4),…,(10,10)},所以除了(2,2),(3,3),(4,4),…,(10,10)以外,都是2个人在不同层离开,故所求概率 P==.故选D.二、填空题(每小题5分,共20分)13.某课题组进行城市空气质量调查,按地域把24个城市分成甲、乙、丙三组,对应城市数分别为4,12,8.若用分层抽样方法抽取6个城市,则甲组中应抽取的城市数为个.解析:甲组中应抽取的城市数为×4=1(个).答案:114.利用秦九韶算法,求当x=23时,多项式7x3+3x2-5x+11的值的算法.①第一步:x=23,第二步:y=7x3+3x2-5x+11,第三步:输出y;②第一步:x=23,第二步:y=((7x+3)x-5)x+11,第三步:输出y;③算6次乘法,3次加法;④算3次乘法,3次加法.以上描述正确的序号为.解析:利用秦九韶算法,y=((7x+3)x-5)x+11,算3次乘法,3次加法,故②④正确.答案:②④15.执行如图所示的程序框图,输出的T= .解析:按照程序框图依次执行为S=5,n=2,T=2;S=10,n=4,T=2+4=6;S=15,n=6,T=6+6=12;S=20,n=8,T=12+8=20;S=25,n=10,T=20+10=30>S,输出T=30.答案:3016.甲、乙两个人玩一转盘游戏(转盘如图①,“C为弧AB的中点”),任意转动转盘一次,指针指向圆弧AC时甲胜,指向圆弧BC时乙胜.后来转盘损坏如图②,甲提议连接AD,∠OAD=,取AD的中点E,若任意转动转盘一次,指针指向线段AE时甲胜,指向线段ED时乙胜.然后继续游戏,你觉得此时游戏还公平吗?答案: ,因为P甲P乙(填“<”“>”或“=”).解析:连接OE(图略),在直角三角形AOD中,∠AOE=,∠DOE=,若任意转动转盘一次,指针指向线段AE的概率是÷=,指针指向线段ED的概率是÷=,所以乙胜的概率大,即这个游戏不公平.答案:不公平<三、解答题(共70分)17.(本小题满分10分)某电视台在一次对收看文艺节目和新闻节目的抽样调查中,随机抽取了100名电视观众,相关的数据如表所示:类别文艺节目新闻节目总计20至40岁40 18 58大于40岁15 27 42 总计55 45 100(1)由表中数据直观分析,收看新闻节目的观众是否与年龄有关?(2)用分层抽样方法在收看新闻节目的观众中随机抽取5名,则大于40岁的观众应该抽取几名?解:(1)由于大于40岁的42人中有27人收看新闻节目,而20至40岁的58人中,只有18人收看新闻节目,故收看新闻节目的观众与年龄、有关.(2)×5=3(名),所以大于40岁的观众应抽取3名.18.(本小题满分12分)某儿童乐园在“六一”儿童节推出了一项趣味活动.参加活动的儿童需转动如图所示的转盘两次,每次转动后,待转盘停止转动时,记录指针所指区域中的数.设两次记录的数分别为x,y.奖励规则如下:①若xy≤3,则奖励玩具一个;②若xy≥8,则奖励水杯一个;③其余情况奖励饮料一瓶.假设转盘质地均匀,四个区域划分均匀.小亮准备参加此项活动.(1)求小亮获得玩具的概率;(2)请比较小亮获得水杯与获得饮料的概率的大小,并说明理由.解:用数对(x,y)表示儿童参加活动先后记录的数,则基本事件空间Ω与点集S={(x,y)|x∈N,y∈N,1≤x≤4,1≤y≤4}一一对应.因为S中元素个数是4×4=16,所以基本事件总数为n=16.(1)记“xy≤3”为事件A.则事件A包含的基本事件共有5个,即(1,1),(1,2),(1,3),(2,1),(3,1),所以P(A)=,即小亮获得玩具的概率为.(2)记“xy≥8”为事件B,“3<xy<8”为事件C,则事件B包含的基本事件共有6个,即(2,4),(3,3),(3,4),(4,2),(4,3),(4,4),所以P(B)==.则事件C包含的基本事件共有5个,即(1,4),(2,2),(2,3),(3,2),(4,1),所以P(C)=.因为>,所以小亮获得水杯的概率大于获得饮料的概率.19.(本小题满分12分)某出租车公司为了解本公司出租车司机对新法规的知晓情况,随机对100名出租车司机进行调查,调查问卷共10道题,答题情况如下表所示.答对题目数[0,8) 8 9 10女 2 13 12 8男 3 37 16 9 (1)如果出租车司机答对题目数大于等于9,就认为该司机对新法规的知晓情况比较好,试估计该公司的出租车司机对新法规知晓情况比较好的概率;(2)从答对题目数小于8的出租车司机中任选出2人做进一步的调查,求选出的2人中至少有一名女出租车司机的概率.解:(1)答对题目数小于9的人数为55,记“答对题目数大于等于9”为事件A,P(A)=1-=0.45.(2)设答对题目数小于8的出租车司机为A,B,C,D,E,其中A,B为女出租车司机,任选出2人包含AB,AC,AD,AE,BC,BD,BE,CD,CE,DE,共10种情况,至少有一名女出租车司机的事件为AB,AC,AD,AE,BC,BD,BE,共7种.记“选出的2人中至少有一名女出租车司机”为事件M,则P(M)==0.7.20.(本小题满分12分)某培训班共有n名学生,现将一次某学科考试成绩(单位:分)绘制成频率分布直方图,如图所示.其中落在[80,90)内的频数为36.(1)请根据图中所给数据,求出a及n的值;(2)从如图5组中按分层抽样的方法选取40名学生的成绩作为一个样本,求在第一组、第五组(从左到右)中分别抽取了几名学生的成绩;(3)在(2)抽取的样本中的第一与第五组中,随机抽取两名学生的成绩,求所取两名学生的平均分不低于70分的概率.解:(1)第四组的频率为1-0.05-0.075-0.225-0.35=0.3,所以a==0.03,n==120.(2)第一组应抽0.05×40=2(名),第五组应抽0.075×40=3(名).(3)设第一组抽取的2个分数记作A1,A2,第五组的3个分数记作B1,B2,B3,那么从这两组中抽取2个的结果有A1A2,A1B1,A1B2,A1B3,A2B1,A2B2,A2B3,B1B2,B1B3,B2B3,共10种,其中平均分不低于70分的有9种,故所求概率为P=.21.(本小题满分12分)某车间为了规定工时定额,需要确定加工零件所花费的时间,为此做了四次试验,得到的数据如表所示:零件的个数x/个 2 3 4 5加工的时间y/h 2.5 3 4 4.5 (1)在给定的坐标系中画出表中数据的散点图;(2)求出y关于x的回归直线方程=x+,并在坐标系中画出回归直线;(3)试预测加工10个零件需要多少时间.解:(1)散点图如图.(2)由表中数据得x i y i=52.5,=3.5,=3.5,=54.代入公式得=0.7,=-=3.5-0.7×3.5=1.05,所以=0.7x+1.05.回归直线如图中所示.(3)将x=10代入回归直线方程,得=0.7×10+1.05=8.05(h).所以预测加工10个零件需要8.05 h.22.(本小题满分12分)某同学利用国庆节期间进行社会实践活动,在[25,55]岁的人群中随机抽取n人进行了一次生活习惯是否符合低碳生活的调查,若生活习惯符合低碳生活的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数的频率分布直方图.组数分组“低碳族”的人数占本组的频率第一组[25,30) 120 0.6第二组[30,35) 195 p第三组[35,40) 100 0.5第四组[40,45) a 0.4第五组[45,50) 30 0.3第六组[50,55] 15 0.3(1)补全频率分布直方图,并求n,a,p的值;(2)从年龄在[40,50)岁的“低碳族”中采用分层抽样的方法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中恰有1人年龄在[40,45)岁的概率.解:(1)第二组的概率为1-(0.04+0.04+0.03+0.02+0.01)×5=0.3,所以==0.06.补全频率分布直方图如图,第一组的人数为=200,频率为0.04×5=0.2,所以n==1 000.因为第二组的频率为0.3,所以第二组的人数为 1 000×0.3=300,所以p==0.65.第四组的频率为0.03×5=0.15,所以第四组的人数为 1 000×0.15=150.所以a=150×0.4=60.(2)因为年龄在[40,45)岁的“低碳族”与[45,50)岁的“低碳族”的人数的比为60∶30=2∶1,所以采用分层抽样法抽取6人,[40,45)中有4人,[45,50)中有2人.设[40,45)中的4人为a,b,c,d,[45,50)中的2人为m,n,则选取2人作为领队的情况有(a,b),(a,c),(a,d), (a,m),(a,n),(b,c),(b,d),(b,m),(b,n),(c,d),(c,m),(c,n),(d,m),(d,n),(m,n),共15种,其中恰有1人年龄在[40,45)岁的情况有(a,m),(a,n),(b,m),(b,n),(c,m),(c,n),(d,m),(d,n),共8种,所以选取的2名领队中恰有1人年龄在[40,45)岁的概率P=.。
2019年人教版高中数学必修三综合测试题(含答案)

必修3综合模拟测试卷A(含答案)一、选择题:(本题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的)1、用冒泡排序算法对无序列数据进行从小到大排序,则最先沉到最右边的数是A、最大数B、最小数C、既不最大也不最小D、不确定2、甲、乙、丙三名同学站成一排,甲站在中间的概率是A、16B、12C、13D、233、某单位有老年人28 人,中年人54人,青年人81人,为了调查他们的身体状况的某项指标,需从他们中间抽取一个容量为36样本,则老年人、中年人、青年人分别各抽取的人数是A、6,12,18B、7,11,19C、6,13,17D、7,12,174、甲、乙两位同学都参加了由学校举办的篮球比赛,它们都参加了全部的7场比赛,平均得分均为16分,标准差分别为5.09和3.72,则甲、乙两同学在这次篮球比赛活动中,发挥得更稳定的是A、甲B、乙C、甲、乙相同D、不能确定5、从1,2,3,4这4个数中,不放回地任意取两个数,两个数都是偶数的概率是A、16B、C、13D、6、如图,是由一个圆、一个三角形和一个长方形构成的组合体,现用红、蓝两种颜色为其涂色,每个图形只能涂一种颜色,则三个形状颜色不全相同的概率为A 、34B 、38C 、14D 、187、阅读下列程序:输入x ;if x <0, then y :=32x π+;else if x >0, then y :=52x π-+;else y :=0; 输出 y .如果输入x =-2,则输出结果y 为A 、3+πB 、3-πC 、π-5D 、-π-5 8、一射手对同一目标独立地进行4次射击,已知至少命中一次的概率为8180,则此射手的命中率是 A 、31 B 、32 C 、41 D 、529、根据下面的基本语句可知,输出的结果T 为 i:=1; T:=1;For i:=1 to 10 do; Begin T:=T+1;End 输出T开始 S :=0 i :=3 i :=i +1S :=S +ii >5 输出S结束是 否A 、10B 、11C 、55D 、56 10、在如图所示的算法流程图中,输出S 的值为 A 、11 B 、12 C 、13 D 、15二、填空题:(本题共4小题,每小题5分,共20分,请把答案填写在答题纸上) 11、一个容量为20的样本数据,分组后,组距与频数如下:(]10,20,2;(]20,30, 3;(]30,40,4;(]40,50,5;(]50,60,4 ;(]60,70,2。
最新人教版高中数学必修3第三章模块综合测评1

模块综合测评(一)(时间:100分钟,满分:100分)一、选择题(每小题4分,共48分)1.某学校有小学生126人,初中生280人,高中生95人,为了调查学生的身体状况,需要从他们当中抽取一个容量为100的样本,采用_________方法较为恰当( ) A.简单随机抽样 B.系统抽样C.分层抽样D.先从小学生中剔除1人,然后分层抽样 答案:D2.下列说法中,不正确的是( )A.简单随机抽样是从个数较少的总体中抽取个体B.系统抽样是从个体较多的总体中将总体均分,再按事先确定的规则在各部分抽取个体C.系统抽样是将差异明显的总体分成几部分再从各部分抽取个体D.分层抽样是将由差异明显的几部分组成的总体分成几层,分层进行抽取个体 答案:C3.输出两个变量a 、b 的值的语句中不正确的是( )A.print(%io(2),a,b)B.print(%io(2),“a,b”)C.print(%io(2),“a,b”,a,b)D.print(%io(2),“a,b=”,a,b) 答案:B4.如果两组数x 1,x 2,…,x n 和y 1,y 2,…,y n 的平均数分别为x 和y ,标准差分别为s 1和s 2,那么合为一组数x 1,x 2,…,x n ,y 1,y 2,…,y n 后的平均数和标准差分别是( )A.2,2221s s y x ++B.2,2221s s y x ++C.2,22221s s y x ++D.2,22221s s y x ++ 答案:D5.把红、黑、白、蓝四张纸牌随机地分给甲、乙、丙、丁四个人,每人得一张,事件“甲分得白牌”与事件“乙分得红牌”是( )A.对立事件B.不可能事件C.互斥但非对立事件D.以上都不对 答案:D6.某学校共有初中生900人,其中初一学生300人,初二学生200人,初三学生400人,现采用分层抽样的方法抽取容量为45的样本,那么初一、初二、初三各年级抽取的人数分别为( )A.15,5,25B.15,15,15C.10,5,30D.15,10,20 答案:D7.关于频率分布直方图中的有关数据,下列说法正确的是( ) A.直方图的高表示该组上的个体在样本中出现的频率 B.直方图的高表示取某数的频率C.直方图的高表示该组上的个体数与组距的比值D.直方图的高表示该组上的个体在样本中出现的频率与组距的比值 答案:D8.在数学考试中,小明的成绩在90分以上的概率是0.18,在80—89分的概率是0.51,在70—79分的概率是0.15,在60—69分的概率是0.09,则小明不及格(60分以下)的概率是( )A.0.93B.0.69C.0.31D.0.07 答案:D9.从甲袋中摸出一个红球的概率是31,从乙袋中摸出一个红球的概率是21,从两个袋中各摸出一球,则32等于( ) A.两球都不是红球的概率 B.两球都是红球的概率C.至少有一个红球的概率D.两球中恰好有一个红球的概率 答案:C10.(2007山东济宁模拟)阅读如图所示的程序框图:输出的结果为( )A.20B.3C.5D.15 ∵a 的初值为5.每循环一次a 的值减1.故循环2次. ∴s=20. 答案:A11.在数轴上的区间[0,3]上任取一点,则此点落在区间[2,3]上的概率是( )A.31 B.21 C.32 D.43 解析:由两区间长度之比得31,∴选A.答案:A12.从甲、乙、丙三人中任选两名代表,则甲被选上的概率为( ) A.31 B.32 C.43 D.61 答案:B二、填空题(每小题4分,共16分)13.某校高中部有学生1 600人,其中高一520人,高二500人,高三580人,如果想抽出80人调查学生情况,考虑到不同年级学生的情况有明显差异,而同一年级学生间差异较小则应采用___________方法抽样,高一学生应抽查___________人. 答案:分层 2614.某人午觉醒来,发现表停了,他打开收音机想听电台报时(电台整点报时),则他等待的时间不多于6分钟的概率是___________. 答案:101 15.把50个数据分成6个组,有一个组有15个数据,那么该组的频数是___________,频率是___________. 答案:15 0.316.(2007山东潍坊期中)下图所示的程序框图的输出结果是____________.当i=1,n=2时,S=2,n=4, 当i=2时,S=6,n=6. 当i=3时,S=12,n=8 当i=4>3时,输出12. 答案:12三、解答题(共36分)17.(8分)某工厂在职人员100人,其中干部10人,科室人员20人,工人70人,为了解工厂改革的意见,从中抽取一个容量为20的样本,试确定如何抽样,并写出具体实施过程. 解析:因为工厂改革关系到不同层次的人的不同利益,故采用分层抽样,各层可采取简单随机抽样. ∵20100=5,∴510=2,570=14,520=4. ∴从干部中抽取2人,科室人员抽取4人,从工人中抽取14人.因干部与科室人员的人数较少,把他们分别按1—10与1—20编号,然后采用抽签法分别抽2人和4人;对工人70人进行00,01,02,…,69编号,然后用随机数表法抽取14人.(2)至少3人排队等候的概率是多少?记事件在窗口等候的人数为0,1,2,3,4,5人及5人以上分别为A 、B 、C 、D 、E 、F. (1)至多2人排队等候的概率是P(A ∪B ∪C)=P(A)+P(B)+P(C)=0.1+0.16+0.3=0.56.(2)方法一:至少3人排队等候的概率是P(D ∪E ∪F)=P(D)+P(E)+P(F)=0.3+0.1+0.04=0.44. 方法二:因为至少3人排队等候与至多2人排队等候是对立事件,故由对立事件的概率公式,至少3人排队等候的概率是P (D ∪E ∪F)=1-P(A ∪B ∪C)=1-0.56=0.44. ∴至多2人排队等候的概率是0.56,至少3个排队等候的概率是0.44. 19.(10分)对任意正整数,设计一个求S=1+n13121+++ 的值的程序框图. 解析:20.(10分)(2007山东临沂模拟)某中学图书馆将图书分为自然科学、文学艺术、社会百科、数学四类.在“深圳读书月”活动期间,为了解图书的借阅情况,图书管理员对本月各类图书的借阅量进行了统计,表甲和图乙是图书管理员通过采集数据后,绘制的两幅不完整的频率分布表与频率分布条形图.请你根据图中和表中提供的信息,解答以下问题:(1)填充表甲频率分布表中的空格;(2)在图乙中,将表示“自然科学”的部分补充完整. 解析:(1)自然科学对应的频率=1-0.50-0.25-0.05=0.20,自然科学对应的频数=50.01000×0.20=400. (2)如图所示导学乐园靠自己小蜗牛问妈妈:为什么我们从生下来,就要背负这个又硬又重的壳呢?妈妈:因为我们的身体没有骨骼的支撑,只能爬,又爬不快.所以要这个壳的保护!小蜗牛:毛虫姊姊没有骨头,也爬不快,为什么她却不用背这个又硬又重的壳呢?妈妈:因为毛虫姊姊能变成蝴蝶,天空会保护她啊.小蜗牛:可是蚯蚓弟弟也没骨头,也爬不快,更不会变成蝴蝶,他为什么不用背这个又硬又重的壳呢?妈妈:因为蚯蚓弟弟会钻土, 大地会保护他啊.小蜗牛哭了起来:我们好可怜,天空不保护,大地也不保护.蜗牛妈妈安慰他:所以我们有壳啊!我们不靠天,也不靠地,我们靠自己.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中数学必修三模块综合测试卷一、选择题(每小题5分,共60分) 1.下列给出的赋值语句中正确的是:( )A 、3=AB 、M=—MC 、B=A=2D 、x+y=0 2.把89化成五进制数的末位数字为 ( ) A 1 B 2 C 3 D 4 3.如右图,是某算法流程图的一部分,其算法的逻辑结构为 ( )A. 顺序结构B. 判断结构C. 条件结构D. 循环结构4.某公司在甲、乙、丙、丁四个地区分别有150个、120个、180个、150个销售点,公司为了调查产品销售的情况,需从这600个销售点中抽取一个容量为100的样本,记这项调查为(1);在丙地区中有20个特大型销售点,要从中抽取7个调查其销售收入和售后服务情况,记这项调查为(2)。
则完成(1)、(2)这两项调查宜采用的抽样方法依次是 ( ) A 、 分层抽样法,系统抽样法 B 、分层抽样法,简单随机抽样法 C 、系统抽样法,分层抽样法 D 、简单随机抽样法,分层抽样法 5.下列对一组数据的分析,不正确的说法是 ( ) A 、数据极差越小,样本数据分布越集中、稳定 B 、数据平均数越小,样本数据分布越集中、稳定 C 、数据标准差越小,样本数据分布越集中、稳定 D 、数据方差越小,样本数据分布越集中、稳定6.有五组变量:①汽车的重量和汽车每消耗1升汽油所行驶的平均路程;②平均日学习时间和平均学习成绩; ③某人每日吸烟量和其身体健康情况; ④正方形的边长和面积; ⑤汽车的重量和百公里耗油量; 其中两个变量成正相关的是 ( )A .①③B .②④C .②⑤D .④⑤7.计算机中常用16进制,采用数字0~9和字母A ~F 共16个计数符号与10进制得对应关系如下表: 例如用16进制表示D+E =1B ,则A ×B=( ) A 6E B 7C C 5F D B08.从一批产品中取出三件产品,设A =“三件产品全不是次品”,B =“三件产品全是次品”,C =“三件产品至少有一件是次品”,则下列结论正确的是( ) A . A 与C 互斥 B . 任何两个均互斥 C . B 与C 互斥D . 任何两个均不互斥9.从一箱产品中随机地抽取一件,设事件A={抽到一等品},事件B ={抽到二等品},事件C ={抽到三等品},且已知 P (A )= 0.65 ,P(B)=0.2 ,P(C)=0.1。
则事件“抽到的不是一等品”的概率为( )A. 0.7B. 0.65C. 0.35D. 0.3 10.先后抛掷质地均匀的硬币三次,则至少一次正面朝上的概率是 ( )A.81B. 83C. 85D. 87 11.在如图所示的“茎叶图”表示的数据中,众数和中位数分别 ( )A.23与26B.31与26C.24与30D.26与3012.从装有2个红球和2个白球的袋内任取2个球,则互斥而不对立的两个事件是( ) A.至少有1个红球和全是白球 B.至少有1个白球和全是白球 C.恰有1个白球和恰有两个白球 D.至少有1个白球和全是红球 二、填空题(每小题5分,共20分)13.计算机的程序设计语言很多,但各种程序语言都包含下列基本的算法语句: , , , , 。
14.为了解某地高一年级男生的身高情况,从其中的一个学校选取容量为60的样本(60名男生的身高,单位:cm),分组情况如下:则表中的, 。
15.如右图,在正方形内有一扇形(见阴影部分),扇形对应的圆心是正方形的一顶点,半径为正方形的边长。
在这个图形上随机撒一粒黄豆,它落在扇形外正方形内的概率为 。
(用分数表示)16.下列说法中正确的有________①平均数不受少数几个极端值的影响,中位数受样本中的每一个数据影响; ②抛掷两枚硬币,出现“两枚都是正面朝上”、“两枚都是反面朝上”、“恰好一枚硬币正面朝上”的概率一样大③用样本的频率分布估计总体分布的过程中,样本容量越大,估计越准确。
④向一个圆面内随机地投一个点,如果该点落在圆内任意一点都是等可能的,则该随机试验的数学模型是古典概型。
三、解答题: 17.(10分)为了参加奥运会,对自行车运动员甲、乙两人在相同的条件下进行了6次测试,测得他们的最大速度的数据如表所示:请判断:谁参加这项重大比赛更合适,并阐述理由。
18.(12分)下面是计算应纳税所得额的算法过程,其算法如下:第一步 输入工资x(注x<=5000);第二步 如果x<=800,那么y=0;如果800<x<=1300,那么 y=0.05(x-800);否则 y=25+0.1(x-1300) 第三步 输出税款y, 结束。
请写出该算法的程序框图和程序。
(注意:程序框图与程序必须对应)1 2 4 2 0 3 5 6 3 0 1 1 4 1 219.(12分)为了调查甲、乙两个网站受欢迎的程度,随机选取了14天,统计上午8:00—10:00间各自的点击量,得如下所示的统计图,根据统计图: (1)甲、乙两个网站点击量的极差分别是多少? (4分) (2)甲网站点击量在[10,40]间的频率是多少? (4分) (3)甲、乙两个网站哪个更受欢迎?并说明理由。
(4分)20. (本题12分)对甲乙两名学生的成绩进行抽样分析,各抽5门功课得到的观测值如下:问甲、乙谁的平均成绩好,谁的各门功课发展较平衡。
甲 60 80 70 90 70 乙806070807521.(12分)假设你家订了一份报纸,送报人可能在早上6点—8点之间把报纸送到你家,你每天离家去工作的时间在早上7点—9点之间(1)你离家前不能看到报纸(称事件A )的概率是多少?(6分,须有过程)(2)请你设计一种随机模拟的方法近似计算事件A 的概率(包括手工的方法或用计算器、计算机的方法)(6分)茎叶图122.(本小题满分12分)给出50个数,1,2,4,7,11,…,其规律是:第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,…,以此类推. 要求计算这50个数的和. 先将下面给出的程序框图补充完整,再根据程序框图写出程序.1. 把程序框图补充完整:(1)________________________ (3分)(2)________________________ (4分)2. 程序:(5分)高中数学必修三模块综合测试卷(二)参考答案一、选择题(每小题5分,共60分)二、填空题(每小题5分,共20分)11.输入语句 ,输出语句 , 赋值语句 , 条件语句 , 循环语句 。
12.=m 6 , =a 0.45 。
13.44π- 14. ③ 。
三、解答题: 15.(12分)为了参加奥运会,对自行车运动员甲、乙两人在相同的条件下进行了6次测试,测得他们的最大速度的数据如表所示:请判断:谁参加这项重大比赛更合适,并阐述理由。
解:336313537303827=+++++=甲X茎叶图336362834382933=+++++=乙X ( 4分)S 甲=958.3694≈, S 乙=559.3338≈ (8分) 乙甲X X =,S 甲>S 乙 (10分)乙参加更合适 (12分)16.(13分)下面是计算应纳税所得额的算法过程,其算法如下:第一步 输入工资x(注x<=5000);第二步 如果x<=800,那么y=0;如果800<x<=1300,那么 y=0.05(x-800);否则 y=25+0.1(x-1300) 第三步 输出税款y, 结束。
请写出该算法的程序框图和程序。
(注意:程序框图与程序必须对应) 解:框图7分,程序6分(不对应扣3-4分)17.(13分)为了调查甲、乙两个网站受欢迎的程度,随机选取了14天,统计上午8:00—10:00间各自的点击量,得如下所示的统计图,根据统计图:(1)甲、乙两个网站点击量的极差分别是多少? (4分) (2)甲网站点击量在[10,40]间的频率是多少? (5分) (3)甲、乙两个网站哪个更受欢迎?并说明理由。
(4分) 解:(1)甲网站的极差为:73-8=65; (2分)乙网站的极差为:61-5=56 (4分)(2)甲网站点击量在[10,40]间的频率为4/14=2/7=0.28571 (9分)(3)甲网站的点击量集中在茎叶图的下方,而乙网站的点击量集中在茎叶图的上方。
从数据的分布情况来看,甲网站更受欢迎。
(13分)18.(本小题满分14分)在人群流量较大的街道,有一中年人吆喝“送钱”,只见他手拿一黑色小布袋,袋中有3只黄色、3只白色的乒乓球(其体积、质地完成相同),旁边立着一块小黑板写道:摸球方法:从袋中随机摸出3个球,若摸得同一颜色的3个球,摊主送给摸球者5元钱;若摸得非同一颜色的3个球,摸球者付给摊主1元钱。
(1)摸出的3个球为白球的概率是多少?(2)摸出的3个球为2个黄球1个白球的概率是多少?(3)假定一天中有100人次摸奖,试从概率的角度估算一下这个摊主一个月(按30天计)能赚多少钱?解:把3只黄色乒乓球标记为A、B、C,3只白色的乒乓球标记为1、2、3。
从6个球中随机摸出3个的基本事件为:ABC、AB1、AB2、AB3、AC1、AC2、AC3、A12、A13、A23、BC1、BC2、BC3、B12、B13、B23、C12、C13、C23、123,共20个(1)事件E={摸出的3个球为白球},事件E包含的基本事件有1个,即摸出123号3个球,P(E)=1/20=0.05(2)事件F={摸出的3个球为2个黄球1个白球},事件F包含的基本事件有9个,P (F)=9/20=0.45(3)事件G={摸出的3个球为同一颜色}={摸出的3个球为白球或摸出的3个球为黄球},P(G)=2/20=0.1,假定一天中有100人次摸奖,由摸出的3个球为同一颜色的概率可估计事件G发生有10次,不发生90次。
则一天可赚⨯-⨯,每月可赚1200元。
90=10540119.(14分)假设你家订了一份报纸,送报人可能在早上6点—8点之间把报纸送到你家,你每天离家去工作的时间在早上7点—9点之间(1)你离家前不能看到报纸(称事件A)的概率是多少?(8分,须有过程)(2)请你设计一种随机模拟的方法近似计算事件A的概率(包括手工的方法或用计算器、计算机的方法)(6分)Array解:如图,设送报人到达的时间为X,小王离家去工作的时间为Y。
(X,Y)可以看成平面中的点,试验的全部结果所构成的区域为YXX,,(一个正方形区域,ΩY)86/7={≤≤≤≤}9面积为SΩ=4,事件A表示小王离家前不能看到报纸,所构成的区域为A={(X,Y)/≤X>≤≤,即图中的阴影部分,≤,Y9X}786Y面积为S A=0.5。
这是一个几何概型,所以P(A)=S A/SΩ=0.5/4=0.125。
