《111探索勾股定理》导学案
《探索勾股定理》第一课时(完整版)精品导学案

精品"正版〞资料系列,由本公司独创 .旨在将"人教版〞、〞苏教版"、〞北师大版"、〞华师大版"等涵盖几乎所有版本的教材教案、课件、导学案及同步练习和检测题分享给需要的朋友 .本资源创作于2021年8月,是当前最||新版本的教材资源 .包含本课对应内容,是您备课、上课、课后练习以及寒暑假预习的最||正确选择 .1.1 探索勾股定理(1 )学习目标:1.了解勾股定理的发现过程,掌握勾股定理的内容,会用面积法证明勾股定理. 2.培养在实际生活中发现问题总结规律的意识和能力.了解我国古代在勾股定理研究方面所取得的成就.学习重点:勾股定理的内容及证明.学习难点:勾股定理的证明.自助探究1、相传2500年前,古希腊的数学家毕达哥拉斯在朋友家做客时,发现朋友家用地砖铺成的地面中反映了直角三角形三边的某种数量关系. 请同学们也观察一下,看看能发现什么?(1) 引导学生观察三个正方形之间的面积的关系;(2) 引导学生把面积的关系转化为边的关系.结论:等腰直角三角形三边的特殊关系:斜边的平方等于两直角边的平方和. 2、等腰直角三角形有上述性质,其它直角三角形也有这个性质吗?3、猜想:4、动手操作、验证猜想:(二)动手在纸上作出几个直角三角形,分别测量它们的三条边,填写好下表.观察三条边的平方有什么关系?(其中a、b是两直角边长,c是斜边长)a2 b2 c2结论.我们古代把直角三角形中较短的直角边称为,较长的直角边称为,斜边称为.从而得到著名的勾股定理:.如果用a、b和c分别表示直角三角形的两直角边和斜边,那么.课题检测1. 求出以下直角三角形中未知边的长度.2、求斜边长17厘米、一条直角边长15厘米的直角三角形的面积.稳固练习1.在△ABC中,∠C=90° , (l )假设a=5 ,b=12 ,那么c=(2 )假设c=5 ,a=3 ,那么b=2.等腰△ABC的腰长AB=10cm ,底BC为16cm ,那么底边上的高为,面积为.3.△ABC中,AB=15 ,AC=13 ,高AD=12 ,那么△ABC的周长为.4.一个抽斗的长为24cm ,宽为7cm ,在抽斗里放铁条,铁条最||长能是多少?总结评价:今天的学习,我学会了:,我在方面的表现很好,在方面表现不够,以后要注意的是:.总体表现 (优、良、差 ) ,愉悦指数 (快乐、一般、痛苦 ) .以下为赠送内容别想一下造出大海,必须先由小河川开始 .成功不是只有将来才有,而是从决定做的那一刻起,持续积累而成!人假设软弱就是自己最||大的敌人,人假设勇敢就是自己最||好的朋友 .成功就是每天进步一点点!如果要挖井,就要挖到水出为止 .即使爬到最||高的山上,一次也只能脚踏实地地迈一步 .今天拼搏努力,他日谁与争锋 .在你不害怕的时候去斗牛,这不算什么;在你害怕的时候不去斗牛,这没什么了不起;只有在你害怕的时候还去斗牛才是真正的了不起 .行动不一定带来快乐,但无行动决无快乐 .只有一条路不能选择- -那就是放弃之路;只有一条路不能拒绝|| - -那就是成长之路 .坚韧是成功的一大要素,只要在门上敲得够久够大声,终会把人唤醒的 .只要我努力过,尽力过,哪怕我失败了,我也能拍着胸膛说:"我问心无愧 ."用今天的泪播种,收获明天的微笑 .人生重要的不是所站的位置,而是所朝的方向 .弱者只有千难万难,而勇者那么能披荆斩棘;愚者只有声声哀叹,智者却有千路万路 .坚持不懈,直到成功!最||淡的墨水也胜过最||强的记忆 .凑合凑合,自己负责 .有志者自有千计万计,无志者只感千难万难 .我中|考,我自信!我尽力我无悔!听从命运安排的是凡人;主宰自己命运的才是强者;没有主见的是盲从,三思而行的是智者 .相信自己能突破重围 .努力造就实力,态度决定高度 .把自己当傻瓜,不懂就问,你会学的更多 .人的活动如果没有理想的鼓舞,就会变得空虚而渺小 .安乐给人予舒适,却又给人予早逝;劳作给人予磨砺,却能给人予长久 .眉毛上的汗水和眉毛下的泪水,你必须选择一样!假设不给自己设限,那么人生中就没有限制你发挥的藩篱 .相信自己我能行!任何业绩的质变都来自于量变的积累 .明天的希望,让我们忘了今天的痛苦 .世|界上最||重要的事情,不在于我们身在何处,而在于我们朝着什么方向走 .爱拼才会赢努力拼搏,青春无悔!。
探索勾股定理导学案

课题:探索勾股定理(1)【学习目标】1.通过测量,数格子等方法探索得到勾股定理.2.利用勾股定理解决生活中的一些问题,培养学生数学应用意识.3.阅读了解古代人民对勾股定理的研究及聪明才智.激发学习的兴趣.【学习重点】探索勾股定理,应用勾股定理.【学习难点】探索勾股定理【知识链接】阅读课本第4页,回答下列问题:1.我国古代把直角三角形中较短的直角边称为______,较长的直角边称为_______,斜边称为_______.2.勾股定理:直角三角形两直角边的平方和等于斜边的___________.如果用a ,b 和c 分别表示直角三角形的两条直角边和斜边,那么a ,b ,c 满足关系式________________. 学法指导:勾股定理只适用于直角三角形,揭示的是直角三角形三边之间的关系,只要已知直角三角形某两条边的长,即可得出第三边的长.【自主学习】1.画一个直角三角形,使它的两条直角边分别为3㎝和4㎝,斜边的长固定了吗?大家测量比较一下.归纳:在直角三角形中,任意两条边确定了,另外一条边也就随之________了.【合作探究】探究1:1.分别作出直角边为①5㎝,12㎝;②6㎝,8㎝的二个直角三角形,测量各斜边长,并填空:(a,b 是两直角边长,c 是斜边长)①a2=_____.b2=_____.c2=_____. ②a2=_____.b2=_____.c2=_____. 你发现三边长的平方之间有什么关系?用式子可以表示为____________________.2.观察下图,回答问题.图1 图2(2)图1、图2中直角三角形三边的平方分别是多少,它们满足上面所猜想的数量关系吗?你是如何计算的?小组交流一下.(3)如果直角三角形的两直角边不是整数而分别是1.6个和2.4个单位长度,上面的猜想的数量关系还成立吗?归纳:1.我国古代把直角三角形中较短的直角边称为______,较长的直角边称为_______,斜边称为_______.2.勾股定理:直角三角形两直角边的平方和等于斜边的___________.如果用a ,b 和c 分别表示直角三角形的两条直角边和斜边,那么a ,b ,c 满足关系式________________. 探究2: 从电线杆距离地面12米处向地面拉一条13米长的钢缆,如图,求地面钢缆固定点A 到电线杆底部B 的距离. 解:在R t △ABC 中,由勾股定理得:222__________-=AB =25121322=-∴AB =________.∴钢缆固定点A 到电线杆底部B 的距离是_____米.归纳:在R t △ABC 中,∠C =90°,∠A 、∠B 、∠C 的对边分别为a 、b 、c ,则(1)=2c ____________;(2)=2a _____________;(3)=2b ______________.【巩固提升】1、已知一个直角三角形三边长的平方和为18002cm ,则斜边长为( )A 、30cmB 、80cmC 、90cmD 、120cm2、如图所示,在△ABC 中,AD ⊥BC 于点D ,AB =13,BC =14,BD =5,求AC 的长.【学案整理】A B C A B DC课题:探索勾股定理(2)【学习目标】1. 进一步一般化,通过拼图验证勾股定理.2. 利用勾股定理解决生活中的一些数学问题.3. 了解勾股定理对人类发展重要作用,体会它的重大意义和文化价值.【学习重点】验证勾股定理及运用勾股定理解决一些实际问题.【学习难点】运用勾股定理解决一些实际问题.【知识链接】阅读课本8-9页,回答下列问题:1、勾股定理的验证方法很多,图1-5用的方法是________,图1-6用的方法是_________.2、我国历史上将图1-6中弦上的正方形称为_________.学法指导:本课中验证勾股定理,关键是利用两种不同的方法求同一个图形的面积,从而推导出勾股定理.【自主学习】准备材料:5个全等的直角三角形纸片(边长为a、b、c),一个边长为a的正方形,一个边长b为的正方形,一个边长为c的正方形纸片。
探索勾股定理导学案

第一讲:探索勾股定理导学案(总4页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--第一讲:探索勾股定理导学案【教学重点与难点】重点:探索勾股定理并能简单的运用.难点:利用数形结合的方法验证勾股定理.【教学过程】 一、引入新课引例:从电线杆离地面8m 处向地面拉一条钢索,如果这条钢索在地面的固定点距离电线杆底部6m ,那么需要多长的钢索?二、讲授新课(一)探索勾股定理1、分别以图中的直角三角形三边为边向外作正方形, 求这三个正方形的面积?C2、这三个面积之间是否存在什么样的未知关系,如果存在, A 那么它们的关系是是什么?B3、是否所有的直角三角形都有这个性质呢?请动手验证。
【小组成员在方格纸上任意作出一个直角三角形,90C ∠=,将所得的数据填入表格】4、结论5、练一练(1)、判断题①若a 、b 、c 是任意直角三角形的三边,则222a b c +=. ( )A SB SC S 12勾股定理:图形:②直角三角形中,两边的平方和等于第三边的平方. ( ) 2、求下列直角三角形中未知边的长.3、求下列图中表示边的未知数x 、y 、z 的值.例1、如图,在四边形ABCD 中,∠︒=90BAD ,∠︒=90DBC ,12,4,3===BC AB AD ,求CD .例2、在Rt △ABC 中,∠A 、∠B 、∠C 所对的边分别是a 、b 、c ,a=3,b=4,求2c的值。
例3、如图,在Rt △ABC 中,∠ACB=90゜,∠A 、∠B 、∠C 所对的边分别是a 、b 、c ,(1)若a :b=3:4,c=15,求b;(2)若a=6,b=8,求c 的长及斜边的高。
例4、如图,将长方形的一边AD 沿AE 折叠,使点D 落在BC 边上的点F 处,已知AB=8cm ,BC=10cm,求EC 的长?(二)验证勾股定理xyz57662514416914481x16x8175CB A1、方法1:四个三角形面积之和+中间正方形的面积=外正方形的面积。
《1.1.1探索勾股定理(一)》导学案

《1.1.1探索勾股定理》导学案设计者: 班级: 姓名: 时间:学习目标:1、运用各种办法体验勾股定理的探索过程并理解勾股定理反映的直角三角形的三边之间的数量关系,会初步运用勾股定理进行简单的计算和实际运用.2、让学生经历勾股定理的探究过程,体会数形结合和特殊到一般的思想方法.3、进一步发展学生的说理和简单推理的意识及能力。
4、通过介绍勾股定理在中国古代的研究,激发学生热爱祖国,热爱祖国悠久文化的思想。
学习重点:探索勾股定理及简单应用。
学习难点:网格中图形面积的计算。
一、课前自学:认真阅读课本2页的引例,回答下列问题1、要计算旗杆的高,我们需要哪些线段的长度?我们能得到吗?并在小组内交流。
2.思考:直角三角形的三边之间有什么关系呢?二、合作探究:认真阅读课本2页做一做,并回答下列问题。
1.任意画一个直角三角形,分别测量他们的三条边,并计算它们的平方,看看有何关系?小组交流。
2. 你有哪些计算下列个图中各正方形的面积的方法,试试看,小组交流。
3.每个图形的面积与中间的直角三角形的边各有什么关系?4. 还能进一步得到直角三角形三边有何关系?独立思考、小组交流、展示。
三、回顾应用:想一想:课本图1-1的问题中,旗杆有多高?你能解决吗?四、总结反思五、拓展训练1.(口答)求下列图形中未知正方形的面积或未知边的长度:?225100x17C B2. 小明妈妈买了一部29英寸(74厘米)的电视机. 小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了.你同意他的想法吗?你能解释这是为什么吗?3.为迎接新年的到来,同学们做了许多拉花布置教室,准备召开新年晚会,小刚搬来一架高为2.5米的木梯,准备把拉花挂到2.4米的墙上,则梯脚与墙角的距离应为 米.4.如图,小张为测量校园内池塘A ,B 两点的距离,他在池塘边选定一点C ,使∠ABC =90°,并测得AC 长26m ,BC 长24m ,则A ,B 两点间的距离为 m .5.如图,阴影部分是一个半圆,则阴影部分的面积为 .( 不取近似值)6.底边长为16cm ,底边上的高为6cm 的等腰三角形的腰长为 cm .7.一艘轮船以16km/h 的速度离开港口向东北方向航行,另一艘轮船同时离开港口以12km/h 的速度向东南方向航行,它们离开港口半小时后相距 km .8.如图,求等腰三角形ABC 的面积。
八上11探索勾股定理1导学案.doc

8厘米的直角三角形。
①请你量出斜边c的长1. 1.1探索勾股定理导学案【学习目标】1、经历用数格子的办法探索勾股定理的过程,进一步发展学生的合情推力意识, 主动探究的习惯,进一步体会数学与现实生活的紧密联系。
2、探索并理解直角三角形的三边之间的数量关系,进一步发展学生的说理和简单的推理的意识及能力。
3、【学习重点】了结勾股定理的由来,并能用它来解决一些简单的问题。
【学前准备】1、画一个直角三角形并测量三边的长。
2、准备一张坐标纸【自学探究】1、分别作出直角边长为3厘米和4厘米直角三角形以及直角边长为6厘米和②、进行有关的计算。
⑴a2+b2= c2=(2) a2+b2= c2=③、得出结论:2、思考:如果下图中小方格的边长是1,观察图形,完成下表,并与同学交流:你是怎样得到的?(1)(2)/\/\/\// (、、\7(、A\/\/ 、/、B/E/ C/A\(f/ 、/(£9-/ X、、/L B打3-14图形A的面积B的面积C的面积A、B、C面积的关系图1-1图1-2图1-3图1-4如果直角三角形的两直角边分别为1.6个单位长度和2.4个长度单位,上面所猜想的数量关系还成立吗?说明你的理由。
【今日作业】1.求出下列直角三角形中未知边的长度。
2、求斜边长17厘米、一条直角边长15厘米的直角三角形的面积3、求下图中字母所代表的正方形的面积2、求出下列各图中x 的【巩固练习】1.在ZXABC 中,ZC = 90°, (1)若 a = 5, b = 12,贝U c= ________________ (2)若 c = 41,a = 9,贝ljb= ______________2.等腰AABC的腰长AB = 10cm,底BC为16cm,则底边上的高为__________ ,面积为3.AABC 中,AB = 15, AC = 13,高AD = 12,则AABC 的周长为()A. 42B. 32C. 42 & 32D. 37 & 334.一个抽斗的长为24cm,宽为7cm,在抽斗里放铁条,铁条最长能是多少?【延伸拓展】1.若正方形的面积为2cm2,则它的对角线长为2cm ()2.已知四边形ABCD 中,AD〃BC, ZA = 90° , AB = 8, AD = 4, BC = 6,则以DC为边的正方形面积为____3.在AABC 中,ZACB = 90° , AC = 12, CB = 5, M、N 在AB 上且AM=AC, BN= BC则MN 的长为()A. 2B. 26C. 3D. 46.___________________________________________ 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A, B, C, D的面积之和为_________________________________________________ c m2.7.___________________________________________________________________ —个直角三角形的三边长为3、4和a,则以a为半径的圆的面积是 __________________________。
探索勾股定理导学案
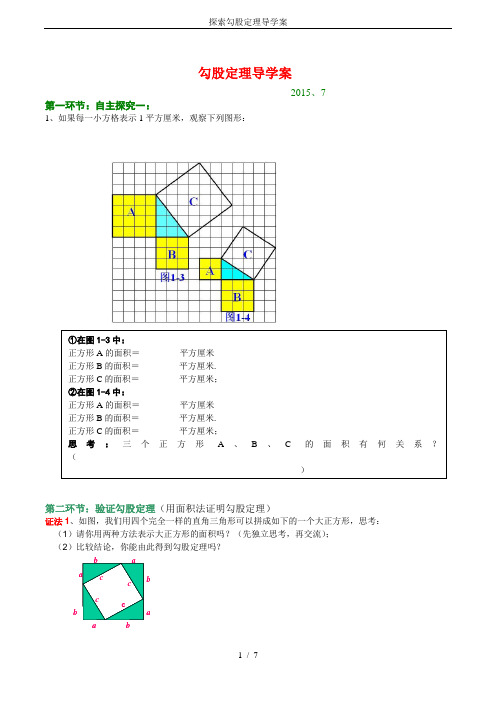
勾股定理导学案2015、7第一环节:自主探究一:1、如果每一小方格表示1平方厘米,观察下列图形:第二环节:验证勾股定理(用面积法证明勾股定理)证法1、如图,我们用四个完全一样的直角三角形可以拼成如下的一个大正方形,思考:(1)请你用两种方法表示大正方形的面积吗?(先独立思考,再交流);(2)比较结论,你能由此得到勾股定理吗?aaaab bb bcc cc①在图1-3中:正方形A的面积=_________平方厘米正方形B的面积=_________平方厘米.正方形C的面积=_________平方厘米;②在图1-4中:正方形A的面积=_________平方厘米正方形B的面积=_________平方厘米.正方形C的面积=_________平方厘米;思考:三个正方形A、B、C的面积有何关系?(___________________________________________________________________________________ _____________________________________________________)证法2、(1)赵爽利用弦图证明。
.....显然4个 的面积+中间小正方形的面积=该图案的面积.即4×21× +﹝ ﹞2=c 2,化简后得到 .证法3:第三环节、自我归纳勾股定理:对于任意的直角三角形,如果的它的两条直角边分别是a 、b ,斜边为c ,那么一定有: 变形则有a= b= c=勾股定理的应用是本节教学的重点,一定要让学生熟练地掌握在直角三角形中已知两边求第三边的方法。
练习1(填空题)已知在Rt △ABC 中,∠C=90°。
①若a=3,b=4,则c=________;②若a=40,b=9,则c=________; ③若a=6,c=10,则b=_______;④若c=25,b=15,则a=________。
练习2如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm ,则正方形A ,B ,C ,D 的面积之和为___________cm 2。
探索勾股定理导学案

化简得:
化简得:
拼图法思路: 1.用全等的直角三角形去拼图 2.图形进行割补拼接后,只要没有重叠、没有缝隙,面积不会改变 3.根据同一个图形的面积,不同的表示方法,列出等式,化简后推导出勾股定理
4
【议一议】
观察下图,用数格子的方法判断图中三角形的三边长是否满足 a2 + b2 = c2 .
c a
b
第一章 勾股定理导学案
1.1 探索勾股定理(1) 【学习目标】 1、会计算网格中正方形的面积。(方法:割、补成直角三角形 技巧:从正方形顶点处出发,横竖分割) 2、通过测量法、数格子法来探索勾股定理。 3、掌握勾股定理,并能运用勾股定理解决一些实际问题。 【课前准备】 1、 你能快速说出 1---20 各整数的平方吗?试一试。
2、如图,在 Rt ABC 中,AB=1,则 AB 2 BC 2 AC 2 的值为(
)
A、2
B、4
C、6
D、8
3、如图,在 ABC 中, B = 90 ,AC=17,BC=15,求AB 的长。
5
4、1876 年,美国总统伽菲尔德利用如图梯形的面积验证了勾股定理。请你把他的验证过程写下来。
5、飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶正上方 4000 米处,过了 20 秒,飞机距离这个 男孩 5000 米,飞机每小时飞行多少千米?(分析:把实际问题转化为数学问题,把实物抽象为几何图 形,在此题中,应把小王和飞机看成一个点,距离看成是线段,画出图形)
间有怎样的关系: _____________________
3、总结结论: (1)勾股定理的文字语言叙述:直角三角形两直角边的平方和等于斜边的平方。 (2)勾股定理的符号语言叙述:在 Rt△ABC 中,∠C=90o,AB=c,AC=b,BC=a,
八年级数学上册 1.1 探索勾股定理导学案1(新版)北师大版

探索勾股定理学习目标:1.探索直角三角形的三边关系,进一步发展学生的说理合简单推理的意识合能力。
2.经历用测量合数格子的方法探索勾股定理的过程,进一步提高学生的合情推理意识,培养主动探究的思想。
3.培养数形结合的思想,体会数学与现实的紧密联系,感受其价值。
学习重点:掌握勾股定理并能利用它来解决实际问题。
学习难点:探索勾股定理。
预习指导:1.先精读教材P2,用红色笔勾画知识点。
再针对学案二次阅读教材,完成教材助读设置的问题,依据发现的问题,查阅资料,解决有关问题。
2.找出自己的疑惑和需要讨论的问题,记录在预习学案上,准备课上讨论质疑。
3.预习目标:独立,限时完成预习自测,并把自己的疑惑写出来.学习环节:一.自学导航:1.在纸上任意作出两个直角三角形,分别测量它们的三边长,且动笔算一下,三条边长的平方有什么样的关系,你能猜想一下吗?2.观察课本第三页图1—2,思考在两个直角三角形ABC中,三边的平方分别是多少?你是怎样得到的?它们满足上面的结论吗?3.在图1—3中的两个直角三角形中,是否仍满足这样的关系?若能,试说明你是如何求出正方形的面积?4.通过以上的活动,你得到了什么结论?请你把结论写下来。
二.合作探究1.总结勾股定理_____________________2.在这个定理中我们应该注意些什么?(1)勾股定理揭示的是直角三角形的关系;(2)勾股定理只适合于三角形;(3)在使用勾股定理时,先要弄清边和边。
3.例题:如图所示,强大的台风使得一根旗杆在离地面9米处折断倒下,旗杆顶部落在离旗杆底部12米处。
旗杆折断之前有多高?三.学以致用1.求下图中字母所代表的正方形的面积。
CBAc400 2252.在Rt △ABC 中,∠C=90°,AC=5,BC=12,求AB 的长。
3.在Rt △ABC 中,∠C=90°,AB=25,AC=20,求△ABC 的面积。
4.若直角三角形的两直角边之比为3:4,斜边长为20㎝,则斜边上的高为 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《1.1.1探索勾股定理》导学案
【学习目标】
1、用数格子的办法探索勾股定理的过程,进一步发展学生的推理意识,主动探究的习惯,进一步体会数学与现实生活的紧密联系。
2、理解直角三角形的三边之间的数量关系,进一步发展学生的说理和简单推理的意识及能力。
【重点】了解勾股定理的由来并能用它解决一些简单问题 【难点】了解勾股定理的由来并能用它解决一些简单问题
预 习 案
一、预习自学
1、三角形如何分类?
2、三角形的三条边、三个角有什么关系?
3、等腰三角形有两边的长分别为4cm 、8cm,则它的周长是。
等腰三角形有一个角是0
110,则它的另两个角分别是,如果有一个角是0
60、
070呢?
探究案
(阅读P2,并思考下面两个问题 (1)、为什么在直角三角形中,任意两条边确定了,另外一条边也就随之确定? (2)、三边之间存在什么样的特殊关系?
2、动手做一做 (1)、在纸上画几个直角三角形,测量出它们各自三条边的长度,计算三边长的平方之间有什么关系?
(2)、(阅读P2做一做(2),P2图1—2,图1—3),计算并回答 ①A 、B 、C 各个图形的面积分别是多少?
②A 、B 、C 之间的面积之间有什么关系?
③、思考如果直角三角形两直角边是1.6个单位长度和2.4个单位长度时,上面所猜想的数量关系还成立吗?为什么?
④、思考以直角三角形两直角边为边的正方形面积和,与以斜边为边的正方形面积之间有什么关系?。
三、议一议(小组讨论)
1、直角三角形三边长度之间有什么关系?
2、分别以5厘米和12厘米为直角边作出一个直角三角形,你知道斜边的长吗?说说你是怎么做的?
巩固练习
1、练习1已知在Rt △ABC 中,∠C=90°。
①若a=3,b=4,则c=________; ②若a=40,b=9,则c=________; ③若a=6,c=10,则b=_______; ④若c=25,b=15,则a=________。
2、1、已知一个Rt △的两边长分别为3和4,则第三边长的平方是。
2、如图,从电线杆离地面6米处向地面拉一条长10米的缆绳,这条缆绳在地面的固定点距离电线杆底部为米。
3、小华和小红都从同一点O 出发,小华向北走了9米到A 点,小红向东 走了12米到了B 点,则________=AB 米。
五、提高练习 (1)、已知在Rt △ABC 中,∠C=90°,若4:3:=b a ,10=c ,则=a ,=b 。
(2)、如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长是a ,则图中四个小正方形的A 、B 、C 、D 面积之和是。
课堂小结:
学习反思:
D A B
C。
