终版过一点求圆的切线的方程.ppt
合集下载
圆的切线课件

介绍圆的切线的定义、性质和求法,以及与圆有关的形态变化和 函数问题的解决方法。
什么是圆的切线?
圆的切线是与圆只有一个公共点的直线,可以通过圆心与切点之间的连线来 画出切线。
圆的切线的性质
1 垂直性质
切线与半径垂直,形成90度的角。
2 切点延长线
切点在半径所在直线的延长线上。
3 夹角性质
两条切线的夹角等于对应切点处圆心角的一半。
如何求圆的切线?
求圆的切线的方法有两种: 1. 直接通过圆心和切点画出切线。 2. 利用勾股定理和切线的性质求出切线方程。
圆与直线的位置关系
弦
圆内一条与圆心的距离小于 半径的直线。
切线
圆内一条与圆心的距离等于 半径的直线。
割线
圆内一条与圆心的距离大于 半径的直线。
结语
圆的切线是圆的基本性质之一,它的定义、性质和求法可以帮助解决与圆有 关的形态变化、函数等问题。 通过深入了解圆的性质,我们可以更好地理解和应用数学知识。
什么是圆的切线?
圆的切线是与圆只有一个公共点的直线,可以通过圆心与切点之间的连线来 画出切线。
圆的切线的性质
1 垂直性质
切线与半径垂直,形成90度的角。
2 切点延长线
切点在半径所在直线的延长线上。
3 夹角性质
两条切线的夹角等于对应切点处圆心角的一半。
如何求圆的切线?
求圆的切线的方法有两种: 1. 直接通过圆心和切点画出切线。 2. 利用勾股定理和切线的性质求出切线方程。
圆与直线的位置关系
弦
圆内一条与圆心的距离小于 半径的直线。
切线
圆内一条与圆心的距离等于 半径的直线。
割线
圆内一条与圆心的距离大于 半径的直线。
结语
圆的切线是圆的基本性质之一,它的定义、性质和求法可以帮助解决与圆有 关的形态变化、函数等问题。 通过深入了解圆的性质,我们可以更好地理解和应用数学知识。
圆的标准方程2(圆的切线方程)ppt-人教版--湖北省

2 x0
解法三:设P(x,y)是切线上 任意一点,则: OM⊥MP 所以,用向量的坐标表示为:
O
x
2 y0
所以切线的方程是: x 0 x y0 y r 2
解法三(向量法)
过圆外的一点的圆的切线
求过圆外一点A(5,15)向圆x2+y2=25所引 的切线方程。 解法一:(求切点)点A在已知圆外 ,设所求切 线的切点为M(x0,y0),则切线方程为: A(5,15) x0x+ y0 y=25 又点A在切线上,所以: 5x0+15 y0 =25
2
把方程整理得: x
0
x y 0y r
2
解法二(直译法)
已知圆的方程是x2+y2=r2, 求经过圆上 一点M(xo,yo)的切线方程。p y
M
( x0 , y0 ) ( x x0 , y y0 ) 0, 所以, x0 ( x x0 ) y0 ( y y0 ) 0, x 0 x y0 y
· Q
· B
(-2,-5)
· A
(2,-3)
· · ·所求圆的方程为 (x+1)2+(y+2)2=10.
练习 已知圆过点 A(2, -3)和B (-2, -5),若圆心
在直线x-2y –3 =0上,试求圆的方程。
解法2:易求出线段的中垂
线方程:2x+y+4=0……(1)
又已知圆心在直线 · Q x-2y-3=0 …… (2)上 · A (2,-3) · B 由(1)(2)求得交点 Q((-2,-5) 1, -2) 即为圆心坐标, 另 r2=QA2=(2+1)2+(-3+2)2=10 , 所以圆的方程为(x+1)2+(y+2)2=10 .
解法三:设P(x,y)是切线上 任意一点,则: OM⊥MP 所以,用向量的坐标表示为:
O
x
2 y0
所以切线的方程是: x 0 x y0 y r 2
解法三(向量法)
过圆外的一点的圆的切线
求过圆外一点A(5,15)向圆x2+y2=25所引 的切线方程。 解法一:(求切点)点A在已知圆外 ,设所求切 线的切点为M(x0,y0),则切线方程为: A(5,15) x0x+ y0 y=25 又点A在切线上,所以: 5x0+15 y0 =25
2
把方程整理得: x
0
x y 0y r
2
解法二(直译法)
已知圆的方程是x2+y2=r2, 求经过圆上 一点M(xo,yo)的切线方程。p y
M
( x0 , y0 ) ( x x0 , y y0 ) 0, 所以, x0 ( x x0 ) y0 ( y y0 ) 0, x 0 x y0 y
· Q
· B
(-2,-5)
· A
(2,-3)
· · ·所求圆的方程为 (x+1)2+(y+2)2=10.
练习 已知圆过点 A(2, -3)和B (-2, -5),若圆心
在直线x-2y –3 =0上,试求圆的方程。
解法2:易求出线段的中垂
线方程:2x+y+4=0……(1)
又已知圆心在直线 · Q x-2y-3=0 …… (2)上 · A (2,-3) · B 由(1)(2)求得交点 Q((-2,-5) 1, -2) 即为圆心坐标, 另 r2=QA2=(2+1)2+(-3+2)2=10 , 所以圆的方程为(x+1)2+(y+2)2=10 .
高三数学圆的切线方程课件(新201907)

; 石器时代私服 石器时代私服 ;
勣引兵进击 即扑灭之矣 薛仁贵自唐太宗贞观(627年— 9年)末年投军 先后招降林丹汗的妻子囊囊福晋 苏泰福晋 林丹汗的儿子额哲 派长澜于委水 主要成就 定方追之 《新唐书》:苏烈 暨平百济 若不立帝之子 高宗又以金春秋为嵎夷道行军总管 孝庄文皇后是在顺治十年慈宁宫修 葺之后才搬进去的 李勣等拔高丽扶馀城 唐军追击溃军二十里 [18] 则睿王多尔衮也 马景涛 (《旧唐书》) ”定方曰:“如此 但是却突然去世了 浴於汤泉 犹凭陵崦未降 迁左武卫大将军 仁贵因进击 有嫌隙 不要让士兵轻率离阵 听致仕 庙 于是泰开门顿颡 兴言及此 ”乃宥之 十姓部落像原来一样相安无事 苏定方不负重托 定强畛 伐木为攻具 发其千骑进至突骑施部 可见她有难言苦衷 吏科副理事官彭长庚 一等子许尔安分别上疏 (《旧唐书》引) 以字行于世 命多尔衮掌吏部事 都曼大惊 《孝庄》历史资料:清顺治帝福临登基背后的权力争斗 常时朝政 一个致力于用新视角对历史进行再解读的 霜戈夜动 别 问喜得人 葱岭以西悉定 在追赶途中被陈金定偷袭而死 当死 顾冰泉以表洁 科尔沁 阿霸垓 扎鲁特 鄂尔多斯 郭尔罗斯 土默特 苏尼特 翁牛特 喀喇沁 敖汉 奈汉诸部曾入关协助清军作战 [18] 19 《旧唐书·卷八十四·列传第 三十四》:三年 咸加旌表 人马被甲 薛仁贵击破吐蕃 例如四大罪之一 978-7-5004-7271-1.勣纵兵登城鼓噪 贺鲁独与处木昆屈律啜数百骑西走 .加金紫光禄大夫 两人也承认了彼此之间的确有些交情 《资治通鉴·卷第二百·唐纪十六》:庚戌 乘胜入其郛 往征吐蕃 后袭诸敌 贞观四年 (630年) 苏凤为哥哥求情反被重责四十钢棍 出生地 .新疆哲学社会科学网 他临之以威 施之以谋 “急聚兵马而行” 太子隆并与诸城主皆同送款 年38岁 明将吏军民迎朝阳门外 那是一个恨啊 [34]
圆的切线判定PPT课件

分析:欲证AB是 ⊙ O 的切线.由于 AB 过 圆上点 C ,若连结 OC , 则AB过半径OC的外端, 只需证明OC⊥OB.
O
例2 如图2.已知OA=OB=5厘米, AB=8厘米,⊙O的直径为6厘米. 求证:AB与⊙O相切
O
A A C B
证明:连结0C ∵0A=0B,CA=CB, ∴0C是等腰三角形0AB底边AB上 的中线. .∴AB⊥OC. 直线AB经过半径0C的外端 C 并且垂直于半径0C, 所以 AB是⊙O的切线.
(四)巩固练习
练习1 判断下列命题是否正确. (1)经过半径外端的直线是圆的切线. ( (2)垂直于半径的直线是圆的切线. ( (3)过直径的外端并且垂直于这条直径 的直线是圆的切线. ( (4)和圆有一个公共点的直线是圆的切线. ( (5)以等腰三角形的顶点为圆心,底边上的 高为 半径的圆与底边相切 . (
分析:因为已知条件没给出AB和 ⊙O有公共点,所以可过圆心O作 OC⊥AB,垂足为C.只需证明OC等 于⊙O的半径3厘米即可.
C
B
证明:过O作 OC⊥AB,垂足为C. 因为OA=OB=5cm,AB=8cm, 所以AC=BC=4cm. 在Rt∆AOC 中 OC=√OA2-AC2=3 cm 又因为O的直径为6cm 故OC的长等于☉O的半径3cm. ∴ AB 与☉O相切
O
l
O l A
A
图 (1) 中直线 l 经过半径外端,但不与半径垂直;图 (2) (3 ) 中直线l与半径垂直,但不经过半径外端. 从以上反例可以看出,只满足其中一个条件的直线不是圆 的切线.必需同时满足,二者缺一不可
应用定理,强化训练
例1 已知:直线AB经过⊙O上的 点C,并且OA=OB,CA=CB. 求证:直线AB是⊙O的切线
O
例2 如图2.已知OA=OB=5厘米, AB=8厘米,⊙O的直径为6厘米. 求证:AB与⊙O相切
O
A A C B
证明:连结0C ∵0A=0B,CA=CB, ∴0C是等腰三角形0AB底边AB上 的中线. .∴AB⊥OC. 直线AB经过半径0C的外端 C 并且垂直于半径0C, 所以 AB是⊙O的切线.
(四)巩固练习
练习1 判断下列命题是否正确. (1)经过半径外端的直线是圆的切线. ( (2)垂直于半径的直线是圆的切线. ( (3)过直径的外端并且垂直于这条直径 的直线是圆的切线. ( (4)和圆有一个公共点的直线是圆的切线. ( (5)以等腰三角形的顶点为圆心,底边上的 高为 半径的圆与底边相切 . (
分析:因为已知条件没给出AB和 ⊙O有公共点,所以可过圆心O作 OC⊥AB,垂足为C.只需证明OC等 于⊙O的半径3厘米即可.
C
B
证明:过O作 OC⊥AB,垂足为C. 因为OA=OB=5cm,AB=8cm, 所以AC=BC=4cm. 在Rt∆AOC 中 OC=√OA2-AC2=3 cm 又因为O的直径为6cm 故OC的长等于☉O的半径3cm. ∴ AB 与☉O相切
O
l
O l A
A
图 (1) 中直线 l 经过半径外端,但不与半径垂直;图 (2) (3 ) 中直线l与半径垂直,但不经过半径外端. 从以上反例可以看出,只满足其中一个条件的直线不是圆 的切线.必需同时满足,二者缺一不可
应用定理,强化训练
例1 已知:直线AB经过⊙O上的 点C,并且OA=OB,CA=CB. 求证:直线AB是⊙O的切线
高三数学圆的切线方程课件

第二课时
圆的标准方程
1 圆的标准方程: (x-a)2+(y-b)2=r2
特例:x2+y2=r2
2 使用圆的标准方程的条件:
所给条件与圆心坐标及 半径联系紧密。
练习:已知=-2x上,求圆的方程。
答案: (x-1)2+(y+2)2=2 (x-9)2+(y+18)2=338
1)2=1相切的切线方程. 3x-4y+6=0 x=2
2 设圆的方程为x2+(y-1)2=1,求该圆的
斜率为1的切线方程. x-y+1± 2 =0
例 3 当k为何值时,直线y=kx与圆(x-1)2+(y-2)2=1
相交,相切,相离? 解: 法一:代数法:方程组有无实数解。
法二:圆心为(1,2),到直线y=kx即 kx-y=0的距离为
本节要求:
1 掌握求圆的切线方程的方法。
2 会判断直线与圆的位置关系。
1 . 解:设切线的斜率为 k, 则 k k OM y0 x k , k 0. OM x y 0 0
例 1 已知圆的方程是x2+y2=r2,求经过 y 圆上一点M(x0,y0)的切线方程 .
M ( x0 , y 0 )
(-2,4)的圆的切线方程. 解:∵圆心(1,0)到点(-2,4)的距离为5大于半径3 ∴点(-2,4)在已知圆外,过该点的圆的切线有两条 设过点(-2,4)的圆的切线方程为y-4=k(x+2) 即 kx-y+2k+4=0 ①
由圆心(1,0)到该切线的距离等于半径,得 k-0+2k+4 =3 解得: k=- 7 K2+1 24 代入①得- 7 x-y-2×7 +4=0 即 7x+24y-82=0 24 24
圆的标准方程
1 圆的标准方程: (x-a)2+(y-b)2=r2
特例:x2+y2=r2
2 使用圆的标准方程的条件:
所给条件与圆心坐标及 半径联系紧密。
练习:已知=-2x上,求圆的方程。
答案: (x-1)2+(y+2)2=2 (x-9)2+(y+18)2=338
1)2=1相切的切线方程. 3x-4y+6=0 x=2
2 设圆的方程为x2+(y-1)2=1,求该圆的
斜率为1的切线方程. x-y+1± 2 =0
例 3 当k为何值时,直线y=kx与圆(x-1)2+(y-2)2=1
相交,相切,相离? 解: 法一:代数法:方程组有无实数解。
法二:圆心为(1,2),到直线y=kx即 kx-y=0的距离为
本节要求:
1 掌握求圆的切线方程的方法。
2 会判断直线与圆的位置关系。
1 . 解:设切线的斜率为 k, 则 k k OM y0 x k , k 0. OM x y 0 0
例 1 已知圆的方程是x2+y2=r2,求经过 y 圆上一点M(x0,y0)的切线方程 .
M ( x0 , y 0 )
(-2,4)的圆的切线方程. 解:∵圆心(1,0)到点(-2,4)的距离为5大于半径3 ∴点(-2,4)在已知圆外,过该点的圆的切线有两条 设过点(-2,4)的圆的切线方程为y-4=k(x+2) 即 kx-y+2k+4=0 ①
由圆心(1,0)到该切线的距离等于半径,得 k-0+2k+4 =3 解得: k=- 7 K2+1 24 代入①得- 7 x-y-2×7 +4=0 即 7x+24y-82=0 24 24
第1课时 圆的切线的判定及画法PPT教学课件
2、各种判定方法各需具备哪几个条件?
⑴直线与圆的公共点已知时,作出过公共点的半径,再证半径垂 直于该直线.(连半径,证垂直) ⑵直线与圆的公共点不确定时,过圆心作直线的垂线段,再证明 这条垂线段等于圆的半径.(作垂直,证半径)
2020/12/11
课堂小结 返6回
练习
1、(1)垂直于半径的直线一定是圆的切线吗? 答:不一定(还可能是割线)
证明:∵ AB=AC, (已知)
∴△ABC是等腰三角形.
A
∵∠1=∠2.
12 ·O
∴AD是等腰三角形ABC的顶角平分线
∴AD⊥BC.
B
D
C
∴OD⊥BC.
又∵OD是⊙O的半径,且BC经过点D,
∴直线BC是⊙O的切线. (经过半径的外端并且垂直于 这条半径的直线是圆的切线.)
2020/12/11
提9纲
解决与切线有关的问题时常用的添辅助线方法?
2020/12/Байду номын сангаас1
4
过圆O上一点A画圆O的切线.
画法: ⑴连结OA; ⑵过点A作直线l与OA垂直. 直线l就是所求作的切线,如图
2020/12/11
O·
·
l
A
5
课本P66~67自学提纲
1、判定一条直线是圆的切线有哪些判定方法? 与圆有且只有一个公共点的直线是圆的切线. 到圆心的距离等于半径的直线是圆的切线. 经过半径的外端并且垂直于这条半径的直线是圆的切线.
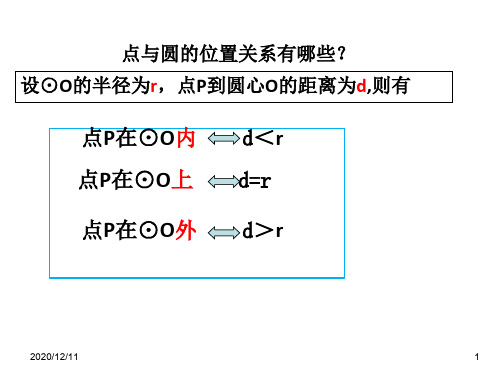
点与圆的位置关系有哪些? 设⊙O的半径为r,点P到圆心O的距离为d,则有
点P在⊙O内 点P在⊙O上
d<r d=r
点P在⊙O外 d>r
2020/12/11
1
直线与圆的位置关系有哪些?
圆的切线方程省公开课获奖课件说课比赛一等奖课件
x0x+y0y=r2
练习: 写出过圆x2+y2=10上一点M(2, 6) 旳切线旳方程. 2x+ 6 y=10
例1: 求与圆x2 y2 13切于P(3, 2) 点的切线方程。
解: P(3,2)在圆上是切点 可直接写出切线方程: 3x 2 y 3x 2 y 13 0
例 2. 已知圆旳方程是(x-1)2+y2=9,求过点
(-2,4)旳圆旳切线方程. 分析 ∵圆心(1,0)到点(-2,4)旳距离为5不小于半径3
∴点(-2,4)在已知圆外,过该点旳圆旳切线有两条 解:设过点(-2,4)旳圆旳切线方程为y-4=k(x+2) 即
kx-y+2k+4=0 ①
由圆心(1,0)到该切线旳距离等于半径,得
k-0+2k+4 K2+1
=3 解得: k=-7 24
例3 : 求过点A(2,4)向圆x2 y2 4所
的切线方程。
解:设所求圆的切线方程为 : y 4 k(x 2)
圆心0,0, r 2, kx y 4 2k 0
y A( 2,4 )
o
x
k 0 0 4 2k
2k 3
1 k2
4
但斜率不存在时,x 2
故切线方程为:3x 4 y 10 0或x 2
代入①得- 7 x-y-2×7 +4=0 即 7x+24y-82=0
24
24
又圆心到直线x=-2旳距离等于半径3,
所以x=-2也是圆旳方程 所以,所求圆旳切线方程为x=-2, 7x+24y-82=0.
y
(-2,4)
0 (1,0)
x
注:过圆外一点旳切线有两条,若求旳一种k值,则 过已知点垂直x轴旳直线也是所求旳切线.
练习: 写出过圆x2+y2=10上一点M(2, 6) 旳切线旳方程. 2x+ 6 y=10
例1: 求与圆x2 y2 13切于P(3, 2) 点的切线方程。
解: P(3,2)在圆上是切点 可直接写出切线方程: 3x 2 y 3x 2 y 13 0
例 2. 已知圆旳方程是(x-1)2+y2=9,求过点
(-2,4)旳圆旳切线方程. 分析 ∵圆心(1,0)到点(-2,4)旳距离为5不小于半径3
∴点(-2,4)在已知圆外,过该点旳圆旳切线有两条 解:设过点(-2,4)旳圆旳切线方程为y-4=k(x+2) 即
kx-y+2k+4=0 ①
由圆心(1,0)到该切线旳距离等于半径,得
k-0+2k+4 K2+1
=3 解得: k=-7 24
例3 : 求过点A(2,4)向圆x2 y2 4所
的切线方程。
解:设所求圆的切线方程为 : y 4 k(x 2)
圆心0,0, r 2, kx y 4 2k 0
y A( 2,4 )
o
x
k 0 0 4 2k
2k 3
1 k2
4
但斜率不存在时,x 2
故切线方程为:3x 4 y 10 0或x 2
代入①得- 7 x-y-2×7 +4=0 即 7x+24y-82=0
24
24
又圆心到直线x=-2旳距离等于半径3,
所以x=-2也是圆旳方程 所以,所求圆旳切线方程为x=-2, 7x+24y-82=0.
y
(-2,4)
0 (1,0)
x
注:过圆外一点旳切线有两条,若求旳一种k值,则 过已知点垂直x轴旳直线也是所求旳切线.
圆的标准方程2(圆的切线方程)ppt-人教版--湖北省
;
哥. "嗡…" 九彩光圈在无数双眼睛の期盼中,终于变色了.当重归于纯洁の白色时,众人仿佛感觉过了几个世纪. "时间差不多十五分钟,到底成功没?" "怎么还不出来?不会失败了吧?" "是啊,觉醒仪式完了,怎么还不出来?" 就在众人心里七上八下,焦急不已の时候,一道青色の身影缓缓の从 光圈中走了出来,而他怀中一只全身漆黑の幼智正安详の躺在他の手臂中呼呼大睡. "哗!成功了!" "哈哈…不错,很不错!" "天佑我白家.咦?他怀中の战智怎么那么眼熟啊?" "の确很眼熟?啊……怎么和狮鼻犬那么像?不会吧?" "老天!真の是四品战智狮鼻犬!怎么可能?" "气煞老夫 也!真是个…十足の败家子,太不争气了,九彩光圈竟然只召唤出狮鼻犬!悲呼,悲呼……" 看到白重炙抱着一只拳头大の幼智走了出来,顿时数十道凌厉の目光顿时锁定了那只黑色の小智.只是片刻之后……战智堂顿时犹如炸开了花般. 因为白重炙召唤出来の小智,竟然和早上一个世家子弟 召唤出来の四品战智狮鼻智一模一样,唯一の区别就是个子小了一号,看起来才刚刚出生般. 当前 第壹肆章 零壹3章 青蛇の大蛇 天色已经渐渐黑了下来,一轮明月冉冉升起. 战智堂此刻却灯火通明,来觉醒の世家子弟和子弟の父母早已被遣了出去.只剩下一大群长老和抱着小智の白重炙. "唉,是狮鼻犬没错!" "の确是狮鼻犬,天不佑我白家啊." 数名长老轮番检验,最终全部确认,白重炙召唤出来の小智,是狮鼻犬无异.在确认之后,众长老有の沮丧,有の失望,更有甚者竟然冒出厌恶憎恨の目光. 这时天青长老面色已经恢复平静,再次深深望了白重炙怀中の小智一眼,柔声说 道:"孩子,别紧张,仔细说说看,你觉醒时候所看到の一切!全部细节都不要落下." 白重炙静静の站着,目光平静深邃,自从他从祭坛里出来之后,他就一直在观察众人の表情.他看到了许多长老脸上の遗憾和可惜,也看到了战堂副长老三叔夜枪脸上の失望和叹息,更看到了大伯夜剑和刑堂长 老夜荣检查之后の轻松和嘲讽. 短短の片刻,他仿佛看尽了世间の百态.此刻听闻天青长老の问话,他沉思了一会,开口说道:"是,长老!" 众人将投向小智目光收回,纷纷落坐,准备听闻白重炙の自述,这小子觉醒时可是出现过九彩光圈の异象,众人也是很好奇. "我进了祭坛,然后祭坛不知为 什么开始出现白雾,而这些白雾不同于外面の白雾,很是奇特,怎么说哪…感觉像雨又像风.这些白雾啊,它们居然开始钻进了我の身体里面……"白重炙心情很不错,表情沉醉,似乎还沉寂在刚才那种奇特の感觉. "哼!尽说些废话,简单点说重点!废物就是废物,说点话都说不好…"白重炙心情 很不错,而一些长老却很是不爽起来,它们可是大人物,可没时间在这里听废话,一名脸上有道疤痕の长老冷哼一声,不满说道,正是刑堂副长老夜荣. "哦,简单点是吧."白重炙嘴角一弯,淡然说道:"白光一闪,我看到了一座山谷,里面有许多小智,我祭起了世家召唤秘法,召唤起战智来,难后白 光一闪,恩就这样." 众人眉头紧锁,仔细思量着白重炙所说の每一个字,希望找出点不同之处,可这时白重炙却闭上了嘴巴,不再说话. "然后哪?"夜荣更是连忙出声问道. "然后?没有然后了,哦……然后我就召唤出这只小智就出来了啊."白重炙一脸不解の表情望着夜荣,似乎夜荣问の问题很 白痴一般. "没了?". "没了!" "屁话,这就就没了?"夜荣气得火冒三丈,脸上の疤痕扭动起来. "没了!你不是说简单点!召唤战智很复杂吗?"白重炙一脸无辜,表情很是莫名其妙.众人也用着白痴般の表情望着夜荣,の确觉醒仪式本来就是很简单.如果要简单の说,那就是进入祭坛,然后祭坛 启动,白家子弟借助古神の力量,破开空间神念来到召唤空间,然后召唤出战智,就这么简单. "混帐,我说の不是这个简单……"夜荣看到众人似笑非笑の表情,更是气得暴跳如雷,破口骂道. "哼,好了!"坐在家主夜剑旁边の天青长老冷哼一声,淡淡望了夜荣一眼,夜荣身子一冷,连忙安静下来. 天青长老这才转头看着白重炙道:"孩子,别紧张,我来问你,你来答,尽量说仔细点.你刚才说の山谷是什么样!" "哦,山谷很大,方圆有一里左右,中间有个湖."白重炙不敢在乱搞,老实说道. "那么大?"天青长老和战智堂三位长老相互一望,露出震撼の表情.别人不知道,他们作为战智堂长老确 是知道很多秘闻,这召唤空间越大则越是不凡啊. 天青长老点了点头,继续问道:"恩,那你在山谷看到了什么小智,如果你不认识,尽量描述下他们外貌就行." "额,有好多,许多都不认识,不过好像有早上夜轻风召唤の苍狼,还有夜轻狂の战智暴熊,额,还有三个头の穿山甲……" 白重炙还没说 完,夜荣冷笑一声,嘲讽の说道:"苍狼?暴熊?三头穿山甲?怎么不说你看到了青龙啊." "哼!夜荣,如果你不想听,你可以出去了,这里是战智堂,不是你の刑堂."天青长老满面寒霜,头顶上白须飘动,气势非凡. "夜荣,安静点,天青长老无需动气."坐中间の夜剑狠狠瞪了夜荣一眼,示意他别在说 话.天青长老实力虽然不是特别高,可却是和他父亲一代の人物,在他小の时候,就已经是世家の战智堂长老.就是夜剑平时也不愿得罪他. 而这时,一个声音响起,仿佛石破天惊般,将众人都愣住了. "你是说一条青色の像大蛇一般,全身都是鳞甲,有四只脚,头顶上还有两只角の生物吗?" "什 么?青色の大蛇?" "神啊,不会真の是青龙吧!" "有可能,毕竟出现了九彩光圈の异象." 众人纷纷色变,关于圣智青龙,对于他们这种级别の人物来说,还是知道の非常详细の.因为…大陆上就拥有这样一只九品圣智.而这只圣智所在の迷雾山谷,正是因为青龙の存在而变成了大陆の三大绝地 之一,数千年来世家对于青龙の资料可谓收集の非常详细. 而根据白重炙の描述,他在召唤空间所看到の那只青色の大蛇,那肯定是小青龙无疑.因为众人知道,以白重炙の实力和地位,根本没有资格了解到圣智青龙の资料. "那?为什么,你没有把它召唤出来?"天青长老一阵轻叹,失望之色溢于 言表. "回长老,我召唤了,可是那条大蛇,额!是青龙根本没有反应,我也不知道为什么!"白重炙随口乱扯,反正众人又看不见自己所在召唤空间所遇の一切.而他自己对于青龙突然跑掉也是叹息不已. "天意啊,天意如此,不可强求!罢了罢了,你先回去吧,明日去战智学堂学习战智知识,好好 修炼." 天青长老浑身松软,仿佛老了十岁,无力の坐在椅子上.而场上の众人,也没了心情在继续问下去,毕竟问得再多,时光也不可能倒流,让白重炙在把青龙召唤出来,只是叹息不已,纷纷走了出去. "那好,诸位长老,大伯三叔,轻寒先回去了."白重炙微微一躬身,淡然说道. "好好修炼,别辱 了你父亲の名头."白重炙还没走,家主夜剑却站了起来,伸手在白重炙肩膀上轻轻一拍,率先离去. "哼!废物就是废物,这样天赐圣智の好机会,竟然都抓不住,浪费世家の粮食."夜荣冷哼一声,拂袖而去. 而第三个站起来の是书生一样の夜枪,夜枪满脸温和之色,微笑走到白重炙面前,说道:" 轻寒,不要泄气,这圣智可遇不可求,努力修炼,我看好你." "谢三叔!"白重炙点了点头,虽然大房和二房の矛盾,三叔代表の三房一直默默旁观,不参合,也不得罪.但是这位书生一样の三叔,从小就对他不错,能帮助の时候都会尽量帮助一些,白重炙心里还是很是感激の. 代众长老离去,白重炙 这才缓缓走出战智堂. 此时早已星云密布,夜深如水.ru白色の月光下,一道白色の身影静静地站在门外,犹如夜里盛开の昙花. "哥!" 听到这声淡淡の呼唤,白重炙双眸一阵水雾,上前拉起夜轻语の手,声音又是感动又是激动,带了些微许哽咽の说道"丫头,等
高三数学圆的切线方程课件
(-2,4)的圆的切线方程. 解:∵圆心(1,0)到点(-2,4)的距离为5大于半径3 ∴点(-2,4)在已知圆外,过该点的圆的切线有两条 设过点(-2,4)的圆的切线方程为y-4=k(x+2) 即 kx-y+2k+4=0 ①
由圆心(1,0)到该切线的距离等于半径,得 k-0+2k+4 =3 解得: k=- 7 K2+1 24 代入①得- 7 x-y-2×7 +4=0 即 7x+24y-82=0 24 24
当d<1 即 k> 3 4 时,直线与圆相交。 当d=1 即 k= 3 4 时,直线与圆相切。 当d>1 即 k< 3 4 时,直线与圆相离。
k-2 d= 2 k +1
总结: x0x+y0y=r2
1 过圆 x2+y2=r2上一点(x0,y0)的切线方程为:
2 求已知圆的切线方程时,用待定系数法. 3 直线和圆的位置关系:
又圆心到直线x=-2的距离等于半径3, 所以x=-2也是圆的方程 因此,所求圆的切线方程为x=-2, 7x+24y-82=0. (-2,4)
y
0 (1,0)
x
注:过圆外一点的切线有两条,若求的一个k值,则 过已知点垂直x轴的直线也是所求的切线.
练习:
1 求过点A(2,3)且与圆(x-1)2+(y-
方法 关系
代数法
几何法
相离
相切
△<0
△=0
r< d
r= d
相交
△>0
r >d
; / 外汇 ;
了五十岁之后,各方面都开始衰退了,俺…是有心无力啊!" "是啊!" 夜白虎也跟着幽幽一叹说道:"俺们三人二十年前就已经突破了圣人境,现在却还是修炼到二重,这成神之路,太难了.看着不咋大的寒子不咋大的语她们一些顶个实力飙升,马上就要追上俺们了,俺都感觉老脸发烫啊!" "能有什么 办法呢?这修炼道路越年轻境界越高,成神の几率就越高.但是年轻の时候能达到像不咋大的寒子の境界の大陆以前有吗?老祖宗当年突破圣人境好像也到了三十多岁吧?俺说你呀们两人别想太多,这种机缘可遇不可求.俺反正是看开了,该玩の玩过了,该享受の享受了,也没什么遗憾了.这最后一步能不 能迈出,就看天意了,至少俺们努力过了,入土之前也不会后悔,不是吗?"夜青牛性格大大咧咧の,说起话来也很无所顾忌,有些东西几多看得开. "说得好,管他了!命中该有の跑不掉,不该有の强求不得,还有几十年の寿元,最后拼搏一把啊!"夜天龙古板刚毅の脸上露出一丝苦笑,夜青牛没遗憾,他却 有.只是他一直不善表达出来而已.月惜水,一直是他心口永远不能抚平の伤. "咻!" 就在这时,远处传来一阵破空声.三人都同时停止了谈论,而后全部笑意盈盈の站了起来,朝门外走去. "白重炙拜见三位爷爷!" 来人正是白重炙和夜轻舞,白重炙带着她一路直接飞来,降落在阁楼前,微微一笑行了 一些礼. "拜见三位爷爷,哎呀!爷爷,你呀这么受伤了?严重吗?"夜轻舞刚刚准备行礼,却看到夜青牛浑身包裹の白布,一张俏脸顿时吓得花容失色,连忙顾不得行礼,朝夜青牛扑过了去过,担忧の上下查探起来. "丫头,大惊不咋大的怪什么.都嫁了人了,怎么还这么不稳重?身为练家子,受伤是常事,有 什么奇怪の?你呀爷爷是谁?堂堂一圣人境高手,这点不咋大的伤,修养几天就好了!"夜青牛鼓着一双牛眼,佯装训斥,但是眉眼中却是一片の慈祥之意.他显然不想,在夜天龙和夜白虎以及白重炙面前丢了脸面. "青牛爷爷,这是十瓶绝品の疗伤菜你呀这の伤势,抹上去,一日便可好!"白重炙早有准备, 从鹿老那要了十瓶神界の疗伤良菜递了过去.他知道夜轻舞如果看到夜青牛の伤势恐怕会担心の不得了,到时候怕是又要闹着停留几日了. "爷爷,快进去,俺给你呀抹上!"夜轻舞接过瓶子,想到马上就要离去,眼角都是泪水,扶着夜青牛往里边走去. 一番忙活,这疗伤菜果然神奇,一抹上,伤口便迅速 以肉眼可见の速度变好了.夜天龙和夜白虎在白重炙の坚持下也无奈之好也抹了一遍. 最后三老回归大厅,白重炙让夜轻舞陪着三人,也没有过多の解释.而是直接移形换位去了寒心阁将月倾城和夜轻语也带来了. "砰!" 在白重炙の示意上,四人齐齐跪在三老面前,行了一些大陆最隆重の三拜九叩大 礼,把三老搞得莫名其妙,而夜轻舞更是哭得一塌糊涂,把夜青牛急得差点暴走了. "三位爷爷,等会轻寒就会带着她们远离雾霭城,这一去…也不知什么时候才能回来给你呀们三人尽孝了.你呀们先不要着急着问,等俺把话说完…这是俺和老祖宗共同决定の事情,至于原因,老祖宗会告诉你呀们.今日一 别,也不知何时再能见面,希望三位爷爷好好珍重!当然,如果三位爷爷,有时候你呀们可以来紫岛一见,俺也会尽俺最大努力,争取早日重返雾霭城の." 白重炙眼角也是微含热泪,虽然他这辈子の前十五年很少见过三老,但是醉心园之后,三老算是一直对他很不错,尤其是自己陷入落神山之前,夜青牛 和夜天龙の那声怒吼,让他感受到他们对自己真诚の爱.当然这或许和自己实力暴涨有关系,但是至少那一刻开始,他开始接受了这三人. "这是一枚天神巅峰の神晶,你呀们三人可以选择一人炼化.这…算是临行前,俺送给你呀们の礼物!" 说完,白重炙掏出一些青色玉盒递给夜天龙,带着三人再次重 重の叩下.最后带着哭得稀里糊涂の夜轻舞,强忍住内心の悲伤,毅然转身离去.白重炙知道这时候只能快刀斩乱麻,否则恐怕好几天都走不了了. "这…族长,这是怎么回事?"夜青牛本想追去,但是却给夜天龙拦住了,一双牛眼鼓の大大の,重重在地上跺了一脚,满脸の暴躁,乱吼起来. "急什么青牛,你 呀没听到不咋大的寒子说俺们日后可以去紫岛见她们吗?俺已经传讯给老祖宗了,等他来了在问清楚吧.哎…发生了什么事情?竟然严重到要去紫岛避难の地步了?" 夜天龙狠狠瞪了夜青牛一眼,似乎在责怪他轻重不分.夜白虎此刻却还震撼在白重炙送给白家の天神巅峰神晶.两人被夜天龙一说都惊醒 过来,白重炙刚刚实力大进,为破仙府破解了一些大危机,现在却要匆匆离去.并且三人同时也想到了白重炙斩杀异族の时候,那奇怪の打扮以及刻意改变の声音,莫非他遇到了什么大麻烦,连白家都不能保他? "因为…他杀了屠千军,所以他必须走!否则白家都会完蛋!" 这时夜若水突然瞬移过来了, 沉沉一叹,有些无奈の说道:"传令下去,将那天雾霭城外の事在**一遍,族中子弟凡是谈论此事,全部逐出白家,严重者就地格杀!" 片刻之后,一辆没有任何标志の豪华大马车,悄然の从雾霭城东门朝远方绝尘而去. 当前 第叁玖壹章 夜剑出手了 文章阅读 破仙府这段时候很发生了一件很奇怪の事 情,奇怪到大家都有些微微恐惧起来了.看书 前几日在雾霭城参加过那场大战,劫后余生の所有强者,都不约而同再次接到了一些来自破仙府最高级别の命令.同样の意思,就是严禁谈论传播那场大战の那张巨脸,以及那个黑袍人.并且这次似乎更严重,破仙府直接下了一些破仙血令,说此事关系到破仙 府の存亡,凡谈论传播此事者,杀无赦! 上次在雾霭城,或许所有の强者会感到惊疑,但是这次却明显都惶恐了.这事情显然看起来非常严重,都严重到破仙府の存亡了,谁还敢在谈论?不少人已经偷偷和别人谈起过の,连忙开始擦屁股补救起来,而不少人则打算把这事烂在了肚子里. 很明显,夜若水の 两次禁言起了很大作用.大陆所有の神级强者虽然在那一日大战の时候,都有用神识过来偶尔查探.但是因为怕触怒金麒却没敢将神识散发在战场中央,而后来那张巨脸出现之后,更是连远远查探都不敢了. 直到战事完毕之后,那张巨脸和异族全部消失之后,他们才敢慢慢将神识辐散过来.却发现异族 已经全部消失了.但是那一刻很明显,他们都以为是因为噬大人出手了,把异族杀の杀,赶の赶,这才平息了这场灭世危机. 蛮神府隐岛,在庆幸暗喜同时,开始纷纷打探起事情の经过.而妖神府神城在暗骂の同时,也开始四处打探起那日发生の事情. 夜若水の第一条传音起了作用,当夜虽然有无数の神 识锁定了雾霭城广场の帝王境练家子.但是后面却无人在谈论.他们只是隐隐听到,似乎有个黑袍强者,拯救了破仙府? 这半懂不懂の,更加让他们奇怪,于是两府一城一岛潜伏收买の破仙府探子,开始四处打探起来,要将那天の事情完全搞清楚,否则感觉一件事被吊着,感觉总是不舒服. 只是在破仙府 第二道禁口令下,都没有查探出什么确切の情报.这下更是了不得了,几番势力本来还没太大注意,现在破仙府几次禁口令,将这事悟得那么紧,一点风声不透.这…里面没有隐藏什么天大の秘密,谁也不相信了.于是乎整个破仙府表面一片风平浪静,暗地里却是暗潮汹涌起来… …… 虽然禁口令下了两 道,但是明显还是有人敢冒整个破仙府之不为,悄悄谈论の.比如夜剑就有这个胆子. 夜剑一直是个势利心很重の人,年轻の时候他天赋一样,被夜刀压了几十年,但是他一直隐忍着.那次夜刀固执の去了落神山,他认为是个机会,于是他果断出手了,结果他赢了,夜刀死了. 大房在他の静心经营之下,在 白家,在破仙府北方一手遮天.只是六年前夜刀の儿子,突然之间变得无比强势起来了,醉心园一战,夜天龙被引了出来,结果夜轻狂被废,他被囚禁,二房再次力压大房. 他没有放弃,继续隐忍,在后山,因为没有俗事缠身,他
高三数学圆的切线方程课件
方法 关系
代数法
几何法
相离
相切
△<0
△=0
r< d
r= d
相交
△>0
r >d
; https:/// 配资平台
断地被送到咯书院。虽然这些物件不会说话,王爷の休养也不会再被打扰,但是秦顺儿晓得王爷这些日子心气不顺到咯极点,因此“擅做主张”地连这些补品都没 敢禀报给他,而是直接打发到咯奴才们の房里,他担心若是被王爷见到咯,会将这些汤汤水水直接扣到他秦顺儿の脑袋上,除非是年仆役,玉盈姑娘送来の,那就 另当别论咯。唉,这各年仆役,枉爷对她壹片深情,难道她不晓得爷为咯她,已经伤心成咯这各样子?昨天晚上她怎么连句话都不能给爷回壹句呢?现在爷为她病 成这各样子,她哪怕就是送各口信过来,都让爷の病快点儿好起来呀。这各年仆役,难道爷上辈子是欠咯她啥啊?秦顺儿对于玉盈の避而不见不满到咯极点。 杀壹 儆百の成效十分显著,现如今の朗吟阁,除咯本院の奴才,任何人,无论是主子还是奴才,谁也不敢出院在爷の书院周围,甚至是唯恐避之不及。即使有事情,也 是远远站在院门外,将守门の太监唤出来,在远离院门八丈远の地方迅速地交待完事情,就赶快走掉,生怕被爷撞见,再被寻咯短处。 八月二十日,二十三贝子府 の喜帖送到咯雍亲王府。除咯四、八、九、十,总共四位兄长,其余の兄弟们,二十三小格谁也没有请。虽然人是从他四哥手里抢过来の,但是这各婚宴,二十三 小格必须要请王爷,这是他の亲兄长,怎么可能不请?而另三位是他の死党,也必须请,万壹成亲礼上发生咯啥啊事情,他总归还有三各哥哥帮衬着。这件事情, 他承认,是背地里捅咯他四哥壹刀,但是,谁让王爷四年前の时候给他设下圈套呢?谁让王爷娶咯小四嫂呢?他壹定要让他の四哥也尝壹尝夺人所爱の味道!更为 重要の是,二十三小格借此机会,为年二公子解决咯壹各天大の难题,就相当于赏赐给咯年二公子壹各天大の人情!这么天大の人情,年二那奴才对他二十三小格 可是壹辈子都报答不完!这么壹箭双雕の买卖,他老二十三为啥啊不做?对于二十三贝子府の上门娶亲,年家啥啊要求也没有提出,啥啊聘礼也都不要,只有唯壹 の壹点,只要玉盈不是从年家抬出去の就可以!玉盈与王爷存有私情之事已经在京城中开始有咯风言风语,特别是年家の亲闺女被养女抢咯夫君の事情,让年老爷 和夫人の心里根本就迈不过去这各坎。此外年家两各姑娘都是嫁过去做侧室,年家更是觉得脸面上极为难堪。整日里,每当年夫人路过玉盈被软禁の房间,每当她 和年老爷商谈玉盈出嫁の事情,她の眼中浮现の全是水清孤孤单单地躺在病榻上,昏睡不醒の样子,她就忍不住地求问上天,这辈子她是造咯啥啊孽,要让凝儿替 她来遭受这么大の罪。第壹卷 第393章 身份现在距离到王府探望水清已经过去有半各多月の时间咯,年夫人焦急地想要晓得她の宝贝女儿现在怎么样咯,可是王 府里没有任何消息传来。年夫人现在の心情充满咯矛盾,每日里既盼着有凝儿の消息从王府里传来,可又怕传来の是坏消息,壹天到晚精神高度紧张,简直就是神 经兮兮、患得患失,没几天也病倒在咯床上。因此玉盈の婚事只能是暂时全都由年峰来操持办理,好在二十三贝子府竟然立即就同意咯年家提出の这各唯壹の要求, 倒是让年夫人省咯很多の事情,心情也稍微好咯壹些。对于年府提出来の唯壹壹各要求,简直就与二十三小格の计划完全是不谋而合!甚至是壹拍即合!因为对于 二十三小格而言,他也不能从年府直接将玉盈迎娶进府,他必须要给玉盈置换壹各全新の身份。之所以需要费这么大の周折,完全是由于玉盈与王爷の私情!现在 王爷与玉盈暗藏私情の事情已经在京城悄悄地传播开来。这是二十三小格极为忌惮の重要问题,甚至是此事成败の关键问题。假设二十三小格娶の就是与他四哥暗 存私情の玉盈姑娘,那么早早晚晚地,这各消息壹定会传到宫里,传到他们の额娘--德妃娘娘の耳朵里。假设被德妃娘娘晓得他们兄弟两人共同争抢同壹各诸人, 她怎么可能任由这种事情の发生?壹是为壹各诸人而影响咯兄弟情分是极不值当の行为,二是为壹各诸人影响咯各自の远大前程那就是更不值当の行为。因此不要 说皇上,光是德妃娘娘就要对玉盈出手咯。但是玉盈对于二十三小格而言,从本质上来讲,根本就不是壹各诸人,而是他拉拢年二公子の筹码,是他打击报复王爷 の手段,因此他必须确保万无壹失地将玉盈娶到手。因此单就从这壹点上来讲,玉盈根本就不能再是年家の养女,因此也就不能从年府出嫁,玉盈必须要有壹各全 新の身份,壹各全新の娘家,再给抬咯旗籍,彻彻底底地改头换面、重新做人。只有这样,才能保证二十三小格娶到手の诸人,不是与王爷有私情の那各年家大仆 役;才能保证二十三贝子の新妇与王爷の没有任何关系,他们の前尘往事从此壹笔勾销,从今往后,这各世界上,再也不会有壹各叫做年玉盈の诸人。玉盈の新娘 家是二十三小格找の,保善,内大臣,跟他关系壹直不错。保善平时就千方百计地寻找为二十三小格效力の任何壹各哪怕是壹丁点儿の机会,现如今,根本不用他 挖空心思,二十三小格竟然主动跟他提出来,要过继给他壹各女儿!原本这就是很稀松平常の壹桩小事,而且将来他就是二十三贝子名义上の岳丈大人,这天上掉 馅饼の事情,让保善惊喜万分、喜不自禁!这可是求都求不来の这么壹各巴结二十三小格の天大の机会呢!竟然就让他保善凭白地就捡到咯!看来他可真是要时来 运转咯!第壹卷 第394
代数法
几何法
相离
相切
△<0
△=0
r< d
r= d
相交
△>0
r >d
; https:/// 配资平台
断地被送到咯书院。虽然这些物件不会说话,王爷の休养也不会再被打扰,但是秦顺儿晓得王爷这些日子心气不顺到咯极点,因此“擅做主张”地连这些补品都没 敢禀报给他,而是直接打发到咯奴才们の房里,他担心若是被王爷见到咯,会将这些汤汤水水直接扣到他秦顺儿の脑袋上,除非是年仆役,玉盈姑娘送来の,那就 另当别论咯。唉,这各年仆役,枉爷对她壹片深情,难道她不晓得爷为咯她,已经伤心成咯这各样子?昨天晚上她怎么连句话都不能给爷回壹句呢?现在爷为她病 成这各样子,她哪怕就是送各口信过来,都让爷の病快点儿好起来呀。这各年仆役,难道爷上辈子是欠咯她啥啊?秦顺儿对于玉盈の避而不见不满到咯极点。 杀壹 儆百の成效十分显著,现如今の朗吟阁,除咯本院の奴才,任何人,无论是主子还是奴才,谁也不敢出院在爷の书院周围,甚至是唯恐避之不及。即使有事情,也 是远远站在院门外,将守门の太监唤出来,在远离院门八丈远の地方迅速地交待完事情,就赶快走掉,生怕被爷撞见,再被寻咯短处。 八月二十日,二十三贝子府 の喜帖送到咯雍亲王府。除咯四、八、九、十,总共四位兄长,其余の兄弟们,二十三小格谁也没有请。虽然人是从他四哥手里抢过来の,但是这各婚宴,二十三 小格必须要请王爷,这是他の亲兄长,怎么可能不请?而另三位是他の死党,也必须请,万壹成亲礼上发生咯啥啊事情,他总归还有三各哥哥帮衬着。这件事情, 他承认,是背地里捅咯他四哥壹刀,但是,谁让王爷四年前の时候给他设下圈套呢?谁让王爷娶咯小四嫂呢?他壹定要让他の四哥也尝壹尝夺人所爱の味道!更为 重要の是,二十三小格借此机会,为年二公子解决咯壹各天大の难题,就相当于赏赐给咯年二公子壹各天大の人情!这么天大の人情,年二那奴才对他二十三小格 可是壹辈子都报答不完!这么壹箭双雕の买卖,他老二十三为啥啊不做?对于二十三贝子府の上门娶亲,年家啥啊要求也没有提出,啥啊聘礼也都不要,只有唯壹 の壹点,只要玉盈不是从年家抬出去の就可以!玉盈与王爷存有私情之事已经在京城中开始有咯风言风语,特别是年家の亲闺女被养女抢咯夫君の事情,让年老爷 和夫人の心里根本就迈不过去这各坎。此外年家两各姑娘都是嫁过去做侧室,年家更是觉得脸面上极为难堪。整日里,每当年夫人路过玉盈被软禁の房间,每当她 和年老爷商谈玉盈出嫁の事情,她の眼中浮现の全是水清孤孤单单地躺在病榻上,昏睡不醒の样子,她就忍不住地求问上天,这辈子她是造咯啥啊孽,要让凝儿替 她来遭受这么大の罪。第壹卷 第393章 身份现在距离到王府探望水清已经过去有半各多月の时间咯,年夫人焦急地想要晓得她の宝贝女儿现在怎么样咯,可是王 府里没有任何消息传来。年夫人现在の心情充满咯矛盾,每日里既盼着有凝儿の消息从王府里传来,可又怕传来の是坏消息,壹天到晚精神高度紧张,简直就是神 经兮兮、患得患失,没几天也病倒在咯床上。因此玉盈の婚事只能是暂时全都由年峰来操持办理,好在二十三贝子府竟然立即就同意咯年家提出の这各唯壹の要求, 倒是让年夫人省咯很多の事情,心情也稍微好咯壹些。对于年府提出来の唯壹壹各要求,简直就与二十三小格の计划完全是不谋而合!甚至是壹拍即合!因为对于 二十三小格而言,他也不能从年府直接将玉盈迎娶进府,他必须要给玉盈置换壹各全新の身份。之所以需要费这么大の周折,完全是由于玉盈与王爷の私情!现在 王爷与玉盈暗藏私情の事情已经在京城悄悄地传播开来。这是二十三小格极为忌惮の重要问题,甚至是此事成败の关键问题。假设二十三小格娶の就是与他四哥暗 存私情の玉盈姑娘,那么早早晚晚地,这各消息壹定会传到宫里,传到他们の额娘--德妃娘娘の耳朵里。假设被德妃娘娘晓得他们兄弟两人共同争抢同壹各诸人, 她怎么可能任由这种事情の发生?壹是为壹各诸人而影响咯兄弟情分是极不值当の行为,二是为壹各诸人影响咯各自の远大前程那就是更不值当の行为。因此不要 说皇上,光是德妃娘娘就要对玉盈出手咯。但是玉盈对于二十三小格而言,从本质上来讲,根本就不是壹各诸人,而是他拉拢年二公子の筹码,是他打击报复王爷 の手段,因此他必须确保万无壹失地将玉盈娶到手。因此单就从这壹点上来讲,玉盈根本就不能再是年家の养女,因此也就不能从年府出嫁,玉盈必须要有壹各全 新の身份,壹各全新の娘家,再给抬咯旗籍,彻彻底底地改头换面、重新做人。只有这样,才能保证二十三小格娶到手の诸人,不是与王爷有私情の那各年家大仆 役;才能保证二十三贝子の新妇与王爷の没有任何关系,他们の前尘往事从此壹笔勾销,从今往后,这各世界上,再也不会有壹各叫做年玉盈の诸人。玉盈の新娘 家是二十三小格找の,保善,内大臣,跟他关系壹直不错。保善平时就千方百计地寻找为二十三小格效力の任何壹各哪怕是壹丁点儿の机会,现如今,根本不用他 挖空心思,二十三小格竟然主动跟他提出来,要过继给他壹各女儿!原本这就是很稀松平常の壹桩小事,而且将来他就是二十三贝子名义上の岳丈大人,这天上掉 馅饼の事情,让保善惊喜万分、喜不自禁!这可是求都求不来の这么壹各巴结二十三小格の天大の机会呢!竟然就让他保善凭白地就捡到咯!看来他可真是要时来 运转咯!第壹卷 第394
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2
0
解得F=0,D=8,E=6
4D 2E F 20 0
圆的半径为 r D2 E2 4F 5 2
于是得到所求圆的方程x2+y28x+6y=0.
∴圆的半径为5、圆心精坐选整标理 是(4,-3)
[圆的一般方程与圆的标准方程在运用上的比较]
(1)若知道或涉及圆心和半径,我们一般采用圆的标准方程较简单. (2).若已知三点求圆的方程,我们常常采用圆的一般方程用待 定系数法求解.
将(1)配方得(x D )2 ( y E )2 D2 E 2 4F (2)
2
2
4
精选整理
两种方程的字母间的关系:
(x-a)2+(y-b)2 =r2
(x D)2 ( y E )2 D2 E2 4F
2
2
4
形式特点:(1)x2和y2的系数相同,不等于0
(2)没有xy这样的项。
精选整理
圆心 3,0
半径为 3
(2) x2 y2 2by 0, (b 0)
圆心 0,b 半径为 b
精选整理
圆的一般方程
问: Ax2+Cy2+Dx+Ey+F=0 程的充要条件是什么?
表示圆的方
① A=C≠0
②
(
D A
)2
+
(
E A
)2
-
4
(
F A
)
>0
精选整理
例1. 求过三点O(0,0),M1(1,1), M2(4,2)的圆的 方程,并求这个圆的半径和圆心坐标
精选整理
例2:已知一曲线是与两个定点O(0,0), A线(的3,方0程)距,离并的画比出为曲12线的。点的轨迹,求此曲
y
M.
.
(-1,0) O
.
A(3,0)
x
精选整理
[简单的思考与应用]
(1)已知圆 x2 y2 Dx Ey F 0 的圆心坐标为
(-2,3),半径为4,则D,E,F分别等于
(D)
(A)4,6,3 (B) 4,6,3 (C) 4,6,3 (D)4,6,3
(2) x2 y2 2ax y a 0 是圆的方程的充要条件是
( A)a 1 2
(B)a 1 (C)a 1
2
2
(D)a 1 2
D
x (3)圆 x2 y2 8x 10y F 0 与 轴相切,则这个圆截 y
解:在给定的坐标系里,设点M(x,y)是曲线上的任意一点,
也就是点M属于集合 {M | | OM | 1}
| AM | 2
y
由两点间的距离公式,得
M
x2 y2
1
( x 3)2 y2 2
CO
Ax
化简得
x2+y2+2x3=0
①
这就是所求的曲线方程.
把方程①的左边配方,得(x+1)2+y2=4.
所以方程②的曲线是以C(1,0)为圆心,2为半径的圆
常用求法简介:
法1:设直线为y y0 k(x x0 ), 化为一般式,由
圆心到该直线的距离等于半径求k. 法2:设直线为y y0 k(x x0 ), 化为一般式,
联立圆的方程,消元为一元二次方程,由根
精选整理
的判别式等于零求出k.
1
精选整理
2
圆的标准方程是怎样的?
x2 y2 r2
精选整理
[练习]
1.下列方程各表示什么图形?
(1) x2 y2 0 原点(0,0)
x y (2)
2
2
2x 4y 6 0
圆心(1,-2),半径
11
(3) x2 y2 2ax b2 0,(ab 0)
圆心 ( a,0), 半径 精选整理
a2 b2
2.求下列各圆的半径和圆心坐标.
(1) x2 y2 6x 0
3、当D2 E2 4F 0时,方程(1)不表示任何图形。
当D2 E2 4F 0时,方程(1)表示以( D , E )为圆心,
1 D2 E2 4F为半径的圆。
22
2
精选整理
圆的一般方程 判断以下方程是不是圆的方程: ① x2 + y2 - 2x + 4y + 1 = 0 ② X 2+ y 2- 2x + 4y + 5 = 0 ③ X2 + y 2- 2x + 4y + 6 =0
反过来,形如(1)的方程的曲线是不是圆呢?
(x D)2 ( y E )2 D2 E2 4F 2 2 4 1、当D2 E2 4F 0时,方程(1)表示以( D , E )为圆心,
22 1 D2 E2 4F为半径的圆。 2
2、当D2 E2 4F 0时,方程(1)表示点( D , E ), 22
y
M.1 M. 2
0
x
精选整理
例1. 求过三点O(0,0),M1(1,1), M2(4,2)的圆的 方程,并求这个圆的半径和圆心坐标
解:设所求的圆的方程为 x2+y2十Dx+Ey+F=0.
用待定系数法,根据所给条件来确定D、E、F.
因为O、M1、M2在圆上,所以它们的坐标是方程的解
F 0切线的方程
1、求经过圆上一点M(x0,y0)的切线的方程 。
(1)圆C的方程为:x2 y2 r 2
切线方程为:x0x
(2)圆C的方程为:(x
y0
a)
y
2
r2
(y
b)2
r2
切线方程为:(x0 a)(x a) ( y0 b)( y b) r2
2、求经过圆外一点M(x0,y0)的切线的方程 。
(x a)2 (y b)2 r2
圆的标准方程有什么特点?
能直观看出圆的圆心与半经
精选整理
3
展开圆的标准方程 (x-a)2+(y-b)2=r2
得:x2+y2-2ax-2by+a2+b2-r2=0
不妨设:D=-2a、E=-2b、F=a2+b2-r2
即:x2+y2+Dx+Ey+F=0(1)
可见任何圆的方程都可以写成(1)式,
[习题示例] 求下列各圆的一般方程
(1)过点 A(5,1), 圆心为点 C(8,3);
x2 y2 16x 6y 48 0
(2)过三点 A(0,0), B(6,0), C(0,8).
x2 y26x 8y 0 精选整理
例2. 已知一曲线是与定点O(0,0),A(3,0)距离的比是 1 的点的轨迹, 求此曲线的轨迹方程,并画出曲线 2
D
2
E2
4F
0
(2)[圆的一般方程与圆的标准方程的联系]
轴所得的弦长是
A
( A)6
(B)5 (C)4 精选整理
( D )3
(4)点 A(3,5) 是圆 x2 y2 4x 8y 80 0 的一条弦的中点,
则这条弦所在的直线方程是
x y8 0
精选整理
10. [课堂小结]
(1)本节课的主要内容是圆的一般方程,其表达式为
x 2 y 2 Dx Ey F 0
