圆的切线的判定
2.3、 圆的切线的性质及判定定理
即B一定点在圆外.由点B的任意性可知,圆与直线 只有一个公共点,因此l 是圆的切线.由此可得:
切线的判定定理:
经过半径的外端并且垂直于这 条半径的直线是圆的切线.
O
l
AB
例1 如图,AB是⊙O的直径, ⊙O过BC的中点D, DE⊥AC.求证:DE是⊙O是切线.
证明:连接OD.
∵BD=CD,OA=OB, ∴OD是△ABC的中位线,
D C
A
O
B
P322
思考:切线的性质定理逆命题“经过半径的外端并且 垂直于这条半径的直线是圆的切线.”是否成立?
已知:点A是⊙O与直线l 的公共点,且 l ⊥OA .
求证:圆与直线只有一个公共点 证明:在l 上任取异于点A的点B,则△OAB是Rt△
而OB是Rt△ OAB的斜边,因此,都有OB>OA,
C P321
∴OD//AC.
又∵∠DEC=90º ∴∠ODE=90º 又∵D在圆周上,
∴DE是⊙O是切线..E D NhomakorabeaB
A
O
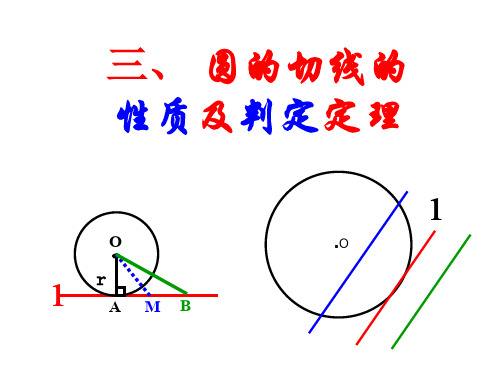
三、 圆的切线的 性质及判定定理
O
r
l A MB
l
.O
1 切线的性质定理:圆的切线垂直于经过切点的半径.
l
AM
反证法
假设不垂直, 作OM⊥l
因“垂线段最 故OA>OM,
O
即短圆”心, 到直线距离小于半径.
这与线圆相切矛盾.
因为经过一点只有一条直线与已知直线垂直,所 以经过圆心垂直于切线的直线一定过切点;反之,过切 点且垂直于切线的直线也一定过圆心.由此得到:
推论1: 经过圆心且垂直于切线的直线必经过切点.
推论2: 经过切点且垂直于切线的直线必经过圆心.
中考与切线有关的定理

1与切线有关的定理一、切线的性质及判定 1. 切线的性质:定理:圆的切线垂直于过切点的半径.推论1:经过圆心且垂直于切线的直线必经过切点. 推论2:经过切点且垂直于切线的直线必经过圆心. 2. 切线的判定:定义法:和圆只有一个公共点的直线是圆的切线; 距离法:到圆心距离等于半径的直线是圆的切线;定理:经过半径的外端并且垂直于这条半径的直线是圆的切线. 3. 切线长和切线长定理:⑴ 切线长:在经过圆外一点的圆的切线上,这点和切点之间的线段的长,叫做这点到圆的切线长.⑵ 切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角.①切线的判定定理设OA 为⊙O 的半径,过半径外端A 作l ⊥OA ,则O 到l 的距离d=r ,∴l 与⊙O 相切.因此,我们得到:切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线. 注:定理的题设①“经过半径外端”,②“垂直于半径”,两个条件缺一不可.结论是“直线是圆的切线”.举例说明:只满足题设的一个条件不是⊙O 的切线.l AlAl证明一直线是圆的切线有两个思路:(1)连接半径,证直线与此半径垂直;(2)作垂线,证垂足在圆上②切线的性质定理及其推论切线的性质定理:圆的切线垂直于过切点的半径. 二、内切圆1. 定义:和三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.P22. 多边形内切圆:和多边形的各边都相切的圆叫做多边形的内切圆,这个多边形叫做圆的外切多边形.3.直角三角形的内切圆半径与三边关系OF ED C BACBA CBAcbacba(1) (2)图(1)中,设a b c ,,分别为ABC ∆中A B C ∠∠∠,,的对边,面积为S 则内切圆半径(1)s r p=,其中()12pa b c =++;图(2)中,90C∠=︒,则()12r a b c =+-cm,BC=14 cm ,CA=13 cm ,求AF 、BD 、CE 的长例2. 如图所示,已知:AB是⊙O的直径,BC是⊙O的切线,切点为B。
圆的切线、切线长、线切角

CA圆的切线、切线长定理与弦切角定理一、圆的切线: 1.切线的判定:2.切线的性质:【运用举例】例1.如图,已知⊙O 所内接△ABC ,过点B 作直线BD ,∠DBC =∠A ,试说明,BD 与⊙O 相切。
例2.如图,已知CB 是⊙O 的切线,C 是切点,OB 交⊙O 于点D ,∠B =30,BD =6㎝,求BC 。
例3、如图,PA 、PB 切⊙O 于点A 、B ,点C 是⊙O 上一点,且∠ACB =65°,求∠P 的度数.例4、已知:如图AB 是⊙O 的直径,P 是AB 上的一点(与A 、B 不重合),QP ⊥AB ,垂足为P ,直线QA 交⊙O 于点C 点,过C 点作⊙O 的切线交直线QP 于点D ,求证:△CDQ 是等腰三角形.当P 点在AB 的延长线上时,其他条件不变,这个结论还成立吗?试说明.二、切线长定理 1、切线长:我们把圆的切线上某一点与切点之间的线段的长叫做这点到圆的切线长2、切线长定理:符号语言:∵PA 、PB 是O ⊙的切线,A 、B 是切点,∴,PA=PB 【运用举例】例1.在△ABC 中,AB=5cm BC=7cm AC=8cm, ⊙O 与BC 、AC 、 AB 分别相切于 D 、 E 、F ,则 AF=_____, BD=_______ 、CF=________例2、如图,PA 、PB 是⊙O 的切线,切点分别是A 、B ,直线EF 也是⊙O 的切线,切点为Q ,交PA 、PB 为E 、F 点,已知12PA cm ,求△PEF 的周长.例3、已知:如图,P 为⊙O 外一点,PA ,PB 为⊙O 的切线,A 和B 是切点,BC 是直径. 求证:AC∥OP.例4.如图,AB 、CD 分别与半圆O 切于点A 、D ,BC 切⊙O 于点E ,若AB =4,CD =9,求⊙O 的半径。
OCB AP三、弦切角定理及其推论1、弦切角:________________________________________________________________。
圆的切线的性质及判定定理完整版课件

证明:连接OD. ∵BD=CD,OA=OB,
∴OD是△ABC的中位线,
C
∴OD//AC.
又∵∠DEC=90º ∴∠ODE=90º 又∵D在圆周上,
∴DE是⊙O是切线..
E D
B
A
O
例2 如图. AB为⊙O的直径,C为⊙O上一点,AD和 过C点的切线互相垂直,垂足为D.
求证:AC平分∠DAB.
证明:连接OC, ∵CD是⊙O的切线,
C
2.已知:OA和OB是⊙O的半径,并且OA⊥OB,P是OA 上任意一点,BP的延长线交⊙O于Q.过Q作⊙O的切 线交OA的延长线于R,.
求证:RP=RQ
B
PA
O
R
Q
∠AQO= ∠APQ
3.AB是⊙O的直径,BC是⊙O的切线,切点为B,OC 平行于弦AD. 求证:DC是⊙O的切线.
C
D
3
1
42
A
∴OC⊥CD.
又∵AD⊥CD, ∴OC//AD.由此得 ∠ACO=∠CAD. ∵OC=OA. ∴ ∠CAO=∠ACO.
D C
A
O
B
∴ ∠CAD=∠CAO. 故AC平分∠DAB.
习题2.3
1.如图,△ABC为等腰三角形,O是底边BC的中点, ⊙O与腰AB相切于点D.
求证:AC与⊙O相切.
A
E D
B
O
推论2: 经过切点且垂直于切线的直线必经过圆心.
思考: 切线的性质定理逆命题是否成立?
切线的判定定理: 经过半径的外端并且垂直于这条半径的直线是圆的切线.
在直线上任取异于A的点B.
l
A
B
连OB.
则在Rt△ABO中
OB>OA=r
圆的切线知识点总结

圆的切线知识点总结一、切线的定义在欧式几何中,对圆的切线有以下几种定义:1. 如果一条直线与圆相交于两点,那么这条直线就被称为圆的切线。
2. 一条直线与圆相交于圆上的一点,那么这条直线就是圆的切线。
3. 一条直线与圆相切于圆上的一点,且直线上的其他点都在圆的外部,那么这条直线就是圆的切线。
这三种定义表达了切线与圆的位置关系,指出了切线与圆的相交情况以及位置特征。
二、切线的性质1. 切线与半径垂直圆的半径与切线的交点处相互垂直。
2. 切线定理若直线l与圆相切于点P,直线l与直径所夹的角为直角。
3. 切线长度相等过圆外一点作一切线与圆相交于A、B两点,连接线A、B,若CA=CB,则线段CA与线段CB构成圆的切线。
4. 切线的判定若直线l经过圆外一点,分别与圆上两点A、B相连,若线段AB的中点恰好是圆心O,那么直线l即为圆的切线。
5. 切线的唯一性圆外一点到圆的切线唯一。
以上是切线的主要性质,这些性质在解题时常常起到重要的作用,特别是在证明几何问题时,能够帮助我们理解和应用切线的知识。
三、切线与圆的位置关系1. 内切线如果一条直线与圆相交于圆上的一点,但直线上的其他点都在圆的内部,那么这条直线就是圆的内切线。
2. 外切线如果一条直线与圆相交于圆上的一点,且直线上的其他点都在圆的外部,那么这条直线就是圆的外切线。
3. 相切线如果一条直线与圆相切于圆上的一点,且直线上的其他点都在圆的外部,那么这条直线就是圆的相切线。
切线与圆的位置关系在解题时十分重要,通过分析切线和圆的位置关系,可以帮助我们求解许多几何问题。
四、切线的判定方法1. 切线与圆的位置关系我们可以通过切线与圆的位置关系来判断一条直线是否为圆的切线,如切线的定义所述,可以分析直线与圆的相交情况以及位置特征来判定切线。
2. 对于圆外一点到圆的切线的判定,我们可以利用中位线作图,利用几何思维判定出直线是否为圆的切线。
3. 切线定理的应用切线定理是判定切线的重要原理之一,通过利用切线定理,可以判定一条直线是否为圆的切线。
证明圆的切线的两种方法

证明圆的切线的两种方法方法一:利用圆的性质和向量的知识证明。
首先,根据圆的性质可知,圆心到切点的线段与切线垂直。
设圆心为O,切点为A,切线为l,则OA垂直于l。
又因为向量OA与向量l的内积为0,即OA·l=0,所以向量OA与l互相垂直。
又因为圆心到切点的线段与切线垂直,所以向量OA与切线方向相同。
因此,切线的方向可以表示为向量l=λOA,其中λ为常数。
再根据圆的性质可知,向量OA与圆的半径向量R的夹角为90度,即OA·R=0。
因此,向量l=λOA与向量R的内积也为0,即l·R=0。
这就证明了切线与圆的半径向量垂直。
方法二:利用微积分的知识证明。
首先,设圆的方程为(x-a)+(y-b)=r,其中(a,b)为圆心坐标,r为半径。
假设切线的斜率为k,则切线的方程为y=kx+c,其中c为常数。
为了使切线与圆相切,需要满足两个条件:一是切线经过圆上的某个点,即(x-a)+(y-b)=r;二是切线与圆的半径向量垂直,即切线的斜率为-k=-(x-a)/(y-b)。
将这两个条件代入切线方程y=kx+c中,得到(x-a)+(kx+c-b)=r,且k=-(x-a)/(y-b)。
将k代入上式,整理得到(x-a)+(c-b)/(1+k)=r。
由于切点坐标(x,y)满足(x-a)+(y-b)=r,因此有(x-a)+(c-b)/(1+k)=(x-a)+(y-b),即(c-b)/(1+k)=(y-b)。
将k带入上式,有c-b=±r/√(1+k)。
因此,切线的方程可以表示为y=±r/√(1+k)x+(b-c)/√(1+k),即y=±(r/√(1+k))x+(b-c)/√(1+k)。
这就证明了切线的方程。
- 1 -。
圆的切线判定定理及性质定理讲义
O ATO MTA B圆的切线判定定理及性质定理讲义一、基础知识归纳1.切线的判定定理切线的判定定理:经过半径的外端并且垂直于这条半径的直 线是圆的切线。
注:定理的题设①“经过半径外端”,②“垂直于半径”,两个 条件缺一不可。
结论是“直线是圆的切线”。
2.切线的性质定理及其推论切线的性质定理:圆的切线垂直于过切点的半径。
我们分析:这个定理共有三个条件:一条直线满足(1)垂直于切线 (2) 过切点 (3)过圆心 任意知道两个,这可以推出第三个。
即知2推1。
定理:①过圆心,过切点⇒ 垂直于切线 OA 过圆心,OA 过切点A ,则OA ⊥AT②经过圆心,垂直于切线⇒过切点()()12AB M AB M T ⎫⎪⇒⎬⊥⎪⎭过圆心为切点③ 经过切点,垂直于切线⇒过圆心()()12A M M T AM M ⊥⎫⎪⇒⎬⎪⎭过圆心为切点二、典型例题解析【例1】PB 切⊙O 于B ,OP 交⊙O 于A ,BC ⊥OP 于C ,OA=6cm,OP=10cm,求AC的长.lAOAOB PCM【例2】如图,⊙O 的直径A B =6cm ,点P 是A B 延长线上的动点,过点P 作⊙O 的切线,切点为C ,连结AC .若CPA 的平分线交AC 于点M ,你认为∠CMP 的大 小是否发生变化?若变化,请说明理由;若不变,求出∠CMP 的度数【例3】如图,若⊙的直径AB 与弦AC 的夹角为30°,切线CD 与AB 的延长线交于点D,且⊙O 的半径为2,则CD 的长是多少?【例4】如图,AB 为半圆O 的直径,CB 是半圆O 的切线,B 是切点,AC•交半圆O 于点D ,已知CD=1,AD=3,那么cos ∠CAB=________.BDAC【例5】设直线ι到⊙O的圆心的距离为d,半径为R,并使x2-2d x+R=0,试由关于x的一元二次方程根的情况讨论ι与⊙O的位置关系.【例6】在Rt ABC∠=°,D是A B边上一点,以B D为直径的O △中,90ACB⊙与边AC相切于点E,连结D E并延长,与BC的延长线交于点F.(1)求证:B D B F=;(2)若64,,求O==BC AD⊙的面积.。
切线的判定和性质
切线的判定和性质
切线的性质与判定
1.主要性质
(1)切线和圆只有一个公共点;
(2)切线和圆心的距离等于圆的半径;
(3)切线垂直于经过切点的半径;
(4)经过圆心垂直于切线的直线必过切点;
(5)经过切点垂直于切线的直线必过圆心;
(6)从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项。
其中(1)是由切线的定义得到的,(2)是由直线和圆的位置关系定理得到的,(6)是由相似三角形推得的,也就是切割线定理。
2.判定
切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线。
圆的切线垂直于这个圆过切点的半径。
专题7圆的切线的判定与性质-重难点题型(举一反三)
专题2.2 圆的切线的判定与性质--重难点题型【知识点1 切线的判定】(1)切线判定:①经过半径的外端并且垂直于这条半径的直线是圆的切线②和圆只有一个公共点的直线是圆的切线(定义法)③如果圆心到一条直线的距离等于圆的半径,那么这条直线是圆的切线(2)切线判定常用的证明方法:①知道直线和圆有公共点时,连半径,证垂直;②不知道直线与圆有没有公共点时,作垂直,证垂线段等于半径.【题型1 切线判定(连半径,证垂直)】【例1】(2021•新兴县一模)如图,AD是⊙O的弦,AB经过圆心O,交⊙O于点C,连接BD,∠DAB=∠B=30°,求证:直线BD是⊙O的切线.【变式1-1】(2020秋•思明区校级期末)如图,AB是圆O的一条弦,点E是劣弧AB的中点,直线CD经过点E 且与直线AB平行,证明:直线CD是圆O的切线.【变式1-2】(2020秋•福州期末)如图,AB是⊙O的直径,C为半圆O上一点,直线l经过点C,过点A作AD ⊥l于点D,连接AC,当AC平分∠DAB时,求证:直线l是⊙O的切线.【变式1-3】(2021•芜湖模拟)如图,在△ABC中,AB=AC,⊙O是△ABC的外接圆,过点C作∠BCD=∠ACB 交⊙O于点D,连接AD交BC于点E,延长DC至点F,使CF=AC,连接AF.(1)求证:ED=EC;(2)求证:AF是⊙O的切线.【题型2 切线判定(作垂直,证半径)】【例2】(2020秋•原州区期末)如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB.求证:直线AB是⊙O 的切线.【变式2-1】(2020秋•北京期末)如图,以点O为圆心作圆,所得的圆与直线a相切的是()A.以OA为半径的圆B.以OB为半径的圆C.以OC为半径的圆D.以OD为半径的圆【变式2-2】(2020秋•曲靖期末)如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC、AC边于点D、F.过点D作DE⊥CF于点E.求证:DE是⊙O的切线;【变式2-3】(2021•南平模拟)如图,在△ABC中,D为BC边上的一点,过A,C,D三点的圆O交AB于点E,已知,BD=AD,∠BAD=2∠DAC=36°.(1)求证:AD是圆O的直径;(2)过点E作EF⊥BC于点F,求证:EF与圆O相切.【题型3 切线判定(定义法)】【例3】(2020秋•北塘区期中)给出下列说法:(1)与圆只有一个公共点的直线是圆的切线;(2)与圆心的距离等于半径的直线是圆的切线;(3)垂直于圆的半径的直线是圆的切线;(4)过圆的半径的外端的直线是圆的切线.其中正确的说法个数为()A.1B.2C.3D.4【变式3-1】(2020秋•锡山区校级月考)下列直线是圆的切线的是()A.与圆有公共点的直线B.到圆心的距离等于半径的直线C.到圆心的距离大于半径的直线D.到圆心的距离小于半径的直线【变式3-2】给出下列说法:①与圆只有一个公共点的直线是圆的切线;②与圆心的距离等于半径的直线是圆的切线;③垂直于圆的半径的直线是圆的切线;④过圆的半径的外端的直线是圆的切线;⑤经过圆心和切点的直线垂直于这条切线.其中正确的是.(填序号)【变式3-3】(2020•龙川县二模)如图,P A和⊙O相切于A点,PB和⊙O有公共点B,且P A=PB,求证:PB是⊙O的切线.【知识点2 切线的性质】(1)切线性质定理:圆的切线垂直于过切点的半径(2)切线性质的推论:①经过圆心且垂直于切线的直线必经过切点②经过切点且垂直于切线的直线必经过圆心【题型4 切线的性质(求长度问题)】【例4】(2020秋•衢江区期末)如图,直线AB与⊙O相切于点C,OA交⊙O于点D,连结CD.已知OD=CD =5,求AC的长.【变式4-1】(2021•温州三模)在等腰三角形ABC 中,AC =BC =2,D 是AB 边上一点,以AD 为直径的⊙O 恰好与BC 相切于点C ,则BD 的长为( )A .1B .2√33C .2D .2√55【变式4-2】(2021•湖州一模)如图,以△ABC 的边AB 为直径作⊙O ,交BC 于点D ,过点D 的切线DE ⊥AC 于点E .(1)求证:AB =AC ;(2)若AB =10,BD =8,求DE 的长.【变式4-3】(2021•陕西模拟)如图,AB 是⊙O 的直径,C 是⊙O 上的一点,连接BC ,F 为BC 的中点,连接FO 并延长交⊙O 于点D ,过点D 的切线与CA 的延长线交于点E .(1)求证:四边形CEDF 是矩形;(2)若AC =OA =2,求AE 的长.【题型5 切线的性质(求半径问题)】【例5】(2020秋•市中区期末)如图,BE 是⊙O 的直径,点A 和点D 是⊙O 上的两点,过点A 作⊙O 的切线交BE 延长线于点C .(1)若∠ADE =28°,求∠C 的度数;(2)若AC =2√3,CE =2,求⊙O 半径的长.【变式5-1】(2020秋•沂水县期末)如图,已知⊙O 上三点A ,B ,C ,∠ABC =15°,切线P A 交OC 延长线于点P ,AP =√3,则⊙O 的半径为( )A .√33B .√32C .√3D .3【变式5-2】(2021•河南模拟)如图,AB 为⊙O 的直径,C 为BA 延长线上一点,CD 是⊙O 的切线,D 为切点,作OF ⊥AD 于点E ,交CD 于点F .(1)在不增加辅助线的情况下,请直接写出图中一对相等的角,并证明;(2)若BD =8,EF =2,求⊙O 的半径.【变式5-3】(2021•贵池区模拟)已知:在⊙O 中,AB 为直径,P 为射线AB 上一点,过点P 作⊙O 的切线,切点为点C ,D 为弧AC 上一点,连接BD 、BC 、DC .(1)如图1,求证:∠D =∠PCB ;(2)如图2,若四边形CDBP 为平行四边形,BC =5,求⊙O 的半径.【题型6 切线的性质(求角度问题)】【例6】(2021•红桥区三模)在△ABC中,以AB为直径的⊙O分别与边AC,BC交于点D,E,且DE=BE.(Ⅰ)如图①,若∠CAB=38°,求∠C的大小;(Ⅱ)如图②,过点E作⊙O的切线,交AB的延长线于点F,交AC于点G,若∠CAB=52°,求∠BEF的大小.【变式6-1】(2021•三明模拟)从⊙O外一点A作⊙O的切线AB,AC,切点分别为B,C,D是⊙O上不同于B,C的点,∠BAC=60°,∠BDC的度数是()A.120°B.60°C.90°或120°D.60°或120°【变式6-2】(2021•北辰区二模)如图,在⊙O中,直径AB与弦CD相交于点E,∠ABC=58°.(Ⅰ)如图①,若∠AEC=85°,求∠BAD和∠CDB的大小;(Ⅱ)如图②,若CD⊥AB,过点D作⊙O的切线DF,与AB的延长线相交于点F,求∠F的大小.【变式6-3】(2021•天津)已知△ABC内接于⊙O,AB=AC,∠BAC=42°,点D是⊙O上一点.(Ⅰ)如图①,若BD为⊙O的直径,连接CD,求∠DBC和∠ACD的大小;(Ⅱ)如图②,若CD∥BA,连接AD,过点D作⊙O的切线,与OC的延长线交于点E,求∠E的大小.。
圆的切线、切线长、线切角
圆的切线、切线长定理与弦切角定理一、圆的切线:1切线的判定:________________________________________________________2 .切线的性质: _________________________________【运用举例】、切线长定理1、切线长:我们把圆的切线上某一点与切点之间的线段的长叫做这点到圆的 切线长2、切线长定理:符号语言::PA PB 是0O 的切线,A 、B 是切点,二,PA=PB 【运用举例】例 1.在厶 ABC 中, AB=5cm BC=7cm AC=8cr ® O 与 BC ACAB 分别相切于 D 、E 、F ,则 AF= ________ , BD= _______ 、CF=____________________________例2.如图,已知CB 是。
O 的切线,C 是切点,0B 交。
O 于点D ,/ B = 30,BD = 6 cm,求BC例3、如图,PA 、PB 切。
0于点A 、B ,点C 是。
0上一点,且/ ACB=65°,求/ P 的度数.例2、如图,PA PB 是。
0的切线,切点分别是A 、B ,直线EF 也是。
0的切线,切点为Q,交PA PB 为E 、F 点,已知PA=12cm ,求△ PEF 的周长.例4、已知:如图AB 是。
0的直径,P 是AB 上的一点(与A 、B 不重合),QP 丄AB ,垂足为P , 直线QA 交。
0于点C 点,过C 点作。
0的切线交直线QP 于点D ,求证:△ CDQ 是等腰当P 点在AB 的延长线上时,其他条件不变,这个结论还成立吗?试说明 例3、已知:如图,P 为。
0外一点,PA PB 为。
0的切线,A 和B 是切点,BC 是直径.求证:AC// 0P例4.如图,AB 、CD 分别与半圆0切于点A 、D , BC 切。
0于点E ,若AB = 4, CD = 9,求O O的半径。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
有切点, 连半径, 证垂直。
如图,在△ABC中,∠A=∠C=30°,AB是⊙O的弦,
AC过圆心O。
求证:BC是⊙O的切线。
有切点,
连半径,
证垂直。
如图,OA是∠CAD的平分线,AC与⊙O相切于B。
求证:AD与⊙点, 作垂直,证半径。
AC是⊙O的直径,点D在⊙O上,过点D的直线BD与AC 的延长线交于点B,AE⊥BD,垂足为点E, AD平分∠BAE。 求证:BD是⊙O的切线。
有切点, 连半径,证垂直。
如图,AB是⊙O的直径,⊙O过BC的中点D,DE⊥AC。 求证:DE是⊙O的切线。
切线的判定
切线的判定
1、与圆只有一个交点。
2、圆心到直线的距离等于半径。
3、经过半径的外端且垂直于 这条半径的直线为圆的切线。
判断
× ×
×
利用判定定理时,要注意直线需具备以下两个条件, 缺一不可。
(1)直线经过半径的外端。 (2)直线与半径垂直。
例:已知,直线AB经过⊙O上的点C, 并且OA=OB,CA=CB。
