晶体学基础 3
合集下载
晶体学基础第三章-晶体的定向和晶体学符号

晶体定向的几个基本概念:
(1)结晶轴:晶体坐标系中的坐标轴,需满足晶体对称性 特征。用x轴、y轴、z轴或X轴、Y轴、Z轴表示。 (2)轴角:两个结晶轴正向之夹角。用a,b,g 表示。
(3)轴单位:晶体坐标系中结晶轴的长度单位。是相应 晶体点阵中平行于晶轴的行列上相邻节点间距。用a, b, c分 别表示x轴位之连比。用a:b:c 表示。
(5)晶体几何常数:轴率a:b:c和轴角a,b,g的合称。表 示晶体坐标系特征的一组参数,用以区分不同的晶系。
第三章 晶体的定向和晶体学符号
➢ 晶体学坐标系 ➢ 各晶系的定向方法 ➢ 晶胞与原子坐标 ➢ 晶面指数 ➢ 晶向指数 ➢ 晶带指数
3.1 晶体学坐标系
晶体定向的目的:
建立坐标系,简单明确地描述晶体中晶面、晶列的 空间方位。为研究晶体的结构特性提供定量标记。
晶体的定向:
在晶体中设置符合晶体对称特征或与晶体点阵参数 一致的坐标系,并将晶体按相应的空间取向关系进行安 置。
(完整版)1《材料科学基础》第一章晶体学基础

一、晶向指数 二、晶面指数 三、六方晶系的晶向指数和晶面指数 四、晶带 五、晶面间距
晶向、晶
钯的PDF卡片-----Pd 89-4897
crystal system,space
图 2 CdS纳米棒的TEM照片(左)和 HRTEM照片(右)
图2 选区电子衍射图
图1. La(Sr)3SrMnO7的低 温电子衍射图
晶向、晶面、晶面间距
晶向:空间点阵中行列的方向代表晶体中原子排 列的方向,称为晶向。
晶面:通过空间点阵中任意一组结点的平面代表 晶体中的原子平面,称为晶面。
L M
P点坐标?
(2,2,2)或222
N
一、晶向指数
1、晶向指数:表示晶体中点阵方向的指数,由晶向上结点的 坐标值决定。
2、求法 1)建立坐标系。 以晶胞中待定晶向上的某一阵点O为原点,
联系:一般情况下,晶胞的几何形状、大小与对应的单胞是 一致的,可由同一组晶格常数来表示。
不区分 图示
晶 胞
空间点阵
单
胞
•NaCl晶体的晶胞,对应的是立方面心格子 •晶格常数a=b=c=0.5628nm,α=β=γ=90°
大晶胞
大晶胞:是相对 于单位晶胞而言 的
例:六方原始格子形式的晶胞就是常见的大晶胞
① 所选取的平行六面体应能反映整个空间点阵的对称性; ② 在上述前提下,平行六面体棱与棱之间的直角应最多; ③ 在遵循上两个条件的前提下,平行六面体的体积应最小。
具有L44P的平面点阵
单胞表
3、单胞的表征
原点:单胞角上的某一阵点 坐标轴:单胞上过原点的三个棱边 x,y,z 点阵参数:a,b,c,α,β,γ
准晶
是一种介于晶体和非晶体之间的固体。准晶具有长程定向有 序,然而又不具有晶体所应有的平移对称性,因而可以具有 晶体所不允许的宏观对称性。
晶向、晶
钯的PDF卡片-----Pd 89-4897
crystal system,space
图 2 CdS纳米棒的TEM照片(左)和 HRTEM照片(右)
图2 选区电子衍射图
图1. La(Sr)3SrMnO7的低 温电子衍射图
晶向、晶面、晶面间距
晶向:空间点阵中行列的方向代表晶体中原子排 列的方向,称为晶向。
晶面:通过空间点阵中任意一组结点的平面代表 晶体中的原子平面,称为晶面。
L M
P点坐标?
(2,2,2)或222
N
一、晶向指数
1、晶向指数:表示晶体中点阵方向的指数,由晶向上结点的 坐标值决定。
2、求法 1)建立坐标系。 以晶胞中待定晶向上的某一阵点O为原点,
联系:一般情况下,晶胞的几何形状、大小与对应的单胞是 一致的,可由同一组晶格常数来表示。
不区分 图示
晶 胞
空间点阵
单
胞
•NaCl晶体的晶胞,对应的是立方面心格子 •晶格常数a=b=c=0.5628nm,α=β=γ=90°
大晶胞
大晶胞:是相对 于单位晶胞而言 的
例:六方原始格子形式的晶胞就是常见的大晶胞
① 所选取的平行六面体应能反映整个空间点阵的对称性; ② 在上述前提下,平行六面体棱与棱之间的直角应最多; ③ 在遵循上两个条件的前提下,平行六面体的体积应最小。
具有L44P的平面点阵
单胞表
3、单胞的表征
原点:单胞角上的某一阵点 坐标轴:单胞上过原点的三个棱边 x,y,z 点阵参数:a,b,c,α,β,γ
准晶
是一种介于晶体和非晶体之间的固体。准晶具有长程定向有 序,然而又不具有晶体所应有的平移对称性,因而可以具有 晶体所不允许的宏观对称性。
晶体学基础 3

4
2
6
间
隙
• 从晶体原子排列的刚球模型可以看到,在原子球与原子球 之间存在着不同形貌的间隙。主要有两类间隙即:四面体 间隙和八面体间隙。 • 晶体结构中间隙的数量、位置和每个间隙的大小等也是晶 体的一个重要特征,对于了解金属的性能、合金相结构、 扩散、相变等问题很有用处。
面心立方
配位数
CN=12
八面体间隙
体心立方
bcc 晶体的八面体间隙如图所示,其位置和形状不同于 fcc 晶胞的八面 体间隙。间隙的中心位于晶胞的面心和晶胞棱的中点(对 bcc 晶体,这
些都是等同点),一个晶胞中八面体间隙的数量是6(个),故八面体间 隙数与原子数之比为6∶2 = 3∶1。
间隙原子只和相距它为a/2的两个原子相切,既和体心原子相切。 而不和相距为 2 a 的四个原子(顶点原子)相切。
和
D2 是晶体学上的等
价方向,但其晶向指 数却分别是[100]和 [110]。
• 由于等价晶面或晶向不具有类似的指数, 人们就无法从指数判断其等价性,也无法 由晶面族或晶向族指数写出它们所包括的 各种等价晶面或晶向,这就给晶体研究带 来很大的不便。为了克服这一缺点,或者 说,为了使晶体学上等价的晶面或晶向具 有类似的指数,对六方晶体来说,就得放 弃三指数表示,而采用四指数表示。
• 填在四面体间隙的最大间隙原子是和4个顶 点的原子同时相切,故二者半径之和为:
密排六方间隙
八面体间隙
• hcp 晶体的八面体间隙如图所示。其形状与fcc 晶胞的八面体间隙完全相似,而间隙的位置不同 。从图看出,在一个hcp 晶胞内有6个八面体间隙 ,故八面体间隙数与原子数之比为6∶6 = 1∶1。
面心立方致密度
原子直径是a/2<110>的长度,即 面心立方结构的晶胞体积为a3,晶 胞内含4个原子,所以它的致密度η 为
《晶体学基础》课件

《晶体学基础》ppt课件
CONTENTS
目录
• 晶体学简介 • 晶体结构 • 晶体性质 • 晶体缺陷 • 晶体生长与制备 • 晶体应用
CHAPTER
01
晶体学简介
晶体学定义
晶体学是一门研究晶体材料、 晶体结构和晶体性能的科学。
晶体是由原子、分子或离子按 照一定的规律周期性排列而成 的固体。
晶体学的研究内容包括晶体的 几何结构、物理性质、化学性 质以及晶体生长、相变等。
观结构和应力分布有关。
疲劳强度
断裂韧性是衡量物质抵抗脆性断裂的能力的物理量。 不同晶体的断裂韧性不同,与晶体的缺陷类型和扩散 机制有关。
CHAPTER
04
晶体缺陷
点缺陷
01
晶体中一个或多个原子离开其平 衡位置,形成局部的、小的原子 排列异常。
02
点缺陷的形成与温度、压力、杂 质等因素有关。在晶体中,点缺 陷可以移动、聚集和消失,对晶 体的物理性质产生影响。
线缺陷
晶体中沿某一特定方向,原子排列出 现异常。
线缺陷通常表现为晶体的裂纹或位错 ,对晶体的力学性质有显著影响。位 错是晶体中常见的线缺陷,其运动和 相互作用会影响材料的加工和性能。
面缺陷
晶体中沿某一平面的原子排列出现异常。
面缺陷包括晶界、相界和表面等。晶界是晶体内部不同晶粒之间的界面,相界是 晶体中不同相之间的界面。这些面缺陷会影响晶体的光学、电学和热学性质。
19世纪,X射线和电子显微镜的发明 为晶体学的研究提供了新的手段,推 动了晶体学的发展。
17世纪,随着显微镜技术的发展,人 们开始对晶体进行更深入的研究,发 现了晶体的对称性和空间格子。
21世纪,随着计算机技术和材料科学 的快速发展,晶体学在理论和实验方 面都取得了重要进展,为新材料的研 发和应用提供了有力支持。
CONTENTS
目录
• 晶体学简介 • 晶体结构 • 晶体性质 • 晶体缺陷 • 晶体生长与制备 • 晶体应用
CHAPTER
01
晶体学简介
晶体学定义
晶体学是一门研究晶体材料、 晶体结构和晶体性能的科学。
晶体是由原子、分子或离子按 照一定的规律周期性排列而成 的固体。
晶体学的研究内容包括晶体的 几何结构、物理性质、化学性 质以及晶体生长、相变等。
观结构和应力分布有关。
疲劳强度
断裂韧性是衡量物质抵抗脆性断裂的能力的物理量。 不同晶体的断裂韧性不同,与晶体的缺陷类型和扩散 机制有关。
CHAPTER
04
晶体缺陷
点缺陷
01
晶体中一个或多个原子离开其平 衡位置,形成局部的、小的原子 排列异常。
02
点缺陷的形成与温度、压力、杂 质等因素有关。在晶体中,点缺 陷可以移动、聚集和消失,对晶 体的物理性质产生影响。
线缺陷
晶体中沿某一特定方向,原子排列出 现异常。
线缺陷通常表现为晶体的裂纹或位错 ,对晶体的力学性质有显著影响。位 错是晶体中常见的线缺陷,其运动和 相互作用会影响材料的加工和性能。
面缺陷
晶体中沿某一平面的原子排列出现异常。
面缺陷包括晶界、相界和表面等。晶界是晶体内部不同晶粒之间的界面,相界是 晶体中不同相之间的界面。这些面缺陷会影响晶体的光学、电学和热学性质。
19世纪,X射线和电子显微镜的发明 为晶体学的研究提供了新的手段,推 动了晶体学的发展。
17世纪,随着显微镜技术的发展,人 们开始对晶体进行更深入的研究,发 现了晶体的对称性和空间格子。
21世纪,随着计算机技术和材料科学 的快速发展,晶体学在理论和实验方 面都取得了重要进展,为新材料的研 发和应用提供了有力支持。
第3讲 晶体化学基础

(1)聚片双晶(若干个单体按同一双晶律所组 成) 例:斜长石的钠长石律聚片双晶 (2)轮式双晶(环状双晶) 例:金红石的六连 晶、白铅矿的三连晶。
斜长石的聚片双晶:
双晶轴(010) (只针对长石)
斜长石聚片双晶
角闪石
正长石卡氏双晶
堇青石矿物的轮式双晶(六连晶);4×(+)
金绿宝石的轮式双晶
3.1 最紧密堆积原理 球体空隙:
第二层球排列堆积在第一层之上时,每球只有与第一层的三个 球同时接触才算是最稳定的。即位于三角形空隙的位置。
八面体空隙
四面体空隙
3.1 最紧密堆积原理
两层球作最紧密堆积,出现了两种不同的空隙:一是由六个球 围成的空隙,称为八面体空隙 。另一种是由四个球围成的空 隙,称为四面体空隙。 第三层球的排列(C):
1 双晶面 :
假想的平面,若双晶 中的一个单体经过它 的反映能够与另一个 单体重合或者平行
6.2 双晶要素 2 双晶轴:
若双晶中的单体围绕此轴旋转180°,可与 另外一个单晶平行或者重合;
一般来说双晶轴都是二次ห้องสมุดไป่ตู้.
3 双晶中心:
假想的点,双晶的单体通过它的反伸操作可 与另一个单体重合;(在实际的双晶分析中 很少用到)
位于配位多面体中心的阳离子充填于被分布在八面体顶角 上的六个阴离子围成的八面体空隙中,并且恰好与周围的六个阴 离子均紧密接触。取八面体中包含两个四次轴的平面。
3.2 配位数和配位多面体
图中直角三角形ABC可以算出: Rk∕Ra = 2 -1=0.414。此值是阳离子作为六次配位的下限值。
Rk∕Ra <0.414时,表明阳离子过小,不能同时与周围的六个阴离 子都紧密接触,离子可在其中移动,结构是不稳定的。
晶体学基础

2020/3/3
3
1.1 晶体及其基本性质
晶体结构 = 点阵 + 结构基元
2020/3/3
4
空间点阵的四要素
1. 阵点: 空间点阵中的点; 2. 阵列: 结点在直线上的排列; 3. 阵面: 阵点在平面上的分布。
2020/3/3
5
空间点阵的四要素
4. 阵胞: 结点在三维空间形成的平行六面体。
原胞:最小的平行六面体,只考虑周期性,不考虑对称性; 晶胞:通常满足对称性的前提下,选取体积最小的平行六面体。
ur b/k
P
a/h A
v
a
2020/3/3
25
倒易点阵的应用
uur dhkl 1/ r *hkl
1、计算面间距
1
d2 hkl
r rhkl
r .rhkl
h
k
av*
l
r bcv**
av*
r b*
h
cv*
k
l
h
h
k
l
G
*
k
2020/3/3
3
c
28
倒易点阵的应用
2、计算晶面夹角
• 两晶面之间的夹角,可以用各自法线之间的夹角来表示, 或用它们的倒易矢量的夹角来表示:
c((ohhs21kk12ll12)c)osrvrv(hh2rv1kk2h1l1l21k1l1 ,hhrv21hav2avk*2*l+2+)kk21bvbv*rvv*+h+1kl12ll11cvcv*vrv*h2k2l2
4. 若已知两个晶带面,则晶带轴;
5. 已知两个不平行的晶向,可以求出过这两个晶向的晶面;
2-3晶体学基础

• • • • 对照片中各对弧对进行编号、标注。 测量有效周长(半周长L)。 测量并计算各弧对的间距(S/2)。 S 90 1 计算 和 d。 d
2 L
2 sin i
• 指数标定,计算晶胞参数。
a d ( HKL ) H 2 K 2 L2
2 sin
Fhkl = fa e2i(h0+k0+l0) = fa [cos2(0)+isin2(0)] = fa
讨论点阵消光的时候,只考虑每个 点阵点对应一个原子的最简单情况。 讨论结构消光的时候,考虑到一个 点阵点对应多个原子的情况。
欧拉公式: e+ix = cos(x) +isin(x) e-ix = cos(x) -isin(x).
4
面心点阵
(相同)
cos2n+isin2n = 1
cos(2n+1)+isin(2n+1) =-1
结论:在面心点阵情况下,hkl 为全奇或全偶时,都 能产生衍射。奇偶混合时出现消光。
5
• 底心点阵
– 每个晶胞中有2个同类原子,其坐标分别为0,0,0 和1/2,1/2,0。 – 在底心点阵中,h + k 为奇数时出现消光。
H 2 K 2 L2
33
f. •
•
34
衍射角为 7.5
35
2. 聚焦法
利用发散度较大的入射 X 射线束,照射试样上较大区域,由多晶体试 样中某一组 (hkl) 晶面族所发生的衍射线束在照相底片上仍然聚焦到一 点 (或一条细线) 的衍射方法,称为聚焦法。该方法比德拜-谢乐法具有 更高的灵敏度。
不对称装片法计算 时,不需要相机半径 数据,可减少误差来源。
2 L
2 sin i
• 指数标定,计算晶胞参数。
a d ( HKL ) H 2 K 2 L2
2 sin
Fhkl = fa e2i(h0+k0+l0) = fa [cos2(0)+isin2(0)] = fa
讨论点阵消光的时候,只考虑每个 点阵点对应一个原子的最简单情况。 讨论结构消光的时候,考虑到一个 点阵点对应多个原子的情况。
欧拉公式: e+ix = cos(x) +isin(x) e-ix = cos(x) -isin(x).
4
面心点阵
(相同)
cos2n+isin2n = 1
cos(2n+1)+isin(2n+1) =-1
结论:在面心点阵情况下,hkl 为全奇或全偶时,都 能产生衍射。奇偶混合时出现消光。
5
• 底心点阵
– 每个晶胞中有2个同类原子,其坐标分别为0,0,0 和1/2,1/2,0。 – 在底心点阵中,h + k 为奇数时出现消光。
H 2 K 2 L2
33
f. •
•
34
衍射角为 7.5
35
2. 聚焦法
利用发散度较大的入射 X 射线束,照射试样上较大区域,由多晶体试 样中某一组 (hkl) 晶面族所发生的衍射线束在照相底片上仍然聚焦到一 点 (或一条细线) 的衍射方法,称为聚焦法。该方法比德拜-谢乐法具有 更高的灵敏度。
不对称装片法计算 时,不需要相机半径 数据,可减少误差来源。
材料科学导论-第一章 晶体学基础3
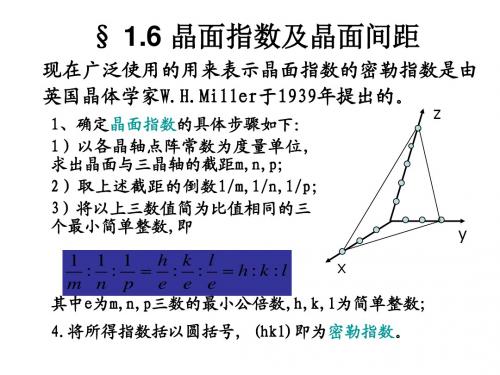
3、六方晶系晶面指数标定
根据六方晶系的对称特点,对六方晶系采用a1,a2,a3 及c四个晶轴,a1,a2,a3之间的夹角均为120度,这样, 其晶面指数就以(h k i l)四个指数来表示。 根据几何学可知,三维空间独立的坐标轴最多不超过三 个。前三个指数中只有两个是独立的,它们之间存在以 下关系:i =- ( h + k ) 。
三轴晶面指数(h k l) 四轴晶面指数(h k i l) i=- ( h + k )
立方晶系:
d hkl
a h k l
2 2 2
§ 1.6 晶面指数及晶面间距 范例:
m/l
c
a
m/k
b
m/h
画出晶面 (100),(110),(111),(201),(211),(321)
பைடு நூலகம்
c a
(100)
b
画出晶面 (100),(110),(111),(201),(211),(321)
d V [h b c sin k a c sin l a b sin
2 2 2 2 2 2 2 2 2 2 2 2
2hkabc (cos cos cos )
2
2kla bc(cos cos cos )
2
2hlab c(cos cos cos )]
2
2 2 2
1
2
1 2
V abc(1 cos cos cos 2cos cos cos )
单斜晶系:d=sinβ(h2/a2+k2sin2β/b2+l2/c2-2hlcosβ/ac)-1/2 正交晶系:d=[h2/a2+k2/b2+l2/c2]-1/2 四方晶系:d=[(h2+k2)/a2+l2/c2]-1/2 六方晶系:d=[4(h2+hk+k2)/3a2+l2/c2]-1/2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
η=nv/V
n:晶胞原子数 v:每个原子所占的体积 V:晶胞的体积
一个晶胞内的原子数n
• 这可从晶胞图中直观看出。但要注意,位于晶胞顶点的原子 是相邻的8个晶胞共有的,故属于一个晶胞的原子数是1/8。 位于晶胞的棱上原子是相邻的4个晶胞共有的,故属于一个 晶胞的原子数是1/4。位于晶胞外表面上的原子是两个晶胞 共有的,故属于一个晶胞的原子数是1/2。
• 填在四面体间隙的最大间隙原子是和4个顶 点的原子同时相切,故二者半径之和为:
密排六方间隙
八面体间隙
• hcp 晶体的八面体间隙如图所示。其形状与fcc 晶胞的八面体间隙完全相似,而间隙的位置不同 。从图看出,在一个hcp 晶胞内有6个八面体间隙 ,故八面体间隙数与原子数之比为6∶6 = 1∶1。
和
D2 是晶体学上的等
价方向,但其晶向指 数却分别是[100]和 [110]。
• 由于等价晶面或晶向不具有类似的指数, 人们就无法从指数判断其等价性,也无法 由晶面族或晶向族指数写出它们所包括的 各种等价晶面或晶向,这就给晶体研究带 来很大的不便。为了克服这一缺点,或者 说,为了使晶体学上等价的晶面或晶向具 有类似的指数,对六方晶体来说,就得放 弃三指数表示,而采用四指数表示。
共3个等价面(Ⅱ型棱柱面)。 •而{0001}只包括(0001) 一个晶面,称为基面。六 方晶体中比较重要的晶面 族还有 ,请读者写 出其全部等价面。
四指数表示晶向指数
• 用四个轴分量来表示一个空间矢量的方法有无穷多种,现在 行走法的方法的困难来自共面的三个轴。 • 看OA矢量,两轴的唯一表示是[-2,-1]。但三轴则有无限多种 • [-1,0,1],[0,1,2],[-2,-1,0],[1,2,3]等。 • 看OB矢量,两轴的唯 • 一表示是[-4,-3],但三 • 轴则有[-1,0,3],[-4,-3,0] • 一定要附加一个约束 • 条件,才能是指数唯 • 一。因 • a1 + a2 + a3 = 0 • 所以约束条件是: • u+ v + t = 0 • 这样,正确的指数是 • OA是 [1 0-1] , • OB是[-5-2 7]
• 4)fcc 和 hcp 中的八面体间隙远大于 bcc 中的八面体或 四面体间隙,因而间隙原子在 fcc 和 hcp 中的溶解度往 往比在 bcc 中大得多。 • (5) fcc 和 hcp 晶体中的八面体间隙大小彼此相等,四 面体间隙大小也相等,其原因在于这两种晶体的原子堆垛 方式非常相像。
• 在原子半径相同的条件下,hcp 晶体的八面体间隙大小与fcc 晶胞的八面体间隙大小相同。
四面体间隙
• hcp 晶体的四面体间隙位置如图所示。其形状与 fcc 晶胞的四 面体间隙完全相似,而间隙的位置不同,位于c 轴上有两个四面 体间隙。由于平行于c 轴的6条棱上的原子排列情况是和 c 轴完 全相同的,故在每条棱上与c 轴上间隙对应的位置也有两个四面 体间隙。
面心立方致密度
原子直径是a/2<110>的长度,即 面心立方结构的晶胞体积为a3,晶 胞内含4个原子,所以它的致密度η 为
a 2
体心立方
配位数
CN=8
体心立方致密度
• 原子直径是a/2<111>的 长,即 面心立 方结构的晶胞体积为a3 ,晶胞内含2个原子,所 以它的致密度η为
密排六方
配位数 •• • • • • •• • •• • • • ••
2
体心立方四面体间隙
bcc 晶体的四面体间隙如图所示,它是位于由两个相邻晶胞的体心 原子以及它们的公共棱上的两个原子所构成的四面体的中间,图 中的红色三角形表示间隙的中心位置。显然,每个表面({100}面) 上都有 4 个和中心点等同的点,故一个晶胞中的四面体间隙数为 6×4×1/2 (个),四面体间隙数与原子数之比为12∶2 = 6∶1。
• 四指数表示是基于4个坐标轴:a1,a2, a3 和 c 轴,如图所示,其中,a1,a2 和 c 轴就是原胞的 a,b 和c 轴,而 a3 = -(a1+a2)。下面就分别讨论用四指 数表示的晶面及晶向指数。
四指数表示晶面指数
• 六方晶系晶面指数的标定原理和方法同立方晶系中的一样,步 骤如下: • (1)先找出该面在四个坐标轴上的截距长度(以晶胞的点阵 常数 a,c 为单位长); (2)求其倒数并化为最简整数,即得(hkil)指数这样得到的 晶面指数称为 Miller-Bravais 指数。 从图所示的4个轴的几何关系 不难看出,只要晶面在a1和a2 轴上的截距一定,它在a3上的 截距也就随之而定。可见, h,k和i三个指数不是独立的。 事实上,可以证明
3
面心立方间隙
八面体间隙
fcc 晶胞的八面体间隙位于6个面心
原子组成的正八面体中间,间隙的
中心就是晶胞的体心位置,如图所 示。由于 fcc 晶胞的每条棱的中点
和晶胞体心是等同的位置,故它们
都是八面体间隙的中心。显然一个 晶胞中八面体间隙的数量为 12× ¼+1=4 (个),故八面体间隙数与原子数 之比为1∶1。
•• •• • •• • • • • • •• •• • ••
•
• •
• •
• • •• CN=12
• • ••
密排六方致密度
c 2 2 3 a ( ) a 2 3 2
2 2
c 8 1.633 a 3 4 a 12 3 2 0.74 1 3 2 8 6 a a 2 2 3
i=-(h+k)。
• 六方晶体中常见晶面及其四指数(亦称六方指数)标于图 。从图看出,采用四指数后,同族晶面(即晶体学上等价 的晶面)就具有类似的指数。例如:
1010 1010 1100 0110
• 共3个等价面(Ⅰ型棱柱面)。
1120 1120 1210 2110
• 但是,用三指数表示六方晶系的晶面和晶向有一个很大的缺点,
即晶体学上等价的晶面和晶向不具有类似的指数。这一点可以从 图看出。图中六棱柱的两个相邻表面(红面和绿面)是晶体学上
等价的晶面,但其密勒指数(Miller Indices)却分别是
(100)。 •图中夹角为 60°的 两个密排方向 D1 和
• 相邻的原子相互接触,原子中心就是八面体的各个角顶。
根据几何学关系可以求出间隙能够容纳的最大圆球半径。 假设原子半径为 r,间隙中能容纳的最大圆球半径为 rx ,
则可以算出八面体间隙相对大小rx / r。
四面体间隙
fcc 晶胞的四面体间隙位于 4 个 原子组成的正四面体的中间,如 图 所示。如果用(200),(020)和
单质晶它是每个原子的最近邻数目,晶体中最大的配位数为12 ,但在一些非单质的晶体中CN可以大于12 。因为金属结构一 般有高的对称性,单质金属的CN没有11、10、9等数值 。 CN 顺序分别为12、8、6、4、2、1。金属结构大部分是密堆的,它 们的CN大多是12或8。
致密度
• 致密度又称堆垛密度或空间填充的效率η,它表示原子排 列的密集程度。它定义为晶体结构中单位体积中原子所占 的体积。假如把金属晶体中的原子看成是有一定直径的刚 球,则紧密系数可以用刚球所占空间的体积百分数来表示 。若以一个晶胞来计算,致密度就等于晶胞中原子所占体 积与晶胞体积之比,即: • 致密度 =晶胞中原子所占体积之和/晶胞的体积。
0.127nm,按上式求得γ-Fe的四面体和八面体间隙的球半径
分别为0.028nm和0.052nm。由于碳原子半径为0.077nm,氮 原子半径为0.070nm,虽稍大于 -Fe的八面体间隙的球半径, 但只要将铁原子稍微挤开使间隙扩大一点,碳、氮原子即可 进入八面体间隙之中,因此,γ-Fe中能溶入碳、氮原子形成 间隙固溶体。
(002)三个平面将 fcc 晶胞分为8
个相同的小立方体,则每个小立 方体的中心就是四面体间隙的中
心,显然一个晶胞内有 8 个四面
体间隙,故四面体间隙数与原子 数之比为 2∶1。
• 根据图可算出四面体间隙相对于点阵原子 的大小:rx/r:
OD = (3/4)例进行分析:γ-Fe的原子半径为
此外,以晶胞中部三个原子中的每一个为顶点
,以其上方(顶层)和下方(底层)的三个原
子构成的三角形为底,分别可作一四面体,其 中心就是四面体间隙的中心。这样,一个六方 晶胞内的四面体间隙总数应是 c 轴上的间隙数 、6 条平行于 c 轴的棱上的间隙数以及通过晶 胞中部的三个原子而平行于c 轴的三条竖直线 上的间隙数之和。其值为2+6×2×1/3+2×3
四轴坐标系中,晶向指数的 确定,首先要求出三轴坐标 系的晶向指数[U V W],然 后利用上述关系,换算成四 轴坐标系中的晶向指数 [u v t w]。
常见晶体结构
一、常见晶体结构在金属晶体中,金属键使原子的排列趋于尽 可能地紧密,构成高度对称性的简单的晶体结构。最常见的金 属晶体结构有以下三类。 面心立方:Al,γ-Fe,Ni,贵金属以及奥氏体不锈钢等。 体心立方:碱金属、难熔金属(V,Nb,Ta,Cr,Mo,W) 、α-Fe 等等。 密排六方 :α-Be, α-Ti, α-Zr等
4
2
6
间
隙
• 从晶体原子排列的刚球模型可以看到,在原子球与原子球 之间存在着不同形貌的间隙。主要有两类间隙即:四面体 间隙和八面体间隙。 • 晶体结构中间隙的数量、位置和每个间隙的大小等也是晶 体的一个重要特征,对于了解金属的性能、合金相结构、 扩散、相变等问题很有用处。
面心立方
配位数
CN=12
八面体间隙
体心立方
bcc 晶体的八面体间隙如图所示,其位置和形状不同于 fcc 晶胞的八面 体间隙。间隙的中心位于晶胞的面心和晶胞棱的中点(对 bcc 晶体,这
些都是等同点),一个晶胞中八面体间隙的数量是6(个),故八面体间 隙数与原子数之比为6∶2 = 3∶1。
