作单跨静定梁的弯矩图和剪力图资料讲解

梁的剪力和弯矩剪力图和弯矩图课件

静力平衡条件的意义
静力平衡条件是物体受力分析的基本依据，通过它我们可以分析物体在受到外力作用时的运动状态，并计算出物体所受到的合力。
梁的剪力和弯矩的静力平衡条件的推导和应用
梁的剪力和弯矩的静力平衡条件的推导
在梁的受力分析中，我们可以通过对梁进行截面切开、移除切块并代之以作用相反的力等步骤，得到梁的内力——剪力和弯矩。当梁处于静力平衡状态时，其剪力和弯矩也必须满足一定的平衡条件。
梁的剪力和弯矩剪力图和弯矩图课件
目
CONTENCT
录
• 引言 • 梁的剪力分析 • 梁的弯矩分析 • 梁的剪力和弯矩组合分析 • 梁的剪力和弯矩的静力平衡条件 • 梁的剪力和弯矩的相互作用和影响
01
引言
课程背景
建筑力学是建筑设计和施工的重要基础，而梁的剪力和弯矩是建筑力学中的重要概念。
通过学习梁的剪力和弯矩，可以更好地理解建筑结构的设计和施工方法。
梁的剪力和弯矩的静力平衡条件的应用
通过应用静力平衡条件，我们可以分析梁在受到外力作用时的剪力和弯矩，进而计算出梁的应力、应变等物理量，为结构设计提供依据。
梁的剪力和弯矩的静力平衡条件的应用实例
简支梁受垂直均布荷载作用
对于简支梁受垂直均布荷载作用的情况，通过应用静力平衡条件，我们可以得到梁的剪力图和弯矩图，并计算出梁的最大剪力和最大弯矩。
简单梁分析
以简单梁为例，说明如何进行剪力和弯矩的组合分析。
复杂梁分析
通过有限元模型，对复杂梁进行剪力和弯矩的组合分析，讨论各种因素对梁内力的影响。
05
梁的剪力和弯矩的静力平衡条件
静力平衡条件的概念和意义
静力平衡条件的概念
静力平衡条件是指物体在受到外力作用时，如果处于静止状态，则物体内部的力也处于平衡状态，即所有作用在物体上的外力矢量和为零。

快速准确绘制单跨静定梁内力图

快速准确绘制单跨静定梁内力图摘要:单跨静定梁的内力图是弯曲杆件强度、刚度计算及做超静定结构内力图的基础。

本文作者从四方面阐述,提出快速准确绘制单跨静定梁内力图的方法。

关键词:内力图;校核;截面内力;图线类型;叠加法一、引言弯曲变形是工程中常见的一种基本变形,以弯曲变形为主要变形的杆件称为梁。

例如房屋建筑中,梁受到楼面荷载和梁自重的作用,将发生弯曲变形;其它如阳台挑梁、梁式桥的主梁等,都是以弯曲变形为主的构件。

在对梁进行强度和刚度计算时,通常要先画出剪力图和弯矩图,以便清楚地看出梁的各个截面上剪力和弯矩的大小、正负以及最值所在截面的位置。

而单跨静定梁的内力图是弯曲杆件强度、刚度计算及做超静定结构内力图的基础,如果这一部分没有学好,弯曲杆件的强度、刚度就无从计算,超静定结构的内力图也就很难做出。

在多年的教学实践中,根据学生信息反馈,本人探索、研究、试行,提出快速准确绘制单跨静定梁内力图的方法以供学生和同行商榷。

二、支座反力计算一定要校核能否正确画出单跨静定梁的内力图,支座反力的对错是关键。

怎样求支座反力是静力学的主要内容,这里不再赘述。

总的来说,支座反力由静力平衡方程解出,求解过程中,在正确的受力图上,列出独立并包含最少未知量的方程,尽量避免解方程组,求出支座反力后一定要用同解方程校核。

例如图1所示简支梁:反力计算正确。

在这个例子中,大多数学生在第二步计算RB 时就用方程,即RB=10+10×2-RA,如果RA 算错了,则RB 肯定也会跟着出错,所以在教学中建议学生尽量用力矩方程求支座反力,用投影方程校核,保证计算正确。

三、熟练掌握截面法求指定截面内力要做出结构的内力图,还必须能正确计算出控制截面的内力。

所谓控制截面指的是:杆端截面、集中力、集中力偶作用面、分布荷载集度变化处。

用截面法求这些截面的内力是做内力图的基础。

这一部分比较容易掌握,许多教材介绍的也比较少,但大部分学生在做内力图时又算不出特定截面的内力,因此,这一部分应投入比较多的精力。

单跨超静定梁的杆端弯矩和杆端剪力

已知梁的eiea解1选取基本结构原结构是三次超静定梁去掉支座b的固定端约束并代之以相应的多余未知力x1x2和x3得到图1911b2建立力法方程根据原结构支座b处位移为零的11x112x213x31p021x122x223x32p031x132x233x33p03计算系数和自由项分别作基本结构的荷载弯矩图mp图和单位弯矩图m1图m2图m3图如图1911cdef利用图乘法求得力法方程中各系数和自由项分别为11l33ei22lei33lea1221l22ei13310233201pql48ei2pql36ei3p04求多余未知力将以上各系数和自由项代入力法解得3241223123xx0328xx026x0llqleieieillqleieieilea?????212311xxx0212qlql???5作内力图作mmm1x1m2x2m3x3mp计算abmab112ql2上拉mba112ql2上拉m跨中124ql2下拉根据三点竖标连以光滑曲线q相对应m为抛物线得图1911g所示m图
Δ1=δ11X1+δ12X2+δ13X3+Δ1P=0
Δ2=δ21X1+δ22X2+δ23X3+Δ2P=0
b
Δ3=δ31X1+δ32X2+δ33X3+Δ3P=0
式(b)就是由位移条件所建立的求解X1、X2和X3
对于n次超静定结构有n个多余约束，也就是有n 个多余未知力x1，x2，…，xn，且在n个多余约束处有n个已知的位移条件，故可建立n个方程，例如原结构在荷载作用下各多余约束处的位移为零时，有
11E 1 I
M 1 2dx1(1ll2l)l3 E I2 3 3E I
1
11q l2 3 q l4
1 P E IM 1 M P d x E I(3 2l l 4 l) 8 E I

浅述单跨静定梁弯矩图的快速绘制

浅述单跨静定梁弯矩图的快速绘制摘要：梁是结构的主要受力单元，在计算梁的承载及破坏时，弯矩图的作用至关重要。

而弯矩图的绘制是学生在学习的一个弱点，因此针对静定粱结构的弯矩图快速绘制进行探讨，可以大大提高作图速度和效率。

关键词：静定梁弯矩弯矩图引言：力学课程是工科专业学生的一门必不可少的基础课程，它对于后续钢筋混凝土等课程的学习起十分重要的作用。

就建筑本身来说，就是一个力学模型，要保证结构的安全就必须确保每个受力构件的计算准确。

因此学好力学课程有非常重要的意义，而在日常力学课程的学习中，梁的弯矩图绘制却是学生在学习中的难点，文章通过总结各种弯矩图绘制的方法后，给出一种能够较为快速的绘制弯矩图的方法，对于梁的后续计算打下基础。

1理论知识1、1 单跨静定梁的种类（如图1）：（a)悬臂梁(b)简支梁(c) 外伸梁[1]图1 ：单跨静定梁的种类(Figure 1: The single-span beam statically determinate types)1、2弯矩出现的原因：弯矩伴随梁的弯曲变形而出现1、3弯矩的位置：弯矩出现在梁的截面上1、4弯矩的正方向规定：弯矩使梁的下侧（以梁的轴线为分界）纤维受拉为正1、5弯矩计算的基本方法：利用截面法计算，通过分段列弯矩图的函数表达式求解1、6 弯矩图绘制的方法：先绘制梁的轴线，弯矩图绘制在梁的受拉侧，不需要标明正负号2静定梁弯矩图绘制的实用结论2、1 弯矩的本质：弯矩是为了平衡所有外界力对截面的转动效果2、2弯矩分段的位置：弯矩作为内力的一种，与外力作用密切相关。

因此，绘制梁的弯矩图时，在有外力（）作用的位置分段进行[2]2、3 需要求解弯矩的截面位置：通常出现在梁的两端以及分段位置的截面处2、4 弯矩图形的特点：梁上的荷载分为四种情况：无荷载区段、均布荷载区段、集中力作用点和集中力偶作用点。

可以对梁的弯矩图特点总结出以下规律（如表1）：2、4、1、当某段梁上无分布荷载（无荷载区段），即时，是与无关的常数，是的一次函数。

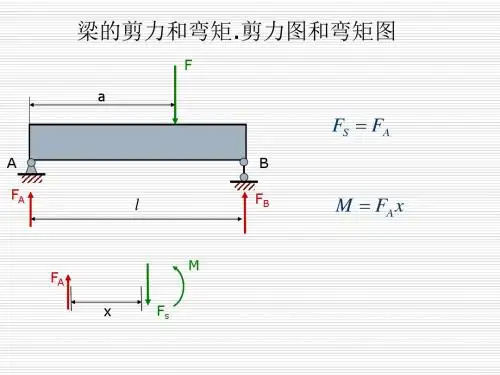
《材料力学》课件4-2梁的剪力和弯矩.剪力图和弯矩图

C D
F
B
FCs F FCs F
M C Fl M C Fl
l
l
FCs
MA FA
A
M C 2Fl Fl 0
FDs F
F
B
l
FCs
C
MA
MC
MC 2 Fl
D
MD 0
FDs
F
D

C
l
MD
B
截开后取左边为示力对象：
向上的外力引起正剪力，向下的外力引起负剪力；
向上的外力引起正弯矩，向下的外力引起负弯矩；
图示外伸梁,,试作剪力图和弯矩图.
10kN m
X2
40 kN m
A
35kN
B
FS x1 20kN
M x1 20 x1
0 x1 1 0 x1 1
1m
15
4m
2.5
25kN
FS x2 25 10 x2
25
2 x2 M x2 25 x2 10 2
突变，顺下逆上，大小与M 同，FS图不发生变化。
例题
4.9
作图示梁的内力图
3kN
D
4.5kN m
A
2kN m
B E
C
FA 10kN 1m 2m
2m
FB 2kN 1m
7
kN
3 3
x 1.56
2 2
kNm
2.44
2
例题
4.10
4kN m
6kN
2kN m
1m
1m
2m
4.5 kN 1.5
x
l
FB
ql FS qx 2

第5章梁的剪力图与弯矩图 ppt课件

FQ/kN
e
1.11 f
1.11
O
0.89 a
0a
O
0.89 b ,c 0.89 d d,e
1.335 b 1.665 c
0.335
x
fx
0
5．确定剪力与弯矩的最大绝对值从图中不难得到剪力与弯矩的绝对值的最大值分别为
(发生在EF段)
(发生在D、E截面上)
M/kN.m
ppt课件
34
例题2
FRA
ppt课件
13
控制面的概念
外力规律发生变化截面—集中力、集中力偶作用点、分布荷载的起点和终点处的横截面。
ppt课件
14
控制面的概念
根据以上分析，在一段杆上，内力按某一种函数规律变化，这一段杆的两个端截面称为控制面（control cross-section）。据此，下列截面均可为控制面：
集中力作用点的两侧截面；集中力偶作用点的两侧截面；均布载荷（集度相同）起点和终点处的截面。
其中任一点作平行于x 轴的直线而得。
ppt课件
39
例题3 A FAy FQ a 9qa/4 O
a
O
M
q
E
4a
B
a FBy
e
qa
c
b 7qa/4
e
81qa2/32
qa2 b,c
D
5．根据微分关系连图线
对于弯矩图：在AB段，因
有均布载荷作用，图形为
ql 二次抛物线。又因为q向下为负，弯矩图为凸向M
坐标正方向的抛物线。于
第5章
梁的剪力图与弯矩图
2019年10月20日
ppt课件
1
目录

单跨静定梁

［弯矩图的叠加］
基本弯矩图
弯矩图的叠加，为弯矩图竖标的叠加。

［单跨静定梁］
三种基本形式：
（1）简支梁（2）外伸梁（3）悬臂梁
其它形式：
［作剪力图］
梁的剪力图简易作法：先求出全部的支座反力。

然后根据外力和反力的指向，从梁的左端零点出发，顺着力的方向，依次绘出剪力图，最终到达梁的右端零点。

剪力图绘在梁的上方为正，下方为负。

［作弯矩图］
先求出各控制截面的弯矩，然后根据弯矩图的叠加，分段作出结构的全部弯矩图。

求控制截面弯矩的固定截面法：先求出全部的支座反力。

欲求某控制截面的弯矩，只要将该截面假想固定，可取左半部或右半部为对象，根据悬臂结构的弯矩，判断受拉边，求出弯矩值。

剪力图和弯矩图(史上最全面)ppt课件

1.25 1
q=2kN/m
+
x
_
1
26
§4–5 按叠加原理作弯矩图
一、叠加原理：多个载荷同时作用于结构而引起的内力等于每个载荷单独
作用于结构而引起的内力的代数和。
Q(P1P2 Pn) Q1(P1) Q2(P2) Qn(Pn)
M (P1P2 Pn) M1(P1) M2(P2) Mn(Pn)
分区点A： Q qa; M qa2
M 的驻点： Q 0 ; M 3 qa2 2
x
右端点： Q 0; M 3 qa2 2
22
[例5] 用简易作图法画下列各图示梁的内力图。AB=BC=CD=a
q AB
RA qa Q qa/2
+ – qa/2
qa2 CD
RD
– qa/2
M
qa2/2
+
–
3qa2/8 qa2/2
1
第四章弯曲内力
§4–1 平面弯曲的概念及梁的计算简图 §4–2 梁的剪力和弯矩 §4–3 剪力方程和弯矩方程 ·剪力图和弯矩图 §4–4 剪力、弯矩与分布荷载集度间的关系及应用 §4–5 按叠加原理作弯矩图 §4–6 平面刚架和曲杆的内力图
弯曲内力习题课
2
§4–1 平面弯曲的概念及梁的计算简图
求支反力qa2qa2qa2241练习直接画内力图p12944dj对称载荷m反对称载荷同时可以提前讲内力图的对称关系2改错见下页ppt3由q图作m图和载荷图p135416b由m图作q图和载荷图p135417a4讲解组合梁的内力图p13046aqa4qa43qa47qa4qa323qa已知q图求外载及m图梁上无集中力偶
qL 1
2q
解：截面法求内力。 1--1截面处截取的分离体

梁的内力图剪力图和弯矩图ppt正式完整版

VA<D0段时3：向q右<0上，方V倾图斜为，x向V=下=30.斜时1m直为线水，平线。
3.8
3
2.2
(kN·m)
1.41 3.8
AD段：q<0， V 图为向下斜直线， M图为下凸抛物线。
谢谢观看
vv vv
vv v v
v
利用上述规律：
1、可以检查剪力图和弯矩图是否正确。 2、可以快速的绘制剪力图和弯矩图，步骤如下：（1）将梁正确分段（2）根据各段梁上的荷载情况，判断剪力图和弯矩图的形状
（3）寻找控制面，算出各控制面的V和M （4）逐段绘制出V和M图即梁的V和M图
快速绘制剪力图和弯矩图 q
画剪力图和弯矩图时，一定要将梁正确分段，分段建立方程，依方程而作图
例题1 简支梁受均布荷载作用，如图示，作此梁的剪力图和弯矩图。
解：1.求约束反力由对称关系，可得：
2、建立内力方程
Vx
RAq
x1q 2
l q
x
(0<x<l)
3、依方程作剪力图和弯矩图
Vmax=
1 ql 2
Mmax 1 ql 2 8
例2 简支梁受集中荷载作用，如图示，作此梁的剪力图和弯矩图。
1.求约束反力 2、分段建立方程 AC段： V
CB段： V
3、依方程而作图
例题3 简支梁受集中力偶作用，如图示，试画梁的剪力图和弯矩图。解：1.求约束反力
2.列剪应力方程和弯矩方程 AC段: V
CB段：V
3、依方程而作图
荷载图、剪力图、弯矩图的规律
A
C
D
B
FA
ac
l
FA
b
FB
FB