材料力学梁弯曲时内力和应力第3节 剪力图和弯矩图
合集下载
材料力学弯曲应力_图文
§5-3 横力弯曲时的正应力
例题6-1
q=60kN/m
A
1m
FAY
C
l = 3m
FS 90kN
120
1.C 截面上K点正应力 2.C 截面上最大正应力
B
x
180
K
30 3.全梁上最大正应力 z 4.已知E=200GPa，
FBY
C 截面的曲率半径ρ y
解：1. 求支反力
x 90kN M
x
（压应力）
目录
目录
§5-2 纯弯曲时的正应力
正应力分布
z
M
C
zzy
x
dA σ
y
目录
§5-2 纯弯曲时的正应力
常见截面的 IZ 和 WZ
圆截面 空心圆截面
矩形截面 空心矩形截面
目录
§5-3 横力弯曲时的正应力
横力弯曲
6-2
目录
§5-3 横力弯曲时的正应力
横力弯曲正应力公式
弹性力学精确分析表明 ，当跨度 l 与横截面高度 h 之比 l / h > 5 （细长梁）时 ，纯弯曲正应力公式对于横 力弯曲近似成立。 横力弯曲最大正应力
§5-3 横力弯曲时的正应力
q=60kN/m
A
1m
FAY
C
l = 3m
FS 90kN
120
2. C 截面最大正应力
B
x
180
K
30 C 截面弯矩 z
FBY
y
C 截面惯性矩
x 90kN M
x
目录
§5-3 横力弯曲时的正应力
q=60kN/m
A
1m
FAY
C
l = 3m
梁的弯曲(应力、变形)
2
回顾与比较
内力
应力
F
A
FAy
编辑ppt
T
IP
M
?
?
FS
3
§9-6 梁的弯曲时的应力及强度计算
一、弯曲正应力 Normal stress in bending beam
梁段CD上，只有弯矩，没有剪力－－纯弯曲Pure bending
梁段AC和BD上，既有弯矩，又有剪力－－剪力弯曲Bending by
transverse force
编辑ppt
4
研究对象：等截面直梁 研究方法：实验——观察——假定
编辑ppt5Leabharlann 实验观察——梁表面变形特征
横线仍是直线，但发生 相对转动，仍与纵线正交
纵线弯成曲线，且梁的 下侧伸长，上侧缩短
以上是外部的情况，内部如何？ 想象 —— 梁变形后，其横截面仍为平面，且垂直
x
61.7106Pa61.7MPa
编辑ppt
13
q=60kN/m
A
1m
FAY
C
l = 3m
FS 90kN
M ql /867.5kNm 2
x
2. C 截面最大正应力
120
B
x
180
K
30 C 截面弯矩
z
MC60kN m
FBY
y
C 截面惯性矩
IZ5.83120 5m 4
x 90kN
C max
M C y max IZ
于变形后梁的轴线，只是绕梁上某一轴转过一个角度 透明的梁就好了，我们用计算机模拟 透明的梁
编辑ppt
6
编辑ppt
7
总之 ，由外部去 想象内部 —— 得到
弯曲内力—利用内力图规律绘制剪力图和弯矩图(材料力学)
2 分段定形
在控制截面处将梁分段，判断各段剪力图和弯矩图的大致形状。
3 求控制截面的内力值
利用计算截面内力的代数和法，求出各控制截面上的Fs和M值。
4 连线绘图
利用荷载、剪力和弯矩之间的微分关系及内力图规律，逐段绘出梁的Fs图和M图。
分布荷载集度、剪力与弯矩之间的微分关系
[例1] 利用内力图特征绘制梁的内力图
2
1
3
1m
1.5m
5kN
0.5m
1m 1kN
dFS(x) q(x) dx
dM (x) dx
FS (x)
q＝0，FS = 常数，平直线； M(x)为 x 一次函数，斜直线；
q=2kN/m
1.25 1
q常数，FS (x) 为 x 一次函数，斜直线；
M(x) 为 x 二次函数，抛物线；
集中力作用处，剪力图突变。
分布荷载集度、剪力与弯矩之间的微分关系
2.内力图特征规律
dFS(x) q(x) dx
dM (x) dx
FS (x)
dM 2 (x) dx2
dFS (x) dx
q(x)
梁上情 无外力 内力图 况 区段
均布荷载qy 集中荷载
作用区段
Fy作用处
剪 力 图
常数 斜直线
有突变(突
零 (水平线) (自左至右)
qL
q
解： FSA右 qL
A
C
L/2
B L/2
FS
FSC qL
FSB
qL
q
L 2
3 2
qL
MA 0
qL
qL
3qL/2
L MC qL 2
qL2 2
9qL2 /8
在控制截面处将梁分段，判断各段剪力图和弯矩图的大致形状。
3 求控制截面的内力值
利用计算截面内力的代数和法，求出各控制截面上的Fs和M值。
4 连线绘图
利用荷载、剪力和弯矩之间的微分关系及内力图规律，逐段绘出梁的Fs图和M图。
分布荷载集度、剪力与弯矩之间的微分关系
[例1] 利用内力图特征绘制梁的内力图
2
1
3
1m
1.5m
5kN
0.5m
1m 1kN
dFS(x) q(x) dx
dM (x) dx
FS (x)
q＝0，FS = 常数，平直线； M(x)为 x 一次函数，斜直线；
q=2kN/m
1.25 1
q常数，FS (x) 为 x 一次函数，斜直线；
M(x) 为 x 二次函数，抛物线；
集中力作用处，剪力图突变。
分布荷载集度、剪力与弯矩之间的微分关系
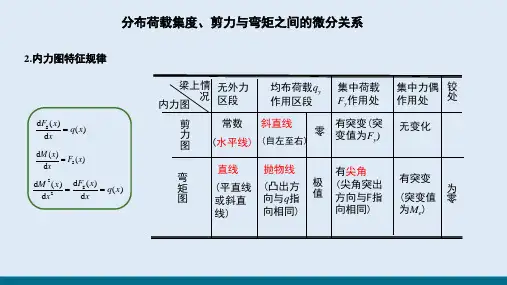
2.内力图特征规律
dFS(x) q(x) dx
dM (x) dx
FS (x)
dM 2 (x) dx2
dFS (x) dx
q(x)
梁上情 无外力 内力图 况 区段
均布荷载qy 集中荷载
作用区段
Fy作用处
剪 力 图
常数 斜直线
有突变(突
零 (水平线) (自左至右)
qL
q
解： FSA右 qL
A
C
L/2
B L/2
FS
FSC qL
FSB
qL
q
L 2
3 2
qL
MA 0
qL
qL
3qL/2
L MC qL 2
qL2 2
9qL2 /8
梁的弯曲(工程力学课件)
02 弯曲的内力—弯矩与剪力
3-3截面
M 3 q 2a a 2qa 2
4-4截面
qa 2
5qa 2
2
M 4 FB 2a M C
3qa
2
2
5-5截面
qa 2
M 5 FB 2a
2
02 弯曲的内力—弯矩与剪力
由以上计算结果可以看出：
（1）集中力作用处的两侧临近截面的弯矩相同，剪力不同，说明剪力在
后逐段画出梁的剪力图和弯矩图。
04 弯矩、剪力与载荷集度之间的关系
例8 悬臂梁AB只在自由端受集中力F作用，如图（a）所示，
试作梁的剪力图和弯矩图。
解：
1-1截面： Q1＝-F M1＝0
2-2截面： Q1＝-F M1＝－Fl
04 弯矩、剪力与载荷集度之间的关系
例9 简支梁AB在C点处受集中力F作用，如图（a）所示，作此梁的剪力
（2）建立剪力方程和弯矩方程；
（3）应用函数作图法画出剪力Q（x），弯矩M（x）的图线，即为剪力
图和弯矩图
03 弯矩图和剪力图
例9.3 悬臂梁AB在自由端B处受集中载荷F作用，如图（a）所示，试作
其剪力图和弯矩图。
解 ：（1）建立剪力方程和弯矩方程
() = ( < < )
() = −( − ) ( ≤ ≤ )
方程和弯矩方程，并作剪力图和弯矩图。
解：（1）求支反力
（2）建立剪力方程和弯矩方程
03 弯矩图和剪力图
（3）绘制剪力图、弯矩图
计算下列5个截面的弯矩值：
03 弯矩图和剪力图
二、用简便方法画剪力图、弯矩图 (从梁的左端做起)
1.无载荷作用的梁段上 剪力图为水平线。 弯矩图为斜直线（两点式画图）。
《材料力学》 第五章 弯曲内力与弯曲应力
第五章 弯曲内力与应力 §5—1 工程实例、基本概念一、实例工厂厂房的天车大梁，火车的轮轴，楼房的横梁，阳台的挑梁等。
二、弯曲的概念：受力特点——作用于杆件上的外力都垂直于杆的轴线。
变形特点——杆轴线由直线变为一条平面的曲线。
三、梁的概念：主要产生弯曲变形的杆。
四、平面弯曲的概念：受力特点——作用于杆件上的外力都垂直于杆的轴线，且都在梁的纵向对称平面内（通过或平行形心主轴且过弯曲中心）。
变形特点——杆的轴线在梁的纵向对称面内由直线变为一条平面曲线。
五、弯曲的分类：1、按杆的形状分——直杆的弯曲；曲杆的弯曲。
2、按杆的长短分——细长杆的弯曲；短粗杆的弯曲。
3、按杆的横截面有无对称轴分——有对称轴的弯曲；无对称轴的弯曲。
4、按杆的变形分——平面弯曲；斜弯曲；弹性弯曲；塑性弯曲。
5、按杆的横截面上的应力分——纯弯曲；横力弯曲。
六、梁、荷载及支座的简化（一）、简化的原则：便于计算，且符合实际要求。
（二）、梁的简化：以梁的轴线代替梁本身。
（三）、荷载的简化：1、集中力——荷载作用的范围与整个杆的长度相比非常小时。
2、分布力——荷载作用的范围与整个杆的长度相比不很小时。
3、集中力偶（分布力偶）——作用于杆的纵向对称面内的力偶。
（四）、支座的简化：1、固定端——有三个约束反力。
2、固定铰支座——有二个约束反力。
3、可动铰支座——有一个约束反力。
（五）、梁的三种基本形式：1、悬臂梁：2、简支梁：3、外伸梁：（L 称为梁的跨长） （六）、静定梁与超静定梁静定梁：由静力学方程可求出支反力，如上述三种基本形式的静定梁。
超静定梁：由静力学方程不可求出支反力或不能求出全部支反力。
§5—2 弯曲内力与内力图一、内力的确定（截面法）：[举例]已知：如图，F ，a ，l 。
求：距A 端x 处截面上内力。
解：①求外力la l F Y l FaF m F X AYBY A AX)(F, 0 , 00 , 0-=∴==∴==∴=∑∑∑ F AX =0 以后可省略不求 ②求内力xF M m l a l F F F Y AY C AY s ⋅=∴=-==∴=∑∑ , 0)( , 0∴ 弯曲构件内力：剪力和弯矩1. 弯矩：M ；构件受弯时，横截面上存在垂直于截面的内力偶矩。
材料力学第5章-剪力图与弯矩图
第5章 梁的强度问题
剪力方程与弯矩方程
建立剪力方程和弯矩方程的方法与过程，实际上与前面所 介绍的确定指定横截面上的剪力和弯矩的方法和过程是相似的 ，所不同的，现在的指定横截面是坐标为x的横截面。
需要特别注意的是，在剪力方程和弯矩方程中，x是变量， 而FQ(x)和M(x)则是x的函数。
第5章 梁的强度问题
剪力方程与弯矩方程
例题2
MO=2FPl
FP
B
A
C
l
l
悬臂梁在B、C两处分别承受集中力FP和集中力偶M＝2FPl
的作用。梁的全长为2l。 试写出：梁的剪力方程和弯矩方程。
第5章 梁的强度问题
剪力方程与弯矩方程
y
MO=2FPl
O
A
C
l
FP
B l
解：1．确定控制面和分段
本例将通过考察截开截面的右
边部分平衡建立剪力方程和弯矩方 程，因此可以不必确定左端的约束 力。
本章首先介绍如何建立剪力方程和弯矩方程；讨论载荷、 剪力、弯矩之间的微分关系；怎样根据载荷、剪力、弯矩之间 的微分关系绘制剪力图与弯矩图；然后应用平衡、变形协调以 及物性关系，建立确定弯曲的应力和变形公式；最后介绍弯曲 强度设计方法。
第5章 梁的强度问题
工程中的弯曲构件 梁的内力及其与外力的相互关系 剪力方程与弯矩方程 载荷集度、剪力、弯矩之间的微分关系 剪力图与弯矩图 刚架的内力与内力图 结论与讨论(1)
根据以上分析，不难得到结论： 杆件各截面上内力变化规律随着外力的 变化而改变。
第5章 梁的强度问题
梁的内力及其与外力的相互关系
所谓剪力和弯矩变化规律是指表示剪力和弯矩变 化的函数或变化的图线。这表明，如果在两个外力 作用点之间的梁上没有其他外力作用，则这一段梁 所有横截面上的剪力和弯矩可以用同一个数学方程 或者同一图线描述。
剪力图和弯矩图(史上最全面)解析
三、 叠加原理： 多个载荷同时作用于结构而引起的内力等于每个载荷单
独作用于结构而引起的内力的代数和。
Q(P1P2 Pn) Q1(P1) Q2(P2) Qn(Pn)
M(P1P2 Pn) M1(P1) M2(P2) Mn(Pn)
M (P1P2 Pn) M1(P1) M2(P2) Mn(Pn)
适用条件：所求参数（内力、应力、位移）必然与荷载满 足线性关系。即在弹性限度内满足虎克定律。
27
二、材料力学构件小变形、线性范围内必遵守此原理 ——叠加方法
步骤： ①分别作出各项荷载单独作用下梁的弯矩图； ②将其相应的纵坐标叠加即可（注意：不是图形的简单
四、对称性与反对称性的应用： 对称结构在对称载荷作用下，Q图反对称，M图对称；对称
结构在反对称载荷作用下，Q图对称，M图反对称。
M 的驻点： Q 0 ; M 3 qa2 2
x
右端点： Q 0; M 3 qa2 2
22
[例5] 用简易作图法画下列各图示梁的内力图。AB=BC=CD=a
q AB
RA qa Q qa/2
+ – qa/2
qa2 CD
RD
– qa/2
M
qa2/2
+
–
3qa2/8 qa2/2
qa2/2
RB
Pa l
Y
0,
YA
P(l a) l
XA A YA
P B
P B
RB
11
②求内力——截面法
Y
0,
Q YA
P(l a) l
mC 0 , M YA x
m XA A
材料力学第五章
l
F l a x
l
材料力学
第五章 梁的剪力图与弯矩图
梁的横截面上位于横截面 内的内力FS是与横截面左右两 侧的两段梁在与梁轴相垂直方 向的错动(剪切)相对应，故称 为剪力；梁的横截面上作用在 纵向平面内的内力偶矩是与梁 的弯曲相对应，故称为弯矩。
材料力学
第五章 梁的剪力图与弯矩图
为使无论取横截面左边或右边为分离体，求得同一横
截面上的剪力和弯矩其正负号相同，剪力和弯矩的正负号
要以其所在横截面处梁的微段的变形情况确定，如下图。
材料力学
第五章 梁的剪力图与弯矩图
综上所述可知： (1) 横截面上的剪力——使截开部分梁产生顺时针方向
转动为正；产生逆时针方向转动为负。
(2) 横截面上的弯矩——作用在左侧面上使截开部分 逆时针方向转动，或者作用在右侧截面上使截开部分顺时 针方向转动者为正；反之为负。
图d，e所示梁及其约束力不能单独利用平衡方程确定， 称为超静定梁。
材料力学
第五章 梁的剪力图与弯矩图
§5.2 梁的内力及其与外力的相互关系
Ⅰ. 梁的剪力和弯矩(梁的横截面上的两种内力)
图a所示跨度为l的简支梁其
约束力为：
FA
Fl
l
a,
FB
Fa l
梁的左段内任一横截面m－
m上的内力，由m－m左边分离
杆件：某一方向尺寸远大于其它方向尺寸的构件。 直杆：杆件的轴线为直线。 杆的可能变形为：
轴向拉压—内力为轴力。如拉、撑、活塞杆、钢缆、柱。
扭转 —内力为扭矩。如各种传动轴等。
(轴)
弯曲 —内力为弯矩。如桥梁、房梁、地板等。(梁)
材料力学
梁的分类
F
q
第五章 梁的剪力图与弯矩图
F l a x
l
材料力学
第五章 梁的剪力图与弯矩图
梁的横截面上位于横截面 内的内力FS是与横截面左右两 侧的两段梁在与梁轴相垂直方 向的错动(剪切)相对应，故称 为剪力；梁的横截面上作用在 纵向平面内的内力偶矩是与梁 的弯曲相对应，故称为弯矩。
材料力学
第五章 梁的剪力图与弯矩图
为使无论取横截面左边或右边为分离体，求得同一横
截面上的剪力和弯矩其正负号相同，剪力和弯矩的正负号
要以其所在横截面处梁的微段的变形情况确定，如下图。
材料力学
第五章 梁的剪力图与弯矩图
综上所述可知： (1) 横截面上的剪力——使截开部分梁产生顺时针方向
转动为正；产生逆时针方向转动为负。
(2) 横截面上的弯矩——作用在左侧面上使截开部分 逆时针方向转动，或者作用在右侧截面上使截开部分顺时 针方向转动者为正；反之为负。
图d，e所示梁及其约束力不能单独利用平衡方程确定， 称为超静定梁。
材料力学
第五章 梁的剪力图与弯矩图
§5.2 梁的内力及其与外力的相互关系
Ⅰ. 梁的剪力和弯矩(梁的横截面上的两种内力)
图a所示跨度为l的简支梁其
约束力为：
FA
Fl
l
a,
FB
Fa l
梁的左段内任一横截面m－
m上的内力，由m－m左边分离
杆件：某一方向尺寸远大于其它方向尺寸的构件。 直杆：杆件的轴线为直线。 杆的可能变形为：
轴向拉压—内力为轴力。如拉、撑、活塞杆、钢缆、柱。
扭转 —内力为扭矩。如各种传动轴等。
(轴)
弯曲 —内力为弯矩。如桥梁、房梁、地板等。(梁)
材料力学
梁的分类
F
q
第五章 梁的剪力图与弯矩图
《材料力学》课件4-2梁的剪力和弯矩.剪力图和弯矩图
实例1
实例2
实例3
03
剪力图和弯矩图的解读
剪力图和弯矩图的解读方法
截面法
通过在梁上选择若干个截面，分别计算出每个截面的剪力 和弯矩值，然后以这些值为纵坐标，以截面位置为横坐标， 绘制出剪力图和弯矩图。
微分关系法
利用剪力和弯矩的微分关系，通过积分求解出剪力图和弯 矩图。
叠加法
对于分段常数的情况，将每一段的剪力和弯矩分别叠加， 得到整体的剪力图和弯矩图。
在机械工程中，梁的剪力和弯矩分析用于设计和优化各种机 械设备，如起重机、输送机和机床等，以提高设备的性能和 可靠性。
梁的剪力和弯矩在科研中的应用
在科研领域，梁的剪力和弯矩分析也是重要的研究内容之 一。通过深入研究梁的剪力和弯矩的分布规律和影响因素 ，可以揭示材料的力学性能和结构行为的本质。
科研人员利用先进的实验技术和数值模拟方法，对梁的剪 力和弯矩进行深入探索，为材料科学、固体力学和结构工 程等领域的发展提供理论支持和实践指导。
选择截面位置
在梁上选择若干个具有代表性的截面，用于 计算剪力和弯矩。
计算剪力和弯矩
对每个截面进行受力分析，计算出剪力和弯 矩的大小。
绘制剪力图和弯矩图
根据计算结果，绘制出相应的剪力图和弯矩 图。
剪力图和弯矩图的绘制实例
悬臂梁在集中力作用下的 剪力和弯矩图
简支梁在均布载荷作用下 的剪力和弯矩图
简支梁在集中力作用下的 剪力和弯矩图
感谢您的观看
THANKS
截面法
通过在梁上选择若干个截面，计算每个截面的剪 力和弯矩，然后绘制相应的图形。
微元法
将梁分成若干个微元段，对每个微元段进行受力 分析，计算剪力和弯矩，然后绘制图形。
解析法
材料力学-5-弯矩图与剪力图
从所得到的剪力图和 弯矩图中不难看出:
在集中力作用点两 侧截面上的剪力是不相 等的，而在集中力偶作 用处两侧截面上的弯矩 是不相等的，其差值分 别为集中力与集中力偶 的数值。
例题5
q
A
4a FAy
梁由一个固定铰链支座和一个辊轴支座所
支承，但是梁的一端向外伸出，这种梁称为外 伸梁(overhanging beam)。梁的受力以及各部 分尺寸均示于图中。
工程中的弯曲构件
工程中可以看作梁的杆件是很多的:
桥式吊车的大梁 可以简化为两端饺支 的简支梁。在起吊重 量(集中力FP)及大梁自 身重量(均布载荷q)的 作用下,大梁将发生弯 曲。
工程中可以看作梁的杆件是很多的:
石油、化工设备中各种直立式反应塔，底部与地面固定 成一体，因此，可以简化为一端固定的悬臂梁。在风力载荷 作用下，反应塔将发生弯曲变形。
Nanjing University of Technology
材料力学 课堂教学(5)
2020年8月12日
第5章 梁的弯曲问题(1)－剪力图与弯矩图
杆件承受垂直于其轴线的外力或位于其轴线所在平面内的 力偶作用时，其轴线将弯曲成曲线，这种受力与变形形式称为 弯曲（bending）。
主要承受弯曲的杆件称为梁（beam）。
得到梁的剪力方程和弯 矩方程分别为：
M(x)
FQ x＝FRA qx＝ql－qx 0 x 2l
FRA x
M x＝qlx－qx2
0 x 2l
2
这一结果表明，梁上的剪力方程是x的线性函数；弯矩方程是x的 二次函数。
载荷集度、剪力、弯矩之间的 微分关系
绘制剪力图和弯矩图有两种方法：
第一种方法是：根据剪力方程和弯矩方程，在FQx和M-x坐标系中绘制出相应的图线，便得到所需要的 剪力图与弯矩图。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
0.6F (0 x a) FS ( x) 0.4F (a x l )
x
(a)
0.6Fx (0 x a) M ( x) 0.4F (l x) (a x l )
3）作剪力图和弯矩图
(b)
(c)
例5-5 如图所示，简支梁AB受载荷集度为 q 的 均布载荷作用，试作梁AB的剪力图和弯矩图。 解： 1）求支座反力
M FS ( x) l
(0 x l )
x
M x ( 0 x a ) l M ( x) M (l x) (a x l ) l
3）作剪力图和弯矩图
注意：弯矩图是两斜 直线，在 C 截面处有突 变，突变量为 M 。
例5-4 如图所示简支梁，C 截面处作用集中力 F ， 且 a 0.4l ，试作梁的剪力图和弯矩图。
剪力图和弯矩图 的特点和规律
2. q = 常数的梁段：∵ dFS / dx q ，∴ FS 为 x 的一次 函数，剪力图为斜直线，斜率由 q 值确定；而M ( x) 是 x的二次函数，则弯矩图为二次抛物线。
2 2 • 当分布载荷向上 （即 q > 0） 时， d M (x)/ d x q 0 ， 弯矩图为凹曲线。此时，因为 dM ( x) / dx FS， ∴ 当 FS 时，弯矩图存在极小值。 0
1 FA FB ql 2
2）求剪力方程和 弯矩方程
x
1 FS ( x) ql qx (0 x l ) 2 1 1 2 M ( x) qlx qx (0 x l ) 2 2
3）作剪力图和弯矩图
1 FS ( x) ql qx 2
剪力图：是一斜直线
(0 x l )
解： 1）求支座反力
M B (Fi ) 0
i 1
n
FA l F (l a) 0 FA 0.6F FB l F a 0
M A (Fi ) 0
i 1
n
FB 0.4 F
2）求剪力方程和弯矩方程 C截面作用有集中力，AC 梁段和BC梁段的剪 力方程表达式不一样，需分段建立方程。
例5-3 如图所示简支梁，C截面处作用有集中力 偶M，作梁的剪力图和弯矩图。 解： 1）求支座反力
n
M A (Fi ) 0
i 1
FB l M 0
M FB lLeabharlann M B (Fi ) 0
i 1
n
FA l M 0
M FA l
2）求剪力方程和弯矩方程（分段建立方程） AC段
一、剪力、弯矩方程与剪力、弯矩图 • 剪力方程和弯矩方程：为了描述剪力与弯矩沿梁 轴线变化的情况，沿梁轴线选取坐标 x 表示梁截 面位置，则剪力和弯矩是 x 的函数，函数的解析 表达式分别称为剪力方程和弯矩方程。
FS FS ( x)
M M ( x)
• 剪力图和弯矩图：以梁轴线为横坐标，分别以剪 力值和弯矩值为纵坐标，按适当比例作出剪力和 弯矩沿轴线的变化曲线，称作剪力图和弯矩图。 • 剪力、弯矩方程便于分析和计算，剪力、弯矩图 形象直观，两者对于解决梁的弯曲强度和刚度问 题都非常重要，四者均是分析弯曲问题的基础。
• 当分布载荷向下 （即 q < 0） 时， d 2 M (x)/ d 2 x q 0 ， 弯矩图为凸曲线。此时，因为 dM ( x) / dx FS， ∴ 当 FS 时，弯矩图存在极大值。 0
表 5-1 各种形式载荷作用下的剪力图和弯矩图
FS 0 FS 0
q0
FS 0
分段建立方程： AC 段 x
FS ( x) 0.6F (0 x a)
M ( x) FA x 0.6Fx
CB 段
(0 x a ) (a x l ) (a x l )
FS ( x) FB 0.4F
M ( x) FB (l x) 0.4F (l x)
1. q = 0的梁段：∵ dFS / dx 0 ，∴ FQ 为常数，剪力 图为水平直线；而 dM ( x) / dx FS 为常数，则 M ( x) 是 x的一次函数，即弯矩图为斜直线，斜率由 FS值确定。
剪力图和弯矩图 的特点和规律
1. q = 0的梁段：∵ dFS / dx 0 ，∴ FQ 为常数，剪力 图为水平直线；而 dM ( x) / dx FS 为常数，则 M ( x) 是 x的一次函数，即弯矩图为斜直线，斜率由 FS值确定。 • 当梁上仅有集中力作用时，剪力图在集中力作用 处有突变，突变量是集中力的大小；弯矩图在集 中力作用处产生尖角。 • 当梁上仅有集中力偶作用时，剪力图在集中力偶 作用处不变；弯矩图在集中力偶作用处有突变， 突变量是集中力偶的大小。
dM ( x) 1 ql qx 0 dx 2 1 得 x l 2 1 2 M max ql 8
弯矩图如图所示。
二、弯矩、剪力与分布载荷集度之间的微分关系
剪力、弯矩与载荷 集度的微分关系 剪力图和弯矩图 的特点和规律
dFS ( x) q ( x) dx dM ( x) FS ( x) dx d 2 M ( x) q( x) 2 d x
FS 0
q0
q0
q 常数
M FS ( x) FA l (0 x a )
x
M M ( x) FA x x (0 x a ) l M FS ( x) FB CB段 (a x l ) l M M ( x) FB (l x) (l x) (a x l ) l
当x 0 时
1 FS (0) ql 2 当 x l时 1 FS (l ) ql 2
剪力图如图所示。
弯矩图：是一抛物线
当x 0时 当x l 时
M (0) 0
M (l ) 0
1 1 2 M ( x) qlx qx 2 2 (0 x l )
确定抛物线的极值点