工力第三章 平衡
工程力学(范钦珊-蒋永莉-税国双-著)-清华大学出版社.pdf

工程力学——课后练习题讲解教师张建平第一章静力学基础课后习题:1. P32习题1-12. P32习题1-23. P33习题1-8图a和b所示分别为正交坐标系Ox解:图():F分力:图与解图,两种情形下受力不同,二者的1-2a解图示压路机的碾子可以在推力或拉力作用下滚过):θ解图第二章力系的简化课后习题:1. P43习题2-12. P43习题2-23. P44习题2-4由作用线处于同一平面内的两个力F和习题图所示一平面力系对A(30),B(0,图示的结构中,各构件的自重都略去不计。
1图2-4解习题)中的梁∑0,F0,1m习题3-3图解:根据习题3-3第三章附加习题课后习题:1. P69习题3-52. P69习题3-63. P70习题3-74. P71习题3-135. P71习题3-143-14 图示为凸轮顶杆机构,在凸轮上作用有力偶,其力偶矩确定下列结构中螺栓的指定截面Ⅰ-Ⅰ上的内力分量,,产生轴向拉伸变形。
,产生剪切变形。
如习题4-2图所示直杆A、C、B在两端A、B处固定,在C解:首先分析知,该问题属于超静定问题,受力图如图所示:试用截面法计算图示杆件各段的轴力,并画轴力图,单解:(a)题题-3一端固定另一端自由的圆轴承受四个外力偶作用,如5-3解:将轴划分为四个截面扭矩平衡方程im m 扭矩平衡方程+m3-3扭矩平衡方程5-5 试写出图中所示各梁的剪力方程、弯矩方程图3建立坐标系并确定两个控制面,如图左侧为研究对象:−=)取根据力平衡方程和弯矩平衡方程得出4ql弯矩方程:1解建立坐标系,并取两个控制面,如图ql ql1Q。
第三章力系的平衡介绍

工 程 力 学
§3-2
平面力系的平衡条件
F1 Fn F3
1、平面任意力系的平衡方程 F2 平面任意力系平衡的充要条件是: 力系的主矢和对任意点的主矩都等于零。
0 FR
第 三 章 力 系 的 平 衡
Mo 0
平面任意力系
FR ( Fx ) 2 ( Fy ) 2
M O M O (F )
2
0
F
x
0,
F
y
0,
F
z
0
即:汇交力系的平衡条件是力系中所有各力在各个坐
标轴中每一轴上的投影的代数和分别等于零。
工 程 力 学
三、空间平行力系的平衡方程
第 三 章 力 系 的 平 衡
F
z
0,
M (F ) 0, M (F ) 0
x
y
工 程 力 学
四、空间力偶系的平衡方程
第 三 章 力 系 的 平 衡
工 程 力 学
例:如图所示为一种起吊装置的结构简图。图中尺寸d , 载荷F, <FAD =60均为已知。若不计各杆自重,试求杆AF与杆AD在各 自的约束处所受的约束力。
第 三 章 力 系 的 平 衡
工 程 力 学
第 三 章 力 系 的 平 衡
工 程 力 学
例:滑轮支架系统如图所示。已知G,a,r,θ ,其余物体重 量不计,试求A和B的约束力。
工 程 力 学
3、平面汇交力系的平衡方程
F
x
0,
F
y
0
4、平面力偶系的平衡条件
第 三 章 力 系 的 平 衡
M 0
即:力偶系各力偶力偶矩的代数和等于零。
工 程 力 学
《工程力学》课后习题与答案全集

由 ,作出速度平行四边形,如图示:
即:
7.图示平行连杆机构中, mm, 。曲柄 以匀角速度 2rad/s绕 轴转动,通过连杆AB上的套筒C带动杆CD沿垂直于 的导轨运动。试示当 时杆CD的速度和加速度。
解:取CD杆上的点C为动点,AB杆为动系。对动点作速度分析和加速度分析,如图(a)、(b)所示。图中:
解:设该力系主矢为 ,其在两坐标轴上的投影分别为 、 。由合力投影定理有:
=-1.5kN
kN
kN
;
由合力矩定理可求出主矩:
合力大小为: kN,方向
位置: m cm,位于O点的右侧。
2.火箭沿与水平面成 角的方向作匀速直线运动,如图所示。火箭的推力 kN与运动方向成 角。如火箭重 kN,求空气动力 和它与飞行方向的交角 。
(d)由于不计杆重,杆AB在A、C两处受绳索作用的拉力 和 ,在B点受到支座反力 。 和 相交于O点,
根据三力平衡汇交定理,
可以判断 必沿通过
B、O两点的连线。
见图(d).
第二章力系的简化与平衡
思考题:1.√;2.×;3.×;4.×;5.√;6.×;7.×;8.×;9.√.
1.平面力系由三个力和两个力偶组成,它们的大小和作用位置如图示,长度单位为cm,求此力系向O点简化的结果,并确定其合力位置。
则
(mm/s)
故 =100(mm/s)
又有: ,因
故:
即:
第四章刚体的平面运动
思考题
1.×;2.√; 3.√;4.√;5.×.
习题四
1.图示自行车的车速 m/s,此瞬时后轮角速度 rad/s,车轮接触点A打滑,试求点A的速度。
工程力学(静力学和材料力学)第2版课后习题答案 范钦珊主编 第3章 静力学平衡问题

FP
FP
FA
FB
习题 3-13 图
解:分析轴承受力为一组平行力系,由平衡方程:
习题 3-13 解图
∑ M B (F ) = 0 : − FP ×1380 − FA ×1020 + (G + Pδ ) × 640 = 0
解得, FA = 6.23kN (↑)
∑ Fy = 0 : FP + FA − (G + Pδ ) = 0
∑ M B (F ) = 0 : FT 50 − FW (300 cos 60D + 200) = 0
FT = 100(300 cos 60D + 200) / 50 = 700N
FT
FT
习题 3-17 图
Fw
习题 3-17 解图
∑ Fx = 0 : FT sin 30D − FB cosθ = 0 ∑ Fy = 0 : FT cos 30D − FB sinθ − FW = 0
α
FQ Cx FN
习题 3-11b 解图
取节点C为研究对象,见习题3-11b解图,
∑ Fy = 0 : F'BC cosα = FN
∴ FN
=
FP cosα 2 sin α
=
FP 2 tan α
=
3 × 15 2×2
= 11.25kN
3-12 蒸汽机的活塞面积为0.1m2,连杆AB长2m,曲柄BC长0.4m。在图示位置时, 活塞两侧的压力分别为p0=6.0×105Pa, p1=1.0×105Pa, ∠ABC=90D 。试求连杆AB作用于曲柄 上 的 推 力 和 十 字 头 A对 导 轨 的压力(各部件之间均为光滑接触)。
习题 3-14 解图
工程力学_笔记

第一篇静力平衡分析第一章静力分析基础1.1静力分析的基本概念1.2静力分析公理公理一(二力平衡公理):作用在刚体上的两个力,使刚体处于平衡的充分必要条件是:两个力大小相等方向相反,且作用在同一直线上。
(只受两个力作用而平衡的构件,称为二力构件。
)公理二(加减平衡力系公理):在作用刚体的力系上,加上或减去任一个平衡力系,并不改变原力系对刚体的作用效应。
推论1 (力的可传性原理):作用于刚体上的力可沿其作用线移至刚体内任一点,而不改变该力对于刚体的作用效应。
公理三(力的平行四边形公理):作用在刚体上同一点的两个力可以合成为一个合力,合力也作用于该点,其大小和方向可以由以这两个力为邻边所构成的平行四边形的共点对角线所确定。
推论2(三力平衡汇交原理)当刚体受三力作用而平衡时,若其中任意两个力的作用线相交于一点,则三力必然共面,且第三力的作用线通过该汇交点。
公理四(作用与反作用定律):两个物体间的相互作用力,总是大小相等,方向相反,作用线相同且分别作用在两个物体上。
公理五(刚化公理):如果变形体在某力系作用下平衡,若将此物体刚化为刚体,其平衡不受影响。
(对于变形体而言,刚体的平衡条件只是必要条件而不是充分条件)1.3约束与约束反力阻碍物体运动的限制条件称为约束。
约束对被约束物体的作用力,称为约束反力,或称约束力。
约束反力作用在被约束物体与约束的接触处,其方向总是与约束所阻碍的运动方向相反。
(1)柔性约束柔索只能承受拉力,因而只能阻止物体沿柔索伸长方向的运动。
柔性约束的约束反力作用于连接点,且方向沿着柔索而背离物体。
(2)理想光滑面接触构成的约束光滑接触约束只能阻止物体沿接触面公法线方向的运动。
光滑接触约束反力通过接触点,沿着接触点的公法线指向被约束的物体。
(3)光滑圆柱铰链约束约束反力在垂直于构建销孔轴线的横截面内,且通过销孔中心。
一般而言,由于接触点的位置无法预先确定,所以铰链约束反力的方向不能预先确定。
工程力学第三章-力系的平衡

将上式两边向x、y、z 轴投影,可得平衡方程
F F F
可以求解3个未知量。
x y
z
0 0 0
• 2.平面汇交力系
力系的平衡
• 力偶系的平衡方程 • 1.空间力偶系
平衡的充要条件(几何条件) M Mi 0 将上式两边向x、y、z 轴投影,可得平衡方程
M M M
可以求解3个未知量。
ix iy iz
0 0 0
• 2.平面力偶系
力系的平衡
• 平衡的充要条件:力偶系中各力偶矩的代数和等于零.
m 0
i
• 任意力系的平衡方程 空间任意力系: • 平衡的充要条件:力系的主矢和对任一点的主矩均为零。
FR 0
MO 0
G3 a
e
G 3(a b) FNAb G1e G 2L 0 G 3(a b) G1e G 2L FNA 2 b
由(1)、(2)式 得:
G1 G2 L
G1e G 2L G3 ab
3
A FN A b
B FN B
(2)空载时
不翻倒条件:FNB≥0 (4) 由 mA 0 得:
FAB = 45 kN
600
y B TBC 15 15 30 TBD
0 0 0
x
C
D
150
B
300
TBD=G E
A
E
FAB G
解题技巧及说明:
1、一般地,对于只受三个力作用的物体,且角度特殊时用 几 何法(解力三角形)比较简便。 2、一般对于受多个力作用的物体,且角度不特殊或特殊, 都用解析法。 3、投影轴常选择与未知力垂直,最好使每个方程中只有一 个未知数。
工力C第三章力系的平衡方程及应用

M
静力学
第三章 力系的平衡方程及其应用
静力学
例3-3 伸臂式起重机,已知匀质梁AB 重P =4kN,吊车连 同吊起重物重P1=10kN。有关尺寸如图。
y
试求:拉索BD 的拉力及铰链 A 的约束力。
D
解:取AB梁连同重物为研究对象,
FAy
FT
C 30°
A
FAx
画受力图。 取坐标,列平衡方程。
B
x由: X 0
• 空间任意力系平衡方程:基本形式、四矩式、五矩式 和六矩式。
• 应当注意:每一种形式最多只能列6个独立平衡方程, 解6个未知数,任何多于6个的方程都是这些方程的线性 组合。
• 空间任意力系平衡方程是平衡方程的一般形式。汇交 力系、平行力系、力偶系及平面力系是其特殊形式。
第三章 力系的平衡方程及其应用
对图(d):
FT1
由 M B (F ) 0 0.4FT cos 1YH 0
(d)
X H
H
由 X 0
FT sin X H X B 0
(e)
YH
FT2 由 Y 0
FT cos YH YB 0
(f )
(c)
YB E X B
B
F'T
但若系统的n物体中,有n1个物体为二力构件或受平面 力偶系, n2个受平面汇交力系或平面平行力系、n3个受平 面任意力系作用,则最多可列的独立平衡方程的数目m为
m n1 2n2 3n3
可解m个未知数。
第三章 力系的平衡方程及其应用
静力学
设k为物体系统的未知量数目
若k = m,未知量数目等于可列独立平衡方程的数
FB
《工程力学(工程静力学与材料力学)(第3版)》习题解答:第3章 力系的平衡
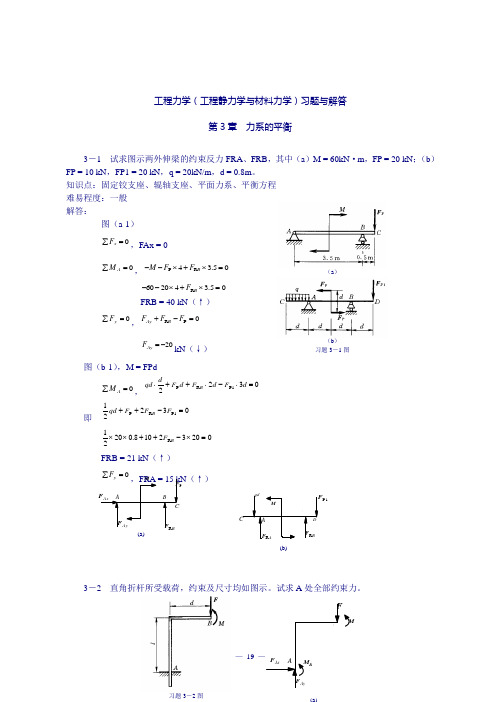
工程力学(工程静力学与材料力学)习题与解答第3章 力系的平衡3-1 试求图示两外伸梁的约束反力FRA 、FRB ,其中(a )M = 60kN ·m ,FP = 20 kN ;(b )FP = 10 kN ,FP1 = 20 kN ,q = 20kN/m ,d = 0.8m 。
知识点:固定铰支座、辊轴支座、平面力系、平衡方程 难易程度:一般 解答:图(a-1) 0=∑x F ,FAx = 00=∑A M ,05.34R P =⨯+⨯--B F F M 05.342060R =⨯+⨯--B F FRB = 40 kN (↑)=∑y F ,0P R =-+F F F B Ay20-=Ay F kN (↓)图(b-1),M = FPd 0=∑A M ,03221P R P =⋅-⋅++⋅d F d F d F dqd B即 032211P R P =-++F F F qd B 02032108.02021R =⨯-++⨯⨯B FFRB = 21 kN (↑)=∑y F ,FRA = 15 kN (↑)3-2 直角折杆所受载荷,约束及尺寸均如图示。
试求A 处全部约束力。
A MB Ay F B R F CAx F PF(a) M A B B R F A R F P 1F C qdBD(b)(a )(b ) 习题3-1图FMB习题3-3图sF W A F ABF BF AN F(a)知识点:固定端约束、平面力系、平衡方程 难易程度:一般 解答: 图(a ): 0=∑x F ,0=Ax F=∑y F ,=Ay F (↑)0=∑A M ,0=-+Fd M M AM Fd M A -=3-3 图示拖车重W = 20kN ,汽车对它的牵引力FS = 10 kN 。
试求拖车匀速直线行驶时,车轮A 、B 对地面的正压力。
知识点:固定端约束、平面力系、平衡方程 难易程度:一般解答: 图(a ):0)(=∑F A M 08.214.1NB S =⨯+⨯-⨯-F F W6.13NB =F kN=∑y F ,4.6NA =F kN3-4 图示起重机ABC 具有铅垂转动轴AB ,起重机重W = 3.5kN ,重心在D 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
FC C
F
FB B
未知力数: 平衡方程数 < 未知力数: 静不定问题(超静定问题) 静不定问题(超静定问题) 将在材料力学中研究
任艳荣
§3-2 静定与静不定问题的概念
刚体系统的平衡 刚体系统的平衡
工程力学
(Engineering Mechanics)
一、 静定与静不定问题的概念
静定
一次 静不定
静不定次数 = 未知力数 – 独立平衡方程数 衡量静不定问题的程度
FAy = −W
y
= 0, FB sin 450 + FAy − W = 0
§3-1
平面任意力系的平衡条件
工程力学
(Engineering Mechanics)
平面任意力系的平衡方程: 二、 平面任意力系的平衡方程:
1、基本形式 一矩式) (一矩式) 2、其他形式
∑F
∑F
x
x
=0
=0
∑F
y
=0
i
∑M (F ) = 0
工程力学
第三章 力系的平衡条件与平衡方程(Engineering Mechanics)
基本要求: 基本要求:
1、能熟练应用平衡方程求解物体系统的平衡问 题。 2、正确理解静定、超静定概念,并会判断具体 正确理解静定、超静定概念, 问题的静定性。 问题的静定性。
重点: 重点:
物体和物体系统平衡问题的求解。 物体和物体系统平衡问题的求解。
任艳荣
§3-2 静定与静不定问题的概念
刚体系统的平衡 刚体系统的平衡
工程力学
(Engineering Mechanics)
特点: 特点:
3、根据题意,灵活选择研究 根据题意, 对象——“是先合后拆, 对象——“是先合后拆,还是 先拆后合? 先拆后合?” 系统平衡与单个物体 平衡的异同点: 平衡的异同点: 区别:需从物系中选取若干个研究对象。 区别:需从物系中选取若干个研究对象。 共性:研究对象一旦确定, 共性:研究对象一旦确定,其解题方法 与单个物体的平衡完全相同。 与单个物体的平衡完全相同。
E FE
C D FC
l/4 l/4
∑M (F) = 0,
C
l l l − q × × − M + FE × = 0 4 8 2
∑F
y
= 0,
l FC − q × + FE = 0 4
4、联立求解
FE = 2.5 kN, FC= 2.5 kN kN,
任艳荣
例 题 分 析
MA A
工程力学
(Engineering Mechanics) q
O i
∑M (F ) = 0 ∑MB(Fi ) = 0
A
应用条件: 连线) 连线 (二矩式) (应用条件: x 轴 不能 “⊥” AB连线) 二矩式) (三矩式) 三矩式)
∑M (F ) = 0 ∑MB(Fi ) = 0
A i
(应用条件:A、 应用条件: 、 应用条件 B、C 不共线 、 不共线)
∑M (F ) = 0
任艳荣
§3-1
平面任意力系的平衡条件 (Engineering Mechanics)
工程力学
平面任意力系平衡的充要条件: 一、 平面任意力系平衡的充要条件:
F =0
, R
MO = 0
即:
, FR = (∑Fx )2 + (∑Fy )2 = 0
MO = ∑MO 1
平面任意力系的平衡条件 (Engineering Mechanics)
任艳荣
思考题
确定图示系统的静定性。 确定图示系统的静定性。
F
工程力学
(Engineering Mechanics)
A
B
C
M
任艳荣
§3-2 静定与静不定问题的概念
刚体系统的平衡 刚体系统的平衡
工程力学
(Engineering Mechanics)
二、 物体系统的平衡
物体系统(物系): 物体系统(物系): 由若干个物体通过 约束所组成的系统。 约束所组成的系统。
任艳荣
§3-2 静定与静不定问题的概念
刚体系统的平衡 刚体系统的平衡
工程力学
(Engineering Mechanics)
一、 静定与静不定问题的概念
q
FAy A FAx
F
FB B
平衡方程数≥未知力数: 平衡方程数≥未知力数: 静定问题(静力学可求解) 静定问题(静力学可求解)
FAy A FAx
q
任艳荣
例 题 分 析
例 4 A,B,C,D处 均为光滑铰链, 均为光滑铰链,物块 重为G 重为G,通过绳子绕 过滑轮水平地连接于 杆AB的E点,各构件 AB的 自重不计,试求A 自重不计,试求A、 B、C三处的约束力。 处的约束力。
工程力学
(Engineering Mechanics)
任艳荣
例 题 分 析
(Engineering Mechanics)
q E FE
A H
C
D
M C D l/4 l/4 E
FC
l/4
l/4
B l/4
l/8 l/8
CE” 为研究对象。 解: 1、取“CE” 为研究对象。 2、分析受力
任艳荣
例 题 分 析
q M
工程力学
(Engineering Mechanics)
3、列平衡方程
为活动铰支座。如图所示。已知: 为活动铰支座。如图所示。已知: l =8 m,F=5 kN, , , q=2.5 kN/m,M= 5 kN•m,试求 、C、E三处的约束 , ,试求A、 、 三处的约束 力。
F
q
A H B C D
M
E
l/8 l/8
l/4
l/4
l/4
任艳荣
例 题 分 析
q M F
工程力学
工程力学
平面任意力系平衡的充要条件: 一、 平面任意力系平衡的充要条件:
, FR = (∑Fx )2 + (∑Fy )2 = 0
MO = ∑MO (Fi ) = 0
平面任意力系的平衡方程: 二、 平面任意力系的平衡方程:
1、基本形式
(一矩式) 一矩式)
∑F = 0 ∑F = 0 ∑M (F ) = 0
x
y
O
i
任艳荣
§3-1
平面任意力系的平衡条件
工程力学
(Engineering Mechanics)
求杆A 处的约束力。 例1:结构如图,已知W,a,求杆 、B处的约束力。 结构如图,已知 处的约束力 A a a D B a C 解:1、画受力图 、 2、建立平衡方程 、 C W
∑ F x = 0 ∑ F y = 0 ∑ M O (F ) = 0
工程力学
(Engineering Mechanics)
二、 物体系统的平衡 特点: 特点:
1、分析系统平衡的受力时, 分析系统平衡的受力时, 不计内力。 不计内力。 2、系统平衡,组成系统的各 系统平衡, 个物体也一定平衡。 个物体也一定平衡。 个物体组成的系统, 即:由n个物体组成的系统,则可列出 个平衡方 个物体组成的系统 则可列出3n个平衡方 程,可求得3n个未知力。 可求得 个未知力。 个未知力
q
解: “AB” ∑ Fx =0 FAx + P⋅ sinα = 0 FAx = - P⋅ sin300 = - 2.5 kN
MA A L A L FAy FAx
B
αP
Q=(1/2)qL
B
α P
任艳荣
§3-1
平面任意力系的平衡条件
Q=(1/2)qL
工程力学
(Engineering Mechanics)
问题: 问题:一结构的受力和
尺寸如图所示, 尺寸如图所示,试求平 衡时, 、 、 处的约 衡时,A、B、C处的约 束力。 束力。
外力:系统以外物体对 外力:
系统的作用力。 系统的作用力。
内力: 内力:系统内部各物体之
间的相互作用力。 间的相互作用力。
任艳荣
§3-2 静定与静不定问题的概念
刚体系统的平衡 刚体系统的平衡
O
或
∑MA(F) = 0 A、B两点连线不得与各力平行 ∑MB (F) = 0 任艳荣
§3-1
平面任意力系的平衡条件
工程力学
(Engineering Mechanics)
四、分布载荷的简化: 分布载荷的简化: 集度q:单位长度上载荷的大小。 集度 :单位长度上载荷的大小。 单位: 单位:N / m kN / m 合成结果:合成为一个合力 合成结果: 1、方向与分布力相同; 、方向与分布力相同; 2、大小等于分布载荷组成的几何图形的面积; 、大小等于分布载荷组成的几何图形的面积; 3、作用点通过分布载荷组成的几何图形的几何中心。 、作用点通过分布载荷组成的几何图形的几何中心。
工程力学
(Engineering Mechanics)
平衡问题求解要点: 平衡问题求解要点:
1、正确选取研究对象 —— 一定要包含待求的未知力 2、画出其正确的受力图 3、选择合适的平衡方程 4、恰当选择投影轴和矩心(通常选在多个 恰当选择投影轴和矩心( 未知力的交点上) 未知力的交点上) ——尽量使一个方程只含一个未知数 ——尽量使一个方程只含一个未知数
FAy FAx FCy FCx
工程力学
(Engineering Mechanics)
解: 1、取整体为研究对象。 整体为研究对象。 2、画受力图。 受力图。 3、列平衡方程。 平衡方程。
G
∑M (F) = 0,
C
∑F
x
=0 ,
5r ×G − 2r × FAx = 0
