特殊角的三角比计算公式
三角函数公式大全

三角函数公式1.设扇形的圆心角为(02),,,.r l s ααπ<<半径为弧长为面积为则:___________,___________________________.ls ===2.同角的三角比关系:平方关系:__________________,_________________________,_____________________. 商数关系:__________________,_________________________. 3.诱导公式:4.特殊角的三角比:5.两角和、差的正弦、余弦、正切公式:cos()___________________αβ+=,cos()___________________αβ-= sin()___________________αβ+=,sin()___________________αβ-= tan()___________________,tan()_____________________.αβαβ+=-=6.辅助角公式:sin cos ___________.a b αα+=7.二倍角的正弦、余弦,正切公式:sin 2________________.cos 2______________________________________tan 2________________.ααα===== 8.半角公式:22sin sin ___________.cos ____________.tan.222sin ααααα====9.正弦定理:______________________.sin aA===10.余弦定理:222___________________.___________________.____________________.a b c ===cos __________________.cos __________________.cos __________________.A B C === 11.面积公式:_____________________________________________.ABC S ∆===12. 三角函数的图象和性质三角函数公式1. 角度与弧度的互换关系:360°=2π180°=π1°=0.01745 1=57.30°=57°18′2. 三角函数的定义域:3. 三角函数的公式:(一)基本关系公式组二公式组三sin(2)sincos(2)costan(2)tank x xk x xk x xπππ+=+=+=sin()sincos()costan()tanx xx xx x-=--=-=-公式组四公式组五公式组六sin()sincos()costan()tanx xx xx xπππ+=-+=-+=sin(2)sincos(2)costan(2)tanx xx xx xπππ-=--=-=-sin()sincos()costan()tanx xx xx xπππ-=-=--=-(二)角与角之间的互换公式组一公式组二βαβαβαsinsincoscos)cos(-=+αααc o ss i n22s i n=βαβαβαsinsincoscos)cos(+=-ααααα2222s i n211c o s2s i nc o s2c o s-=-=-=βαβαβαsincoscossin)sin(+=+ααα2t a n1t a n22t a n-=βαβαβαsincoscossin)sin(-=-2c o s12s i nαα-±=βαβαβαtantan1tantan)tan(-+=+2cos12cosαα+±=βαβαβαtantan1tantan)tan(+-=-公式组三公式组四2tan12tan2sin2αα+=αααααααsincos1cos1sincos1cos12tan-=+=+-±=ααπsin)21cos(=-ααπcos)21sin(=-2tan 12tan 1cos 22ααα+-=2tan 12tan2tan 2ααα-=42675cos 15sin -== ,42615cos 75sin +== ,3275cot 15tan -== ,3215cot 75tan +== .5. 正弦、余弦、正切、余切函数的图象的性质:②x y sin =与x y cos =的周期是π.③)sin(ϕω+=x y 或)cos(ϕω+=x y (0≠ω)的周期ωπ2=T .④)sin(ϕω+=x y 的对称轴方程是2ππ+=k x (Z k ∈),对称中心(0,πk );)c o s (ϕω+=x y 的对称轴方程是πk x =(Z k ∈),对称中心(0,21ππ+k );)t a n (ϕω+=x y 的对称中心(0,2πk ). (5).函数x y tan =在R 上为增函数.(×) [只能在某个单调区间单调递增]ααπsin )21cos(-=+ααπcos )21sin(=+ααπcot )21tan(-=+ααπcot )21tan(=-。
2.2 30°,45°,60°角的三角比 课件 青岛版数学九年级上册

则AB=13x,由勾股定理得 BC=12x, ∴ tanA=BACC=152xx=152.
知2-练
感悟新知
3-1.
已知tanα
=5,则2
3 sinα cosα sin2α+cos2α
5 =____1_7____.
知2-练
感悟新知
知识点 3 互余两角的三角比之间的关系
∵ sinα=ac,cosα=bc,tanα=ab, ∴ sin2α+cos2α=(ac)2+(bc)2=a2+c2 b2=cc22=1,
sinα cosα
a =bc
=ab=
tanα,即sin2α+cos2α=1,tanα=
csoinsαα.
c
感悟新知
特别提醒 已 知 sinα,cosα, tanα 中 的
知2-讲
关系
平方 关系 商的 关系
项目
速记内容
同一个锐角α 的正弦值与 余弦值的平方和等于1
同一个锐角α 的正弦与余 弦的比值等于它的正切值
巧记关系式 sin2α+cos2α=1
tanα=csoinsαα
感悟新知
同一锐角的三角比之间的关系的推导:
知2-讲
如图2 .2-2 所示,在Rt △ ABC 中,∠ C= 90°,∠ A=α .
感悟新知
知1-讲
特别提醒 1. 能利用特殊锐角的三角比的值进行计算,也可由特殊角的三
角比的值求出相应的锐角. 2. 2sin60°表示sin60°的2倍,书写时省略2 与sin60°之间的乘
号,且应将数字2放在前面,不要写成sin60°·2,以免误以 为是sin120° .
感悟新知
直角三角形的特殊角度计算

直角三角形的特殊角度计算直角三角形是一种特殊的三角形,其中一个角为90度。
在直角三角形中,两个直角边之间的夹角可以通过三角函数来计算。
本文将介绍如何计算直角三角形中的特殊角度,即30度、45度和60度角。
1. 30度角计算:在直角三角形中,30度角的边长比例是1:2:√3。
假设直角边的长度为a,斜边的长度为c,则另一个直角边的长度为2a。
根据勾股定理可得c²=a²+(2a)²=5a²。
因此,斜边的长度c为a√5。
2. 45度角计算:在直角三角形中,45度角的边长比例是1:1:√2。
假设直角边的长度为a,斜边的长度为c,则根据勾股定理可得c²=a²+a²=2a²。
因此,斜边的长度c为a√2。
3. 60度角计算:在直角三角形中,60度角的边长比例是1:√3:2。
假设直角边的长度为a,斜边的长度为c,则另一个直角边的长度为a√3。
根据勾股定理可得c²=a²+(a√3)²=4a²。
因此,斜边的长度c为2a。
通过以上计算,我们可以得到直角三角形中的特殊角度的边长比例。
这些特殊角度在数学和几何学中经常被使用,并在实际应用中起到重要作用。
除了边长比例,我们还可以通过三角函数来计算直角三角形中的特殊角度的正弦、余弦和正切值。
1. 30度角的三角函数值:正弦值sin(30°) = 1/2余弦值cos(30°) = √3/2正切值tan(30°) = 1/√32. 45度角的三角函数值:正弦值sin(45°) = √2/2余弦值cos(45°) = √2/2正切值tan(45°) = 13. 60度角的三角函数值:正弦值sin(60°) = √3/2余弦值cos(60°) = 1/2正切值tan(60°) = √3这些三角函数值在计算和测量过程中使用广泛,并具有许多实际应用,如建筑设计、物理学、工程学等。
2.2特殊角的三角比

2 2 2 + = + AC BC 1 1 = 2. 2
B 1
BC 1 2 = = sin45°= ; AB 2 2
cos45°=
AC 1 2 = = ; AB 2 2
2
BC 1 = =1 . tan45°= AC 1
A
45° 1
C
sin30°,cos30 °,tan30 °的值分别是多少?
45°
60°
sin α cosα
1 2
3 2 3 3
2 2
2 2 1
要能记 住有多 好
3 2 1 2
3
tanα
这张表还包含许多知识之间 的内在联系,你能发现那些 规律,请同学交流一下。
找到规律,事半功倍
角α
30°
45°
60°
三角比
sin α cosα tanα
1 2 3 2 3 3
2 2 2 2
0 1
4
课堂小测
3 30° 填空(1)若A为锐角, tanA= ,则A=_____ 3 1 3
sinA= _____,cosA=______ 2 2 ⑵已知cosB= 3 ,且∠A=90﹣∠B,则 sinA=____ 3 2
2
3 选择1 、 已知为锐角,cos = , 则 sin 的值为( B ) 2 3 1 3 A B C D 3 2 2 3 2 3 2、 在ABC中, 若 sin A = ,tan B = , 则这个三角形一定是 ( 2 3 A 锐角三角形 B 直角三角形 C 钝角三角形 D 等腰三角形
3Hale Waihona Puke 2,解:因为A是锐角,并且sinA =
3
sin60 ° = 3
高中数学三角比公式归纳(最全)
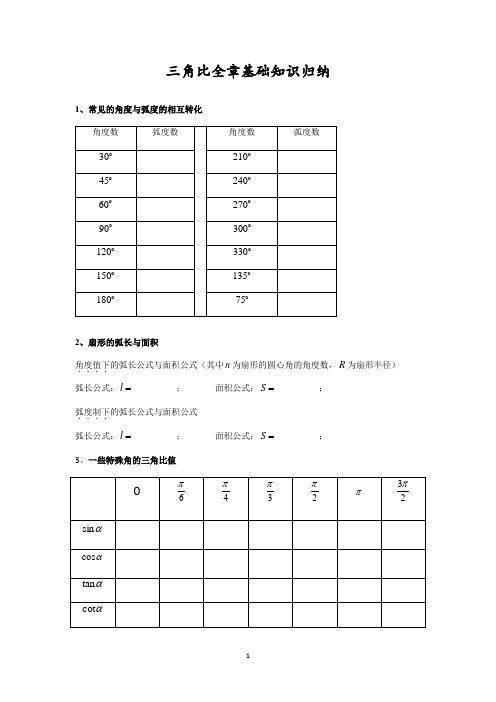
三角比全章基础知识归纳1、常见的角度与弧度的相互转化2、扇形的弧长与面积角度值下....的弧长公式与面积公式(其中n 为扇形的圆心角的角度数,R 为扇形半径) 弧长公式:________=l ;面积公式:________=S ;弧度制下....的弧长公式与面积公式 弧长公式:________=l ;面积公式:________=S ;3、一些特殊角的三角比值4、各三角比在每个象限的符号5、诱导公式(奇变偶不变,符号看象限) 第1组()=+απk 2sin ____________________;()=+απk 2cos ____________________; ()=+απk 2tan ____________________;()=+απk 2cot ____________________;第2组()=-αsin ____________________;()=-αcos ____________________; ()=-αtan ____________________;()=-αcot ____________________;第3组()=-απsin ____________________;()=-απcos ____________________; ()=-απtan ____________________;()=-απcot ____________________;第4组()=+απsin ____________________;()=+απcos ____________________; ()=+απtan ____________________;()=+απcot ____________________;第5组=⎪⎭⎫ ⎝⎛-απ2sin ____________________;=⎪⎭⎫⎝⎛-απ2cos ____________________; =⎪⎭⎫ ⎝⎛-απ2tan ____________________;=⎪⎭⎫⎝⎛-απ2cot ____________________; 第6组=⎪⎭⎫ ⎝⎛+απ2sin ____________________;=⎪⎭⎫⎝⎛+απ2cos ____________________; =⎪⎭⎫ ⎝⎛+απ2tan ____________________;=⎪⎭⎫⎝⎛+απ2cot ____________________; 6、同角三角比关系 【商数关系】________cos sin =αα; ________sin cos =αα; 【平方关系】=+αα22cos sin ____________________; =+α2t a n 1____________________;=+α2cot 1____________________;【倒数关系】=αsec ____________________;αcsc ________________;=αtan ____________________; 三点总结:①切割化弦,“切”通过商数关系化为“弦”,“割”通过倒数关系化为“弦”; ②弦化切,一般和“齐次式”有关,通过分式上下同时除以cos 或2cos 得到“切”; ③1的代换,通过平方关系,将1带换成所需的三角比;7、三角恒等变换【两角和与差的正弦、余弦、正切公式】()=+βαsin ____________________; ()=-βαsin ____________________; ()=+βαcos ____________________; ()=-βαcos ____________________;()=+βαtan ____________________; ()=-βαtan ____________________;【辅助角公式】sin cos a b αα+=_____________________________________________;常见类型:⎪⎭⎫ ⎝⎛±=±4sin 2cos sin πααα⎪⎭⎫ ⎝⎛±=±6sin 2cos sin 3πααα⎪⎭⎫ ⎝⎛±=±3sin 2cos 3sin πααα【倍角公式】=α2sin ____________________;=α2cos ____________________=____________________=____________________;=α2tan ____________________;【半角公式】=2sinα____________________; =2cosα____________________;=2tanα____________________; =2cotα____________________;=2tanα____________________=____________________;8、其他公式及恒等变换 【降幂公式】=2sin 2α____________________; =2cos 2α____________________;【升幂公式】=+αcos 1____________________; =-αcos 1____________________; =+αsin 1____________________; =-αsin 1____________________; =1____________________; =αsin ____________________;【万能置换公式】=αsin ___________________; =αcos ___________________;=αtan ___________________;【常见公式变形】_________cos 1=+α;_________cos 1=-α; _________2sin 1=+α;_________2sin 1=-α _______tan 1tan 1=-+αα;_______tan 1tan 1=+-αα;【常见角的变换】()ββαα-+=;22αα⋅=;⎪⎭⎫⎝⎛-+⎪⎭⎫ ⎝⎛+=απαππ442; ()()βαβαα-++=2;()()βαβαβ--+=2;⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛-=+βαβαβα222;⎪⎭⎫⎝⎛+-⎪⎭⎫ ⎝⎛+=-βαβαβα2229、解三角形【三角形面积计算公式】=S ___________________=___________________=___________________;18、【正弦定理公式】=Aasin ________=_______=__________=_________; 19、【余弦定理公式】=2a ___________________; =A cos ___________________; =2b ___________________; =B cos ___________________; =2c ___________________; =C cos ___________________;10、三角形中常见结论。
特殊角的三角函数值公式大全

特殊角的三角函数值公式大全三角函数是数学中一类基础且重要的函数,它们在几何、物理、工程等各个领域都有着广泛的应用。
在三角函数中,特殊角所对应的三角函数值往往是我们熟知的,今天我们来总结一下特殊角的三角函数值公式。
正弦函数值正弦函数是一种常见的三角函数,用于表示直角三角形中的对边与斜边之比。
对于特殊角来说,它们的正弦函数值是固定的,常见的特殊角有0度、30度、45度、60度和90度。
下面是它们的正弦函数值公式:•正弦0度:sin(0) = 0•正弦30度:sin(30) = 1/2•正弦45度:sin(45) = √2/2•正弦60度:sin(60) = √3/2•正弦90度:sin(90) = 1余弦函数值余弦函数也是一种常见的三角函数,用于表示直角三角形中的邻边与斜边之比。
特殊角的余弦函数值也是固定的,和正弦函数值相似,下面是特殊角的余弦函数值公式:•余弦0度:cos(0) = 1•余弦30度:cos(30) = √3/2•余弦45度:cos(45) = √2/2•余弦60度:cos(60) = 1/2•余弦90度:cos(90) = 0正切函数值正切函数是三角函数中的另一个重要函数,它表示直角三角形的对边与邻边之比。
正切函数的特殊角值也是固定的,下面是特殊角的正切函数值公式:•正切0度:tan(0) = 0•正切30度:tan(30) = √3/3•正切45度:tan(45) = 1•正切60度:tan(60) = √3•正切90度:tan(90) = 无穷大总结通过以上内容,我们总结了特殊角的正弦、余弦和正切函数值公式,这些特殊角值在数学计算中应用非常广泛,能够帮助我们解决各种问题。
熟练掌握这些特殊角的三角函数值公式,将对我们理解和运用三角函数起到很大的帮助。
希望本文对特殊角的三角函数值公式有一个清晰的了解,也希望读者能够在学习和工作中充分利用这些知识,提高数学应用能力。
三角比

三角比本章知识网络一、 任意角的三角比 1、 角的概念 定义:(1)正角、负角、零角例1、当主动轮与从动轮的齿数之比为3:5时,若主动轮按逆时针方向旋转5周,求:(1)主动轮OA 绕O 点形成的角;(2)从动轮上B O '绕'O 点形成的角。
(2)象限角,轴线角,与α终边相同的角例2、判断下列各角分别属于哪个象限:(1)200-;(2)2000;(3)1060;(4)1350-。
例3、依下列条件,写出与角α终边相同的角的集合:(1) 角α终边在x 轴上;(2)角α终边在坐标轴上;(3)角α终边在射线)0(≤=x x y 上。
例4、下列说法正确的是 ( )A .小于90°的角是锐角B .大于90°的角是钝角C .0°~90°间的角一定是锐角D .锐角一定是第一象限的角 例5、设A={钝角},B={小于180°的角},C={第二象限的角}, D={小于180°而大于90°的角},则 下列等式中成立的是( )A .A=CB .A=BC .C=D D .A=D例6、已知角θ的终边与1775角的终边相同,求的最大负角与最小正角。
(3)如果α分别是第一、二、三、四象限,则2α的位置2、 弧度与度(1)弧度的定义:(2)弧度制与角度制的转换关系:(3)特殊角的角度数与弧度数的对应关系:用弧度数表示角时,通常省略“弧度”两字,而只写这个角的弧度数。
用弧度数表示象限角与弧度角:例7、已知α是钝角,且α与α9终边相同,则的弧度数是 。
例8、若α是第二象限角,则2πα-是第 象限角;πα-是第 象限角;2α是第 象限角。
例9、若α,β的终边互为反向延长线,则有 [ ]A .α=-βB .α=2k π+β(k ∈Z)C .α=π+βD .α=(2k+1)π+β(k ∈Z) 例10、在直角坐标系中,若角α与角β的终边关于y 轴对称,则α与β的关系一定是 [ ]A .α+β=πB .α+β=2k π(k ∈Z)C .α+β=n π(n ∈Z)D .α+β=(2k+1)π(k ∈Z)例11、终边在第一、三象限角的平分线上的角可表示为 [ ]A .k ²180°+45°(k ∈Z)B .k ²180°±45°(k ∈Z)C .k ²360°+45°(k ∈Z)D .以上结论都不对例12、(1)若角β与角α的终边关于x 轴对称,则β与α的关系式为 。
特殊角的三角函数

2 - 3 2
1 - 2 2
36 tan2 300 -
3 sin 600 - 2 cos450.
填空: (1)已知tana= 3 ,则a=(
600
)
3 (2)已知a为锐角,sin(a-20°)= ,则a=( 2
800 )
68页习题9.2A组 必做:第2题 选做:从第1题中选3个
1 tan 22.5 = = 2 -1 2 1
o
A
D
E
B
C
三角比
锐角α
sinα
cosα
tanα
300 450
600
1 2
3 2 2 2 1 2
3 3
1
2 2 3 2
3
请贡献出你的学习方法,
以便大家共同进步。
计算; (1)tan450-sin300; (2) -3tan300+sin450;
1 2
2.求下列各式的值:
(1)sin30°+cos60°; (2)tan30 °· tan60 °;
(3) 2sin60°- tan30 °;(4) sin45°· cos45°+ tan45 °. 3 2 3 . (1)1; (2)1; (3) ; ( 4) 2 3
求下列各式中锐角A的值:
1 (1) cos A 2
能力目标:
情感目标:
亲自动手探索30°、45°、60°角的三角比,提高探索能力。
在积极探索新知的过程中思考、总结、掌握知识,提高学生 数学学习的兴趣何时要探究的能力,感受数学的魅力。
特殊角的三角比
三角比
锐角α
sinα
cosα
tanα
300 450
1 2
3 2 2 2
