八年级数学上册5.3.2用待定系数法求一次函数表达式同步测试(新版)浙教版【含解析】
初中数学浙教版八年级上册5.3 一次函数-待定系数法求一次函数解析式 同步训练D卷

初中数学浙教版八年级上册5.3 一次函数-待定系数法求一次函数解析式同步训练D卷姓名:________ 班级:________ 成绩:________一、基础夯实 (共8题;共26分)1. (2分) (2019八上·贵阳期末) 在精准扶贫中,某乡镇实施产业扶贫,帮助贫困户承包荒山种植猕猴桃.到了收获季节,已知猕猴桃销售量y(千克)与销售单价x(元/千克)之间的函数关系如图所示.则y与x的函数关系式为().A . y=-10x-300B . y=10x+300C . y=-10x+300D . y=10x-3002. (2分) (2018八上·合肥期中) 过和两点的直线一定()A . 垂直于轴B . 与轴相交但不平行于轴C . 平行于轴D . 与轴、轴都不平行3. (2分)如图,一次函数图象经过点A,且与正比例函数y=-x的图象交于点B,则该一次函数的表达式为()A . y=-x+2B . y=x+2C . y=x-2D . y=-x-24. (2分) (2019八上·陇西期中) 下面哪个点不在函数y=-2x+3的图象上()A .B .C .D .5. (1分) (2018八上·重庆期中) 平面直角坐标系中,点(n,3)在一次函数y=2x ﹣1的图象上,则n的值是________.6. (1分) (2019九上·靖远期末) 已知函数y=y1+y2 , y1与x成正比例,y2与x 成反比例,且当x=1时,y=4;当x=2时,y=5. y与x之间的函数关系式________,当x=4时,求y=________.7. (1分) (2018八上·达州期中) 某一次函数的图象经过点(﹣1,2),且函数y 的值随x的增大而减小,请你写出一个符合上述条件的函数关系式:________.8. (15分)(2019·铁西模拟) 如图,Rt△AOB在平面直角坐标系中,点O与坐标原点重合,点A在x轴上,点B在y轴上, ,将△AOB沿直线BE折叠,使得OB边落在AB上,点O与点D重合.(1)求直线BE的解析式;(2)求点D的坐标;(3) x轴上是否存在点P,使△PAD为等腰三角形?若存在,请直接写出点P的坐标,若不存在,请说明理由。
初中数学浙教版八年级上册5.3 一次函数-待定系数法求一次函数解析式 同步训练B卷
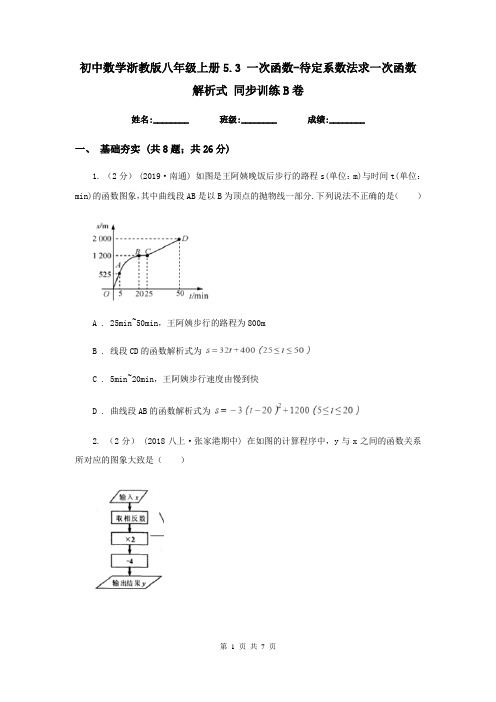
初中数学浙教版八年级上册5.3 一次函数-待定系数法求一次函数解析式同步训练B卷姓名:________ 班级:________ 成绩:________一、基础夯实 (共8题;共26分)1. (2分)(2019·南通) 如图是王阿姨晚饭后步行的路程s(单位:m)与时间t(单位:min)的函数图象,其中曲线段AB是以B为顶点的抛物线一部分.下列说法不正确的是()A . 25min~50min,王阿姨步行的路程为800mB . 线段CD的函数解析式为C . 5min~20min,王阿姨步行速度由慢到快D . 曲线段AB的函数解析式为2. (2分) (2018八上·张家港期中) 在如图的计算程序中,y与x之间的函数关系所对应的图象大致是()A .B .C .D .3. (2分)(2014·四川理) 如果一个正比例函数的图象经过点A(3,-1),那么这个正比例函数的解析式为()A . y=3xB . y=-3xC . y=xD . y=-x4. (2分) (2019八上·陇西期中) 下面哪个点不在函数y=-2x+3的图象上()A .B .C .D .5. (1分) (2018八上·辽阳月考) 点,在函数的图象上,则 ________.6. (1分) (2018八上·深圳期中) 如图,直线与轴、轴分别交于两点,点是第二象限内一点,连接。
若,则直线的解析式为________。
7. (1分)已知一次函数的图象过点与(-4, -9),那么这个函数的解析式是________,则该函数的图象与轴交点的坐标为________.8. (15分)(2019·广西模拟) 在平面直角坐标系x0y中,一次函数y=kx+4的图象与y轴交于点A,与x轴的正半轴交于点B,OA=2OB(1)求点A、点B的坐标;(2)求一次函数的解析式.二、提高训练 (共7题;共31分)9. (2分)一次函数y=kx+b(k≠0)的图象经过A(﹣1,﹣4),B(2,2)两点,P 为反比例函数图象上一动点,O为坐标原点,过点P作y轴的垂线,垂足为C,则△PCO的面积为()A . 2B . 4C . 8D . 不确定10. (2分)(2019·嘉定模拟) 若x=﹣1是关于x的方程2x+5a=3的解,则a的值为()A .B . 4C . 1D . ﹣111. (1分)(2019·广西模拟) 如图,在平面直角坐标系中,四边形OABC是边长为2的正方形,顶点A,C分别在x,y轴的正半轴上.点Q在对角线OB上,且QO=OC,连接CQ 并延长CQ交边AB于点P.则点P的坐标为________12. (1分)一次函数y=kx+b的图象与y=x+1的图象平行,且经过点(-3,4),则这个函数的表达式为________.13. (5分)(2018·宜宾) 已知点是直线上一点,其横坐标为 .若点与点关于轴对称,则点的坐标为________.14. (10分)(2017·启东模拟) 如图,在平面直角坐标系中,一次函数y=kx+b与反比例函数y= (m≠0)的图象交于点A(3,1),且过点B(0,﹣2).(1)求反比例函数和一次函数的表达式;(2)如果点P是x轴上一点,且△ABP的面积是3,求点P的坐标.15. (10分) (2018八下·柳州期末) 如图,已知直线l:y=﹣ x+b与x轴,y轴的交点分别为A,B,直线l1:y= x+1与y轴交于点C,直线l与直线ll的交点为E,且点E的横坐标为2.(1)求实数b的值和点A的坐标;(2)设点D(a,0)为x轴上的动点,过点D作x轴的垂线,分别交直线l与直线ll 于点M、N,若以点B、O、M、N为顶点的四边形是平行四边形,求a的值.参考答案一、基础夯实 (共8题;共26分)1、答案:略2、答案:略3、答案:略4、答案:略5、答案:略6、答案:略7、答案:略8、答案:略二、提高训练 (共7题;共31分)9、答案:略10、答案:略11、答案:略12、答案:略13、答案:略14、答案:略15、答案:略。
浙教版八年级数学上册.3一次函数同步练习题(二).docx

5.3一次函数同步练习题(二)第一课时1.一次函数的图象经过点A(-2,-1),且与直线y=2x-3平行,•则此函数的解析式为()A.y=x+1 B.y=2x+3 C.y=2x-1 D.y=-2x-52.已知一次函数y=kx+b,当x=1时,y=2,且它的图象与y•轴交点的纵坐标是3,则此函数的解析式为()A.0≤x≤3 B.-3≤x≤0 C.-3≤x≤ D.不能确定☆我能填4.已知一次函数的图象经过点A(1,4)、B(4,2),•则这个一次函数的解析式为___________.5.如图1,该直线是某个一次函数的图象,•则此函数的解析式为_________.(1) (2)6.已知y-2与x成正比例,且x=2时,y=4,则y与x的函数关系式是_________;当y=3时,x=__________.7.若一次函数y=bx+2的图象经过点A(-1,1),则b=__________.8.如图2,线段AB的解析式为____________.☆我能答9.已知直线m与直线y=2x+1的交点的横坐标为2,与直线y=-x+2•的交点的纵坐标为1,求直线m的函数关系式.10.已知一次函数的图象经过点A(-3,2)、B(1,6).①求此函数的解析式,并画出图象.②求函数图象与坐标轴所围成的三角形面积11.某一次函数的图象与直线y=6-x交于点A(5,k),且与直线y=2x-3无交点,•求此函数的关系式.第二课时☆我能选1.已知点(a,b)、(c,d)都在直线y=2x+1上,且a>c,则b与d的大小关系是( • )A.b>d B.b=d C.b<d D.b≥d2.已知自变量为x的一次函数y=a(x-b)的图象经过第二、三、四象限,则( • )A.a>0,b<0 B.a<0,b>0 C.a<0,b<0 D.a>0,b>03.如图所示的图象中,不可能是关于x的一次函数y=mx-(m-3)的图象的是()☆我能填4.一条平行于直线y=-3x的直线交x轴于点(2,0),则该直线与y•轴的交点是_________.5.已知一次函数y=kx+b的图象经过点(0,-4),且x=2时y=0,则k=______,b=•_______.初中数学试卷。
新浙教版八年级上册初中数学 第2课时 用待定系数法求一次函数表达式 教学课件

所以在弹性限度内:y=0.5x+14.5
当x=4时,y=0.5×4+14.5=16.5 答:物体的质量为4千克时,弹簧长度为16.5厘米。
新课讲解
2.下表列出了一项试验统计数据,表示将皮球从高
处落下时,弹跳高度b与下落高度d的关系.试问:
下面哪个式子能表示这种关系( C )
当堂小练
3.已知正比例函数y=kx(k≠0); (1) 若比例系数为-5,则函数关系式为 y=-5x 。 (2) 若当x=1时,y=5,则函数关系式为 y=5x 。
当堂小练
4.已知函数y=(m-3)xm-1; (1) 当m = 2 时,y是x的正比例函数; (2) 若x=-2, y=a 满足(1)中所求的函数关系式, 则a= 2 .
1、设:设所求的一次函数表达式为y=kx+b; 2、列:根据已知列出关于k、b的方程组; 3、解:解方程组,求得k、b; 4、写:把k、b的值代入y=kx+b ,写出一次函数表达式。
新课讲解
典例分析
例 已知y是 x的正比例函数,当x=-2时,y=8,求 y关于x的函数表达式,以及当x=3时的函数值. 解:设y=kx. 把x=-2,y=8 代入 y=kx, ∴ -2k=8, ∴k=-4, ∴y=-4x. 当x=3时, y=-4×3=-12.
新课讲解
知识点1 待定系数法求一次函数表达式 问题1. 若y与x成正比例,即y=kx(k为常数,k≠0),且当x=0.5时, y=3,求k的值并写出y与x的关系式 问题2 已知y是x的一次函数, 当x=3时,y=1;x=-2时, y=-14 , (1)求这个一次函数的关系式,
新课讲解
用待定系数法求一次函数解析式的一般步骤是怎样的呢
5.3一次函数待定系数法求一次函数的表达式课件2023-2024学年浙教版数学八年级上册++

求这个一次函数的表达式. 解:
因为y是x的一次函数,所以设所求表达式为y=kx+b(k≠0).
将x=0时,y=5和x=2,y=-5分别代入上式,得:
5=b,
k=-5,
-5=2k+b,解这个方程组,得 b=5,
所以,所求的一次函数表达式为y=-5x+5.
你能总结用待定系数法求函数解析式的一般步骤吗?
待定系数法求一次函数表达式的步骤
典例精讲
例1 已知一次函数y=kx+b,当x=0时,y=1;当x=1时, y=0. 试确定这个函数的表达式. 分析:分别将x=0,y=1和x=1,y=0代入y=kx+b中, 得到关于k、b的二元一次方程组,解之即可.
解:将x=0,y=1和x=1,y=0分别代入y=kx+b,
b=1,
k=-1,
得
解得
b的值.这两个条件通常是两个点的坐标或两对x,y的值. (2)确定方法:
将两对已知变量的对应值分别代入y=kx+b中,建立关于k、b 的方程组,通过解这个方程组求出k、b,从而确定其表达式.
感谢观看!
2. 正比例函数的概念是什么? 当b=0时,一次函数y=kx+b就成为y=kx( k为常数, k≠0),叫做正比例函数.
复习引入
3. 已知y是x的正比例函数,当x=-2时,y=8. 求y与x之间的 函数关系式. 解:设正比例函数关系式是 y=kx,
把x=-2,y=8代入上式,得8=-2k, 解得 k=-4, 所求的正比例函数关系式是 y=-4x .
解:(1)设y与x之间的函数关系式为y=kx+b,
因为当x=20时,y=1 600;当x=30时,y=2 00,
所以
1 600=20k+b, 2 000=30k+b,
浙教版八年级上册数学第5章 用待定系数法求一次函数表达式

8 【中考·湖州】已知y是x的一次函数.当x=3时,y=1; 当x=-2时,y=-4.求这个一次函数的表达式.
解:设这个一次函数的表达式为 y=kx+b(k≠0), 将 x=3,y=1 和 x=-2,y=-4,代入上式得 3-k+2kb+=b1=,-4,解得kb==1-,2. 所以这个一次函数的表达式为 y=x-2.
解:设所求一次函数的表达式为 y=kx+b(k,b 为常数,k≠0), 任取表中的两组数据,不妨取 x=37.0,y=70.0 和 x=42.0, y=78.0,代入,得7708==3472kk++bb,,解得kb==11.06.,8. ∴所求一次函数的表达式为 y=1.6x+10.8.
(2)小明回家后,测量了家里的写字台和凳子.写字台的高 度为77cm,凳子的高度为43.5cm,请你判断它们是否 配套,并说明理由.
13 小明受“乌鸦喝水”故事的启发,利用量桶和体积相同 的小球进行了如下操作:
请根据图中给出的信息,解答下列问题. (1)放入一个小球,量桶中水面升高____2____cm;
(2) 求 放 入 小 球 后 量 桶 中 水 面 的 高 度 y(cm) 关 于 小 球 个 数 x(个)的一次函数表达式;(水未溢出,不要求写出自变 量的取值范围)
时,x 的值为( A )
A.92
B.29
C.2
D.12
2 【杭州期末】若y关于x的函数关系式为y=kx+1,当 x=1时,y=2,则当x=-3时,y的值为( ) B A.-1B.-2C.-3D.-4
3 一次函数 y=kx+b,经过点(1,1), (2,-4),则 k 与
b 的值为( C )
k=3 A. b=-2
(2)已知某“快递小哥”的日收入不少于110元,则他至少要 派送快递多少件?
2019年秋浙教版初中数学八年级上册《一次函数》单元测试(含答案) (202)
浙教版初中数学试卷2019-2020年八年级数学上册《一次函数》测试卷学校:__________题号 一 二 三 总分 得分评卷人 得分一、选择题1.(2分) 如图 ,在凯里一中学生耐力测试比费中,甲、乙两名学生测试的路程s (米)与时间t (秒)之间的函数关系图象分别为折线 OABC 和线段OD ,下列说法中,正确确的是( )A .乙比甲先到终点B .乙测试的速度随时间增大而增大C .比赛进行到29.4秒时,两人出发后第一次相遇D .比赛全程甲的测试速度始终比乙的测试速度快2.(2分)下列函数解析式中,是一次函数的有( ) ①2y x=;②22y x =--;③22x y =+;④122y x =-.A .1个B .2个C .3个D .4个3.(2分)一次函数21y x =-+的图象与两坐标轴所围成的三角形的面积为( ) A .1B .12C .14D .184.(2分)下列图像不是..函数图象的是( )5.(2分)已知,一次函数by+=的图象如图,下列结论正确的是()kxA.0>k,0b D.0b<<<k,0b C.0k,0>b B.0><k,0>6.(2分)如图,在光明中学学生耐力测试比赛中,甲、乙两学生测试的路程s(m)与时间t(s)之间的函数关系图象分别为折线OABC和线段OD,下列说法正确的是()A.乙比甲先到达终点B.乙测试的速度随时间增加而增大C.比赛进行到29.4 S时,两人出发后第一次相遇D.比赛全程甲的测试速度始终比乙的测试速度快7.(2分)如图是某人骑自行车的行驶路程s(km)与行驶时间t(h)的函数图象,下列说法不正确的是()A.从0 h到3 h,行驶了30 kmB.从l h到2 h匀速前进C.从l h到2 h在原地不动D.从0 h到l h与从2 h到3 h的行驶速度相同8.(2分)函数y=3x-6的图象是()A.过点(0,-6),(0,-2)的直线B.过点(0,2),(1,-3)的直线C.过点(2,O),(1,3)的直线D.过点(2,0),(0,-6)的直线9.(2分)如图,某电信公司提供了A B,两种方案的移动通讯费用y(元)与通话时间x(元)之间的关系,则以下说法错误..的是()A.若通话时间少于120分,则A方案比B方案便宜20元B.若通话时间超过200分,则B方案比A方案便宜12元C.若通讯费用为60元,则B方案比A方案的通话时间多D.若两种方案通讯费用相差10元,则通话时间是145分或185分10.(2分)如图,直线AB对应的函数表达式是()A.3y x32=-+B.3y x32=+C.2y x33=-+D.2y x33=+11.(2分)下列函数中,自变量x的取值范围是x≥2的是()A.y=B.y=C.y=D.y=二、填空题12.(3分)若直线5y x=--与x轴交于点A,直线上有一点M,若△AOM的面积为l0,则点M的坐标为 .解答题13.(3分)若一次函数y x a=+与一次函数y x b=-+的图象的交点坐标为(m,4),则a b+= .14.(3分)已知关于x的函数同时满足下列三个条件:①函数的图象不经过第二象限;②当2x<时,对应的函数值0y<;③当2x<时,函数值y随x值的增大而增大.你认为符合要求的函数的解析式可以是: (写出一个即可).15.(3分)直线y=kx+b经过点A(-2,0)和y轴正半轴上的一点B,若△ABO(0为坐标原点)的面积为2,则b的值为.16.(3分)已知一次函数y=-2x+7,当y≤2时,自变量x的取值范围是.17.(3分)已知一次函数y=kx-k+4的图象与y轴的交点坐标是(0,-2),那么这个一次函数的表达式是.18.(3分)函数y=3x+5中,自变量x的取值范围为.19.(3分)钢筋的横截面面积是0.25π,长度为h,则钢筋的体积V=0.257πh,这里常量是,变量是.20.(3分)某汽车每小时耗油6 kg ,该车在行驶t(h)后耗去了Q(kg)油,即Q=6t ,其中常量是,变量是 . 评卷人 得分三、解答题21.(6分) 有两条直线y ax b =+(a 、b 为常数,且0a ≠)和3(y cx =-c 为常敖,且0c ≠),学生甲求得它们的交点坐标为(3,-2),学生乙因抄错c 而解得它们的交点为(5,2),求这两条直线的解析式.22.(6分)一次函数) y kx b =+(k 、b 为常数,且k≠0)的图象经过点A(3,-2)和点B ,其中点`B 是直线21y x =+和4y x =-+的交点,求这个一次函数的解析式,并画出其函数图象.23.(6分)已知一次函数的图象经过A(-2,-3),B(1,3)两点. (1)求这个函数的解析式;(2)试判断点P(-1,1)是否在这个一次函数的图象上.24.(6分)某气象研究中心观测一场沙尘暴从发生到结束的全过程,开始时风速平均增加2 km /h ,4 h 后,沙尘暴经过开阔的荒漠地,风速平均增加4 km /h ,一段时间风速保持不变.当沙尘暴遇到绿色植被区时,其风速平均减少l km /h ,最终停止.结合风速与时间的图象(如图所示)回答下列问题:(1)在y 轴括号内填入相应的数值;(2)沙尘暴从发生到结束,共经过多少时间?(3)求出当x≥25时,风速y(km/h)与时间x(h)之间的函数解析式.25.(6分)求下列问题中两个变量的函数解析式,并写出自变量的取值范围,判断其是否为一次函数:现要利用64 m长的旧围栏建一个长方形的花圃.设花圃一边长x(m),分别写出下列变量和x的函数解析式:(1)花圃另一边长y(m);(2)花圃的面积S(m2).26.(6分)已知一次函数图象经过点(1,1)和(-1,-5).(1)求该一次函数的表达式;(2)求此一次函数图象与两坐标轴围成的三角形面积;(3)另一条直线与该一次函数图象交于点A(-1,m),且与y轴交点的纵坐标为4,求这条直线的解析式.27.(6分)衢州是中国历史文化名城,衢州烂柯山是中国围棋文化的重要发源地.如图是棋子摆成的“巨”字.求:(1)第四个“巨”字需要的棋子数;(2)按以上规律继续摆下去,求第n个“巨”字所需的棋子数m.28.(6分)为调动销售人员的积极性,A、B两公司采取如下工资支付方式:A公司每月2000元基本工资,另加销售额的2%作为奖金;B 公司每月l600元基本工资,另加销售额的4%作为奖金.已知A 、B 公司两位销售员小李、小张l ~6月份的销售额如下表:(1)请问小李与小张3月份的工资各是多少?(2)小李l ~6月份的销售额y 1与月份x 的函数解析式是y 1=l200x+10400,小张1~6月份的销售额y 2也是月份x 的一次函数,请求出y 2与x 的函数解析式;(3)如果7~12月份两人的销售额也分别满足(2)中两个一次函数的关系,问几月份起小张的工资高于小李的工资.29.(6分)求下列函数的自变量的取值范围: (1)22y x x =+; (2)3xy x =+;(3)33x y +=(4)12y x x =-+.30.(6分)举出两个常量和变量的实际例子.【参考答案】***试卷处理标记,请不要删除评卷人 得分一、选择题1.C 2.C 3.C 4.C5.B 6.C 7.B 8.D 9.D 10.A 11.B二、填空题12.(-9,4)或(-1,-4) 13.814.答案不唯一,如2y x =- 15.216.52x ≥17.y=6x-2 18.任何实数 19.0.25π;V,h 20.6;Q 、t三、解答题21.把3x =,2y =-代入3y ax b y cx =+⎧⎨=-⎩,得23(1)233(2)a b c -=+⎧⎨-=-⎩,把5x =,2y =代入y ax b =+,得25a b =+…(3), 由(1)和(3),得28a b =⎧⎨=-⎩,由(2)得13c =.∴所求的这两条直线的解析式分别为28y x =-,133y x =-.22.由214y x y x =+⎧⎨=-+⎩,得13x y =⎧⎨=⎩,∴点B(1,3),∴233k b k b -=+⎧⎨=+⎩,解得52112k b ⎧=-⎪⎪⎨⎪=⎪⎩, ∴这个一次函数的解析式为51122y x =-+.图象略.23.(1)21y x =+ (2)点P(-1,1)不在这个一次函数的图象上 24.(1)8,32;(2)57 h ;(3)y=-x+57(25≤x ≤57)25.(1)y=x+32(0<x<32)是一次函数;(2)232S x x =-+(O<x<32)不是一次函数 26.(1)y=3x-2;(2)23;y=9x+4 27.(1)34颗;(2)m=10+8(n-l)28.(1)2280元,2040元;(2)y 2=1800x+5600;(3)9月份 29.(1)任何实数;(2)x ≠-3;(3)x ≥-l 且x ≠2;(4)x ≥1 30.略。
八年级数学上册5-3一次函数第2课时用待定系数法求一次函数表达式习题课件新版浙教版
10
(1)小明经过研究,发现课桌高度 y (cm)是椅子高度 x (cm)的
一次函数,请你帮小明求出这个函数关系式.
【解】设 y = kx + b ( k ≠0).
把 x =37, y =70和 x =40, y =74.8分别代入,得
= .,
= +,
ቊ
解得ቊ
= ..
8
9
10
7. 周日上午,小俊从外地乘汽车回嘉兴,一路上,小俊记下
了如下数据:
观察时间
9:00( t =0)
9:06( t =6)
9:18( t =18)
路牌内容
嘉兴90 km
嘉兴80 km
嘉兴60 km
(注:“嘉兴90 km”表示离嘉兴的距离为90 km)
假设汽车离嘉兴的距离 s (km)是行驶时间 t (min)的一次函
. = +,
∴这个函数关系式为 y =1.6 x +10.8.
1
2
3
4
5
6
7
8
9
10
(2)小明回家后,测量了自己家里的写字台和椅子,测得
写字台的高度为77 cm,椅子的高度为43.5 cm,请你
判断它们是否符合(1)中的函数关系,为什么?
【解】不符合.理由:当 x =43.5时, y =1.6×43.5
例,当 x = m 时, y =1,当 x =2时, y = n ,则 m n 的
值为(
A
)
A. 2
B. -2
1
2
3
4
C. 1
5
6
7
8
9
D. 4
10
3. 已知 y 是 x 的一次函数,下表列出了部分对应值,则 m =
2019年秋浙教版初中数学八年级上册《一次函数》单元测试(含答案) (353)
14.如 y = −x +1(答案不唯一)
15.(-1,0)或(1,O)
16.y=2x+7
17.(1)1000;(2)1000
18.三
19.M=7.8v
20.y=18x,2016
21.y=2.2x,33,用水量为 15 吨时所付水费为 33 元,l6
22.14
23.180、 ; l 、 n 、r
浙教版初中数学试卷
2019-2020 年八年级数学上册《一次函数》测试卷
学校:__________ 姓名:__________ 班级:__________ 考号:__________
题号 一
二
三 总分
得分
评卷人 得分
一、选择题
1.(2 分)若正比例函数 y = (2m −1)x 的图象经过点 A( x1 , y1 )和点 B( x2 , y2 ),当 x1 x2 时, y1 y2 ,则 m 的取值范围是( )
29.(6 分)衢州是中国历史文化名城,衢州烂柯山是中国围棋文化的重要发源地.如图是棋 子摆成的“巨”字.
求: (1)第四个“巨”字需要的棋子数; (2)按以上规律继续摆下去,求第 n 个“巨”字所需的棋子数 m.
30.(6 分)在计算器上按下面的程序进行操作:
请问:y 是 x 的函数吗?如果是,写出它的表达式;如果不是,说明理由.
求:(1)这个函数的解析式;
(2)当 x = 4 时, y 的值.
28.(6 分)已知一次函数图象经过点(1,1)和(-1,-5). (1)求该一次函数的表达式; (2)求此一次函数图象与两坐标轴围成的三角形面积; (3)另一条直线与该一次函数图象交于点 A(-1,m),且与 y 轴交点的纵坐标为 4,求这条直 线的解析式.
八年级数学上册5.3一次函数同步练习(新版)浙教版【含解析】
5.3 一次函数一、选择题(共10小题;共50分)1. 若y=(m−3)x+1是一次函数,则( )A. m=3B. m=−3C. m≠3D. m≠−32. 在同一平面直角坐标系中,若一次函数y=−x+3与y=3x−5的图象交于点M,则点M的坐标为 ( )A. (−1,4)B. (−1,2)C. (2,−1)D. (2,1)3. 下列四组点中,可以在同一个正比例函数图象上的一组点是 ( )A. (2,−3),(−4,6)B. (−2,3),(4,6)C. (−2,−3),(4,−6)D. (2,3),(−4,6)4. 某油箱容量为60 L的汽车,加满汽油后行驶了100 km时,油箱中的汽油大约消耗了15,如果加满汽油后汽车行驶的路程为x km,油箱中剩油量为y L,则y与x之间的函数解析式和自变量的取值范围分别是( )A. y=0.12x,x>0B. y=60−0.12x,x>0C. y=0.12x,0≤x≤500D. y=60−0.12x,0≤x≤5005. 如图,一次函数图象经过点A,且与正比例函数y=−x的图象交于点B,则该一次函数的表达式为 ( )A. y=−x+2B. y=x+2C. y=x−2D. y=−x−26. 下列函数:① y=πx,② y=2x−1,③ y=1x ,④ y=1x−3x,⑤ y=x2−1中,是一次函数的有( )A. 4个B. 3个C. 2个D. 1个7. 根据下表中一次函数的自变量x与函数y的对应值,可得p的值为 ( )A. 1B. −1 D. −38. 若实数m,n满足4m2+12m+n2−2n+10=0,则函数y=x2m+4n+n+2是 ( )A. 正比例函数B. 一次函数C. 反比例函数D. 二次函数9. 在密码学中,直接可以看到内容为明码,对明码进行某种处理后得到的内容为密码.有一种密码,将英文26个字母a,b,c,⋯,z(不论大小写)依次对应1,2,3,⋯,26这26个自然数(见表格).当明码对应的序号x为奇数时,密码对应的序号y=x+12;当明码对应的序号x为偶数时,密码对应的序号y=x+13.A. gawqB. shxcC. sdriD. love10. 八个边长为1的正方形如图摆放在平面直角坐标系中,经过原点的一条直线l将这八个正方形分成面积相等的两部分,则该直线l的解析式为 ( )A. y=−xB. y=−34x C. y=−34x D. y=−910x二、填空题(共10小题;共50分)11. 正比例函数y=−12x的图象过点(1, ).在横线处应填.12. 已知函数y=(m+2)x∣m∣−1−1是一次函数,则m的值为.13. 当m=时,关于x的函数y=(m−2)x m2−3+5是一次函数.14. 如图,在平面直角坐标系中,正方形ABCD的对称中心与原点重合,顶点A的坐标为(−1,1),顶点B在第一象限,若点B在直线y=kx+3上,则k的值为.15. 已知y=(m−3)x m2−8+m+1是一次函数,则m=.16. 已知一次函数y=kx+b的图象经过两点A(0,1),B(2,0),则当x时,y≤0.17. 如图,在平面直角坐标系中,△ABC的两个顶点A,B的坐标分别为(−2,0),(−1,0),BC⊥x轴,将△ABC以y轴为对称轴作轴对称变换,得到△AʹBʹCʹ(A和Aʹ,B和Bʹ,C和Cʹ分别是对应顶点),直线y=x+b经过点A,Cʹ,则点Cʹ的坐标是.18. 当m=时,函数y=(m+3)x2m+1+4x−5(x≠0)是一个一次函数.19. 如图,在x轴上有五个点,它们的横坐标依次为1,2,3,4,5.分别过这些点作x轴的垂线与三条直线y=ax,y=(a+1)x,y=(a+2)x相交,其中a>0,则图中阴影部分的面积是.20. 在平面直角坐标系中,有三条直线l1,l2,l3,它们的函数解析式分别是y=x,y=x+1,y=x+2.在这三条直线上各有一个动点,依次为A,B,C,它们的横坐标分别为a,b,c,则当a,b,c满足条件( )时,这三点不能构成△ABC.三、解答题(共5小题;共65分)21. 已知一次函数y=kx+b,当x=1时,y=−1;当x=−1时,y=3,求k和b的值.22. 甲、乙两地相距50 km,小明骑自行车以10 km/h的速度从甲地驶往乙地.写出小明离乙地的距离s(km)与行驶时间t(h)之间的关系式. s是否为t的一次函数?是否为正比例函数?23. 已知关于x的函数y=kx−2k+3−x+5是一次函数,求k的值.x−6与x轴相交于点A,与y轴相交于点B,求这条直线与坐标轴围成的三24. 已知直线y=−12角形的面积.25. 如图,直线y=kx+b经过A,B两点.Ⅰ求此直线表达式;Ⅱ若直线y=kx+b绕着点A旋转,旋转后的直线y=kʹx+bʹ与y轴交于点M,若△OAM 的面积为S,且3<S<5,分别写出kʹ和bʹ的取值范围(只要求写出最后结果).答案第一部分1. C2. D3. A4. D5. B6. C7. A8. B9. B 10. D 第二部分 11. −12 12. 2 13. −2 14. −2 15. −3 16. ≥2 17. (1,3)18. −3 或 −12 或 0 19. 12.520. a =b =c 或 a =b +1=c +2 或 a−ca−b =2 第三部分21. 由题意可得 {k +b =−1,−k +b =3.∴k =−2;b =1 .22. s =50−10t ,s 是 t 的一次函数,s 不是 t 正比例函数. 23. 当 k =0 时,y =−x +5,是一次函数. 当 −2k +3=0,即 k =32 时,y =−x +132,是一次函数.当 −2k +3=1,即 k =1 时,y =5,不是一次函数.所以 k 的值为 0 或 32.24. ∵ 直线 y =−12x −6 与 x 轴相交于点 A ,与 y 轴相交于点 B ,∴A (−12,0),B (0,−6) . ∴OA =12,OB =6 .∴ 这条直线与坐标轴围成的三角形的面积 =12×12×6=36 . 25. (1) 依题意,得{b =4,−2k +b =0.解得{b =4,k =2.所以直线表达式为 y =2x +4.(2) 32<kʹ<52,3<bʹ<5 或 −52<kʹ<−32,−5<bʹ<−3.。
