正四面体内切球和外接球(好用)精品PPT课件
合集下载
外接球与内切球 PPT

②有一个面是直角三角形,且一条棱垂直该面的三棱锥的外接球 可以补成长方体的外接球
③对棱两两相等的三棱锥的外接球可以补成长方体的外接球(所有 的棱为长方体的面对角线)
④有一侧棱垂直于底面的三棱锥的外接球可以补成直三棱柱。
Eg1(1)(2011.辽高考宁)已知球的直径 SC=4,A,B 是该球球面上的两点,
本例(3)中,改为∠BAC=60°,其他条件不变,如何求?若 ∠BAC=90°呢?
解析:若∠BAC=60°,如图,设 O1,O2 分 别为上、下底面的中心,且球心 O 为 O1O2 的中 点,得 AD= 23×2= 3,AO2=23AD=233,OO2 =1.设球的半径为 R,则 R2=AO2=AO22+OO22=43+1=73.
AB= 3 , ASC BSC 30, 则
C 棱锥 S—ABC 的体积为( ) A 3 3 B 2 3 C 3
D1
(2)(2012 课标全国)已知三棱锥 S—ABC 的所有顶点都在球 O的球面上, ABC是边长为 1 的正三角形,SC 为球 O 的直径,且 SC=2,则此棱锥 的体积为
基
础
知
识
V=13(S 上+S 下+ S上S下)h=13π(r21 +r22+r1r2)h
① 圆锥的侧面展开图的扇形的圆心角: r • 2
l
② 圆台的侧面展开图的扇环的圆心角: r2 r1 • 2
l
直棱柱 正棱锥
正棱台 球
S 侧=Ch′
V=Sh
S 侧=12Ch′(h′为 斜高)
V=13Sh
S 侧=12(C+
V=13(S 上+S 下+
C′)h′
S上S下)h
S 球面=4πR2
V=43πR3
2.几何体的表面积 (1)棱柱、棱锥、棱台的表面积就是各面面积之和. (2)圆柱、圆锥、圆台的侧面展开图分别是矩形、扇形、扇环形; 它们的表面积等于侧面积与底面积之和.
③对棱两两相等的三棱锥的外接球可以补成长方体的外接球(所有 的棱为长方体的面对角线)
④有一侧棱垂直于底面的三棱锥的外接球可以补成直三棱柱。
Eg1(1)(2011.辽高考宁)已知球的直径 SC=4,A,B 是该球球面上的两点,
本例(3)中,改为∠BAC=60°,其他条件不变,如何求?若 ∠BAC=90°呢?
解析:若∠BAC=60°,如图,设 O1,O2 分 别为上、下底面的中心,且球心 O 为 O1O2 的中 点,得 AD= 23×2= 3,AO2=23AD=233,OO2 =1.设球的半径为 R,则 R2=AO2=AO22+OO22=43+1=73.
AB= 3 , ASC BSC 30, 则
C 棱锥 S—ABC 的体积为( ) A 3 3 B 2 3 C 3
D1
(2)(2012 课标全国)已知三棱锥 S—ABC 的所有顶点都在球 O的球面上, ABC是边长为 1 的正三角形,SC 为球 O 的直径,且 SC=2,则此棱锥 的体积为
基
础
知
识
V=13(S 上+S 下+ S上S下)h=13π(r21 +r22+r1r2)h
① 圆锥的侧面展开图的扇形的圆心角: r • 2
l
② 圆台的侧面展开图的扇环的圆心角: r2 r1 • 2
l
直棱柱 正棱锥
正棱台 球
S 侧=Ch′
V=Sh
S 侧=12Ch′(h′为 斜高)
V=13Sh
S 侧=12(C+
V=13(S 上+S 下+
C′)h′
S上S下)h
S 球面=4πR2
V=43πR3
2.几何体的表面积 (1)棱柱、棱锥、棱台的表面积就是各面面积之和. (2)圆柱、圆锥、圆台的侧面展开图分别是矩形、扇形、扇环形; 它们的表面积等于侧面积与底面积之和.
正四面体内切球和外接球

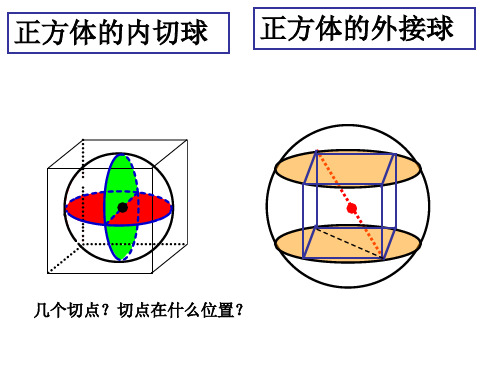
正方体的内切球
几个切点? 切点在什么 位置?
正方体的外接球
求棱长为a的正四面体的高.
P
PO 6 a 3
A
CБайду номын сангаас
D
O
B
典例精析
1、若球O有一棱长为a
球
的内接正四面体,则球
的
组 合
的半径为__________.
体
D
法一:
C
4
3
B
A
法二、
R 6a 4
A●
B ●
R ●O 1
·D ●O M ●
●
C
3、若正四体的棱长都为a,内有一球与四个面都相 切,求球的半径.
VOABC 13SABCOO1,
E
A
O
所以PO1 4r
C
D
O1
r 6a
12
B
求棱长为a的正四面体的外接球和它 的内切球的体积之比
D
O
A
H
B
R 6a 4
6
C
r a 12
典例精析
在一个倒置的正三棱锥容器内放入一个钢球,
A
钢球恰与棱锥的四个面都接触,过棱锥的一条
侧棱和高作截面,正确的截面图形是(
)
B
C
解法1:球被截成的大圆与DP、 DC相切,连结EO,设球半径为r,P
由 RtPEO ∽ RtPO1D
r 6a 12
E
A
O
C
D
O1
B
3、若正四体的棱长都为a,内有一球与四个面都相切,求 球的半径
解法2:连结OA、OB、OC、
OP,那么
P
VPABCVOPABVOPBCVOPCAVOABC
几个切点? 切点在什么 位置?
正方体的外接球
求棱长为a的正四面体的高.
P
PO 6 a 3
A
CБайду номын сангаас
D
O
B
典例精析
1、若球O有一棱长为a
球
的内接正四面体,则球
的
组 合
的半径为__________.
体
D
法一:
C
4
3
B
A
法二、
R 6a 4
A●
B ●
R ●O 1
·D ●O M ●
●
C
3、若正四体的棱长都为a,内有一球与四个面都相 切,求球的半径.
VOABC 13SABCOO1,
E
A
O
所以PO1 4r
C
D
O1
r 6a
12
B
求棱长为a的正四面体的外接球和它 的内切球的体积之比
D
O
A
H
B
R 6a 4
6
C
r a 12
典例精析
在一个倒置的正三棱锥容器内放入一个钢球,
A
钢球恰与棱锥的四个面都接触,过棱锥的一条
侧棱和高作截面,正确的截面图形是(
)
B
C
解法1:球被截成的大圆与DP、 DC相切,连结EO,设球半径为r,P
由 RtPEO ∽ RtPO1D
r 6a 12
E
A
O
C
D
O1
B
3、若正四体的棱长都为a,内有一球与四个面都相切,求 球的半径
解法2:连结OA、OB、OC、
OP,那么
P
VPABCVOPABVOPBCVOPCAVOABC
正四面体内切球和外接球(好用)
A
M
●
D
C
3、若正四体的棱长都为a,内有一球与四个面都相
切,求球的半径.
解法1:球被截成的大圆与DP、DC 相切,连结EO,设球半径为r,
由 Rt PEO ∽ Rt PO1D
E
P
6 r a 12
A D B
O C
O1
3、若正四体的棱长都为a,内有一球与四个面都相切, 求球的半径
解法2:连结OA、OB、OC、 OP,那么
正方体的内切球
正方体的外接球
几个切点?切点在什么位置?
求棱长为a的正四面体的高.
P
6 PO a 3
A D B
C O
典例精析
1、若球O有一棱长为a
的内接正四面体,则球 的半径为__________.
4 3
A
球 的 组 合 体DLeabharlann C法一:B
法二、
6 R a 4
B ●
A●
R ● O1
● ●
O
·
D
6 R a 4
O
A B
H
C
6 r a 12
典例精析
1、在一个倒置的正三棱锥容器内放入一个钢球,
钢球恰与棱锥的四个面都接触,过棱锥的一条
侧棱和高作截面,正确的截面图形是( B )
A
B
C
D
考点练习 3、自球面上一点P作球的两两垂直的三条弦PA,PB, PC,球的半径为R,则PA2+PB2+PC2=( ) A、4 R 2 B、3R 2 C、2 R 2 D、 R2 2
P
VP ABC VOPAB VO PBC VO PCA VO ABC 4VO ABC
正方体内切球、外接球、棱切球、图例演示ppt课件

面积。
略 解 :RtB1D1D中 :
(2R)2 a 2 ( 2a)2 , 得
R 3a 2
S 4R2 3a 2
D A
D1 A1
D A
C B
O C1
B1
C B
D1 A1
O C1
B1
正方体的棱切球
正方体的棱切球直径是切球的直径是棱长
例2.如图,正方体ABCD-A1B1C1D1的棱长为a,它的各 个顶点都在球O的球面上,问球O的表面积。
分析:正方体内接于球,则由球和正方 体都是中心对称图形可知,它们中心重 合,则正方体对角线与球的直径相等。
略 解 :RtB1D1D中 :
(2R)2 a 2 ( 2a)2 , 得 R 3a
球的表面积和体积
D1
A1
d
D
S
Aa
C1
c B1
C
b
B
d2 a2 b2 c2
球的体积
球面:半圆以它的直径为旋转轴,旋转所成的曲面。 球(即球体):球面所围成的几何体。
它包括球面和球面所包围的空间。
半径是R的球的体积:V 4R3
3
2、球的表面积
S 4πR2
练习一:
(1)球的半径伸长为原来的2倍,体积变为原 来的—8—倍.
2
S 4R2 3a 2
D A
D1 A1
D A
D1 A1
C B O
C1
B1
C B O
C1
B1
正方体的外接球
正方体的外接球
D A
D1 A1
C
B O
C1 B1
对角面 A
A1
C
O
内切球与外接球

内切球与外接球
10
内切球与外接球
内切球与外接球
11
内切球与外接球
内切球与外接球
12
内切球与外接球
内切球与外接球
13
内切球与外接球
内切球与外接球
14
内切内切球与外接球
此课件下载可自行编辑修改,供参考! 感谢你的支持,我们会努力做得更好!
内切球与外接球
内切球与外接球
内切球与外接球
内切球与外接球
内切球与外接球
内切球与外接球
内切球与外接球
内切球与外接球
内切球与外接球
内切球与外接球
内切球与外接球
内切球与外接球
6
内切球与外接球
内切球与外接球
7
内切球与外接球
内切球与外接球
8
内切球与外接球
内切球与外接球
9
内切球与外接球
正四面体的外接球和内切球

解题小结: (1) V1:V2=R13:R23; S1:S2=R12:R22. (2) 注意扩大与扩大到的区别.
(3) 解这类问题的关键:找到变化前后 半径的大小关系.
例3. 长方体的三个相邻面的面积分别为2,3, 6,这个长方体的顶点都在同一个球面上,求这个 球的表面积。
例4.在球心同侧有相距9cm的两个平行截面,它们的面 积分别为49πcm² 和400πcm² ,求球的表面积。 若将“球心同侧”这个条件去掉,又如何?
·
M
●
D
2 在RtBOO1中,由O1B2 BO2 OO 得 1
2
C
2 2 3 2 R ( R) , 解得R , 所以S球 4 R2 3 . 3 2 3
1、一个四面体的所有的棱都为 2 ,四个顶点在同 一球面上,则此球的表面积( )
A 3л
B 4л
C 3 3
D1 A1
解:作出过一条侧棱PC和高 PO的截面,则截面三角形PDC 的边PD是斜高,DC是斜高的射 影,球被截成的大圆与DP、DC
P
相切,连结EO,设球半径为r,
由 Rt PEO ∽ Rt PO1D
r PO 6 , 得r , DO1 PD 2
E A D B O C O1
故S球 4 r 6
A D
E
O C O1 B
所以PO1 4r
6 易求PO1 2 6, 所以r . 2
B 4л
C 3 3
D 6л
A●
解:设四面体为ABCD,O1 为其外接 球心。球半径为R,O为A在平面BCD上 的射影,M为CD的中点。 连结B O1
2 2 3 6 BO BM ( BC ) . 3 3 2 3 2 2 2 所以AO AB BO , 3
正四面体的外接球与内切球PPT讲稿
解题小结:
(1) V1:V2=R13:R23; S1:S2=R12:R22.
(2) 注意扩大与扩大到的区别.
(3) 解这类问题的关键:找到变化前 后半径的大小关系.
例3. 长方体的三个相邻面的面积分别为2,3, 6,这个长方体的顶点都在同一个球面上,求这个 球的表面积。
例4.在球心同侧有相距9cm的两个平行截面,它们的面 积分别为49πcm²和400πcm²,求球的表面积。
若将“球心同侧”这个条件去掉,又如何?
O₂
A
O₁
B
O
题组二:
1、一个四面体的所有2的棱都
一球为面上,,则四此个球顶的点表在面同积
( ) A 3л
B 4л C
3 3
D 6л
2、若正四体的棱长都为6,内有一 切球。与求四球个的面表都面相积。
1、一个四面体的所有的2 棱都
一球为面上,,则四此个球顶的点表在A面同积
的外接球,此时球的直径
为 3,
D
S球 =4 (
3 )2 2
3 ,
选A
A
C1 B1
C B
2、若正四体的棱长都为6,内有一
切球,与求四球个的面表都面相积。
解:作出过一条侧棱PC和高PO的截面,则截面三
角形PDC的边PD是斜高,DC是斜高的射影,球被截
P
成的大圆与DP、DC相切,连结EO,设球半径为r,
R2 2 ( 3
2 R)2,解得R 3
3 2
, 所以S球
4
R2
3 .
1、一个四面体的所有的2 棱都 一 (A为球3л面)上,B则四4л 此个C 球顶的点表在3 面同3 积 D 6л
解法2 构造棱长为1的正 方体,如图。则A1、C1、B、D
外接球、内切球模型总结专题课件-高三数学二轮复习备考课件
∴正三棱锥 − 的三条侧棱两两互相垂直
把三棱锥补形为正方体,则正方体外接球即为三棱锥的外接球
其直径为 =
=
1
2 + 2 + 2 + 2 + 2 + 2
2
=
1
2 + 2 + 2 =
2
1
2 + 2 + 2
半径为
6
2
4
球 = ×
找三条两两垂直的线段,直接用公式 2
即2 = 2 + 2 + 2 ,求出
2
= 2 + 2 + 2 ,
例1 (1)已知各顶点都在同一球面上的正四棱柱的高为4,体积为16,则这个球的
表面积是( C )
B. 20
A.16
C. 24
D. 32
= 2 ℎ = 16
则该四面体的外接球的表面积为( D )
A. 11
B. 7
1
C.
10
3
D.
40
3
在
��
2 = 2 + 2 − 2 ⋅ ⋅ cos120∘
=7
= 7
中
的外接球直径为
7 2 7
=
2 =
=
sin∠
3
3
2
∵ ⊥平面 ∴ ⊥ ∴ ∆是直角三角形
是这个球的外切多面体,这个球是这个多面体的内切球.
把三棱锥补形为正方体,则正方体外接球即为三棱锥的外接球
其直径为 =
=
1
2 + 2 + 2 + 2 + 2 + 2
2
=
1
2 + 2 + 2 =
2
1
2 + 2 + 2
半径为
6
2
4
球 = ×
找三条两两垂直的线段,直接用公式 2
即2 = 2 + 2 + 2 ,求出
2
= 2 + 2 + 2 ,
例1 (1)已知各顶点都在同一球面上的正四棱柱的高为4,体积为16,则这个球的
表面积是( C )
B. 20
A.16
C. 24
D. 32
= 2 ℎ = 16
则该四面体的外接球的表面积为( D )
A. 11
B. 7
1
C.
10
3
D.
40
3
在
��
2 = 2 + 2 − 2 ⋅ ⋅ cos120∘
=7
= 7
中
的外接球直径为
7 2 7
=
2 =
=
sin∠
3
3
2
∵ ⊥平面 ∴ ⊥ ∴ ∆是直角三角形
是这个球的外切多面体,这个球是这个多面体的内切球.
正方体内切球、外接球、棱切球、图例演示课件
为原来的——倍。 若球半径变为原来的2倍,则表面积变
比是———。
来的——倍. 若球的表面积变为原来的2倍,则半径变
为原来的——倍。 若两球表面积之比为1:2,则其体积之
8
练习一:
练习一
2.一个正方体的顶点都在球面上,它的棱长是4cm,这个球的体积为___cm3.
8
3.有三个球,一球切于正方体的各面,一球切于正方体的各侧棱,一球过正方体的各顶点,求这三个球的体积之比_________.
单击此处添加文本具体内容,简明扼要地阐述你的观点
202X
球的表面积和体积
D
A
B
C
D1
A1
B1
C1
球(即球体):球面所围成的几何体。
球面:半圆以它的直径为旋转轴,旋转所成的曲面。
它包括球面和球面所包围的空间。
球的体积
半径是R的球的体积:
2、球的表面积
球的半径伸长为原来的2倍,体积变为原
B
C
D
D1
C1
B1
A1
O
A
B
C
D
D1
C1
B1
A1
O
正方体的棱切球
演讲完毕,感谢观看
1.球的半径伸长为原来的2倍,体积变为原来的_倍.
例1.钢球直径是5cm,求它的体积.
变式1:把钢球放入一个正方体的有盖纸盒中,至少要用多少纸?
切球的直径是棱长
例2.如图,正方体ABCD-A1B1C1D1的棱长为a,它的各个顶点都在球O的球面上,问球O的表面积。
A
B
C
D
D1
C1
B1
A1
O
分析:正方体内接于球,则由球和正方体都是中心对称图形可知,它们中心重合,则正方体对角线与球的直径相等。
正四面体内切球和外接球(好用).ppt.ppt
A
[题组冲关] 3.假如某爱国实业家在20世纪初需要了解全国各地商业信
息,可采用的最快捷的方式是
(
)
A.乘坐飞机赴各地了解 B.通过无线电报输送讯息 C.通过互联网 D.乘坐火车赴各地了解
解析:本题考查中国近代物质生活的变迁。注意题干信 息“20世纪初”“最快捷的方式”,因此应选B,火车速度
远不及电报快。20世纪30年代民航飞机才在中国出现,
1.李鸿章1872年在上海创办轮船招商局,“前10年盈和,成
为长江上重要商局,招商局和英商太古、怡和三家呈鼎立
之势”。这说明该企业的创办 A.打破了外商对中国航运业的垄断 B.阻止了外国对中国的经济侵略 C.标志着中国近代化的起步 ( )
D.使李鸿章转变为民族资本家
解析:李鸿章是地主阶级的代表,并未转化为民族资本家; 洋务运动标志着中国近代化的开端,但不是具体以某个企业 的创办为标志;洋务运动中民用企业的创办在一定程度上抵
(2)1924年国民党“一大”召开,标志着第 一
关键词——交通和通讯不断进步、辛亥革命和国民大革命顺应 时 代潮流 图说历史 主旨句归纳 (1)20世纪初,孙中山提出“民族、民权、 民生”三民主义,成为以后辛亥革命 的
指导思想。 (2)三民主义没有明确提出反帝要求,也 没 有提出废除封建土地制度,是一个 不彻 底的资产阶级革命纲领。
报先后发明。
(3)近代以来,交通、通讯工具的进步,推 动了经济与社会的发展。
关键词——交通和通讯不断进步、辛亥革命和国民大革命顺应 时 代潮流 图说历史 主旨句归纳 (1)1911年,革命党人发动武昌起义,辛亥
革命
爆发,随后建立了中华民国,颁布了《中 华
民国临时约法》;辛亥革命是中国近代化
[题组冲关] 3.假如某爱国实业家在20世纪初需要了解全国各地商业信
息,可采用的最快捷的方式是
(
)
A.乘坐飞机赴各地了解 B.通过无线电报输送讯息 C.通过互联网 D.乘坐火车赴各地了解
解析:本题考查中国近代物质生活的变迁。注意题干信 息“20世纪初”“最快捷的方式”,因此应选B,火车速度
远不及电报快。20世纪30年代民航飞机才在中国出现,
1.李鸿章1872年在上海创办轮船招商局,“前10年盈和,成
为长江上重要商局,招商局和英商太古、怡和三家呈鼎立
之势”。这说明该企业的创办 A.打破了外商对中国航运业的垄断 B.阻止了外国对中国的经济侵略 C.标志着中国近代化的起步 ( )
D.使李鸿章转变为民族资本家
解析:李鸿章是地主阶级的代表,并未转化为民族资本家; 洋务运动标志着中国近代化的开端,但不是具体以某个企业 的创办为标志;洋务运动中民用企业的创办在一定程度上抵
(2)1924年国民党“一大”召开,标志着第 一
关键词——交通和通讯不断进步、辛亥革命和国民大革命顺应 时 代潮流 图说历史 主旨句归纳 (1)20世纪初,孙中山提出“民族、民权、 民生”三民主义,成为以后辛亥革命 的
指导思想。 (2)三民主义没有明确提出反帝要求,也 没 有提出废除封建土地制度,是一个 不彻 底的资产阶级革命纲领。
报先后发明。
(3)近代以来,交通、通讯工具的进步,推 动了经济与社会的发展。
关键词——交通和通讯不断进步、辛亥革命和国民大革命顺应 时 代潮流 图说历史 主旨句归纳 (1)1911年,革命党人发动武昌起义,辛亥
革命
爆发,随后建立了中华民国,颁布了《中 华
民国临时约法》;辛亥革命是中国近代化
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
因VP ABC
1 3
SABC
PO1,
VO ABC
1 3
SABC
OO1 ,
E
A
O
所以PO1 4r
C
D
O1
r 6a
B
12
求棱长为a的正四面体的外接球 和它的内切球的体积之比
D
O
A
H
B
R 6a 4
6
r a
C
12
典例精析
1、在一个倒置的正三棱锥容器内放入一个钢球, 钢球恰与棱锥的四个面都接触,过棱锥的一条 侧棱和高作截面,正确的截面图形是( B )
解法1:球被截成的大圆与DP、DC 相切,连结EO,设球半径为r, P
由 RtPEO ∽ RtPO1D
E
A
O
r 6a 12
C
D
O1
B
3、若正四体的棱长都为a,内有一球与四个面都相切, 求球的半径
解法2:连结OA、OB、OC、
OP,那么
P
VPABC VOPAB VOPBC VOPCA VOABC
4VOABC
正方体的内切球 正方体的外接球
几个切点?切点在什么位置?
求棱长为a的正四面体的高.
P
PO 6 a 3
A
C
D
O
B
典例精析
球 的组合体
1、若球O有一棱长为a 的内接正四面体,则球 的半径为__________.
D
法一:
C
4
3
B
A
法二、
R 6a 4
A●
B
R ● O1
·D
●
●O
●
M
●
C
3、若正四体的棱长都为a,内有一球与四个面都相 切,求球的半径.
A
B
C
D
写在最后
成功的基础在于好的学习习惯
The foundation of success lies in good habits
9Leabharlann 谢谢聆听·学习就是为了达到一定目的而努力去干, 是为一个目标去 战胜各种困难的过程,这个过程会充满压力、痛苦和挫折
Learning Is To Achieve A Certain Goal And Work Hard, Is A Process To Overcome Various Difficulties For A Goal
