大学物理电磁学课后作业答案(清华大学出版社) 共19页PPT资料
清华大学《大学物理》题库(第二部分:电磁学)【解答】

第四章真空中的静电场4.1库仑定律4.1.1库仑定律第1题【1440】真空中有两个点电荷M、N,相互间作用力为⃗F,当另一点电荷Q移近这两个点电荷时,M、N两点电荷之间的作用力(A)大小不变,方向改变(B)大小改变,方向不变(C)大小和方向都不变(D)大小和方向都改变4.1.2电场力叠加原理第3题【5093】电荷Q(Q>0)均匀分布在长为L的细棒上,在细棒的延长线上距细棒中心O距离为a的P 点处放一电荷为q(q>0)的点电荷,求带电细棒对该点电荷的静电力。
4.2电场强度4.2.1电场强度的定义的方向与该处电场强度的方向相反。
解析【答案】D【解析】曲线运动,静电力。
依题意,质点做曲线运动,速率递减,所以切向加速度与运动方向相反,而法向加速度一定指向凹侧,所以质点在C点的总的加速度沿C中箭头方向,所以质点所受到的力的方向与加速度的方向一致。
又因为质点带负电荷,所以电场力的方向与电场强度的方向相反,因此图D正确。
4.2.2电场叠加原理解析【答案】0【解析】库仑定律,电场叠加原理。
由于对称性,很容易得到中心处的电场强度为零。
第8题【1262】用绝缘细线弯成的半圆环,半径为R,其上均匀地带有正电荷Q,试求圆心O点的电场强度。
解析【解析】电场叠加原理。
解析【解析】电场叠加原理。
先分别求半无限长带电直线和半圆弧在圆心O点的场强。
如下图。
第13题【1264】一半径为R的半球面,均匀地带有电荷,电荷面密度为σ,求球心O处的电场强度。
4.3电通量高斯定理电通量4.3.14.3.2高斯定理的理解(D)只适用于虽然不具有(C)中所述的对称性、但可以找到合适的高斯面的静电场解析【答案】A【解析】高斯定理。
高斯定理本身适用于任何静电场。
只是对于真空中的静电场,右边的电荷只包括自由电荷,因为真空中并不存在束缚电荷,而对于介质,电荷包含了自由电荷和束缚电荷。
关于对称性,定理本身并不要求一定要具有什么对称性,但在具体的计算过程中,只有某些特殊对称性的电场,才可以取比较适当的高斯面,可以求出通过高斯面的电通量。
清华大学《大学物理》题库(第二部分:电磁学)【题目】

第四章真空中的静电场4.1库仑定律4.1.1库仑定律1【1440】真空中有两个点电荷M、N,相互间作用力为⃗F,当另一点电荷Q移近这两个点电荷时,M、N两点电荷之间的作用力(A)大小不变,方向改变(B)大小改变,方向不变(C)大小和方向都不变(D)大小和方向都改变4.1.2电场力叠加原理第3题【5093】电荷Q(Q>0)均匀分布在长为L的细棒上,在细棒的延长线上距细棒中心O距离为a的P 点处放一电荷为q(q>0)的点电荷,求带电细棒对该点电荷的静电力。
4.2电场强度4.2.1电场强度的定义第4题【1003】下列几个说法中哪一个是正确的?(A)电场中某点场强的方向,就是将点电荷放在该点所受电场力的方向(B)在以点电荷为中心的球面上,由该点电荷所产生的场强处处相同电场叠加原理4.2.2点的电场强度。
【1262】用绝缘细线弯成的半圆环,半径为R,其上均匀地带有正电荷Q,试求圆心O第13题【1264】一半径为R的半球面,均匀地带有电荷,电荷面密度为σ,求球心O处的电场强度。
4.3电通量高斯定理电通量4.3.14.3.2高斯定理的理解第16题【1434】关于高斯定理的理解有下面几种说法,其中正确的是(A)如果高斯面上⃗E处处为零,则该面内必无电荷(B)如果高斯面内无电荷,则高斯面上⃗E处处为零(C)如果高斯面上⃗E处处不为零,则高斯面内必有电荷(D)如果高斯面内有净电荷,则通过高斯面的电场强度通量必不为零4.3.3利用高斯定理求电通量4.3.4利用高斯定理求电场强度37【1373】一半径为R的带电球体,其电荷体密度分布为:ρ=Ar(r⩽R),ρ=0(r>R),A为一常量。
试求球体内外的场强分布。
4.4电势能电势4.4.1电场力做功4.4.2电势差第47题【1266】在已知静电场分布的条件下,任意两点P1和P2之间的电势差决定于(A)P1和P2两点的位置(B)P1和P2两点处的电场强度的大小和方向(C)试验电荷所带电荷的正负(D)试验电荷的电荷大小4.4.3电势第48题【1016】静电场中某点电势的数值等于(A)试验电荷q0置于该点时具有的电势能(B)单位试验电荷置于该点时具有的电势能(C)单位正电荷置于该点时具有的电势能(D)把单位正电荷从该点移到电势零点外力所作的功第49题【1267】关于静电场中某点电势值的正负,下列说法中正确的是(A)电势值的正负取决于置于该点的试验电荷的正负(B)电势值的正负取决于电场力对试验电荷作功的正负(C)电势值的正负取决于电势零点的选取电势值的正负取决于产生电场的电荷的正负(D)第52题【1316】相距为r1的两个电子,在重力可忽略的情况下由静止开始运动到相距为r2,从相距r1到相距r2期间,两电子系统的下列哪一个量是不变的?(A)动能总和(B)电势能总和(C)动量总和(D)电相互作用力电势叠加原理求电势4.4.54.5静电场中的电偶极子第76题【1439】一电偶极子放在均匀电场中,当电偶极矩的方向与场强方向不一致时,其所受的合力⃗F和合力矩⃗M为(A)⃗F=0,⃗M=0(B)⃗F=0,⃗M=0(C)⃗F=0,⃗M=0(D)⃗F=0,⃗M=第五章静电场中的导体与电介质5.1静电场中的导体5.1.1静电平衡条件78【1480】当一个带电导体达到静电平衡时(A)表面上电荷密度较大处电势较高(B)表面曲率较大处电势较高(C)导体内部的电势比导体表面的电势高(D)导体内任一点与其表面上任一点的电势差等于零5.1.2静电平衡时的电荷分布5.1.3静电平衡时的电场分布5.1.4接地5.2电容器电容5.2.1平行板电容器5.2.2电容器的串并联第98题【1460】如果在空气平行板电容器的两极板间平行地插入一块与极板面积相同的金属板,则由于金属板的插入及其相对极板所放位置的不同,对电容器电容的影响为(A)使电容减小,但与金属板相对极板的位置无关(B)使电容减小,且与金属板相对极板的位置有关(C)使电容增大,但与金属板相对极板的位置无关(D)使电容增大,且与金属板相对极板的位置有关5.3静电场中的电介质5.3.1电介质对电场、电容的影响102【1358】设有一个带正电的导体球壳。
大物电磁学课后答案3经典.ppt
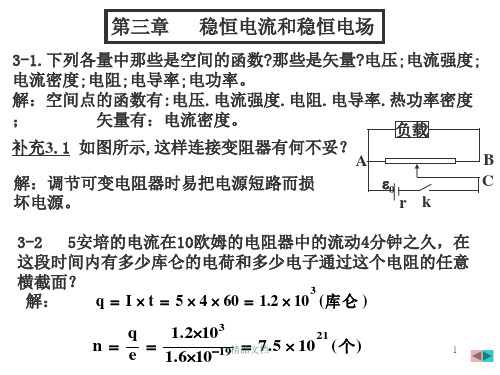
(1)电流强度在10秒内均匀的有零增加到3安培; (2)电流强度从18安培起,每过0.01秒减少一半,直到零。
解:(1)I 3 t 10
q
I dt
010
t 10
dt
15(库 仑)
(2)q I0k
1 2
I
0k
1 4
I0k
I0k(1 1 / 2 1 / 4 ) 180.011/(11/ 2)0.36(库 仑)
安培起,每过0.01秒减少一半,直到零。求导线产生的热量。
解:
3
2
(1) I 10 t dQ I rdt
| Q
t
(
3
t)2 Rdt
3
Rt3
10
180(焦)
0 10
10 0
2
2
2
(2) Q Q1 Q 2 Q 3 I1 Rt I 2Rt I 3Rt
Rt[I02
(
I0
/
2)2
电势差为4.25伏特,当该电池放电时,通过的电流为4安培两极
间的电势差为3.90伏特,求该电池的电动势和电阻。
解:
I1r 4.25 I 2r 3.90
精品文档
r
0.05(欧 4.10(伏
姆) 特)
6
3-10 设在图中所示的电路中,三个电容开始时均不带电,求将 它们与A、B、C点联结后,各极板上的电量。
7
补 Rr;3(2==充330)..3a06.,欧欧4d一姆姆两电,,点R路4求电=如1:势.(图01差欧),通其;姆(过中4,)每bb1点,=个c6接.电两0地伏阻点,,的电rR1电1势==01流差.04.;(00(5欧欧2))a姆姆每,b,,个,c2R电=,28d=源.各20.的伏点5欧端特电姆电势,压。
大学物理:电磁学PPT

N F4
O
F2 B
en
M,N F1
O,P B
F2
en
l1 l1 M F1 sin F2 sin Il2 B l1 sin ISB sin 2 2 M IS B m B 线圈有N匝时 m NIS
2 电流元的磁场
dB
P *
I
Idl
0 Idl dB er 2 4 r
——毕奥-萨伐尔定律
r
3
磁场的叠加原理
B Bi
i
B dB
例 1: 判断下列各点磁感强度的方向和大小.
1 8 2Βιβλιοθήκη dB 0 1、 5 点 :
7
Idl
R
6 5 4
例 5:
一半径为R,均匀带电Q的薄球壳。 求球壳内外任意点的电场强 度。
0 r R 如图,过P点做球面S1 E dS E dS 0 E 0
S1 S1
r
P
+ + +
+
S +1
O
如图,过P点做球面S2 rR E dS E dS Q / 0
rB
(electric potential )
点电荷电场 中的电势:
V
Q 40 r
电势的叠加 原理:
V Vi
i
点电荷电场中常取 无穷远处为电势零点
点电荷的电场线和等势面:
两平行带电平板的电场线和等势面:
+ + + + + + + + + + + +
大学物理第9章 电磁感应和电磁场 课后习题及答案

第9章 电稳感应和电磁场 习题及答案1. 通过某回路的磁场与线圈平面垂直指向纸面内,磁通量按以下关系变化:23(65)10t t Wb -Φ=++⨯。
求2t s =时,回路中感应电动势的大小和方向。
解:310)62(-⨯+-=Φ-=t dtd ε当s t 2=时,V 01.0-=ε由楞次定律知,感应电动势方向为逆时针方向2. 长度为l 的金属杆ab 以速率υ在导电轨道abcd 上平行移动。
已知导轨处于均匀磁场B中,B 的方向与回路的法线成60°角,如图所示,B 的大小为B =kt (k 为正常数)。
设0=t 时杆位于cd 处,求:任一时刻t 导线回路中感应电动势的大小和方向。
解:任意时刻通过通过回路面积的磁通量为202160cos t kl t Bl S d B m υυ==⋅=Φ导线回路中感应电动势为 t kl tmυε-=Φ-=d d 方向沿abcda 方向。
3. 如图所示,一边长为a ,总电阻为R 的正方形导体框固定于一空间非均匀磁场中,磁场方向垂直于纸面向外,其大小沿x 方向变化,且)1(x k B +=,0>k 。
求: (1)穿过正方形线框的磁通量;(2)当k 随时间t 按t k t k 0)(=(0k 为正值常量)变化时,线框中感生电流的大小和方向。
解:(1)通过正方形线框的磁通量为⎰⎰=⋅=Φa S Badx S d B 0 ⎰+=a dx x ak 0)1()211(2a k a +=(2)当t k k 0=时,通过正方形线框的磁通量为)211(02a t k a +=Φ 正方形线框中感应电动势的大小为dt d Φ=ε)211(02a k a += 正方形线框线框中电流大小为)211(02a R k a R I +==ε,方向:顺时针方向4.如图所示,一矩形线圈与载有电流t I I ωcos 0=长直导线共面。
设线圈的长为b ,宽为a ;0=t 时,线圈的AD 边与长直导线重合;线圈以匀速度υ垂直离开导线。
大学物理电磁学习题的总结PPT课件

第28页/共159页
例题. 均匀带电细杆AB,电荷线密度为λ,绕垂直于
直线的轴O以角速度ω匀速转动
求:1. O点的磁感应强度Bo 2. 磁矩m
3. 若a>>b,求Bo及 m
电流强度: dI
dq
dq
dr
T 2
2
1.
dB0
0
2r
dI
0
2r
(设导线本身不带电,且对电场无影响)
A
B
第9页/共159页
例8.在一不带电的金属球旁,有一点电荷+q,金属 球半径为R, 求:(1)金属球上感应电荷在球心处产生的电场强度
及此时球心处的电势U; (2)若将金属球接地,球上的净电荷为何?
已知+q与金属球心间距离为r。
r
o
q
第10页/共159页
例9 :三个“无限长”的同轴导体圆柱面A、B、C,
流
I=20A,求通过斜线面积的磁通量。
x处的(磁感r1强=r度3=1为0:cm,l=25cm )
B
μ0I
2x
2π
μ0I
d
x
I1
dΦm B dS
r1
Φm
d r1
r3
(
μ0I
2x
作业17-5.
1
I
a
O
2I be c
第23页/共159页
作业17-8.无限长同轴电缆由一导体圆柱和一与它同轴的导体圆筒所构成.使用时, 电流I从一导体流入,从另一导体流出,设导体中的电流均匀分布在横截面上.圆柱 的半径为r1,圆筒的内外半径分别为r2和r3,试求空间各处的磁感应强度.
大物电磁学课后答案

6-5 如图一长为l的直导线弯折成夹角为120o相等
长度的两部分,放在垂直于均匀磁场B的平面 上,并绕其一端以角速度在此平面内旋转, 求导线中感应电动势,并指出哪些电势高。
B
l
120o
2
l
解:两部分获感应电动势相当于直线段OA感
应电动势: OA 2 l cos300 3 l
9
6-10在圆柱形空间中存在着均匀磁场,B的方向与柱的轴线平行 ,若B的变化率为dB/dt=0.1特/秒,R=10厘米,问自r=5厘米、15 厘米处的感应电场的电场强度为多大?若将一个电子放在r=5厘 米处,求开始时电子的加速度a。
解:由于B的对称性
r=5厘米时
l
E
dl
E1
指向圆心的内压力。
补充6.1 一块金属板在均匀磁场中平移会不会产生感应电动势? 会不会产生涡电流?若金属板在均匀磁场中旋转,情况怎样?
解:当平板运动方向与磁力线平行时,不产生感应电动势;若
不平行,则有感应电动势,但无涡流产生;若是旋转,则平板
上各点速度所在平面与磁力线平行,无感应电动势,不平行则
有电动势。
1
补充6.2有一个铜环和一个木环,两环尺寸完全相同,放在同一 变化磁场里,问在两环中的感应电动势和感生电场相同吗? 解:产生的感应电场相同,电动势不同,铜环内有自由电子可 形成感应电流,而木环在感应电场作用下受极化。
6-2将一个超导材料作成的小薄片,放在永久磁铁的上方,它会 悬浮起来。你能解释这种现象吗? 解:处于超导态的材料电阻为零,电流分布在外表面上,内部 磁场为零。实际超导电流产生磁场抵抗外磁场的侵入,因而超 导材料受到一个排斥力,它与重力平衡而悬浮在磁场的上方。
大学物理电磁学总结-PPT

U 0点
Ua E dl a
(3)电势差 Uab Ua Ub ab E dl
b
• 静电场力的功 Aab a q0E dl q0Uab q0Ua q01U0 b
(4)电势的计算 令 U 0
①点电荷的电势
q
U P 4 π0r
②点电系的电势
UP
i
U Pi
i
qi
4 π 0ri
Idl
dF
Idl
dF
B
B
不规则的平 面载 流导线在均匀磁场中所受的力
F Fy BIlj
y
dF
B
结论 任意平面载流导线在均匀磁
场中所受的力 , 与其始点和终点相同 I
的载流直导线所受的磁场力相同.
o
Idl
L
Px
23
三、稳恒磁场的基本性质
1、磁场中的高斯定理: m B dS 0
Ei
n i 1
1
4 0
qi ri3
ri
qi qn
ri rn
q0
E E q0
E3 E2
P
E3 1
2)电荷连续分布的带电体
dE
4
1
π 0
dq r3
r
1 dq
qdq
r
P
dE
E dE 4 π0 r3 r
体电荷分布: dq dV
面电荷分布:dq ds 线电荷分布:dq dl
计算步骤: ①建坐标;②取电荷元 dq ;
电体且选无限远处为电势零点.)
②已知场强的分布,利用电势与场强的积分关系, 即电势的定义式计算电势。
U 0点
U P P E dl
12
六、静电场中的导体
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
8.4解: 两根直电流在圆心处 的磁感应强度均为0. I1
I1在圆心处产生
1
I A
2
O
I2 I C
B1
大小:B 12 0 R I12 2 2 R 0I2 2 2
方向: ⊙
I2B在2 圆大心小处:产B 2生2 0R I22 2 R 0I22 2
9.010 4V
(2) 电场力作功为
Aq0AB
9 1 4 0 ( 1 .0 1 8 ) 0 9 1 4 J 0 ∴外力克服电场力作功为
A A M ′和M分别表示挂线
圈的臂和另一臂在第一次 平衡时的质量,则
当q1>0时, 12>0,总有内球电势高于外球电势。 当q1<0时, 12<0,总有内球电势低于外球电势。
这是因为:两球面的电势差由两球面间的 电场分布决定,而这电场又只与q1有关。
3.6(1) 解:
x+dx x
P
X
O
l
a
选坐标轴OX,取微元x-x+dx,如图所示。
设 ∞ = 0 ,则此微元在P点的电势为
1 d1 BdS
B
r1r2
dS
0I1l
d
x
r1 2x
0I1l lnr1 r2
2
r1
∴所求磁通量为
210 I1lln r1r 1r22.210 6Wb
8.28解:
(1)
Id
0S板
dE dt
0R2
dE dt
8 .8 1 5 1 0 2 0 .0 2 5 1 .0 1 10 2 7.0102A
M
MgMgnIlB
电流反向时应有
(Mm)gMgnIlB
两式相减,即可得 B mg
2 nIl
(2) B=0.860T
M′
I
× ×
lF ××B
7.18解:
(1)mNIS 3A 6m2 (2 )M m a m x 1 BN 4m 4
力矩的单位不能用J,只有 功、能、热的单位才能用J.
其在圆心处的场强为 EO1 0.
o
●
R
E0
d
再补上 - d ,可视作点电荷,
其在圆心处的场强为
EO2 .
E O E O 1 E O 2 E O 2
EOEO2
4d 0 R2
4
qd
0R2(2Rd)
0.7V 2/m
方向指向负电荷,即指向缝隙。
1.18解(典型场的叠加): 由Gauss定理,易知
3.4 解:
q2
设 ∞ = 0 ,由均匀带电球面的电场中
R2
的电势分布和电势叠加原理,得
内球面电势:14q1 0 R1 4q2 0 R2
q1 R1
12
外球面电势:2 4q0 1 R2 4q2 0 R2
两球面的电势差:12124q10(R 11R 12)
R2 R1
小柱面产生的场强为
E1
rˆ 2 0r
(r
R1
)
- +
0 (rR1)
大柱面产生的场强为
E2
2 0r
rˆ
(r
R2
)
0 (rR2)
由场强叠加原理,
0 (rR1)
合场强为
E E 1E 220rrˆ (R1rR2)
0 (rR2)
L
o x x+dx r
P
X
dE
dE dx 40(rx)2
所有电荷元在P点的场强方向相同,
∴整个带电直线在P点的场强大小为
E dEL L//2240 (d rxx)240(r2L L2 / 4)
方向沿X轴正向。
1.11解(弥补法):
设电荷线密度为,缝隙宽为d. 先补上 d ,构成完整的圆环,
1.8 解:
一根带电直线在另一带电直线处的场强大小为
E2 0(2a)4 0a
方向⊥直线
单位长度的另一带电直线在此电场中受力大 小为
FqE1E420 a
此力方向⊥直线,为相互吸引力。
1.9 解:
题目应加一个条件:>0. 如图所示,电荷元dq=dx在P点的场强大小为
d dx 4 0 x
∴P点的总电势为
al a
dx 4 0x
4 0
lnal a
2.510 3V
方法2: O
x x+dx
l
P a
Q X
r 选坐标轴OX,取微元x-x+dx,如图所示。
在X轴上任选一点Q,其与杆右端距离为r,则
Q点场强方向向右,大小为
E d E 0 l4 π 0 (r ε λ d l x x )2 4 π λ0(ε 1 r r1 l)
(2) 以极板边缘线作为安培回路L,则
Bdl
0Id
B
0 Id 2R
L
412 0 7 0 7 ..0 0 5 1 0 22.81 0 7T
10.1 解:
选坐标系,取微元, I
如图所示,
O
v a x x+dx
bX
其产生的动生电动势为 d
l
d(vB )dx vBdx
A CB
●
●
方向向左。
Ⅰ ⅡⅢ
平面II和III之间的场强大小为
E 22 1 0(1 2 3) 1.9 6 1 55 V 0 /m方向向右。
如图,有 A BA CC B E 1A C E 2CB
1 .9 6 1 5 5 7 0 1 2 5 0 .6 1 5 5 5 0 1 20
方向:
B1B20 ∴圆心处的总磁感应强度为0.
8.5解:
d
(1)所求磁感应强度方向:⊙ I1 大小为
l I2
B220 dI/24.01 05T
O
x x+dx
X
r1 r2 r3
(2)选坐标系OX和微元x-x+dx,选⊙为正法线方向
则电流I1的磁场通过图中面积的磁通量为
设 ∞ = 0 ,则P点的电势为
λ 1 1
φ Ed r
( )dr
a
a 4π0εr rl
4 0
lnaal
2.510 3V
3.21解:(1) 平面I和II之间的场强大小为
σ1
E1
σ2
E2
σ3
E 12 1 0(2 3 1)5 .6 5 15 V 0/m
