一种新的在线训练神经网络算法

合集下载

离散型Hopfield神经网络学习算法

离散型Hopfield神经网络学习算法朱丽萍;王锋辉;李洪奇;吕洁;Sikandar Ali【摘要】为使得离散型Hopfield神经网络(DHNN)具备更强的联想记忆功能,基于替换函数f(χ),权值求取采用提出的学习算法.通过设计比sgn更强约束能力的函数f(χ),在满足sgn函数要求的同时连续可导,由于f(sχ)连续可导,可根据能量最低点网络状态不再发生变化的特性定义损失函数,用梯度下降算法来求解.使用Matlab编程验证效果,验证结果表明,该学习算法比传统的外积法、正交设计法具有更好的效果,对原始信息还原率提高了5％-11％.%To make the discrete Hopfield neural networks have stronger associative memory ability,a learning algorithm for the weight of DHNN was adopted.Function fCr) was designed with stronger inhibition than sgn function,which satisfied the requirements of sgn function and possessed the continuously differentiable feature at the same time.Because the replace function f(χ) was continuously differentiable,according to the characteristics of the network that the lowest energy state doesn't change any more,the gradient descent algorithm was used to solve the problem.Matlab was used to verify the effects.Results show that the performance of the proposed method is better than outer product method and other traditional methods and the original information reduction rate increases by 5％ to 11 ％.【期刊名称】《计算机工程与设计》【年(卷),期】2018(039)003【总页数】5页(P831-835)【关键词】离散型Hopfield神经网络;外积和法;损失函数;梯度下降算法;联想记忆【作者】朱丽萍;王锋辉;李洪奇;吕洁;Sikandar Ali【作者单位】中国石油大学(北京)石油数据挖掘北京市重点实验室,北京102249;中国石油大学(北京)地球物理与信息工程学院,北京102249;中国石油大学(北京)石油数据挖掘北京市重点实验室,北京102249;中国石油大学(北京)地球物理与信息工程学院,北京102249;中国石油大学(北京)石油数据挖掘北京市重点实验室,北京102249;中国石油大学(北京)地球物理与信息工程学院,北京102249;中国石油大学(北京)石油数据挖掘北京市重点实验室,北京102249;中国石油大学(北京)地球物理与信息工程学院,北京102249;中国石油大学(北京)石油数据挖掘北京市重点实验室,北京102249;中国石油大学(北京)地球物理与信息工程学院,北京102249【正文语种】中文【中图分类】TP3910 引言离散型Hopfield神经网络是递归型神经网络中最基本的模型之一，广泛用于联想记忆[1]和二值无约束二次规划问题[2,3]，其研究具有深刻意义。

基于深度强化学习的微电网在线优化

基于深度强化学习的微电网在线优化
余宏晖;林声宏;朱建全;陈浩悟
【期刊名称】《电测与仪表》
【年(卷),期】2024(61)4
【摘要】针对微电网的随机优化调度问题,提出了一种基于深度强化学习的微电网在线优化算法。

利用深度神经网络近似状态-动作值函数,把蓄电池的动作离散化作为神经网络输出,然后利用非线性规划求解剩余决策变量并计算立即回报,通过Q学习算法,获取最优策略。

为使得神经网络适应风光负荷的随机性,根据风电、光伏和负荷功率预测曲线及其预测误差,利用蒙特卡洛抽样生成多组训练曲线来训练神经网络;训练完成后,保存权重,根据微电网实时输入状态,神经网络能实时输出蓄电池的动作,实现微电网的在线优化调度。

在风电、光伏和负荷功率发生波动的情况下与日前优化结果进行对比,验证了该算法相比于日前优化在微电网在线优化中的有效性和优越性。

【总页数】6页(P9-14)
【作者】余宏晖;林声宏;朱建全;陈浩悟
【作者单位】华南理工大学电力学院
【正文语种】中文
【中图分类】TM71
【相关文献】
1.基于深度强化学习的配电网在线拓扑优化策略研究
2.基于深度强化学习的微电网优化调度研究
3.基于确定性策略梯度深度强化学习和模仿学习的多源微电网经济优化调度策略
4.基于深度强化学习的微电网在线优化调度
5.基于深度强化学习的微电网源-荷低碳调度优化研究
因版权原因，仅展示原文概要，查看原文内容请购买。

ELM算法1 言忧

ELM算法1(20130218 13:25:58)分类：机器学习ELM(Extreme Learning Machine)是一种新型神经网络算法，最早由Huang于2004年提出【Extreme learning machine: a new learning scheme of feedforward neural networks】。

与SVM，传统神经网络相比，ELM的训练速度非常快，需要人工干扰较少，对于异质的数据集其泛化能力很强。

Huang在【Extreme learning machines: a survey，2011】这篇论文中对ELM进行了总结，包括最初的ELM算法和后来被发展延伸的ELM算法(比如在线序列ELM算法、增量ELM算法和集成ELM算法等)，里面的很多知识点值得学习。

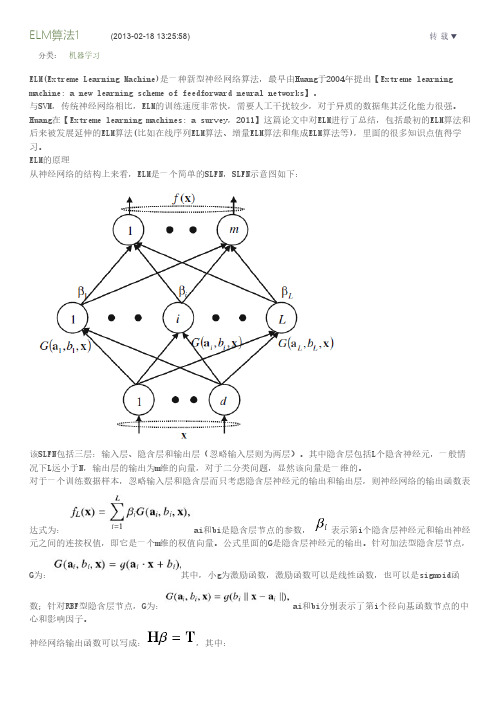
ELM的原理从神经网络的结构上来看，ELM是一个简单的SLFN，SLFN示意图如下：该SLFN包括三层：输入层、隐含层和输出层（忽略输入层则为两层）。

其中隐含层包括L个隐含神经元，一般情况下L远小于N，输出层的输出为m维的向量，对于二分类问题，显然该向量是一维的。

对于一个训练数据样本，忽略输入层和隐含层而只考虑隐含层神经元的输出和输出层，则神经网络的输出函数表达式为：ai和bi是隐含层节点的参数，表示第i个隐含层神经元和输出神经元之间的连接权值，即它是一个m维的权值向量。

公式里面的G是隐含层神经元的输出。

针对加法型隐含层节点，G为：其中，小g为激励函数，激励函数可以是线性函数，也可以是sigmoid函数；针对RBF型隐含层节点，G为：ai和bi分别表示了第i个径向基函数节点的中心和影响因子。

神经网络输出函数可以写成：，其中：转载▼如果神经网络能够无误差的预测训练样本，那么隐含层和输出层的权值是有解的，特别的，当L=N时，肯定有解。

但是实际问题中，L往往是远小于N的，那么求解权值向量的问题是无解的，即网络输出和实际值之间有误差，可以定义代价函数为：接下来如何求解最优的权值向量，使得损失函数J最小呢？针对这个问题ELM分两种情况解决：a.如果H是列满秩的，那么可以通过最小二乘找到最佳的权值，其解为：，其中：b.如果H是非列满秩的，则使用奇异值分解求解H的广义逆来计算最佳权值。

深度学习网络结构与神经网络优化算法的创新与改进

深度学习网络结构与神经网络优化算法的创新与改进摘要：深度学习是机器学习领域的一个重要分支，具有强大的模式识别和表征学习能力。

然而，选择合适的网络结构和有效的优化算法仍然是深度学习的关键挑战。

因此，本论文旨在提出新的创新和改进方法来解决深度学习网络结构和神经网络优化算法方面的问题。

关键词：深度学习；网络结构；神经网络；优化算法；创新与改进引言深度学习作为一种强大的机器学习技术，近年来在各个领域取得了显著的进展和应用。

它通过多层次的神经网络模型，能够自动地学习和表示数据中的复杂模式和抽象特征。

然而，深度学习的成功并不仅仅依赖于数据和计算资源的增加，选择合适的网络结构和有效的优化算法同样至关重要。

1深度学习网络结构1.1前馈神经网络由输入层、隐藏层和输出层组成，数据仅沿单个方向前进。

它是最简单的深度学习网络结构，通常用于解决分类或回归问题。

1.2卷积神经网络主要用于图像处理任务。

它包括卷积层、池化层和全连接层。

卷积层通过局部感受野和共享权重来提取图像的特征，池化层用于降低特征维度，全连接层实现最终的分类或回归。

1.3循环神经网络适用于序列数据处理，如文本和语音。

RNN中的神经元通过时间上的反馈连接，可以处理可变长度的输入序列，并记忆先前的信息。

1.4长短期记忆网络是RNN的一种变体，通过引入门控机制来解决传统RNN模型中的梯度消失或爆炸问题，能够更好地捕捉序列中的长期依赖关系。

1.5生成对抗网络由生成器和判别器组成。

生成器学习生成数据样本，而判别器则学习区分生成的样本和真实的样本。

通过对抗训练过程，GAN能够生成逼真的假样本。

2神经网络优化算法2.1随机梯度下降随机梯度下降是最基本的优化算法之一。

它通过计算每个样本的梯度来更新参数，从而降低损失函数。

SGD在训练过程中的每个迭代步骤都只用到一个样本，因此计算效率高，但收敛速度相对较慢。

2.2动量优化算法在SGD的基础上引入了动量项，可以加快收敛速度，并且有利于跳出局部最小值。

基于嵌入式系统的神经网络在线训练平台实现

便携式特点。同时对于单一变量的测量或处理也有了低成本的解决方案。但神经网络算法复杂、算量大，时，运本文搭建双核嵌入式软硬件系统平台，神经网络的将在线训练成功移植到该双核平台中，并对大量数据集进行
关键词：嵌入式系统；软测量；在线训练；神经网络中图分类号：Ｔ７Ｐ２３文献标识码：Ａ文章编号：１０－７７２１）８９０－４００９８（００ｏ－１００
Ｎｅａｅｗｏｋｏｌｅｔａｎｎｌｔｏｍａｅｎｕｒｌｎｔｒｎｉｒｉｉｇｐａｆｒｂｓｄｏｎ
ａｄｌｒｉｇａｅｔｅｏｔｚｄｎｕ￣ｎｔｏｋＮ）ｓｅｌｅｅｄｕｌｃｒ（ＲａｄｆａｎｏｔＳ）ｎａｎｔ，ｐｉｅｅｒｅｒ（ＮｉｒａｚｄｉｔｏｂｅｏｅＡＭｎｏｔｇｉＰｅｎｒｈｍｉｗｉｎｈ－ｌｉｐｎＤ
摘
要：基于最新的工业应用双核处理器ＯＡ — １７设计了一种神经网络软测量模型在线训练平台。ＭＰＬ３
该平台以ＡＭ与浮点ＤＰ双核控制器为核心。针对神经网络隐含层节点数、ＲＳ训练中止条件、习率等相学
关参数的确定进行了研究与测试，将优化的神经网络算法成功移植到嵌入式平台，支持神经网络软测量模型的在线训练。通过对相关数据集的测试，结果表明：系统具有高速、高精度等优良性能。
ＺｅａｇＵｉｅｓｙＨｎｚｏ１０７，ｈｎ）ｈｊｎｎｖｒｉ，ａｇｈｎ３０２Ｃｉａｉｔ

神经网络的Levenberg-Marquardt算法研究

神经网络的Levenberg-Marquardt算法研究摘要：本文主要介绍LM(Levenberg-Marquardt)神经网络算法，LM算法是梯度下降法和高斯—牛顿法的结合，这种神经网络算法综合了这两种方法的优点，在一定程度上克服了基本的BP网络收敛速度慢和容易陷入局部最小点等问题。

对LM算法的计算步骤作了简要的阐述。

最后介绍了LM神经网络算法再监督控制上的应用。

关键词：神经网络；LM算法；计算步骤；监督控制0 引言神经网络BP学习算法在理论上具有逼近任意非线性连续映射的能力，在非线性系统的建模及控制领域里有着广泛的应用。

然而BP 算法存在一些不足，主要是收敛速度很慢；往往收敛于局部极小点；数值稳定性差，学习率、动量项系数和初始权值等参数难以调整，非线性神经网络学习算法LM可以有效地克服BP算法所存在的这些缺陷[1]。

LM算法是高斯—牛顿法和最速下降法的结合，具有高斯—牛顿法的局部收敛性和梯度下降法的全局特性。

它通过自适应调整阻尼因子来达到收敛特性，具有更高的迭代收敛速度，在很多非线性优化问题中得到了稳定可靠解。

在LM算法的计算过程中，初值是一个很重要的因素。

若选择的初值X0接近真值时，收敛速度很快且能够得到全局最优解，但如果初值远离真解时，优化结果往往过早的陷入局部最优解从而得到的结果完全背离真解。

要解决该问题，一是通过得到大量的原始信息来对真值有一个较准确的估计，但这在实际问题中往往不太可能达到；另外就是选择一种合理的全局最优化算法与其相结合，消除LM算法对初值的依赖且具有很快的收敛速度[2]。

1 神经网络神经网络具有高度的自学习、自组织和自适应能力，能通过学习和训练获取网络的权值和结构。

多层前向神经网络具有理论上可逼近任意非线性连续映射的能力，因而非常适合于非线性系统的建模及控制，是目前使用较多的一种神经网络模型[3]。

BP网络(Back Propagation Network)称为误差反向传播神经网络，它是一种能朝着满足给定的输入/输出关系方向进行自组织的神经网络，其典型的结构图如图1所示，由三部分组成：输入层、隐含层、输出层，三部分之间通过各层节点之间的连接权依次前向连接。

基于互相关函数的神经网络解耦器在线学习算法

ｅｉａｏｔｍｒｌｒｈｃｇｉ
引言
工业生产中的大部分被控系统是ＭＩＭＯ系统，
其各个回路之间会相互影响，这使得系统的控制品１神经网络解耦控制系统结构选取
质急剧下降，严重时将导致系统无法工作。目前，在理论上比较成熟的解耦控制技术主要本文采用分散式神经网络解耦控制系统，整．有：传统解耦、基于现代控制理论的解耦、自适应个系统由控制器ＣＣ，神经网络解耦器ＮＤ，Ｄｚ所解耦和智能解耦，中智能解耦以神经网络解耦为Ｎ和被控过程Ｐ组成，如图１示。图中，被控其
代表。人们提出了各种基于神经网络理论的解耦算
法。于神经网络理论的解耦控制算法和容错解耦基
控制算法 …需要知道对象控制变量关于被控变量
的雅可比矩阵，不便于在工程中应用。于连续非对线性ＭＩＭＯ系统线性化解耦，可利用神经网络阶积分逆系统来实现解耦；对于离散非线性ＭＩＭＯ
ＬｎｌＩＸｉ－ｉ．ＢＡＩｎＹｏ
（ｅａｔｎｆ￣ｔｎｏｔｈｎｌｆ￣ｏｅｎｖｒｔ，ｅｔｇ１２０，ＣｉａＤｐｒｔＡｕｍａｏ，ＮｒＣｉＥｅｉＰｗｒｉｅｓｙＢｉ０２６ｈ）ｍｅｏｉｈａｃＵｉｊｈｎ
Ａｂｉａｔｓｒｃ：ＯｎｉｅｌａｉｇａｇｒｈｉｎｅｒｎｌｏｉｍｏＮｅｒｌｎｔｆｕａＮｅｗｏｋｔｒＤｅｕｌｒｗｈｃｓｄｏＩＯｌＳ — ｏｒｌｔｎｆｎｔｎｏｃｐｅ，ｉｈｈｃｎＭＭａＣＯＳｃｒａｏｕｃｉ．ｅｉｏｉｐｏｏｅｎｔｅｆａｆｉｔｉｕｅｅｃｕｌｇｓｓｅｓｒｐｓｄｏｈｒｍｅｏｄｓｂｔｄｄｏｐｔｔｍ．ＴｈｒｈｙｅａＥｒｔｍｅｉｅｅｆ（ＯＳｃｒｅａｉｎｆｎｔｎｏｅｌ０ｈｄｆｓａｓｔｏ：Ｓ —ｏｒｌｔｕｃｉｆｔｉｎｔｏｏｈＭＩＯｃｅｓｔｅｔｒｅｕｃｉｎｏｅｉｌｄｃｕｌｒＴｅＭａｔｄａｈａｇｔｆｎｔｆｎｕａｅｏｐｅ．ｈｏｒｍｉｇｇｎｔｌｏｔｍｓａｏｔｄｔ＇ｉｅａｅｏｐｅｉｘｎｅｅｃａｇｒｈｉｄｐｅ０ｕａｎｏ］ｄｃｕｌｒｉｉｎｒ

神经网络方法

神经网络方法神经网络是一种模仿人脑神经元网络结构和功能的数学模型，它可以通过学习和训练来完成各种复杂的任务。

在计算机科学和人工智能领域，神经网络方法被广泛应用于图像识别、自然语言处理、语音识别等领域，取得了许多重要的成果。

首先，神经网络方法的核心是神经元。

神经元是神经网络的基本单元，它接收输入信号，并通过激活函数处理后输出结果。

神经网络由多个神经元组成的层次结构，包括输入层、隐藏层和输出层。

通过不断调整神经元之间的连接权重，神经网络可以逐渐学习和优化自己的模型，从而实现对复杂问题的处理和解决。

其次，神经网络方法的训练过程是非常重要的。

神经网络的训练通常采用反向传播算法，通过计算输出结果和实际结果之间的误差，来调整神经元之间的连接权重。

这个过程需要大量的数据和计算资源，同时也需要合适的损失函数和优化算法来指导训练的方向和速度。

在训练过程中，还需要注意防止过拟合和欠拟合的问题，以保证神经网络的泛化能力和准确性。

另外，神经网络方法在实际应用中也面临一些挑战和限制。

例如，神经网络需要大量的数据来进行训练，而且对数据的质量和标注要求较高。

此外，神经网络的模型结构和超参数的选择也需要一定的经验和技巧。

同时，神经网络的计算和存储成本也较高，对硬件设备和算法实现提出了挑战。

最后，随着深度学习和神经网络技术的不断发展，神经网络方法在各个领域都取得了许多重要的成果。

例如，在图像识别领域，深度卷积神经网络已经可以实现对复杂图像的高精度识别和分类。

在自然语言处理领域，循环神经网络和注意力机制已经可以实现对自然语言文本的语义分析和情感识别。

在语音识别领域，端到端的神经网络模型已经可以实现对语音信号的准确识别和转换。

总的来说，神经网络方法是一种强大的工具，它在人工智能和计算机科学领域具有重要的地位和应用前景。

随着技术的不断进步和创新，相信神经网络方法将会在更多领域发挥重要作用，为人类社会带来更多的便利和进步。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

一种新的在线训练神经网络算法速度估计和PMSG风力发电系统的自适应控制最大功率提取*BFernando Jaramillo Lopez，Francoise Lamnabhi Lagarrigue *，godpromesse肯尼，一个该DES signaux等系统，Supelec高原都moulon Gif sur伊维特，91192，法国B该d'automatique等信息学系的精灵appliquee，电气，iut-fv Bandjoun，Universite de姜村，喀麦隆这是一个值得注意的问题。

有一个房间文章历史：在本文中，自适应控制系统最大功率点跟踪单机PMSG风涡轮系统（WTS）了。

一种新的程序来估计风速导出。

实现这一神经网络识别ﬁER（NNI）是为了近似的机械转矩设计WTS。

有了这些信息，风速计算的基础上的最佳机械扭矩点。

NNI接近实时的机械转矩信号，它不需要离线训练得到其最佳参数值。

这样，它可以真正接近任何机械扭矩值精度好。

为了将转子转速调节到最优转速值，采用块反推控制器导出。

使用Lyapunov证明了一致渐近稳定的跟踪误差来源争论。

一个标准的被动为基础的控制器的数值模拟和比较为了显示所提出的自适应方案的良好性能。

1。

介绍使风产业的趋势是设计和建造变量—高速涡轮机的公用事业规模安装[ 2 ]。

可再生能源发电的兴趣增加由于污染排放，在其他原因。

风能源是各种可再生能源中最为成熟的能源之一技术，并得到了很多的青睐，在世界的许多地方[ 1 ]。

根据风速、VST可以在3区域操作，因为它如图1所示。

该地区1是当风速下切入风速Vmin。

没有最大效率发生在EFﬁ这一地区。

区域2是当风速高于Vmin但在额定值V下。

在该区域中，主控制器任务是n有两种类型的风力涡轮机系统：恒速涡轮机（CST）和变速风力涡轮机（VST）。

CST操作恒定的转子速度，并可以连接到公用电网直接，以这种方式电源转换器是没有必要的。

VST可以跟随风的变化，在可变转子速度。

因为变频电源，VST产生，电源转换器将它们连接到公用电网或电阻性负载是必要的。

VST的主要优点是，他们可以操作的大部分时间最大功率点。

这一事实，和低负荷的VST有增加了WTS的EFﬁ效率，它工作在其最大功率点（MPP）。

这是主要的操作区域。

区域3当风速高于V但切出风速下nVmax。

在该区域中，控制器的任务是保持捕获的PO—我们在ﬁ固定或额定值，而不是试图最大化。

另一个重要的控制器任务在这个区域，是保持电气和安全区域的结构条件。

这是通过改变叶片螺距。

当风速高于Vmax，VST关机为了保持系统的完整性。

这里介绍的工作，包括EFﬁ效率增加2区经营WTS在MPP多尔本文的分析是考虑到叶片的变桨角度解决zerod。

然而，这不是一件容易的事，因为系统的动态性具有较强的非线性和广泛的操作系统使线性技术不适合问题。

*本研究已得到欧盟部分支持第七框架计划FP7 / 2007e2013 ] [ 257462号协议下授予hycon2英才网。

*对应作者。

电子邮件地址：jaramillo@lss.supelec.fr（F. Jaramillo Lopez），gokenne @雅虎。

com（G. Kenne），lamnabhi@lss.supelec.fr（F. Lamnabhi Lagarrigue）。

/可再生能源，86（2016）38e48三十九点的大部分时间。

不同的作者面临的最大功率点跟踪忽略发电机动态和使用电气的问题扭矩作为一个实际的控制变量，见参考文献。

[ 6 ]。

有些作品提出了债权取得一定的控制权目标像[ 14e17 ]；但不稳定的理论给出分析。

文献[ 18 ]中，作者提出了一种无位置传感器变速风力发电系统的鲁棒控制方案—最优转矩控制方法。

参见参考文献其他相关控制工程。

文献[ 19 ]中，作者提出了一种基于无源性控制器标准（分），考虑到发电机动力学和平衡的渐近稳定性点证明。

该控制器工作缓慢变化在风输入信号。

为了解决一些参数的不确定性，它是必要的采用鲁棒控制技术实现控制目标。

这些技术之一是滑模控制（标准ﬁRST—阶和高阶）[ 20e25 ]。

在所有的鲁棒控制技术，可以解决目前的问题，后退步进本文选择的技术相对简单[ 21,26 ]。

图1。

VST的操作区域。

本文的主要贡献是一个基于神经网络的风电在线训练新算法速度估计块反步计划，以规范风力机系统的最佳平衡点。

风速度计算与最佳机械转矩值，即用神经网络识别ﬁ二近似。

实时动态—动态非线性学习法（相对于离线训练亲—程序）的权重向量，提出了神经网络，证明了误差源的一致渐近稳定李雅普诺夫稳定性定理。

非线性学习律使神经网络可以近似非常快速变化的数据。

在这形式，脱机培训与广泛的输入数据是没有必要的。

此外，良好的精度在任何操作条件，保证和实现持续学习。

块反推控制器导出以调节最佳平衡点。

大学—整体跟踪误差原点的渐近稳定性系统证明使用Lyapunov参数，性能该控制器是一个分，提出了比较同一制度。

基于风速估计的最大功率点控制跟踪（MPPT）是通过计算最优转速达到以最佳比例值的帮助和参考，估计—风速信号。

几种估算风的方法速度已报告。

功率平衡估计算法其中包括求解代数风功率方程文献[ 3 ]的解释。

文献[ 4 ]利用扩展卡尔曼ﬁ滤波估计，并在文献[ 5 ]的卡尔曼滤波器估计ﬁ阐述了。

文献[ 6 ]对风速的一个有趣的估计提出了采用浸入不变性技术3可再生能源，86（2016）38e48由风力涡轮机捕获的功率是由一一一新世界报u_ M¼下午¼rpr2cðLÞV3PW二J是转子惯量；Tm是机械转矩，T是电磁转矩：E其中R是空气的密度，R是转子扫掠半径，C（L）是功率系数ﬁ高效和大众的风速。

l是尖端速度P比（TSR），下面的表达式3pTE¼4 FIQ：朗姆酒LB（1）的机械转矩之间的比率给出捕获功率和转子转速：大众转子速度在哪里？。

下午一CðLÞ通过实验测量得到的功率系数ﬁ有效数据—测试或使用刀片元矩理论，它de—在尺寸和叶片的几何起。

一些作品P2¼rPR3（2）TM¼v：W嗯l系统的状态是ﬁ内德在dq电流比例—租金和转子速度：已经提出了表征C（L）的表达，喜欢的工作P文献[ 27 ]。

虽然CP的一般特性不仅取决于L，但也对叶片间距Q，目前工作的目的是提高风力发电机在区域2的EFﬁ效率，和q 被视为ﬁ固定，即问≡0。

以下特性取自文献[ 28 ]中使用的工作。

T2j33rXB的Li s Li二Q；SD；嗯一在那里，我¼1,2,3是一个额外的缩放因子。

我CþC该系统的整体模型CP1lP2CðLÞ¼E保罗PP4Llx_¼FðX；VÞþGðXÞU（3）（4）W在¼¼CP1 21，C 125.2165，C 9.7798和C 0.0068¼，¼。

这P3P4哪里函数有一个已知的最高点C¼0:48在争论P *我¼价值8.001。

*这个最大C值给出了最大捕获功率TTFðX；VÞB½F；F；F；GðXÞB½G；G；0W一二三一二P *对于给定的风速v。

这些事实可以利用解决W和TSR的方程（1）UM和获得最佳转速：RXF1¼L3plrs X X1 24ljs S2 3V LR一三三二（5）Wþ嗯¼*然后，对于一个给定的风速，主要控制目标是调节转子转速至其最佳值。

在DQ框架给出了永磁同步发电机模型通过（见参考文献。

【29,30 ]）2 3plrs X X3pfrs2x34js3二一F2¼Lþ（6）（7）（8）4ljs S1 3F3¼TSMðX；VÞg x三W3vli_¼RIþ李U V；DDQEDli_¼侯日立Uþ福Vkdevbx1G1¼lQQDEEQ我和我所在的dq电流；V和V的DQ电压；R DQDQ定子电阻和电感分别为定子电阻和电感永磁ﬂUX；与电频率你了Ekdevbx2lG2¼（9）PUE¼嗯二pfs32lrs2¼G3V（10）用P对的数目对。

与控制信号和缩放机械扭矩，分别：由于所使用的拓扑，PMSG电流单位功率因子和DQ电压由电池电压VB的确定对dcedc转换器的占空比D [ 19 ]：DUB的ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ我二二DV¼问ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃK V DXX二D判定元件B一þ二二QLSLS二我þ我一D它是假定状态X2ℝ3测量的模型；参数是众所周知的，风速大众是未知的。