轻绳、轻杆、轻弹簧三种模型之比较
高中物理必考模型:轻绳、轻弹簧、轻杆联系与区别全解析

高中物理必考模型:轻绳、轻弹簧、轻杆联系与区别全解析轻绳特点轻绳模型的建立轻绳或称为细线,它的质量可忽略不计,轻绳是软的,不能产生侧向力,只能产生沿着绳子方向的力。
它的劲度系数非常大,以至于认为在受力时形变极微小,看作不可伸长。
轻绳模型的特点①轻绳各处受力相等,且拉力方向沿着绳子;②轻绳不能伸长;③用轻绳连接的系统通过轻绳的碰撞、撞击时,系统的机械能有损失;④轻绳的弹力会发生突变。
轻杆特点轻杆模型的建立轻杆的质量可忽略不计,轻杆是硬的,能产生侧向力,它的劲度系数非常大,以至于认为在受力时形变极微小,看作不可伸长或压缩。
轻杆模型的特点①轻杆各处受力相等,其力的方向不一定沿着杆的方向;②轻杆不能伸长或压缩;③轻杆受到的弹力的方式有拉力或压力。
轻弹簧特点轻弹簧模型的建立轻弹簧可以被压缩或拉伸,其弹力的大小与弹簧的伸长量或缩短量有关。
轻弹簧的特点①轻弹簧各处受力相等,其方向与弹簧形变的方向相反;②弹力的大小为F=kx,其中k 为弹簧的劲度系数,x为弹簧的伸长量或缩短量;③弹簧的弹力不会发生突变。
特别提醒:橡皮筋与轻弹簧极为相似,只是橡皮筋不能被压缩静止或匀速运动例1、如图所示,有一质量为m的小球用轻绳悬挂于小车顶部,小车静止或匀速直线运动时,求绳子对小球作用力的大小和方向。
解析:小车静止或匀速直线运动时,小球也处于静止或匀速直线运动状态。
由平衡条件可知,绳子对小球的弹力为F=mg,方向是沿着绳子向上。
若将轻绳换成轻弹簧,其结果是一样的。
例2、如图所示,小车上有一弯折轻杆,杆下端固定一质量为m的小球。
当小车处于静止或匀速直线运动状态时,求杆对球的作用力的大小和方向。
解析:以小球为研究对象,可知小球受到杆对它一个的弹力和重力作用,由平衡条件可知小球受力如图所示。
则可知杆对小球的弹力为F=mg,方向与重力的方向相反即竖直向上。
注意:在这里杆对小球的作用力方向不是沿着杆的方向。
以加速度a做匀加速直线运动时,求轻绳对小球的作用力的大小和方向。
浅析轻绳、轻杆和轻弹簧模型的应用

T-mgcosθ =mv2/l=0 所以,拉力为
T=mgcosθ
请想一想: 这时 OA 的拉力与 OB 断开前的拉力之 比是多少?OB 断开瞬间,小球的运动加速度是 多少?
0 2 -1
分析:在细绳烧断之前,两球受到的平衡力如图所示。 在细绳烧断瞬间间,拉力(T)消失,而弹簧弹力不变, 即
T=2 mg
根据牛顿第二定律,A、B 的加速度分别为 aA=(F-mg)/m=g--方向竖直向上。
aB=mg/m=g--方向竖直向下。
请读者想一想:如果将连接 A、B 球的细绳换成轻 杆或者轻弹簧结果如何?
T= [(ma)2+( mg)2]1/2=m (a2+g2)1/2
拉力与竖直方向的夹角θ 可表示为 θ =tg (a/g). 可以看出:θ 角随加速度 a 的增大而增大。 当 a=0 时:T= mg , θ =0---拉力竖直向上; 当 a=gtgß 时: T= mg(1+tg ß)1 /2= mg/cosθ , θ =ß---拉力沿杆方向; 注意:这个临界加速度,可以利用逆向思维方法。由θ =ß 简捷的得出。 当 a»g 时, T≈ ma,θ ≈90 ――拉力趋于水平方向。 当 a«g 时, T≈ mg,θ ≈0――拉力趋于竖直方向。 请读者想一想:如果小球由一段轻绳或者轻弹簧连接,结果如何? 例 3:如图 4 所示,质量相同的 A、B 两球用细绳相连,然后由轻弹簧竖直悬挂。求 将细绳烧断瞬间,A、B 的加速度是多少?方向如何?
轻杆轻绳轻弹簧模型

等于物体的重力;分别
取C点和G点为研究对象,
细绳EG的张力FTEG之比;
进行受力分析如图甲和
(2)轻杆BC对C端的支持力;
乙所示,根据平衡规律
(3)轻杆HG对G端的支持力。
可求解。
[答案]
(1)2MM12 (2)M1g 方向跟水平方向成 30°指 向右上方
(3) 3 M2g 方向水平向右
点评: 解答本题的关键是抓住:活结中轻绳上各点的拉力大小相
解析: 绳连接时,球由A到C做自由落体运动,A、C关于水平线
对称,设C处的速度为Vc,且方向竖直向下,选取B点为零能,m在vc绳2 突然拉紧的瞬间,将径向的动
能损耗掉,由C到B的过程中机械能守恒,选取B点为零能面,
1 2m12vmg(1 Lsin)1 2mB 2v
则α=37°
即方向与竖直方向成 37°角斜向下,这个力与轻绳的拉力恰好在同一条
直线上。根据物体平衡的条件可知,轻杆对小球的作用力大小为 5 N,方
向与竖直方向成 37°角斜向上
点评: 由于轻杆作用力的方向具有多向性的
特点,先确定其余力的合力,然后再根据 平衡条件判定轻杆作用力的大小和方向。
[典例2]轻杆长为L,一端用光滑轴固定,另一端系一个可视为 质点,质量为的小球,把小球拉至图示的位置,无初速度地自 由释放到最低处的过程中,小球做什么运动?到最低处时速度 多大?弹力多少?若其它条件不变,把轻杆换为细绳,则释放 后小球做什么运动?到最低处时速度多大?弹力为多少?
水平横梁BC右端的定滑轮挂住一个质 量为M1的物体,∠ACB=30°;图乙 中轻杆HG一端用铰链固定在竖直墙上, 另一端G通过细绳EG拉住,EG与水平 方向也成30°,轻杆的G点用细绳GF
轻绳、轻杆和轻弹簧模型(修)

轻绳、轻杆和轻弹簧模型的应用一、三个模型的相同点1、“轻”—不计质量,不受重力。
2、在任何情况下,沿绳、杆和弹簧伸缩方向的张力、弹力处处相等。
二、三个模型的不同点1、形变特点轻绳—可以任意弯曲,但不能伸长,即伸长形变不计。
轻杆—不能任意弯曲,不能伸长和缩短,即伸缩形变不计。
轻弹簧—可以伸长,也可以缩短,且伸缩形变不能忽略不计。
2、施力和受力特点轻绳—只能产生和承受沿绳方向的拉力。
轻杆—不仅能产生和承受沿杆方向的拉力和压力,还能产生和承受不沿杆方向的拉力和压力。
轻弹簧—可以产生和承受沿弹簧伸缩方向的拉力和压力。
3、力的变化特点轻绳—张力的产生、变化、或消失不需要时间,具有突变性和瞬时性。
轻杆—拉力和压力的产生、变化或消失不需要时间,具有突变性和瞬时性。
轻弹簧—弹力的产生、变化或消失需要时间,即只能渐变,不具有瞬时性,且在形变保持瞬间,弹力保持不变。
(注意:当弹簧的自由端无重物时,形变消失不需要时间)4、连接体的运动特点轻绳—轻绳平动时,两端的连接体沿绳方向的速度(或速度分量)总是相等,且等于省上各点的平动速度;轻绳转动并拉直时,连接体具有相同的角速度,而线速度与转动半径成正比。
轻杆—轻杆平动时,连接体具有相同的平动的速度;轻杆转动时,连接体具有相同的角速度,而线速度与转动半径成正比。
轻弹簧—在弹簧发生形变的过程中,两端连接体的速率不一定相等;在弹簧形变最大,即弹性势能最大时,两端连接体的速率相等;在弹簧转动时,连接体的转动半径随弹力变化,速度方向不一定垂直于弹力。
5、作功和能量转化特点轻绳—在连接体作匀速率和变速率圆周运动的过程中,绳的拉力都不作功;在绳突然拉直的瞬间,有机械能转化为绳的内能,即机械能不守恒。
轻杆—在连接体作匀速率和变速率圆周运动的过程中,轻杆的法向力对物体不作功,而切向力既可以对物体作正功,也可以对物体作负功,但系统机械能守恒。
轻弹簧—弹力对物体作功,系统机械能守恒;弹力作正功,弹性势能减少,物体动能增加;弹力作负功,弹性势能增加,物体动能减少。
对轻杆、轻绳、轻弹簧三种模型的深入探讨

‘
’一。、] 引探导航·难点突破
,,
端是否固定.若不固定,则另一端合力必沿 杆方向,若固定,则可以受任何方向的力,应 根据实际情况加以分析.
2.轻弹簧中弹力的大小 在弹簧测力计的两端各用5 N的力对拉, 测力计 的读数是多 少?请 同学们注意 不是 10 N也不是0 N.对于这个问题我们可以做如 下分析:我们可以把弹簧分成很多段,显然在 弹簧 发生伸长 形变时, 相邻两端 之间都互 相
囊:二、三种模型的主要特点
1.轻绳 轻绳或称为细线,它的质量可忽略不计, 轻绳是软的,不能产生侧向力,只能产生沿着 绳子 方向的力 .它的劲 度系数非 常大,以 至 于认为在受力时形变极微小,看作不可伸长. 其特点是: ①轻 绳中各处 受力相 等,且 拉力方向 沿 着绳子. ②轻绳不能伸长. ③用轻 绳连接的 系统通过 轻绳的碰 撞、 撞击时,系统的机械能有损失. ④轻绳的弹力会发生突变. 2.轻杆 轻杆的质量可忽略不计,轻杆是硬的,能 产生侧向力,它的劲度系数非常大,以至于认 为在 受力时形 变极微小 ,看作不 可伸长或 压 缩.其特点是: ①轻杆 各处受力 相等,其 力的方向 不一 定沿 着杆的方向 . ②轻杆不能伸长或压缩. ③轻仟受到 的弹力的力武有:拉力 或匮力. 3.轻弹簧 轻弹簧 可以被压 缩或拉伸 ,其弹力 的大 小与弹簧的伸长量或缩短量有关.其特点是: ①轻 弹簧各处 受力相 等,其 方向与弹 簧 形变的 向相反. ② 弹力 的大 小为 F=k x,其 中 k为弹 簧的
l l!l l i;39’’’。。‘1。。‘’。’~、7…一一一一一一~一 引探导航·难点突破
昌掰疆舀国深氏冁讨
尹秀辉
曩:一、三种模型的相同点
1.轻绳、轻杆和轻弹簧的“轻”就是质量 可忽略,重力不计.
(完整版)轻绳、轻杆和轻弹簧模型

浅析轻绳、轻杆和轻弹簧模型的应用山西泽州县第一中学成文荣李智涛 048000轻绳、轻杆和轻弹簧,是力学中三个重要的理想模型,在高中物理解题中有着重要的地位,为了帮助学生正确地分析和解决与轻绳、轻杆和轻弹簧有关的问题,笔者对三个模型的相同点和不同点进行了总结,并想通过一定的实例,对学生学习和应用给与启迪思考。
一、三个模型的相同点1、“轻”- 不计质量,不受重力。
2、在任何情况下,沿绳、杆和弹簧伸缩方向的张力、弹力处处相等.二、三个模型的不同点1、形变特点轻绳—可以任意弯曲,但不能伸长,即伸长形变不计。
轻杆—不能任意弯曲,不能伸长和缩短,即伸缩形变不计。
轻弹簧—可以伸长,也可以缩短,且伸缩形变不能忽略不计。
2、施力和受力特点轻绳 - 只能产生和承受沿绳方向的拉力.轻杆 - 不仅能产生和承受沿杆方向的拉力和压力,还能产生和承受不沿杆方向的拉力和压力。
轻弹簧—可以产生和承受沿弹簧伸缩方向的拉力和压力。
3、力的变化特点轻绳—张力的产生、变化、或消失不需要时间,具有突变性和瞬时性。
轻杆 - 拉力和压力的产生、变化或消失不需要时间,具有突变性和瞬时性.轻弹簧—弹力的产生、变化或消失需要时间,即只能渐变,不具有瞬时性,且在形变保持瞬间,弹力保持不变。
(注意 :当弹簧的自由端无重物时,形变消失不需要时间)4、连接体的运动特点轻绳 - 轻绳平动时,两端的连接体沿绳方向的速度(或速度分量)总是相等,且等于省上各点的平动速度;轻绳转动并拉直时,连接体具有相同的角速度,而线速度与转动半径成正比。
轻杆—轻杆平动时,连接体具有相同的平动的速度;轻杆转动时,连接体具有相同的角速度,而线速度与转动半径成正比.轻弹簧—在弹簧发生形变的过程中,两端连接体的速率不一定相等;在弹簧形变最大,即弹性势能最大时,两端连接体的速率相等;在弹簧转动时,连接体的转动半径随弹力变化,速度方向不一定垂直于弹力。
5、作功和能量转化特点轻绳 - 在连接体作匀速率和变速率圆周运动的过程中,绳的拉力都不作功;在绳突然拉直的瞬间,有机械能转化为绳的内能,即机械能不守恒.轻杆—在连接体作匀速率和变速率圆周运动的过程中,轻杆的法向力对物体不作功,而切向力既可以对物体作正功,也可以对物体作负功,但系统机械能守恒。
物理建模轻杆轻绳轻弹簧模型
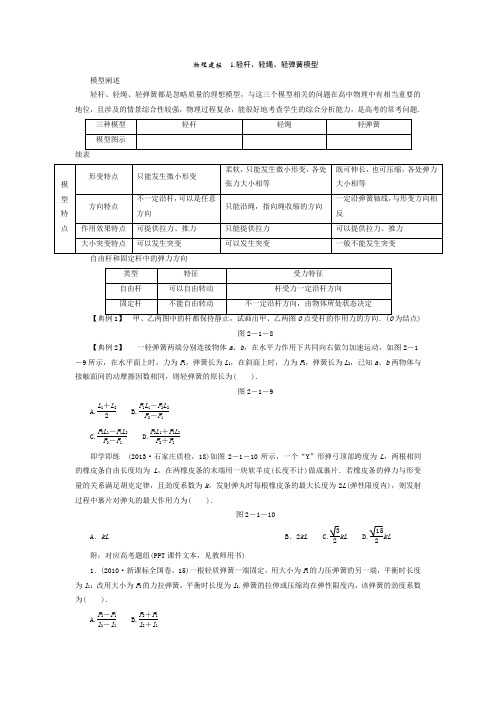
物理建模 1.轻杆、轻绳、轻弹簧模型模型阐述轻杆、轻绳、轻弹簧都是忽略质量的理想模型,与这三个模型相关的问题在高中物理中有相当重要的地位,且涉及的情景综合性较强,物理过程复杂,能很好地考查学生的综合分析能力,是高考的常考问题.为结点)图2-1-8【典例2】 一轻弹簧两端分别连接物体a 、b ,在水平力作用下共同向右做匀加速运动,如图2-1-9所示,在水平面上时,力为F 1,弹簧长为L 1,在斜面上时,力为F 2,弹簧长为L 2,已知a 、b 两物体与接触面间的动摩擦因数相同,则轻弹簧的原长为( ).图2-1-9A.L 1+L 22B.F 1L 1-F 2L 2F 2-F 1C.F 2L 1-F 1L 2F 2-F 1 D.F 2L 1+F 1L 2F 2+F 1即学即练 (2013·石家庄质检,18)如图2-1-10所示,一个“Y”形弹弓顶部跨度为L ,两根相同的橡皮条自由长度均为L ,在两橡皮条的末端用一块软羊皮(长度不计)做成裹片.若橡皮条的弹力与形变量的关系满足胡克定律,且劲度系数为k ,发射弹丸时每根橡皮条的最大长度为2L (弹性限度内),则发射过程中裹片对弹丸的最大作用力为( ).图2-1-10A .kLB .2kL C.32kL D.152kL 附:对应高考题组(PPT 课件文本,见教师用书)1.(2010·新课标全国卷,15)一根轻质弹簧一端固定,用大小为F 1的力压弹簧的另一端,平衡时长度为l 1;改用大小为F 2的力拉弹簧,平衡时长度为l 2.弹簧的拉伸或压缩均在弹性限度内,该弹簧的劲度系数为( ).A.F 2-F 1l 2-l 1 B.F 2+F 1l 2+l 1C.F 2+F 1l 2-l 1 D.F 2-F 1l 2+l 12.(2011·山东卷,19)如图所示,将两相同的木块a 、b 置于粗糙的水平地面上,中间用一轻弹簧连接,两侧用细绳系于墙壁.开始时a 、b 均静止,弹簧处于伸长状态,两细绳均有拉力,a 所受摩擦力F f a ≠0,b 所受摩擦力F f b =0.现将右侧细绳剪断,则剪断瞬间( ).A .F f a 大小不变B .F f a 方向改变C .F f b 仍然为零D .F f b 方向向右3.(2012·山东基本能力,85)力是物体间的相互作用,下列有关力的图示及表述正确的是( ).物理建模 1.轻杆、轻绳、轻弹簧模型模型阐述轻杆、轻绳、轻弹簧都是忽略质量的理想模型,与这三个模型相关的问题在高中物理中有相当重要的地位,且涉及的情景综合性较强,物理过程复杂,能很好地考查学生的综合分析能力,是高考的常考问题.为结点)图2-1-8解析 甲为自由杆,受力一定沿杆方向,如下图甲所示的F N1.乙为固定杆,受力由O 点所处状态决定,此时受力平衡,由平衡条件知杆的支持力F N2的方向与mg 和F 1的合力方向相反,如下图乙所示.答案 如解析图所示【典例2】 一轻弹簧两端分别连接物体a 、b ,在水平力作用下共同向右做匀加速运动,如图2-1-9所示,在水平面上时,力为F 1,弹簧长为L 1,在斜面上时,力为F 2,弹簧长为L 2,已知a 、b 两物体与接触面间的动摩擦因数相同,则轻弹簧的原长为( ).图2-1-9A.L 1+L 22B.F 1L 1-F 2L 2F 2-F 1C.F 2L 1-F 1L 2F 2-F 1 D.F 2L 1+F 1L 2F 2+F 1解析 设物体a 、b 的质量分别为m 1、m 2,与接触面间的动摩擦因数为μ,弹簧原长为L 0,在水平面上时,以整体为研究对象有F 1-μ(m 1+m 2)g =(m 1+m 2)a ,①隔离a 物体有k (L 1-L 0)-μm 1g =m 1a ,② 联立解得k (L 1-L 0)=m 1m 1+m 2F 1,③ 同理可得k (L 2-L 0)=m 1m 1+m 2F 2,④ 联立③④可得轻弹簧的原长为L 0=F 2L 1-F 1L 2F 2-F 1,C 对.答案 C反思总结 如何理解理想化模型——“轻弹簧”与“橡皮筋” (1)弹簧与橡皮筋产生的弹力遵循胡克定律F =kx ,x 是指形变量.(2)“轻”即指弹簧(或橡皮筋)的重力不计,所以同一弹簧的两端及中间各点的弹力大小相等. (3)弹簧既能受拉力,也能受压力(沿弹簧轴线),分析弹簧问题时一定要特别注意这一点,而橡皮筋只能受拉力作用.(4)弹簧和橡皮筋中的弹力均不能突变,但当将弹簧(或橡皮筋)剪断时,其弹力立即消失.即学即练 (2013·石家庄质检,18)如图2-1-10所示,一个“Y”形弹弓顶部跨度为L ,两根相同的橡皮条自由长度均为L ,在两橡皮条的末端用一块软羊皮(长度不计)做成裹片.若橡皮条的弹力与形变量的关系满足胡克定律,且劲度系数为k ,发射弹丸时每根橡皮条的最大长度为2L (弹性限度内),则发射过程中裹片对弹丸的最大作用力为( ).图2-1-10A .kLB .2kL C.32kL D.152kL 解析 对裹片受力分析,由相似三角形可得:kL2L=F2?2L ?2-⎝⎛⎭⎫L 22得:F =152kL 则裹片对弹丸的最大作用力为F 丸=F =152kL ,故选项D 正确. 答案 D附:对应高考题组(PPT 课件文本,见教师用书)1.(2010·新课标全国卷,15)一根轻质弹簧一端固定,用大小为F 1的力压弹簧的另一端,平衡时长度为l 1;改用大小为F 2的力拉弹簧,平衡时长度为l 2.弹簧的拉伸或压缩均在弹性限度内,该弹簧的劲度系数为( ).A.F 2-F 1l 2-l 1B.F 2+F 1l 2+l 1 C.F 2+F 1l 2-l 1 D.F 2-F 1l 2+l 1解析 设弹簧原长为l ,由题意知,F 1=k (l -l 1),F 2=k (l 2-l ),两式联立,得k =F 2+F 1l 2-l 1,选项C 正确. 答案 C2.(2011·山东卷,19)如图所示,将两相同的木块a 、b 置于粗糙的水平地面上,中间用一轻弹簧连接,两侧用细绳系于墙壁.开始时a、b均静止,弹簧处于伸长状态,两细绳均有拉力,a所受摩擦力F f a≠0,b所受摩擦力F f b=0.现将右侧细绳剪断,则剪断瞬间( ).A.F f a大小不变B.F f a方向改变C.F f b仍然为零D.F f b方向向右解析剪断右侧绳的瞬间,右侧细绳上拉力突变为零,而弹簧对两木块的拉力没有发生突变,与原来一样,所以b对地面有向左的运动趋势,受到静摩擦力F f b方向向右,C错误,D正确.剪断右侧绳的瞬间,木块a受到的各力都没有发生变化,A正确,B错误.答案AD3.(2012·山东基本能力,85)力是物体间的相互作用,下列有关力的图示及表述正确的是( ).解析由于在不同纬度处重力加速度g不同,旅客所受重力不同,故对飞机的压力不同,A错误.充足气的篮球平衡时,篮球壳对内部气体有压力作用,即内外气体对篮球壳压力的差值等于篮球壳对内部气体的压力,故B正确.书对桌子的压力作用在桌子上,箭尾应位于桌面上,故C错误.平地上匀速行驶的汽车,其主动轮受到地面的摩擦力是其前进的动力,地面对其从动轮的摩擦力是阻力,汽车受到的动力与阻力平衡时才能匀速前进,故D正确.答案BD。
怎样区别轻绳、轻杆、轻弹簧

一、三种模型的相同点
(1)轻绳、轻杆和轻弹簧的“轻”,指的是质量可 )轻绳、轻杆和轻弹簧的“ 以忽略,重力不计. 以忽略,重力不计 (2)他们对物体的作用力都是弹力,属于接触力、 )他们对物体的作用力都是弹力,属于接触力、 被动力。 被动力。 (3)各处的受力一般认为相同 )各处的受力一般认为相同. (4)都可以连接物体。 )都可以连接物体。
A、由位置A到位置 重力做功为 、由位置 到位置 重力做功为mgh, 到位置B重力做功为 C、由位置A到位置 小球克服弹力做功为 、由位置 到位置 小球克服弹力做功为mgh 到位置B小球克服弹力做功为
1 B、由位置 到位置 重力势能减少 mv2 到位置B重力势能减少 、由位置A到位置 2
1 D、小球到达位置 时弹簧的弹性势能为 时弹簧的弹性势能为mgh、小球到达位置B时弹簧的弹性势能为 2 mv2
(2)轻绳弹力的方向总是指向绳收缩的方向;轻杆弹力 )轻绳弹力的方向总是指向绳收缩的方向; 的方向由运动状态决定; 的方向由运动状态决定;轻弹簧弹力的方向总是沿 弹簧指向反抗形变的方向。 弹簧指向反抗形变的方向。 所示, 例3、如图 所示,小车顶端悬挂 、如图3所示 一个小球,当小车以加速度a做 一个小球,当小车以加速度 做 匀变速运动时, 匀变速运动时,悬线与竖直方 向成某一固定角θ, 向成某一固定角 ,若小球质量 为m,求悬线对小球的拉力。 ,求悬线对小球的拉力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
轻绳、轻杆、轻弹簧三种模型之比较轻绳、轻杆、轻弹簧作为中学物理最常见的三种典型的理想化力学模型, 在各类题目中都会出现,有必要将它们的特点归类,供同学们学习时参考。
.轻绳(或细绳)中学物理中的绳和线,是理想化的模型,具有以下几个特征:(1)轻:即绳(或线)的质量或重力可以视为等于零。
由此特点可知,同一根绳(或线)的两端及其中间各点的张力大小相等;例1.如图1所示,PQ 是固定的水平导轨,两端 小定滑轮,物体A 、B 用轻绳连结,绕过定滑轮, 轮的摩擦,系统处于静止时,a =37°,片53°,10N,A 重20N, A 与水平导轨间摩擦因数=0.2 ,的摩擦力()A •大小为4N ,方向向左B •大小为4N ,方向向右C .大小为2N ,方向向左D .大小为2N解析:要分析A 物体所受摩擦力,必须确定两绳子 的拉力情况。
因为两绳均为轻绳,且滑轮摩擦不计, 绳子两端及其中间各点的张力大小相等,只要对 B 受力分析即可知道绳子拉力大小情况。
如图2所示,B 受重力、两绳拉力F ,、F 2而平衡, 的平衡知识即平行四边形法则可知:F ,=G B S in : =6N , F ,=G B cos 〉=8N 。
再以 A 物体为研 象 ,如图可知,A 物体所受摩擦力为f =F 2 -F^8N -6N =2N ,方向向左。
本题 C 选项符合题意。
(2)软:即绳(或线)只能受拉力,不能承受压力。
由此特点可知:绳(或线)与其他物体的相 互间作用力的方向总是沿着绳子。
注意轻绳“拉紧”和“伸直”的区别:“拉紧”的轻绳,一定而“伸直”的轻绳,还没有发生形变,没有张力。
例2■物体A 质量为m ,用两根轻绳B 、C 连接到墙上,在物体 一个力F ,如图所示,二=60,要使两绳都能伸直,求 小范围。
解析:我们先假设拉力F 较小,则绳C 将松弛,绳B 将有两个 不计滑 若B 重 则A 受因此 物体由力究对 拉紧,因有张力,A 上施加力F 的大图此,拉力F 的最小值F min ,出现在绳C 恰好伸直无弹力,而绳B 张紧时。
此时A 球的受力分析如 图4所示,F B 为绳B 的拉力。
由力的正交分解,有:水平方向: F min COST = F B COS V ,竖直方向: F min sinv+F B sinr 二mg再假设拉力F 较大,则绳B 将松弛,绳C 将拉紧,拉力F 的最大值F max ,出现在绳B 恰好伸 直无弹力,而绳C 张紧时。
此时A 球的受力分析如图5所示,F c 为绳C 的拉力。
由力的正交分解, (3)轻绳伸长不计:即无论轻绳(或线)所受拉力多大,绳子(或线)的形变量忽略不计,认为 轻绳长度不变。
由此特点可知,绳(或线)中的张力可以突变。
-——w u/例3.如图6所示,一质量为m 的物体系于长度分别为L i 、 上, L i 的一端悬挂在天花板上,与竖直方向夹角为9, L 2水于平衡状态。
现将L 2线剪断,求剪断瞬间物体的加速度。
下面是某同学对该题的一种解法: 分析与解:设L i 线上拉力为T i ,L 2线上拉力为T 2。
重力为 作用下保持平衡,有:T i cos 4mg ,T i sin &T 2,T 2 = mgtan 9剪断线的瞬间,T 2突然消失,物体即在T 2反方向获得加速度。
因为 mgtama ,所以加速度 a = gtan 0方向与T 2方向相反。
你认为这个结果正确吗?请对该解法作出评价并说明理由。
解得: F minmg 2sin vf mg在竖直方向有: F max Sin 二二mg解得: F maxmg sin v因此,要使两绳都能伸直,求力F 的大小范围为 fmg 汗23:: ----- mg 。
L 2的两根细线mg ,物体在三力平拉直,物体处图6精心整理解析:该同学做法是错误的。
因为 L 2被剪断前,L i 、L 2 小T i 、T 2满足T i cos 4mg , T i sin 丰T 2,可解得 T 1= mg , T 2= mgtan Q cos 6 后, T 2瞬间突变为零,而此时,T i 也将发生突变。
如图7细线瞬间,物体只受重力与细线 L i 的拉力T/的作用,由 伸长,因此沿L i 方向物体加速度为零,垂直于 L i 方向物 度,因此将物体重力分解为沿 L i 方向和垂直于L i 方向的沿L i 方向物体加速度为零,有:T )=mgcos^ 沿垂直于细线方向(切线方向)有:mgsinv = ma ,a=gsinr ,与细线垂直斜向右下方。
可见,剪断L 2瞬间,L i 上的张力由「=-mg-突变为T ,=mgcosr ,物体加速度为a=gs inn 。
cos 6二•轻杆具有以下几个特征:1 z-_ i 、 /(1) 轻:即轻杆的质量和重力可以视为等于零。
由此特点可知,同一轻杆的两端及其中间各点的 张力大小相等;例4.如图8所示,A 、B 两物体用水平杆C 相连,置于水平地面上,已知 m A = m B = 4kg ,上的张力大剪断细线 所示,剪断 于L i 不可 体具有加速 两个分力。
A 、B 与水平地面的动摩擦因数均为 J =0.i 。
现用F=20N 的水平恒力作用在A 物体上,(i )若杆为轻杆,求杆对 A 、B 作用力的 大小 (2) 若杆的质量m C = 2kg ,求杆对A 、B 作用力的大小 解析:(i)对A 、B 及杆整体分析,由牛顿 第二定律,有:解得:a _F 二艸mA+m B )g = 20_0■仆(4+4)"0(m A m B )m s 2 =i.5m s 2隔离A ,设杆对A 拉力为F A ,如图9所示。
由牛顿第二定律:F - F A - 'm A g 二m A a 77777777777图9解得:F A "ON隔离B ,设杆对B 拉力为F B ,如图i0所示由牛顿第二定律:F B - "m B g =m B a —B —I77777777777解得:F B =i0N图i0由此可见,轻杆两端张力大小相同。
这是因为,轻杆质量为零,如果两端张力的合力不为零, 轻杆加速度将无穷大,这是不可能出现的。
(2)若杆的质量m C = 2kg,同样对整体应用牛顿第二定律:隔离A,设杆对A拉力为F A ,由牛顿第二定律:F - F A -」m A g = m A a解得:F A:〉12N隔离B,设杆对B拉力为F B ,由牛顿第二定律:F B"-\m3g =m B a・解得:F B HON由此可见,F/-F A '当杆的质量不为零时,在一个运动系统中,杆两端的张力大小不一定相等。
(2)硬:轻杆不能伸长或压缩。
轻杆既能承受拉力也能承受压力,①对于可以绕一端自由转动的轻杆,其另一端受力一定沿杆方向;②对于一端固定不能转动的轻杆,其另一端受力方向不一定沿着杆的方向;例5.如图11所示,轻杆HG —端用铰链固定在竖直墙上,杆与墙的另一端通过轻质细绳EG拉住,EG与墙的夹角为60°,轻杆的拉住一质量为m的物体A。
试求轻杆对G点的弹力的大小和解析:由于HG是轻杆,且H 端为绕铰链,因此杆的G点受到一定沿杆方向。
现对G点受力分析,如图12所示,杆对G点斜上上。
由共点力的平衡,可知F =mgcos&= —mg。
方向沿2例6.如图13所示,小车上固定一弯折硬杆ABC,C端固定质球,已知:=30恒定。
当小车水平向左以v=0.5ms的速度匀速杆对小球的作用力的大小是,方向是;当小车水平向左以a=g的加速度作匀加速运动时,BC杆对小球的作用力的大小是,方向是。
图12 夹角为30°。
点用细绳GF方向。
杆的作用力的弹力沿杆杆斜向上。
量为m的小运动时,BCEG图11(1)当小车水平向左以v=0.5m s 的速度匀速运动时,由平衡条件,细杆对小球的力必定与重力等大反向,如图14所示。
此时杆的弹力并不沿杆方向(2)当小车水平向左以a=g 的加速度作匀加速运动时,小球所受合力F 合=mg 沿水平方向,则小球 受细杆的弹力F = :2mg ,与水平方向夹角为:=45,如图15所示。
此时杆的弹力也不沿杆方向。
3.轻弹簧中学物理中的轻弹簧,也是理想化的模型。
具有以下几个特征:(1)轻:即弹簧的质量和重力可以视为等于零。
由此特点可知,向一轻弹簧的两端及其中间各点 的张力大小相等;(2)弹簧既能承受拉力也能承受压力,其方向与弹簧的形变的方向相反;例7.如图16所示,质量为m 的质点,与三根相同的螺旋形轻弹 止时,弹簧c 沿竖直方向,相邻两弹簧间的夹角均为 120。
已知 质点的作用力大小均为F ,则弹簧c 对质点的作用力大小可能为B. F + mgC. F — mg解析:由于弹簧对小球施加的是推力还是拉力未知,因此分类讨论如下:(1)弹簧a 、b 对球是拉力,弹簧c 对球是推力,。
此时,a 、b 对球拉力的合力仍为F ,方向竖直 向上,对球有F+F C 二mg ,因此F C = mg - F 。
D 选项正确。
(2) 弹簧a 、b 对球是拉力,弹簧c 对球也是拉力,有:F =F C +mg ,因此F C =F - mg , 选项C 正确13解析:对细杆来说,图14图15是坚硬的物体,可以产生与杆垂直的横向的力,也可以产生与杆任何夹角的弹D . mg — F图16簧相连.静 弹簧a b 对 ()(3)弹簧a、b对球是推力,弹簧c对球也是推力,有:F+mg =F C,选项B正确。
(4) 弹簧a 、b 对球是推力,弹簧c 对球是拉力或处于原长,此时小球不能平衡, (5) 弹簧a 、b 对球是拉力,弹簧c 处于,原长即满足F =mg ,此时F^ 0 0综上,本题正确选项为 BCD o(3)由于弹簧受力时,要发生形变需要一段时间,所以弹簧的弹力不能发生突变。
例8.若将上文例3图6中的细线L i 改为长度相同、质量不计的轻弹簧,如图件不变,求解的步骤和结果与例3中某同学的做法完全相 解析:这种情况下该同学做法是对的。
因为L 2被剪断 的长度来不及发生变化,其大小和方向都不变。
具体请参 做法。
作者联系方式: 姓名:刘坤'| |通信地址:上海市徐汇区番禺路 800弄22号西南高级中学,刘坤 邮编:200030你认为这个结果正确吗?请说明理由17所示,其他条同,即 a = gtan 0的瞬间,弹簧L 1 考例3中该同学9L 2图17。
