原子物理学第三次作业答案 (7)
原子物理学第三次作业答案 (6)

第五章 磁场中的原子原子的磁矩:μJ =-e m e2g J J ,g J =)1(2)1()1()1(3++++-+J J S S L L J JμJ 和外场B 的作用能:∆E J, B =-μJ ∙ B =-B μJ ,z =g J m J B B μ应用1:施特恩-盖拉赫实验-角动量空间量子化的实验验证1,原理, 2, 装置,3, 结果,4, 意义 应用2:顺磁性:外磁场中原子磁矩规则排列后,原子蒸汽沿磁场方向在宏观上表现出来的磁性。
应用3:塞曼效应:发射原子光谱的光源放入磁场中后,光源的光谱线发生分裂的现象。
1,正常塞曼效应:在弱磁场中,一条光谱线分裂为三条的塞曼效应称为正常塞曼效应(单重态→单重态)。
2,反常塞曼效应: 在弱磁场中,非正常的三线分裂塞曼效应(多重态↔多重态)。
3,帕邢-贝克效应:强磁场中的塞曼效应:一条光谱线分裂为三条。
塞曼效应问题:知道原谱线的跃迁能级后,1),分裂能级:∆E J, B =g J m J B B μ,裂距:g J B B μ;2),分裂后的能级跃迁图;3)分裂后的谱线频率,偏振性质。
拉莫尔进动:原子的角动量(磁矩)在磁场中的运动方式进动角频率:ωL =γ B =e m e2 Bg J ;三种情况:A ,无外磁场时L ,S ,J 的进动;B ,(弱)外磁场B 中,L ,S ,的进动;C ,(强)外磁场B 中,L ,S 的进动。
分裂能级∆E J, B 不一。
有超精细结构时的塞曼能级分裂:情况1:在弱外磁场B 中, ∆E F ,B =-μF ∙ B =g F m F B B μ情况2,在强外磁场B 中,∆E j,I, B =-μj ∙ B -μI ∙ B + a · I ∙j ≈ m j g j B μ B + am j m I 磁共振-塞曼能级(磁能级)之间的直接跃迁磁偶极跃迁的选择定则:∆n = 0;∆l = 0;∆S = 0;∆J = ±1,0(J=0→ J=0除外);∆F = ±1,0。
原子物理学 课后答案

目录第一章原子的位形 (2)第二章原子的量子态:波尔模型 (8)第三章量子力学导论 (12)第四章原子的精细结构:电子的自旋....................... 错误!未定义书签。
第五章多电子原理:泡利原理 (23)第六章X射线 (28)第七章原子核物理概论.......................................... 错误!未定义书签。
1.本课程各章的重点难点重点:α粒子散射实验公式推导、原子能量级、氢原子的玻尔理论、原子的空间取向量子化、物质的波粒二象性、不确定原则、波函数及其物理意义和薛定谔方程、电子自旋轨道的相互作用、两个价电子的原子组态、能级分裂、泡利原理、电子组态的原子态的确定等。
难点:原子能级、电子组态、不确定原则、薛定谔方程、能级分裂、电子组态的原子态及基态的确定等。
2.本课程和其他课程的联系本课程需在高等数学、力学、电磁学、光学之后开设,同时又是理论物理课程中量子力学部分的前导课程,拟在第三学年第一学期开出。
3.本课程的基本要求及特点第一章原子的位形:卢瑟福模型了解原子的质量和大小、原子核式模型的提出;掌握粒子散射公式及其推导,理解α粒子散射实验对认识原子结构的作用;理解原子核式模型的实验验证及其物理意义。
第二章原子的量子态:玻尔模型掌握氢原子光谱规律及巴尔末公式;理解玻尔原子模型的基本假设、经典轨道、量子化条件、能量公式、主量子数、氢能级图;掌握用玻尔理论来解释氢原子及其光谱规律;了解伏兰克---赫兹实验的实验事实并掌握实验如何验证原子能级的量子化;理解索菲末量子化条件;了解碱金属光谱规律。
第三章量子力学导论掌握波粒二象性、德布罗意波的假设、波函数的统计诠释、不确定关系等概念、原理和关系式;理解定态薛定谔方程和氢原子薛定谔方程的解及n,l,m 三个量子数的意义及其重要性。
第四章 原子的精细结构:电子的自旋理解原子中电子轨道运动的磁矩、电子自旋的假设和电子自旋、电子量子态的 确定;了解史特恩—盖拉赫实验的实验事实并掌握实验如何验证角动量取向的量子化;理解碱金属原子光谱的精细结构;掌握电子自旋与轨道运动的相互作用;了解外磁场对原子的作用,理解史特恩—盖拉赫实验的结果、塞曼效应。
《原子物理学》作业参考答案

《原子物理学》作业参考答案一. 填空题1. 1010-m ;1510-m ;17103m kg2. )11(~222m nZ R A-=ν3. 21;53.0;51.14.3;6.13n a A eV eVeV --- 4. nm a eV 0177.03;4.541= 5. 单层;双层;自旋与轨道的相互作用 6. 2;3;4=j7. 12+l 8. 2121S ;2122S ;2323D ;2322P9. 原子的量子态 10. 相对论效应;自旋同轨道的相互作用。
11. j l n ,,12. 23=S ; 2;013. ),(211s s G ,),(212l l G > ),(113s l G ,),(224s l G ;),(211s s G ,),(212l l G < ),(113s l G ,),(224s l G 14. B B J g j j μμμ5353)1(;6=+= 15. 6;6 ;16. n 和l 相同的电子; 17. 32种 18. [1.51eV] 19.ph,h E 20. 6.626×10-34Js 21. 622. )exp(0x I I μ-=,随着X 光子的能量增加,吸收系数下降,吸收限,原子中电子壳层结构的实在性,导致的电子的电离23. 原子中量子态的存在,电子自旋的存在24. 一条谱线在外磁场下分为三且彼此间隔相等(间隔均为B B μ);总自旋角动量等于零()0=S 25. 高能光子与低能电子相碰撞,光子把一部分能量传递给电子从而变为低能光子,波长变长,频率变低 26. 轨道电子俘获、、-+ββ27. α+→--Y X A Z AZ 42 28. 能量和动量守恒29. 光电效应 30. 汤姆逊; 核式结构(或行星)模型 31. 氘)(D 32. 量子化的33. 康普顿效应;吴有训。
34. 液滴模型,费米气体模型,壳层模型, 集体模型35. 0.31nm 36. 电磁辐射与物质交换能量时是量子化的,即νh E = 二. 简答1. 卢瑟福的“核式结构”模型的意义、困难是什么?意义:第一,正确地提出了原子的“核式结构”将原子分为核外与核内两个部分。
原子物理学第三次作业答案 (7)精品文档29页

第一章 量子力学前的原子物理学§1.1 原子的外部和内部特性“原子”的原始慨念:组成物质的最基本单元 (最小,不可再分离:atom -希腊文)提出者:古希腊哲学家-德膜克利特(~B.C. 400) 古代中国人: 金,木,水,火,土 (五行说); 古代云南彝族: 铜,木,水,火,土。
问题:不可再分离?原子→电子、原子核;原子核→质子,中子;质子,中子 基本粒子(中微子、光子、介子、超子,…); 基本粒子夸克弦,…说明:人们对“最基本单元”的认识是无止境的。
意义: 闪烁着人类认识世界的哲学光芒,但是,不具备科学的“实证”特征。
“实证”(有实验证据):多大?多重?内部结构特性?1.1.1 原子的外部特性19世纪初:掌握了原子的外部特性:多大?多重? (i) 摩尔(Mol )定义(1971年国际计量会议):一个系统物质的数量,该系统中包含的基本单元数与0.012 kg C 126的原子数相同。
说明: 1,“基本单元”可以是原子、分子或带电粒子等;2,0.012 kg C 126的原子数=6.022×1023, 或N A (阿伏伽德罗常数)=6.022×1023/Mol 。
(ii) 原子的相对质量(原子量,A )定义(1971年国际计量会议):1摩尔某种物质的质量[M(A)]和1摩尔C 126的质量[M(C 126)]的1/12的比值,是这种物质的原子量(A )。
(iii) 原子的绝对质量(原子质量,m A ) 已知: N A ,A按定义:A=M(A)/[M(C 126)/12], M(A)= A M(C 126)/12= A (g )则: m A =A (g )/ N A =A ×1.661×10-24(g )=A ×1.661×10-27(kg ) 例:C 126,A =12.0000, 一个C 126原子的重量:12×1.661×10-27(kg)=19.93×10-27(kg);H 11, A =1.0078,一个H 11原子的重量:1.0078×1.661×10-27(kg)=1.674×10-27(kg);(vi )原子的尺寸已知: N A ,A ,(g/cm 3);则:一个摩尔的原子所占的体积:V mol =A(g)/;另一方面,设r A 为原子半径,一个原子的体积(球体)=(4r A 3/3);一个摩尔的原子所占的体积:V mol =N A (4r A 3/3)所以,r A = (3A/4 N A )1/3 ~10-8cm 10-10 m=1 A例:H (H 11) , A =1.0078, =0.09(g/cm 3)r H ~1.6×10-8 (cm) =1.6 A量子力学计算值: r H =a =0.53 A1.1.2 原子的内部特性19世纪末-20世纪初:基本掌握了原子的内部特性:原子由带正电的原子核和带负电的电子组成,整体呈电中型;电子绕着原子核做圆周运动。
原子物理学第七章习题解答

原子物理学第七章习题解答第七章习题解答7-1 试计算核素40Ca 和56Fe 的结合能和比结合能。
解:402020Ca结合能 22(2020)p n ca E mc m m m c ?=?=+-[]220(1.008665 1.007277)39.96259c =+-(40.3188439.96259)931.5mev =-?331.85mev =比结合能331.88.340E mev A ε?=== 562630Fe结合能: 2(2630)p n Fe B m m m c =+-0.51425931.5479.024mev =?=比结合能:479.0248.55456B mev A ε===7-2 1mg 238U 每分钟放出740个α 粒子,试证明:1g 238U 的放射性活度为0.33 Ci μ,238U 的半衰期为94.510a ?证明:1mg 238U 的放射性强度 A=74060可知1g 238U 的放射强度x 为: 374010:1:60x -= ∴x = 74060×310= 43.7103次/s =13Ci μ= 0.33Ci μ7-3 活着的有机体中,14C 对12C 的比与大气中是相同的,约为1.3×1210-,有机体死亡后,由于14C 的放射性衰变,14C 的含量就不断少,因此,测量每克碳的衰变率就可计算有机体的死亡时间。
现测得:取之于某一骸骨的100g 碳的β衰变率为300次衰变/min ,试问该骸骨已有多久历史?解:由于12C 的丰度高达98.89%,可以近似认为自然界的碳全部由12C 组成故1g 碳中,12C 的原子数目为:2322(12)11 6.0210 5.02101212A N N ==??=?个根据题意:1g 碳中,14C 的原子数目为:12122210(14)(12)1.3010 1.3010 5.0210 6.5310N N --=?==?个根据衰变率的定义(单位时间内发生的核衰变数),1g 碳中,14C 的衰变率,在t=0时为: 100(14)0.693 6.531057303652460A N λ== 150=次衰变/Min由题知t 时刻测得的衰变率为(1g 14C 在t 时刻的衰变率) 3003.00100A ==次衰变/Min 因放射性强度服从指数衰变规律 1/20.69300t T t A A e A e λ--== ∴41/20573015.0 1.3100.6930.693 3.00T A t In In y A ==?=?7-4 一个放射性元素的平均寿命为10d ,试问在第5d 内发生衰变的数目是原来的多少?解:放射性衰变规律为0N N = t e λ-。
原子物理学第三次作业答案 (9)

第三章 碱金属原子结构及光谱碱金属原子: Li, Na, K, Rb, Cs, Fr (周期表中I 族元素) 特点: 最外层只有一个电子, 内层形成“闭合壳层”(中学化学:原子中电子分层排列,每层排满2n 2个电子形成“闭合壳层”,第四章介绍)。
只考虑最外层的那一个电子和“闭合壳层+原子核=原子实”的作用。
§3.1 能级和光谱---最外层电子和原子实作用形成 3.1.1 能级和能级图(玻尔理论为基础的维象理论) 1, 能级 对氢原子:E n = -2nhcR H , (和l, m 无关)对碱金属原子,和最外层电子的状态有关: E n = E n,l = - 2)(l n Rhcδ-。
(1)Note : (i) R = R ∞ →R H ; (n -δl )→ n ; δl (量子数亏损),和n , l 有关;(ii) E n 对l 的“简并”消除,E =E n,l 。
一个n , 对应l (0,1,2,3,…n -1)个E n,l 。
对: l = 0, 1, 2, 3, 4, …,描述的电子 表示: s, p, d, f, g, …, δl : δs , δp , δd , δf , δg ,…。
2, N a 原子(Z=11)的能级图 − 格罗春图 纵轴:E n,l / eV最右边一列:H (对比, 只和n 有关); 第一列 (S 能级): s 电子; n =3,4,5,…,(无 n =1,2, Why ?:2n 2) 。
第四列 (F 能级):f 电子; n =4,5,6,…,(无 n =3,2,1 , Why ?: l max = n-1 ) 问题:Li 、K 、。
能级图特点? 3.1.2 光谱和能级跃迁规律- Na 原子为例 仅存在: ∆ l =±1 (2-67)的跃迁,由此构成四个主要线系。
1, 锐线系(nS →3P, n =4,5,6,…, ) ∆ l =-1nS 能级能量: E n,s = - 2)(s n Rhc δ-; 3P 能级能量:E 3,p = - 2)3(p Rhcδ- ;nS →3P 的波数:由, E n,s - E 3,p = h ν=hc/λ= hc σσ = 2)3(p Rδ--2)(s n Rδ- (2)2, 主线系(nP →3S, n =3,4,5,…, ) ∆ l =1σ = 2)3(s Rδ--2)(p n Rδ- (3)3, 漫线系(nD →3P, n =3,4,5,…, ) ∆ l =1σ = 2)3(p Rδ--2)(d n Rδ- (4)4, 柏格曼线系(nF →3D, n =4,5,6,…, ) ∆ l =1σ = 2)3(d Rδ--2)(f n Rδ- (5)问题:Li 、K 、。
原子物理学第三章题解

m=
p=
p=
1 1 1 E 2 − m02 c4 = ( Ek + m0 c2 )2 − m02 c4 = c c c
kh da
课 后
λ= λc = h hc hc = = m0c m0c 2 E 0 hc E0 hc
( E 2 − E 20 )
1 1 1 E 2 − m02 c4 = ( Ek + m0 c 2 ) 2 − m0 2 c 4 = Ek ( Ek + 2m0 c 2 ) c c c
整理后得:
答 案
(4)
w.
8
网
x>a ,
V ( x) = V0
薛定 谔 方 程 为 :
则 (6) 式 可 改 为 : uctgu = −v
w.
u 和 v 还必须满足下列关系式: (8)
2b
为: N
2
∫e
0
−2
2a
dx ∫ e
−∞
−2
dy ∫ e
−∞
+∞
−2
z
2c
dz
ww
= N 2 4abc − (e −1 − 1) =
(3) 粒子的
−2
[
]
1 1 (1 − ) 2 e
+c −2Fra biblioteky ∈ (−b, b), z ∈ ( −c, c) 区域内的几率为:
y z
2c
N
2
∫
+∞
x
−∞
e
2a
dx∫ e
w.
λ=
掠射角(入射束与布喇格面之间的夹角)为 30°,试求这些热中子的能
nλ=d sinθ
ww
原子物理学第三次作业答案 (8)
第二章 量子力学初步为什么要学?量子力学已经从理论物理的一个分支学科,发展成为技术专家手中的一门有力的工具:纳米(10-9M )科学与技术, STM 和AFM ,…对物理专业的学生,导论和准备;对应用物理专业的学生,掌握量子力学的基本知识。
为什么在这时候学?在波尔与索末菲的旧量子理论中:问题1:L (轨道角动量数值)=n ϕℏ,L z (轨道角动量的方向)= m ℏ;即:定态条件,作为“规定”的量子化条件引入。
这种强制性“规定”不符合数学逻辑。
问题2:氢原子基态的电子空间分布: 波尔理论:n =1的“轨道”,r n =n 2a 1=a 1=0.53A ; 中学物理中的“电子云”。
孰是孰非?“电子云”概念是正确的,“轨道”概念是错误的。
正确的原子概念的建立,必须学习量子力学。
§2.1 光的波动粒子二象性(duality)光从何来? 圣经:上帝创造;玻尔,爱因斯坦:能级跃迁,。
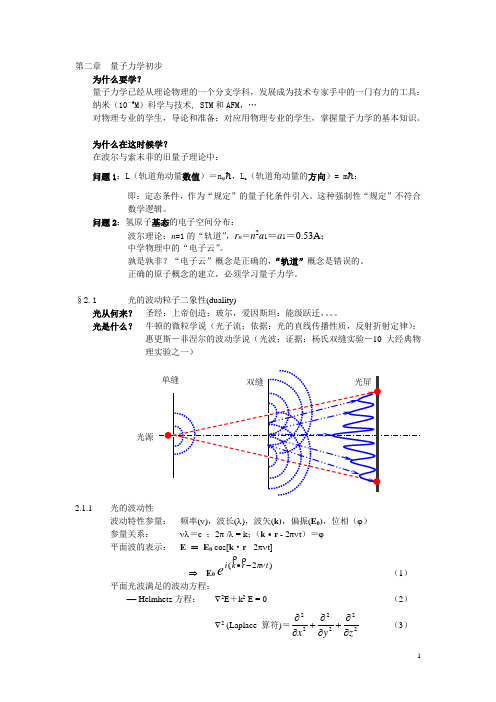
光是什么? 牛顿的微粒学说(光子流;依据:光的直线传播性质,反射折射定律);惠更斯-菲涅尔的波动学说(光波;证据:杨氏双缝实验-10大经典物理实验之一)2.1.1 光的波动性波动特性参量: 频率(ν),波长(λ),波矢(k),偏振(E 0),位相(ϕ) 参量关系: νλ=c ;2π /λ = k ;(k ·r - 2πνt )=ϕ 平面波的表示: E = E 0 cos[k ·r - 2πνt]⇒ E 0)2(t r k i eπν-∙(1)平面光波满足的波动方程:− Helmhetz 方程: ∇2E +k 2 E = 0 (2)∇2(Laplace 算符)=222222zy x ∂∂+∂∂+∂∂(3)光源2.1.2光的粒子性粒子特性参量:能量E ,动量p 。
粒子特性参量(E ,p )和波动特性参量(ν,λ)由Einstein 关系联系起来: E = h ν =hc / λ (4)p = h / λ = h ν / c = ℏk(5) p =ℏk = (h / λ) k 0 (k 0 :光传播的方向)(5')光子能量(4)式的实验证实:光电效应实验装置:结果:仅当入射光的频率 ν > νmin ,才有光电流(光电子)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章 量子力学前的原子物理学§1.1 原子的外部和内部特性“原子”的原始慨念:组成物质的最基本单元 (最小,不可再分离:atom -希腊文) 提出者:古希腊哲学家-德膜克利特(~B.C. 400)古代中国人: 金,木,水,火,土 (五行说); 古代云南彝族: 铜,木,水,火,土。
问题:不可再分离?原子→电子、原子核;原子核→质子,中子;质子,中子→ 基本粒子(中微子、光子、介子、超子,…); 基本粒子→夸克→弦,…说明:人们对“最基本单元”的认识是无止境的。
意义: 闪烁着人类认识世界的哲学光芒,但是,不具备科学的“实证”特征。
“实证”(有实验证据):多大?多重?内部结构特性? 1.1.1 原子的外部特性19世纪初:掌握了原子的外部特性:多大?多重? (i) 摩尔(Mol )定义(1971年国际计量会议):一个系统物质的数量,该系统中包含的基本单元数与0.012 kg C 126的原子数相同。
说明: 1,“基本单元”可以是原子、分子或带电粒子等;2,0.012 kgC 126的原子数=6.022×1023,或N A (阿伏伽德罗常数)=6.022×1023/Mol 。
(ii) 原子的相对质量(原子量,A )定义(1971年国际计量会议):1摩尔某种物质的质量[M(A)]和1摩尔C 126的质量[M(C 126)]的1/12的比值,是这种物质的原子量(A )。
(iii) 原子的绝对质量(原子质量,m A ) 已知: N A ,A按定义:A=M(A)/[M(C 126)/12], M(A)= A M(C 126)/12= A (g )则: m A =A (g )/ N A =A ×1.661×10-24(g )=A ×1.661×10-27(kg )例:C 126,A =12.0000,一个C 126原子的重量:12×1.661×10-27(kg)=19.93×10-27(kg);H 11, A =1.0078,一个H 11原子的重量:1.0078×1.661×10-27(kg)=1.674×10-27(kg);(vi )原子的尺寸已知: N A ,A ,ρ(g/cm 3); 则: 一个摩尔的原子所占的体积:V mol =A(g)/ρ;另一方面,设r A 为原子半径,一个原子的体积(球体)=(4πr A 3/3); 一个摩尔的原子所占的体积:V mol =N A (4πr A 3/3)所以,r A = (3A/4πρ N A )1/3 ~10-8cm ~ 10-10m=1 A例:H (H 11) , A =1.0078, ρ =0.09(g/cm 3)r H ~1.6×10-8 (cm) =1.6 A 量子力学计算值: r H =a =0.53 A 1.1.2 原子的内部特性19世纪末-20世纪初:基本掌握了原子的内部特性:原子由带正电的原子核和带负电的电子组成,整体呈电中型;电子绕着原子核做圆周运动。
做出如上认识的三个著名实验:(一) 汤姆逊(英国,Thomson ,1897)的阴极射线实验装置原图:轴线管壁发光(忽略“阴极射线”的重量)加偏转电场E 后,射线向上偏转:说明带负电,受力=qE加偏转磁场B 后,射线向下偏转:说明带负电,受力=qVB电场和磁场力平衡时,qE=qVB → V=E/B ;撤去电场,阴极射线受罗伦滋力作用,在磁场内做半径为R 的圆周运动;在磁场外做直线运动并偏离轴线。
由偏转角θ 测量出R ;由 mV 2/R=qVB → q/m=V/RB= E/RB 2结果: 1,阴极射线是一种带负电的粒子流; 2,求出了阴极射线的荷质比,此值和发出阴极射线的材料无关;3,Thomson 认为,阴极射线是一种比原子小的粒子(电子)流,阴极射线的荷质比就是电子的荷质比。
意义: 发现了电子,并由此发现获得1905年度的诺贝尔物理学奖。
问题: 物体带电量是否存在一个最小数值?q min= e (electron) = ?,(二)密里根(美国,Milikan, 1910)的油滴实验装置原图:装置原理图:基本思想:带电油滴在电场力QE和重力Mg作用下处于静止状态,Q=Mg/E;油滴带电量如果是某个最小电量q min = e的倍数,即:Q=N e(N为整数),则平衡电场E=Mg/Ne 应该是一系列分离的数值,反之亦然;由这些分离的数值可求出油滴的最小带电量q min,即电子电量e。
实验结果:1,油滴带电量确实是一系列分离数值,即,物体带电量是“量子化”的;2,物体带电量的最小值q min = e=1.6×10-19 C; m e=9.1*10-31 kg。
意义:从实验上证实了油滴带电量的“量子化”,测量出了电子电量。
密里根由此获得1915年度的诺贝尔物理学奖。
(三) 卢瑟福(新西兰,Rutherford,1909)的α粒子散射实验背景:1, 汤姆逊(剑桥大学卡文的许实验室主任)的“面包葡萄干”原子模型(西瓜子模型):在原子尺度r 0~10-10M 内,原子的正电部分均匀分布(面粉),电子就如葡萄干,崁嵌在正电核(面粉)中。
2, 卢瑟福是汤姆逊的研究生,熟悉“面包葡萄干”原子模型。
3, 1908年,卢瑟福由于对铀元素放射性的研究,获得诺贝尔化学奖。
发现铀放射性由三个部分组成:(1)α射线(H e 核:H e ++粒子流);(2)β射线(-e :电子流);(3)γ射线(电磁辐射:光子流)。
其中,α粒子的速度达C/10000, 是高能粒子,可以作为“炮弹”轰击并研究其他粒子。
卢瑟福设想1:如果“葡萄面包干”模型正确,α粒子被原子的散射只能是小角度的散射(θ小)。
(Why?)1, α粒子的动量大,电子对α粒子的动量无影响(-e: 无斥力;m e : M α/ m e ~4M p / m e =4×1836),只需考虑“面粉”的影响; 2, α粒子受力:20041)(r ZeQ r r F out απε=> (库仑定律);r r ZeQ r r F in 300041)(απε=<=(高斯定律)。
10-10M αF α装置原图:实验结果:发现大角度散射,甚至背向散射(θ=180o )的α粒子。
结果说明:汤姆逊的“葡萄面包干”原子模型是错误的。
卢瑟福设想2: 如果原子的正电部分集中于一个非常小的空间区域r n 中,r n << r 0,当r → r n ,2041r ZeQ F ααπε=将很大,可以解释α粒子的大角度散射和背向散射。
由实验结果结合的α粒子散射公式,可知这个“非常小的空间区域”的尺度r n ~10-14M ,在此区域内集中了原子的正电部分和绝大部分原子质量,Rutherford 将此区域称为“原子核”。
意义:发现原子核在此基础上,Rutherford 提出原子的核式模型:原子中,正电部分集中在 “原子核”中,电子绕核作圆周运动--原子的行星运动模型。
F n = F c ,即:α220241rZe r V m e e πε=。
“伽里略发现了宇宙,卢瑟福发现了原子!” 原子核式模型的困境:(1) 原子的不稳定性;根据经典电动力学,带电粒子做加速运动将向外辐射能量。
电子在动能耗尽后,将落入原子核中,导致原子的湮灭。
(2) 不能解释原子的线状光谱的特性。
按“核式模型”,电子的辐射频率f e =V e /2πr ;V e 的连续变化导致电子的辐射频率是连续的。
和实验观察不符合。
原子光谱和太阳光谱的比较困境意味着旧的理论体系出现了问题,新的理论体系即将诞生。
§1.2 玻尔(Bohr ,丹麦,1913)的氢原子理论 1.2.1 玻尔氢原子理论的三个要点(1) 定态假设:定态:原子中的一些特殊的状态,处于定态的原子,电子绕核做圆周运动而不辐射能量(解决原子的稳定问题);(2) 定态条件(量子化条件):氢原子的角动量必须满足:L =nh/2π=n ℏ (n>=1的整数);h (普朗克常数)=6.63×10-34(JS )(3)定态跃迁:原子从一个定态跃迁到另一个定态时,以光子形式辐射或吸收能量。
说明: A ,光子是爱因斯坦于1905为解释光电效应提出。
光子能量满足:E =h ν,式中,ν: 光波的频率;B ,辐射过程:E 2-E 1=h ν;吸收过程:E 1+ h ν=E 2;C ,定态↔非定态;非定态↔非定态的跃迁是不存在的。
1.2.2 由玻尔理论求定态能量和轨道半径 E n =?;r n =?(A) 电子绕核运动的向心力由核电荷(+e )和电子电荷(-e )间的库仑力提供;220241r e r V m e e πε=(1)⇒e k E(电子动能)=221e e V m =r e 204121πε; r =22041ee V m e πε (1,)E k (原子的动能)=pk E (氢核动能)+ek E (电子动能)~ek E (核不动!)E p (原子的势能)==-=⎰⎰∞∞-dr r e dr F rre 22041πεre 2041πε-;E(原子的总能)=E k +E p =re 204121πε-;(负值!)(2)(B) L(原子的角动量)=L e +L N ~L e (核不动!) =m e r 2ω=m e rV e (V e =r ω)=n ℏ (定态条件)(n>=1整数)(3)联立(1,),(2),(3)得:) E 2> E 1h ν= E 2-E 1E 1+h ν= E 2-222041)4(21n e m E e πε-==E n (定态能量是分离值) (4)22204em n r e πε==r n(定态轨道半径是分离值) (5)问题及作业:1,证明:在pk E (氢核动能)≠0(核在动!)的条件下,用μ=pe p e M m M m +(折合质量,M p : 质子质量)代替(4),(5)式中的m e ,可得氢原子的定态能量和轨道半径满足:222041)4(21n e E n πεμ-= (4,)r n =22204en μπε(5,)提示:氢核不动的条件下,才有E k (原子的动能)=E k (电子动能)。
但是,氢核不动是不合理的(因为有反作用力!)。
为计算E k (原子的动能)=E k (氢核动能)+E k (电子动能),以原子的不动点r c (质心)基点。
L(原子角动量)=I p ωN +I e ωe =M p r c 2ω+ m e (r-r c )2ω=r 2ωμ =n ℏ (定态条件);(ωN = ωe = ω: why?)(用质心公式:r c =pe e M m rm +)E k (原子的动能)=pk E +ek E =221NP V M +221e e V m =21μ(r ω)2(V p = r c ω; V e = (r-r c )ω) E p (原子的势能)= re 2041πε-=-μ(r ω)2,(由 220241r e r V M c p p πε=关系得到)-e m e2, 对类氢粒子(核外只有一个电子的带电粒子),如:H e (Z =2)一次电离后→H e +;L i(Z =3)二次电离后→ L i ++;B e (Z =4)三次电离后→ B e +++。
