工程光学第二章理想光学系统
合集下载
工程光学第二章
B
①平行于光轴的光线经理想光学系统后必通过像方焦点； 过物方焦点的光线经理想光学系统后必为平行于光轴的光线。 （焦点性质 ） ②任意方向的一束平行光经理想光学系统后必交于像方焦平面上点； 过物方焦平面上一点的光线经理想光学系统后必为一束平行光。 （焦面性质） ③过节点的光线方向不变。（节点性质） ④共轭光线在主面上的投射高度相等。（主面性质）
1 1.6745 1 1.6140
三片式照相物镜基点计算
（２）求系统的像方参数，沿正向光路从左到右追 迹一条平行于光轴的近轴光线， 初始参数取为： l1 (u1 0)
r1 26.67mm
h1 10 mm h 10 i1 1 (rad ) r1 26 .67
i1
l1
h1 10mm
三片式照相物镜基点计算
利用近轴光线计算公式逐面计算结果为：
l F l 67.4907mm, u 0.121869
则： f h1
tgu
10 82.055(mm) 0.121869
像方主点的位置：lH lF f 14.5644mm
B A y F H H F B y A
x
l
f
f
x l
y f l 高斯公式的垂轴放大率公式： y f l 注意：高斯公式中物方和像方截距的原点为各方主点。
二、解析法求像
当系统的物像方介质相同时有: 则高斯公式为:
1 1 1 l l f
f f
l1
h1 10mm
u 0.121869
H
lH lF f
F
lF l
f 82.055mm
三片式照相物镜基点计算
①平行于光轴的光线经理想光学系统后必通过像方焦点； 过物方焦点的光线经理想光学系统后必为平行于光轴的光线。 （焦点性质 ） ②任意方向的一束平行光经理想光学系统后必交于像方焦平面上点； 过物方焦平面上一点的光线经理想光学系统后必为一束平行光。 （焦面性质） ③过节点的光线方向不变。（节点性质） ④共轭光线在主面上的投射高度相等。（主面性质）
1 1.6745 1 1.6140
三片式照相物镜基点计算
（２）求系统的像方参数，沿正向光路从左到右追 迹一条平行于光轴的近轴光线， 初始参数取为： l1 (u1 0)
r1 26.67mm
h1 10 mm h 10 i1 1 (rad ) r1 26 .67
i1
l1
h1 10mm
三片式照相物镜基点计算
利用近轴光线计算公式逐面计算结果为：
l F l 67.4907mm, u 0.121869
则： f h1
tgu
10 82.055(mm) 0.121869
像方主点的位置：lH lF f 14.5644mm
B A y F H H F B y A
x
l
f
f
x l
y f l 高斯公式的垂轴放大率公式： y f l 注意：高斯公式中物方和像方截距的原点为各方主点。
二、解析法求像
当系统的物像方介质相同时有: 则高斯公式为:
1 1 1 l l f
f f
l1
h1 10mm
u 0.121869
H
lH lF f
F
lF l
f 82.055mm
三片式照相物镜基点计算
工程光学第二章
高斯公式
1 1 1 l l f
y l yl
牛顿与高斯公式的转换: x l f ......x l f
当系统确定时，f
可根据公式，改变 x(l) 可得到不同β， 或β按要求，可计算出相应的 x(l) .
例:有一理想光组,其焦距为 f f 75mm
其前方150mm处有一物高为20mm的物体,
求像的位置和大小.若要求 0.5x 问物体应位于何处?
解:
1)根据 1 1 1 l l f
Q Q' B y
A
F
H H'
F
A'
l 150mm
-y'
f 75mm
R
R'
-x
-f
f'
B' x'
l 150mm
-l
l 1 l
一个理想光学系统可以用其基点（面）来表示，而 不需考虑其具体结构如何。
O
B O2
O1 A
A'
O' B' O'2
M
图2-3 两对共轭面已知的情况
O
B
A
O3
O1 O2
O'
A'
B'
M
图2-4 一对共轭面及两对共轭点已知的情况
第二节 理想光学系统的基点和基面
一.焦点与焦平面
1.像方焦点与像方焦平面（对应 L＝－∞）
l x f 902.605mm
以O1为原点! 以H 为原点!
x f 8.2055mm l x f 90.2605mm
L=-∞ F'
第2章 理想光学系统
如果已知共轴光 学系统的一对主 平面和两个焦点 的位置，就能根 据它们找出物空 间任意物点的像！
理想光组可有任意多个折、反射球面或多个光组组成。 寻找理想光组的特征点、面——基点、基面，就可以代 表整个光组的光学特性，用以讨论成像规律。
※ 若 f ’ >0，为正光组（会聚光组） 若 f ’ <0，为负光组（发散光组）
B
F
H
B H
F
•
•
节点就是主轴上角 放大率正1（=+1） 的物像共轭点。 通过节点的光线方 向不变。
H
H
P
u
P
A
• •• •M M
K K
A
u
•
若：光学系统在空气中(光学系统两边介质 相同)， 由亥姆霍兹—拉格朗日定理可知 当 =1 时， =1 。
因此：这时两节点分别与两主点重合。
• 总能找到：在像方折射光 线中一定有一条光线与入 P 射光线平行,即u = u 。 • 根据主平面的性质，存在一对共轭点M、M' • 即入射光线PAM与出射光线M'B'F'平行，并且共轭。 （过M点只有一条光线平行于光束。）
A
M
• • M K
u
F
• 节点：这两条光线的延长线与光轴的交点K和 K'，分别称为物方节点和像方节点。
B A’ 2F ’ F’ H
H’
F
A 2F
B’
作图题都要写出作图步骤
第三节:理想光学系统的物像关系 3.解析法求像： x—以物方焦点 为原点的物距。 称为焦物距。 以F为起始点， x 方向与光线方向 一致为正。（图 中为-）
11
三、基点、基面的概念
工程光学习题参考答案第二章理想光学系统
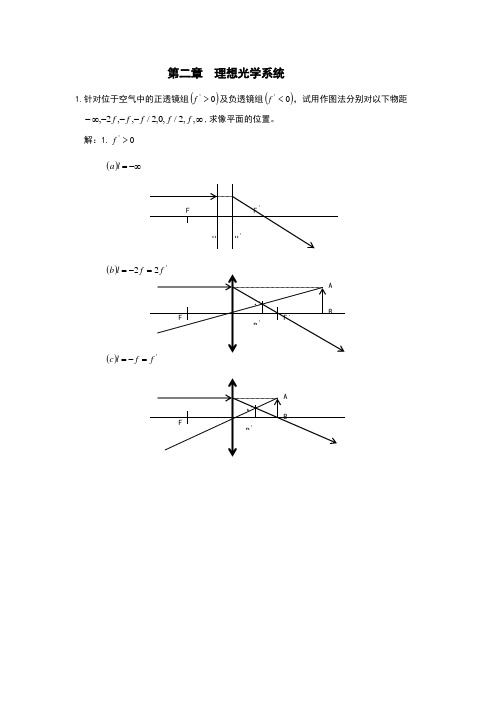
第二章 理想光学系统1.针对位于空气中的正透镜组()0'>f 及负透镜组()0'<f ，试用作图法分别对以下物距 ∞---∞-,,2/,0,2/,,2,f f f f f ,求像平面的位置。
解：1.0'>f ()-∞=l a()'2f l b -=()f f l c =-=()/f l d -=()0=l e()/f l f =')(f f l g -=='22)(f f l h -==+∞=l i )(2.0'<f -∞=l a )(l b )(=l c =)(/)(f l d -=0 el(=)f=l2/ (f)()fg=l(=h)ll i)(+∞=2. 已知照相物镜的焦距f’＝75mm,被摄景物位于（以F 点为坐标原点）=x ,2,4,6,8,10,m m m m m -----∝-处，试求照相底片应分别放在离物镜的像方焦面多远的地方。
解： （1）x= -∝ ，xx ′=ff ′ 得到：x ′=0 （2）x ′= （3）x ′= （4）x ′= （5）x ′=（6）x ′=3.设一系统位于空气中，垂轴放大率*-=10β，由物面到像面的距离（共轭距离）为7200mm ， 物镜两焦点间距离为1140mm 。
求该物镜焦距，并绘出基点位置图。
解:∵ 系统位于空气中，f f -='10''-===ll y y β 由已知条件：1140)('=+-+x f f7200)('=+-+x l l解得：mm f 600'= mm x 60-=4.已知一个透镜把物体放大*-3投影到屏幕上，当透镜向物体移近18mm 时，物体将被放大*-4，试求透镜的焦距，并用图解法校核之。
解：方法一：31'11-==l l β ⇒ ()183321'1--=-=l l l ①42'22-==l l β ⇒ 2'24l l -= ② 1821+-=-l l ⇒ 1821-=l l ③ '/1/1/11'1f l l =-'/1/1/12'2f l l =-将①②③代入④中得 mm l 2702-= mm l 1080'2-= ∴ mm f 216'=方法二： 311-=-=x fβ 422-=-=x fβ ⇒ mm f 216-= 1812=-x x方法三： 12)4)(3(21''=--==∆∆=ββαnn x x2161812'-=⨯=∆x''fx -=β143''''2'121=+-=∆=+-=-∴fx fx x ββ mm x f 216''=∆=∴5.一个薄透镜对某一物体成实像，放大率为⨯-1,今以另一个薄透镜紧贴在第一个透镜上，则见像向透镜方向移动，放大率为原先的3/4倍，求两块透镜的焦距为多少 解：⇒ 2'21'1/1/1/1/1l l l l -=- ④6.有一正薄透镜对某一物成倒立的实像，像高为物高的一半，今将物面向物体移近100mm ， 则所得像与物同大小，求该正透镜组的焦距。
工程光学课件第02章
第一节 理想光学系统与共线成像理论
理想光学系统理论是在1841年由高斯提出来的，所以理想 光学系统理论又被称为“高斯光学”。 理想光学系统中，任何一个物点发出的光线在系统的作用 下所有的出射光线仍然相交于一点。每个物点对应于唯一的 一个像点，这种物像对应关系叫做“共轭”。
物空间 像空间 点 直线 平面 共轭
F'：像方焦点，过F'垂直于光轴的平面为像方焦平面， 这个焦平面是与无限远处垂直于光轴的物平面共轭的 像平面。
第二节 理想光学系统的基点与基面
H'：像方主点，过H'垂直于 光轴的平面为像方主平面。
从像方主点H'到像方焦点 的距离为像方焦距f' 无限远轴外物点发出一束 平行光线，通过光学系统 后交于像方焦平面上一点。
A
F
H
H′ F′
A A′
H
H′ F′
A′
F
A F
H
H′ F′
A A′ F
H
H′ F′
A′
第三节
理想光学系统的物像关系
（三）轴上点经过两个光组的图解法求像
第三节
练习：作图求像
A
理想光学系统的物像关系
A
H′ H F H′ F′
A′
H
F′
A′
F
A′ A
H
H′ F′
A A′
F F′ H H′ F
第三节
理想光学系统的物像关系
用作图法求以下双光组等效系统的基点、基面
F1
H1
H1’ F1’ F2 H2
F2’ H2’
d Q H F Q’
F1
H1
H1’ F1’ F2 H2
F2’ H2’
理想光学系统
第三节 理想光学系统的物像关系
几何光学的基本内容之一是求像，即对于确定的 光学系统，给定物体的位置、大小、方向，求像的位 置、大小、正倒及虚实。常用的用以求取物象位置关 系的方法有二种：一为图解法，一为解析法。 一、图解法求像
图解法求像的定义
已知一个光学系统的主点(主面)和焦点的位置， 利用光线通过这些基点后表现的性质，对物空间给 定的点、线和面，通过画图追踪典型光线的方法求 像。
工程光学
石家庄铁道大学
机械工程学院
总第三讲
第二章 理想光学系统
Perfect Optical System
光学系统的具体结构（r、d、n） 实际光学系统与高斯（近轴）光学系统 研究光学系统成像的目的在于将高斯光学 完善成像的理论推广到任意大的空间，本 章的主要内容即介绍建立在高斯光学之上 的所谓理想光学系统，并研究理想光学系 统的主要光学参数、成像关系、放大率以 及光组组合和透镜。
可选择的典型光线和可利用的性质： ①平行于光轴入射的光线，经系统后过像方焦点； ②过物方焦点的光线，经过系统后平行于光轴； ③倾斜于光轴入射的平行光束经过系统后会交于像 方焦平面上的一点； ④自物方焦平面上一点发出的光束经系统后成倾斜 于光轴的平行光束； ⑤共轭光线在主面上的投射高度相等。 欲在理想光学系统条件下确定像点位置，只需 求出其对应物点发出的两条特定光线在像空间的共 轭光线，其交点即为所求像点。
总第三讲
３、主点与主平面
Q
Q'
h
f
'
h tanU '
F
U
H
H'
U
'
h'
F'
f
h tan U
工程光学 第二章 理想光学系统
第二节 理想光学系统的基点和基面 2、理想光学系统的像方参数
定义：像方焦点、焦平面；像方主点、主平面；像方焦距
A h B E’ Q’ H’
U’
f’
F’
像方焦距f’：从像方主点H’到像方焦点F’之间的距离。
其符号遵从符号法则，像方焦距f’的起算原点是像方主点H’ 。
光线AB的投射高度为h，出射光线的孔径角为U’。
即在垂直于光轴的同一平面内，物体的各部分具有相同 的放大率β。
正因如此，在讨论共轴系统的成像性质时，总是取垂直于光 轴的物平面和像平面。
二、共轴理想光学系统的成像性质
3、利用已知的共轭点/面求物像关系
（1）已知两对共轭面的位置和放大率：
O O1
A
O2
B
O1' O' A '
B'
O2'
★ 利用光轴上的已知共轭点；
第三节
理想光学系统的物像关系
1 ①焦点间隔或光学间隔 ：第一光组的像方焦点F1’到第二光组物 方焦点F2的距离。 符号规定：以前一光组的像方焦点为原点， 若它到下一光组物方焦点的方向与光线方向 相同，则为正；反之为负。
第三节 理想光学系统的物像关系
②过渡关系式：
③光学间隔与主面间隔之间的关系：
依据：理想的成像情况下，从一点发出的一 束光线 经光学系统作用后仍交于一点。
2、典型光线及性质（5条） a、平行于光轴入射的光线， 经过系统后过像方焦点;
b、过物方焦点的光线，
经过系统后平行于光轴；
焦点 定义
c、倾斜于光轴入射的平行光束， 经过系统后会交于像方焦平面上的一点；
d、自物方焦平面上一点发出的光束，
牛顿公式：
工程光学第二章+2012
20
2.2 理想光学系统的基点与基面 二、无限远轴上物点对应的物点F
物方焦平面上任意一点发出的光线通过理想光学系统后， 也是相互平行的光线，它们与光轴的夹角大小反应了轴外 物点的离轴距离。
三、物方主平面与像方主平面间的关系
作一投射高度为 h 且平行 于光轴的入射线，出射光 线必经过像方焦点；过物 方焦点作一入射线，使其 出射光线的投射高度也是h。 这样，两条入射光线都经过Q点，相应的两条出射光线都经 过Q’点。所以，Q与Q’点是一对共轭点，物方主平面QH与像 方主平面Q’H’是一对共轭面。
l ' 67.4907 mm, u ' 0.121869
由所以，l’F=67.4907，即系统的像方焦点在系统最后一个折射 面右边67.4907mm处。系统的像方焦距为
f ' 10 0.121869 82.055mm
27 Engineering Optics
2.2 理想光学系统的基点与基面 四、实际光学系统的基点和焦距的计算
28
Engineering Optics
2.2 理想光学系统的基点与基面 四、实际光学系统的基点和焦距的计算
（3）求物方焦距f、物方焦点F、物方主点H
' ' ' f 、 l 和 l 再作上述光路追迹，求得相应的 F' H ' 将其值反号即
得该系统的物方焦距f、物方焦点位置lF和物方主点位置lH。
（二）像方焦点、焦平面；像方主点、主平面；像方焦距 AB 是一条平行于光轴的入 射光线，它通过理想光学 系统后，出射光线E’F’交 光轴于F’，F ’ 就是无限远 轴上物点的像点，称像方 焦点。过F ’ 点作垂直于光 轴的平面，称为像方焦平 面。它是无限远处垂直ຫໍສະໝຸດ 于光轴的物平面的共轭 像平面。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
二、共轴理想光学系统的成像性质
性质1：位于光轴上物点的共轭像点必然在光轴上；过光轴的 任意截面成像性质相同。 由此得到：
（1）可用一个过光轴的截面来代表一个共轴系统； （过光轴的截面一般称为子午面）
（2）垂直于光轴的物平面，其共轭像面必然垂直于光轴；
性质2：垂直于光轴的平面物与其共轭平面像必然是几何相似， 具有相同的放大率
第二节 理想光学系统的基点和基面
一、无限远的轴上物点和它对应的像点F′
内容提要：先讨论无限远物体轴上物点发出的光线 通过光学系统的特征→定义焦点、焦平面→主点、主平 面；再讨论位于无限远的物体轴外物点发出的光线通 过光学系统的特征及成像位置。
（一）无限远轴上物点发出的光线
A
-U
-L
A
B
E′
h
物方截距L→∞
焦平 面性 质
（5）共轭光线在一对主面上的投射高度相等。——主面性质
▲ 依据：理想的成像情况下，从一点发出的一束光线经光学 系统作用后仍交于一点。
▲ 方法：求物点发出的两条特定光线在像方空间的共轭光线， 二者的交点为共轭像点。
（一）轴外点B或一垂轴线段AB的图解法求像
（二）轴上物点成像——利用焦平面的性质 解法1：
F′
孔径角U→0
（二）像方焦点、焦平面；像方主点、主平面；像方焦距
1、像方焦点、焦平面
A
B
E′
F′
像方焦点F′——无限远轴上 物点的像点
像方焦平面——无限远处垂直于 光轴的物平面的共轭像。
2、像方主点、主平面、像方焦距
A
B
Q′
E′
h
f ' h tanU '
H′
像方主点H′
F′ f′
像方主平面
像方焦距f′——起算原点是像
★ 用六次近轴光线的光路计算公式和过渡公式求像距和倾角
i l r u, i' n i, u'uii', l'r(1 i' )
r
n'
u'
ni1 ni＇, ui1 ui＇, li1 li＇di
lH '
h
H′
u′
F′
f′
lF
★ 像距和倾角
l' F'
l
'
67.4907mm
u' 0.121869
★ 像方焦距
-f
理想光学系统的物方参数
三、物方主平面与像方主平面间的关系
Q Q′
h
h
F
H
H′
F′
1、主平面的物理意义 ▲ QH 与 Q’H’为共轭面
▲ 垂轴放大率β=Q’H’/QH =+1，出射光线在像方主平面的 投射高度与入射光线在物方主平面的投射高度相等。
2、共轴理想光学系统的基点和基面
★一对主点、一对主平面；（共轭）
第三节 理想光学系统的物像关系
几何光学的基本内容之一：已知物求其像。 一、图解法求像
▲ 典型光线及性质（5条）
（1）平行于光轴入射的光线，经系统后必经过像方焦点； 焦点
（2）过物方焦点的入射光线，经系统后平行于光轴；
定义
（3）倾斜于光轴入射的平行光束，经过系统后出射光束 交于像方焦平面上的一点；
（4）自物方焦平面上一点发出的光束，经系统后成倾 斜于光轴的平行光束出射。
第一节 理想光学系统与共线成像理论
一、理想光学系统 ▲ 理想光学系统——任意大的空间、以任意宽的光 束都成完善像的光学系统。
▲ 1841年高斯提出理想光学系统理论，故理想光学 系统理论被称为“高斯光学（Gaussian Optics）”
▲ 共轭——任意物点经理想光学系统都成完善像点。
▲ 如果物像空间皆为均匀介质，理想光学系统具有 共线成像性质。共线成像——物像变换为点对点，线 对线，面对面的关系。
★一对焦点、一对焦平面；（非共轭） F
H H’
F’
共轴理想光学系统的简化图：用基点和基面的位置表征。
四、实际光学系统的基点位置和焦距计算
▲ 共轴球面系统的近轴区就是实际的理想光学系统，在实际 系统的近轴区追迹平行于光轴的光线，就可计算出实际系统近 轴区的基点位置和焦距。
例：三片型照相物镜
l =-∞
方主点H′
理想光学系统的像方参数
（三）无限远轴外物点发出的光线
▲ 由于光学系统的口径大小 有限，无限远轴外物点发出的、 能进入光学系统的光线总是相 互平行的，且与光轴有一定夹 角，夹角常用ω表示。
▲ 无限远轴外物点的共轭像点位于像方焦平面上。
二、无限远轴上像点对应的物点F
Q
F
-U
h H
f h tanU
第二章 理想光学系统
什么是理想光学系统？ 把光学系统在近轴区成完 善像的理论推广到任意大的空间、以任意宽的光束都 成完善像的光学系统。
第一节 理想光学系统与共线成像理论 第二节 理想光学系统的基点与基面 第三节 理想光学系统的物像关系 第四节 理想光学系统的放大率
第五节 理想光学系统的组合 第六节 透镜
性质3：利用已知的共轭点/面求物像关系
（1）已知两对共轭面的位置和放大率
O
A
O2
O1
B
O1'
B'
O' A'
O2'
（2）已知一对共轭面的位置和放大率，及轴上两对共轭点的位置
O B
A
O3
O1 O2
O1' O2'
O' B' A'
O3'
M
注意：上面的论证并没有限定要预知什么样的共轭面和共轭点，
它们可以是任意的。实际中，为了应用方便，一般采用一些特殊 的共轭面和共轭点作为共轴系统的基面和基点。
（1）结构参数
r/mm 26.67 189.67 -49.66 25.47 72.11 -35.00
d/mm n 5.20 1.6140 7.95 1.6 1.61745 6.7 2.8 1.6140
F′
方法：在近轴区追迹 平行于光轴的光线。
（2）求物镜像方焦距、像方焦点、像方主点
★ 起始坐标 l1 u1 0 h1 10mm i1 h1 / anU '
10 mm82.055mm 0.121869
★ 像方主点
l' H
'
l' F
'
f
'
14.5644mm
特别注意：l 或 l'都是以球面顶点为起算原点！！
（3）求物镜物方焦距、物方焦点、物方主点 方法：原则上要作反向光路计算，但通常是把系统倒转，即
把第一面作为最后一面，把最后一面作为第一面，并随之将曲 率半径改变符号。
★ 起始坐标 l1 , u1 0, h1 10mm, i1 h1 r1
★ 物距和倾角 l ' 70.0184 mm, u' 0.121869 ★ 物方焦点位置 lF 70.0184 mm ★ 物方焦距 f 82.055mm
★ 物方主点 lH 12.0366 mm
注意：上面计算出的物方焦距和像方焦距的量值是相同的， 这不是偶然的巧合，其原因留待后续内容中解释。