平行四边形和梯形的关系
平行四边形和梯形的认识和计算
平行四边形和梯形的认识和计算平行四边形和梯形是几何学中常见的两种多边形。
它们在实际生活和各行各业中都有广泛的应用。
本文将详细介绍平行四边形和梯形的定义、性质以及计算方法。
一、平行四边形的认识和计算平行四边形是指有四条边两两平行的四边形。
平行四边形的性质如下：1. 对边平行性质：平行四边形的任意两对对边都是平行的。
2. 对角线性质：平行四边形的对角线互相平分，并且长度相等。
3. 对顶角性质：平行四边形的对顶角互补，即相邻的对顶角之和为180°。
平行四边形的面积计算公式为：面积 = 底边长 ×高。
在使用平行四边形的面积计算公式时，需要将平行四边形的一条边作为底边，再通过垂直于底边的高线求得高的长度。
二、梯形的认识和计算梯形是指有两边平行的四边形。
梯形的性质如下：1. 底边平行性质：梯形的两条底边是平行的。
2. 对角线性质：梯形的对角线互相平分。
3. 高性质：梯形的高线是连接两条底边，且垂直于底边的线段。
梯形的面积计算公式为：面积 = (上底长 + 下底长) ×高 ÷ 2。
在使用梯形的面积计算公式时，需要将两条底边的长度相加，再除以2，最后乘以高的长度。
三、平行四边形和梯形的计算实例下面通过两个计算实例来说明平行四边形和梯形的计算方法：1. 平行四边形的计算实例：假设有一个平行四边形，其中底边长为5cm，高为8cm。
根据平行四边形的面积计算公式，可以计算得到该平行四边形的面积为：面积 = 5cm × 8cm = 40cm²。
2. 梯形的计算实例：假设有一个梯形，其中上底长为3cm，下底长为7cm，高为4cm。
根据梯形的面积计算公式，可以计算得到该梯形的面积为：面积 =(3cm + 7cm) × 4cm ÷ 2 = 20cm²。
通过上述两个实例，我们可以看到如何利用平行四边形和梯形的面积公式进行计算。
只需要知道底边、高的长度，就可以轻松计算出平行四边形和梯形的面积。
平行四边形和梯形知识点归纳
平行四边形和梯形知识点归纳1.平行四边形的定义及性质平行四边形是指具有两对对边平行的四边形。
以下是平行四边形的一些性质：-对角线相互平分-对角线相等-相邻角互补（和为180度）-同位角相等-任意一对相邻内角互补-对边相等2.平行四边形的判定方法判定一个四边形是否为平行四边形可以使用以下方法：-两组对边分别平行-对角线互相平分-一组对边相等且对角线互相分割成相等的部分3.梯形的定义及性质梯形是指至少有一对对边平行的四边形。
以下是梯形的一些性质：-底边平行-顶角互补（和为180度）-一对对边相等的梯形为等腰梯形-高线平行于底边且等于底边长度乘以高线对应的比例4.梯形的判定方法判定一个四边形是否为梯形可以使用以下方法：-一对对边平行-一对对边相等且没有其他平行边-底边长度与高线长度成比例5.平行四边形和梯形的应用5.1平行四边形的应用平行四边形的性质和判定方法在几何学的各个分支中常常被应用，例如：-在解决平面图形的计算问题中，我们经常会遇到平行四边形的形状，通过了解平行四边形的性质和判定方法，可以更快地解决问题。
-在建筑和土木工程中，平行四边形的形状常常出现，例如建筑物的立面图等。
了解平行四边形的性质可以帮助我们更好地设计和构建建筑物。
5.2梯形的应用梯形也在几何学的各个领域中被广泛应用，例如：-在计算梯形的面积时，我们可以通过将梯形分割成平行四边形和直角三角形，从而简化计算。
-在图形的投影中，梯形的形状常常出现，通过了解梯形的性质，可以更好地理解和分析图像的特点。
结论平行四边形和梯形是几何学中重要的概念，它们具有独特的性质和判定方法。
通过了解这些知识点，我们可以更好地理解和应用于实际问题中。
在解决几何学问题时，熟练掌握平行四边形和梯形的性质和判定方法是非常重要的。
希望通过本文库文档的详细介绍，您对平行四边形和梯形有了更深入的理解。
《平行四边形和梯形》课件(共18张PPT)四年级上册数学人教版
视察与思考
下面的图形哪些是平行四边形，哪些是梯形？
平行四边形（ ① ② ⑥ ⑧ ） 梯形（ ④ ⑤ ）
视察与思考
四边形之间的关系：
平行四边形 长方形 正方形
梯形 四边形
我们可以用左面的图 来表示四边形之间的
关系
长方形和正方形是特殊的平行四边形。
视察与思考
做一做，想一想。
我发现平行四边形容易变 形，具有不稳定性。
智力大比拼
做一做： 1. 说一说日常生活中应用平行四边形容易变形这一特性的例子． 2. 画出下面两个图形的高．
智力大比拼
做一做： 1. 说一说日常生活中应用平行四边形容易变形这一特性的例子． 2. 画出下面两个图形的高．
智力大比拼
判断：对的做“√”，错的做“×” ：
× 1. 两组对边分别平行的图形是平行四边形。
视察与思考
做一做，想一想。
高 底
从平行四边形一条边上的一点 到对边引一条垂线，这点和垂 足之间的线段叫做平行四边形 的高，垂足所在的边叫做平行
四边形的底。
视察与思考
做一做，想一想。
上底
腰
高
来给梯形的各部分起 个名字吧！
腰
下底
两腰相等的梯形叫做等腰梯形。
智力大比拼
做一做： 1. 说一说日常生活中应用平行四边形容易变形这一特性的例子． 2. 画出下面两个图形的高．
平行四边形和梯形
2. 有一组对边平行的四边形是梯形。
×
3. 平行四边形的两组对边分别平行并且相等。√
4. 长方形、正方形都是特殊的平行四边形。 √
智力大比拼
从右面图形中找出平行四 边形和梯形，并画出它们 的高.
梯形
平行四边形
梯形与平行四边形的区别
梯形与平行四边形的区别梯形和平行四边形是几何中常见的两种多边形形状，它们在外观和性质上有着一些显著的区别。
本文将就梯形和平行四边形的定义、性质和应用进行详细比较。
一、梯形的定义和性质梯形是一个四边形，其中两边是平行的，但其余两边不一定平行。
我们可以通过以下定义和性质来更好地理解梯形。
1. 定义：梯形是一个四边形，其中两边是平行边，而其余两边则不平行。
2. 性质：（a）只有两条边是平行的，其余两条边不平行。
（b）梯形的对角线不相等，并且两条对角线的交点是梯形的中心。
（c）梯形的每个内角之和为180度。
（d）梯形的面积可以通过底边长度、顶边长度和高来计算，即面积=（底边长度+顶边长度）×高除以2。
二、平行四边形的定义和性质平行四边形是一个四边形，其中四个边都是平行的。
下面是关于平行四边形的定义和性质的详细解释。
1. 定义：平行四边形是一个四边形，其中四个边都是平行的。
2. 性质：（a）四个边都是平行的。
（b）相邻两个角的和为180度。
（c）对角线相等且互相平分。
（d）对角线的交点是平行四边形的中心。
（e）平行四边形的面积可以通过底边长度和高来计算，即面积=底边长度×高。
三、梯形与平行四边形的区别梯形和平行四边形在几何形状上有一些明显的区别。
1. 边的平行性质：梯形只有两条边是平行的，而平行四边形的四条边都是平行的。
2. 对角线的相等与平分性质：梯形的对角线不相等，而平行四边形的对角线则相等且互相平分。
3. 角的性质：梯形的各个内角之和为180度，而平行四边形的相邻两个角之和也为180度。
4. 面积的计算方式：梯形的面积计算公式为面积=（底边长度+顶边长度）×高除以2，而平行四边形的面积计算公式为面积=底边长度×高。
四、梯形与平行四边形的应用梯形和平行四边形在实际生活和工程中都有广泛的应用。
1. 梯形的应用：梯形常常用于建筑和工程设计中，例如台阶的设计、屋顶的设计等。
平行四边形和梯形知识点总结
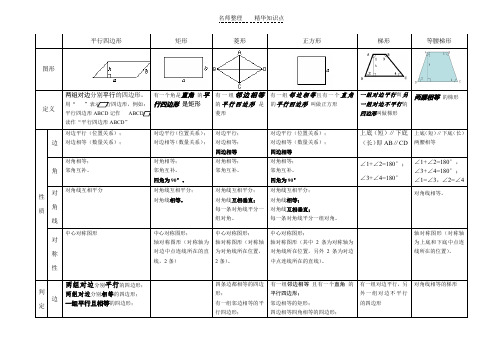
平行四边形矩形菱形正方形梯形等腰梯形图形定义两组对边分别平行的四边形。
用“”表示平行四边形，例如：平行四边形ABCD记作ABCD，读作“平行四边形ABCD”有一个角是直角的平行四边形是矩形有一组邻边相等的平行四边形是菱形有一组邻边相等且有一个直角的平行四边形叫做正方形一组对边平行而另一组对边不平行的四边形叫做梯形两腰相等的梯形性质边对边平行（位置关系）；对边相等（数量关系）；对边平行（位置关系）；对边相等（数量关系）；对边平行；对边相等；四边相等对边平行（位置关系）；对边相等（数量关系）；四边相等上底（短）∥下底（长）即AB∥CD上底（短）∥下底（长）两腰相等角对角相等；邻角互补。
对角相等；邻角互补。
四角为90°。
对角相等；邻角互补。
对角相等；邻角互补。
四角为90°∠1+∠2=180°；∠3+∠4=180°∠1+∠2=180°，∠3+∠4=180°；∠1=∠3，∠2=∠4 对角线对角线互相平分对角线互相平分；对角线相等。
对角线互相平分；对角线互相垂直；每一条对角线平分一组对角。
对角线互相平分；对角线相等；对角线互相垂直；每一条对角线平分一组对角。
对角线相等。
对称性中心对称图形中心对称图形；轴对称图形（对称轴为对边中点连线所在的直线，2条）中心对称图形；轴对称图形（对称轴为对角线所在位置，2条）。
中心对称图形；轴对称图形（其中2条为对称轴为对角线所在位置，另外2条为对边中点连线所在的直线）。
轴对称图形（对称轴为上底和下底中点连线所在的位置）。
判定边两组对边分别平行的四边形；两组对边分别相等的四边形；一组平行且相等的四边形；四条边都相等的四边形；有一组邻边相等的平行四边形；有一组邻边相等且有一个直角的平行四边形；邻边相等的矩形；四边相等四角相等的四边形；有一组对边平行，另外一组对边不平行的四边形对角线相等的梯形角两组对角分别相等的四边形；有一个角是直角的平行四边形；四个角都相等的四边形。
认识平行四边形与梯形
认识平行四边形与梯形平行四边形和梯形是几何学中常见的两种特殊四边形。
它们具有独特的性质和特点，在数学中起到重要的应用和作用。
本文将介绍平行四边形和梯形的定义、性质以及它们的区别。
一、平行四边形平行四边形是指具有两组对边分别平行的四边形。
下面给出平行四边形的定义和性质。
1. 定义平行四边形的定义是：具有两组对边分别平行的四边形。
2. 性质（1）相对边相等：平行四边形的对边长度相等。
（2）相对角相等：平行四边形的对角线所夹的角相等。
（3）同位角相等：同位角是指相邻并位于同一边的两个内角，平行四边形的同位角相等。
（4）对角线的交点连线是平分线：对于平行四边形ABCD，其对角线AC和BD的交点O，连接OA、OB、OC、OD，这四条线段互相平分。
（5）对边平行：平行四边形的对边互相平行。
二、梯形梯形是指具有一对平行边的四边形。
下面给出梯形的定义和性质。
1. 定义梯形的定义是：具有一对平行边的四边形。
2. 性质（1）底角相等：梯形的两个底角相等。
（2）顶角相等：梯形的两个顶角相等。
（3）对边平行：梯形的对边互相平行。
（4）对角线的交点连线是中位线：对于梯形ABCD，其对角线AC 和BD的交点O，连接OA、OB、OC、OD，这四条线段相互平分。
三、平行四边形与梯形的区别尽管平行四边形和梯形都是具有平行边的四边形，但它们的不同之处在于：平行四边形的对边长度相等，而梯形的两个底角和两个顶角相等。
以ABCD为例，若AB∥CD，BC∥AD，且AB=CD，BC ≠ AD，则ABCD是平行四边形，反之若两个底角相等，两个顶角相等，但底边和顶边不平行，则ABCD是梯形。
四、总结平行四边形和梯形是几何学中的两个重要概念。
平行四边形具有对边平行、相对边相等、同位角相等和对角线互相平分等性质；而梯形具有对边平行、底角相等、顶角相等和对角线互相平分等性质。
通过对它们的认识和理解，我们能更好地应用它们解决实际问题。
通过本文的学习，我们对平行四边形和梯形有了更深入的了解。
人教版四年级上册数学课件-第五单元第7课时认识梯形、平行四边形的关系(共15张PPT)
教科书第66页例4
我们认识了长方形、正方形……
长方形和正方形可以看成特殊 的平行四边形吗？为什么？
四年级上册数学课件-第五单元第7课 时 认识梯形、平行四边形的关系 人教版(共15张PPT)
四年级上册数学课件-第五单元第7课 时 认识梯形、平行四边形的关系 人教版(共15张PPT)
我们可以用下面的图来表示四边形之间的关系。
正方形 长方形 平行四边形
平行四边形 长方形
正方形
长方形 平行四边形
正边形
①
②
③
四年级上册数学课件-第五单元第7课 时 认识梯形、平行四边形的关系 人教版(共15张PPT)
四年级上册数学课件-第五单元第7课 时 认识梯形、平行四边形的关系 人教版((将正确答案的序号填在括号里)
二、在图中各画一条线段，把图形分成两个不 同的梯形。
四年级上册数学课件-第五单元第7课 时 认识梯形、平行四边形的关系 人教版(共15张PPT)
答案不唯一。
四年级上册数学课件-第五单元第7课 时 认识梯形、平行四边形的关系 人教版(共15张PPT)
五 课堂小结 这节课你们都学会了哪些知识？
只有一组对边平行的四边形叫做梯形。 特殊梯形：两个腰相等的等腰梯形；有 一个角是直角的直角梯形。
一 复习导入
你能写出下面这图形的名称吗？
圆 平行四边形 三角形 正方形
四年级上册数学课件-第五单元第7课 时 认识梯形、平行四边形的关系 人教版(共15张PPT)
四年级上册数学课件-第五单元第7课 时 认识梯形、平行四边形的关系 人教版(共15张PPT)
二 新课探究
教科书第66页例3
你见过下面这样的图形吗？他们有什么
▷ 特殊的梯形： 两腰相等的梯形叫做等腰梯形。 有一个角是直角的梯形叫做直角梯形。
三角形平行四边形梯形的知识整理
三角形、平行四边形和梯形都是平面几何中的基本图形，它们具有不同的特点和性质。
1. 三角形
三角形是由三条线段组成的图形，它有三个顶点和三条边。
三角形的内角和为180度，可以根据它的边长和角度计算它的面积和周长。
根据三个内角的大小，可以将三角形分为锐角三角形、直角三角形和钝角三角形三种。
2. 平行四边形
平行四边形是四边形中特殊的一种，四条边都是平行的，对角线互相平分，相邻两角之和为180度。
平行四边形的对边长度相等，面积可以使用底边长与高的乘积计算。
3. 梯形
梯形是由两个并排的平行四边形和它们之间的四边形组成的图形。
两条平行边的长度分别为上底和下底，不在同一直线上的两个角称为梯形的腰角，它们的对边叫做梯形的腰。
梯形的面积也可以使用上底、下底和高的公式计算。
此外，一个特殊的情况是当梯形上下底相等时，梯形就变成了平行四边形。
4. 三角形与平行四边形的关系
如果一条直线与一个平行四边形平行，则这条直线所截下的平行四边形两个角之和等于180度，这是因为它们是同旁内角。
如果在平行四边形的两边上各取一条等于其中一边的线段，则它们所围成的三角形是等边三角形。
5. 平行四边形与梯形的关系
如果一个平行四边形和一条直线平行，则这条直线所截下来的线段之间的距离等于平行四边形的高。
如果在梯形的两边上各取一条相等的线段，则它们所围成的三角形是全等三角形。
因此，在梯形中两边平行的两个线段的比例相等。
人教版四年级数学上册平行四边形和梯形练习(一)
人教版四年级数学上册平行四边形和梯形练习（一）学校:___________姓名：___________班级：___________考号：___________一、选择题1．关于平行四边形与梯形的关系，下面（）的表述是正确的。
A．平行四边形与梯形是不同的四边形B．有些梯形是平行四边形C．平行四边形是特殊的梯形D．梯形是特殊的平行四边形2．下面说法正确的有（）个。
①线段和射线都可以看成直线上的一部分，所以射线比直线短。
①用一副三角尺可以画出105°的角，但不能画出15°的角。
①两条直线相交成的4个角中，有一个是直角，就可以说这两条直线互相垂直。
①两条平行线间有无数条垂直线段且都相等。
A．1B．2C．3D．都不正确3．在两条平行线之间有4条垂线，这4条垂线之间的关系是（）。
A．只平行不相等B．平行且相等C．不平行D．无法比较4．如图，画和直线l平行的直线，可以画()条．A．1B．2C．无数5．铅垂线可以用来检验（）A．直线与平面垂直B．直线与平面平行C．平面与水平面垂直D．平面与平面垂直6．图形A被两张纸遮住了一部分（如图），它可能是（）。
①长方形①正方形①梯形①平行四边形A．①①①B．①①①C．①①①D．①①①7．如图中有（）个不同的平行四边形。
A．2B．3C．48．下图中，属于平行四边形都找到的有（）。
A．①①B．①①①C．①①①D．①①①①二、填空题9．两条直线相交，有一个角是直角，其他三个角的度数都是( )，这两条直线的位置关系是( )。
10．下图中有( )个梯形，有( )个三角形。
11．直线a与直线b互相垂直，记作( )，读作( )。
12．数一数，图中有( )个平行四边形，( )个梯形．13．黑板左右两条边是互相的，相邻两条边是互相的．14．在( )内( )的两条直线叫做( )，也可以说这两条直线( )．15．长方形的邻边互相( )，平行四边形的对边互相( )。
16．下图中有( )组平行线，有( )组线段互相垂直。
人教版四年级上册《梯形的认识及四边形间的关系》
四边形间的关系
用集合图表示各种四边形之间的关系。
平行四边形 长方形 梯形 四边形
正方形
1. 下面哪些图形是梯形？画出每个梯形的高，分别 指出它们的上底、下底和腰。
梯形
梯形
梯形
小结：梯形的特征及四边形间关系
只有一组对边平行的四边形，叫做梯形。
平行四边形 长方形 梯形 四边形
正方形
梯形的认识及四边形间的关系
平行四边形和梯形的认识
生活中梯形
这些梯形有哪些共同特征？梯形的特征一组对边平但长度不相等梯形的特征
另一组对边不平行
只有一组对边平行的四边形，叫做梯形。
梯形各部分名称
上底
腰
高
腰
下底
梯形各部分名称
上底
腰
高
腰
下底
等腰梯形、直角梯形
等腰梯形
直角梯形
直角梯形的高就是它的那条垂直于上底、下底的腰。
平行四边形和梯形的不同点
平行四边形和梯形的不同点平行四边形和梯形是几何学中常见的两种多边形，它们在形状和性质上有许多不同之处。
本文将从各个方面详细比较平行四边形和梯形的不同点。
从形状上来看，平行四边形是由四条边构成的四边形，其中相邻的两条边互相平行。
这意味着平行四边形的对边长度相等，对角线相互平分，并且具有相等的内角和外角。
而梯形则是由四条边组成的四边形，其中两条边平行，另外两条边不平行。
梯形的对边不相等，内角和外角也不相等。
平行四边形和梯形的性质也有所不同。
平行四边形的特点是对边平行且相等，对角线相等，并且具有相等的内角和外角。
平行四边形的特殊情况是正方形，即四条边相等且四个角都是直角。
梯形的特点是两条平行边不相等，且没有对角线相等的性质。
梯形的特殊情况是等腰梯形，即两条非平行边相等。
第三，平行四边形和梯形的面积计算方式也不同。
平行四边形的面积可以通过底边长乘以高得到，即S = 底边× 高。
梯形的面积计算公式为底边和顶边之和的一半乘以高，即S = (底边 + 顶边) × 高 / 2。
在计算面积时，需要注意底边和顶边的长度以及高的测量单位要保持一致。
平行四边形和梯形在实际应用中有不同的用途。
平行四边形常用于建筑和工程设计中，例如建筑物的地基和墙体结构。
平行四边形的特性使其具有较好的稳定性和承重能力。
而梯形则常用于制造业和机械设计中，例如传送带和机器工作台的设计。
梯形的形状使其具有适合放置物体和进行加工的特点。
平行四边形和梯形在对称性和旋转对称性方面也有所不同。
平行四边形具有旋转对称性，即将平行四边形绕其对角线旋转180度后，仍然保持原来的形状。
而梯形则没有旋转对称性，即旋转梯形后，形状会发生变化。
平行四边形和梯形的边长和角度可以通过测量工具进行准确测量。
在实际应用中，可以使用尺子或测角器来测量平行四边形和梯形的边长和角度，以便进行准确的计算和设计。
平行四边形和梯形在形状、性质、面积计算、应用和对称性等方面存在显著的不同。
平行四边形与梯形
平行四边形与梯形平行四边形与梯形是几何学中常见的两类多边形。
它们具有一些共同的特点和性质，同时也有着一些不同之处。
本文将对平行四边形和梯形的定义、性质以及应用进行探讨。
一、平行四边形平行四边形是一类具有特殊性质的四边形。
它的定义为：如果一个四边形的对边两两平行，则这个四边形就是平行四边形。
1.1 基本性质平行四边形有以下基本性质：a) 两组对边分别平行；b) 两组对边长度相等；c) 两组对角线互相平分；d) 相邻两个内角互补，即和为180°；e) 对角线相等的平行四边形是矩形；f) 对角线垂直的平行四边形是菱形。
1.2 应用举例平行四边形的性质使得它们在实际应用中有着广泛的用途。
例如，在建筑工程中，我们常常需要利用平行四边形的性质来确定地面的平行与垂直方向，从而保证建筑物的结构稳定。
此外，在日常生活中，平行四边形的概念还可以应用于制作桌子、柜子等家具，以确保其坚固且美观。
二、梯形梯形是一类特殊的四边形，它具有以下定义：如果一个四边形的两边是平行的，则这个四边形是梯形。
2.1 基本性质梯形的基本性质如下：a) 两条底边平行；b) 上底与下底互相平行；c) 上底与下底长度不相等；d) 两腰边之间的夹角不相等；e) 对角线不相交。
2.2 应用举例梯形在几何学中是一个常见的形状，具有一些重要的应用。
例如，在建筑设计中，梯形的概念常被应用于楼梯的设计，通过合理利用梯形的性质和比例，可以确保楼梯的安全性和舒适性。
此外，在工业生产中，梯形的结构也常常被用于设计输送带、坡道等设备，以实现物料的顺利运输。
综上所述，平行四边形和梯形是几何学中重要的两类多边形。
它们具有一些共同的性质，同时也有一些独特的特点。
了解和掌握这些多边形的性质和应用，对于我们理解几何学的基本原理，以及在实际问题中的应用具有重要意义。
无论是在建筑设计、工程制造还是日常生活中，平行四边形和梯形的概念和性质都扮演着重要的角色，我们应该深入学习和研究它们，以提高我们的几何学水平和解决实际问题的能力。
平行四边形 梯形关系
平行四边形梯形关系
平行四边形和梯形都是四边形，但它们有一些重要的区别和关系。
平行四边形和梯形之间的关系可以总结如下：
1. 定义：平行四边形是两组相对边平行，而梯形只有一组相对边平行。
2. 对角线：平行四边形的对角线互相平分，而梯形的对角线不一定互相平分。
3. 分类：根据定义，所有平行四边形都是特殊的梯形（具有一组相对边平行）。
反过来，并不是所有梯形都是平行四边形，因为梯形只需要有一组相对边平行。
4. 面积计算：虽然两种形状都是四边形，它们的面积计算方法有所不同。
简而言之，平行四边形是梯形的一个子集，这意味着所有平行四边形都是梯形，但不是所有梯形都是平行四边形。
小学数学四年级平行四边形和梯形知识点
平行四边形和梯形知识点1、平行四边形：两组对边互相平行的四边形;它的对边平行且相等;对角相等。
从一个顶点向对边可以作两种不同的高。
底和高一定要对齐、一个平行四边形有无数条高。
2、用两块完全一样的三角尺可以拼成一个平行四边形。
3、平行四边形容易变形（不稳定性）。
生活中许多物体都利用了这样的特性。
如：（电动伸缩门、铁拉门、升降机）把平行四边形拉成一个长方形;周长不变;面积变了。
平行四边形不是轴对称图形。
4、梯形：只有一组对边平行的四边形。
平行的一组对边较短的叫做梯形的上底;较长的叫做梯形的下底;不平行的一组对边叫做梯形的腰;两条平行线之间的距离叫做梯形的高（无数条）。
5、等腰梯形：两条腰相等的梯形;它的两个底角相等;是轴对称图形;有一条对称轴。
直角梯形有且只有两个直角。
6、两个完全一样的梯形可以拼成一个平行四边形。
7、正方形、长方形数属于特殊的平行四边形。
平行与垂直1、在同一个平面内不相交的两条直线叫做平行线;也可以说这两条直线互相平行。
记作：a∥b 读作：a平行于b2、两条直线相交成直角;就说这两条直线互相垂直;其中一条直线叫做另一条直线的垂线;这两条直线的交点叫做垂足。
记作：a⊥b 读作：a垂直于b3、从直线外一点到这条直线所画的垂直线段最短;它的长度叫做这点到直线的距离。
实际应用4、与两条平行线互相垂直的线段长度都相等。
或者说：两条平行线之间的距离处处相等。
经过直线上一点（或外一点）作垂线;只能画一条。
经过直线外一点作平行线;只能画一条。
5、同一平面内;与同一条直线平行（或垂直）的两条直线也互相平行。
平行四边形1、两组对边分别平行的四边形;叫做平行四边形。
2、平行四边形的特点：对边平行且相等；对角相等；邻角相加得180度。
具有不稳定性;易变形。
3、从平行四边形一条边上的一点向对边引一条垂线;这点和垂足之间的线段叫做平行四边形的高;垂足所在的边叫做平行四边形的底。
平行四边形有两种高。
4、一个长方形;用两手捏住长方形的两个对角;向相反方向拉;可以拉成不同形状的平行四边形;形状变了;高变短；边长不变;是周长不变。
平行四边形与梯形的联系分析
平行四边形与梯形的联系分析一、平行四边形的定义及性质1.定义：在同一平面内，有两组对边分别平行且相等的四边形叫平行四边形。
（1）对边平行且相等；（2）对角相等；（3）对边上的高相等；（4）对角线互相平分。
二、梯形的定义及性质1.定义：在同一平面内，一组对边平行，另一组对边不平行且不平行的两边相等的四边形叫梯形。
（1）一组对边平行，另一组对边不平行；（2）平行边互相平行且相等；（3）对角相等；（4）梯形的对角线互相平分。
三、平行四边形与梯形的联系1.转化：在特定条件下，平行四边形可以转化为梯形，梯形也可以转化为平行四边形。
2.共同性质：（1）都有两组对边；（2）都有对角；（3）都有对边上的高；（4）对角线互相平分。
3.不同点：（1）平行四边形的两组对边都平行，梯形只有一组对边平行；（2）平行四边形的对边相等，梯形的平行边相等，但非平行边不一定相等。
四、平行四边形与梯形的判定1.平行四边形的判定：（1）有两组对边分别平行且相等的四边形是平行四边形；（2）有一组对边平行且相等，且另一组对边也平行的四边形是平行四边形。
2.梯形的判定：（1）有一组对边平行，另一组对边不平行且不平行的两边相等的四边形是梯形；（2）在同一底边上，两腰不等且不平行，腰和底边不垂直的四边形是梯形。
1.计算平行四边形与梯形的面积；2.证明平行四边形与梯形的性质；3.转化平行四边形与梯形解决问题。
通过以上分析，我们可以看出平行四边形与梯形在性质、判定和应用方面有很多相似之处，但也存在不同点。
掌握这些知识点，有助于我们更好地理解和解决几何问题。
习题及方法：1.习题：已知平行四边形ABCD中，AB=CD，AD=BC，AC=6cm，BD=8cm，求平行四边形ABCD的面积。
方法：利用平行四边形的性质，对边相等，对角相等。
因为AC=6cm，BD=8cm，所以平行四边形的对角线互相平分，即AC和BD是平行四边形的对角线。
根据对角线互相平分的性质，可以得到平行四边形的面积S=1/2AC BD=1/26cm8cm=24cm²。
小学数学四年级平行四边形和梯形知识点
小学数学四年级平行四边形和梯形知识点平行四边形和梯形知识点1、平行四边形：两组对边互相平行的四边形;它的对边平行且相等;对角相等。
从一个顶点向对边可以作两种不同的高。
底和高一定要对齐、一个平行四边形有无数条高。
2、用两块完全一样的三角尺可以拼成一个平行四边形。
3、平行四边形容易变形（不稳定性）。
生活中许多物体都利用了这样的特性。
如：（电动伸缩门、铁拉门、升降机）把平行四边形拉成一个长方形;周长不变;面积变了。
平行四边形不是轴对称图形。
4、梯形：只有一组对边平行的四边形。
平行的一组对边较短的叫做梯形的上底;较长的叫做梯形的下底;不平行的一组对边叫做梯形的腰;两条平行线之间的距离叫做梯形的高（无数条）。
5、等腰梯形：两条腰相等的梯形;它的两个底角相等;是轴对称图形;有一条对称轴。
直角梯形有且只有两个直角。
6、两个完全一样的梯形可以拼成一个平行四边形。
7、正方形、长方形数属于特殊的平行四边形。
平行与垂直1、在同一个平面内不订交的两条直线叫做平行线;也能够说这两条直线互相平行。
记作：a∥b读作：a平行于b2、两条直线相交成直角;就说这两条直线互相垂直;其中一条直线叫做另一条直线的垂线;这两条直线的交点叫做垂足。
记作：a⊥b读作：a垂直于b3、从直线外一点到这条直线所画的垂直线段最短;它的长度叫做这点到直线的距离。
实际应用4、与两条平行线互相垂直的线段长度都相等。
或者说：两条平行线之间的距离处处相等。
经过直线上一点（或外一点）作垂线;只能画一条。
经过直线外一点作平行线;只能画一条。
5、同一平面内;与同一条直线平行（或垂直）的两条直线也互相平行。
平行四边形1、两组对边分别平行的四边形;叫做平行四边形。
2、平行四边形的特征：对边平行且相等；对角相等；邻角相加得180度。
具有不不乱性;易变形。
3、从平行四边形一条边上的一点向对边引一条垂线;这点和垂足之间的线段叫做平行四边形的高;垂足所在的边叫做平行四边形的底。
四边形正方形长方形平行四边形梯形的关系
四边形正方形长方形平行四边形梯形的关系示例文章篇一：《四边形大家族：正方形、长方形、平行四边形和梯形的关系》嘿，小伙伴们！今天咱们来聊聊四边形这个大家族里的一些成员，就是正方形、长方形、平行四边形还有梯形。
这几个图形呀，就像一家人一样，有着千丝万缕的关系呢。
我先来说说平行四边形吧。
平行四边形就像一个很有个性的家伙，它的两组对边呀，都是平行的。
你看，就像两条铁轨一样，永远不会相交。
我记得有一次上数学课，老师拿着平行四边形的教具在黑板上比划着，说：“同学们，这平行四边形的对边平行，这可是它最大的特点哦。
”我当时就在想，这就好像是两个好朋友，总是并肩前行，谁也不偏离谁的方向。
那长方形呢？长方形呀，其实是一种特殊的平行四边形。
我同桌就问过我：“长方形和平行四边形有啥不一样呢？”我就跟他说：“你看啊，长方形除了对边平行，它的四个角还都是直角呢。
”这就好比是平行四边形穿上了一件规规矩矩的衣服，把自己的角都弄得方方正正的。
长方形在我们生活中可常见啦，像我们的书本，课桌的桌面，很多都是长方形的。
这时候，前桌的同学转过头来说：“哦，我懂了，那长方形就像是平行四边形里的好学生，把自己的角都管理得很好。
”哈哈，这个比喻虽然有点搞笑，但还挺贴切的呢。
再来说说正方形。
正方形可就更厉害了，它不仅是特殊的平行四边形，还是特殊的长方形呢。
它的四条边都相等，四个角也都是直角。
我觉得正方形就像是一个超级规规矩矩的小方块，每个边都一样长，就像四个小伙伴手拉手，围成了一个完美的小天地。
我在家里玩积木的时候，那些小正方形的积木块就特别好拼搭，不管怎么组合都很整齐。
有一次我拼了一个小房子，全是用正方形的积木搭的，妈妈看了还夸我有创意呢。
我跟妈妈说：“妈妈，正方形就是这么神奇，它又整齐又好看。
”妈妈笑着说：“是呀，宝贝，正方形是很规则的图形呢。
”最后就是梯形啦。
梯形这个家伙和前面几个有点不一样。
它只有一组对边平行。
我在做数学作业的时候，就老是会把梯形和平行四边形搞混。
平行四边形与梯形的相同点
平行四边形与梯形的相同点平行四边形和梯形，看起来两者有点差别吧？但你知道吗，它们居然有一些挺相似的地方哦。
说实话，可能一开始你会觉得它们不太搭边，一个四条边都一样长，一个只有两条平行的边。
可是，真要说起来，这俩形状其实有很多“共同点”，要是你不小心，就会把它们的相似之处忽略掉。
咱们就从“平行”这点说起。
平行四边形最显著的特点，就是它对边平行。
你想啊，左边对右边，底边对顶边，它们永远是平行的，离得老远也不碰头。
而梯形呢，虽然上下两条边不一样长，但它的上下边也是平行的。
所以，这俩形状有个共同点——平行！只是一个是四条边都平行，另一个只有两条。
嘿，别看平行这一点简单，真要画起来，光这一条就能让你摊上不少麻烦呢。
记得小时候画梯形或者平行四边形，总得小心翼翼的，生怕两条边跑偏，结果一不小心，画成了个“歪歪扭扭”的四边形，简直让人想哭。
再说它们的角。
平行四边形的对角是相等的，哎呀，感觉就像是老朋友见面，总是有那么些共同点。
而梯形呢，虽然不是所有角都相等，但它的上下角有些地方也像极了平行四边形。
你仔细看看，梯形的上底和下底那两边角，有的也能对应得上。
你说它们是不是有点“投缘”呢？你看，角度虽然不全等，但也是“心有灵犀”的。
别忘了这俩形状的面积公式。
哈哈，讲到公式，你是不是有点头大？不过别担心，其实它们的面积公式也挺有意思。
平行四边形的面积，算起来就是底边乘以高。
而梯形呢，虽然有上下两条边，但它的面积也差不多，算的是上下底边的平均值乘以高。
所以，虽然它们的形状不完全一样，算面积时用的思路其实挺像的。
像是做饭，虽然材料不一样，但最终做出来的菜，口感上竟然有点相似。
除了这些，从几何角度看，它们的对称性也有点共同之处。
平行四边形虽然没有严格意义上的对称轴，但它的对角线总是互相平分，感觉就像是默契十足的情侣，走到哪儿都在一起，哪里都不分开。
而梯形呢，虽然整体不是对称的，但有些特殊的梯形，比如等腰梯形，它的对称性也很强。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
梯形 四边形
从上图可以知道：
1、平行四边形、长方形、正方形、梯形都是（ 四边形
2、（ 长方形 ）和（
）。
正方形 ）是特殊的平行四边形。
3、（ 正方形
）形是特殊的长方形。
4、梯形（
不是
）特殊的平行四边形。注：填是或不是
1.判断下面说法正确吗？说说你的想法。
（1）正方形和长方形都是特殊的平行四边形。 （√ ） （2）长方形也是平行四边形。（ √ ）
人教版数学四年级上册
平行四边形和梯形
长方形
正方形
平行四边形 梯形
在下表内适当的空格内填上“√”，再说一说几 种图形之间的联系和区别。 四边形 正方形 长方形 平 行 四边形 梯形 四边相等 两组对边 只有一组 两组对边 分别相等 对边平行 分别平行 有四个 直角
√
√ √ √ √
√ √ √
√ √
平行四边形 长方形 正方形
（3）平行四边形是特殊的梯形。（ Х ） （4）两个完全相同的梯形可以拼成一个长方形 。（ Х ）