2014《热点重点难点专题透析》高考二轮数学第5专题(文)立体几何

合集下载

安徽省阜阳三中2014-2015高考数学二轮复习立体几何 .

二轮复习专题五：立体几何§5.2空间中的平行关系（1）【学习目标】1.理解数列的概念和几种简单的表示方法（列表、图象、通项公式）．2.了解数列通项公式的意义（数列是自变量为正整数的一类函数．）3.理解数列的函数特征，能利用数列的周期性，单调性解决数列的有关问题。

4.以极度的热情投入到课堂学习中，体验学习的快乐。

【学法指导】1.先认真阅读教材和一轮复习笔记，处理好知识网络构建，构建知识体系，形成系统的认识；2.限时30分钟独立、规范完成探究部分，并总结规律方法；3.找出自己的疑惑和需要讨论的问题准备课上讨论质疑；4.重点理解的内容：【高考方向】1.以三视图为载体，考查空间几何体面积、体积的计算.2.考查空间几何体的侧面展开图及简单的组合体问题．【课前预习】：一、知识网络构建二、高考真题再现（2013年普通高等学校招生统一考试安徽数学（理）试题（纯WORD版））如图,圆锥顶点为p.底面圆心为o,其母线与底面所成的角为22.5°.AB和CD是底面圆O上的两条平行的弦,轴OP与平面PCD所成的角为60°.∠.(Ⅰ)证明:平面PAB与平面PCD的交线平行于底面; (Ⅱ)求cos COD三、基本概念检测1.下列命题中，正确命题的个数是 .①若直线l上有无数个点不在平面α内，则l∥α;②若直线l与平面α平行，则l与平面α内的任意一条直线都平行；③如果两条平行直线中的一条直线与一个平面平行，那么另一条直线也与这个平面平行；④若直线l与平面α平行，则l与平面α内的任意一条直线都没有公共点.2.下列条件中，不能判断两个平面平行的是（填序号）. ①一个平面内的一条直线平行于另一个平面 ②一个平面内的两条直线平行于另一个平面 ③一个平面内有无数条直线平行于另一个平面 ④一个平面内任何一条直线都平行于另一个平面3.对于平面α和共面的直线m 、n ，下列命题中假命题是（填序号）. ①若m ⊥α，m ⊥n ，则n ∥α ②若m ∥α，n ∥α，则m ∥n ③若m ⊂α，n ∥α，则m ∥n④若m 、n 与α所成的角相等，则m ∥n4.[2014·北京卷] 如图13，正方形AMDE 的边长为2，B ，C 分别为AM ，MD 的中点．在五棱锥P ABCDE 中，F 为棱PE 的中点，平面ABF 与棱PD ，PC 分别交于点G ，H .(1)求证：AB ∥FG ；(2)若PA ⊥底面ABCDE ，且PA ＝AE ，求直线BC 与平面ABF 所成角的大小，并求线段PH 的长．图13解：(1)证明：在正方形AMDE 中，因为B 是AM 的中点，所以AB ∥DE .又因为AB ⊄平面PDE ，所以AB ∥平面PDE .因为AB ⊂平面ABF ，且平面ABF ∩平面PDE ＝FG ，所以AB ∥FG .(2)因为PA ⊥底面ABCDE ，所以PA ⊥AB ，PA ⊥AE .建立空间直角坐标系Axyz ，如图所示，则A (0，0，0)，B (1，0，0)，C (2，1，0)，P (0，0，2)，F (0，1，1)，BC →＝(1，1，0)．设平面ABF 的法向量为n ＝(x ，y ，z )，则⎩⎪⎨⎪⎧n ·AB →＝0，n ·AF →＝0，即⎩⎪⎨⎪⎧x ＝0，y ＋z ＝0. 令z ＝1，则y ＝－1.所以n ＝(0，－1，1)．设直线BC 与平面ABF 所成角为α，则 sin α＝|cos 〈n ，BC →〉|＝⎪⎪⎪⎪⎪⎪⎪⎪n ·BC→|n ||BC →|＝12. 因此直线BC 与平面ABF 所成角的大小为π6.设点H 的坐标为(u ，v ，w )．因为点H 在棱PC 上，所以可设PH →＝λPC →(0<λ<1)．即(u ，v ，w －2)＝λ(2，1，－2)，所以u ＝2λ，v ＝λ，w ＝2－2λ. 因为n 是平面ABF 的一个法向量，所以n ·AH →＝0，即(0，－1，1)·(2λ，λ，2－2λ)＝0，解得λ＝23，所以点H 的坐标为⎝ ⎛⎭⎪⎫43，23，23. 所以PH ＝⎝ ⎛⎭⎪⎫432＋⎝ ⎛⎭⎪⎫232＋⎝ ⎛⎭⎪⎫－432＝2.【课中研讨】：例1.[2014·新课标全国卷Ⅱ] 如图13，四棱锥P ABCD 中，底面ABCD 为矩形，PA ⊥平面ABCD ，E 为PD 的中点．(1)证明：PB ∥平面AEC ；(2)设二面角D AE C 为60的体积．解：(1)证明：连接BD 交AC 于点O ，连接EO . 因为ABCD 为矩形，所以O 为BD 的中点．又E 为PD 的中点，所以EO ∥PB . 因为EO ⊂平面AEC ，PB ⊄平面AEC ，所以PB ∥平面AEC .(2)因为PA ⊥平面ABCD ，ABCD 为矩形，所以AB ，AD ，AP 两两垂直．如图，以A 为坐标原点，AB →，AD ，AP 的方向为x 轴、y 轴、z 轴的正方向，|AP →|为单位长，建立空间直角坐标系A xyz ，则D ()0，3，0，E ⎝ ⎛⎭⎪⎫0，32，12，AE →＝⎝⎛⎭⎪⎫0，32，12.设B (m ，0，0)(m >0)，则C (m ，3，0)，AC →＝(m ，3，0)．设n 1＝(x ，y ，z )为平面ACE 的法向量，则⎩⎪⎨⎪⎧n 1·AC →＝0，n 1·AE →＝0，即⎩⎪⎨⎪⎧mx ＋3y ＝032y ＋12z ＝0可取n 1＝⎝ ⎛⎭⎪⎫3m ，－1，3.又n 2＝(1，0，0)为平面DAE 的法向量，由题设易知|cos 〈n 1，n 2〉|＝12，即33＋4m 2＝12，解得m ＝32. 因为E 为PD 的中点，所以三棱锥E ACD 的高为12.三棱锥E ACD 的体积V ＝13×12×3×32×12＝38.例2.[2014·山东卷] 如图13所示，在四棱柱ABCD A 1B 1C 1D 1中，底面ABCD 是等腰梯形，∠DAB ＝60°，AB ＝2CD ＝2，M 是线段AB 的中点．图13(1)求证：C 1M ∥平面A 1ADD 1；(2)若CD 1垂直于平面ABCD 且CD 1＝3，求平面C 1D 1M 和平面ABCD 所成的角(锐角)的余弦值．例3.(理)如图，在三棱柱ABC —A 1B 1C 1中，AA 1⊥平面ABC ，AB ⊥BC ，且AB ＝BC ＝2，点N 为B 1C 1的中点，点P 在棱A 1C 1上运动．(1)试问点P 在何处时，AB ∥平面PNC ，并证明你的结论；(2)在(1)的条件下，若AA 1<AB ，直线B 1C 与平面BCP 所成角的正弦值为1010，求二面角A －BP －C 的大小.[解析] (1)当点P 为A 1C 1的中点时，AB ∥平面PNC . ∵P 为A 1C 1的中点，N 为B 1C 1的中点，∴PN ∥A 1B 1∥AB ∵AB ⊄平面PNC ，PN ⊂平面PNC ，∴AB ∥平面PNC . (2)设AA 1＝m ，则m <2，∵AB 、BC 、BB ，两两垂直，∴以B 为原点，BA 、BC ，BB 1为x 轴、y 轴，z 轴建立空间直角坐标系，则A (2,0,0)，C (0,2,0)，B 1(0,0，m )，A 1(2,0，m )，C 1(0,2，m )，∴P (1,1，m )，设平面BCP 的法向量n ＝(x ，y ，z )，则由n ·BP →＝0，n ·BC →＝0，解得y ＝0，x ＝－mz ，令z ＝0，则n ＝(－m,0，－1)，又B 1C →＝(0,2，－m )，直线B 1C 与平面BCP 所成角正弦值为1010， ∴1010＝|n ·B 1C ||n |·|B 1C |，解之得m ＝1 ∴n ＝(－1,0,1)易求得平面ABP 的法向量n 1＝(0，－1,1)cos α＝n ·n 1|n |·|n 1|＝12，设二面角的平面角为θ，则cos θ＝－12，∴θ＝120°.例4.（2013年普通高等学校招生全国统一招生考试江苏卷（数学）（已校对纯WORD 版含附加题））本小题满分14分.如图,在三棱锥ABC S -中,平面⊥SAB 平面SBC ,BC AB ⊥,AB AS =,过A 作SB AF ⊥,垂足为F ,点G E ，分别是棱SC SA ，的中点. 求证:(1)平面//EFG 平面ABC ; (2)SA BC ⊥.【答案】证明:(1)∵AB AS =,SB AF ⊥∴F 分别是SB 的中点 ∵E.F 分别是SA.SB 的中点 ∴EF∥AB又∵EF ⊄平面ABC, AB ⊆平面ABC ∴EF∥平面ABC 同理:FG∥平面ABC又∵EF FG=F, EF.FG ⊆平面ABC∴平面//EFG 平面ABC (2)∵平面⊥SAB 平面SBC 平面SAB 平面SBC =BC AF ⊆平面SABAF⊥SB∴AF⊥平面SBC 又∵BC ⊆平面SBC ∴AF⊥BC又∵BC AB ⊥, AB AF=A, AB.AF ⊆平面SAB ∴BC⊥平面SAB 又∵SA ⊆平面SAB∴BC⊥SA例5.[2014·湖北卷] 如图14，在棱长为2的正方体ABCD A 1B 1C 1D 1中，E ，F ，M ，N 分别是棱AB ，AD ，A 1B 1，A 1D 1的中点，点P ，Q 分别在棱DD 1，BB 1上移动，且DP ＝BQ ＝λ(0<λ<2)．(1)当λ＝1时，证明：直线BC 1∥平面EFPQ .(2)是否存在λ，使面EFPQ 与面PQMN 所成的二面角为直二面角？若存在，求出λ的值；若不存在，说明理由．解：方法一(几何方法)：(1)证明：如图①，连接AD 1，由ABCD A 1B 1C 1D 1是正方体，知BC 1∥AD 1.当λ＝1时，P 是DD 1的中点，又F 是AD 的中点，所以FP ∥AD 1，所以BC 1∥FP . 而FP ⊂平面EFPQ ，且BC 1⊄平面EFPQ ，故直线BC 1∥平面EFPQ.ABSGFE(2)如图②，连接BD .因为E ，F 分别是AB ，AD 的中点，所以EF ∥BD ，且EF ＝12BD .又DP ＝BQ ，DP ∥BQ ，所以四边形PQBD 是平行四边形，故PQ ∥BD ，且PQ ＝BD ，从而EF ∥PQ ，且EF ＝12PQ .在Rt △EBQ 和Rt △FDP 中，因为BQ ＝DP ＝λ，BE ＝DF ＝1，于是EQ ＝FP ＝1＋λ2，所以四边形EFPQ 也是等腰梯形．同理可证四边形PQMN 也是等腰梯形．分别取EF ，PQ ，MN 的中点为H ，O ，G ，连接OH ，OG ，则GO ⊥PQ ，HO ⊥PQ ，而GO ∩HO ＝O ，故∠GOH 是面EFPQ 与面PQMN 所成的二面角的平面角．若存在λ，使面EFPQ 与面PQMN 所成的二面角为直二面角，则∠GOH ＝90°. 连接EM ，FN ，则由EF ∥MN ，且EF ＝MN 知四边形EFNM 是平行四边形．连接GH ，因为H ，G 是EF ，MN 的中点，所以GH ＝ME ＝2.在△GOH 中，GH 2＝4，OH 2＝1＋λ2－⎝ ⎛⎭⎪⎫222＝λ2＋12，OG 2＝1＋(2－λ)2－⎝ ⎛⎭⎪⎫222＝(2－λ)2＋12，由OG 2＋OH 2＝GH 2，得(2－λ)2＋12＋λ2＋12＝4，解得λ＝1±22，故存在λ＝1±22，使面EFPQ 与面PQMN 所成的二面角为直二面角．方法二(向量方法)：以D 为原点，射线DA ，DC ，DD 1分别为x ，y ，z 轴的正半轴建立如图③所示的空间直角坐标系．由已知得B (2，2，0)，C 1(0，2，2)，E (2，1，0)，F (1，0，0)，P (0，0，λ)．BC 1→＝(－2，0，2)，FP ＝(－1，0，λ)，FE ＝(1，1，0)． (1)证明：当λ＝1时，FP ＝(－1，0，1)，因为BC 1→＝(－2，0，2)，所以BC 1→＝2FP →，即BC 1∥FP .而FP ⊂平面EFPQ ，且BC 1⊄平面EFPQ ，故直线BC 1∥平面EFPQ .(2)设平面EFPQ 的一个法向量为n ＝(x ，y ，z )，则由⎩⎪⎨⎪⎧FE →·n ＝0，FP →·n ＝0可得⎩⎪⎨⎪⎧x ＋y ＝0，－x ＋λz ＝0.于是可取n ＝(λ，－λ，1)．同理可得平面MNPQ 的一个法向量为m ＝(λ－2，2－λ，1)．若存在λ，使面EFPQ 与面PQMN 所成的二面角为直二面角，则m ·n ＝(λ－2，2－λ，1)·(λ，－λ，1)＝0，即λ(λ－2)－λ(2－λ)＋1＝0，解得λ＝1±22. 故存在λ＝1±22，使面EFPQ 与面PQMN 所成的二面角为直二面角．【课后巩固】1.已知直线a,b,平面α，则以下三个命题： ①若a ∥b,b ⊂α,则a ∥α; ②若a ∥b,a ∥α,则b ∥α; ③若a ∥α,b ∥α,则a ∥b.其中真命题的个数是 .2.下列命题，其中真命题的个数为 . ①直线l 平行于平面α内的无数条直线，则l ∥α； ②若直线a 在平面α外，则a ∥α; ③若直线a ∥b,直线b ⊂α,则a ∥α；④若直线a ∥b,b ⊂α,那么直线a 就平行于平面α内的无数条直线.3．已知m ，n 是平面α外的两条直线，且m ∥n ，则“m ∥α”是“n ∥α”的________条件． 4.（2013年浙江试题）如图,在四面体BCD A -中,⊥AD 平面B C D,22,2,==⊥BD AD CD BC .M 是AD 的中点,P 是BM 的中点,点Q 在线段AC 上,且QC AQ 3=.(1)证明://PQ 平面BCD ;(2)若二面角D BM C --的大小为060,求BDC ∠的大小.【答案】解:证明(Ⅰ)方法一:如图6,取MD 的中点F ,且M 是AD 中点,所以3AF FD=.因为P 是BM 中点,所以//PF BD ;又因为(Ⅰ)3AQ QC =且3AF FD =,所以//QF BD ,所以面//PQF 面BDC ,且PQ ⊂面BDC ,所以//PQ 面BDC ;ABCDPQM（第20题图）方法二:如图7所示,取BD 中点O ,且P 是BM 中点,所以1//2PO MD ;取CD 的三等分点H ,使3DH CH =,且3AQ QC =,所以11////42QH AD MD ,所以////P O Q H P Q O H ∴,且OHBCD ⊂,所以//PQ 面BDC ; (Ⅱ)如图8所示,由已知得到面ADB ⊥面BDC ,过C 作CG BD ⊥于G ,所以CG BMD ⊥,过G 作GH BM ⊥于H ,连接CH ,所以CHG ∠就是C BM D --的二面角;由已知得到3BM ==,设BDC α∠=,所以cos ,sin ,sin ,,CD CG CBCD CG BC BD CD BDαααααα===⇒===,在RT BCG ∆中,2sin BGBCG BG BCααα∠=∴=∴=,所以在RT BHG ∆中, 2133HG α=∴=,所以在RT CHG ∆中tan tan 6033CG CHGHG ∠==== tan (0,90)6060BDC ααα∴=∈∴=∴∠=;5.[2014·北京卷] 正方形AMDE的边长为2，B，C分别为AM，MD的中点．在五棱锥P ABCDE中，F为棱PE的中点，平面ABF与棱PD，PC分别交于点G，H.(1)求证：AB∥FG；(2)若PA⊥底面ABCDE，且PA＝AE，求直线BC与平面ABF所成角的大小，并求线段PH的长．【反思与疑惑】：请同学们将其集中在典型题集中。

高三数学二轮复习专题《立体几何》

高三数学二轮复习专题《立体几何》专题热点透析高考中立体几何主要考查学生的空间想象能力，在推理中兼顾考查逻辑思维能力，解决立体几何的基本方法是将空间问题转化为平面问题。

近几年高考立体几何试题以基础题和中档题为主，热点问题主要有证明点线面的关系，如点共线、线共点、线共面问题；证明空间线面平行、垂直关系；求空间的角和距离；利用空间向量，将空间中的性质及位置关系的判定与向量运算相结合，使几何问题代数化等等。

考查的重点是点线面的位置关系及空间距离和空间角，突出空间想象能力，侧重于空间线面位置关系的定性与定量考查，算中有证。

其中选择、填空题注重几何符号语言、文字语言、图形语言三种语言的相互转化，考查学生对图形的识别、理解和加工能力；解答题则一般将线面集中于一个几何体中，即以一个多面体为依托，设置几个小问，设问形式以证明或计算为主。

热点题型范例一、平行与垂直的证明例1．如图，在四棱锥P —ABCD 中，底面ABCD 是正方形，侧棱PD ⊥底面ABCD ，PD =DC ，E 是PC 的中点，作EF ⊥PB 交PB 于点F . （1）证明P A //平面EDB ；（2）证明PB ⊥平面EFD 解：（1）连结AC ，AC 交BD 于O ，连结EO . ∵底面ABCD 是正方形，∴点O 是AC 的中点在PAC ∆中，EO 是中位线，∴P A // EO而⊂EO 平面EDB 且⊄PA 平面EDB ，所以，P A // 平面EDB （2）∵PD ⊥底面ABCD 且⊂DC 底面ABCD ，∴DC PD ⊥∵PD =DC ，可知PDC ∆是等腰直角三角形，而DE 是斜边PC 的中线，∴PC DE ⊥. ①同样由PD ⊥底面ABCD ，得PD ⊥BC .∵底面ABCD 是正方形，有DC ⊥BC ，∴BC ⊥平面PDC .而⊂DE 平面PDC ，∴DE BC ⊥. ②由①和②推得⊥DE 平面PBC .而⊂PB 平面PBC ，∴PB DE ⊥ 又PB EF ⊥且E EF DE = ，所以PB ⊥平面EFD .例2．四棱锥S ABCD -中，底面ABCD 为平行四边形，侧面SBC ⊥底面ABCD ，已知45ABC ∠=︒，2AB =，BC =，SA SB ==（Ⅰ）证明：SA BC ⊥；（Ⅱ）求直线SD 与平面SBC 所成角的大小．解：（1）作SO BC ⊥，垂足为O ，连结AO ，由侧面SBC ⊥底面ABCD ，得SO ⊥底面ABCD ．因为A CDBCASOESA SB =，所以AO BO =，又45ABC =∠，故AOB △为等腰直角三角形，AO BO ⊥，由三垂线定理，得SA BC ⊥．（Ⅱ）由（Ⅰ）知SA BC ⊥，依题设AD BC ∥，故SA AD ⊥，由AD BC ==，SA =SD sin 452AO AB ==DE BC ⊥，垂足为E ，则DE ⊥平面SBC ，连结SE ．ESD ∠为直线SD 与平面SBC 所成的角．sin 11ED AO ESD SD SD ====∠，所以直线SD 与平面SBC所成的角为． 1.1已知四棱锥P -ABCD 的底面为直角梯形，AB ∥DC ，⊥=∠PA DAB ,90底面ABCD ，且P A =AD =DC =21AB =1，M 是PB 的中点. （Ⅰ）证明：面P AD ⊥面PCD ；（Ⅱ）求AC 与PB 所成的角；（Ⅲ）求面AMC 与面BMC 所成二面角的大小. 解：（Ⅰ）∵P A ⊥面ABCD ，CD ⊥AD ，∴由三垂线定理得：CD ⊥PD .因而，CD 与面P AD 内两条相交直线AD ，PD 都垂直，∴CD ⊥面P AD .又CD ⊂面PCD ，∴面P AD ⊥面PCD .（Ⅱ）过点B 作BE //CA ，且BE =CA ，则∠PBE 是AC 与PB 所成的角.连结AE ，可知AC =CB =BE =AE =2，又AB =2，所以四边形ACBE 为正方形. 由P A ⊥面ABCD 得∠PEB =90° 在Rt △PEB 中BE =2，PB =5， .510cos ==∠∴PB BE PBE .510arccos 所成的角为与PB AC ∴ （Ⅲ）作AN ⊥CM ，垂足为N ，连结BN .在Rt △P AB 中，AM =MB ，又AC =CB ，∴△AMC ≌△BMC ，∴BN ⊥CM ，故∠ANB 为所求二面角的平面角.∵CB ⊥AC ，由三垂线定理，得CB ⊥PC ，在Rt △PCB 中，CM =MB ，所以CM =AM .在等腰三角形AMC 中，AN ·MC =AC AC CM ⋅-22)2(，5625223=⨯=∴AN . ∴AB =2，322cos 222-=⨯⨯-+=∠∴BN AN AB BN AN ANB 故所求的二面角为).32arccos(-ADCBNM EP二、空间角与距离例3．如图，在四棱锥O ABCD -中，底面ABCD 四边长为1的菱形，4ABC π∠=， OA ABCD ⊥底面， 2OA =，M 为OA 的中点。

高考数学二轮复习立体几何的知识点

高考数学二轮复习立体几何的知识点平面几何是3维欧氏空间的几何的传统称号。

下面是平面几何的知识点的相关内容，希望对考生温习有协助。

(1)棱柱：定义：有两个面相互平行，其他各面都是四边形，且每相邻两个四边形的公共边都相互平行，由这些面所围成的几何体。

分类：以底面多边形的边数作为分类的规范分为三棱柱、四棱柱、五棱柱等。

表示：用各顶点字母，如五棱柱或用对角线的端点字母，如五棱柱几何特征：两底面是对应边平行的全等多边形;正面、对角面都是平行四边形;侧棱平行且相等;平行于底面的截面是与底面全等的多边形。

(2)棱锥定义：有一个面是多边形，其他各面都是有一个公共顶点的三角形，由这些面所围成的几何体分类：以底面多边形的边数作为分类的规范分为三棱锥、四棱锥、五棱锥等表示：用各顶点字母，如五棱锥几何特征：正面、对角面都是三角形;平行于底面的截面与底面相似，其相似比等于顶点到截面距离与高的比的平方。

(3)棱台：定义：用一个平行于棱锥底面的平面去截棱锥，截面和底面之间的局部分类：以底面多边形的边数作为分类的规范分为三棱态、四棱台、五棱台等表示：用各顶点字母，如五棱台几何特征：①上下底面是相似的平行多边形②正面是梯形③侧棱交于原棱锥的顶点(4)圆柱：定义：以矩形的一边所在的直线为轴旋转，其他三边旋转所成的曲面所围成的几何体几何特征：①底面是全等的圆;②母线与轴平行;③轴与底面圆的半径垂直;④正面展开图是一个矩形。

(5)圆锥：定义：以直角三角形的一条直角边为旋转轴，旋转一周所成的曲面所围成的几何体几何特征：①底面是一个圆;②母线交于圆锥的顶点;③正面展开图是一个扇形。

(6)圆台：定义：用一个平行于圆锥底面的平面去截圆锥，截面和底面之间的局部几何特征：①上下底面是两个圆;②正面母线交于原圆锥的顶点;③正面展开图是一个弓形。

(7)球体：定义：以半圆的直径所在直线为旋转轴，半圆面旋转一周构成的几何体几何特征：①球的截面是圆;②球面上恣意一点到球心的距离等于半径。

高考数学二轮复习立体几何多选题知识归纳总结及解析

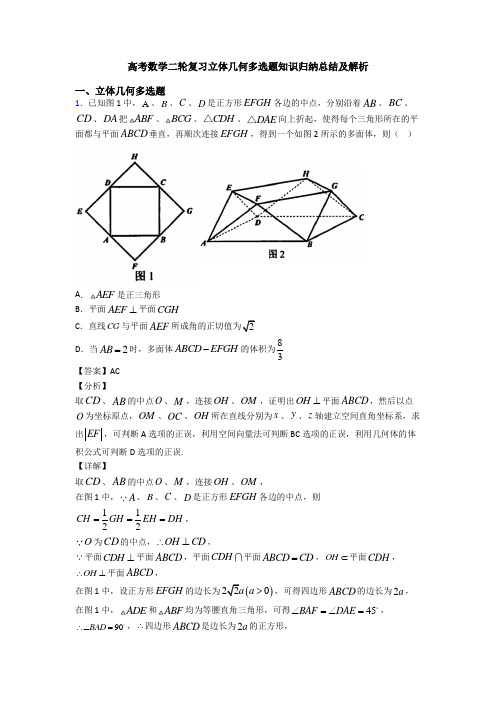
高考数学二轮复习立体几何多选题知识归纳总结及解析一、立体几何多选题1．已知图1中，A 、B 、C 、D 是正方形EFGH 各边的中点，分别沿着AB 、BC 、CD 、DA 把ABF 、BCG 、CDH △、DAE △向上折起，使得每个三角形所在的平面都与平面ABCD 垂直，再顺次连接EFGH ，得到一个如图2所示的多面体，则（）A ．AEF 是正三角形B ．平面AEF ⊥平面CGHC ．直线CG 与平面AEF 2D ．当2AB =时，多面体ABCD EFGH -的体积为83【答案】AC 【分析】取CD 、AB 的中点O 、M ，连接OH 、OM ，证明出OH ⊥平面ABCD ，然后以点O 为坐标原点，OM 、OC 、OH 所在直线分别为x 、y 、z 轴建立空间直角坐标系，求出EF ，可判断A 选项的正误，利用空间向量法可判断BC 选项的正误，利用几何体的体积公式可判断D 选项的正误. 【详解】取CD 、AB 的中点O 、M ，连接OH 、OM ，在图1中，A 、B 、C 、D 是正方形EFGH 各边的中点，则1122CH GH EH DH ===，O 为CD 的中点，OH CD ∴⊥，平面CDH ⊥平面ABCD ，平面CDH 平面ABCD CD =，OH ⊂平面CDH ，OH ∴⊥平面ABCD ，在图1中，设正方形EFGH 的边长为()220a a >，可得四边形ABCD 的边长为2a ，在图1中，ADE 和ABF 均为等腰直角三角形，可得45BAF DAE ∠=∠=， 90BAD ∴∠=，∴四边形ABCD 是边长为2a 的正方形，O 、M 分别为CD 、AB 的中点，则//OC BM 且OC BM =，且90OCB ∠=，所以，四边形OCBM 为矩形，所以，OM CD ⊥，以点O 为坐标原点，OM 、OC 、OH 所在直线分别为x 、y 、z 轴建立空间直角坐标系，则()2,,0A a a -、()2,,0B a a 、()0,,0C a 、()0,,0D a -、(),,E a a a -、()2,0,F a a 、(),,G a a a 、()0,0,H a .对于A 选项，由空间中两点间的距离公式可得2AE AF EF a ===，所以，AEF 是正三角形，A 选项正确；对于B 选项，设平面AEF 的法向量为()111,,m x y z =，(),0,AE a a =-，()0,,AF a a =，由11110m AE ax az m AF ay az ⎧⋅=-+=⎪⎨⋅=+=⎪⎩，取11z =，则11x =，11y =-，则()1,1,1m =-，设平面CGH 的法向量为()222,,n x y z =，(),0,CG a a =，()0,,CH a a =-，由222200n CG ax az n CH ay az ⎧⋅=+=⎪⎨⋅=-+=⎪⎩，取21z =-，可得21x =，21y =-，则()1,1,1n =--，()22111110m n ⋅=+--⨯=≠，所以，平面AEF 与平面CGH 不垂直，B 选项错误；对于C 选项，6cos ,23CG m CG m a CG m⋅<>===⨯⋅，设直线CG 与平面AEF 所成角为θ，则sin 6θ=，23cos 1sin θθ=-=，所以，sin tan 2cos θθθ==，C 选项正确；对于D 选项，以ABCD 为底面，以OH 为高将几何体ABCD EFGH -补成长方体1111ABCD A B C D -，则E 、F 、G 、H 分别为11A D 、11A B 、11B C 、11C D 的中点，因为2AB =，即1a =，则1OH =，长方体1111ABCD A B C D -的体积为2214V =⨯=，11211111113326A A EF A EF V S AA -=⋅=⨯⨯⨯=△，因此，多面体ABCD EFGH -的体积为111044463ABCD EFGH A A EF V V V --=-=-⨯=， D 选项错误. 故选：AC. 【点睛】方法点睛：计算线面角，一般有如下几种方法：（1）利用面面垂直的性质定理，得到线面垂直，进而确定线面角的垂足，明确斜线在平面内的射影，即可确定线面角；（2）在构成线面角的直角三角形中，可利用等体积法求解垂线段的长度h ，从而不必作出线面角，则线面角θ满足sin hlθ=（l 为斜线段长），进而可求得线面角；（3）建立空间直角坐标系，利用向量法求解，设a 为直线l 的方向向量，n 为平面的法向量，则线面角θ的正弦值为sin cos ,a n θ=<>.2．如图所示，正三角形ABC 中，D ，E 分别为边AB ，AC 的中点，其中AB ＝8，把△ADE 沿着DE 翻折至A 'DE 位置，使得二面角A '-DE -B 为60°，则下列选项中正确的是（）A ．点A '到平面BCED 的距离为3B ．直线A 'D 与直线CE 所成的角的余弦值为58C ．A 'D ⊥BDD ．四棱锥A '-BCED 237【答案】ABD 【分析】作AM ⊥DE ，交DE 于M ,延长AM 交BC 于N ,连接A'M ,A'N .利用线面垂直的判定定理判定CD ⊥平面A'MN ,利用面面垂直的判定定理与性质定理得到'A 到平面面BCED 的高A'H ,并根据二面角的平面角，在直角三角形中计算求得A'H 的值，从而判定A;根据异面直线所成角的定义找到∠A'DN 就是直线A'D 与CE 所成的角，利用余弦定理计算即可判定B;利用勾股定理检验可以否定C;先证明底面的外接圆的圆心为N ,在利用外接球的球心的性质进行得到四棱锥A'-BCED 的外接球的球心为O ,则ON ⊥平面BCED ,且OA'=OC ,经过计算求解可得半径从而判定D. 【详解】如图所示，作AM ⊥DE ，交DE 于M ,延长AM 交BC 于N ,连接A'M ,A'N . 则A'M ⊥DE ,MN ⊥DE , ,∵'A M ∩MN =M ,∴CD ⊥平面A'MN , 又∵CD ⊂平面ABDC ,∴平面A'MN ⊥平面ABDC , 在平面A'MN 中作A'H ⊥MN ,则A'H ⊥平面BCED , ∵二面角A'-DE -B 为60°，∴∠A'EF =60°，∵正三角形ABC 中，AB =8,∴AN =∴A'M ,∴A'H =A'M sin60°=3，故A 正确；连接DN ,易得DN ‖EC ,DN =EC =4, ∠A'DN 就是直线A'D 与CE 所成的角，DN =DA'=4,A'N =A'M ,cos ∠A'DN =22441252448+-=⨯⨯,故B 正确；A'D =DB =4,==,∴222A D DB A B '≠'+,∴A'D 与BD 不垂直，故C 错误’ 易得NB =NC =ND =NG =4，∴N 为底面梯形BCED 的外接圆的圆心，设四棱锥A'-BCED 的外接球的球心为O ,则ON ⊥平面BCED ,且OA'=OC , 若O 在平面BCED 上方，入图①所示：设ON =x ,外接球的半径为R ,过O 作A'H 的垂线，垂足为P ,则HP =x ,易得()2222243x x R +=-+=,解得23x =-,舍去；故O 在平面BCED 下方，如图②所示：设ON =x ,外接球的半径为R ,过O 作A'H 的垂线，垂足为P ,则HP =x ,易得()2222243x x R +=++=, 解得23x =,∴244371699R ⨯=+=,R ∴=故D 正确. 故选:ABD .【点睛】本题考查立体几何中的折叠问题，涉及二面角问题，异面直线所成的角，用到线面、面面垂直的判定与性质及外接球的球心的性质和有关计算，余弦定理等，属综合性较强的题目，关键是利用线面垂直，面面垂直的判定和性质进行空间关系和结构的判定，注意球心在四棱锥的底面上方和下方的讨论与验证.3．如图，直三棱柱11,ABC A B C -，ABC 为等腰直角三角形，AB BC ⊥，且12AC AA ==，E ，F 分别是AC ，11A C 的中点，D ，M 分别是1AA ，1BB 上的两个动点，则（）A ．FM 与BD 一定是异面直线B ．三棱锥D MEF -的体积为定值14C ．直线11B C 与BD 所成角为2π D ．若D 为1AA 中点，则四棱锥1D BB FE -55【答案】CD 【分析】A 当特殊情况M 与B 重合有FM 与BD 相交且共面；B 根据线面垂直、面面垂直判定可证面1BEFB ⊥面11ACC A ，可知EMFS、D 到面1BEFB 的距离，可求D EMF V -；C 根据线面垂直的判定及性质即可确定11B C 与BD 所成角；D 由面面垂直、勾股、矩形性质等确定外接球半径，进而求体积，即可判断各项的正误. 【详解】A ：当M 与B 重合时，FM 与BD 相交且共面，错误； B ：由题意知：BE AC ⊥，AC EF ⊥且BEEF E =，则AC ⊥面1BEFB ，又AC ⊂面11ACC A ，面1BEFB ⋂面11ACC A EF =，所以面1BEFB ⊥面11ACC A ，又1121122EMFSEF BE =⋅⋅=⨯⨯=，D 到面1BEFB 的距离为1h =，所以1133D EMF EMFV h S-=⋅⋅=，错误； C ：由AB BC ⊥，1BC B B ⊥，1B BAB B =，所以BC ⊥面11ABB A ，又11//BC B C ，即11B C ⊥面11ABB A ，而BD ⊂面11ABB A ，则11BD B C ⊥，正确；D ：由B 中，面1BEFB ⊥面11ACC A ，即面DEF ⊥面1BEFB ，则D 到面1BEFB 的距离为1h =，又D 为1AA 中点，若1,BF EB 交点为O ，G 为EF 中点，连接,,OG GD OD ，则OG GD ⊥，故2252OD OG GD =+=，由矩形的性质知：15OB OE OF OB ====令四棱锥1D BB FE -的外接球半径为R ，则52R =，所以四棱锥1D BB FE -的外接球体积为35435V R π==，正确. 故选：CD. 【点睛】关键点点睛：利用线面、面面关系确定几何体的高，结合棱锥体积公式求体积，根据线面垂直、勾股定理及矩形性质确定外接球半径，结合球体体积公式求体积.4．在正方体1111ABCD A B C D -中，M 、N 分别是棱AB 、1CC 的中点，1MB P 的顶点P 在棱1CC 与棱11C D 上运动，有以下四个命题正确命题的序号是（）A ．平面1MB P 1ND ⊥ B ．平面1MB P ⊥平面11ND AC ．1MB P 在底面ABCD 上的射影图形的面积为定值 D ．1MB P 在侧面11D C CD 上射影图形是三角形【答案】BC 【分析】取N 与P 重合，结合勾股定理可判断A 选项的正误；利用面面垂直的判定定理可判断B 选项的正误；分点P 在棱1CC 、11C D 上运动两种情况讨论，利用三角形的面积公式可判断C 选项的正误；取点P 与点1C 重合，判断1MB P 在侧面11D C CD 上射影图形形状，可判断D 选项的正误. 【详解】对于A 选项，设正方体1111ABCD A B C D -的棱长为2，如下图所示：当点P 与点N 重合时，若1ND ⊥平面1MB P ，1B N ⊂平面1MB P ，则11ND B N ⊥，由勾股定理可得2211115D N C N C D =+=，同理可得15B N =，1122B D =，2221111B N D N B D ∴+≠，则1ND 与1B N 不垂直，假设不成立，A 选项错误；对于B 选项，取1BB 的中点E ，连接1A E 、EN ，在正方体1111ABCD A B C D -中，11//BB CC ，且E 、N 分别为1BB 、1CC 的中点，则11//B E C N 且11B E C N =，所以，四边形11B ENC 为平行四边形，则11//EN B C 且11EN B C =，1111//A D B C 且1111A D B C =，所以，11//A D EN 且11A D EN =，所以，四边形11A END 为平行四边形，所以，11//A E D N ，111A B BB =，1B E BM =，11190A B E B BM ∠=∠=，所以，111Rt A B E Rt B BM ≅△△，所以，111B A E BB M ∠=∠，所以，111111190A EB BB M A EB B A E ∠+∠=∠+∠=，190B FE ∴∠=，所以，11B M A E ⊥，11A D ⊥平面11AA B B ，1B M ⊂平面11AA B B ，111B M A D ∴⊥， 1111A D A E A =，11A D 、1A E ⊂平面11ND A ，1MB ∴⊥平面11ND A ，1MB ⊂平面1MB P ，所以，平面1MB P ⊥平面11ND A ，B 选项正确；对于C 选项，设正方体1111ABCD A B C D -的棱长为a .若点P 在棱1CC 上运动时，1MB P 在底面ABCD 上的射影为MBC △，此时，射影图形的面积为21224MBCa a S a =⋅=△；若点P 在棱11C D 上运动时，设点P 在底面ABCD 上的射影点为G ，则G CD ∈，且点G 到AB 的距离为a ,1MB 在底面ABCD 内的射影为MB ，则1MB P 在底面ABCD 内的射影为MBG △，且21224MBGa a S a =⋅⋅=△.综上所述，1MB P 在底面ABCD 内的射影图形的面积为定值，C 选项正确；对于D 选项，当点P 与1C 重合时，P 、1B 两点在平面11D C CD 上的射影重合，此时，1MB P 在侧面11D C CD 上的射影不构成三角形，D 选项错误. 故选：BC. 【点睛】方法点睛：证明面面垂直常用的方法：（1）面面垂直的定义；（2）面面垂直的判定定理.在证明面面垂直时，一般假设面面垂直成立，然后利用面面垂直转化为线面垂直，即为所证的线面垂直，组织论据证明即可.5．如图四棱锥P ABCD -，平面PAD ⊥平面ABCD ，侧面PAD 是边长为26的正三角形，底面ABCD 为矩形，23CD =，点Q 是PD 的中点，则下列结论正确的是（）A ．CQ ⊥平面PADB ．PC 与平面AQC 22C ．三棱锥B ACQ -的体积为62D ．四棱锥Q ABCD -外接球的内接正四面体的表面积为3【答案】BD 【分析】取AD 的中点O ，BC 的中点E ，连接,OE OP ，则由已知可得OP ⊥平面 ABCD ，而底面ABCD 为矩形，所以以O 为坐标原点，分别以,,OD OE OP 所在的直线为x 轴，y 轴，z 轴，建立空间直角坐标系，利用空间向量依次求解即可. 【详解】解：取AD 的中点O ，BC 的中点E ，连接,OE OP ，因为三角形PAD 为等边三角形，所以OP AD ⊥, 因为平面PAD ⊥平面ABCD ，所以OP ⊥平面 ABCD ，因为AD OE ⊥，所以,,OD OE OP 两两垂直，所以，如下图，以O 为坐标原点，分别以,,OD OE OP 所在的直线为x 轴，y 轴，z 轴，建立空间直角坐标系，则(0,0,0),(6,0,0),(6,0,0)O D A ，(0,0,32),6,23,0),(6,23,0)P C B ，因为点Q 是PD 的中点，所以632,0,)22Q ，平面PAD 的一个法向量为(0,1,0)m =，632(23,2QC =-，显然 m 与QC 不共线，所以CQ 与平面PAD 不垂直，所以A 不正确；3632(6,23,32),(,0,),(26,23,0)PC AQ AC =-==，设平面AQC 的法向量为(,,)n x y z =，则3602260n AQ x zn AC ⎧⋅=+=⎪⎨⎪⋅=+=⎩，令=1x ，则y z ==，所以(1,2,n =-，设PC 与平面AQC 所成角为θ，则21sin 36n PCn PC θ⋅===，所以cos θ=，所以B 正确；三棱锥B ACQ -的体积为1132B ACQ Q ABC ABC V V S OP --==⋅1116322=⨯⨯⨯=，所以C 不正确；设四棱锥Q ABCD -外接球的球心为)M a ，则MQ MD =，所以222222a a ⎛++-=++ ⎝⎭⎝⎭，解得0a =，即M 为矩形ABCD 对角线的交点，所以四棱锥Q ABCD -外接球的半径为3，设四棱锥Q ABCD -外接球的内接正四面体的棱长为x ，将四面体拓展成正方体，其中正四面体棱为正方体面的对角线，故正方体的棱长为2x，所以22362x ⎛⎫= ⎪ ⎪⎝⎭，得224x =，所以正四面体的表面积为24x =，所以D 正确. 故选：BD【点睛】此题考查线面垂直，线面角，棱锥的体积，棱锥的外接球等知识，综合性强，考查了计算能力，属于较难题.6．如果一个棱锥的底面是正方形，且顶点在底面内的射影是底面的中心，那么这样的棱锥叫正四棱锥．若一正四棱锥的体积为18，则该正四棱锥的侧面积最小时，以下结论正确的是（）．A 2B ．侧棱与底面所成的角为4π C 2D ．侧棱与底面所成的角为3π 【答案】AB【分析】设四棱锥S ABCD -的高为h ，底面边长为a ，由21183V a h ==得254h a =，然后可得侧242108a a+32a =时侧面积取得最小值，此时3h =，然后求出棱锥的高与底面边长的比和SAO ∠即可选出答案.【详解】设四棱锥S ABCD -的高为h ，底面边长为a 可得21183V a h ==，即254h a= 所以其侧面积为2222244215410842244a a a h a a a⋅⋅+=+=+令()242108f a a a =+，则()23321084f a a a ⨯'=- 令()233210840f a a a ⨯'=-=得32a = 当(0,32a ∈时()0f a '<，()f a 单调递减当()32,a ∈+∞时()0f a '>，()f a 单调递增所以当32a =时()f a 取得最小值，即四棱锥的侧面积最小此时3h = 所以棱锥的高与底面边长的比为22，故A 正确，C 错误侧棱与底面所成的角为SAO ∠，由3h =，32a =可得3AO = 所以4SAO π∠=，故B 正确，D 错误故选：AB【点睛】本题考查的知识点有空间几何体的体积和表面积、线面角及利用导数求最值，属于综合题.7．如图所示，正方体ABCD A B C D ''''-的棱长为1，E ，F 分别是棱AA '，CC '的中点，过直线EF 的平面分别与棱BB '，DD '交于点M ，N ，以下四个命题中正确的是（）A ．0MN EF ⋅=B ．ME NE =C ．四边形MENF 的面积最小值与最大值之比为2:3D ．四棱锥A MENF -与多面体ABCD EMFN -体积之比为1:3【答案】ABD【分析】证明EF ⊥平面BDD B ''，进而得EF MN ⊥，即可得A 选项正确；证明四边形MENF 为菱形即可得B 选项正确；由菱形性质得四边形MENF 的面积12S MN EF =⋅，再分别讨论MN 的最大值与最小值即可；根据割补法求解体积即可.【详解】对于A 选项，如图，连接BD ，B D ''，MN ．由题易得EF BD ⊥，EF BB '⊥，BD BB B '⋂=，所以EF ⊥平面BDD B ''，又MN ⊂平面BDD B ''，所以EF MN ⊥，因此0MN EF ⋅=，故A 正确．对于B 选项，由正方体性质得：平面''//BCC B 平面''ADD A ，平面''BCC B 平面EMFN MF =，平面''ADD A 平面EMFN EN =，所以//MF EN ，同理得//ME NF ，又EF MN ⊥，所以四边形MENF 为菱形，因此ME NE =，故B 正确．对于C 选项，由B 易得四边形MENF 的面积12S MN EF =⋅，所以当点M ，N 分别为BB '，DD '的中点时，四边形MENF 的面积S 最小，此时2MN EF ==，即面积S 的最小值为1；当点M ，N 分别与点B （或点B '），D （或D ）重合时，四边形MENF 的面积S 最大，此时3MN =，即面积S 的最大值为6，所以四边形MENF 的面积最小值与最大值之比为2:6，故C 不正确．对于D 选项，四棱锥A MENF -的体积1112123346M AEF N AEF AEF V V V DB S --=+=⋅=⨯⨯=△；因为E ，F 分别是AA '，CC '的中点，所以BM D N '=，DN B M '=，于是被截面MENF 平分的两个多面体是完全相同的，则它们的体积也是相同的，因此多面体ABCD EMFN -的体积21122ABCD A B C D V V ''''-==正方体，所以四棱锥A MENF -与多面体ABCD EMFN -体积之比为1:3，故D 正确．故选：ABD ．【点睛】本题考查立体几何与向量的综合、截面面积的最值、几何体的体积，考查空间思维能力与运算求解能力，是中档题.本题解题的关键在于证明四边形MENF 为菱形，利用割补法将四棱锥A MENF -的体积转化为三棱锥M AEF - 和N AEF -的体积之和，将多面体ABCD EMFN -的体积转化为正方体的体积的一半求解.8．半正多面体（semiregularsolid ）亦称“阿基米德多面体”，是由边数不全相同的正多边形围成的多面体，体现了数学的对称美．二十四等边体就是一种半正多面体，是由正方体切截而成的，它由八个正三角形和六个正方形构成（如图所示），若它的所有棱长都为2 ）A ．BF ⊥平面EABB ．该二十四等边体的体积为203C ．该二十四等边体外接球的表面积为8πD ．PN 与平面EBFN 2 【答案】BCD【分析】 A 用反证法判断；B 先补齐八个角成正方体，再计算体积判断；C 先找到球心与半径，再计算表面积判断；D 先找到直线与平面所成角，再求正弦值判断．【详解】解：对于A ，假设A 对，即BF ⊥平面EAB ，于是BF AB ⊥，90ABF ∠=︒，但六边形ABFPQH 为正六边形，120ABF ∠=︒，矛盾，所以A 错；对于B ，补齐八个角构成棱长为2的正方体，则该二十四等边体的体积为3112028111323-⋅⋅⋅⋅⋅=，所以B 对；对于C ，取正方形ACPM 对角线交点O ，即为该二十四等边体外接球的球心，其半径为2R =248R ππ=，所以C 对；对于D ，因为PN 在平面EBFN 内射影为NS ，所以PN 与平面EBFN 所成角即为PNS ∠，其正弦值为22PS PN =，所以D 对．故选：BCD ．【点睛】本题考查了正方体的性质，考查了直线与平面所成角问题，考查了球的体积与表面积计算问题．。

2014年高考试题分析及2015年复习备考建议立体几何

立体几何
【典例2】[2014•安徽卷] 一个多面体的三视图如图12所示，则该多面体的表面积为( ) A．21＋√�� B．8＋√�� C．21 D．18 【解析】该题主要考查正方体三棱锥的三视图识别与其表面积的求解. 【典例3】】[2014· 浙江卷] 几何体的三视图(单位：cm)如图11所示，则此几何体的表面积是 ( ) A．90 cm2 B．129 cm2 C．132 cm2 D．138 cm2 【解析】该题主要考查长方体与三棱柱的三视图识别与其表面积的求解.
1.文科重在空间线面关系的逻辑证明，与几何体的表面积、体积等问题综合
【典例1】[2014•山东卷] 如图14所示，四棱锥 PABCD中，AP⊥平面PCD，AD∥BC，AB＝BC＝ 12AD，E，F分别为线段AD，PC的中点．(1)求证： AP∥平面BEF；(2)求证：BE⊥平面PAC.
【分析】本题以棱锥为载体主要考查空间线面关系的逻辑证明，考查了空间想象能力以及基本的推理证明能力.
立体几何
【典例4】[2014•广东卷] 如图12所示，四边形ABCD为矩形，PD⊥平面ABCD，AB＝1，BC＝PC＝2，作如图折叠：折痕EF∥DC，其中点 E，F分别在线段PD，PC上，沿EF折叠后点P叠在线段AD上的点记为M，并且MF⊥CF. (1)证明：CF⊥平面MDF； (2)求三棱锥M -CDE的体积．【分析】本题以三棱锥为载体主要考查几何体体积的求解以及以及空间线面垂直的证明、平面图形的翻折问题，考查了空间想象能力以及基本的推理证明能力.
5
文理同题文理载体相同 1 问相同，2 问不同
以四棱锥为载体，考查线面 15 垂直的证明和线面角的求解
以四棱锥为载体，考查线面垂直的证 15 明和二面角的求解

2014届高考数学专题复习课件：第三篇专题5 立体几何

查缺补漏
第三篇 5
BC 与 AE 是相交直线，所以 BC 一定不与平面 PAE 平行， ③错误；
本讲
直线 PD 与平面 ABC 所成角为∠PDA，
栏目
在 Rt△PAD 中，AD＝PA，
开
关 ∴∠PDA＝45°，④正确．
答案 ④
查缺补漏
第三篇 5
8．对于四面体 ABCD，给出下列四个命题：
①若 AB＝AC，BD＝CD，则 BC⊥AD；
目
开关
∴∠BSA＝90°，以 S 为顶点，将三棱锥补成
一个正方体，如图所示，
故外接球的直径 2R＝ 3·SA，即 R＝3，
∴S＝4πR2＝36π.
查缺补漏
第三篇 5
10．如图，在四棱锥 P－ABCD 中，平面 PAD⊥
平面 ABCD，AB＝AD，∠BAD＝60°，E，
F 分别是 AP，AD 的中点．
目开
②若 α∥β，l⊂α，则 l∥β；
关 ③α⊥γ，β⊥γ，则 α∥β；
④若 m，n 为异面直线，m⊂α，n⊂β，m∥β，n∥α，则 α∥β.
其中正确命题的个数是________．
查缺补漏
第三篇 5
解析因为平行于同一平面的两条直线除了平行，还可能相交或成异面直线，所以命题①错误；
由直线与平面平行的定义知命题②正确；
求证：(1)直线 EF∥平面 PCD；
本讲
(2)平面 BEF⊥平面 PAD.
栏目
证明 (1)因为 E，F 分别是 AP，AD 的中点，∴EF∥PD.
开关
又∵PD⊂面 PCD，EF⊄面 PCD，
∴直线 EF∥平面 PCD.
(2)连结 BD，∵AB＝AD，∠BAD＝60°，

2014年高考数学二轮复习专题07 立体几何教学案文

2014年高考数学（文）二轮复习精品教学案：专题07 立体几何一．考场传真1.【2012年北京卷数学（文）】某三棱锥的三视图如图所示，该三梭锥的表面积是（）A. 28+65B. 30+65C. 56+ 125D. 60+1252. 【2013年普通高等学校招生全国统一考试（广东卷）文科】设l为直线，,αβ是两个不同的平面，下列命题中正确的是（）A ．若//l α，//l β，则//αβB ．若l α⊥，l β⊥，则//αβC ．若l α⊥，//l β，则//αβD ．若αβ⊥，//l α，则l β⊥3.【2013年普通高等学校招生全国统一考试（辽宁卷）文科】已知三棱柱111ABC A B C -的六个顶点都在球O 的球面上，若34AB AC ，，==,AB AC ⊥112AA O =，则球的半径为 A ．3172B ．210C ．132D ．3104. (2012年高考山东卷文科13)如图，正方体1111ABCD A B C D -的棱长为1，E 为线段1B C 上的一点，则三棱锥1A DED -的体积为＿＿＿＿＿.5. 【2013年全国高考新课标（I ）文科】已知H 是球O 的直径AB 上一点，:1:2AH HB =，AB ⊥平面α，H 为垂足，α截球O 所得截面的面积为π，则球O 的表面积为_______.6. 【2013年普通高等学校招生全国统一考试（安徽卷文科）】如图，四棱锥P ABCD -的底面ABCD 是边长为2的菱形，60BAD ∠=.已知2,6PB PD PA === . （Ⅰ）证明：PC BD ⊥（Ⅱ）若E 为PA 的中点，求三菱锥P BCE -的体积.7. 【2013年高考新课标Ⅱ数学（文）卷】如图，直三棱柱ABC-A1B1C1中，D,E分别是AB，BB1的中点.（Ⅰ）证明： BC1//平面A1CD;（Ⅱ）设AA1= AC=CB=2，AB=22，求三棱锥C一A1DE的体积.8. (2012年高考福建卷文科19)（本小题满分12分）如图，在长方体ABCD-A1B1C1D1中，AB=AD=1，AA1=2，M为棱DD1上的一点。

高三数学总复习二轮专题5立体几何知识归纳

• 注意：利用空间向量方法求二面角时，注意结合图形判断二面角是锐角还是钝角．
• 4．点到平面的距离
• (1)定义：一个点到它在一个平面内的正射影的距离叫做这个点到平面的距离．
• (2)求法：一是根据定义，按照作(或找)— 证—求的步骤求解；二是利用空间向量，首先求出平面的单位法向量n0，再任意找一个从该点出发的平面的斜线对应的向量 v，则点到平面的距离为d＝|n0·v|.
• (3)证明平面与平面平行的方法是转化为直线与直线平行和直线与平面平行，然后利
用向量方法证明．也可以用如下方法：若平面α和β的法向量分别为n1和n2，则 α∥β⇔n1∥n2. • (4)证明直线和直线垂直的方法是：若直线 l1和l2的方向向量分别为v1和v2，则 l1⊥l2⇔v1⊥v2⇔v1·v2＝0.
• 2．证明线面平行问题的常用方法：
• (1)利用定义证明，即若a∩α＝∅，则a∥α；
• (2)利用线面平行的判定定理证明，即a∥b， a⊄α，b⊂α⇒a∥α；由线线平行⇒线面平行；
• (3)利用面面平行的重要结论证明，即α∥β， a⊂α⇒a∥β，由面面平行⇒线面平行．
• (4)利用空间向量法，又有三种方法：一是证明直线方向向量与平面法向量垂直；二是证明直线方向向量与平面内两不共线向量是共面向量；三是证明直线方向向量与平面内一向量共线．
• 6．求柱、锥、台体的体积时，根据体积公式，需要具备已知底面积和高两个重要条件，底面积一般可由底面边长或半径求出，但当高不知道时，求高比较困难，一般要转化为平面几何知识求出高．
• 7．有关球的组合体
• 与球有关的组合体问题，近几年高考命题
中常出现，特别是球的外接与内切问题，
解题时要认真分析图形，明确切点和接点

(四川专用)2014高考数学二轮 (热点重点难点专题透析)第5专题立体几何课件文

【解析】由三视图知三棱锥有从一个顶点出发的三条棱两两互相垂直，所以可补形为一个长方体，长、宽、高均为 2，故体对角线的长为 2 3 ，外接球的半径为 3 ，体积为 4 3 π.
【答案】4 3 π 4．在如图所示的组合体中，三棱柱 ABC—A1B1C1 的侧面 ABB1A1 是圆柱的轴截面，C 是圆柱底面圆周上不与 A、B 重合的一个点．
(1)求证：无论点 C 如何运动，平面 A1BC⊥平面 A1AC； (2)当点 C 是弧 AB 的中点时，求四棱锥 A1—BB1C1C 与圆柱的体积比．
【解析】 (1)∵侧面 ABB1A1 是圆柱的轴截面， C 是圆柱底面圆周上不与 A、B 重合的一个点，∴AC⊥BC，又圆柱母线 AA1⊥平面 ABC， BC⊂平面 ABC， ∴AA1⊥BC，又 AA1∩AC＝A， ∴BC⊥平面 A1AC. ∵BC⊂平面 A1BC， ∴平面 A1BC⊥平面 A1AC. (2)设圆柱的底面半径为 r，母线长度为 h，当点 C 是弧 AB 的中点时，AC＝BC＝ 2r， 1 2 2 VA1－BB1C1C＝ ·( 2r)·h·( 2 r)＝ r h， 3 3
【诊断参考】 1．线面位置关系的判断或证明是立体几何初步的重要内容之一，也是高考的必考点，试题难度不大，经常作为解答题的第一问出现，或以选择题或填空题的形式出现．易错点是平面几何知识有些不能迁移到立体几何中，如两条直线的位置关系有异面直线这种情况，垂直不一定相交，等等．在推证线面位置关系时，一定要严格遵循其判定定理或性质定理，注意其成立条件，否则极易出错． 2．空间几何体的表面积、体积与三视图的综合是每年高考的必考内容，此类问题解答易错点有三：一是对平行投
【考情报告】
【考向预测】立体几何是高考考查的重点内容之一，主要考查空间想象能力，在推理中兼顾考查逻辑思维能力.2013 年是四川实行新课标的第一年高考，文科的立体几何主要考查两部分：一是空间几何体，主要是以三视图为主展开，考查三视图的识别、判断，考查通过三视图给出的空间几何体的表面积和体积的计算等问题，以选择题的形式出现；二是空间点、直线、平面的位置关系，以解答题的形式考查，在条件的设问上有一些创新点，考查的重点是空间线面平行关系和垂直关系的证明，求多面体的体积．预测 2014 年高考对立体几何

(全国卷地区专用)2014届高考数学二轮复习专题五立体几何课件文

返回目录
第11讲
空间几何体
命题考向探究
【答题步骤】第一步：分别计算长方体和锥体的体积；第二步：利用“削减”的方法求得空间几何体 A1B1C1D1－ABCD剩余部分的体积；第三步：分类求得不同情形下的两个几何体的体积之比．
返回目录
第11讲
空间几何体
命题考向探究
小结：求规则几何体的体积，只需确定底面与相应的高，而求不规则几何体的体积时，要采取分割或补形思想，转化为规则几何体来运算．
返回目录
第11讲
核心知识聚焦
空间几何体
—— 体验高考 ——
4．[2013· 天津卷] 已知
④
——主干知识 ——
⇒ 几何体的外接和内切问题关键词：球的内接正方体和长方体、柱体和锥体的内切球，如④⑤.
一个正方体的所有顶点在一个球面上
9π ，若球的体积为 2 ，则正方体的棱长为________． [答案] 3
——主干知识 ——
⇒ 空间几何体的三视图关键词：三视图的画法与应用，如①.
[答案] 3 [解析]正视图的长为 3，侧视图的长为 3，它们的高为 1，因此，该四棱锥底面是边长 1 为 3 的正方形，且高为 1，因此 V＝3× (3×3)×1＝3.
图 5－11－1
返回目录
第11讲
核心知识聚焦
返回目录
第11讲
空间几何体
命题考向探究
► 考向三多面体与球的关系问题考向：多面体的棱长与外接球(或内切球)的半径的关系运算．考例：2010年T7、2011年T16、2012年T8、2013年卷ⅠT15、2013年卷ⅡT15，近五年新课标全国卷共考查了5次．

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

热点重点难点专题透析· 数学(文科)
专题5
平面 ABCD∩平面 ABEF＝AB，∴CB⊥平面 ABEF. ∵AF⊂平面 ABEF，∴AF⊥CB，又 AB 为圆 O 的直径，∴AF⊥BF，BF∩CB＝B， ∴AF⊥平面 CBF. (2)由(1)知 CB⊥平面 ABEF，即 CB⊥平面 OEF， ∴三棱锥 C—OEF 的高是 CB，又 CB＝AD＝1，又 OE＝OF＝EF＝1， 3 ∴△OEF 为正三角形，∴△OEF 的高是， 2 1 1 1 3 3 ∴VC—OEF＝ CB×S△OEF＝ ×1× × ×1＝ . 3 3 2 2 12
热点重点难点专题透析· 数学(文科)
专题5
在等腰梯形 PDCB 中，DC∥PB，PB＝3DC＝3，PD＝ 2， DA⊥PB， ∴PA＝1，AB＝2，AD＝ PD2－PA2＝1. 设 MN＝h，则有 1 1 1 1 1 VM—ABC＝ S△ABC·h＝ × ×AB×DA×h＝ × ×2×1×h＝ 3 3 2 3 2 1 h. 3 1 1 （DC＋AB）×AD 1 VP — ABCD ＝ S 梯形 ABCD ·PA＝ × × PA＝ × 3 3 2 3 1＋2 1 ×1×1＝ . 2 2
热点重点难点专题透析· 数学(文科)
专题5
【解析】A 中两条直线可能异面；B 不正确；C 满足“一个平面经过另一个平面的一条垂线，则两个平面互相垂直” ； D 中 l 可能在平面α内．【答案】C 2．(2013 湖南卷)已知棱长为 1 的正方体的俯视图是一个面积为 1 的正方形，则该正方体的正(主)视图的面积不可．．能等于( ． A．1 )． B. 2 2－1 C. 2 2＋1 D. 2
热点重点难点专题透析· 数学(文科)
专题5
1 ②锥体的体积 V＝ Sh(S 为底面面积，h 为锥体的高 )； 3 1 ③台体的体积 V＝ (S′＋ SS′＋S)h(S′，S 分别为 3 上、下底面面积，h 为台体的高)； 4 3 ④球的体积 V＝ πR (球的半径为 R)． 3 (3)正四面体： 2 对于棱长为 a 的正四面体可将它补成一个边长为 a 的 2 正方体．
热点重点难点专题透析· 数学(文科)
专题5
【诊断参考】 1．线面位置关系的判断或证明是立体几何初步的重要内容之一，也是高考的必考点，试题难度不大，经常作为解答题的第一问出现，或以选择题或填空题的形式出现．易错点是平面几何知识有些不能迁移到立体几何中，如两条直线的位置关系有异面直线这种情况，垂直不一定相交，等等．在推证线面位置关系时，一定要严格遵循其判定定理或性质定理，注意其成立条件，否则极易出错． 2．空间几何体的表面积、体积与三视图的综合是每年高考的必考内容，此类问题解答易错点有三：一是对平行投
热点重点难点专题透析· 数学(文科)
专题5
6．在等腰梯形 PDCB(如图 1)中， DC∥PB， PB＝3DC＝3， PD＝ 2 ，DA⊥PB，垂足为 A，将△PAD 沿 AD 折起，使得 PA ⊥AB，得到四棱锥 P—ABCD(如图 2)． (1)证明：平面 PAD⊥平面 PCD； (2)点 M 在棱 PB 上，平面 AMC 把四棱锥 P—ABCD 分成两个几何体(如图 2)，当这两个几何体的体积之比为 VPM－ACD∶
PM VM－ABC＝5∶4 时，求的值． MB
热点重点难点专题透析· 数学(文科)
专题5
【解析】(1)∵在图 1 的等腰梯形 PDCB 中，DA⊥PB， ∴在四棱锥 P—ABCD 中，DA⊥AB.又 PA⊥AB， ∴AB⊥平面 PAD，又 DC∥AB，∴DC⊥平面 PAD.∵DC⊂平面 PCD， ∴平面 PAD⊥平面 PCD. (2)∵DA⊥PA，且 PA⊥AB， ∴PA⊥平面 ABCD，又 PA⊂平面 PAB， ∴平面 PAB⊥平面 ABCD. 过 M 作 MN⊥AB，垂足为 N，则 MN⊥平面 ABCD.
热点重点难点专题透析· 数学(文科)
专题5
【解析】正(主)视图转化为长方形 A1ACC1 的正投影，设 A1C1 的正投影长为 l，则 S＝1×l＝l，可知 l∈[1， 2]，故 2－1 S∈[1， 2]，则 ∉[1， 2]，故正(主)视图的面积不 2 2－1 可能等于，故选 C. 2
【答案】C
热点重点难点专题透析· 数学(文科)
专题5
【解析】 (1)∵侧面 ABB1A1 是圆柱的轴截面， C 是圆柱底面圆周上不与 A、B 重合的一个点，∴AC⊥BC，又圆柱母线 AA1⊥平面 ABC， BC⊂平面 ABC， ∴AA1⊥BC，又 AA1∩AC＝A， ∴BC⊥平面 A1AC. ∵BC⊂平面 A1BC， ∴平面 A1BC⊥平面 A1AC. (2)设圆柱的底面半径为 r，母线长度为 h，当点 C 是弧 AB 的中点时，AC＝BC＝ 2r， 1 2 2 VA1－BB1C1C＝ ·( 2r)·h·( 2 r)＝ r h， 3 3
热点重点难点专题透析· 数学(文科)
专题5
3．已知一个三棱锥的三视图如图所示，其中俯视图是等腰直角三角形，则该三棱锥的外接球的体积为________．
【解析】由三视图知三棱锥有从一个顶点出发的三条棱两两互相垂直，所以可补形为一个长方体，长、宽、高均为 2，故体对角线的长为 2 3 ，外接球的半径为 3 ，体积为 4 3 π.
热点重点难点专题透析· 数学(文科)
专题5
线．画三视图的基本要求：正俯(主俯)一样长，俯侧(俯左)一样宽，正侧(主左)一样高；长对正，高平齐，宽相等． (2)三视图排列规则：俯视图放在正(主)视图的下面，长度与正(主)视图一样；侧(左)视图放在正(主)视图的右面，高度和正(主)视图一样，宽度与俯视图一样． 2．直观图斜二测画法：在坐标系 x′O′y′中画直观图时，已知图形中平行于坐标轴的线段保持平行性不变，平行于 x 轴 (或在 x 轴上)的线段保持长度不变，平行于 y 轴(或在 y 轴上)的线段长度减半．
热点重点难点专题透析· 数学(文科)
专题5
2 对棱间的距离为 a(正方体的边长)． 2 6 2 正四面体的高为 a( l 正方体体对角线长)． 3 3
2 3 1 正四面体的体积为 a (V 正方体－4V 小三棱锥＝ V 正方体)． 12 3
热点重点难点专题透析· 数学(文科)
专题5
1 正四面体的中心到底面与顶点的距离之比为 1∶3(即 l 6 1 正方体体对角线长∶ l 正方体体对角线长) ． 2 6 1 外接球的半径为 a(是正方体的外接球，则半径等于 4 2 l 正方体体对角线长)． 6 内切球的半径为 a(是正四面体中心到四个面的距离， 12 1 则半径等于 l 正方体体对角线长)． 6
热点重点难点专题透析· 数学(文科)
专题5
【考情报告】
热点重点难点专题透析· 数学(文科)
专题5
热点重点难点专题透析· 数学(文科)
专题5
【考向预测】立体几何是高考考查的重点内容之一，主要考查空间想象能力，在推理中兼顾考查逻辑思维能力.2013 年是四川实行新课标的第一年高考，文科的立体几何主要考查两部分：一是空间几何体，主要是以三视图为主展开，考查三视图的识别、判断，考查通过三视图给出的空间几何体的表面积和体积的计算等问题，以选择题的形式出现；二是空间点、直线、平面的位置关系，以解答题的形式考查，在条件的设问上有一些创新点，考查的重点是空间线面平行关系和垂直关系的证明，求多面体的体积．预测 2014 年高考对立体几何
热点重点难点专题透析· 数学(文科)
专题5
1 1 VPM—ACD＝VP—ABCD－VM—ABC＝－ h. 2 3 ∵VPM—ACD∶VM—ABC＝5∶4， 1 1 1 2 ∴( － h)∶ h＝5∶4，解得 h＝ . 2 3 3 3 BM MN 2 2 1 在△PAB 中，＝＝，∴BM＝ BP，MP＝ BP. BP PA 3 3 3 PM 1 ∴ ＝ . MB 2
热点重点难点专题透析· 数学(文科)
专题5
பைடு நூலகம்
6．翻折问题体现了平面问题和空间问题间的相互转化，能够很好地考查学生的空间想象能力、图形变换能力及识图能力．在解题过程中，若不能分清翻折前后基本量间的位置关系或数量关系则易造成错解．
【知识整合】一、空间几何体 1．三视图 (1)三视图的正(主)视图、侧(左)视图、俯视图分别是从几何体的正前方、正左方、正上方观察几何体画出的轮廓
热点重点难点专题透析· 数学(文科)
专题5
二、点、直线、平面之间的位置关系 1．直线与平面的位置关系 (1)线线平行的判断： ①平行于同一条直线的两条直线平行． ②如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线和交线平行． ③如果两个平行平面同时和第三个平面相交，那么它们的交线平行． ④垂直于同个一平面的两条直线平行． ⑤如果一条直线与两个相交平面都平行，那么这条直线必与它们的交线平行．
热点重点难点专题透析· 数学(文科)
专题5
V 圆柱＝πr2h，∴VA1—BB1C1C∶V 圆柱＝2∶3π. 5．如图，AB 为圆 O 的直径，点 E、F 在圆 O 上，矩形 ABCD 所在的平面和圆 O 所在的平面互相垂直，AB∥EF，且 AB＝2，AD＝EF＝1.
(1)求证：AF⊥平面 CBF； (2)求三棱锥 C—OEF 的体积．【解析】(1)平面 ABCD⊥平面 ABEF，CB⊥AB，
热点重点难点专题透析· 数学(文科)
专题5
4．求空间几何体的体积除了利用公式法外，还常用到分割、补形、转化法等．特别是利用转化法(或等积法)求三棱锥高的问题，用补形法解决球内接多面体的问题，是一种好方法．但在利用“割” “补”法求几何体的体积时一定要辨清“割” “补”后几何体的结构特征，若辨析不清则易出现错解． 5．探索型(或开放性)试题是近年高考试题命制的“新宠” ，此类问题的命制非常灵活，角度新颖，能够很好地考查学生对知识的灵活运用及知识的迁移能力．解答开放性问题的基本策略是先猜结论，后证明，因此大胆假设，严格证明是解决开放性问题的基本策略．此类问题不知如何作答是同学们常见的困惑．