数理统计在植保试验研究中的应用第五讲方差分析及多重比较
方差分析之多重比较

方差分析之多重比较目前对于均数的多重比较的方法较多,例如SPSS软件共提供18种均数的多重比较的方法。
对于均数多重比较,当资料满足正态性方差齐性时,可采用的比较方法有LSD法、Bonferroni法、Sidak法、Scheffe法、R-E-G-W F法、R-E-G-W Q法、S-N-K法、Tukey法、Tukey-b法、Duncan法、Hochberg GT2法、Gabriel法、Waller Duncan法、Dunnett法;当资料满足正态性但不符合方差齐性时,可采用Tamhane T2法、Dunnett T3、Games-Howell法、Dunnett C法。
1.常见的多重比较方法介绍1.1 LSD法原理:LSD与独立样本t检验非常相近,主要差别在于LSD法在首先满足F检验达到显著的基础上,将F检验的误差均方作为合并方差。
优点:在ANOVA中F检验显著时,LSD方法是检验效率最高的多重比较方法.缺点:①涉及过多的要比较均数对;②犯I型错误的概率较高;③这种方法只控制了每次比较犯I型错误概率,没有对总犯I型错误概率进行控制。
1.2 Bonferroni法原理:利用Bonferroni不等式来控制多次比较的总I型错误,Bonferroni不等式是指一个或多个事件发生的总概率不高于这些事件各自发生概率的加和。
通过将每次检验的α设置为总α除以检验次数,从而控制总α。
优点:用途最广,几乎可用于任何多重比较的情形,包括组间例数相等或不等、成对两两比较或综合多重比较等。
缺点:会增加犯Ⅱ型错误的概率。
1.3 Sidak法原理:基本思路与Bonferroni法接近,只是在调整仅值时采用不同的策略。
若控制单次比较犯I型错误的概率为αpc,一次比较不犯I型错误的概率为1-αpc,n次比较均不犯I型错误的概率为(1-αpc)n,则n次比较总的犯I型错误的概率为1-(1-αpc)n。
优点:调整多重比较的显著性水平,提供比Bonferroni 更严密的边界。
方差分析中的多重比较

XD XC
XB XE XA
67 69.5 71.5 74 74.5
XC 2.5 XB 4.5 2.0 XE 7.0* 4.5 XA 7.5* 5.0
2 .5 3.0 0.5
等级排列为:
1、2、3、4、5
(2)根 据 比 较 等 级 r, 自 由 度 df w ,
在
附
表
中
查
相
应
的
q
0
或
.05
q
的
0.01
值
。
比 较 等 级 r ri -rj 1, 如 :
X
与
B
X
比
C
较,
r
2-1
1;
X
A
与
X
比
D
较
,
r
5
3
1
3;
[应用心理学专业必修课 心理统计学 淮北煤师院教育学院 李怀龙] Email:lihlong@
由 上 述 结 果 ,可 以 作 出 统 计 结 论
[应用心理学专业必修课 心理统计学 淮北煤师院教育学院 李怀龙] Email:lihlong@
6
Psychology Statistics
2、N-K法(q检验)
步骤:
(1)把要比较的各个平均数从小到大作等级排列;
如5个平均数从小到大顺序是XB,XC,XA,XE,XD, 则
27.3 29.6 26.4 31.5
[应用心理学专业必修课 心理统计学 淮北煤师院教育学院 李怀龙] Email:lihlong@
植物营养研究方法 第六章-3 方差分析

Sx
对前面例题进行q检验:
四种肥料玉米产量LSR值(q检验) P q0.05 q0.01 LSR0.05 LSR0.01 2 3.00 4.13 31.02 42.70 3 3.65 4.78 37.74 49.43 4 4.05 5.19 41.88 53.66
四种肥料玉米产量差异显著性(q法)
字母标记法:
就是对没有显著差异的平均数标以相同字母,对有显著差异 的标以不同字母。 具体方法:首先是将欲比较的平均数按大小次序排列。然后 在最大的平均数上标上字母a(=0.05)或A(=0.01);将该平 均数与以下平均数逐个相比,凡差异不显著者都标以字母a 或A,直至相差显著的平均数则标以字母b或B;再以标有b或 B的平均数为标准,与其上方比它大的平均数逐个相比,凡 相差不显著者一律标以字母b或B;再以标有b或B的最大平均 数为标准,与其下方未标记字母的平均数相比,凡相差不显 著者继续标以字母b或B,直至与之相差显著的平均数则标以 字母c或C,再与上面的平均数比较。如此重复进行,直至最 小的平均数有了标记字母并与上面的平均数比较后为止。
对上例题的各组平均值作新复极差检验:
四种肥料玉米产量LSR值(SSR检验) P 2 3 4
SSR0.05 SSR0.01 LSR0.05 LSR0.01
3.00 4.13 31.02 42.70
3.14 4.31 32. 47 44.57
3.24 4.42 33.50 45.70
四种肥料玉米产量差异显著性(SSR法)
差异显著性
肥料 A1 A4 A2 A3
平均数 311.8 279.8 262.8 247.4
=0.05 a b b b
=0.01 A AB B B
数理统计-方差分析

例1
H 1 : 1 , 2 , 3不全相等.
检验假设
H 0 : 1 2 3 , H 1 : 1 , 2 , 3不全相等.
进一步假设各总体均为正态变量,且各总体的 方差相等,但参数均未知. 问 题——检验同方差的多个正态总体均 值是否相等.
解决方法——方差分析法,一种统计方法.
2 SA /( r 1) 在检验水平 下, 由p F 2 k 得 S E /( n r ) k F1 ( r 1, n r )
H0的拒绝域为 :
2 SA /( r 1) F1 ( r 1, n r ) F 2 S E /( n r )
自由度 2
12 14
均
方
F
比
素A 0.00105333
0.00052667 32.92
0.000016
随机误差 0.000192 总 和 0.00124533
F 32.92 F0.05 ( 2,12) 3.89.在水平0.05下拒绝 H 0 . 各机器生产的薄板厚度有显著差异.
在MATLAB中的求解 函数:anova1 格式:p=anova1(x) 说明:对样本X中的多列数据进行单因素方差分析, 比较各列的均值,返回“零假设”成立的概率值,如果 概率值接近于零,则零假设值得怀疑,表明各列的均 值事实上是不同的. 源程序: x=[0.236,0.238,0.248,0.245,0.243; 0.257,0.253,0.255,0.254,0.261; 0.258,0.264,0.259,0.267,0.262]; p=anova1(x’) 助 程序运行结果 方差分析表 Box 图检验 帮
1. 各水平效应 i 的点估计
方差分析与与多重比较
平均 12.76aA 12.04abAB 11.48bcBC 11.45bcBC 11.25bcdBC 11.21bcdBCD 11.17bcdBCD 11.15cdBCD 11.09cdBCD 10.90cdBCD 10.83cdeCD 10.75cdeCD 10.69cdeCD 10.62cdeCD 10.40deCD 10.00eD
0.13 0.35 0.75 12
0.07 0.29 0.69 13
0.22 0.62 14
0.40 1516 Nhomakorabea1718
* 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
19
20
21
22
23
24
25
26
27
28
29
30
27
28
29
30
0.59 0.81 1.21 6
0.55 0.77 1.17 7
0.53 0.75 1.15 8
0.47 0.69 1.09 9
** ** ** ** ** ** ** ** ** ** ** ** ** ** 1
* * * ** ** ** ** ** ** 2
* ** 3
* ** 4
** 5
* 6
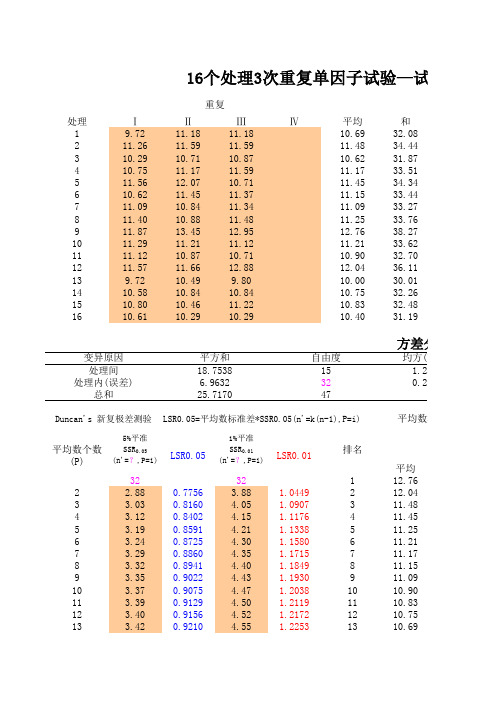
16个处理3次重复单因子试验— 16个处理3次重复单因子试验—试验结果方 个处理
重复 处理 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 Ⅰ 9.72 11.26 10.29 10.75 11.56 10.62 11.09 11.40 11.87 11.29 11.12 11.57 9.72 10.58 10.80 10.61 Ⅱ 11.18 11.59 10.71 11.17 12.07 11.45 10.84 10.88 13.45 11.21 10.87 11.66 10.49 10.84 10.46 10.29 Ⅲ 11.18 11.59 10.87 11.59 10.71 11.37 11.34 11.48 12.95 11.12 10.71 12.88 9.80 10.84 11.22 10.29 Ⅳ 平均 10.69 11.48 10.62 11.17 11.45 11.15 11.09 11.25 12.76 11.21 10.90 12.04 10.00 10.75 10.83 10.40 和 32.08 34.44 31.87 33.51 34.34 33.44 33.27 33.76 38.27 33.62 32.70 36.11 30.01 32.26 32.48 31.19
方差分析(ANOVA)、 多重比较(LSD Duncan)、q检验(student)

方差分析(ANOV A)、多重比较(LSD Duncan)、q检验(student)实际研究中,经常需要比较两组以上样本均数的差别,这时不能使用t检验方法作两两间的比较(如有人对四组均数的比较,作6次两两间的t检验),这势必增加两类错误的可能性(如原先a定为0.05,这样作多次的t检验将使最终推断时的a>0.05)。
故对于两组以上的均数比较,必须使用方差分析的方法,当然方差分析方法亦适用于两组均数的比较。
方差分析可调用此过程可完成。
Least-significant difference(LSD):最小显著差法。
a可指定0~1之间任何显著性水平,默认值为0.05;Bonferroni:Bonferroni修正差别检验法。
a可指定0~1之间任何显著性水平,默认值为0.05;Duncan’s multiple range test:Duncan多范围检验。
只能指定a为0.05或0.01或0.1,默认值为0.05;Student-Newman-Keuls:Student-Newman-Keuls检验,简称N-K检验,亦即q 检验。
a只能为0.05;(以前都以SNK法最为常用,但研究表明,当两两比较的次数极多时,该方法的假阳性非常高,最终可以达到100%。
因此比较次数较多时,包括SPSS和SAS在内的权威统计软件都不再推荐使用此法。
) Tukey’s honestly significant difference:Tukey显著性检验。
a只能为0.05;Tukey’s b:Tukey另一种显著性检验。
a只能为0.05;Scheffe:Scheffe差别检验法。
a可指定0~1之间任何显著性水平,默认值为0.05。
根据对相关研究的检索结果,除了参照所研究领域的惯例外,一般可以参照如下标准:如果存在明确的对照组,要进行的是验证性研究,即计划好的某两个或几个组间(和对照组)的比较,宜用Bonferoni(LSD)法;若需要进行的是多个平均数间的两两比较(探索性研究),且各组样本数相等,宜用Tukey法,其他情况宜用Scheffe法。
方差分析与多重比较
方差是表示变异的量,在一个多处理试验 中,可以得出一系列不同的观测值,造成它们 不同的原因是多方面的。 • 由处理不同引起的,叫处理效应(或叫 条件变异) • 由试验过程中偶然性因素的干扰和测量 误差所致,这一类误差称试验误差。
• 方差分析的最大优点是在于它可以全面分 析差异的原因。
方差分析的基本思想:
二、方差分析的基本原理
• 重复数相等的几个均数的比较
符号:
nn knk knn k k
xxiijj xxijij x为ij 表中所有观测数据之和
ii11 jij111 jii11 j1j1
n
xij 为各列(重复)之和
i 1
k
xij 为各行(处理)之和
j 1
1. 自由度的分解
设有k组样本,每样本具有n个观察值, 则总共有nk个观察值,其自由度df
ijj111 ji11 j1 j1
St2=SSt/(k-1)
(xij
nn n nkk
SxSi )t2=nk k
k
n
(((xx(xiixjiijj xx)x)22xi ))2=20.73(1x i
x)2
k
=0.731/3 1 =0.2437
i i11i ij1j111j 1
2
i 1
j1
(x x) SSeini1n1ij1jikkn11j((1ijxkn1x1ij(jiikxjj1ij(xx)i2xjx)i )2x2 )=20k.i3n10(9x i
总自由度:dfT=nk-1 组间自由度:dft=k-1 组内自由度:dfe=k(n-1)
总自由度:dfT=dft+dfe =(k-1)+k(n-1)
=k-1+kn-k=nk-1
报告中的ANOVA分析和多重比较
报告中的ANOVA分析和多重比较引言:ANOVA(方差分析)是一种经典的统计方法,用于比较两个或多个组别之间的差异。
在报告中使用ANOVA进行数据分析时,为了更全面地揭示结果,通常需要进行多重比较。
本文将就报告中使用ANOVA分析和多重比较方法的相关问题展开论述,包括效应大小的解读、假设检验的细节、多重比较的必要性以及选择合适的多重比较方法。
一、效应大小的解读在报告中,除了给出显著性检验的结果外,也需要对实验效应的大小进行解读。
效应大小可以通过η²或ω²指标来衡量,它们分别表示了解释变量(组别)对因变量的解释程度。
η²指标的取值范围是0到1,表示了变量解释的百分比;而ω²指标的取值范围是-1到1,它修正了样本偏差的影响。
二、假设检验的细节在报告中呈现ANOVA分析结果时,需要清晰地陈述研究者所采用的假设以及相应的检验方法。
具体而言,首先要明确零假设(H0)和备择假设(H1),以及选择合适的统计检验(如一元ANOVA、双因素ANOVA等)。
此外,还需提及所使用的显著性水平和效应大小指标。
三、多重比较的必要性多重比较是为了进一步分析差异显著的组别之间的具体差异。
在进行多重比较时,可以利用事前比较和事后比较两种方法。
事前比较是在进行方差分析之前,对组别进行两两比较;而事后比较是在方差分析结果显著时,对不同组别之间进行比较。
四、多重比较的方法选择在报告中选择合适的多重比较方法非常重要。
有多种方法可以选择,包括Bonferroni校正、Tukey HSD、Scheffe法等。
具体选择哪种方法取决于研究者的需求和实验设计的特点。
文章中可以简要介绍每种方法的原理和应用场景,以帮助读者选择适合自己研究的方法。
五、多重比较的结果描述在报告中对进行多重比较的结果进行准确和全面的描述至关重要。
可以使用表格或图表来展示多个组别之间的差异,同时注明置信区间和显著性水平等信息。
此外,还可以使用文字对发现的差异进行解释和解读。
统计学系列讲座第5讲多组样本均数比较的方差分析
3
随机单位组设计资料的方差分析(randomized block des ign)
第6期
安胜利 . 统计学系列讲座
第5讲
多组样本均数比较的方差分析
95
又称随机区组设计、 配伍组设计 。 这 种 设 计 相 当 于 配 对 设计的扩大。具体做法是将受试对象按性质( 如性别、 体质 量、 年龄及病情等对试验结果有影响的非实验因素) 相同或 相 近者组成 b 个单位组 , 每个单位组中有 k 个 受 试 对 象 , 分 别随机地分配到 k 个处理组。这种设计使得各处理组内受试 对象数量相同 , 生物学特点也较为均衡。由于减少了误差 , 试 验效率提高了。 例 2 为研究注射不同剂量雌激素对大白鼠子宫质量的 影响 , 取 4 窝不同种系的大白鼠 ( b=4 ) , 每窝 3 只 , 随机地分配 到 3 个 组 内 ( k=3 ) 接 受 不 同 剂 量 的 雌 激 素 的 注 射 , 然 后 测 定 其子宫质量 , 见表 5 , 问注射不同剂量的雌激素对大白鼠子宫 质量是否不同 ? 表5
分析: 本例多处数据标准差是均数的 2 倍以上, 基本上 可以认为此资料不服从正态分布 , 而且 各 指 标 内 不 同 组 间 标 准差相差悬殊 , 也不满足方差齐性条件 , 所以不宜用 t 检验和 方差分析。这两个条件具体可通过正态性检验和方差齐性检 验证实 ( 此略 ) 。另外 , 本资料分为 3 组 , 而原作者反复用 t 检 验进行各两组间的比较也是错误的, t 检验不能用于分析多 组资料间的两两比较。此例可考虑用无前提条件要求的非参 数检验( 将在以后的讲座中介绍) , 如果有统计学意义, 接着 用非参数检验中相应的两两比较方法。
SS SS 处 理 SS 单 位
CEA CA19- 9 (μ g/L) (103U/L) 术前 58 34.0± 79.0 209.0± 739.0 术后 30 2.0± 1.2* 11.0± 10.9* 转移复发 19 88.0± 107.0 212.0± 529.0 与术前组比较 : *P<0.05,**P<0.01 n
数理统计在植保试验研究中的应用第五讲方差分析及多重比较
“试验统计 ” “随 然后在系统菜单下选择 4 机区组设计 ”4“单向分组试验统计分析 ”功
植保技术与推广
!"#$% !&’%()%*’$ +(),$’"’-. #$/ 01%($2*’$, 3445 , 6’"7 358 9’7 54
!"
能, 可立即得到如下分析结果 # 表 & 、 表 "$。
表& 变异 方差分析表 均方 !值 显著水平 # "$
(3!" 1 (3"" 1 (,’" $ ) * 2 !, "’-. -,* % (". "0- -, 自由度 *" % ! 2 ( % *, 均方 +%- % (". "0- - ) * % !. -,* *。 试 验 误 差 平 方 和 %%. / %%# ( %%! ( %%" % 自由度 *. % &,. 3(’ & 2 0-. ’’’ & 2 (". "0 % (’, 均方 +%. % (’ ) ’ % ". ’’’ &。 (( 2 " 2 * % ’, +%. 是 试 验 误 差 估 计 值 ; 处 理 间 均 方 +%! % "0. *** * 是 不 同 药 剂 对 苗 高 效 应 的 差 异, 查 0 值表, 得 0-. -0 0 值 % +%! 1 +%. % 3. 0-。 # ",’ $ % 0. (!, 0-. -( # ",’ $ % (-. 3",这里 02 表明处理间差异显著。 0-. -0 # ", ’$, 区组间均方 +%! % !. -,* * 是不同环境对 苗高效应的差异,0 值 % +%" 1 +%. % (. 0*( -。 查 0 分布表得,0-. -0 # *, ’ $ % !. &’,0-. -( # *, ’$ 这里 0 3 0-. -0 # *, ’ $ 则表明组间环境条 % 3. &,, 件无显著差异。 因处理间差异显著, 我们可进一步作 4567 896 : ; 新复极差比较。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(3!" 1 (3"" 1 (,’" $ ) * 2 !, "’-. -,* % (". "0- -, 自由度 *" % ! 2 ( % *, 均方 +%- % (". "0- - ) * % !. -,* *。 试 验 误 差 平 方 和 %%. / %%# ( %%! ( %%" % 自由度 *. % &,. 3(’ & 2 0-. ’’’ & 2 (". "0 % (’, 均方 +%. % (’ ) ’ % ". ’’’ &。 (( 2 " 2 * % ’, +%. 是 试 验 误 差 估 计 值 ; 处 理 间 均 方 +%! % "0. *** * 是 不 同 药 剂 对 苗 高 效 应 的 差 异, 查 0 值表, 得 0-. -0 0 值 % +%! 1 +%. % 3. 0-。 # ",’ $ % 0. (!, 0-. -( # ",’ $ % (-. 3",这里 02 表明处理间差异显著。 0-. -0 # ", ’$, 区组间均方 +%! % !. -,* * 是不同环境对 苗高效应的差异,0 值 % +%" 1 +%. % (. 0*( -。 查 0 分布表得,0-. -0 # *, ’ $ % !. &’,0-. -( # *, ’$ 这里 0 3 0-. -0 # *, ’ $ 则表明组间环境条 % 3. &,, 件无显著差异。 因处理间差异显著, 我们可进一步作 4567 896 : ; 新复极差比较。
( (
是否成立。计算 4 值时,总是要将测验的那一 (一 项变异因素的均方作分子, 而以另一项变异 般是试验误差,但有时不是,这与试验设计有
!"
植保技术与推广
!"#$% !&’%()%*’$ +(),$’"’-. #$/ 01%($2*’$, 3445 , 6’"7 358 9’7 54
表( 处理 K L M G・ / I ’0 ’! ’(,3
55555555555555555555555555555555555555555555 & 防治方法 ’ ’ ’ ’&
病虫 动态
&))% 年 , 月北京市顺义、延庆等区县在玉米田发 现一种以前未发生过的新害虫,经中国科学院动物研 究 所 专 家 鉴 定 为 褐 足 角 胸 叶 甲 > $%&’()"#% *+(,’")& # ?@A:8B6C:DE $ F 。 % 田间为害状 褐足角胸叶甲以成虫啃食玉米叶片,从玉米苗期 至成株期均可受害,但以玉米抽雄前受害最重。据观 察,成虫怕光,喜欢集中在心叶内为害,啃食叶肉造成 许多小孔, 有时被啃食的小孔连接起来, 使叶片横向被 切断, 或叶片呈破碎状。玉米苗期受害, 褐足角胸叶甲 在心叶内为害,使心叶卷缩在一起,呈牛尾状,生长受 到严重抑制。 据顺义区植保站 &))% 年 , 月 %) 日调查 , 块玉米地, 有虫地块 %)). 。 全区发生面积 )’ +, 万 BG& , 其中受害较重的 )’ "" 万 BG& 。平均百株有虫 "% 头, 最 平均被害株率 "%. , 最高的 *). 。延庆县 高的 %") 头, 山区春玉米受害严重,其中有 "" BG& 玉米叶被吃成花 叶, 一般百株虫量 ")) H !)) 头, 多的达千头。
新复极差测验表 (. 显著水平 %. 极显著水平 / / 2 0 01 1
这里对结果的解释更直观: ! 处理间差异 的 显 著 水 平 " 值 等 于 )’ )%" * , )’ )% 3 " 3)’ )( ,故差异显著。 " 区组间差异不显著 # " 4 )’ ")) % $ 。# 5678/7 9 : 新复极差比较: 两 个处理与对照相比有显著差异,但两个处理间 的差异不显著。 ! ’’’’& ! 检验应用条件及注意事项
"
处理间平方和 ++" , )$( ,・ # / %,自由度
,
均方 1+" , ++" - 0" 0" , " / " ,
# ’ 区组间平方和 ++# & )$・ - " / %,自由度 -
均方 1+# & ++# - 0# 0# , # / " , 剩 余 变 异 为 试 验 误 差 ++2 & ++$ / ++" / 自由度 02 , 0$ . 0" . 0#, 均方 1+2 & ++2 - 02 ++#, 第二步, 给出原假设 3%/ ! ! , ! 2, 即各个 处理间不存在差异,并应用 4 测验检验原假设
不同处理的试验结果 区 II ’0 ’& ’" (3! 组 III ’, ’* ’( (3" IJ ’0 ’( ’(,’ GH ・ "’* "00 "!* &’(
已知处理 4 均值 ’4 % ’0. &0,处理 5 均值 ’5 % ’*. &0,对照 # 未处理 $ 均值 ’) % ’-. &0, 查 456896 : ; 新复 +% . % ". ’’’ & 。当 6 % " 时, 极 差 表 , 计 算 7%8-. -0, " / %%8-. -0 , " 3+%. " % 当 6 % * 时, *. !’ + -. ,(’ 0 % ". ,"0, 7%8-. -0,* % %%8-. -0, * 3+% . " % *. 0, + -. ,(’ 0 % ". 3"*。 当 6 % " 时, ’4 2 ’5 % ", ’4 2 ’5 < 7%8-. -0 , ", 0= 水平不显著; ’5 2 ’) % *, ’5 2 ’) > 7%8-. -0 , ", 水平显著。 0= 当 6 % * 时, ’4 2 ’) % 0, ’4 2 ’) > 7%8-. -0 , *, 0= 水平显著。 结论:两个处理与对照相比有显著差异, 但两个处理间的差异不显著。 * 用统计软件进行方差分析 目前,多个处理的试验统计分析一般借助 于统计软件进行。如 4?@ 数据处理系统 # 可从 网站 AAA. ;B9BCDE5F. 8DF 下载或与作者联系 $ 可 同时进行方差分析和多重比较。借助于 4?@ 软 件,可立即得到按试验设计方案剖分的各个变 异因素的相应平方和、 自由度、 均方、0 值及其 显著水平 6 的概率值。 根据显著水平 6 值大小 可直接进行统计推断:如 6 值小于或等于 表示差异显著; 如 6 值小于或等于 -. -(, -. -0, 表示差异极显著。最后, 采用字母标记法, 给出 456896 : ; 新复极差等方法的多重比较结果。 根据试验设计类型不同, 所采用的方差分 析方法也不同。 读者只要按系统的使用说明所 描述的数据编辑格式正确输入数据, 并调用适 当的统计分析方法, 4?@ 软件会给出所有的分 析结果。如本例,只需在 4?@ 的电子表格中, ( 行 ( 个处理地输入数据,并用鼠标将数据选 定为数据块, 图示如下。
收稿日期: &))% = )* = %)
平方和 自由度 " & + %%
区组间 %&’ &() ) 处理间 ()’ +++ , 误差 %+’ ))) 总变异 ,*’ -%+ , 表" 处理 处理 % 处理 & 处理 " 平均 +(’ ,( +"’ ,( +)’ ,(
!’ )*" " %’ ("% ) )’ ")) % &(’ """ " -’ ()) ) )’ )%" * &’ +++ ,
植保技术与推广
!"#$% !&’%()%*’$ +(),$’"’-. #$/ 01%($2*’$, 3445 , 6’"7 358 9’7 54
!"
’’’’&
’ ’ ’ ’&
植保 讲座
"
方差分析基本原理
两个样本平均数的差异比较可采用 ! 检验 (样本) 的方法。 但处理个数 大于 ( 时, 则需用方 差分析进行统计检验。 方差分析分为以下几个步骤: 第一步,将试验数据总变异按试验设计方 案剖分为各个处理因素的相应均方 (即离均差 平方和除以自由度的商 ) ,剩余变异为试验误 差, 作为假设检验的依据。 这里以最常用的单因素随机区组试验 # " 个处理, 说明平方和、 自由度及 # 次重复 ’ 为例, 均方的计算过程: 先计算试验 数据总 和 $、矫正 系数 % & 各重复的和 $)・ 、 再计 $ ( ) "# * 及各处理、 *・ + , 算:
资料呈正态分布是应用方差分析前提之 一。因此,和 # 检验一样,常需对数据进行转 换。数据转换方式可参考上一讲。 室内农药药效试验一般采用单因素完全随 机试验设计,而田间农药药效试验采用本文介 绍的单因素随机区组试验设计进行试验和方差 分析。田间药效试验结果解释时,区组间差异 是否显著并不影响处理间差异显著性的结论。 经假设检验, 若发现某因素的作用不显著, 不能简单地理解为该因素在此试验中是无用的 因素。因素在试验中是否有用,取决于专业知 识;而假设检验的结果只能说明因素的各水平 对试验结果所产生的影响在统计学上相差是否 足够的大。因此,由于所取的处理水平过于接 近, 常会导致某因素的作用不显著。 如因不可抗拒的事件造成小区缺失,且无 法弥补时,可应用 5;< 里面提供的线性模型技 术对有缺失的试验数据进行方差分析。
