工程力学20-j8b(例题)
(完整版)工程力学课后习题答案

工程力学练习册学校学院专业学号教师姓名第一章静力学基础 1第一章静力学基础1-1 画出下列各图中物体A,构件AB,BC或ABC的受力图,未标重力的物体的重量不计,所有接触处均为光滑接触。
(a)(b)(c)2 第一章静力学基础(d)(e)(f)(g)第一章静力学基础 3 1-2 试画出图示各题中AC杆(带销钉)和BC杆的受力图(a)(b)(c)(a)4 第一章静力学基础1-3 画出图中指定物体的受力图。
所有摩擦均不计,各物自重除图中已画出的外均不计。
(a)第一章静力学基础 5 (b)(c)(d)6 第一章静力学基础(e)第一章静力学基础7 (f)(g)8 第二章 平面力系第二章 平面力系2-1 电动机重P=5000N ,放在水平梁AC 的中央,如图所示。
梁的A 端以铰链固定,另一端以撑杆BC 支持,撑杆与水平梁的夹角为30 0。
如忽略撑杆与梁的重量,求绞支座A 、B 处的约束反力。
题2-1图∑∑=︒+︒==︒-︒=PF F FF F F B A yA B x 30sin 30sin ,0030cos 30cos ,0解得: N P F F B A 5000===2-2 物体重P=20kN ,用绳子挂在支架的滑轮B 上,绳子的另一端接在绞车D 上,如第二章 平面力系 9图所示。
转动绞车,物体便能升起。
设滑轮的大小及轴承的摩擦略去不计,杆重不计,A 、B 、C 三处均为铰链连接。
当物体处于平衡状态时,求拉杆AB 和支杆BC 所受的力。
题2-2图∑∑=-︒-︒-==︒-︒--=030cos 30sin ,0030sin 30cos ,0P P F FP F F F BC yBC AB x解得: PF P F AB BC 732.2732.3=-=2-3 如图所示,输电线ACB 架在两电线杆之间,形成一下垂线,下垂距离CD =f =1m ,两电线杆间距离AB =40m 。
电线ACB 段重P=400N ,可近视认为沿AB 直线均匀分布,求电线的中点和两端的拉力。
工程力学例题ppt课件

解得
M A 10.37kN
11
例4-8
已知: P1, P2, P=2P1, r, R=2r, 200;
求: 物C 匀速上升时,作用于轮I
上的力偶矩M;轴承A,B处的
约束力.
解: 取塔轮及重物C,画受力图.
M B 0 Pr F R 0
解得 由
F
Pr R
10P1
Fr tan 200
F
解得 Fr F tan 200 3.64P1 12
解得
FBy 8kN
20
用截面法,取桁架左边部分.
M E 0 F1 1 cos 300 FAy 1 0
解得 F1 10.4kN(压)
Fiy 0 FAy F2 sin 600 P1 0
解得
F2 1.15kN(拉)
Fix 0 F1 F3 F2 cos 600 0
解得
5 8
P
Fiy 0 FEy P FA sin 450 0
解得
13 FEy 8 P
取DCE杆,画受力图.
MC 0 FDB cos 450 2l FK l FEx 2l 0
解得
FDB
32 8
P
(拉)
17
例4-11 已知: P=10kN,尺寸如图; 求: 桁架各杆件受力.
解: 取整体,画受力图.
xx FAB P b P b P 0
解得 FAB P(压) 29
例4-17 已知:q ,a ,M , 且M qa2, P作用于销钉B上;
求:固定端A处的约束力和销钉B对
BC杆,AB杆的作用力.
解:取CD杆,画受力图.
MD 0
a FCx a qa 2 0
得
1 FCx 2 qa
清华出版社工程力学答案-第5章 杆件的内力分析与内力图

eBook工程力学习题详细解答教师用书(第5章)2011-10-1范 钦 珊 教 育 教 学 工 作 室FAN Qin-Shan ,s Education & Teaching Studio习题5-1 习题5-2 习题5-3 习题5-4 习题5-5 习题5-6工程力学习题详细解答之五第5章 杆件的内力分析与内力图5-1 试用截面法计算图示杆件各段的轴力,并画轴力图。
5-2 圆轴上安有5个皮带轮,其中轮2为主动轮,由此输入功率80 kW ;1、3、4、5均为从动轮,它们输出功率分别为25 kW 、15 kW 、30 kW 、10 kW ,若圆轴设计成等截面的,为使设计更合理地利用材料,各轮位置可以互相调整。
1. 请判断下列布置中哪一种最好?(A) 图示位置最合理;(B) 2轮与5轮互换位置后最合理; (C) 1轮与3轮互换位置后最合理; (D) 2轮与3轮互换位置后最合理。
2. 画出带轮合理布置时轴的功率分布图。
30kN 20kN10kN20kN10kN 5kNBAD CB A DC BACBA C(a)(b)(c)(d)F NF ACBF N xDACB102030ACF N x210ADCF N -10习题5-1图解: 1. D2. 带轮合理布置时轴的扭矩图如图(b )所示。
5-3 一端固定另一端自由的圆轴承受4个外力偶作用,如图所示。
各力偶的力偶矩数值均示于图中。
试画出圆轴的扭矩图。
固定固定(kN.m)习题5-3图P x (kW)2540(b)习题5-2图5-4 试求图示各梁中指定截面上的剪力、弯矩值。
(a)题解:取1-1截面左段为研究对象,1-1截面处的剪力和弯矩按正方向假设:22222211qa qa qa a qa M M qaF Q =−=⎟⎠⎞⎜⎝⎛⋅−=−= 取2-2截面左段为研究对象,2-2截面处的剪力和弯矩按正方向假设:222222222qa qa qa a qa M M qaqa qa F Q =−=⎟⎠⎞⎜⎝⎛⋅−=−=−−= (b)题解:取1-1截面右段为研究对象,1-1截面处的剪力和弯矩按正方向假设:21P 12322qa a qa a qa M qa qa qa qa F F Q −=⋅−⋅−==+=+= 取2-2截面右段为研究对象,2-2截面处的剪力和弯矩按正方向假设:2222222qa qa a qa a qa M qaF Q −=+⋅−⋅−== (c)题解:(1)考虑整体平衡,可解A 、C 支座约束力0m kN 5.4124m kN 4,0)(=⋅××−×+⋅=∑C i A F F M得 kN 25.1=C F0kN 12,0=×−+=∑C A iyF F F得 kN 75.0=A F(2)取1-1截面左段为研究对象,1-1截面处的剪力和弯矩按正方向假设:BB5kN1 m34AAB(b)(a)(c)(d)习题5-4图0,01=−=∑Q A iyF F F得 kN 75.01=Q F02,0)(11=+×−=∑M F F MQ i A得 m kN 5.11⋅=M(3) 取2-2截面左段为研究对象,2-2截面处的剪力和弯矩按正方向假设:0,02=−=∑Q A iyF F F得 kN 75.02=Q F0m kN 42,0)(22=+⋅+×−=∑M F F M Q i A得 m kN 5.22⋅−=M(4) 取3-3截面右段为研究对象,3-3截面处的剪力和弯矩按正方向假设:0kN 12,03=×−+=∑C Q iyF F F得 kN 75.03=Q F0m kN 1221,0)(23=⋅××−−=∑M F M i C得 m kN 13⋅−=M (5) 取4-4截面右段为研究对象,4-4截面处的剪力和弯矩按正方向假设:0kN 12,04=×−=∑Q iyF F得 kN 24=Q F0m kN 1221,0)(24=⋅××−−=∑M F Mi C得 m kN 14⋅−=M (d)题解:(1)考虑整体平衡,可解A 、B 支座约束力03m kN 2m kN 15,0)(=×+⋅+⋅×−=∑B i A F F M 得 kN 1=B F0kN 5,0=+−=∑B A iyF F F得 kN 4=A F(2)取1-1截面左段为研究对象,1-1截面处的剪力和弯矩按正方向假设:0,01=−=∑Q A iyF F F得 kN 41=Q F01,0)(11=+×−=∑M FF M Ai得 m kN 41⋅=M(3) 取2-2截面左段为研究对象,2-2截面处的剪力和弯矩按正方向假设:0kN 5,02=−−=∑Q A iyF F F得 kN 12−=Q F01,0)(22=+×−=∑M F F M A i得 m kN 42⋅=M(4) 取3-3截面右段为研究对象,3-3截面处的剪力和弯矩按正方向假设:0,03=+=∑B Q iyF F F得 kN 13−=Q F1m kN 2,0)(33=×+⋅+−=∑B iF M F M得 m kN 33⋅=M(5) 取4-4截面右段为研究对象,4-4截面处的剪力和弯矩按正方向假设:0,04=+=∑B Q iyF F F得 kN 14−=Q F1,0)(44=×+−=∑B i F M F M得 m kN 14⋅=M5-5 试写出以下各梁的剪力方程、弯矩方程。
工程力学19-j8a(例题)

位形 ri , xi 广义坐标位形 q j ( j = 1,2⋯, k )
用独立的广义虚位移表示出来。 将各点虚位移 δ ri 或δ x i用独立的广义虚位移表示出来。
4. 单个刚体上各点的虚位移之间关系表示方法 与刚体上各点的速度关系类似 虚速度法 任意点的虚 位移均相等
平动 刚体
δri
c
δrC
例题
例 题 1
§8 虚位移原理
F D C A ϕ B E
刚体系统如图所示, 刚体系统如图所示, AE=DB=2DF=2EF=2l C为AE和DB的中点, 的中点, 为 和 的中点 求F 和B两点虚位移的 两点虚位移的 关系。 关系。
例题
例 题 1
y F D C A ϕ E
§8 虚位移原理
解:1.解析法 解析法 建立xy坐标系 坐标系, 建立 坐标系,选择广义坐标 ϕ 写出B, 点的位形 点的位形: 写出 ,F点的位形:
实位移表示为: 实位移表示为:
∂ri ∂ri dri = ∑ dq j + dt ∂t i =1 ∂q j
k
(i = 1,2,⋯, n)
(i = 1,2, ⋯ ,3n)
∂xi ∂xi dxi = ∑ dq j + dt ∂t i =1 ∂q j
k
虚位移表示为: 虚位移表示为:
δ ri =
∑
k
k
j =1
§8 .1
位形、 位形、约束方程及约束分类
1.质点系的位形 质点系的位形 n个自由质点组成的质点系 个自由质点组成的质点系——任一质点 Di 的位置 个自由质点组成的质点系 任一质点 确定,称这3n个 可由其直角坐标 xi , yi , zi (i = 1 ~ n) 确定,称这 个 坐标的集合为该质点系的位形, 坐标的集合为该质点系的位形,位形给定则质点系 中每一质点的位置就可确定。 中每一质点的位置就可确定。 n个质点的非自由质点系 个质点的非自由质点系——设自由度 k ≤ 3n , 个质点的非自由质点系 设自由度 确定质点系的位形: 可用广义坐标 q 1 ~ q k 确定质点系的位形: i = 1,..., n (8.1) ri = ri (q1 , q2 , ⋯, qk , t ) 或 xi = xi (q1 , q2 ,⋯, qk , t ) i = 1,...,3n (8.2) 2. 约束方程及分类 用数学方程式表示的约束条件,称为约束方程。 用数学方程式表示的约束条件,称为约束方程。 系统自由度 k = 3n − l 其中 为独立的完整约束方程数。 其中l 为独立的完整约束方程数。
工程力学练习题及参考答案.doc

)一、判断题(正确的在括号中打“√”,错误的在括号中打“×”。
1、加减平衡力系公理一般不适用于一个变形体。
(√)2、合力一定比分力大。
(×)3、物体相对于地球静止时,它一定平衡;物体相对于地球运动时,它一定不平衡。
(×)4、约束力的作用位置在约束与被约数物体的相互接触处。
(√)5、凡是只受到两个力作用的杆件都是二力杆件。
(×)6、汇交力系中各个力的作用点为同一点。
(×)7、力偶矩的单位与力矩的单位是相同的。
(√)8、力偶不能够合成为一个力,也不能用一个力来等效替代。
(√)9、平面一般力系的主矢与简化中心无关。
(√)10、平面力系与其作用面内的两个不同点简化,有可能得到主矩相等,但力系的主矢和主矩都不为零。
(×)11、平面汇交力系中各力在任意轴上投影的代数和分别等于零,则该力系平衡。
(√)12、一个汇交力系如果不是平衡力系,则必然有合力。
(√)13、在应用平面汇交力系的平衡方程解题时,所选取的两个投影轴必须相互垂直。
(×)14、平面力系的平衡方程可以是三个彼此独立的投影式的平衡方程。
(×)15、材料力学的任务是尽可能保证构件的安全工作。
(√)16、作用在刚体上的力偶可以任意平移,而作用在变形固体上的力偶一般不能平移。
(√)17、线应变是构件中单位长度的变形量。
(√)18、若构件无位移,则其内部不会产生内力。
(×)19、用圆截面低碳钢试件做拉伸试验,试件在颈缩处被拉断,断口呈杯锥形。
(√)20、一般情况下,脆性材料的安全系数要比塑性材料取得小些。
(×)21、胡克定律只适用于弹性变形范围内。
(√)22、塑性材料的应力 - 应变曲线中,强化阶段的最高点所对应的应力为强度极限。
(√)23、发生剪切变形的构件都可以称为剪切构件。
(×)24、在剪切构件中,挤压变形也是一个次要的方面。
(×)25、构件的挤压面和剪切面一般是垂直的。
《工程力学》复习题及答案课件.doc

《工程力学》复习题及答案一、填空题1、工程力学包括、、和动力学的有关内容。
2、力的三要素是力的、、。
用符号表示力的单位是或。
3、力偶的三要素是力偶矩的、和。
用符号表示力偶矩的单位为或。
4、常见的约束类型有约束、约束、约束和固定端约束。
5、低碳钢拉伸时的大致可分为、、和阶段。
6、剪切变形的特点是工件受到一对大小、方向、作用线且相距很近的外力作用。
7、圆轴扭转的变形特点是:杆件的各横截面绕杆轴线发生相对,杆轴线始终保持。
8、平面弯曲变形的变形特点是杆的轴线被弯成一条。
9、静定梁可分为三种类型,即、和。
10、是指由无数个点组成的不变形系统。
11、规定动点对于定参考系的运动称为运动。
动点对于动参考系的运动称为运动,把动参考系对于定参考系的运动称为运动。
12、平面汇交力系平衡的解析条件是:力系中所有的力在投影的代数均为。
13、在工程中受拉伸的杆件,其共同的特点是:作用于杆件上的外力或外力的合力的作用线与构件轴线,杆件发生方向,伸长或压缩。
14、空间汇交力系的合力在任意一个坐标轴上的投影,等于在同一轴上投影的,此称为空间力系的。
15、力矩的大小等于和的乘积。
通常规定力使物体绕矩心时力矩为正,反之为负。
16、大小,方向,作用线的两个力组成的力系,称为力偶。
力偶中二力之间的距离称为,力偶所在的平面称为。
17、力的平将作用在刚体某点的力平移到刚体上别指定一点,而不改变原力对刚体的作用效果,则必须附加一力偶,其力偶矩等于。
18、构件的强度是指的能力;构件的刚度是指的能力;构件的稳定性是指的能力。
二、判断题:(对的画“√”,错的画“×”)1、力的可传性定理,只适用于刚体。
()2、两物体间相互作用的力总是同时存在,并且两力等值、反向共线,作用在同一个物体上。
()3、力的大小等于零或力的作用线通过矩心时,力矩等于零。
()4、力偶无合力,且力偶只能用力偶来等效。
()5、柔体约束特点是限制物体沿绳索伸长方向的运动,只能给物体提供拉力。
(完整版)工程力学习题解答(详解版)
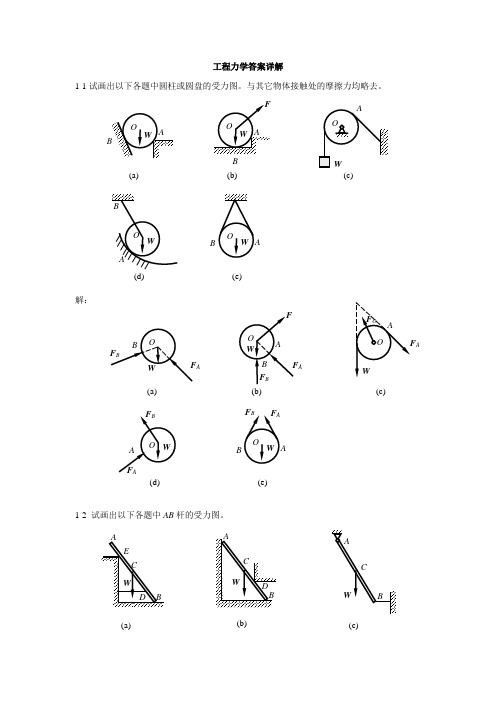
工程力学答案详解1-1试画出以下各题中圆柱或圆盘的受力图。
与其它物体接触处的摩擦力均略去。
解:1-2 试画出以下各题中AB 杆的受力图。
(a) B(b)(c)(d)A(e) A(a)(b) A(c)A(d)A(e)(c)(a)(b)解:1-3 试画出以下各题中AB 梁的受力图。
(d)(e)BB(a)B(b)(c)F B(a)(c)F (b)(d)(e)解:1-4 试画出以下各题中指定物体的受力图。
(a) 拱ABCD ;(b) 半拱AB 部分;(c) 踏板AB ;(d) 杠杆AB ;(e) 方板ABCD ;(f) 节点B 。
解:(a)F (b)W(c)(d) D(e)F Bx(a)(b)(c)(d)D(e)W(f)(a)D(b)B(c)BF D BF1-5 试画出以下各题中指定物体的受力图。
(a) 结点A,结点B;(b) 圆柱A和B及整体;(c) 半拱AB,半拱BC及整体;(d) 杠杆AB,切刀CEF及整体;(e) 秤杆AB,秤盘架BCD及整体。
解:(a)(b)(c)(d)ATF BAF(b)(e)(c)(d)(e)CAA C’CDDB2-2 杆AC 、BC 在C 处铰接,另一端均与墙面铰接,如图所示,F 1和F 2作用在销钉C 上,F 1=445 N ,F 2=535 N ,不计杆重,试求两杆所受的力。
解:(1) 取节点C 为研究对象,画受力图,注意AC 、BC 都为二力杆,(2) 列平衡方程:12140 sin 600530 cos6005207 164 o y AC o x BC AC AC BC F F F F F F F F F N F N=⨯+-==⨯--=∴==∑∑ AC 与BC 两杆均受拉。
2-3 水平力F 作用在刚架的B 点,如图所示。
如不计刚架重量,试求支座A 和D 处的约束力。
解:(1) 取整体ABCD 为研究对象,受力分析如图,画封闭的力三角形:(2)F 1F FDF F AF D211 1.122D A D D A F F FF F BC AB AC F F F F F =====∴===2-4 在简支梁AB 的中点C 作用一个倾斜45o 的力F ,力的大小等于20KN ,如图所示。
08B材料力学试题
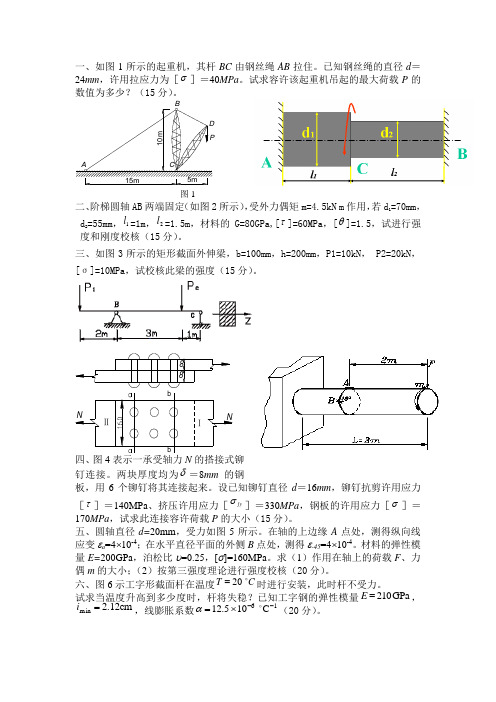
一、如图1所示的起重机,其杆BC 由钢丝绳AB 拉住。
已知钢丝绳的直径d =24mm ,许用拉应力为[σ]=40MPa 。
试求容许该起重机吊起的最大荷载P 的数值为多少?(15分)。
15m5m10mPABCDb PABCD15m5m10mN ABX CY C d图2-28 例题2-13图图1二、阶梯圆轴AB 两端固定(如图2所示),受外力偶矩m=4.5kN m 作用,若d 1=70mm ,d 2=55mm ,1l =1m ,2l =1.5m ,材料的G=80GPa,[τ]=60MPa ,[θ]=1.5,试进行强度和刚度校核(15分)。
三、如图3所示的矩形截面外伸梁,b=100mm ,h=200mm ,P1=10kN , P2=20kN ,[σ]=10MPa ,试校核此梁的强度(15分)。
88ⅠNⅡbbN板Ⅰ的图64P62P Pcb6P 6P 6P6P 6P6P bbⅠN=P 图2-49 例题2-20图长度单位:Ⅰσbb N 8截面d四、图4表示一承受轴力N 的搭接式铆钉连接。
两块厚度均为δ=8mm 的钢板,用6个铆钉将其连接起来。
设已知铆钉直径d =16mm ,铆钉抗剪许用应力[τ]=140MPa 、挤压许用应力[jyσ]=330MPa ,钢板的许用应力[σ]=170MPa ,试求此连接容许荷载P 的大小(15分)。
五、圆轴直径d=20mm ,受力如图5所示。
在轴的上边缘A 点处,测得纵向线应变εa =4⨯10-4;在水平直径平面的外侧B 点处,测得ε-45=4⨯10-4。
材料的弹性模量E=200GPa ,泊松比υ=0.25,[σ]=160MPa 。
求(1)作用在轴上的荷载F 、力偶m 的大小;(2)按第三强度理论进行强度校核(20分)。
六、图6示工字形截面杆在温度C T20=时进行安装,此时杆不受力。
试求当温度升高到多少度时,杆将失稳?已知工字钢的弹性模量GPa 210=E ,cm 12.2min =i ,线膨胀系数16C 105.12--⨯= α(20分)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
C
B
v P
v v 拆除弹簧AB, 拆除弹簧 ,用 F 、F ′ 表示弹簧对刚体系统的作用 弹簧伸长量 λ = 2l sin θ − 2l sin θ 0 故弹簧力的大小为 F = F ' = kλ = 2l (sinθ − sinθ0 )k
例题
例 题 5
§8 虚位移原理
O
δ ′WF = Fδx A δ ′WF ′ = − F ′δxB
例题
例 题 5
§8 虚位移原理
系统的虚功方程为 δ ′W = ∑ δ ′Wi = PδxB + Fδx A − F ′δxB = 0 即 由于
( Fl cosθ − 3F ' l cosθ + 3Pl cosθ )δθ = 0
Fl cosθ − 3F ' l cosθ + 3Pl cosθ = 0 δθ ≠ 0 2 4 ∴ P = F = l (sinθ − sinθ0 )k
v QE 1
v T
v Q2
B
v T' H v
Q3
C
r r 且 T = −T ' , T = T ′
G
D v
δ ′W = ∑ δ ′Wi
2.列虚功方程 几何法) 列虚功方程(几何法 列虚功方程 几何法) n
T'
= r ir 1 r r r r r r r r = Q ⋅1 δrE + Q2 ⋅ δrG + Q3 ⋅ δrH + T ⋅ δrE + T '⋅δrH = 0
x A = l sin θ
建立坐标系Oxy,各 各 建立坐标系 力的虚功表示为: 力的虚功表示为: δ ′WP = PδxB
C
x l
B
θ
l l
A
l l
v v F F′
D
l
v P
E
y
利用解析法建立虚位移的关系: 利用解析法建立虚位移的关系:
xB = 3l sinθ
求变分
δxA = l cosθδθ
δxB = 3l cosθδθ
v T
例题
例 题 6
§8 虚位移原理
=0
r r r r r r r r r r Q ⋅1 δrE + Q2 ⋅ δrG + Q3 ⋅ δrH + T ⋅ δrE + T '⋅δrH
此机构中, 为定轴转动, 为平动, 此机构中,杆AB,DC为定轴转动,杆BC为平动,可 , 为定轴转动 为平动 v 判断E, , 各点的虚位移方向 各点的虚位移方向。 判断 ,G,H各点的虚位移方向。 Q E 1 A 且 δ rG = δ rE B v
工程力学(C 工程力学(C)
(20)
北京理工大学理学院力学系
韩斌
§8.4 虚位移原理
1. 虚位移原理 具有双面理想约束的质点系, 具有双面理想约束的质点系,在某一位置能继续 保持静止平衡的充要条件是: 保持静止平衡的充要条件是: 作用于质点系的主动力在该位置任何一组虚位 移上做的虚功之和等于零。 移上做的虚功之和等于零。即: n r r 虚功方程 δ ′W = ∑ Fi ⋅ δ ri = 0 (8.32) )
A
l l
v v F F′
D
l
v P
E
y
例题
例 题 6
§8 虚位移原理
A E B
AB、BC、CD为三根等 、 、 为三根等 等重的均质杆, 长、等重的均质杆,与铅 垂墙壁连成正方形ABCD, 垂墙壁连成正方形 , 并用柔绳EH拉住 拉住, 、 并用柔绳 拉住,E、H 分别为AB、 的中点 的中点, 分别为 、BC的中点,各 杆重Q,求柔绳的拉力。 杆重 ,求柔绳的拉力。
对于有弹簧连接的刚体系统或变形体: 对于有弹簧连接的刚体系统或变形体:
δ ′W = ∑ δ ′Wi ( 外) + ∑ δ ′Wi (内) = 0
i =1 i =1
n
m
对于非理想约束,可将其约束力视为主动力。 对于非理想约束,可将其约束力视为主动力。 若系统全部为有势力作功时, 若系统全部为有势力作功时,虚功方程为
B
r Q
杆AB、CD由光滑铰 、 由光滑铰 相连, 杆的B 链C相连,在AB杆的 相连 杆的 r 端作用一铅垂力 Q ,在 CD杆上作用一力偶,其 杆上作用一力偶, 杆上作用一力偶 力偶矩为M,不计杆重, 力偶矩为 ,不计杆重, 端的约束反力。 求A端的约束反力。 端的约束反力
A
b
D
M
例题
例 题 7
r ∂ri ∑ Fi ⋅ ∂q = 0 i =1 j
n
k个独立方程 r 个独立方程
j=1,…k
已知平衡位置,求此时各主动 已知平衡位置, 力之间关系 已知各主动力, 已知各主动力,求平衡时的位置
(2)对自由度为零的系统(静定结构)——求约 )对自由度为零的系统(静定结构) 求约 束处的约束力 自由度为零, 自由度为零,系统无虚位移 解除一个约束, 解除一个约束,代之以 相应的待求约束力( 相应的待求约束力(视 为未知大小的主动力) 为未知大小的主动力) 系统变为k=1的机构, 的机构, 系统变为 的机构 按(1)求解未知约束力 求解未知约束力
AB定轴转动,CD一般 定轴转动, 一般 定轴转动 平面运动,瞬心为P, 平面运动,瞬心为 , AB的虚转角 δϕ1 的虚转角 CD的虚转角为 δϕ 2 的虚转角为
r Q
B
δϕ1
δrC
δϕ 2
D
则 δrC = AC ⋅ δϕ1 = PC ⋅ δϕ 2
∴δϕ 2 = 2δϕ1
例题
例 题 7
列虚功方程: 列虚功方程:
同理可得
O
δ ′W = δ ′W + δ ′W = 0 δ ′W 外 = δ ′W P = 3Pl cos θδθ 由 λ = 2l sin θ − 2l sin θ 0 = δ ′W 内 δ ′WT= −kλδλ
C
x l
B
2 ∴P= F 4 3 = l (sinθ − sinθ0 )k 3
θ
l l
i
∑ δ ′W
的虚位移, 的虚位移,必须表示为独立的虚位移的形式 (3)整理虚功方程,令虚功方程中各独立虚位移前 )整理虚功方程, 面的系数为零。 面的系数为零。
i =1
例题
例 题 5
O
§8 虚位移原理
C
A
θ
B
v P
E
D
杆OD、CE、CB、DB,弹簧 ,刚度为 ,弹 ,弹簧AB,刚度为k, 簧未变形时 θ = θ 0 ,OA=AE=AD=AC=CB=DB=l,求 求 角为平衡位置时, =? 当θ角为平衡位置时,P=? 角为平衡位置时
例题
例 题 5
§8 虚位移原理
O
解:1.分析 分析 l l l 系统自由度为1, 系统自由度为 ,可 A θ v v F F′ 为广义坐标。 选θ为广义坐标。 为广义坐标 系统中作功的力: 系统中作功的力: l l l r 弹簧力, 主动力 P ,弹簧力, E D 系统为理想约束系统, 系统为理想约束系统,各铰处的约束力不作功 。 2.列虚功方程 列虚功方程
若求多个约束力,可依次解除相应约束, 若求多个约束力,可依次解除相应约束,每次求出 一个约束力
解题指导 (1)对系统,正确写出虚功方程: )对系统,正确写出虚功方程:
δ ′W = ∑ δ ′W i = 0
(8.32) )
是全部作功的力的虚功之和 ——正确找出 正确找出 全部作功之力, 全部作功之力, 正确写出虚功 n r r (2)虚功方程 δ ′W = ∑ δ ′Wi = ∑ Fi ⋅ δ ri = 0 中 )
a
A
a
P
v δrC
C
M
a
v δrB
B
r Q
FAy
AB平动,CD瞬心为 AB平动,CD瞬心为P 瞬心为P 平动 设CD的虚转角为δϕ 的虚转角为 则有 δ rC = δ rA = δ rB = a δ ϕ 列虚功方程: 列虚功方程:
nbDFra bibliotekδϕδWQ = −QδrB
∑ δW
i =1
i
=0
δWF = FAyδrA
δϕ 2
∴ M A = 3aQ + 2 M 1 ( )
例题
例 题 7
§8 虚位移原理
a
A A
r (2)求 FAx 求 FAx 去掉A端的水平约束 端的水平约束, 去掉 端的水平约束, 用约束力F 代替。 用约束力 Ax 代替。 系统的自由度为1 系统的自由度为v v 主动力 FAx , M , Q AB、CD只能作平动 v、 只能作平动 v v
相对惯性系静止
2. 虚位移原理的应用
r r 虚功方程 δ ′W = ∑ Fi ⋅ δ ri = 0 (8.32) )
n i =1
的系统( (1)对自由度为 的系统(机构)——有k个独立的广 )对自由度为k的系统 机构) 有 个独立的广 义坐标、 个独立的广义虚位移 义坐标、k个独立的广义虚位移 r n n k r r r ∂ ri δq j ) 虚功方程 δ ′W = ∑ Fi ⋅ δ ri = ∑ Fi ⋅ ( ∑ i =1 i =1 j =1 ∂ q j r k n r ∂ ri = ∑ ( ∑ Fi ⋅ )δ q j = 0 (8.34) ) ∂q j j =1 i =1
3 3
O
C
x l
B
θ
l l
A
l l
v v F F′
D
l
v P
E
y
例题
例 题 5
虚功方程为
§8 虚位移原理
内 外
方法二 不拆除弹簧(弹簧包括在系统内,有内力作功) 不拆除弹簧(弹簧包括在系统内,有内力作功)
