2016版频率分布直方图课件PPT
合集下载
频率分布直方图与折线图课件

优缺点分析
分别分析两种图表在展示 数据方面的优缺点,以便 在实际应用中选择合适的 图表。
实例对比
通过对比实际数据实例, 展示两种图表在展示数据 时的差异和效果。
感谢您的观看
THANKS
频率分布直方图的缺点
对于连续型数据或数据量较小的情况,直方图的表现力可能不够理想。
折线图的优点
能够直观地展示数据随时间或其他变量的变化趋势。能够清晰地展示 数据的趋势和变化。
折线图的缺点
对于数据点较少或数据变化不大的情况,折线图的表现力可能不够理 想。
05
实践练习
制作频率分布直方图
收集数据
首先需要收集一组数据,可以是 关于某班级学生的考试成绩、某
频率分布直方图与折线图课 件
目录
• 引言 • 频率分布直方图 • 折线图 • 比较频率分布直方图与折线图 • 实践练习
01
引言
课程目标
掌握频率分布直方图 和折线图的绘制方法
能够根据实际数据选 择合适的图表进行展 示
理解频率分布直方图 和折线图在数据分析 中的应用
学习内容概述
01
02
03
04
频率分布直方图的概念、特点 和绘制步骤
品牌产品的销售数据等。
确定组距
根据数据的特点和需求,确定 合适的组距,以便将数据分成 若干个区间。
计算频率
根据每个区间的数据个数,计 算出每个区间的频率。
绘制直方图
使用适当的图表软件,根据区间 和频率绘制出直方图,每个矩形
的高度代表该区间的频率。
制作折线图
01
02
03
04
准备数据
准备一组有序的数据点,可以 是时间序列数据或有序分类数
频率分布与直方图PPT课件
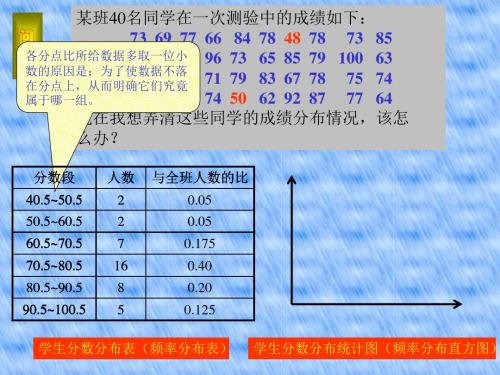
某班40名同学在一次测验中的成绩如下: 问 73 69 77 66 84 78 48 78 73 85 题 各分点比所给数据多取一位小 98 81 52 96 73 65 85 79 100 63 数的原因是:为了使数据不落 88 57 99 71 79 83 67 78 75 74 在分点上,从而明确它们究竟 71 89 76 74 50 62 92 87 77 64 属于哪一组。 现在我想弄清这些同学的成绩分布情况,该怎 么办?
总质量
想 一 想
练 习 一
已知一组数据如下:
25 21 23 25 27 29 25 28 30 29 26 24 25 27 26 22 24 25 26 28
填写下面的频率分布表,绘出频率分布直方图。
组别
频数累计
频数
频率
20.5~22.5
22.5~24.5
24.5~26.5
260名15岁女学生的身高做 了测量,结果如下(单位:cm): 142 154 159 175 159 156 149 162 166 158 159 156 166 160 164 155 157 146 147 161 158 158 153 158 154 158 163 154 153 153 162 162 151 154 165 164 152 151 146 151 158 160 165 158 163 163 162 161 154 165 162 162 159 157 159 149 164 149 159 153 列出频率分布表,绘出频率分布直方图。
分数段
40.5~50.5 50.5~60.5 60.5~70.5
人数
2 2 7 16
与全班人数的比
0.05 0.05 0.175 0.40
总质量
想 一 想
练 习 一
已知一组数据如下:
25 21 23 25 27 29 25 28 30 29 26 24 25 27 26 22 24 25 26 28
填写下面的频率分布表,绘出频率分布直方图。
组别
频数累计
频数
频率
20.5~22.5
22.5~24.5
24.5~26.5
260名15岁女学生的身高做 了测量,结果如下(单位:cm): 142 154 159 175 159 156 149 162 166 158 159 156 166 160 164 155 157 146 147 161 158 158 153 158 154 158 163 154 153 153 162 162 151 154 165 164 152 151 146 151 158 160 165 158 163 163 162 161 154 165 162 162 159 157 159 149 164 149 159 153 列出频率分布表,绘出频率分布直方图。
分数段
40.5~50.5 50.5~60.5 60.5~70.5
人数
2 2 7 16
与全班人数的比
0.05 0.05 0.175 0.40
《频数分布表与直方图》PPT课件

直方图是为了把表中的结果直观地表示出来,它
们是频数分布的“数”与“形”的两种不同形式,
互相补充.
(来自《点拨》)
知2-练
1 某学校八年级共有你n名男生. 现测量他们的身高 (单位:cm. 结果精确到1 cm),依据数据绘制的 频数分布直方图如图所示(为了避免有些数据落 在分组的界限上,对作为分点的数保留一位小数).
的学生为正常,试求身高正常的学生的百分比.
知2-讲
导引知:先识确点定最大值与最小值的差为180-140=40(cm),故可
将数据按组距为5进行分组,可分40÷5=8(组). 解:(1)计算这组数据的最大值与最小值的差为180-140=
40(cm). 确定组数与组距,将数据按组距为5进行分组,可分 为40÷5=8(组),即每个小组的范围分别是140≤x< 145,145≤x<150,150≤x<155,155≤x<160,160≤ x<165,165≤x<170,170≤x<175,175≤x≤180. 其中x为学生身高.
C.8组
D.10组
导引:因为这组数据的最大值是187,最小值是140,最 大值与最小值的差是47,且 47 7 5 ,所以应 66 分为8组. 答案:C
总结
知1-讲
确定组数的方法:若最大值与最小值的差除 以组距所得的商是整数,则这个商即为组数;若 最大值与最小值的差除以组距所得的商是小数, 则这个商的整数部分+1即为组数.
知2-讲
知2-讲
例2 某中学部分同学参加全国初中数学竞赛,取得了优异的成
绩,指导老师统计了所有参赛同学的成绩(成绩都是整数, 试题满分120分),并且绘制了如图所示的频数分布直方图 (每组中含最低分数,但不含最高分数),请回答: (1)该中学参加本次数学竞
频率分布直方图 PPT

频组频率距率 0.5 组距
0.4 0.3 0.2 0.1
O 0.5 1 1.5 2 2.5 3 3.5 4 4.5 月均用水量/t
各小长方形的面积=频率
各小长方形的面积之和=1
频率分布直方图的优点是能够非常直观明了 地反映样本数据的分布情况,缺点是原始数据不 能在图中表示出来.
你能根据频率分布直方图估计居民月均用水量 的一些数据特点吗?
(2)大部分居民的月均用水量集中在一个中间值 附近,只有少数居民的月均用水量很多或很少;
(3)居民月均用水量的分布有一定的对称性等.
样本数据的频率分布直方图是根据频率分布表画出来的,一般地,频率分布直方图的 作图步骤如下
第一步,画平面直角坐标系. 第二步,在横轴上均匀标出各组分点,在纵轴上标出单位长度.
频率 频组组率距距
0.5 0.4 0.3 0.2 0.1
O 0.5 1 1.5 2 2.5 3 3.5 4 4.5 月均用水量/t
频率 频组组率距距
0.5 0.4 0.3 0.2 0.1
O 0.5 1 1.5 2 2.5 3 3.5 4 4.5 月均用水量/t
(1)居民月均用水量的分布是“山峰”状的,而 且是“单峰”的;(说明样本的数据非常集中)
第三步,以组距为宽,各组的频率与组距的商为高,分别画出各组对应的小长方形.
练习
高一某班有50名学生,在数学必修②结业考试后随机抽取10名,其考试成绩如下: 82, 75, 61, 93, 62, 55, 70, 68, 85, 78.
要求根据上述抽样数据,(1).作出频率分布列表和频率分布直方图.(2)估计该班对数 学模块②的总体学习水平。
高度:
频率 组距
宽度:组距
O 0.5 1 1.5 2 2.5 3 3.5 4 4.5 月均用水量/t
0.4 0.3 0.2 0.1
O 0.5 1 1.5 2 2.5 3 3.5 4 4.5 月均用水量/t
各小长方形的面积=频率
各小长方形的面积之和=1
频率分布直方图的优点是能够非常直观明了 地反映样本数据的分布情况,缺点是原始数据不 能在图中表示出来.
你能根据频率分布直方图估计居民月均用水量 的一些数据特点吗?
(2)大部分居民的月均用水量集中在一个中间值 附近,只有少数居民的月均用水量很多或很少;
(3)居民月均用水量的分布有一定的对称性等.
样本数据的频率分布直方图是根据频率分布表画出来的,一般地,频率分布直方图的 作图步骤如下
第一步,画平面直角坐标系. 第二步,在横轴上均匀标出各组分点,在纵轴上标出单位长度.
频率 频组组率距距
0.5 0.4 0.3 0.2 0.1
O 0.5 1 1.5 2 2.5 3 3.5 4 4.5 月均用水量/t
频率 频组组率距距
0.5 0.4 0.3 0.2 0.1
O 0.5 1 1.5 2 2.5 3 3.5 4 4.5 月均用水量/t
(1)居民月均用水量的分布是“山峰”状的,而 且是“单峰”的;(说明样本的数据非常集中)
第三步,以组距为宽,各组的频率与组距的商为高,分别画出各组对应的小长方形.
练习
高一某班有50名学生,在数学必修②结业考试后随机抽取10名,其考试成绩如下: 82, 75, 61, 93, 62, 55, 70, 68, 85, 78.
要求根据上述抽样数据,(1).作出频率分布列表和频率分布直方图.(2)估计该班对数 学模块②的总体学习水平。
高度:
频率 组距
宽度:组距
O 0.5 1 1.5 2 2.5 3 3.5 4 4.5 月均用水量/t
《频率分布直方图》课件

《频率分布直方图》PPT 课件
欢迎来到本节课的《频率分布直方图》PPT课件。本课件将详细介绍频率分布 直方图的概念、数据收集、构建和解读,帮助您更好地理解和运用这一重要 统计工具。
课件目标
通过本课件,您将学习以下内容:
1 掌握频率分布直方图的定义和用途
2 了解数据收集的方法和重要性
3 学会如何整理数据以构建频率分布
直方图
4 掌握如何解读直方图并获取有用的
统计信息
频率分布直方图介绍
• 频率分布直方图是一种图表,用于显示数据的分布情况和频率。 • 直方图以数据的范围为横轴,频率为纵轴,通过矩形的高度来表示频率。 • 直方图可以帮助我们更直观地了解数据的分布特征和趋势。
数据收集
在构建频率分布直方图之前,我们需要收集一定数量的数据。
1 确定需要收集的数据类型和范围 2 选择合适的数据收集方法(例如调查、观察、实验等) 3 确保数据的准确性和完整性
数据整理
在构建频率分布直方图之前,我们需要对数据进行适当的整理和分类。
1 将收集到的数据进行排序
2 确定数据的分组间隔和组数
3 计算每个数据分组的频率
构建频率分布直方图
1
绘制矩形并标出各个分组的频率
2
3
确定横轴和纵轴的范围 为直方图添加标题和标签
解读直方图
通过观察直方图,我们可以得到有关数据分布的重要信息。
1 查看直方图的对称、偏态或多
分布范围
和离群点
峰性
课件总结
通过本课件,您已经了解了频率分布直方图的概念、数据收集、构建和解读。 希望这些知识能帮助您更好地进行数据分析和统计。 谢谢观看!
欢迎来到本节课的《频率分布直方图》PPT课件。本课件将详细介绍频率分布 直方图的概念、数据收集、构建和解读,帮助您更好地理解和运用这一重要 统计工具。
课件目标
通过本课件,您将学习以下内容:
1 掌握频率分布直方图的定义和用途
2 了解数据收集的方法和重要性
3 学会如何整理数据以构建频率分布
直方图
4 掌握如何解读直方图并获取有用的
统计信息
频率分布直方图介绍
• 频率分布直方图是一种图表,用于显示数据的分布情况和频率。 • 直方图以数据的范围为横轴,频率为纵轴,通过矩形的高度来表示频率。 • 直方图可以帮助我们更直观地了解数据的分布特征和趋势。
数据收集
在构建频率分布直方图之前,我们需要收集一定数量的数据。
1 确定需要收集的数据类型和范围 2 选择合适的数据收集方法(例如调查、观察、实验等) 3 确保数据的准确性和完整性
数据整理
在构建频率分布直方图之前,我们需要对数据进行适当的整理和分类。
1 将收集到的数据进行排序
2 确定数据的分组间隔和组数
3 计算每个数据分组的频率
构建频率分布直方图
1
绘制矩形并标出各个分组的频率
2
3
确定横轴和纵轴的范围 为直方图添加标题和标签
解读直方图
通过观察直方图,我们可以得到有关数据分布的重要信息。
1 查看直方图的对称、偏态或多
分布范围
和离群点
峰性
课件总结
通过本课件,您已经了解了频率分布直方图的概念、数据收集、构建和解读。 希望这些知识能帮助您更好地进行数据分析和统计。 谢谢观看!
频率分布直方图课件

由于频率分布直方图是基于数据的近似离 散化,因此无法准确地反映数据的分布情 况,特别是对于具有复杂分布的数据。
无法表示数据间的相关性
无法进行参数估计和假设检验
频率分布直方图只能展示单个变量的分布 情况,无法表示两个或多个变量之间的相 关性。
频率分布直方图主要用于数据的描述性分 析,无法进行参数估计和假设检验等推断 性分析。
于反映数据的中心趋势。频率பைடு நூலகம்布直方图可以直观地展示数据在不同区
间的分布情况,从而更好地理解数据的分布特征。
03
众数
众数是数据中出现次数最多的数值。频率分布直方图可以清晰地展示众
数所在区间的数据分布情况,帮助我们更好地理解众数的含义和作用。
与箱线图、折线图等其他图形的比较
要点一
箱线图
要点二
折线图
箱线图是一种用于展示一组数据分散情况的统计图,它包 括数据的最大值、最小值、中位数和异常值等统计量。频 率分布直方图和箱线图各有优缺点,箱线图可以展示数据 的分散情况和异常值,但无法展示数据的具体分布情况; 频率分布直方图可以清晰地展示数据的分布情况,但无法 很好地展示数据的分散情况和异常值。
数据中心位置与离散程度判断
确定数据的中位数和众数
频率分布直方图可以显示数据的频数分布,从而确定数据的 中位数和众数,了解数据的中心位置。
评估数据的离散程度
通过观察频率分布直方图中数据的分散程度,可以评估数据 的离散程度,进一步了解数据的稳定性。
数据异常值检测
识别异常值
频率分布直方图可以显示数据的频数分布,通过观察直方图的形状和异常的数据点,可 以识别出异常值。
纵轴
表示频数或频率,即落在每个数 据范围内的数据点的个数。
《频率分布直方图》示范公开课教学课件【高中数学北师大版】

146 141 139 140 145 141 142 131 142 140 144 140138 139 147 139 141 137 141 132 140 140 141 143134 146 134 142 133 149 140 140 143 143 149 136141 143 143 141 138 136 138 144 136 145 143 137142 146 140 148 140 140 139 139 144 138 146 153148 152 143 140 141 145 148 139 136 141 140 139158 135 132 148 142 145 145 121 129 143 148 138149 146 141 142 144 137 153 148 144 138 150 148138 145 145 142 143 143 148 141 145 141
宽度的最大值是158mm,最小值是121mm.
计算极差:mm.
这说明样本观测数据的变化范围是37mm.
146 141 139 140 145 141 142 131 142 140 144 140138 139 147 139 141 137 141 132 140 140 141 143134 146 134 142 133 149 140 140 143 143 149 136141 143 143 141 138 136 138 144 136 145 143 137142 146 140 148 140 140 139 139 144 138 146 153148 152 143 140 141 145 148 139 136 141 140 139158 135 132 148 142 145 145 121 129 143 148 138149 146 141 142 144 137 153 148 144 138 150 148138 145 145 142 143 143 148 141 145 141
宽度的最大值是158mm,最小值是121mm.
计算极差:mm.
这说明样本观测数据的变化范围是37mm.
146 141 139 140 145 141 142 131 142 140 144 140138 139 147 139 141 137 141 132 140 140 141 143134 146 134 142 133 149 140 140 143 143 149 136141 143 143 141 138 136 138 144 136 145 143 137142 146 140 148 140 140 139 139 144 138 146 153148 152 143 140 141 145 148 139 136 141 140 139158 135 132 148 142 145 145 121 129 143 148 138149 146 141 142 144 137 153 148 144 138 150 148138 145 145 142 143 143 148 141 145 141
频率分布直方图课件

绘制直方图的步骤
收集数据
如何收集数据,以及注意事项
确定组距
如何选择合适的组距
分组
如何将数据分为不同的组
统计频数或频率
如何计算每个组的频数或频率
绘制直方图
如何用数据绘制直方图
直方图的解读和应用
1
分布分析
2
如何利用直方图对数据分布进行分析和
解读
3
形状和特征
各种形状的直方图代表了不同的数据分 布形态和特征
频率分布直方图ppt课件
# 频率分布直方图PPT课件
目的和背景
1 数据分析的基础
介绍直方图在数据分析中的重要作用
2 可视化数据
将数据可视化有助于更好的理解和解释数据
直方图的构成
横轴和纵轴
介绍直方图的两个轴,以及它们的作用
组数和组距
解释如何选择合适的组数和组距
频率和频率密度
解释什么频率和频率密度,以及它们的区别
比较和评价
如何利用直方图进行数据比较和评价
结语
数据可视化的重要性
强调用直方图等数据可视化工具帮助人们更好地理 解和解释数据
更多学习资料和实例
提供其他学习资源和实例,以便更多人学习利用直 方图进行数据分析
参考文献
统计学基础知识
一本专门介绍统计学基础知识的书籍
直方图绘制方法和解读教程
一份详细的直方图绘制方法和解读教程
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
月均用水量 /t 4.5
当样本容量无限增大,分组的组距无限缩小,那么频率分
布直方图就会无限接近一条光滑曲线——总体密度曲线.
频率 组距
总体在区间(a , b)内取值的概率
S
a b
月均用水量 (mm)
应用举例:
例1对某电子元件进行寿命追踪调查,情况如下:
寿命 个数
100~200 200~300 300~400 400~500 500~600
200~300 300~400 400~500 500~600
合计
频率/组距
(3)电子元件寿命在 100h~400h 以内的频率为 0.65 (4)电子元件寿命在 400h以上的频率为0.35
0
寿命(h) 100 200 300 400 500 600
小结
1.求极差 步骤 2.决定组距与组数 3.将数据分组 4.列频率分布表
频率 组距
频数 3 8 9 11 10 5 4 50
频率 0.06 0.16 0.18 0.22 0.20 0.10 0.08 1
频率/ 组距 0.020 0.053 0.060 0.073 0.067 0.033 0.027
0.070 0.060 0.050 0.040 0.030 0.020 0.010
(1)列出样本的频率分布表; (2)画出频率分布直方图; (3)根据频率分布直方图估计,数据落在[15.5, 24.5)的 百分比是多少?
解:组距为3
分组 [12.5, [15.5, [18.5, [21.5, [24.5, [27.5, [30.5, 合计
15.5) 18.5) 21.5) 24.5) 27.5) 30.5) 33.5]
频率分布直方图的特征:
优点:从频率分布直方图可以清楚地看出数据分布的总体趋势 缺点:从频率分布直方图得不出原始的数据内容,把数据表示成直 方图后,原有的具体数据就被抹掉了
分组 [0,0.5) [0.5,1) [1,1.5) [1.5,2) [2,2.5)
频数 频率 累积频率 4 8 15 22 25 0.04 0.08 0.15 0.22 0.25
用水量 /t
如果当地政府希望85%以上的居民每月的用水量不超出 标准,根据频率分布表和频率分布直方图,你能对制定 月用水量提出建议吗?
居民月用水量标准应定为3t.
频率分布折线图如下:
频率
组距
连接频率分布直方图 中各小长方形上端的 中点,得到频率分布折 线图
0.50
0.40
0.30 0.20 0.10 0.5 1 1.5 2 2.5 3 3.5 4
极差 4.1 组数= = 8.2 = 组距 0.5 3.将数据分组(左闭右开)
[0,0.5 ),[0.5,1 ),…,[4,4.5]
4.列频率分布表
频率分布表一般分“分 组”,“频数累计” (可省),“频数”, “频率”, “频率/组 距””五列,最后一行 频数 是合计
分组 频数累计 频数 频率 频率/组距
车速
O
60 70 80 90 100 110
A100辆
C300辆
B200辆
D400辆
5.有一个容量为50的样本数据的分组的频数如下: [12.5, 15.5) 3
[15.5, [18.5, [21.5, [24.5, [27.5, [30.5, 18.5) 8 21.5) 9 24.5) 11 27.5) 10 30.5) 5 33.5 ] 4
请计算每个小矩形的面积 ,它代表什么 所有小矩形的面积的和是多少 ? 1 ?为什么?
频率 = 频率 小矩形的面积 = 组距× 组距
频率/组距
0.50 0.40 0.30 0.20 0.10
用水量/t
O
0.5
1
1.5
2
2.5
3
3.5
4
4.5
频率分布直方图,显示了样本数据落在各个小组的比例的大小, 图中最高的小矩形说明了什么? 月均用水量在[2,2.5)内的居民最多. 大部分居民的月均用水量都集中在什么之间? [1,3)之间.
通过抽样,我们获得了100位居民某年的月平均用水量 (单位:t) ,如下表:
这些数字告诉我们什么信息?
1.求极差(即一组数据中最大值与最小值的差) 4.3 - 0.2 = 4.1 2.决定组距与组数
组数:将数据分组,当数据在100个以内时,
按数据多少常分5-12组。
组距:指每个小组的两个端点的距离,
教学目标
1 通过实例体会分布的意义和作用。 2 在表示样本数据的过程中,学会列频率分 布表,画频率分布直方图,频率分布折线 图 3 能通过样本的频率分布估计总体的分布。
引入
我国是世界上严重缺水的国家之一, 城市缺水问题较为突出。
2000年全国主要城市中缺水情况排在前10位的城市
政府为了节约生活用水,计划在本市试行居民生 活用水定额管理,即确定一个居民月用水量标准 a , 用水量不超过a的部分按平价收费,超过a的 部分按议价收费。 ①如果希望大部分居民的日常生活不受影响,那 么标准a定为多少比较合理呢? ②为了较合理地确定这个标准,你认为需要做 哪些工作?
20
30
80
40
30
(1)列出频率分布表; (2)画出频率分布直方图及频率分布折线图; (3)估计电子元件寿命在100h~400h以内的频率; (4)估计电子元件寿命在400h以上的频率;
(1)列出频率分布表;
寿命 100~200 频数 20 30 80 40 30 200 频率 0.10 0.15 0.40 0.20 0.15 1 频率/组距 0.001 0.0015 0.004 0.002 0.0015
频率=
样本容量
注意频数的合计应 是样本容量,频率 合计应是1
0.02 1.00
0.04
100
5. 画频率分布直方图:
分组 [0,0.5) 频数 4 频率 频率/组距 0.04 0.08 频率/组距
0.50 0.40 0.30 0.20 0.10
注意 纵坐标是 频率/组距
[0.5,1)
[1,1.5) [1.5,2) [2,2.5)
频率分布直方图
5.画频率分布直方图
检测
1. 右图是容量为100的 样本的频率分布直方图, 试根据图中的数据填空: (1)样本数据落在范围 [6,10)内的频率为0.32 ____;
(2)样本数据落在范围 36 [10,14)内的频数为____; (3)总体在范围[2,6)内的 0.08 概率约为_______;
数据落在[15.5, 的百分比是56%
24.5)
12.5
15.5 18.5
21.5
24.5
27.5
30.5
33.5
[0,0.5) [0.5,1)
[1,1.5) [1.5,2) [2,2.5) [2.5,3) [3,3.5) [3.5,4) [4,4.5] 合计
4
0.04
0.08
8 15
22 25 14 6 4 2
0.08
0.15 0.22 0.25 0.14 0.06 0.04
0.16 0.30 0.44
0.50 0.28 0.12 0.08
频率
组距
0.09
0.08
0.03 0.02
样本 数据
O
2
6 10 14 18
2.一个容量为35的样本,分组后,组距与频数如下: [5,10)5,[10,15)12,[15,20)7,[20,25)5,[25,30)4, [30,35)2,则样本在区间[20,+∞)上的频率为( C ) A.20% B.69% C.31% D.27% 3.一个容量为32的样本,已知某组样本的频率
为0.125,则该组样本的频数为( B )
A.2
B.4
C.6
D.8
4.某路段检查监控录象 显示,在某时段内,有 1000辆汽车通过该站, 现在随机抽取其中的 200辆汽车进行车速分 析,则估计在这一时段 内通过该站的汽车中速 度不小于90km/h的约 有( C )
频率
组距
0.04
0.02 0.01
[2.5,3)
[3,3.5) [3.5,4)
14
6 4
0.14
0.06 0.04
[4,4.5)
合计
2
100
0.02
1.00
0.04 0.12 0.27 0.49 0.74 0.88 0.94 0.98 1.00
频率/组距
0.50 0.40 0.30 0.20 0.10
O 0.5 1 1.5 2 2.5 3 3.5 4 4.5
8
15 22 25
0.08
0.15 0.22 0.25
0.16
0.30 0.44 0.50
[2.5,3)
[3,3.5) [3.5,4) [4,4.5] 合计
14
6 4 2 100
0.14
0.06 0.04 0.02
0.28
0.12 0.08 0.04
用水量
O 0.5
1
1.5 2
2.5 3
3.5 4 4.5
