北师大版九年级数学下册第一章三角函数知识点总结(超级详细)
北师大版九年级数学下册第一章三角函数知识点总结(超级详细)
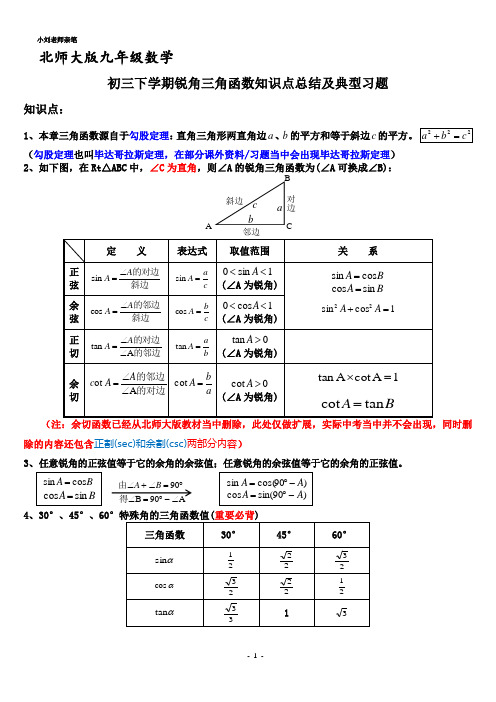
北师大版九年级数学初三下学期锐角三角函数知识点总结及典型习题知识点:1、本章三角函数源自于勾股定理:直角三角形两直角边a 、b 的平方和等于斜边c(勾股定理也叫毕达哥拉斯定理,在部分课外资料/习题当中会出现毕达哥拉斯定理) 2、如下图,在Rt △ABC 中,∠C 为直角,则∠A 的锐角三角函数为(∠A 可换成∠B):除的内容还包含正割(sec)和余割(csc)两部分内容)3、任意锐角的正弦值等于它的余角的余弦值;任意锐角的余弦值等于它的余角的正弦值。
4、30°、45°、60A 90B 90∠-︒=∠︒=∠+∠得由B A对边邻边 C6、正弦、余弦的增减性:当0°≤α≤90°时,sin α随α的增大而增大,cos α随α的增大而减小。
7、正切、的增减性:当0°<α<90°时,tan α随α的增大而增大,解直角三角形的定义1、:已知边和角(两个,其中必有一边)→所有未知的边和角。
依据:①边的关系:222c b a =+;②角的关系:A+B=90°;③边角关系:三角函数的定义。
(注意:尽量避免使用中间数据和除法)2、应用举例:(1)仰角:视线在水平线上方的角;俯角:视线在水平线下方的角。
仰角水平线视线视线俯角(2)坡面的铅直高度h 和水平宽度l 的比叫做坡度(坡比)。
用字母i 表示,即h i l=。
坡度一般写成1:m 的形式,如1:5i =等。
把坡面与水平面的夹角记作α(叫做坡角),那么tan hi lα==。
3、从某点的指北方向按顺时针转到目标方向的水平角,叫做方位角。
如图 ,OA 、OB 、OC 、OD 的方向角分别是:45°、135°、225°。
指北或指南方向线与目标方向 线所成的小于90°的水平角,叫做方向角。
所以,OA 、OB 、OC 、OD 的方向角分别是:北偏东30°(东北方向) , 南偏东45°(东南方向), 南偏西60°(西南方向), 北偏西60°(西北方向)。
(完整版)新北师大九年级数学下册知识点总结

新北师大版九年级数学下册知识点总结第一章直角三角形边的关系一•锐角三角函数 1.正切:定义:在Rt △ ABC 中,锐角/A 的对边与邻边的比叫做/A的正切,记作tanA ,① tanA 是一个完整的符号,它表示/A的正切,记号里习惯省去角的符号“/”;② tanA 没有单位,它表示一个比值,即直角三角形中/A 的对边与邻边的比;③ tanA 不表示"tan ”乘以"A ”;④ 初中阶段,我们只学习直角三角形中,/A是锐角的正切;⑤ tanA 的值越大,梯子越陡,ZA 越大;ZA 越大,梯子越陡,tanA 的值越大。
2. 正弦:定义:在Rt △ ABC 中,锐角/A 的对边与斜边的比叫做/A 的正弦,记作sinA ,即sin AA的对边................................... """■ 斜边3. 余弦:定义:在Rt △ ABC 中,锐角/A 的邻边与斜边的比叫做/A 的余弦,记作cosA ,即cosA A的邻边 .............................. ■■■■■斜边之变化三•三角函数的计算1. 仰角:当从低处观测高处的目标时,视线与水平线所成的锐角称为 仰角2. 俯角:当从高处观测低处的目标时,视线与水平线所成的锐角称为 俯角值随着角度的增大(或减小)而增大(或减小);余弦值随着角度的增大 < sin a< 1, 0< cos a< 1。
4. 坡度:如图2,坡面与水平面的夹角叫做坡角坡角的正切称为坡度i tan Al5. 方位角:从某点的指北方向按顺时针转到目标方向的水平角,叫做方位角...。
如图3,OA OB OC 的方位角分别为 45 °、135 °、225 °。
6. 方向角:指北或指南方向线与目标方向线所成的小于90°的水平角,叫做方向角.。
北师大版九年级数学下册《30°,45°,60°角的三角函数值》

= −+
=2 −
课堂练习
6.升国旗时,小明站在操场上离国旗20m处行注目礼.当国旗升至
顶端时,小明看国旗视线的仰角为45°(如图所示),若小明双眼
离地面1.60m,你能帮助小明求出旗杆AB的高度吗?
解:由已知得DC=EB=20m
∵tan∠ADC=tan45°=
∴AC=DC∙tan45°
°
(3)
+°
+
°
课堂练习
解: (1)1-2 sin30°cos30°
=1-2× ×
=1-
°
(3)
+°
=
+
+
+
=2- +
=2
°
(2)3tan30°-tan45°+2sin60°
=3×
−+×
O
C
B
A
D
答:最高位置与最低位置的高度差约为0.34m。
随堂练习P12
8
驶向胜利
的彼岸
八仙过海,尽显才能
某商场有一自动扶梯,其倾斜角为300,高为7m,
B
扶梯的长度是多少?
3.如图,在Rt△ABC中,∠C=90°,
∠A,∠B ,∠C的对边分别是a,b,c.
求证:sin2A+cos2A=1
老师期望:
sin30°=
sin60°=
=
2a
2
2a
a
3a 3
1
=2
cos30°=
(完整word版)北师大版九年级数学下册知识点归纳复习提纲,文档

新北师大版九年级数学下册知识点总结第一章 直角三角形边的关系一.锐角三角函数 1. 正切:定义:在中,锐角∠A 的对边与邻边的比叫做∠A的正切 ,记作 tanA ,Rt △ABC..的对边;即tan AA的邻边A① t anA 是一个完满的符号,它表示∠A 的正切,记号里习惯省去角的符号“∠〞;②tanA 没有单位,它表示一个比值,即直角三角形中∠A 的对边与邻边的比;③tanA 不表示“ tan 〞乘以“ A 〞;④初中阶段,我们只学习直角三角形中,∠A 是锐角的正切;⑤tanA 的值越大, 梯子越陡, ∠A 越大; ∠A 越大, 梯子越陡, tanA 的值越大。
2. 正弦:..定义:在 Rt △ABC 中,锐角∠A 的对边与斜边的比叫做∠A的正弦,记作 sinA ,即A 的对边 ; sin A斜边3. 余弦:定义:在 Rt △ABC 中,锐角∠A 的邻边与斜边的比叫做∠A的余弦,记作 cosA ,即A 的邻边 ; cos A斜边锐角 A 的正弦、余弦和正切都是∠A 的三角函数当锐角 A 变化时,相应的正弦、余弦和正 切之也随之变化。
二.特别角的三角函数值30 o45 o60 osin α1 2 3Bi=h:lhcos α321222tan α3133三.三角函数的计算1.仰角 : 当从低处察看高处的目标时,视线与水平线所成的锐角称为仰角..2.俯角:当从高处察看低处的目标时,视线与水平线所成的锐角称为俯角..3.规律:利用特别角的三角函数值表,能够看出,(1) 当角度在 0°~ 90°间变化时,正弦值、正切值随着角度的增大 ( 或减小 ) 而增大 ( 或减小 ) ;余弦值随着角度的增大(或减小 )而减小 ( 或增大 ) 。
(2)0 ≤ sin α≤ 1,0≤ cosα≤ 1。
4.坡度:如图 2,坡面与水平面的夹角叫做坡角坡角的正切称为坡度( 或坡比 ) 。
用字母 i.............表示,即 i htan A l5.方向角:从某点的指北方向按顺时针转到目标方向的水平角,叫做方向角...。
北师大版九年级(下)数学知识点归纳总结

第一章直角三角形的边角关系九年级下册第1节锐角三角函数一、锐角三角函数锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数。
如图所示,在Rt△ABC中,∠C=90°【说明】①三角函数表示的是两边的比值,所以它只是一个数值,没有单位。
②当用一个大写字母表示角时,其三角函数中角的符号省略,如sin A,cos B,tan C;当用一个希腊字母表示角时,其三角函数中角的符号省略,如sinα,cosβ,tanθ;当用三个大写字母表示角时,其三角函数中角的符号不能省略,如sin∠ABC,cos∠DEF,tan∠GHI;当用一个阿拉伯数字表示角时,其三角函数中角的符号不能省略,如sin∠1,cos∠2,tan∠3。
③如果要表示三角函数的倍数与乘方,应分别表示为2 sin A,3cos B,4tan C,sin2A,cos3B,tan4C;2 sin30°,3cos30°,4tan30°,sin230°,cos330°,tan430°。
二、坡度1、坡度的概念如图所示,我们把坡面的铅直高度h和水平宽度l的比值叫做坡度(或坡比),通常用字母i表示。
【说明】坡面的坡度实际上就是坡角的正切值,即i=tanα=hl2、三角函数与坡面的陡峭程度(1)tan A的值越大,坡面越陡。
(2)sin A的值越大,坡面越陡。
(3)cos A的值越小,坡面越陡。
三、锐角三角函数的增减性(0°~90°)1、正弦值随着角度的增大(或减小)而增大(或减小);2、余弦值随着角度的增大(或减小)而减小(或增大);3、正切值随着角度的增大(或减小)而增大(或减小)。
四、同角三角函数的关系1、互余关系:sinA =cos(90°-A) cosA =sin(90°-A)2、平方关系:s in 2A +cos 2A =13、弦切关系:tan A =sin cos AA4、倒数关系:tan A ·tan(90°-A)=1第2节 30°,45°,60°角的三角函数值一、探索30°,45°,60°角的三角函数值求30°角的三角函数值,关键根据“直角三角形中30°的锐角所对的直角边等于斜边的一半”,可设30°的锐角的对边为a ,则斜边为2a ,由勾股定理可求得30°3a ,因此可以求出30°的锐角的各个三角函数值:sin30°=2a a =12 cos30°3a3 tan30°3a 33也可以求出60°的锐角的各个三角函数值:sin60°3a =3 cos60°=2a a =12tan60°3a 3求45°角的三角函数值,关键根据“有一个角是45°的直角三角形是等腰直角三角形”,可设一条直角边为a ,则另一条直角边也为a 2a ,因此可以求出45°的锐角的各个三角函数值:sin45°2a 22 cos45°2a 2 tan45°=aa =1二、熟记特殊角的三角函数值第3节三角函数的计算一、用计算器求任意锐角的三角函数值1、求整数度数的锐角的三角函数值首先使计算器的面板上出现DEG,然后再按sin cos tan这三个键之一,再从高位向低位按出表示度数的整数,再按键=,就可以在显示屏上得到答案。
北师大版九年级下册第一章直角三角函数的边角关系课本知识点

北师大版九年级下册
第一章 直角三角形的边角关系
1、锐角三角函数
在ABC Rt ∆中,如果锐角A 确定,那么A ∠的对边与邻边的比便随之确定,这个比叫做A ∠的正切,记作A tan ,即
的邻边
的对边A A A ∠∠=tan . A tan 的值越大,梯子越陡。
A ∠的对边与斜边的比叫做A ∠的正弦,记作A sin ,即
斜边
的对边A A ∠=sin . A sin 的值越大,梯子越陡。
A ∠的邻边与斜边的比叫做A ∠的余弦,记作A cos ,即
斜边
的邻边A A ∠=cos . A cos 的值越小,梯子越陡。
锐角A 的正弦、余弦和正切都是A ∠的三角函数。
2、30°、45°、60°角的三角函数值
2130sin =︒
2245sin =︒ 2360sin =︒ 2330cos =︒
2245cos =︒ 2160cos =︒ 3330tan =︒ 145tan =︒ 360tan =︒
3、三角函数的计算(略)
4、解直角三角形
直角三角形中有6个元素,分别是三条边和三个角。
由直角三角形中已知的元素,求出所有未知元素的过程,叫做解直角三角形。
5、三角函数的应用(略)
6、利用三角函数测高(略)。
北师大版九年级数学下册各章知识点汇总

第一章 直角三角形的边角关系1 锐角三角函数2 30°,45°,60°角的三角函数值3 三角函数的计算4 解直角三角形5 三角函数的应用6 利用三角函数测高※一. 正切:定义:在Rt △ABC 中,锐角∠A 的对边与邻边的比叫做∠A 的正切..,记作tanA ,即的邻边的对边A A A ∠∠=tan ;①tanA 是一个完整的符号,它表示∠A 的正切,记号里习惯省去角的符号“∠”; ②tanA 没有单位,它表示一个比值,即直角三角形中∠A 的对边与邻边的比; ③tanA 不表示“tan ”乘以“A ”;④初中阶段,我们只学习直角三角形中,∠A 是锐角的正切;⑤tanA 的值越大,梯子越陡,∠A 越大; ∠A 越大,梯子越陡,tanA 的值越大。
※二. 正弦..: 定义:在Rt △ABC 中,锐角∠A 的对边与斜边的比叫做∠A 的正弦,记作sinA ,即斜边的对边A A ∠=sin ;※三. 余弦:定义:在Rt △ABC 中,锐角∠A 的邻边与斜边的比叫做∠A 的余弦,记作cosA ,即斜边的邻边A A ∠=cos ;※余切:定义:在Rt △ABC 中,锐角∠A 的邻边与对边的比叫做∠A 的余切,记作cotA ,即的对边的邻边A A A ∠∠=cot ;※一个锐角的正弦、余弦、正切、余切分别等于它的余角的余弦、正弦、余切、正切。
0º 30 º45 º 60 º 90 º sin α 0 21 22 23 1 cos α 1 23 22 21 0 tan α 0 33 1 3— cot α—3133 0(通常我们称正弦、余弦互为余函数。
同样,也称正切、余切互为余函数,可以概括为:一个锐角的三角函数等于它的余角的余函数)用等式表达:若∠A 为锐角,则 ①)90cos(sin A A ∠-︒=; )90sin(cos A A ∠-︒= ②)90cot(tan A A ∠-︒=; )90tan(cot A A ∠-︒=※当从低处观测高处的目标时,视线与水平线所成的锐角称为仰角.. ※当从高处观测低处的目标时,视线与水平线所成的锐角称为俯角.. ※利用特殊角的三角函数值表,可以看出,(1)当角度在0°~90°间变化时,正弦值、正切值随着角度的增大(或减小)而增大(或减小);余弦值、余切值随着角度的增大(或减小)而减小(或增大)。
北师大版九年级数学下册第一章1锐角三角函数

例3 在Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别是a、b、c,已知 a=12,b=5,求∠A、∠B的正弦与余弦.
分析 在Rt△ABC中,先根据勾股定理求出c的值,然后分别根据正弦和余 弦的定义求得∠A、∠B的正弦与余弦.
解析 在Rt△ABC中,∵a=12,b=5,∠C=90°,∴c= a2 b2 = 122 52 =13,∴
AB 4
BC 3
(2)tan A与tan C互为倒数.理由:
∵tan A·tan C= BC · AB = 3 × 4 =1,
AB BC 4 3
∴tan A与tan C互为倒数.
知识点二 坡度(或坡比)与坡角
坡度
坡角
图形
定义
坡面的铅直高度h和水 斜坡与水平面的夹角
平宽度l的比叫做坡度 叫做坡角,记作α
AB 10 5
AB 10 5
正解 ∵BC2+AC2=62+82=102=AB2,
∴△ABC是直角三角形,且∠C=90°,
∴sin A= BC = 6 = 3,cos B= BC = 6 = 3.
AB 10 5
AB 10 5
错因分析 错解未判断△ABC是不是直角三角形就直接求解.
知识点一 正切
1.在△ABC中,BC=3,AC=4,AB=5,则tan A的值是 ( )
-∠A).
(4)结合图例,有sin
A= a ,sin
c
B= b ,则sin2A+sin2B=
c
a c
2
+
b c
2
= a2
c2
b2
=1,从而
sin2A+sin2(90°-∠A)=sin2A+cos2A=1.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北师大版九年级数学
初三下学期锐角三角函数知识点总结及典型习题
知识点:
1、本章三角函数源自于勾股定理:直角三角形两直角边a 、b 的平方和等于斜边c
(勾股定理也叫毕达哥拉斯定理,在部分课外资料/习题当中会出现毕达哥拉斯定理)2、如下图,在Rt△ABC 中,∠C 为直角,则∠A 的锐角三角函数为(∠A 可换成∠B):
定
义
表达式
取值范围关系
正弦斜边的对边A A ∠=sin c a A =
sin 1sin 0<<A (∠A 为锐角)B A cos sin =B
A sin cos =1
cos sin 22=+A A 余弦斜边的邻边A A ∠=cos c b A =
cos 1cos 0<<A (∠A 为锐角)正切的邻边
的对边A tan ∠∠=
A A b
a A =
tan 0tan >A (∠A 为锐角)余切
的对边
的邻边A ot ∠∠=
A A c a b
A =
cot 0cot >A (∠A 为锐角)
1
A cot A tan =⨯B
A tan cot =(注:余切函数已经从北师大版教材当中删除,此处仅做扩展,实际中考当中并不会出现,同时删除的内容还包含正割(sec)和余割(csc)两部分内容)
3、任意锐角的正弦值等于它的余角的余弦值;任意锐角的余弦值等于它的余角的正弦值。
B
A cos sin =B
A sin cos =)
90cos(sin A A -︒=)
90sin(cos A A -︒=4、30°、45°、60°特殊角的三角函数值(重要必背)
三角函数
30°
45°
60°
α
sin 2
1222
3αcos 232
22
1α
tan 3
31
3
A
90B 90∠-︒=∠︒=∠+∠得由B A 对边邻边
斜边A
C
B
b
a c
6、正弦、余弦的增减性:
当0°≤α≤90°时,sin α随α的增大而增大,cos α随α的增大而减小。
7、正切、的增减性:
当0°<α<90°时,tan α随α的增大而增大,
解直角三角形的定义
1、:已知边和角(两个,其中必有一边)→所有未知的边和角。
依据:①边的关系:222c b a =+;②角的关系:A+B=90°;③边角关系:三角函数的定义。
(注意:尽量避免使用中间数据和除法)
2、应用举例:
(1)仰角:视线在水平线上方的角;俯角:视线在水平线下方的角。
:i h l
=h
l
α
(2)坡面的铅直高度h 和水平宽度l 的比叫做坡度(坡比)。
用字母i 表示,即h
i l
=。
坡度一般写成1:m 的形式,如1:5i =等。
把坡面与水平面的夹角记作α(叫做坡角),那么tan h
i l
α=
=。
3、从某点的指北方向按顺时针转到目标方向的水平角,叫做方位角。
如图,OA、OB、OC、OD 的方向角分别是:45°、135°、225°。
指北或指南方向线与目标方向线所成的小于90°的水平角,叫做方向角。
所以,OA、OB、OC、OD 的方向角分别是:北偏东30°(东北方向),南偏东45°(东南方向),南偏西60°(西南方向),北偏西60°(西北方向)。
例1:已知在Rt ABC △中,3
90sin 5
C A ∠==°,,则tan B 的值为(
)A.43B.45C.54D.
34
【解析】本题考查三角函数的定义和勾股定理,在RTΔABC 中,∠C=90°,则sin a A c =
,tan b
B a
=和222a b c +=;由3sin 5A =知,如果设3a x =,则5c x =,结合222a b c +=得4b x =;∴44
tan 33
b x B a x ===,
所以选A.
例2:104cos30sin 60(2)(20092008)-︒︒+---=______.
【解析】本题考查特殊角的三角函数值.零指数幂.负整数指数幂的有关运算,
104cos30sin 60(2)(20092008)-︒︒+---=3313412222
⎛⎫⨯
⨯+--= ⎪⎝⎭,故填3
2
.
1.某人想沿着梯子爬上高4米的房顶,梯子的倾斜角(梯子与地面的夹角)不能大于60°,否则就有危险,那么梯子的长至少为()
A.8米
B.83米
C.
83
3
米D.
43
3
米2.一架5米长的梯子斜靠在墙上,测得它与地面的夹角是40°,则梯子底端到墙的距离为()
A.5sin 40°B.5cos 40°C.5tan 40°D.
5
cos 40°
3.如图是某商场一楼与二楼之间的手扶电梯示意图.其中AB 、CD 分别表示一楼、二楼地面的水平线,∠ABC =150°,BC 的长是8m,则乘电梯从点B 到点C 上升的高度h 是()
A.
8
33
m B.4m C.43m
D.8m
4.河堤横断面如图所示,堤高BC=5米,迎水坡AB 的坡比是1:3(坡比是坡面的铅直高度BC 与水平宽度AC 之比),则AC 的长是(
)
A.53米B.10米C.15米
D.103米
5.如图,在矩形ABCD 中,DE⊥AC 于E,∠EDC∶∠EDA=1∶3,且AC=10,则DE 的长度是()
A.3
B.5
C.2
5D.
2
25A
B
C
D
150°h
6.如图所示,小明在家里楼顶上的点A处,测量建在与小明家楼房同一水平线上相邻的电梯楼的高,在点A处看电梯楼顶部点B处的仰角为60°,在点A处看这栋电梯楼底部点C处的俯角为45°,两栋楼之间的距离为30m,则电梯楼的高BC为米(精确到0.1).
1.414
≈ 1.732)
7.如图,热气球的探测器显示,从热气球A看一栋大楼顶部B的俯角为30°,看这栋大楼底部C的俯角为60°,热气球A的高度为240米,求这栋大楼的高度.
解:过点A作直线BC的垂线,垂足为点D.
则90
CDA
∠=°,60
CAD
∠=°,30
BAD
∠=°,CD=240米.
在Rt ACD
△中,tan
CD CAD
AD ∠=
,
tan60
CD
AD
∴===
°
在Rt ABD
△中,tan
BD
BAD
AD
∠=
,
tan3080
3
BD AD
∴===
·°.
∴BC CD BD
=-=240-80=160.
答:这栋大楼的高为160
米.
C
8.如图所示,城关幼儿园为加强安全管理,决定将园内的滑滑板的倾斜角由45°降为30°,已知原滑滑板AB 的长为4米,点D、B、C 在同一水平面上.
(1)改善后滑滑板会加长多少米?(2)若滑滑板的正前方能有3米长的空地就能保证安全,原滑滑板的前方有6米长的空地,像这样改造是否可行?请说明理由.
(参考数据:141.12=,732.13=,449.26=,以上结果均保留到小数点后两位.)
解:(1)在Rt△ABC 中,∠ABC=45°
∴AC=BC=AB·sin45°=222
2
4=⨯
在Rt△ADC 中,∠ADC=30°
∴AD=2421
2230
sin =÷=o
AC ∴AD-AB=66
.1424≈-∴改善后滑滑板会加长约1.66米.(2)这样改造能行,理由如下:∵989.46233
2230
tan ≈=÷==
o
AC CD ∴07.22262≈-=-=BC CD BD ∴6-2.07≈3.93>3
∴这样改造能行.
练一练
9
.求值1
01|2|20093tan 303-⎛⎫
-+--+ ⎪⎝⎭
°
2009
12sin 603tan 30(1)3⎛⎫
-++- ⎪⎝⎭
°°原式=.
解:原式=。
