(word完整版)八年级下册勾股定理知识点归纳
人教版数学八年级下勾股定理知识梳理完整版

人教版数学八年级下勾股定理知识梳理HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】勾股定理1.勾股定理:如果直角三角形的两直角边长分别为a ,b ,斜边长为c ,那么a 2+b 2=c 2。
2.勾股定理逆定理:如果三角形三边长a,b,c 满足a 2+b 2=c 2。
,那么这个三角形是直角三角形。
3.经过证明被确认正确的命题叫做定理。
我们把题设、结论正好相反的两个命题叫做互逆命题。
如果把其中一个叫做原命题,那么另一个叫做它的逆命题。
(例:勾股定理与勾股定理逆定理)4.直角三角形的性质(1)、直角三角形的两个锐角互余。
可表示如下:∠C=90°⇒∠A+∠B=90° (2)、在直角三角形中,30°角所对的直角边等于斜边的一半。
∠A=30°可表示如下: ⇒BC=21AB ∠C=90°(3)、直角三角形斜边上的中线等于斜边的一半 ∠ACB=90°可表示如下: ⇒CD=21AB=BD=AD D 为AB 的中点6、常用关系式由三角形面积公式可得:AB •CD=AC •BC 7、直角三角形的判定1、有一个角是直角的三角形是直角三角形。
2、如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形。
3、勾股定理的逆定理:如果三角形的三边长a ,b ,c 有关系222c b a =+,那么这个三角形是直角三角形。
8、命题、定理、证明1、命题的概念判断一件事情的语句,叫做命题。
理解:命题的定义包括两层含义:(1)命题必须是个完整的句子;(2)这个句子必须对某件事情做出判断。
2、命题的分类(按正确、错误与否分)真命题(正确的命题)命题所谓正确的命题就是:如果题设成立,那么结论一定成立的命题。
所谓错误的命题就是:如果题设成立,不能证明结论总是成立的命题。
3、公理人们在长期实践中总结出来的得到人们公认的真命题,叫做公理。
完整版)勾股定理知识点与常见题型总结

完整版)勾股定理知识点与常见题型总结勾股定理复勾股定理是指直角三角形两直角边的平方和等于斜边的平方,表示为a^2 + b^2 = c^2,其中a、b为直角三角形的两直角边,c为斜边。
勾股定理的证明常用拼图的方法。
通过割补拼接图形后,根据同一种图形的面积不同的表示方法,列出等式,推导出勾股定理。
常见的证明方法有以下三种:1.通过正方形的面积证明,即4ab + (b-a)^2 = c^2,化简可证。
2.四个直角三角形的面积与小正方形面积的和等于大正方形的面积,即4ab + c^2 = 2ab + c^2,化简得证。
3.通过梯形的面积证明,即(a+b)×(a+b)/2 = 2ab + c^2,化简得证。
勾股定理适用于直角三角形,因此在应用勾股定理时,必须明确所考察的对象是直角三角形。
勾股定理可用于解决直角三角形中的边长计算或直角三角形中线段之间的关系的证明问题。
在使用勾股定理时,必须把握直角三角形的前提条件,了解直角三角形中,斜边和直角边各是什么,以便运用勾股定理进行计算。
同时,应设法添加辅助线(通常作垂线),构造直角三角形,以便正确使用勾股定理进行求解。
勾股定理的逆定理是:如果三角形三边长a、b、c满足a^2 + b^2 = c^2,那么这个三角形是直角三角形,其中c为斜边。
a^2+b^2=c^2$是勾股定理的基本公式。
如果三角形ABC 不是直角三角形,我们可以类比勾股定理,猜想$a+b$与$c$的关系,并对其进行证明。
勾股定理的实际应用有很多。
例如,在图中,梯子AB靠在墙上,梯子的底端A到墙根O的距离为2m,梯子的顶端B 到地面的距离为7m。
现将梯子的底端A向外移动到A′,使梯子的底端A′到墙根O的距离等于3m。
同时梯子的顶端B下降至B′。
那么BB′的长度是小于1m的(选项A)。
又如,在图中,一根24cm的筷子置于底面直径为15cm,高8cm的圆柱形水杯中。
设筷子露在杯子外面的长度为h cm,则h的取值范围是7cm ≤ h ≤ 16cm(选项D)。
勾股定理可知(最全)word资料

勾股定理可知(最全)word资料由勾股定理可知在浩瀚的数学星空里,勾股定理像是一颗璀璨的明星闪耀在数学的星空上。
我国是最早了解勾股定理的国家之一。
早在三千多年前,周朝数学家商高就提出了“勾三、股四、弦五”。
他被记载于我国古代著名的数学著作《周髀算经》中,这是我国最早对勾股定理的记载。
勾股定理的奥秘:直角三角形两直角边的平方和等于斜边的平方。
如果用a、b和c分别表示直角三角形的两条直角边和斜边,那么就会得到a²+b²=c²。
此公式另可以变形为b²=c²-a²和a²=c²-b²。
当然,学习勾股定理是要学以致用,勾股定理在生活中最大的用处就是证明直角三角形,从而解决一些实际性的问题。
此外,为了方便计算,我们也要记住一些常用的勾股数,如:“3、4、5”,“5、12、13”等等。
值得注意的是,勾股数的倍数也是勾股数,如“6、8、10”也是一组勾股数,它就是“3、4、5”的二倍。
可是,在我们享受着勾股定理为我们的生活带来便利的同时,也要想一想,勾股定理真的是正确的吗?聪明的毕达哥拉斯已经在几千年前给了我们答案。
但是在我国古代却有一种非常奇特无字证明法,它就是青朱出入图。
如图所示以勾为边的的正方形为朱方,以股为边的正方形为青方。
以赢补虚,只要把图中朱方的I移至I′,青方的II移至II′,III移至III′,则刚好拼好一个以弦为边长的正方形,由此便可证得a²+b²=c²。
勾股定理的出现已经有几千年了,应用非常广泛,在古代作为构造直角三角形的工具。
比如分土地时不知道怎样能分出直角三角形,这时就要使用勾股定理。
在现代勾股定理已经融入现代科技中和生活中,比如:在建筑学领域,利用勾股定理可此测量出房屋与地面是否垂直。
另外,如果将勾股定理与物理学中的力学完美的结合起来,勾股定理将会发挥更大更神奇的作用。
(完整版)勾股定理知识点+对应类型
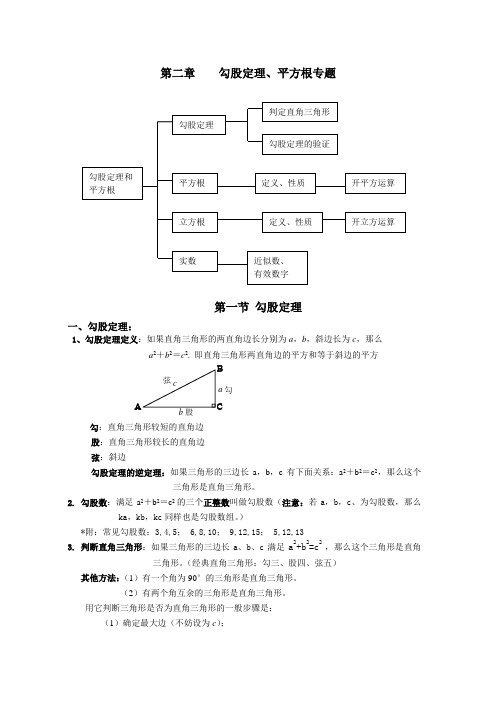
第二章勾股定理、平方根专题第一节勾股定理一、勾股定理:1、勾股定理定义:如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2. 即直角三角形两直角边的平方和等于斜边的平方ABCabc弦股勾勾:直角三角形较短的直角边股:直角三角形较长的直角边弦:斜边勾股定理的逆定理:如果三角形的三边长a,b,c有下面关系:a2+b2=c2,那么这个三角形是直角三角形。
2. 勾股数:满足a2+b2=c2的三个正整数叫做勾股数(注意:若a,b,c、为勾股数,那么ka,kb,kc同样也是勾股数组。
)*附:常见勾股数:3,4,5; 6,8,10; 9,12,15; 5,12,133. 判断直角三角形:如果三角形的三边长a、b、c满足a2+b2=c2 ,那么这个三角形是直角三角形。
(经典直角三角形:勾三、股四、弦五)其他方法:(1)有一个角为90°的三角形是直角三角形。
(2)有两个角互余的三角形是直角三角形。
用它判断三角形是否为直角三角形的一般步骤是:(1)确定最大边(不妨设为c);(2)若c 2=a 2+b 2,则△ABC 是以∠C 为直角的三角形; 若a 2+b 2<c 2,则此三角形为钝角三角形(其中c 为最大边); 若a 2+b 2>c 2,则此三角形为锐角三角形(其中c 为最大边)4.注意:(1)直角三角形斜边上的中线等于斜边的一半(2)在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半。
(3)在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30°。
5. 勾股定理的作用:(1)已知直角三角形的两边求第三边。
(2)已知直角三角形的一边,求另两边的关系。
(3)用于证明线段平方关系的问题。
(4)利用勾股定理,作出长为n 的线段二、平方根:(11——19的平方)1、平方根定义:如果一个数的平方等于a ,那么这个数就叫做a 的平方根。
完整版)八年级数学公式及概念

完整版)八年级数学公式及概念八年级数学公式及概念第一章勾股定理1、勾股定理:直角三角形两直角边a,b的平方和等于斜边c的平方,即a²+b²=c²。
2、勾股定理的逆定理:如果三角形的三边长a,b,c有关系a²+b²=c²,那么这个三角形是直角三角形。
3、勾股数:满足a²+b²=c²的三个正整数,称为勾股数。
第二章实数一、实数的概念及分类1、实数的分类:正有理数、有理数零有限小数和无限循环小数、实数负有理数、正无理数、无理数无限不循环小数、负无理数。
2、无理数:无限不循环小数叫做无理数。
在理解无理数时,要抓住“无限不循环”这一特点,归纳起来有四类:1)开方开不尽的数,如7、32等;2)有特定意义的数,如圆周率π,或化简后含有π的数,如π+8/3等;3)有特定结构的数,如0.xxxxxxxx01…等;4)某些三角函数值,如sin60°等。
二、实数的倒数、相反数和绝对值1、相反数:实数与它的相反数是一对数(只有符号不同的两个数叫做互为相反数,零的相反数是零)。
从数轴上看,互为相反数的两个数所对应的点关于原点对称。
如果a与b互为相反数,则有a+b=0,a=-b,反之亦成立。
2、绝对值:在数轴上,一个数所对应的点与原点的距离,叫做该数的绝对值。
(|a|≥0)。
零的绝对值是它本身,也可看成它的相反数。
若|a|=a,则a≥0;若|a|=-a,则a≤0.3、倒数:如果a与b互为倒数,则有ab=1,反之亦成立。
倒数等于本身的数是1和-1.零没有倒数。
4、数轴:规定了原点、正方向和单位长度的直线叫做数轴(画数轴时,要注意上述规定的三要素缺一不可)。
解题时要真正掌握数形结合的思想,理解实数与数轴的点是一一对应的,并能灵活运用。
5、估算。
三、平方根、算数平方根和立方根21、算术平方根:一般地,如果一个正数x的平方等于a,即x²=a,那么这个正数x就叫做a的算术平方根。
考点梳理:初中勾股定理章节必考点全梳理(精编Word)

B、∵4 t h(b﹣a)2=c2,∴整理得:a2+b2=c2,即能证明勾股定理,故本选项不符合题意;
C、根据图形不能证明勾股定理,故本选项符合题意; D、∵4 t hc2=(a+b)2,∴整理得:a2+b2=c2,即能证明勾股定理,不符合题意;选 C.
【小结】本题考查了勾股定理的证明,能根据图形中各个部分的面积列出等式是解此题的关键.
变式 4: “赵爽弦图”巧妙地利用“出入相补”的方法证明了勾股定理.小明受此启发,探究后发现,若 将 4 个直角边长分别为 a、b,斜边长为 c 的直角三角形拼成如图所示的五边形,用等积法也可以证明勾股 定理,则小明用两种方法表示五边形的面积分别是(用含有 a、b、c 的式子表示) , .
【分析】五边形的面积=边长为 c 的正方形面积+2 个全等的直角边分别为 a,b 的直角三角形的面积,或五 边形的面积=边长为 c 的正方形面积+边长为 c 的正方形面积+2 个全等的直角边分别为 a,b 的直角三角形 的面积,依此列式计算即可求解. 【解析】如图所示:①S=c2h ab×2=c2+ab,②S=a2+b2h ab×2=a2+b2+ab. 故答案为:c2+ab,a2+b2+ab. 【小结】本题考查利用图形面积的关系证明勾股定理,解题关键是利用三角形和正方形边长的关系进行组合 图形.
A.9
B.6
C.5
D.4
【分析】由题意可知:中间小正方形的边长为:a﹣b,根据勾股定理以及题目给出的已知数据即可求出大正 方形的边长.
【解析】由题意可知:中间小正方形的边长为:a﹣b,∵每一个直角三角形的面积为: ab 8=4,∴大
正方形的面积为:4 ab+(a﹣b)2=16+9=25,∴大正方形的边长为 5.选 C. 【小结】本题考查勾股定理的证明,解题的关键是熟练运用勾股定理以及完全平方公式,基础题型.
勾股定理(知识点+题型分类练习)(word文档物超所值)

A B Ca c 弦股勾勾股定理(知识点)【知识要点】1. 勾股定理的概念:如果直角三角形的两直角边长分别为a ,b ,斜边长为c ,那么 a 2+b 2=c 2. 即直角三角形两直角边的平方和等于斜边的平方。
常用关系式由三角形面积公式可得:AB·CD=AC·BC2. 勾股定理的逆定理:如果三角形的三边长a ,b ,c 有下面关系:a 2+b 2=c 2,那么这个三角形是直角三角形,其中为斜c 边。
3. 勾股数:①满足a 2+b 2=c 2的三个正整数叫做勾股数(注意:若a ,b ,c 、为勾股数,那么ka ,kb ,kc 同样也是勾股数组。
)②记住常见的勾股数可以提高解题速度,如;;;;8,15,17等3,4,56,8,105,12,137,24,25③用含字母的代数式表示组勾股数:n (为正整数);221,2,1n n n -+2,n ≥n (为正整数)2221,22,221n n n n n ++++n (,为正整数)2222,2,m n mn m n -+,m n >m n 4.判断直角三角形:(1)有一个角为90°的三角形是直角三角形。
(2)有两个角互余的三角形是直角三角形。
(3)如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形。
(4)如果三角形的三边长a 、b 、c 满足a 2+b 2=c 2 ,那么这个三角形是直角三角形。
(经典直角三角形:勾三、股四、弦五)用勾股定理逆定理判断三角形是否为直角三角形的一般步骤是:(1)确定最大边(不妨设为c );(2)若c 2=a 2+b 2,则△ABC 是以∠C 为直角的三角形;若a 2+b 2<c 2,则此三角形为钝角三角形(其中c 为最大边);若a 2+b 2>c 2,则此三角形为锐角三角形(其中c 为最大边)A5.直角三角形的性质(1)直角三角形的两个锐角互余。
可表示如下:∠C=90°∠A+∠B=90°⇒ (2)在直角三角形中,30°角所对的直角边等于斜边的一半。
人教版八年级数学下册课件勾股定理复习课(课2)

c
(1)如果∠A和∠B是邻补角,那么∠A+∠B=180〫.
重难点3:勾股定理逆定理的应用
Ca B
知识梳理
3. 勾股定理逆定理的应用
② 实质:由“数”到“形”的转化; ③ 应用:判定一个三角形是否为直角三角形.
知识梳理
4. 勾股数
勾股数
正整数
判断一组数是不是勾股数的步骤: 看、找、算、判.
重点解析
反走私艇 B 离走私艇 C 12 海里,若走私艇 C
从边的方面判断:如果已知条件与边有关系,则可以通过勾股定理的逆定理进行判断.
两个角都是40〫
重点解析
1.有些命题在不容易确定题设和结论的情况下,可 以先改写成“如果……那么……”的形式,然后确 定题设和结论. 2.判断一个命题是假命题只需要举出一个反例即可.
重点解析
重难点2:勾股定理的逆定理
判断满足下列条件的三角形是不是直角三角形.如果是, 请指出哪个角是直角. (1)在△ABC中,∠A=25〫、∠B=65〫; 解:(1)在△ABC中,因为∠A=25〫、∠B=65〫,所以 ∠C=180〫-∠A-∠B=90〫,所以这个三角形是直角三角形. ∠C是直角.
重点解析
重难点4:勾股数
判断下列各组数是不是勾股数:
深化练习
1.在△ABC中,∠A、 ∠B 、 ∠C的对边分别是a、b、c,下列判断 错误的是( B ).
A.如果∠C- ∠B= ∠A,则△ABC是直角三角形.
深化练习
A.如果∠C- ∠B= ∠A,则△ABC是直角三角形. 解析:因为∠C- ∠B=∠A,所以 ∠C=∠B+∠A. 因为∠C+∠B+∠A=180〫,所以 ∠C+∠C=180〫. 解得:∠C=90〫,所以△ABC是直角三角形.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
八年级下册勾股定理知识点和典型例习题一、基础知识点:1.勾股定理内容:直角三角形两直角边的平方和等于斜边的平方;表示方法:如果直角三角形的两直角边分别为a ,b ,斜边为c ,那么222ab c +=2.勾股定理的证明勾股定理的证明方法很多,常见的是拼图的方法用拼图的方法验证勾股定理的思路是①图形通过割补拼接后,只要没有重叠,没有空隙,面积不会改变 ②根据同一种图形的面积不同的表示方法,列出等式,推导出勾股定理 常见方法如下: 方法一:4EFGH S S S ∆+=正方形正方形ABCD ,,化简可证.方法二:四个直角三角形的面积与小正方形面积的和等于大正方形的面积.四个直角三角形的面积与小正方形面积的和为221422S ab c ab c =⨯+=+ 大正方形面积为222()2S a b a ab b =+=++ 所以222a b c +=方法三:1()()2S a b a b =+⋅+梯形,2112S 222ADE ABE S S ab c ∆∆=+=⋅+梯形,化简得证3.勾股定理的适用范围勾股定理揭示了直角三角形三条边之间所存在的数量关系,它只适用于直角三角形,对于锐角三角形和钝角三角形的三边就不具有这一特征,因而在应用勾股定理时,必须明了所考察的对象是直角三角形4.勾股定理的应用①已知直角三角形的任意两边长,求第三边在ABC ∆中,90C ∠=︒,则22c a b =+,22b c a =-,22a c b =-②知道直角三角形一边,可得另外两边之间的数量关系③可运用勾股定理解决一些实际问题5.勾股定理的逆定理如果三角形三边长a ,b ,c 满足222a b c +=,那么这个三角形是直角三角形,其中c 为斜边①勾股定理的逆定理是判定一个三角形是否是直角三角形的一种重要方法,它通过“数转化为形”来确定三角形的可能形状,在运用这一定理时,可用两小边的平方和22a b +与较长边的平方2c 作比较,若它们相等时,以a ,b ,c 为三边的三角形是直角三角形;否则,就不是直角三角形。
cbaHG F EDCBAbacbac cabcab a bc cbaE D CBAAB C 30°D CB A AD B C ②定理中a ,b ,c 及222a b c +=只是一种表现形式,不可认为是唯一的,如若三角形三边长a ,b ,c 满足222a c b +=,那么以a ,b ,c 为三边的三角形是直角三角形,但是b 为斜边③勾股定理的逆定理在用问题描述时,不能说成:当斜边的平方等于两条直角边的平方和时,这个三角形是直角三角形 6.勾股数①能够构成直角三角形的三边长的三个正整数称为勾股数,即222a b c +=中,a ,b ,c 为正整数时,称a ,b ,c 为一组勾股数②记住常见的勾股数可以提高解题速度,如3,4,5;6,8,10;5,12,13;7,24,25,8,15,17等 ③用含字母的代数式表示n 组勾股数:221,2,1n n n -+(2,n ≥n 为正整数); 2221,22,221n n n n n ++++(n 为正整数); 2222,2,m n mn m n -+(,m n >m ,n 为正整数)7.勾股定理的应用勾股定理能够帮助我们解决直角三角形中的边长的计算或直角三角形中线段之间的关系的证明问题.在使用勾股定理时,必须把握直角三角形的前提条件,了解直角三角形中,斜边和直角边各是什么,以便运用勾股定理进行计算,应设法添加辅助线(通常作垂线),构造直角三角形,以便正确使用勾股定理进行求解. 8.勾股定理逆定理的应用勾股定理的逆定理能帮助我们通过三角形三边之间的数量关系判断一个三角形是否是直角三角形,在具体推算过程中,应用两短边的平方和与最长边的平方进行比较,切不可不加思考的用两边的平方和与第三边的平方比较而得到错误的结论. 9.勾股定理及其逆定理的应用勾股定理及其逆定理在解决一些实际问题或具体的几何问题中,是密不可分的一个整体.通常既要通过逆定理判定一个三角形是直角三角形,又要用勾股定理求出边的长度,二者相辅相成,完成对问题的解决.常见图形:二、经典例题精讲题型一:直接考查勾股定理 例1.在ABC ∆中,90C ∠=︒.⑴已知6AC =,8BC =.求AB 的长⑵已知17AB =,15AC =,求BC 的长分析:直接应用勾股定理222a b c += 解:⑴2210AB AC BC =+= ⑵228BC AB AC =-= 题型二:利用勾股定理测量长度例题1 如果梯子的底端离建筑物9米,那么15米长的梯子可以到达建筑物的高度是多少米?C BD A解析:这是一道大家熟知的典型的“知二求一”的题。
把实物模型转化为数学模型后,.已知斜边长和一条直角边长,求另外一条直角边的长度,可以直接利用勾股定理!根据勾股定理AC 2+BC 2=AB 2, 即AC 2+92=152,所以AC 2=144,所以AC=12.例题2 如图(8),水池中离岸边D 点1.5米的C 处,直立长着一根芦苇,出水部分BC 的长是0.5米,把芦苇拉到岸边,它的顶端B 恰好落到D 点,并求水池的深度AC.解析:同例题1一样,先将实物模型转化为数学模型,如图2. 由题意可知△ACD 中,∠ACD=90°,在Rt △AC D 中,只知道CD=1.5,这是典型的利用勾股定理“知二求一”的类型。
标准解题步骤如下(仅供参考): 解:如图2,根据勾股定理,AC 2+CD 2=AD 2设水深AC= x 米,那么AD=AB=AC+CB=x +0.5x 2+1.52=( x +0.5)2解之得x =2.故水深为2米.题型三:勾股定理和逆定理并用例题3 如图3,正方形ABCD 中,E 是BC 边上的中点,F 是AB 上一点,且AB FB 41=那么△DEF 是直角三角形吗?为什么?解析:这道题把很多条件都隐藏了,乍一看有点摸不着头脑。
仔细读题会意可以发现规律,没有任何条件,我们也可以开创条件,由AB FB 41=可以设AB=4a ,那么BE=CE=2 a ,AF=3 a ,BF= a ,那么在Rt △AFD 、Rt △BEF 和 Rt △CDE 中,分别利用勾股定理求出DF,EF 和DE 的长,反过来再利用勾股定理逆定理去判断△DEF 是否是直角三角形。
详细解题步骤如下:解:设正方形ABCD 的边长为4a ,则BE=CE=2 a ,AF=3 a ,BF= a 在Rt △CDE 中,DE 2=CD 2+CE 2=(4a )2+(2 a)2=20 a2同理EF 2=5a 2, DF 2=25a 2在△DEF 中,EF 2+ DE 2=5a 2+ 20a 2=25a 2=DF 2∴△DEF 是直角三角形,且∠DEF=90°.注:本题利用了四次勾股定理,是掌握勾股定理的必练习题。
题型四:利用勾股定理求线段长度例题4 如图4,已知长方形ABCD 中AB=8cm,BC=10cm,在边CD 上取一点E ,将△ADE 折叠使点D 恰好落在BC 边上的点F ,求CE 的长.解析:解题之前先弄清楚折叠中的不变量。
合理设元是关键。
解:根据题意得Rt △ADE ≌Rt △AEF ∴∠AFE=90°, AF=10cm, EF=DE设CE=x cm,则DE=EF=CD-CE=8-x在Rt△ABF中由勾股定理得:AB2+BF2=AF2,即82+BF2=102,∴BF=6cm ∴CF=BC-BF=10-6=4(cm)在Rt△ECF中由勾股定理可得:EF2=CE2+CF2,即(8-x) 2=x2+42∴64-16x+x2=2+16∴x=3(cm),即CE=3 cm注:本题接下来还可以折痕的长度和求重叠部分的面积。
题型五:利用勾股定理逆定理判断垂直例题5 如图5,王师傅想要检测桌子的表面AD边是否垂直与AB边和CD边,他测得AD=80cm,AB=60cm,BD=100cm,AD边与AB边垂直吗?怎样去验证AD边与CD边是否垂直?解析:由于实物一般比较大,长度不容易用直尺来方便测量。
我们通常截取部分长度来验证。
如图4,矩形ABCD表示桌面形状,在AB上截取AM=12cm,在AD上截取AN=9cm(想想为什么要设为这两个长度?),连结MN,测量MN的长度。
①如果MN=15,则AM2+AN2=MN2,所以AD边与AB边垂直;②如果MN=a≠15,则92+122=81+144=225,a2≠225,即92+122≠a2,所以∠A不是直角。
例题6 有一个传感器控制的灯,安装在门上方,离地高4.5米的墙上,任何东西只要移至5米以内,灯就自动打开,一个身高1.5米的学生,要走到离门多远的地方灯刚好打开?解析:首先要弄清楚人走过去,是头先距离灯5米还是脚先距离灯5米,可想而知应该是头先距离灯5米。
转化为数学模型,如图6 所示,A点表示控制灯,BM表示人的高度,BC∥MN,BC⊥AN当头(B点)距离A有5米时,求BC的长度。
已知AN=4.5米,所以AC=3米,由勾股定理,可计算B C=4米.即使要走到离门4米的时候灯刚好打开。
题型六:关于翻折问题如图,矩形纸片ABCD的边AB=10cm,BC=6cm,E为BC上一点,将矩形纸片沿AE折叠,点B恰好落在CD边上的点G处,求BE的长.变式:如图,AD是△ABC的中线,∠ADC=45°,把△ADC沿直线AD翻折,点C落在点C’的位置,BC=4,求BC’的长.三、勾股定理练习题(一)、选择题1、下列各组数中,能构成直角三角形的是()A :4,5,6B :1,1,2C :6,8,11D :5,12,232、在Rt △ABC 中,∠C =90°,a =12,b =16,则c 的长为( ) A :26 B :18 C :20 D :213、在平面直角坐标系中,已知点P 的坐标是(3,4),则OP 的长为( )A :3 B :4 C :5 D :74、在Rt △ABC 中,∠C =90°,∠B =45°,c =10,则a 的长为( ) A :5 B :10 C : D :55、已知Rt △ABC 中,∠C=90°,若a+b=14cm ,c=10cm ,则Rt △ABC 的面积是( )A 、24cm 2B 、36cm 2C 、48cm 2D 、60cm 26、若等腰三角形的腰长为10,底边长为12,则底边上的高为( )A 、6 B 、7 C 、8 D 、97、已知,如图长方形ABCD 中,AB=3cm ,AD=9cm , 将此长方形折叠,使点B 与点D 重合,折痕为EF ,则△ABE 的面积为( ) A 、3cm 2B 、4cm 2C 、6cm 2D 、12cm 28、若△ABC 中,13,15AB cm AC cm ==,高AD=12,则BC 的长为 A 、14 B 、4 C 、14或4 D 、 以上都不对9、 如图,正方形网格中的△ABC ,若小方格边长为1,则△ABC 是 ()(A )直角三角形 (B)锐角三角形 (C)钝角三角形 (D)以上答案都不对10、在一棵树的10米高处有两只猴子,一只猴子爬下树走到离树20米处的池塘的A 处。
