土力学-第二章土的渗透性及渗流
合集下载
经典土力学课件渗流清华张丙印
水的性质
水的动力粘滞系数： 温度，水粘滞性，k
饱和度（含气量）：封闭气 泡对k影响很大，可减少有效 渗透面积，还可以堵塞孔隙 的通道
渗透系数的影响因素
§2.2 土的渗流性与渗透规律
仁者乐山 智者乐水
天然土层多呈层状
• 确立各层土的ki • 根据渗流方向确定等效渗流系数
等效渗透系数
多个土层用假想单一土层置换， 使得其总体的透水性不变
达西定律
渗透系数的测定
及影响因素
层状地基的等效
渗透系数
仁者乐山 智者乐水
渗流的驱动能量 反映渗流特点的定律 土的渗透性 地基的渗透系数
土的渗透性与渗透规律
§2.2 土的渗流性与渗透规律
仁者乐山 智者乐水
uB w
u0pa
B
静水 A zB
0 基准面
位置水头：到基准面的竖直距离， 代表单位重量的液体从基准面算起 所具有的位置势能
• 井孔抽水试验 • 井孔注水试验
渗透系数的测定方法
§2.2 土的渗流性与渗透规律
仁者乐山 智者乐水
试验条件: Δh，A，L=const 量测变量: 体积V，t
V=Qt=vAt v=ki
i=Δh/L
h
k VL
土样
L
Aht
A
Q
适用土类：透水性较大的砂性土
V
室内试验方法-常水头试验法
§2.2 土的渗流性与渗透规律
渗透速度v：土体试样全断面的平均渗流速度，也称假想
渗流速度
v
vs
v n
其中，Vs为实际平均流速，孔隙断面的平均流速
达西定律
§2.2 土的渗流性与渗透规律
仁者乐山 智者乐水
适用条件：层流（线性流动） 水 2.0
水的动力粘滞系数： 温度，水粘滞性，k
饱和度（含气量）：封闭气 泡对k影响很大，可减少有效 渗透面积，还可以堵塞孔隙 的通道
渗透系数的影响因素
§2.2 土的渗流性与渗透规律
仁者乐山 智者乐水
天然土层多呈层状
• 确立各层土的ki • 根据渗流方向确定等效渗流系数
等效渗透系数
多个土层用假想单一土层置换， 使得其总体的透水性不变
达西定律
渗透系数的测定
及影响因素
层状地基的等效
渗透系数
仁者乐山 智者乐水
渗流的驱动能量 反映渗流特点的定律 土的渗透性 地基的渗透系数
土的渗透性与渗透规律
§2.2 土的渗流性与渗透规律
仁者乐山 智者乐水
uB w
u0pa
B
静水 A zB
0 基准面
位置水头：到基准面的竖直距离， 代表单位重量的液体从基准面算起 所具有的位置势能
• 井孔抽水试验 • 井孔注水试验
渗透系数的测定方法
§2.2 土的渗流性与渗透规律
仁者乐山 智者乐水
试验条件: Δh，A，L=const 量测变量: 体积V，t
V=Qt=vAt v=ki
i=Δh/L
h
k VL
土样
L
Aht
A
Q
适用土类：透水性较大的砂性土
V
室内试验方法-常水头试验法
§2.2 土的渗流性与渗透规律
渗透速度v：土体试样全断面的平均渗流速度，也称假想
渗流速度
v
vs
v n
其中，Vs为实际平均流速，孔隙断面的平均流速
达西定律
§2.2 土的渗流性与渗透规律
仁者乐山 智者乐水
适用条件：层流（线性流动） 水 2.0
土力学 第2章 土的渗透性
n Vv Av 1 Av V A1 A
A > Av
v
vs
v n
Vs=q/Av V=q/A
(3)适用条件
v
层流(线性流):大部分砂土，粉土；
疏松的粘土及砂性较重的粘性土。
o
v=k i
v
v ki (a) 层流 i
(4)两种特例
密实粘性土：近似适用： v=k(i - i0 ) ( i >i0 ) i0：起始水力梯度
选取几组不同的h1和h2及对应的时间t=t2-t1，利用式(2-11)计算出相 应的渗透系数k，然后取其平均值作为该土样的渗透系数。
2. 现场井孔抽水试验
(1)室内试验的优缺点 优点：设备简单、操作方便、费用低廉。 缺点：取样和制样对土扰动、试样不一定是现场的代表性土，导致室内
测定的渗透系数难以反映现场土的实际渗透性。
☆水工建筑物防渗
一般采用“上堵下疏”原则。即上游截渗，延长渗径；下 游通畅渗透水流，减小渗透压力，防止渗透变形。
☆基坑开挖防渗
工程实例：
2003年7月1日，上海市轨道交通4号线发生一起管涌坍 塌事故，防汛墙塌陷、隧道结构损坏、周边地面沉降、造成 三幢建筑物严重倾斜。直接经济损失高达1.5亿人民币。
(2-34)
式中Fs为流土安全系数，通常取1.5~2.0。
பைடு நூலகம்
流土
(2)管涌(潜蚀) 定义：在渗流作用下土体的细土粒在粗土粒形成的孔隙通道中
发生移动并被带出的现象。 长期管涌破坏土的结构，最终导致土体内形成贯通的渗流 管道，造成土体坍陷。
管涌(土体内部细颗粒被带走)
管涌破坏(土体坍塌)
◆判别
①土类条件
第2章 土的渗透性与渗透变形
【解答】 临界水力坡降
d s 1 2.68 1 icr 0.92 1 e 1 0.82
[i ] icr 0.92 0.37 K 2 .5
允许水力坡降
由于实际水力坡降i <[i]，故土坝地基出口处土体不会发生 流土破坏
31
渗流工程问题与防治措施
渗流工程问题
土力学中与渗透有关的几个重要内容
土体固结的速度 边坡、挡土墙、堤坝的抗滑稳定性 地下施工时的降水 土坝的抗渗透破坏稳定性
3
土石坝坝基坝身渗流
防渗斜墙及铺盖 土石坝 浸润线
透水层
不透水层
4
板桩围护下的基坑渗流
板桩墙
基坑
透水层
不透水层
5
水井渗流
Q
天然水面 透水层
不透水层
6
渠道渗流
渗流时地下水位
Qx k xiH
ix
Q
i 1
n
k1iH1 k2iH 2 kniH n
整个土层与层面平 行的等效渗透系数
1 kx H
k H
i 1 i
n
i
20
2.垂直渗透系数
Qy
根据水流连续定理，通过整个土层 的渗流量等于通过各土层的渗流量
H1
H2 H
k1
k2 k3
Q1y
Q2y Q3y
管内减少水量＝流经试样水量
－adh=kAh/Ldt
分离变量 积分
南55渗透仪·
16
3.现场实验——现场抽水实验
以不变的速率连续抽水，形成降水漏斗 假定：水流为水平流向 流向水井的渗流过水断面为同心圆柱面
地下水进入抽水井的流量与抽 水量相等且维持稳定时，测定 相关数据，计算土层平均k
d s 1 2.68 1 icr 0.92 1 e 1 0.82
[i ] icr 0.92 0.37 K 2 .5
允许水力坡降
由于实际水力坡降i <[i]，故土坝地基出口处土体不会发生 流土破坏
31
渗流工程问题与防治措施
渗流工程问题
土力学中与渗透有关的几个重要内容
土体固结的速度 边坡、挡土墙、堤坝的抗滑稳定性 地下施工时的降水 土坝的抗渗透破坏稳定性
3
土石坝坝基坝身渗流
防渗斜墙及铺盖 土石坝 浸润线
透水层
不透水层
4
板桩围护下的基坑渗流
板桩墙
基坑
透水层
不透水层
5
水井渗流
Q
天然水面 透水层
不透水层
6
渠道渗流
渗流时地下水位
Qx k xiH
ix
Q
i 1
n
k1iH1 k2iH 2 kniH n
整个土层与层面平 行的等效渗透系数
1 kx H
k H
i 1 i
n
i
20
2.垂直渗透系数
Qy
根据水流连续定理，通过整个土层 的渗流量等于通过各土层的渗流量
H1
H2 H
k1
k2 k3
Q1y
Q2y Q3y
管内减少水量＝流经试样水量
－adh=kAh/Ldt
分离变量 积分
南55渗透仪·
16
3.现场实验——现场抽水实验
以不变的速率连续抽水，形成降水漏斗 假定：水流为水平流向 流向水井的渗流过水断面为同心圆柱面
地下水进入抽水井的流量与抽 水量相等且维持稳定时，测定 相关数据，计算土层平均k
2 土力学 第二章 土的渗透性及水的渗流
作用方向与渗流方向一致！
二、临界水力梯度及渗透破坏 当土中水向上渗流时，渗透力垂直向上而与土样重力方向相反，若渗透力 等于土样浮度，即
j = iγ w = γ , 得临界水力梯度： i cr =
γ' γw
土木工程学院 岩土系 冷伍明
第二章 土的渗透性及水的渗流
因此，若土中水向上渗流： ⑴若i>icr，会发生流土破坏，即“管涌”； ⑵若i=icr，流土处于临界状态，即“悬浮”； ⑶若i<icr，不会发生流土破坏。
h = z + hW + hV
由于水在土中渗流的速度一般很小，hv≈0，因此
h = z + hW = z +
u
γw
式中 u为该点的静水压力
土木工程学院 岩土系 冷伍明
第二章 土的渗透性及水的渗流
A、B两点的总水头可分别表示为：
hA = z A +
γω
uA
; hB = z B +
γω
uB
A、B两点间的总水头差：
作业题：P54： 2-7，2-9 补题1：什么是渗透力、临界水力梯度？
土木工程学院 岩土系 冷伍明
第二章 土的渗透性及水的渗流 §2.1 土的渗透定律
土的渗透性：由于土中孔隙是相互连同 的，土体孔隙中的自由水会由于总水头 差而产生流动，这种土体被水透过的性 质，称为土的渗透性(permeability)。 一、土中渗流的总水头与水力梯度 土中一点的总水头由三项组成：势水头 z、静水头hw和动水头hv，即：
土木工程学院 岩土系 冷伍明
第二章 土的渗透性及水的渗流
二、成层土的平均渗透系数 成层土渗透系数的计算方法见P43 三、渗透系数的室内测定方法 渗透系数k不能用理论方法求得，只能通过试验确定。 测定k值室内方法：定水头法、变水头法。 （1）定水头法 保持总水头差Δh不变，在t时间内，量得透过土样的水量为Q，求k： 根据达西定律
二、临界水力梯度及渗透破坏 当土中水向上渗流时，渗透力垂直向上而与土样重力方向相反，若渗透力 等于土样浮度，即
j = iγ w = γ , 得临界水力梯度： i cr =
γ' γw
土木工程学院 岩土系 冷伍明
第二章 土的渗透性及水的渗流
因此，若土中水向上渗流： ⑴若i>icr，会发生流土破坏，即“管涌”； ⑵若i=icr，流土处于临界状态，即“悬浮”； ⑶若i<icr，不会发生流土破坏。
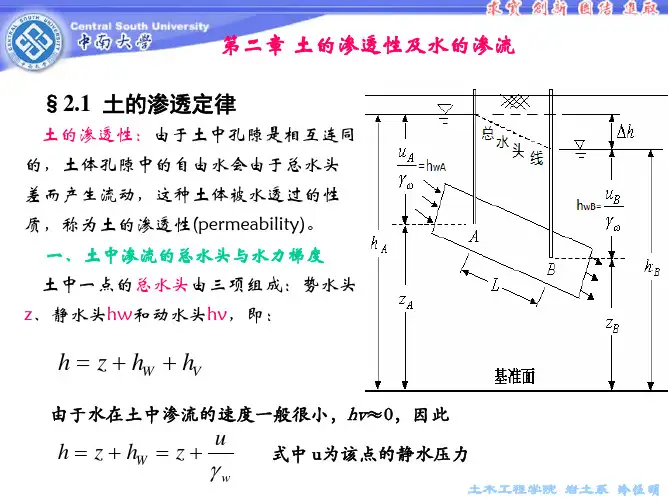
h = z + hW + hV
由于水在土中渗流的速度一般很小，hv≈0，因此
h = z + hW = z +
u
γw
式中 u为该点的静水压力
土木工程学院 岩土系 冷伍明
第二章 土的渗透性及水的渗流
A、B两点的总水头可分别表示为：
hA = z A +
γω
uA
; hB = z B +
γω
uB
A、B两点间的总水头差：
作业题：P54： 2-7，2-9 补题1：什么是渗透力、临界水力梯度？
土木工程学院 岩土系 冷伍明
第二章 土的渗透性及水的渗流 §2.1 土的渗透定律
土的渗透性：由于土中孔隙是相互连同 的，土体孔隙中的自由水会由于总水头 差而产生流动，这种土体被水透过的性 质，称为土的渗透性(permeability)。 一、土中渗流的总水头与水力梯度 土中一点的总水头由三项组成：势水头 z、静水头hw和动水头hv，即：
土木工程学院 岩土系 冷伍明
第二章 土的渗透性及水的渗流
二、成层土的平均渗透系数 成层土渗透系数的计算方法见P43 三、渗透系数的室内测定方法 渗透系数k不能用理论方法求得，只能通过试验确定。 测定k值室内方法：定水头法、变水头法。 （1）定水头法 保持总水头差Δh不变，在t时间内，量得透过土样的水量为Q，求k： 根据达西定律
3清华大学-土力学与地基基础--第02章-土的渗透性和渗流问题
基本要求 绘制方法 主要特点 实际应用
共轭调和，等值线正交
流函数
求解（流网） 边界条件
33
§2 土的渗透性和渗流问题 §2.2 平面渗流与流网
一. 平面渗流的基本方程及求解 1. 基本方程 水头描述
▪ 连续性条件
dq e v xdz v zdx
dq o
(vx
v x x
dx )dz
(vz
v z z
平面渗流 稳定渗流
与y、t无关
对单宽dy=1，取一微小单元dx, dz
z
x
Δh
z
vz
vz z
dz
vx
v
x
v x x
dx
vz
x
32
§2 土的渗透性和渗流问题 §2.2 平面渗流与流网
连续性条件 达西定律 流线方程 假定kx=kz
势函数的 基本方程
Laplace方程 （基本方程）
流函数的 基本方程
势函数
dz )dx
dq e dq o
vx vz 0 x z
z
vz
vz z
dz
vx
v
x
v x x
dx
vz
x
34
§2 土的渗透性和渗流问题 §2.2 平面渗流与流网
一. 平面渗流的基本方程及求解 1. 基本方程 水头描述
▪ 连续性条件 v x v z 0
x z
▪ 达西定律
vx
k x
h x
;
vz
k z
观察井
r2 r r1
dr dh
h1 h
h2
缺点： 费用较高，耗时较长
23
§2 土的渗透性和渗流问题 §2.1 土的渗透性与渗流规律
共轭调和，等值线正交
流函数
求解（流网） 边界条件
33
§2 土的渗透性和渗流问题 §2.2 平面渗流与流网
一. 平面渗流的基本方程及求解 1. 基本方程 水头描述
▪ 连续性条件
dq e v xdz v zdx
dq o
(vx
v x x
dx )dz
(vz
v z z
平面渗流 稳定渗流
与y、t无关
对单宽dy=1，取一微小单元dx, dz
z
x
Δh
z
vz
vz z
dz
vx
v
x
v x x
dx
vz
x
32
§2 土的渗透性和渗流问题 §2.2 平面渗流与流网
连续性条件 达西定律 流线方程 假定kx=kz
势函数的 基本方程
Laplace方程 （基本方程）
流函数的 基本方程
势函数
dz )dx
dq e dq o
vx vz 0 x z
z
vz
vz z
dz
vx
v
x
v x x
dx
vz
x
34
§2 土的渗透性和渗流问题 §2.2 平面渗流与流网
一. 平面渗流的基本方程及求解 1. 基本方程 水头描述
▪ 连续性条件 v x v z 0
x z
▪ 达西定律
vx
k x
h x
;
vz
k z
观察井
r2 r r1
dr dh
h1 h
h2
缺点： 费用较高，耗时较长
23
§2 土的渗透性和渗流问题 §2.1 土的渗透性与渗流规律
土力学-土的渗透性
14
⑵试验结论
层流sheet flow状态下 紊流turbulent flow
v v=ki
O
达西定律
v = k ⋅i
砂土
i
渗透系数coefficient of permeability cm/s
Q q v= = At A
discharge velocity
v v′ = n
seepage velocity
30 i1 = = 1.5 20 10 i2 = = 0.25 40
单位时间渗流量q按下式计算：
q = 2.5 ×10 −2 ×1.5 × 300 = 11.25cm 3 /s q = 1.5 ×10 −1 × 0.25 × 300 = 11.25cm 3 /s
19
课内练习
图示渗透试验，水由底部流经土样后从顶部溢出。在a—a处引 一测压管，测得管内的水柱高 ha = 3cm ，试问若在c—c处引 测压管，相应的水柱高为多少？
4
一、概述
一、土的渗透性permeability及土中渗流seepage
碎散性 多孔介质 三相体系 能量差
孔隙流体流动
水在土体孔隙中流动的现象 土具有被水透过的性质
渗流seepage 渗透性permeability
5
二、 为什么要研究土的渗透性
Teton大坝， 位于美国爱达 荷州的东南 部，为高93m的 土坝。1976年6 月5日该坝完成 后第一次蓄水 时即发生破 坏，造成11人 死亡及数百万 美元的损失。 破坏是由右岸 距坝顶约40m处 的一个漏洞引 起的。
v≈0
h = z +u /γw
单位流程的水头损失。
10
z与hw之和称为测压管水头，可见，测压管水头等于总水头h
土力学2.土的渗透性与渗透问题
水力坡降 由于渗流过程中存在能量损失，测管水头线沿渗流方向下降。两 点间的水头损失，可用一无量纲的形式来表示，即
i=h/L
i 称为水力坡降，L为两点间的渗流路径，
水力坡降的物理意义为单位渗流长度上的水头损失。
(二) 达西定律与渗透试验 达西根据对不同尺寸的圆筒和不同类 型及长度的土样所进行的试验发现,渗出量 Q与圆筒断面积A和水力坡降i成正比，且 与土的透水性质有关。即
在渗透水流作用下，土中的细颗粒在粗颗粒形成的孔隙中移动．以 至流失；随着土的孔隙不断扩大，渗透流速不断增加．较粗的颗粒也相 继被水流逐渐带走，最终导致土体内形成贯通的渗流管道，造成土体塌 陷，这种现象称为管涌。管涌破坏一般有个时间发展过程，是一种渐进 性质的破坏。管涌发生在一定级配的无粘性土中，发生的部位可以在渗 流逸出处，也可以在土体内部，故也称之为渗流的潜蚀现象 土的渗透变形的发生和发展过程有其内因和外因。内因是土的颗粒 组成和结构,即几何条件；外因是水力条件，即作用于土体渗透力的大小。 1.流土可能性的判别 任何土，包括粘性土或无粘性土,在自下而上的渗流逸出处，只要满 足渗透坡降大于临界水力坡降这一个事实，均要发生流土。 可按下列条件，判别流土的可能性： 若 i < ic 土体处于稳定状态 i > ic 土体发中流土破坏 i = ic 土体处于临界状态
土的渗透系数范围
土的类型 砾石、粗砂 中 砂 细纱、粉沙 粉土 粉质粘土 粘 土 渗透系数 k(cm/s) a×10-1 ~ a×10-2 a×10-2 ~ a×10-3 a×10-3 ~ a×10-4 a×10-4 ~ a×10-6 a×10-6 ~ a×10-7 a×10-7 ~ a×10-10
2.管涌可能性的判别 土是发生管涌，首先决定于土的性质。一般粘性土(分散性土例外)． 只会发生流土而不会发生管涌，故属于非管涌土；无粘性土中产生管涌 必须具备下列两个条件。 (1)几何条件 土中粗颗粒所构成的孔隙直径必须大于细颗粒的直径，才可能让细 颗粒在其中移动，这是管涌产生的必要条件。 (2)水力条件 渗透力能够带动细颗粒在孔隙间滚动或移动是发生管涌的水力条件，
土力学与地基基础-第二章土的渗透性图文
2h x2
2h y 2
0(各向异性：kx
2h x2
ky
2h y 2
0)
上式就是著名的拉普拉斯(Laplace)方程，它是描述稳定渗流的基本方程式。
二、流网及其特征
就渗流问题来说，一组曲线称为等势线，在任一条等势线上各点的总水 头是相等的；另一组曲线称为流线，它们代表渗流的方向。等势线和流线交 织在一起形成的网格叫流网。
得出：流量Q与过水面积A和水头 （h1-h2）成正比与渗透路径L成反比，
即达西定律： Q kA h1 h2 vA kiA l
达西渗透实验装置
二、达西渗透定律
达西定律是由砂质土体实验得到的，后来推广应用于其他土体如粘土和具有细 裂隙的岩石等。
①砂土、一般粘土
②颗粒极细的粘土
细粒土的v-i关系
经验估算法
●1991年 哈森提出用有效粒径d10计算较均匀砂土的公式:
K d2 10
●1955年，太沙基提出考虑土体孔隙比e的经验公式:
K 2d 2 e2 10
成层土的渗透系数(补充)
天然沉积土往往由渗透性不同的土层所组成。对于与土层层面平行和垂直的 简单渗流情况，当各土层的渗透系数和厚度为已知时，我们可求出整个土层 与层面平行和垂直的平均渗透系数，作为进行渗流计算的依据。
v k h ki l
是单位时间内流过单位土截面积的水量，
i—水头梯度或水力坡降。
k—渗透系数，cm/s。
由于土体中的孔隙一般非常微小，水在土体中流动时的粘滞阻力很大、流速
缓慢，因此，其流动状态大多属于层流。
二、达西渗透定律
达西渗透实验
装置中①是面积为A的直立圆筒，其侧壁装有 两支相距为L的侧压管。滤板②填放颗粒均匀 的砂土。水由上端注入圆筒，多余的水从溢 水管③溢出，使筒内的水位维持恒定。渗透 过砂层的水从短水管④流入量杯⑤中，并以 此来计算渗流量Q。
《土力学》教案——第二章 土的渗透性和渗透问题
教学内容设计及安排第一节达西定律【基本内容】渗透——在水位差作用下，水透过土体孔隙的现象。
渗透性——土具有被水透过的性能。
一、达西定律v =ki =k Lh或用渗流量表示为q =vA =kiA式中 v ――渗透速度，cm/s 或m/d ；q ――渗流量，cm 3/s 或m 3/d ；i =h /L ――水力坡降（水力梯度），即沿渗流方向单位距离的水头损失，无因次； h ――试样两端的水头差，cm 或m ； L ――渗径长度；cm 或m ；k ――渗透系数，cm/s 或m/d ；其物理意义是当水力梯度i 等于1时的渗透速度； A ――试样截面积，cm 2或m 2。
【注意】由上式求出的v 是一种假想的平均流速，假定水在土中的渗透是通过整个土体截面来进行的。
水在土体中的实际平均流速要比达西定律采用的假想平均流速大。
二、达西定律的适用范围与起始水力坡降对于密实的粘土：由于结合水具有较大的粘滞阻力，只有当水力梯度达到某一数值，克服了结合水的粘滞阻力后才能发生渗透。
起始水力梯度――使粘性土开始发生渗透时的水力坡降。
(a ) 砂土 (b ) 密实粘土 (c )砾石、卵石粘性土渗透系数与水力坡降的规律偏离达西定律而呈非线性关系，如图（b ）中的实线所示，常用虚直线来描述密实粘土的渗透规律。
()b i i k v -= (2-3)式中 i b ――密实粘土的起始水力坡降；对于粗粒土中（如砾、卵石等）：在较小的i 下，v 与i 才呈线性关系，当渗透速度超过临界流速v cr 时，水在土中的流动进入紊流状态，渗透速度与水力坡降呈非线性关系，如图（c ）所示，此时，达西定律不能适用。
第二节 渗透系数及其确定方法【基本内容】一、渗透试验1．常水头试验常水头试验适用于透水性大（k >10-3cm/s ）的土，例如砂土。
常水头试验就是在整个试验过程中，水头保持不变。
试验时测出某时间间隔t 内流过试样的总水量V ，根据达西定律At LhkkiAt qt V === 即 hAtVL k =2．变水头试验粘性土由于渗透系数很小，流经试样的总水量也很小，不易准确测定。
土的渗透性和渗流
一、平面渗流的连续性分析
对于一个稳定的渗流来说，渗流场中各点的测管水头h 及流速v等仅是位置的函数而与时间无关，即： h = f (x, z)，v = g(x, z)。
z
vz+
v z z
dz
dz vx
图2-9 二维稳定 渗流场中
vz
的某微元
dx
vx+
vx x
dx
x
单位时间流入微元的水量为：
(b) 等效图
图2-8 层状土的垂直渗流情况
其特点有：
（1）通过各层土的流量与等效土层的流量均相 同，即：
qz = q1z = q2z = q3z = ∙∙∙∙∙，v = v1 = v2 = v3 = ∙∙∙∙∙∙ （2）流经等效土层的水头损失等于各土层的水
头损失之和，即：
Δh = Δh1 + Δh2 + Δh3 + ∙∙∙∙∙ = Σhi
分布规律，结合一定的边界条件后，求解该方
程即可得到此条件下的渗流场。
以上就是教材P50-51三个式子的由来。
求解拉普拉斯方程有以下四种方法：
（1）解析法 — 边界条件复杂时，难以求解；
（2）数值解法 — 差分法和有限元方法已应用越 来越广；
（3）实验法 — 用一定比尺的模型实验来模拟渗 流场，应用较广的是电比拟法等；
有
vx
kx
h x
，vz
kz
h z
，将这两式代入连续
方程(2-12)可得：
kx
2h x 2
kz
2h z 2
0
(2-13)
对于各向同性的均质土kx = kz，(2-13)还可变为：
土力学 2土的渗透性与渗透问题
流砂
粉细沙随地下水流入基 坑，产生流砂
在基坑开挖和地下结构施工中，必须防止流砂，以 免发生重大基坑坍塌事故。
流砂形成条件：i < icr : i > icr : i = icr :
土体处于稳定状态 土体发生流土破坏 土体处于临界状态
工程经验判断：
➢粘性土中，渗透力的作用往往使渗流逸出处某一范围内的土体出现 表面隆起变形 ；
γwhw+ γwL + j L= γwh1
P2
结论： 渗透力是一种体积力，
其大小与水力梯度成正比。 其方向与渗透方向一致。
j
w (h1
hw L
L)
w h L
wi
二.流砂破坏及其防治
j
w (h1
hw L
L)
w h L
wi
流砂（流土）：渗流力的方向自下而上时，若渗流力大 于向下的重力，土发生浮起、悬浮并随水流移动的现象。
i 1
达西定律 qx k xiH
n
qix k1iH1 k2iH 2 kniH n
i 1
整个土层与层面平
行的等效渗透系数
1n
kx
H
ki Hi
i 1
1
q1x q2x q3x
1 L
2 Δh x
z k1 k2
H1 H2 H
k3 2
H3
不透水层
与土层平行向渗流时，平均渗透系数的大小受渗透系数最大的控制
为防止发生渗透破坏，采取适当的措施，进行控制。 所以：主要内容为：渗透规律、渗透系数测定、工程中渗 透破坏类型及控制。
主要内容
2.1 概述 2.2 土的渗透系数及其确定方法 2.3 土的渗流和流网 （只讲概念） 2.4 渗透破坏与控制
土力学-土的渗透性及渗流
• 防止发生流土破坏的设计要求
所需入土深度
水力梯度 i h h 2h
临界水力梯度 i c r
w
所需入土深度 h Fs w h 2
地下连续墙
h
坑底
渗
透
h
力
向
上
地表
渗 透 力 向 下
• 管涌 piping 在渗流作用下，土中的细粒在粗粒形成的孔隙中移动以至流失→孔
z
（1）连续方程的建立
流入微单元的水量（厚度为1）
dqxvxdz1vxdz dqz vzdx dqxdqzvxdzvzdx
vx
dz
流出微单元的水量
(vz v zzdz)dx(vx v xxdx)dz
vz
vz z
dz
vx
vx x
dx
vz
dx
x
对稳定流，流入量＝流出量（忽略土体的变形） z
v x d z v z d x ( v z v z zd z )d x ( v x v x xd x )d z dz vx vx vz 0 x z
（2）水力梯度 水头 hydraulic head：单位重量的水所具有的能量。（故量纲为长度）
测压管水头
总水头 hzhwhv zu/wv2/2g hzu/w
势静 动
孔
渗
水水 水
隙
流
土中渗流速度通常较小，可忽略
头头 头
水
速
头位头压 头速
压
度
置力 度
水水 水
• 水力梯度
uA w
hA zA
测压管 piezometer tube
隙增大，渗流速度增加→粗粒流走→贯通的水流通道→土体塌陷。
管涌
土力学-知识单元二(土的渗透性及渗流)
0 基准面
u w
z
0
位置势能： mgz
压力势能： 动能： 总能量：
mg u w
1 mv2 2 E mgz mg u 1 mv2
w 2
单位重量水流的能量：
h z u v2 w 2g
称为总水头，是水流动 的驱动力
水流动的驱动力 - 水头
知识点一 土的渗流性与渗透规律
仁者乐山 智者乐水
B
静水 A zB
0 基准面
位置水头：到基准面的竖直距离， 代表单位重量的液体从基准面算起 所具有的位置势能
uA 压力水头：水压力所能引起的自由
w
水面的升高，表示单位重量液体所
具有的压力势能
测管水头：测管水面到基准面的垂
zA
直距离，等于位置水头和压力水头
0
之和，表示单位重量液体的总势能
在静止液体中各点的测管水头相等
在微观结构上，当孔隙比相同 时，凝聚结构将比分散结构具 有更大的透水性
渗透系数的影响因素
知识点一 土的渗流性与渗透规律
仁者乐山 智者乐水
土的性质
• 粒径大小及级配 • 孔隙比 • 矿物成分 • 结构
干容重 d max
1
絮状结构 分散结构
Wop
含水量 w
渗透系数 k
水的性质
含水量 w
渗透系数的影响因素
头高处流向水头低处
uA w
hA zA
A
B L
基准面
渗流问题的水头
知识点一 土的渗流性与渗透规律
仁者乐山 智者乐水
•
A点总水头： h A
zA
uA
w
•
B点总水头： h B
zB
uB
w
u w
z
0
位置势能： mgz
压力势能： 动能： 总能量：
mg u w
1 mv2 2 E mgz mg u 1 mv2
w 2
单位重量水流的能量：
h z u v2 w 2g
称为总水头，是水流动 的驱动力
水流动的驱动力 - 水头
知识点一 土的渗流性与渗透规律
仁者乐山 智者乐水
B
静水 A zB
0 基准面
位置水头：到基准面的竖直距离， 代表单位重量的液体从基准面算起 所具有的位置势能
uA 压力水头：水压力所能引起的自由
w
水面的升高，表示单位重量液体所
具有的压力势能
测管水头：测管水面到基准面的垂
zA
直距离，等于位置水头和压力水头
0
之和，表示单位重量液体的总势能
在静止液体中各点的测管水头相等
在微观结构上，当孔隙比相同 时，凝聚结构将比分散结构具 有更大的透水性
渗透系数的影响因素
知识点一 土的渗流性与渗透规律
仁者乐山 智者乐水
土的性质
• 粒径大小及级配 • 孔隙比 • 矿物成分 • 结构
干容重 d max
1
絮状结构 分散结构
Wop
含水量 w
渗透系数 k
水的性质
含水量 w
渗透系数的影响因素
头高处流向水头低处
uA w
hA zA
A
B L
基准面
渗流问题的水头
知识点一 土的渗流性与渗透规律
仁者乐山 智者乐水
•
A点总水头： h A
zA
uA
w
•
B点总水头： h B
zB
uB
w
土力学第二章土的渗透性和渗透问题
三．渗透系数的测定及影响因素
§2.1 土的渗透性与渗透规律 Permeability and seepage law of soil
Ch2 土的渗透性和渗流问题 Permeability and seepage problem of soil
Ch2 土的渗透性和渗流问题 Permeability and seepage problem of soil
A
B
L
h1
h2
zA
zB
Δh
0
0
基准面
水力坡降线
总水头－单位质量水体所具有的能量
流速水头≈0
A点总水头：
B点总水头：
总水头：
水力坡降：
一．渗流中的水头与水力坡降
§2.1 土的渗透性与渗透规律 Permeability and seepage law of soil
概述
Ch2 土的渗透性和渗流问题 Permeability and seepage problem of soil
概述
Teton坝
渗流量
渗透变形
渗水压力
渗流滑坡
土的渗透性及渗透规律
二维渗流及流网
渗透力与渗透变形
扬压力
土坡稳定分析
挡水建筑物 集水建筑物 引水结构物 基坑等地下施工 边坡渗流
§2.3 渗透力与渗透变形 Seepage force and seepage deformaton
学习目标
学习基本要求
参考学习进度
学习指导
学习目标
掌握土的渗透定律与渗透力计算方法，具备对地基渗透变形进行正确分析的能力。
掌握土的渗透定律
01
掌握二维渗流及流网绘制
§2.1 土的渗透性与渗透规律 Permeability and seepage law of soil
Ch2 土的渗透性和渗流问题 Permeability and seepage problem of soil
Ch2 土的渗透性和渗流问题 Permeability and seepage problem of soil
A
B
L
h1
h2
zA
zB
Δh
0
0
基准面
水力坡降线
总水头－单位质量水体所具有的能量
流速水头≈0
A点总水头：
B点总水头：
总水头：
水力坡降：
一．渗流中的水头与水力坡降
§2.1 土的渗透性与渗透规律 Permeability and seepage law of soil
概述
Ch2 土的渗透性和渗流问题 Permeability and seepage problem of soil
概述
Teton坝
渗流量
渗透变形
渗水压力
渗流滑坡
土的渗透性及渗透规律
二维渗流及流网
渗透力与渗透变形
扬压力
土坡稳定分析
挡水建筑物 集水建筑物 引水结构物 基坑等地下施工 边坡渗流
§2.3 渗透力与渗透变形 Seepage force and seepage deformaton
学习目标
学习基本要求
参考学习进度
学习指导
学习目标
掌握土的渗透定律与渗透力计算方法，具备对地基渗透变形进行正确分析的能力。
掌握土的渗透定律
01
掌握二维渗流及流网绘制
土力学第2章
第2章土的渗透性与渗流2.1概述由于土体本身具有连续的孔隙，如果存在水位差的作用时，水就会透过土体孔隙而产生孔隙内的流动，这一现象称为渗透。
土具有被水透过的性能称为土的渗透性。
这里所论及的水是指重力水。
水是在土的孔隙中流动的，本章假定土颗粒骨架形成的孔隙是固定不变的，并且认为，在孔隙中流动的水是具有粘滞性的流体。
也就是说，把土中水的流动，简单地看成是粘滞性的流体在土烧制成的素陶磁管似的刚体的孔隙中流动。
这种思考方法，在被称为达西定律的试验中反映出来。
达西定律是土中水的运动规律的最重要的公式。
这个公式采用了“水是从水头(总水头)高的地方流向低处”这一水流的基本原理。
根据达西定律和连续方程，再考虑边界条件，一般的透水问题都可以得到解决，即可以求出土中水的流量(透水量)及土中水压力的分布。
如图2-1 所示为土木、水利工程中典型渗流问题。
此外，土的渗透性的强弱，对土体的固结、强度以及工程施工都有非常重要的影响。
为此，我们必须对土的渗透性质、水在土中的渗透规律及其与工程的关系进行很好的研究，从而给土工建筑物或地基的设计、施工提供必要的资料。
图2-1土木、水利工程中的渗流问题2.2土的渗透性土是由固体相的颗粒、孔隙中的液体和气体三相组成的，而土中的孔隙具有连续的性质，当土作为水土建筑物的地基或直接把它用作水土建筑物的材料时，水就会在水头差作用下从水位较高的一侧透过土体的孔隙流向水位较低的一侧。
渗透：在水头差作用下，水透过土体孔隙的现象。
渗透性：土允许水透过的性能称为土的渗透性。
水在土体中渗透，一方面会造成水量损失，影响工程效益；另一方面将引起土体内部应力状态的变化，从而改变水土建筑物或地基的稳定条件，甚者还会酿成破坏事故。
此外，土的渗透性的强弱，对土体的固结、强度以及工程施工都有非常重要的影响。
2.2.1土的渗透定律地下水在土体孔隙中渗透时，由于渗透阻力的作用，沿程必然伴随着能量的损失。
为了揭示水在土体中的渗透规律，法国工程师达西(H.darcy)经过大量的试验研究，1856年总结得出渗透能量损失与渗流速度之间的相互关系即为达西定律。
土力学 第二章、土的渗流
解：已知A=120cm2，k =2.5×10-2cm/sec，t =10sec，h =45cm，l =25cm
根据常水头渗透试验透水量公式（2.9），得10sec内土的透水量为
V k h At 2.5102 45 12010 54cm3
l
25
k h Adt a(dh) l
A t2
h2 dh
2 土的渗透性
土的渗透性和土中渗流 当饱和土中的两点存在
能量差时，水就在土的孔 隙中从能量高的点向能量 低的点流动。 渗 流：水在土体中流动 的现象。 渗透性：土具有被水等液 体透过的性质。
2.1 达西定律
一、伯努利定律 ：
所谓贝努力定律是指水的 流动符合能量守恒原理，如果 忽略不计由摩擦等引起的能量 损失，则贝努力定律可以用下 式表示。
v2 z u h 常数
2g
w
z u h
w
-△h =h1-h2=(z1+u1/γw)-(z2+u2/γw)
2.1 达西定律
二、达西定律（H.Darcy,1856） 层流渗透定律是由法国学
者达西（Darcy）根据砂土实 验得到
v ki k( h ) L
式中：υ--水在土中的渗透速度， cm/s。ik----水土头的梯渗度透，系i数 ，Lhcm/s， 与土的渗透性质有关的待定系 数。
k
q
ln(r2 (h22
r1 ) h12 )
q
2.3lg(r2 r1 ) (h22 h12 )
2.3q (h22 h12 )
பைடு நூலகம்
lg(r2
r1
)
例题2.3某水平堆积而成的成层土的层厚自上而下分别为H1
，H2，…，Hn，水平渗透系数分别是Kx1，Kx2，…，Kxn，垂
根据常水头渗透试验透水量公式（2.9），得10sec内土的透水量为
V k h At 2.5102 45 12010 54cm3
l
25
k h Adt a(dh) l
A t2
h2 dh
2 土的渗透性
土的渗透性和土中渗流 当饱和土中的两点存在
能量差时，水就在土的孔 隙中从能量高的点向能量 低的点流动。 渗 流：水在土体中流动 的现象。 渗透性：土具有被水等液 体透过的性质。
2.1 达西定律
一、伯努利定律 ：
所谓贝努力定律是指水的 流动符合能量守恒原理，如果 忽略不计由摩擦等引起的能量 损失，则贝努力定律可以用下 式表示。
v2 z u h 常数
2g
w
z u h
w
-△h =h1-h2=(z1+u1/γw)-(z2+u2/γw)
2.1 达西定律
二、达西定律（H.Darcy,1856） 层流渗透定律是由法国学
者达西（Darcy）根据砂土实 验得到
v ki k( h ) L
式中：υ--水在土中的渗透速度， cm/s。ik----水土头的梯渗度透，系i数 ，Lhcm/s， 与土的渗透性质有关的待定系 数。
k
q
ln(r2 (h22
r1 ) h12 )
q
2.3lg(r2 r1 ) (h22 h12 )
2.3q (h22 h12 )
பைடு நூலகம்
lg(r2
r1
)
例题2.3某水平堆积而成的成层土的层厚自上而下分别为H1
，H2，…，Hn，水平渗透系数分别是Kx1，Kx2，…，Kxn，垂
土力学第二章
第二章 土的渗透性和渗流问题
2.1 概述 2.2 土的渗透性 2.3 二维渗流与流网
2.4 渗透力与渗透变形
2.1 概述
2.1 概述
碎散性
多孔介质 能量差
土颗粒 土中水 渗流
三相体系
孔隙流体流动
水、气等在土体孔隙中流动的现象 土具有被水、气等流体透过的性质
渗流 渗透性
2.1 概述
土石坝坝基坝身渗流 防渗斜墙及铺 盖
1 kx H
kz
1 k j H j （0.0011 0.2 1 101 ） 3.4m/d 3 j 1
3 1 1 1 0.001 0.2 10 0.003m/d
n
k
j 1
H n H j
j
水平渗流kx：渗透系数大的土层起主导作用 竖直渗流kz：渗透系数小的土层起主导作用 kx恒大于kz，实际工程中，一定要注意渗流水流的流向
Q lg(r2 / r1 ) k 2.3 h22 h12
优点：可获得现场较为可 靠的平均渗透系数 缺点：费用较高，耗时较长
2.2 土体的渗透性
4、影响渗透系数的因素
k f (土粒特性、流体特性）
粒径大小及级配 孔隙比 矿物成分 结构 饱和度（含气量） 水的动力粘滞系数
2.2 土体的渗透性
2.2 土体的渗透性
2.2.2
渗透系数的测定和影响因素
常水头试验法
室内试验测定方法
变水头试验法
野外试验测定方法
井孔抽水试验 井孔注水试验
2.2 土体的渗透性
1、常水头试验法
试验条件: Δh，A，L已知 量测变量: V，t 结果整理
V=Qt=vAt v=ki
i=Δh/L
2.1 概述 2.2 土的渗透性 2.3 二维渗流与流网
2.4 渗透力与渗透变形
2.1 概述
2.1 概述
碎散性
多孔介质 能量差
土颗粒 土中水 渗流
三相体系
孔隙流体流动
水、气等在土体孔隙中流动的现象 土具有被水、气等流体透过的性质
渗流 渗透性
2.1 概述
土石坝坝基坝身渗流 防渗斜墙及铺 盖
1 kx H
kz
1 k j H j （0.0011 0.2 1 101 ） 3.4m/d 3 j 1
3 1 1 1 0.001 0.2 10 0.003m/d
n
k
j 1
H n H j
j
水平渗流kx：渗透系数大的土层起主导作用 竖直渗流kz：渗透系数小的土层起主导作用 kx恒大于kz，实际工程中，一定要注意渗流水流的流向
Q lg(r2 / r1 ) k 2.3 h22 h12
优点：可获得现场较为可 靠的平均渗透系数 缺点：费用较高，耗时较长
2.2 土体的渗透性
4、影响渗透系数的因素
k f (土粒特性、流体特性）
粒径大小及级配 孔隙比 矿物成分 结构 饱和度（含气量） 水的动力粘滞系数
2.2 土体的渗透性
2.2 土体的渗透性
2.2.2
渗透系数的测定和影响因素
常水头试验法
室内试验测定方法
变水头试验法
野外试验测定方法
井孔抽水试验 井孔注水试验
2.2 土体的渗透性
1、常水头试验法
试验条件: Δh，A，L已知 量测变量: V，t 结果整理
V=Qt=vAt v=ki
i=Δh/L
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
Δh=h1-h2
q=V/t
Δh↑，q↑ A↑，q↑ L↑， q↓
q A h L
断面平均流速 v q A
水力梯度 i h L
vi
23
2.达西定律
渗透定律
vi
k: 反映土的透水性能的比例系数，称为渗透系数
物理意义：水力梯度i＝1时的渗流速度 单位：mm/s, cm/s, m/s, m/day 在层流状态的渗流中，渗透速度v与水力梯度i 的一次方成正比，并与土的性质有关。
29
一、渗透系数的影响因素
k f (土粒特性、流体特性)
➢粒径大小及级配 ➢孔隙比 ➢矿物成分 ➢结构
➢饱和度（含气量） ➢水的动力粘滞系数
30
土粒特性对渗透系数的影响
（1）土颗粒的粒径、级配和矿物成分
a. 砂土的渗透性由其中的小颗粒控制 土中孔隙直径大小是主要影响因素； 因由粗颗粒形成的大孔隙可被细颗粒 充填，故土体孔隙的大小一般由细颗 粒所控制。
土的力学性质
渗透特性
强度特性
变形特性
3
为什么要学习土的渗透性和水的渗流？
土的渗透性和水的渗流 工程活动
直接影响
（1） 渗透变形（破坏）问题 （2） 渗流量的计算问题 （3） 渗流变形控制问题
4
1、渗透变形（破坏）问题
因渗流造成土体变形甚至破坏
Teton大坝， 位于美国爱达 荷州的东南部， 为高93m的土坝。 1976年6月5日 该坝完成后第 一次蓄水时即 发生破坏，造 成11人死亡及 数百万美元的 损失。破坏是 由右岸距坝顶 约40m处的一个 漏洞引起的。
27
两种特例：
（1）粗粒土：
v
①砾石类土中的渗流常不符合达西定律 vcr
②砂土中渗透速度
o
vcr=0.3-0.5cm/s
（2）粘性土： 致密的粘土
i > i0
修正：v = k(i - i0 )
v
o i0
v kim (m 1)
i
i
28
第二节 渗透系数及其测定
一、渗透系数的影响因素 二、渗透系数的测定方法 三、成层土的平均渗透系数
v ki
A
Av
注意：
v：假想渗流速度，土体试样全断面的平均渗流速度
vs：实际平均渗流速度，孔隙断面的平均渗流速度
土截面
n Av
A
v
A > Av q＝vA ＝ vsAv
v vs n
24
四、达西渗透定律的适用范围 适用条件： 层流（线性流）
按地下水的渗流状态
线性流（层流） 地下水的渗流速度 与水力梯度成正比
uB
w
hB
zB
21
二、水力梯度
uA
w
hA zA
测压管 piezometer tube
总水头线
A B
L
h
uB
w
hB
zB
水力梯度（坡降） hydraulic gradient
i hA hB h LL
单位流程的水头损失。
22
三、达西渗透定律
1.达西渗透试验
▪试验前提：层流 ▪试验装置：如图 ▪试验条件: h1，A，L=const ▪量测变量: h2，V，t ▪试验结果
1.渗流量Q？ 2.降水深度？
不透水层
14
2、渗流量的计算及渗透变形控制问题
渠道渗流
渗流时地下水位
渗流问题：
1.渗流量？ 2.地下水影响 范围？
原地下水位
15
2、渗流量的计算及渗透变形控制问题
降雨入渗引发滑坡
降雨入渗 引发滑坡
16
2、渗流量的计算及渗透变形控制问题
2003年7月三峡库区 湖北省秭归县发生 的千将坪滑坡，该 滑坡造成24人死 亡，22艘船翻沉。
适用范围：
岩土工程中的绝大多数渗流问题，包括砂土或一般 粘土，均属层流范围
在粗粒土孔隙中，水流形态可能会随流速增大呈紊 流状态，渗流不再服从达西定律。
可用雷诺数Re进行判断：
雷诺数Re ：是流体力学中用来判别流体流动状态的重要参数
Re＜5~10时层流 Re ＞100~200时紊流 100~200＞ Re ＞5~10时为过渡区
库水位升降引发滑坡
17
第一节 土的渗透定律
一、水头 二、水力梯度 三、达西渗透定律 四、达西定律的适用范围
18
水流动的驱动力
水往低处流
位置：使水流从位置势能 高处流向位置势能低处
速度v
水往高处“跑”
压力u
流速：水具有的动能 压力：水所具有的压力势能
19
一、水头
水头 hydraulic head：单位重量的水所具有的能量。
非线性流（紊流） 地下水的渗流速度与 水力梯度成非线性关系
线性稳定流
线性非稳定流
非线性稳定流 非线性非稳定流
我们现在需要掌握和理解的达西定律
25
四、达西渗透定律的适用范围
水 2.0 力 坡 1.5 降
1.0 0.5
0
达西定律 适用范围
0 0.5 1.0 1.5 2.0 2.5 流速 (m/h)
26
板桩墙
基坑
A
透水层
L
不透水层
B
20
土体中一点总水头
动水头速度水头
h z hw hv z u / w v2 / 2g
势水头 位置水头
静水头 孔隙水压
渗流速度
压力水头
测压管 piezometer tube
uA
w
hA zA
总水头线
A B
LHale Waihona Puke 土中渗流速度 通常较小， 可忽略，故有
h zu/w
h
九江大堤决口
1998年8月7日13:10 发生管涌险情，很快 形成宽62m的溃口 原因 堤基管涌
8
土石坝坝基坝身渗流破坏实例
位于青海省，高71 米，长265米，建 于1989年。 1993年8月7日突然 发生溃坝，是现代 碾压堆石坝垮坝的 先例。
面板砂砾石坝
溃坝原因： 面板止水失效，下游坝体排水不畅， 造成坝坡失稳
5
Teton坝失事现场现状
土坝，高93m， 长1000m， 1975年建成， 次年6月失事 原因
渗透破坏：管涌 水力劈裂
6
2、渗流量的计算及渗透变形控制问题
土石坝坝基坝身渗流
防渗斜墙及铺盖 不透水层
土石坝
浸润线
透水层
渗流问题：
1. 渗流量？ 2. 渗透破坏？ 3. 渗透力？
7
土石坝坝基坝身渗流破坏实例
9
2、渗流量的计算及渗透变形控制问题
基坑围护结构下的渗流
板桩墙
基坑
透水层
渗流问题：
1. 渗流量？ 2. 渗透破坏？ 3. 渗水压力？
不透水层
10
基坑开挖降水
井点降水
11
管井降水
12
工程实例 湖南浯溪水电站二期基坑出现管涌
13
2、渗流量的计算及渗透变形控制问题
水井渗流 Q
天然水面
含水层
渗流问题：
第二章 土的渗透性及水的渗流
1
主要内容
第一节 土的渗透定律 第二节 渗透系数及其测定 第三节 渗透力及临界水力梯度 第四节 二维稳定渗流问题（自学）
2
什么是土的渗透性和水的渗流？
土
多孔介质
渗流
三相体系 能量差
孔隙流体流动
土颗粒 土中水
水在土体孔隙中流动的现象
渗流
土具有被水透过的性质
渗透性