【全国市级联考】河南省新乡市2020届高三第一次模拟考试数学(理)试题
河南省新乡市2019-2020学年高考数学一模考试卷含解析
河南省新乡市2019-2020学年高考数学一模考试卷一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.一个几何体的三视图如图所示,则该几何体的体积为( )A .103B .3C .83D .73【答案】A【解析】【分析】根据题意,可得几何体,利用体积计算即可.【详解】由题意,该几何体如图所示:该几何体的体积11110222222323V =⨯⨯⨯-⨯⨯⨯=.故选:A.【点睛】本题考查了常见几何体的三视图和体积计算,属于基础题.2.设数列{}n a 是等差数列,1356a a a ++=,76a =.则这个数列的前7项和等于() A .12 B .21 C .24 D .36【答案】B【解析】【分析】根据等差数列的性质可得3a ,由等差数列求和公式可得结果.【详解】因为数列{}n a 是等差数列,1356a a a ++=,所以336a =,即32a =,又76a =, 所以73173a a d -==-,1320a a d =-=, 故1777()212a a S +== 故选:B【点睛】本题主要考查了等差数列的通项公式,性质,等差数列的和,属于中档题.3.袋中装有标号为1,2,3,4,5,6且大小相同的6个小球,从袋子中一次性摸出两个球,记下号码并放回,如果两个号码的和是3的倍数,则获奖,若有5人参与摸球,则恰好2人获奖的概率是( ) A .40243 B .70243 C .80243 D .38243【答案】C【解析】【分析】先确定摸一次中奖的概率,5个人摸奖,相当于发生5次试验,根据每一次发生的概率,利用独立重复试验的公式得到结果.【详解】从6个球中摸出2个,共有2615C =种结果,两个球的号码之和是3的倍数,共有(1,2),(1,5),(2,4),(3,6),(4,5)∴摸一次中奖的概率是51153=, 5个人摸奖,相当于发生5次试验,且每一次发生的概率是13, ∴有5人参与摸奖,恰好有2人获奖的概率是35222180()()33243C ⋅⋅=, 故选:C .【点睛】 本题主要考查了n 次独立重复试验中恰好发生k 次的概率,考查独立重复试验的概率,解题时主要是看清摸奖5次,相当于做了5次独立重复试验,利用公式做出结果,属于中档题.4.若函数()3cos 4sin f x x x =+在x θ=时取得最小值,则cos θ=( )A .35B .45-C .45D .35- 【答案】D【解析】【分析】利用辅助角公式化简()f x 的解析式,再根据正弦函数的最值,求得()f x 在x θ=函数取得最小值时cos θ的值.【详解】 解:34()3cos 4sin 5cos sin 5sin()55f x x x x x x α⎛⎫=+=+=+ ⎪⎝⎭,其中,3sin 5α=,4cos 5α=, 故当22k πθαπ+=-()k ∈Z ,即2()2k k Z πθπα=--∈时,函数取最小值()5f θ=-, 所以3cos cos(2)cos()sin 225k ππθπααα=--=--=-=-, 故选:D【点睛】 本题主要考查辅助角公式,正弦函数的最值的应用,属于基础题.5.已知实数,x y 满足不等式组10240440x y x y x y +-≥⎧⎪-+≥⎨⎪+-≤⎩,则34x y +的最小值为( )A .2B .3C .4D .5 【答案】B【解析】【分析】作出约束条件的可行域,在可行域内求34z x y =+的最小值即为34x y +的最小值,作34y x =-,平移直线即可求解.【详解】 作出实数,x y 满足不等式组10240440x y x y x y +-≥⎧⎪-+≥⎨⎪+-≤⎩的可行域,如图(阴影部分)令34z x y =+,则344z y x =-+, 作出34y x =-,平移直线,当直线经过点()1,0A 时,截距最小, 故min 3103z =⨯+=, 即34x y +的最小值为3.故选:B【点睛】本题考查了简单的线性规划问题,解题的关键是作出可行域、理解目标函数的意义,属于基础题. 6. “1sin 2x =”是“2()6x k k Z ππ=+∈”的( ) A .充分不必要条件 B .必要不充分条件C .充要条件D .既不充分也不必要条件 【答案】B【解析】【分析】1sin 2x =⇔2()6x k k Z ππ=+∈或52()6x k k Z ππ=+∈,从而明确充分性与必要性. 【详解】, 由1sin 2x =可得:2()6x k k Z ππ=+∈或52()6x k k Z ππ=+∈, 即2()6x k k Z ππ=+∈能推出1sin 2x =, 但1sin 2x =推不出2()6x k k Z ππ=+∈ ∴“1sin 2x =”是“2()6x k k Z ππ=+∈”的必要不充分条件 故选B【点睛】本题考查充分性与必要性,简单三角方程的解法,属于基础题.7.设2,(10)()[(6)],(10)x x f x f f x x -≥⎧=⎨+<⎩,则(5)f =( ) A .10B .11C .12D .13【答案】B【解析】【分析】根据题中给出的分段函数,只要将问题转化为求x≥10内的函数值,代入即可求出其值.【详解】 ∵f (x )()()()210610x x f f x x ⎧-≥⎪=⎨⎡⎤+⎪⎣⎦⎩<, ∴f (5)=f[f (1)]=f (9)=f[f (15)]=f (13)=1.故选:B .【点睛】本题主要考查了分段函数中求函数的值,属于基础题.8.已知()5x a +展开式的二项式系数和与展开式中常数项相等,则2x 项系数为( )A .10B .32C .40D .80【答案】D【解析】【分析】根据二项式定理通项公式1r r n r r n T C a b -+=可得常数项,然后二项式系数和,可得a ,最后依据1r r n r r n T C a b -+=,可得结果. 【详解】由题可知:515r r r r T C x a -+=当0r =时,常数项为51T a =又()5x a +展开式的二项式系数和为52由5522a a =⇒=所以5152r r r r T C x -+=当2r =时,223235280T C x x ==所以2x 项系数为80故选:D【点睛】本题考查二项式定理通项公式,熟悉公式,细心计算,属基础题.9.集合{2,0,1,9}的真子集的个数是( )A .13B .14C .15D .16【答案】C【解析】【分析】根据含有n 个元素的集合,有2n 个子集,有21n -个真子集,计算可得;【详解】解:集合{2,0,1,9}含有4个元素,则集合{2,0,1,9}的真子集有42115-=(个),故选:C【点睛】考查列举法的定义,集合元素的概念,以及真子集的概念,对于含有n 个元素的集合,有2n 个子集,有21n -个真子集,属于基础题.10.一个空间几何体的正视图是长为4,宽为3的长方形,侧视图是边长为2的等边三角形,俯视图如图所示,则该几何体的体积为( )A 43B .3C 23D .23【答案】B【解析】 【分析】由三视图确定原几何体是正三棱柱,由此可求得体积.【详解】由题意原几何体是正三棱柱,1234432V =⨯=. 故选:B .本题考查三视图,考查棱柱的体积.解题关键是由三视图不愿出原几何体.11.阅读如图所示的程序框图,运行相应的程序,则输出的结果为( )A .1112B .6C .112D .223【答案】D 【解析】【分析】用列举法,通过循环过程直接得出S 与n 的值,得到8n =时退出循环,即可求得.【详解】执行程序框图,可得0S =,2n =,满足条件,12S =,4n =,满足条件,113244S =+=,6n =,满足条件,1111124612S =++=,8n =,由题意,此时应该不满足条件,退出循环,输出S 的值为11228123⨯=. 故选D .【点睛】本题主要考查了循环结构的程序框图的应用,正确依次写出每次循环得到的S 与n 的值是解题的关键,难度较易.12.某几何体的三视图如图所示,则该几何体的体积为( )A .83π3B .4π1633C 16343π+D .43π163 【答案】D【解析】结合三视图可知,该几何体的上半部分是半个圆锥,下半部分是一个底面边长为4,高为4的正三棱柱,分别求出体积即可.【详解】由三视图可知该几何体的上半部分是半个圆锥,下半部分是一个底面边长为4,高为4的正三棱柱,则上半部分的半个圆锥的体积1114π233V =⨯⨯⨯=,下半部分的正三棱柱的体积21442V =⨯⨯=故该几何体的体积123V V V =+=+故选:D.【点睛】本题考查三视图,考查空间几何体的体积,考查空间想象能力与运算求解能力,属于中档题.二、填空题:本题共4小题,每小题5分,共20分。
河南省新乡市新乡一中2020届高三数学上学期第一次质量预测试题文[含答案]
![河南省新乡市新乡一中2020届高三数学上学期第一次质量预测试题文[含答案]](https://img.taocdn.com/s3/m/4485e5aa67ec102de3bd897c.png)
定值.
23.[选修 4—5 不等式选讲](10 分) 已知函数 f(x)=|x-1|-|2x+1|+m. (Ⅰ)求不等式 f(x)≥m 的解集; (Ⅱ)若恰好存在 4 个不同的整数 n,使得 f(n)≥0,求 m 的取值范围.
一、选择题:1---12 二、填空题:
(文科) BDACB BAADC DB
题.每个试题考生都必须作答.第 22、23 题为选考题,考生根据要求作答. (一)必考题:共 60 分
17.(12 分)
已知等差数列{ an }为递增数列,且满足 a1=2, a32 + a42 = a52 .
(Ⅰ)求数列{ an }的通项公式;
(Ⅱ)令
bn
=
1 (an+1+)(an-1
1) (n∈N*), Sn 为数列{ bn }的前 n 项和,求 Sn .
x2 y2 9.已知椭圆: +=
1 (a>b>0)的离心率为 3 ,直线 2x+y+10=0 过椭圆的左顶点,
a2 b2
5
则椭圆方程为
A. x2 +=y2 1 B. x2 +=y2 1
54
25 9
C. x2 +=y2 1 16 9
D. x2 +=y2 1 25 16
10.已知三棱锥 P—ABC 的四个顶点均在球面上,PB⊥平面 ABC.PB=2 3 ,△ABC
3
x=a,cos
在平面直角坐标系
xOy
中,已知曲线
E
经过点
P(1,
2
),其参数方程为
y=,3
sin
(α 为参数),以原点 O 为极点,x 轴的正半轴为极轴建立极坐标系. (Ⅰ)求曲线 E 的极坐标方程;
1
1
(Ⅱ)若直线 l 交 E 于点 A,B,且 OA⊥OB,求证:
2020年河南省六市高三数学第一次联考(理科)试题【含答案】
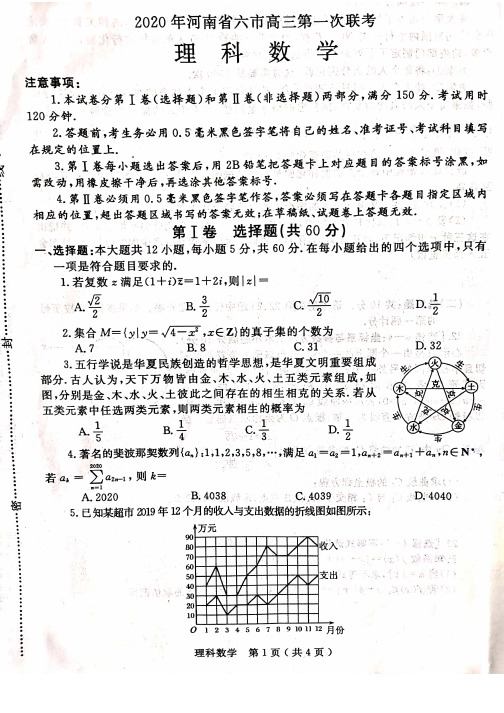
2a
理科数学答案 第 3 页 (共 6 页)
(2)方法一:由(1)知,
x1,
x2
是方程
x 1 ex
2a
的两根,
∴ 1
x1
0
x2
,则
x1
x2
0
x2
x1
0
因为
h(x)
在(0,
)单减,
h( x2
)
h(
x1
), 又h( x2
23. 解:(1)当 a 1时,
2x 1, x 1 f (x) 3,1 x 2
2x 1, x 2
…………………………2 分
当 x 1时,由 f (x) 7 得 2x 1 7 ,解得 x 3 ;
当 1 x 2 时, f (x) 7 无解;
当 x 2 时,由 f (x) 7 得 2x 1 7 ,解得 x 4 ,
1)
即 t ln t t 1 (ln t t 1) 0恒成立 ................................8 分
令 g(t) t ln t t 1 (ln t t 1)
理科数学答案 第 4 页 (共 6 页)
g ' (t)
ln t
1 t t
, g '' (t)
1 t t2
t t2
.............................9 分
当 1 时, g '' (t) 0 , g ' (t) 单减,故 g ' (t) g ' (1) 0
故 g(t)在(0,1)上为增函数 , g(t) g(1) 0 ........................10 分
(全国卷)高三数学第一次大联考试题理

(全国卷)2020届高三数学第一次大联考试题 理考生注意:1.本试卷共150分,考试时间120分钟。
2.请将试卷答案填在试卷后面的答题卷上。
3.本试卷主要考试内容:集合与常用逻辑用语、函数与导数。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
{}{}223,,1A x x x N B x x =-<<∈=> ,则集合A∩B=A.{2}B.{-1,0,1)C.{-2,2}D.{-1,0,1,2}2.命题“∀x>0,x(x +1)>(x -1)2”的否定为;A.20,(1)(1)x x x x ∀>+≤-B.20,(1)(1)x x x x ∀≤+≤-C.20,(1)(1)x x x x ∃>+≤-D.20,(1)(1)x x x x ∃≤+≤- 3.21232x dx x -+=+⎰ A.2+ln2 B.3-ln2 C.6-ln2 D.6-ln44.设集合A 、B 是全集U 的两个子集,则“A B ⊆”是“U AB φ= ”的2,0()0x x f x x -⎧≤⎪=> ,若f(x 0)<2,则x 0的取值范围是A.(-∞,-1)B.(-1,0]C.(-1,+∞)D.(-∞,0)01021:1,log ;:,2x p x x q x R e x ∃>>∀∈>,则下列说法中正确的是 A.p∨q 是假命题 B.p∧q 是真命题 C.p∨(⌝q)是真命题 D.p∧(⌝q)是假命题 {}{}12,15A x x B x x =-<≤=≤-≤, 定义集合{},,A B z z x y x A y B *==+∈∈,则()B A B **等于 A.{}61x x -<≤ B.{}112x x <≤ C.{}110x x -<≤ D.{}56x x -<≤8.已知定义在R 上的奇函数f(x)和偶函数g(x)满足f(x)+g(x)=a x - a -x +2(a>0且a≠1),若g(2)=a ,则函数f(x 2+2x)的单调递增区间为A(-1.1) B.(-∞,1) C.(1,+∞) D.(-1,+∞)9.如图是二次函数f(x)=x 2-bx +a 的部分图象,则函数g(x)=alnx + f’(x)的零点所在的区间是 A.(14,12) B.(12,1) C.(1,2) D.(2,3) ∈R ,函数f(x)满足f(2-x)=-f(x),且当x≧1时,函数f(x)=1x -。
2020年河南高考模拟题理数(附答案)

2020年高中毕业年级第一次质量预测数学(理科)参考答案一、选择题1-12BDACB CBCDB DA 二、填空题13.10;x y -+=14.4;15.;53016.{}.66,2,0--三、解答题17.解析:(I)222(sinsin )()sin .R A B a c C -=-∴2222(sinsin )()sin 2,R R A B a c C R ⋅-=-⋅即:222.a c b ac +-=……3分∴2221cos .22a c b B ac+-==因为0,B π<<所以3B π∠=……6分(II)若12,8b c ==,由正弦定理,sin sin b c B C=,3sin 3C =,由b c >,故C ∠为锐角,6cos 3C =……9分3613323sin sin()sin().323236A B C C π+=+=+=⋅+⋅=……12分18.解析:(I )如图所示:连接OM ,在ABC ∆中:2,22AB BC AC ===,则90,2ABC BO ∠=︒,OB AC ⊥.……2分在MAC ∆中:2M A M C A C ===O 为AC 的中点,则OM AC ⊥,且 6.O M ……4分在MOB ∆中:2,6,22BO OM MB =222BO OM MB +=根据勾股定理逆定理得到OB OM⊥,AC OM 相交于O ,故OB ⊥平面AMC ………………….6分(Ⅱ)因为,,OB OC OM 两两垂直,建立空间直角坐标系 㜠Ꮉ婈Ӭ如图所示.因为2M A M B M C A C ====,2AB BC ==则(0,2,0),(2,0,0),2,0),6)A B C M -……8分由23BN BC = 所以,222(,33N 设平面MAN 的法向量为(,,)m x y z = ,则252252(,,0)(,,)0,33332,6)(,,)260AN n x y z x y AM n x y z z ⎧⋅=⋅=+=⎪⎨⎪⋅=⋅==⎩ 令3y =(53,3,1)m =-- ……10分因为BO ⊥平面AMC ,所以(2,0,0)OB = 为平面AMC 的法向量,所以(53,3,1)m =-- 与(2,0,0)OB = 所成角的余弦为5653cos ,79279m OB < 所以二面角的正弦值为253279|sin ,|1(797979m OB -<>=-= .……12分19.(I )由题意知1b =,22c a =.……1分又因为222a b c =+解得,2a =.……3分所以椭圆方程为2212y x +=.……4分(Ⅱ)设过点1(,0)3-直线为13x ty =-,设()11,A x y ,()22,B x y 由221312x ty x y ⎧=-⎪⎪⎨⎪+=⎪⎩得()2291812160t ty y +--=,且>0∆.则12212212,918616,918y y y t y t t ⎧+=⎪⎪+⋯⋯⎨⎪=-⎪+⎩分又因为()111,CA x y =- ,()221,CB x y =- ,()()212121212121244416(1)(1)13339CA CB x x y y ty ty y y t y y t y y ⎛⎫⎛⎫⋅=--+=--+=+-++ ⎪⎪⎝⎭⎝⎭ ()22216412161091839189t t t t t -=+-⋅+=++,……10分所以C A C B ⊥ .因为线段AB 的中点为M ,所以||2||AB CM =.……12分20.解析:(I)该混合样本达标的概率是28(39=,……2分所以根据对立事件原理,不达标的概率为81199-=.……4分(II)(i )方案一:逐个检测,检测次数为4.方案二:由(1)知,每组两个样本检测时,若达标则检测次数为1,概率为89;若不达标则检测次数为3,概率为19.故方案二的检测次数记为ξ2,ξ2的可能取值为2,4,6.其分布列如下,2ξ246p 64811681181可求得方案二的期望为26416119822()246818181819E ξ=⨯+⨯+⨯==方案四:混在一起检测,记检测次数为ξ4,ξ4可取1,5.其分布列如下,4ξ15p 64811781可求得方案四的期望为46417149()15818181E ξ=⨯+⨯=.比较可得42()()4E E ξξ<<,故选择方案四最“优”.……9分(ii)方案三:设化验次数为3η,3η可取2,5.3η25p3p 31p -3333()25(1)53E p p p η=+-=-;方案四:设化验次数为4η,4η可取1,54η15p4p 41p -4444()5(1)54E p p p η=+-=-;由题意得34343()()53544E E p p p ηη<⇔-<-⇔<.故当304p <<时,方案三比方案四更“优”.……12分21解析:(I)()ln x e f x x x x=--,定义域(0,)+∞,221(1)(1)()()1x x e x x x e f x x x x---'=--=,由1x e x x ≥+>,()f x 在(0,1]增,在(1,)+∞减,max ()(1)1f x f e ==-……4分(II)1()()e 1x f x x bx x++-≥e e ln e 1x x x x x x bx x x⇔-+-++-≥ln e 10x x x x bx ⇔-++--≥e ln 1x x x x b x --+⇔≥min e ln 1(,x x x x b x--+⇔≥……6分令e ln 1()x x x x x x ϕ--+=,2ln ()x x e x x xϕ+'=令2()ln x h x x e x =+,()h x 在(0,)+∞单调递增,0,()x h x →→-∞,(1)0h e =>()h x 在(0,1)存在零点0x ,即02000()ln 0x h x x e x =+=0001ln 2000000ln 1ln 0(ln )()x x x x x e x x e e x x +=⇔=-=……9分由于x y xe =在(0,)+∞单调递增,故0001ln ln ,x x x ==-即001x e x =()x ϕ在0(0,)x 减,在0(,)x +∞增,000000min00e ln 111()2x x x x x x x x x ϕ--++-+===所以2b ≤.……12分22.解析:(I)将点3(1,)2P 代入曲线E 的方程,得1cos ,3,2a αα=⎧⎪⎨=⎪⎩解得24a =,……2分所以曲线E 的普通方程为22143x y +=,极坐标方程为22211(cos sin )143ρθθ+=.……5分(Ⅱ)不妨设点,A B 的极坐标分别为1212()(00,2A B πρθρθρρ+>>,,,,,则22221122222211(cos sin )1,4311(cos ()sin ()1,4232ρθρθππρθρθ⎧+=⎪⎪⎨⎪+++=⎪⎩即22212222111cos sin ,43111sin cos ,43θθρθθρ⎧=+⎪⎪⎨⎪=+⎪⎩……8分2212111174312ρρ+=+=,即22117||||12OA OB +=……10分23.解:(I)由()f x m ≥,得,不等式两边同时平方,得221)(21)x x ≥(-+,……3分即3(2)0x x +≤,解得20x -≤≤.所以不等式()f x m ≥的解集为{|20}x x -≤≤.……5分(Ⅱ)设g (x )=|x -1|-|2x +1|,……8分()0()f n g n m ≥⇔≥-因为(2)(0)0g g -==,(3)1,(4)2,(1) 3.g g g -=--=-=-又恰好存在4个不同的整数n ,使得()0f n ≥,所以2 1.m -<-≤-故m 的取值范围为[1,2).……10分12,,21()3,1,22,1,x x g x x x x x ⎧+≤-⎪⎪⎪=--<≤⎨⎪-->⎪⎪⎩。
2020年河南省新乡市镇第一中学高三数学理模拟试卷含解析

2020年河南省新乡市镇第一中学高三数学理模拟试卷含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 某公园有一个人工湖,湖中有4个人造岛屿甲、乙、丙、丁,要求驾船游遍4个岛屿,且每个岛屿只游览一次,则首先游岛屿甲,最后游岛屿丁的概率是()A. B. C. D.参考答案:D2. 执行如右图所示的程序框图,若输出m的值是25,则输入k的值可以是A.4 B.6 C.8 D.10参考答案:C3. 已知y=f(2x)的定义域为-1,1,则y=f(log2x)的定义域为( )A.-1,1 B.,2 C.1,2 D.,4参考答案:D4. 某班级有50名学生,其中有30名男生和20名女生,随机询问了该班五名男生和五名女生在某次数学测验中的成绩,五名男生的成绩分别为86,94,88,92,90,五名女生的成绩分别为88,93,93,88,93.下列说法一定正确的是(A)这种抽样方法是一种分层抽样(B)这种抽样方法是一种系统抽样(C)这五名男生成绩的方差大于这五名女生成绩的方差(D)该班级男生成绩的平均数小于该班女生成绩的平均数参考答案:C5. 已知向量=(cosα,﹣2),=(sinα,1),且∥,则tan(α﹣)等于( )A.3 B.﹣3 C.D.参考答案:B考点:平面向量共线(平行)的坐标表示;两角和与差的正切函数.专题:平面向量及应用.分析:根据两个向量共线的充要条件,得到关于三角函数的等式,等式两边同时除以cosα,得到角的正切值,把要求的结论用两角差的正切公式展开,代入正切值,得到结果.解答:解:∵,∴cosα+2sinα=0,∴tanα=,∴tan()==﹣3,故选B点评:向量知识,向量观点在数学.物理等学科的很多分支有着广泛的应用,而它具有代数形式和几何形式的“双重身份”能融数形于一体,能与中学数学教学内容的许多主干知识综合,形成知识交汇点,所以2015届高考中应引起足够的重视.本题是把向量同三角函数结合的问题.6. 已知向量,,,若∥,则=()A. B. C.D. 5参考答案:D7. 某几何体的三视图如图所示,则该几何体的表面积为()A.36+12πB.36+16πC.40+12πD.40+16π参考答案:C【考点】L!:由三视图求面积、体积.【分析】几何体为棱柱与半圆柱的组合体,作出直观图,代入数据计算.【解答】解:由三视图可知几何体为长方体与半圆柱的组合体,作出几何体的直观图如图所示:其中半圆柱的底面半径为2,高为4,长方体的棱长分别为4,2,2,∴几何体的表面积S=π×22×2++2×4+2×4×2+2×4+2×2×2=12π+40.故选C.8. 设随机变量X~N(2,82),且P{2<x<4=0.3,则P{x<0=A.0.8 B.0.2 C.0.5 D.0.4参考答案:B略9. 将正三棱柱截去三个角(如图1所示A、B、C分别是三边的中点)得到的几何体如图2,则该几何体按图2所示方向的侧视图(或称左视图)为参考答案:A略10. 如果执行如图的框图,运行的结果为A.B.3 C.D.4参考答案:B二、填空题:本大题共7小题,每小题4分,共28分11. 设向量,,若,则.参考答案:12. 已知函数对任意的恒成立,则.参考答案:13. 20世纪30年代,里克特(C.F.Richter)制定了一种表明地震能量大小的尺度,就是使用地震仪测量地震能量的等级,地震能量越大,地震仪记录的地震曲线的振幅就越大,这就是我们常说的里氏震级M,其计算公式为:,其中A是被测地震的最大振幅,是“标准地震”的振幅(使用标准地震振幅是为了修正测震仪距实际震中的距离造成的偏差).假设在一次地震中,一个距离震中100km的测震仪记录的最大振幅是20,此时标准地震的振幅为0.001,则此次地震的震级为 (精确到0.1,已知).参考答案:14. 已知(a,b∈R,i为虚数单位),则ab=▲.参考答案:15. 在中,,,为垂足,则,该结论称为射影定理。
河南省新乡市新乡一中2020届高三数学上学期第一次质量预测试题理(含答案)
河南省新乡市新乡一中2020届高三上学期第一次质量预测试题数学理注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上.2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效.3.考试结束后,将本试卷和答题卡一并交回.一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合A={x∈N||x≤2},B={y|y=1-x2},则A∩B的子集个数为A.2 B.4 C.8 D.162.复数z=1ii+在复平面内对应的点位于A.第一象限 B.第二象限 C.第三象限 D.第四象限3.郑州市某一景区为了了解游客人数的变化规律,提高旅游服务质量,收集并整理了2016年1月至2018年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是A.月接待游客逐月增加B.年接待游客量逐年增加C.各年的月接待游客量高峰期大致在7,8月D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳4.定义在R上的函数f(x)=1()3x m-2为偶函数,a=f(21log2),b=f(131()2),c=f(m),则A.c<a<b B.a<c<b C.a<b<c D.b<a<c5.“纹样”是中国艺术宝库的瑰宝,“火纹”是常见的一种传统纹样.为了测算某火纹纹样(如图阴影部分所示)的面积,作一个边长为3的正方形将其包含在内,并向该正方形内随机投掷2 000个点,己知恰有800个点落在阴影部分,据此可估计阴影部分的面积是A.165B.185C .10D .3256.已知向量a 与b 夹角为3,且|a |=1,|2a -b |=3,则|b |= A .3 B .2C .1D .327.宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题:松长三尺,竹长一尺,松日自半,竹日自倍,松竹何日而长等,如图是源于其思想的一个程序框图,若输入 的a ,b 分别为3,1,则输出的n 等于A .5B .4C .3D .28.函数f (x )=2121x x +-·cosx 的图象大致是9.第十一届全国少数民族传统体育运动会在河南郑州举行,某项目比赛期间需要安排3名志愿者完成5项工作,每人至少完成一项,每项工作由一人完成,则不同的安排方式共有多少种A .60B .90C .120D .15010.已知抛物线y 2=2x 的焦点为F ,准线为l ,P 是l 上一点,直线PF 与抛物线交于M ,N 两点,若PF uu u r =3MF uuu r,则|MN |=A .163 B .83C .2D .8311.已知三棱锥P —ABC 内接于球O ,PA ⊥平面ABC ,△ABC 为等边三角形,且边长为3,球O 的表面积为16π,则直线PC 与平面PAB 所成的角的正弦值为 A .157 B .155 C .152 D .151012.f (x )=221(1)1x x x x ⎧⎪⎨⎪⎩+,<1,log -,>,g (x )=54x 3-154x 2+m +2,若y =f (g (x ))-m 有9个零点,则m 的取值范围是A .(0,1)B .(0,3)C .(1,53) D .(53,3) 二、填空题:本大题共4小题,每小题5分,共20分. 13.曲线y =x x e -2x 2+1在点(0,1)处的切线方程为________.14.若n S 是等差数列{n a }的前n 项和,若a 1≠0,a 2=3a 1,则105S S =_______. 15.已知双曲线C :22221x y a b-=(a >0,b >0)的右顶点为A ,以A 为圆心,b 为半径做圆,圆A 与双曲线C 的一条渐近线相交于M ,N 两点,若OM uuu r =32ON uuu r(O 为坐标原点),则双曲线C 的离心率为________.16.已知数列{n a }满足:对任意n ∈N *均有1n a +=p n a +2p -2(p 为常数,p ≠0且p ≠1),若a 2,a 3,a 4,a 5∈{-18,-6,-2,6,11,30},则a 1的所有可能取值的集合是_________. 三、解答题:共70分.解答应写出文宇说明、证明过程或演算步骤.第17~21题为必考题.每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答. (一)必考题:共60分 17.(12分)已知△ABC 外接圆半径为R ,其内角A ,B ,C 的对边长分别为a ,b ,c ,设2R (sin 2A -sin 2B )=(a -c )sinC . (Ⅰ)求角B ;(Ⅱ)若b =12,c =8,求sinA 的值. 18.(12分)已知三棱锥M —ABC 中,MA =MB =MC =AC =,AB =BC =2,O 为AC 的中点,点N 在棱BC 上,且BN uuu r =23BC uu u r.(Ⅰ)证明:BO ⊥平面AMC ;(Ⅱ)求二面角N —AM —C 的正弦值. 19.(12分)已知椭圆E :22221y x a b+=(a >b >0)的离心率为2,且过点C (1,0).(Ⅰ)求椭圆E 的方程; (Ⅱ)若过点(-13,0)的任意直线与椭圆E 相交于A ,B 两点,线段AB 的中点为M ,求证:恒有|AB |=2|CM |.20.(12分)水污染现状与工业废水排放密切相关,某工厂深入贯彻科学发展观,努力提高污水收集处理水平,其污水处理程序如下:原始污水必先经过A 系统处理,处理后的污水(A 级水)达到环保标准(简称达标)的概率为p (0<p <1).经化验检测,若确认达标便可直接排放;若不达标则必须进行B 系统处理后直接排放.某厂现有4个标准水量的A 级水池,分别取样、检测.多个污水样本检测时,既可以逐个化验,也可以将若干个样本混合在一起化验.混合样本中只要有样本不达标,则混合样本的化验结果必不达标.若混合样本不达标,则该组中各个样本必须再逐个化验;若混合样本达标,则原水池的污水直接排放. 现有以下四种方案: 方案一:逐个化验;方案二:平均分成两组化验;方案三:三个样本混在一起化验,剩下的一个单独化验; 方案四:四个样本混在一起化验.化验次数的期望值越小,则方案越“优”. (Ⅰ)若p=3,求2个A 级水样本混合化验结果不达标的概率; (Ⅱ)(ⅰ)若p=3,现有4个A 级水样本需要化验,请问:方案一、二、四中哪个最“优”?(ⅱ)若“方案三”比“方案四”更“优”,求p 的取值范围. 21.(12分)已知函数f (x )=x -lnx -xe x.(Ⅰ)求f (x )的最大值; (Ⅱ)若f (x )+(x +1x)x e -bx ≥1恒成立,求实数b 的取值范围.(二)选考题:共10分.请考生在第22、23题中任选一题做答.如果多做.则按所做的第一题记分.22.[选修4—4:坐标系与参数方程](10分)在平面直角坐标系xOy 中,已知曲线E 经过点P (1,32),其参数方程为cos x a y αα⎧⎪⎨⎪⎩=,,(α为参数),以原点O 为极点,x 轴的正半轴为极轴建立极坐标系.(Ⅰ)求曲线E 的极坐标方程;(Ⅱ)若直线l 交E 于点A ,B ,且OA ⊥OB ,求证:21OA+21OB为定值,并求出这个定值.23.[选修4—5不等式选讲](10分)已知函数f(x)=|x-1|-|2x+1|+m.(Ⅰ)求不等式f(x)≥m的解集;(Ⅱ)若恰好存在4个不同的整数n,使得f(n)≥0,求m的取值范围.NOACM数学(理科) 参考答案一、选择题1-12 BDACB CBCDB DA 二、填空题13. 10;x y -+= 14.4; 15.;53016.{}.66,2,0-- 三、解答题17.解析:(I )222(sin sin )()sin .R A B a c C -=-∴2222(sin sin )()sin 2,R R A B a c C R ⋅-=-⋅即:222.ac b ac +-=……3分∴2221cos .22a cb B ac +-== 因为0,B π<<所以3B π∠=……6分(II )若12,8b c ==,由正弦定理,sin sin b cB C =,3sin C =, 由b c >,故C ∠为锐角,6cos .C =……9分 3613323sin sin()sin().32A B C C π+=+=+=⋅+⋅=……12分18. 解析:(I )如图所示:连接OM , 在ABC ∆中:2,22AB BC AC ===,则90,2ABC BO ∠=︒=,OB AC ⊥.……2分在MAC ∆中:22MA MC AC ===,O 为AC 的中点,则OM AC ⊥,且 6.OM = ……4分在MOB ∆中:2,6,22BO OM MB ===,满足:222BO OM MB +=根据勾股定理逆定理得到OB OM ⊥,AC OM 相交于O , 故OB ⊥平面AMC ………………….6分(Ⅱ)因为,,OB OC OM 两两垂直,建立空间直角坐标系如图所示.因为MA MB MC AC ====2AB BC ==则(0,A B C M ……8分由23BN BC =u u u r u u u r所以,N设平面MAN 的法向量为(,,)m x y z =u r,则(,,)0,3333(,,)0AN n x y z x y AM n x y z ⎧⋅=⋅=+=⎪⎨⎪⋅=⋅=+=⎩u u u r r uu u u r r令y =(1)m =--u r……10分因为BO ⊥平面AMC,所以OB =uuu r为平面AMC 的法向量,所以(1)m =--u r与OB =uuu r所成角的余弦为cos ,m OB <>==u r u u u u r .所以二面角的正弦值为2|sin ,|m OB <>===u r u u u u r .……12分 19.(I )由题意知1b =,2c a =.……1分 又因为222a b c =+解得,a =分所以椭圆方程为2212y x +=. ……4分 (Ⅱ) 设过点1(,0)3-直线为13x ty =-,设()11,A x y ,()22,B x y 由221312x ty x y ⎧=-⎪⎪⎨⎪+=⎪⎩得()2291812160t ty y +--=,且>0∆. 则12212212,918616,918y y y t y t t ⎧+=⎪⎪+⋯⋯⎨⎪=-⎪+⎩分又因为()111,CA x y =-u u u r ,()221,CB x y =-u u u r,()()212121212121244416(1)(1)13339CA CB x x y y ty ty y y t y y t y y ⎛⎫⎛⎫⋅=--+=--+=+-++⎪⎪⎝⎭⎝⎭u u u r u u u r ()22216412161091839189t t t t t -=+-⋅+=++,……10分所以CA CB ⊥u u u ru u u r.因为线段AB 的中点为M ,所以||2||AB CM =.……12分 20. 解析:(I)该混合样本达标的概率是28(39=,……2分 所以根据对立事件原理,不达标的概率为81199-=.……4分 (II )(i )方案一:逐个检测,检测次数为4.方案二:由(1)知,每组两个样本检测时,若达标则检测次数为1,概率为89;若不达标则检测次数为3,概率为19.故方案二的检测次数记为ξ2,ξ2的可能取值为2,4,6. 其分布列如下,可求得方案二的期望为26416119822()246818181819E ξ=⨯+⨯+⨯== 方案四:混在一起检测,记检测次数为ξ4,ξ4可取1,5. 其分布列如下,可求得方案四的期望为46417149()15818181E ξ=⨯+⨯=. 比较可得42()()4E E ξξ<<,故选择方案四最“优”.……9分 (ii )方案三:设化验次数为3η,3η可取2,5.3333()25(1)53E p p p η=+-=-;方案四:设化验次数为4η,4η可取1,54444()5(1)54E p p p η=+-=-;由题意得34343()()53544E E p p p ηη<⇔-<-⇔<. 故当304p <<时,方案三比方案四更“优”.……12分 21解析:(I )()ln xe f x x x x=--,定义域(0,)+∞,221(1)(1)()()1x x e x x x e f x x x x ---'=--=, 由1x e x x ≥+>,()f x 在(0,1]增,在(1,)+∞减,max ()(1)1f x f e ==-……4分 (II )1()()e 1xf x x bx x++-≥ e e ln e 1x x xx x x bx x x⇔-+-++-≥ln e 10x x x x bx ⇔-++--≥e ln 1x x x xb x --+⇔≥min e ln 1(),x x x x b x --+⇔≥……6分令e ln 1()x x x x x x ϕ--+=,2ln ()x x e xx xϕ+'=令2()ln x h x x e x =+,()h x 在(0,)+∞单调递增,0,()x h x →→-∞,(1)0h e =>()h x 在(0,1)存在零点0x ,即02000()ln 0xh x x e x =+=001ln 2000000ln 1ln 0(ln )()x x x x x e x x e e x x +=⇔=-=……9分由于x y xe =在(0,)+∞单调递增,故0001lnln ,x x x ==-即001x e x =- 11 -()x ϕ在0(0,)x 减,在0(,)x +∞增,000000min 00e ln 111()2x x x x x x x x x ϕ--++-+=== 所以2b ≤.……12分22.解析:(I )将点3(1,)2P 代入曲线E 的方程,得1cos ,3,2a αα=⎧⎪⎨=⎪⎩解得24a =,……2分所以曲线E 的普通方程为22143x y +=, 极坐标方程为22211(cos sin )143ρθθ+=.……5分(Ⅱ)不妨设点,A B 的极坐标分别为1212()()00,2A B πρθρθρρ+>>,,,,, 则22221122222211(cos sin )1,4311(cos ()sin ()1,4232ρθρθππρθρθ⎧+=⎪⎪⎨⎪+++=⎪⎩ 即22212222111cos sin ,43111sin cos ,43θθρθθρ⎧=+⎪⎪⎨⎪=+⎪⎩……8分2212111174312ρρ+=+=,即22117||||12OA OB +=……10分23. 解:(I )由()f x m ≥,得,不等式两边同时平方,得221)(21)x x ≥(-+,……3分 即3(2)0x x +≤,解得20x -≤≤.所以不等式()f x m ≥的解集为{|20}x x -≤≤.……5分(Ⅱ)设g (x )=|x -1|-|2x +1|,12,,21()3,1,22,1,x x g x x x x x ⎧+≤-⎪⎪⎪=--<≤⎨⎪-->⎪⎪⎩- 12 -……8分()0()f n g n m ≥⇔≥-因为(2)(0)0g g -==,(3)1,(4)2,(1) 3.g g g -=--=-=- 又恰好存在4个不同的整数n ,使得()0f n ≥,所以2 1.m -<-≤-故m 的取值范围为[1,2). ……10分。
河南省新乡市2019-2020学年高考数学一模试卷含解析

河南省新乡市2019-2020学年高考数学一模试卷一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.若a >b >0,0<c <1,则A .log a c <log b cB .log c a <log c bC .a c <b cD .c a >c b【答案】B【解析】 试题分析:对于选项A ,a b 1gc 1gc log c ,log c lg a lg b==,01c <<Q ,10gc ∴<,而0a b >>,所以lg lg a b >,但不能确定lg lg a b 、的正负,所以它们的大小不能确定;对于选项B ,c lg lg log ,log lg lg c a b a b c c ==,lg lg a b >,两边同乘以一个负数1lg c改变不等号方向,所以选项B 正确;对于选项C ,利用c y x =在第一象限内是增函数即可得到c c a b >,所以C 错误;对于选项D ,利用x y c =在R 上为减函数易得a b c c <,所以D 错误.所以本题选B.【考点】指数函数与对数函数的性质【名师点睛】比较幂或对数值的大小,若幂的底数相同或对数的底数相同,通常利用指数函数或对数函数的单调性进行比较;若底数不同,可考虑利用中间量进行比较.2.已知角a 的终边经过点()()4,30P m m m -≠,则2sin cos a a +的值是( )A .1或1-B .25或25-C .1或25-D .1-或25 【答案】B【解析】【分析】根据三角函数的定义求得sin ,cos a a 后可得结论.【详解】由题意得点P 与原点间的距离5r m ==.①当0m >时,5r m =, ∴3344sin ,cos 5555m m a a m m -====-, ∴3422sin cos 2555a a +=⨯-=. ②当0m <时,5r m =-,∴3344sin ,cos 5555m m a a m m -==-==--,∴3422sin cos 2555a a ⎛⎫+=⨯-+=- ⎪⎝⎭. 综上可得2sin cos a a +的值是25或25-. 故选B .【点睛】 利用三角函数的定义求一个角的三角函数值时需确定三个量:角的终边上任意一个异于原点的点的横坐标x ,纵坐标y ,该点到原点的距离r ,然后再根据三角函数的定义求解即可.3.函数()4sin (0)3f x x πωω⎛⎫=+> ⎪⎝⎭的最小正周期是3π,则其图象向左平移6π个单位长度后得到的函数的一条对称轴是( )A .4x π= B .3x π= C .56x π= D .1912x π= 【答案】D【解析】【分析】 由三角函数的周期可得23πω=,由函数图像的变换可得, 平移后得到函数解析式为244sin 39y x π⎛⎫=+ ⎪⎝⎭,再求其对称轴方程即可. 【详解】 解:函数()4sin (0)3f x x πωω⎛⎫=+> ⎪⎝⎭的最小正周期是3π,则函数2()4sin 33f x x π⎛⎫=+ ⎪⎝⎭,经过平移后得到函数解析式为2244sin 4sin 36339y x x πππ⎡⎤⎛⎫⎛⎫=++=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,由24()392x k k πππ+=+∈Z , 得3()212x k k ππ=+∈Z ,当1k =时,1912x π=. 故选D.【点睛】本题考查了正弦函数图像的性质及函数图像的平移变换,属基础题.4.对于定义在R 上的函数()y f x =,若下列说法中有且仅有一个是错误的,则错误..的一个是( ) A .()f x 在(],0-∞上是减函数B .()f x 在()0,∞+上是增函数C .()f x 不是函数的最小值D .对于x ∈R ,都有()()11f x f x +=-【答案】B【解析】【分析】根据函数对称性和单调性的关系,进行判断即可.【详解】由(1)(1)f x f x +=-得()f x 关于1x =对称,若关于1x =对称,则函数()f x 在(0,)+∞上不可能是单调的,故错误的可能是B 或者是D ,若D 错误,则()f x 在(-∞,0]上是减函数,在()f x 在(0,)+∞上是增函数,则(0)f 为函数的最小值,与C 矛盾,此时C 也错误,不满足条件.故错误的是B ,故选:B .【点睛】本题主要考查函数性质的综合应用,结合对称性和单调性的关系是解决本题的关键.5.已知向量(1,4)a =r ,(2,)b m =-r ,若||||a b a b +=-r r r r ,则m =( )A .12-B .12C .-8D .8【答案】B【解析】【分析】先求出向量a b +r r ,a b -r r 的坐标,然后由||||a b a b +=-r r r r 可求出参数m 的值.【详解】由向量(1,4)a =r ,(2,)b m =-r,则()1,4a b m +=-+r r ,()3,4a b m -=-r r||a b +r r ||a b -=r r又||||a b a b +=-r r r r 12m =. 故选:B【点睛】本题考查向量的坐标运算和模长的运算,属于基础题.6.已知全集U =R ,集合{}{}237,7100A x x B x x x =≤<=-+<,则()U A B ⋂ð=( )A .()(),35,-∞+∞UB .(](),35,-∞+∞UC .(][),35,-∞+∞UD .()[),35,-∞+∞U【答案】D【解析】【分析】 先计算集合B ,再计算A B I ,最后计算()U A B ⋂ð.【详解】 解:{}27100B x x x =-+<Q{|25}B x x ∴=<<, {}37A x x =≤<Q{|35}A B x x ∴=<I „,()[)U ,35(,)A B -∞+∞∴=U I ð.故选:D .【点睛】本题主要考查了集合的交,补混合运算,注意分清集合间的关系,属于基础题.7.已知实数x 、y 满足不等式组2102100x y x y y -+≥⎧⎪--≤⎨⎪≥⎩,则3z x y =-+的最大值为( )A .3B .2C .32-D .2-【答案】A【解析】【分析】画出不等式组所表示的平面区域,结合图形确定目标函数的最优解,代入即可求解,得到答案.【详解】 画出不等式组2102100x y x y y -+≥⎧⎪--≤⎨⎪≥⎩所表示平面区域,如图所示,由目标函数3z x y =-+,化为直线3y x z =+,当直线3y x z =+过点A 时,此时直线3y x z =+在y 轴上的截距最大,目标函数取得最大值,又由2100x y y -+=⎧⎨=⎩,解得(1,0)A -,所以目标函数的最大值为3(1)03z =-⨯-+=,故选A .【点睛】本题主要考查简单线性规划求解目标函数的最值问题.其中解答中正确画出不等式组表示的可行域,利用“一画、二移、三求”,确定目标函数的最优解是解答的关键,着重考查了数形结合思想,及推理与计算能力,属于基础题.8.在平面直角坐标系xOy 中,已知点()0,2A -,()1,0N ,若动点M 满足2MA MO =,则·OM ON u u u u r u u u r 的取值范围是( )A .[]0,2B .0,22⎡⎣C .[]22-,D .22,22-⎡⎣ 【答案】D【解析】【分析】设出M 的坐标为(,)x y ,依据题目条件,求出点M 的轨迹方程22(2)8x y +-=,写出点M 的参数方程,则·22os OM ON θ=u u u u r u u u r ,根据余弦函数自身的范围,可求得·OM ON u u u u r u u u r 结果. 【详解】设(,)M x y ,则 ∵2MA MO =,()0,2A - 2222(2)2x y x y ++=+∴2222(2)2()x y x y ++=+∴22(2)8x y +-=为点M 的轨迹方程∴点M的参数方程为2x y θθ⎧=⎪⎨=+⎪⎩(θ为参数)则由向量的坐标表达式有:·os OM ON θ=u u u u r u u u r又∵cos [1,1]θ∈-∴·[OM ON θ=∈-u u u u r u u u r故选:D【点睛】考查学生依据条件求解各种轨迹方程的能力,熟练掌握代数式转换,能够利用三角换元的思想处理轨迹中的向量乘积,属于中档题.求解轨迹方程的方法有:①直接法;②定义法;③相关点法;④参数法;⑤待定系数法9.已知集合A ={﹣2,﹣1,0,1,2},B ={x|x 2﹣4x ﹣5<0},则A∩B =( )A .{﹣2,﹣1,0}B .{﹣1,0,1,2}C .{﹣1,0,1}D .{0,1,2}【答案】D【解析】【分析】解一元二次不等式化简集合B ,再由集合的交集运算可得选项.【详解】因为集合{2,1,0,1,2},{|(5)(1)0}{|15}A B x x x x x =--=-+<=-<< {}{}{}2,1,0,1,2|150,1,2A B x x ∴⋂=--⋂-<<=,故选:D.【点睛】本题考查集合的交集运算,属于基础题.10.要排出高三某班一天中,语文、数学、英语各2节,自习课1节的功课表,其中上午5节,下午2节,若要求2节语文课必须相邻且2节数学课也必须相邻(注意:上午第五节和下午第一节不算相邻),则不同的排法种数是( )A .84B .54C .42D .18【答案】C【解析】【分析】根据题意,分两种情况进行讨论:①语文和数学都安排在上午;②语文和数学一个安排在上午,一个安排在下午.分别求出每一种情况的安排方法数目,由分类加法计数原理可得答案.【详解】根据题意,分两种情况进行讨论:①语文和数学都安排在上午,要求2节语文课必须相邻且2节数学课也必须相邻,将2节语文课和2节数学课分别捆绑,然后在剩余3节课中选1节到上午,由于2节英语课不加以区分,此时,排法种数为1233232218C A A A =种; ②语文和数学都一个安排在上午,一个安排在下午.语文和数学一个安排在上午,一个安排在下午,但2节语文课不加以区分,2节数学课不加以区分,2节英语课也不加以区分,此时,排法种数为14242224C A A =种. 综上所述,共有182442+=种不同的排法.故选:C .【点睛】本题考查排列、组合的应用,涉及分类计数原理的应用,属于中等题.11.如图是某地区2000年至2016年环境基础设施投资额y (单位:亿元)的折线图.则下列结论中表述不正确...的是( )A .从2000年至2016年,该地区环境基础设施投资额逐年增加;B .2011年该地区环境基础设施的投资额比2000年至2004年的投资总额还多;C .2012年该地区基础设施的投资额比2004年的投资额翻了两番 ;D .为了预测该地区2019年的环境基础设施投资额,根据2010年至2016年的数据(时间变量t 的值依次为127,,…,)建立了投资额y 与时间变量t 的线性回归模型ˆ9917.5y t =+,根据该模型预测该地区2019的环境基础设施投资额为256.5亿元.【答案】D【解析】【分析】根据图像所给的数据,对四个选项逐一进行分析排除,由此得到表述不正确的选项.【详解】对于A 选项,由图像可知,投资额逐年增加是正确的.对于B 选项,20002004-投资总额为1119253537127++++=亿元,小于2012年的148亿元,故描述正确.2004年的投资额为37亿,翻两翻得到374148⨯=,故描述正确.对于D 选项,令10t =代入回归直线方程得9917.510274+⨯=亿元,故D 选项描述不正确.所以本题选D.【点睛】本小题主要考查图表分析能力,考查利用回归直线方程进行预测的方法,属于基础题.12.为研究语文成绩和英语成绩之间是否具有线性相关关系,统计两科成绩得到如图所示的散点图(两坐标轴单位长度相同),用回归直线y bx a =+$$$近似地刻画其相关关系,根据图形,以下结论最有可能成立的是( )A .线性相关关系较强,b 的值为1.25B .线性相关关系较强,b 的值为0.83C .线性相关关系较强,b 的值为-0.87D .线性相关关系太弱,无研究价值【答案】B【解析】【分析】根据散点图呈现的特点可以看出,二者具有相关关系,且斜率小于1.【详解】散点图里变量的对应点分布在一条直线附近,且比较密集,故可判断语文成绩和英语成绩之间具有较强的线性相关关系,且直线斜率小于1,故选B.【点睛】本题主要考查散点图的理解,侧重考查读图识图能力和逻辑推理的核心素养.二、填空题:本题共4小题,每小题5分,共20分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
新乡市2020届高三第一次模拟测试数学(理科)第Ⅰ卷一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{|24}xA x =>,{|015}B x x =<-≤,则()=RC A B I ( ) A .{|25}x x <≤ B .{|5}x x ≤ C .{|12}x x <≤D .{|1}x x > 2.若复数z 满足(2)1811z i i -=+,则z 的实部为( ) A .-5 B . 5 C .-8 D .83.为了参加冬季运动会的5000m 长跑比赛,某同学给自己制定了7天的训练计划:第1天跑5000m ,以后每天比前1天多跑200m ,则这个同学7天一共将跑( )A .39200mB .39300mC .39400mD . 39500m 4.若二项式71()nx x -的展开式存在常数项,则正整数n 的最小值为( ) A . 7 B .8 C. 14 D .16 5.设函数()5xx f x ee x -=--,则不等式2()(6)0f x f x +--<的解集为( )A .(3,2)-B .(,3)(2,)-∞-+∞U C. (2,3)- D .(,2)(3,)-∞-+∞U6.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的表面积为( )A . 28B .30 C. 36 D .427.设不等式组40310x x y y -≤⎧⎪+≥⎨⎪-≥⎩,表示的可行域M 与区域N 关于y 轴对称,若点(,)P x y N ∈,则2z x y =+的最小值为( )A . -9B .9 C. -7 D .78.《镜花缘》是清代文人李汝珍创作的长篇小说,书中有这样一个情节:一座阁楼到处挂满了五彩缤纷的大小灯球,灯球有两种,一种是大灯下缀2个小灯,另一种是大灯下缀4个小灯,大灯共360个,小灯共1200个.若在这座楼阁的灯球中,随机选取两个灯球,则至少有一个灯球是大灯下缀4个小灯的概率为( ) A .1191077 B .160359 C. 9581077 D .2893599.已知点(,)M x y 是抛物线24y x =( )A .3B . 4 C. 5 D .6 10.将函数44()sin cos f x x x =+的图像向左平移8π个单位长度后,得到()g x 的图像,则()g x =( )A .31sin 444x - B .13sin 444x - C. 31cos 444x - D .13cos 244x - 11.设2log 3a =,3log 4b =,5log 8c =,则( )A .a b c >>B .a c b >> C. c a b >> D .c b a >>12.已知函数1,0()3,0x e x f x x ax x -⎧>⎪=⎨⎪+≤⎩,若函数()(())2g x f f x =-恰有5个零点,且最小的零点小于-4,则a 的取值范围是( )A .(,1)-∞-B .(0,)+∞ C. (0,1) D .(1,)+∞第Ⅱ卷二、填空题(每题5分,满分20分,将答案填在答题纸上)13.若向量,a b r r 满足||3a =r ,且()()4a b a b +-=r r r r g,则||b =r.14.设P 为曲线224x y =+上一点,(5,0)A -,(5,0)B ,若||2PB =,则||PA = . 15.设n S 是数列{}n a 的前n 项和,且11a =,1(1)(1)n n n a n S ++=-,则n S = .16.已知,A B 两点都在以PC 为直径的球O 的表面上,AB BC ⊥,2AB =,4BC =,若球O 的体积为86π,则异面直线PB 与AC 所成角的正切值为 .三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17. ABC ∆的内角,,A B C 的对边分别为,,a b c ,已知4sin ()(sin sin )c C b a B A =+-.(1)试问:,,a b c 是否可能依次成等差数列?为什么?(2)若3b c =,且ABC ∆的周长为45+,求ABC ∆的面积.18. 如图,在三棱锥P ABC -中,PA ⊥底面ABC ,3AB AC ==,2CE EA =u u u r u u u r ,BD DC =u u u r u u u r.(1)证明:平面PBC ⊥平面PAD ; (2)若三棱锥P ABD -的体积为94,且AB AC ⊥,求平面PAB 与平面PDE 所成锐二面角的余弦值.19. 某面包推出一款新面包,每个面包的成本价为4元,售价为10元,该款面包当天只出一炉(一炉至少15个,至多30个),当天如果没有售完,剩余的面包以每个2元的价格处理掉,为了确定这一炉面包的个数,该店记录了这款新面包最近30天的日需求量(单位:个),整理得下表:(1)根据表中数据可知,频数y 与日需求量x (单位:个)线性相关,求y 关于x 的线性回归方程;(2)以30天记录的各日需求量的频率代替各日需求量的概率,若该店这款新面包出炉的个数为24,记当日这款新面包获得的总利润为X (单位:元).(ⅰ)若日需求量为15个,求X ;(ⅱ)求X 的分布列及其数学期望.相关公式:∑∑==---=n ii ni iix x y yx x b 121^)())((∑∑==--=n i i ni ii xn x yx n yx 1221 , x by a ^^-= 20. 已知椭圆2222:1(0)x y C a b a b+=>>的左、右焦点分别为21,F F ,12||2F F =,过点1F 的直线与椭圆C 交于,A B 两点,延长2BF 交椭圆C 于点M ,2ABF ∆的周长为8.(1)求C 的离心率及方程;(2)试问:是否存在定点0(,0)P x ,使得PM PB u u u u r u u u rg 为定值?若存在,求0x ;若不存在,请说明理由.21. 已知函数()ln (0)af x x a x a a =--≠. (1)讨论()f x 的单调性;(2)对0a >时,对任意121,[,]x x e e∈,12|()()|2f x f x e -≤-恒成立,求a 的取值范围.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.22.选修4-4:坐标系与参数方程在直角坐标系xOy 中,直线l的参数方程为1222x y ⎧=--⎪⎪⎨⎪=+⎪⎩(t 为参数),以坐标原点O 为极点,以x 轴正半轴为极轴,建立极坐标系,已知曲线C 的极坐标方程为2cos sin ρθθ=. (1)求直线l 的普通方程及曲线C 的直角坐标方程;(2)若直线l 与曲线C 交于,A B 两点,(1,2)P -,求||||PA PB g . 23.选修4-5:不等式选讲已知函数()|1||2|f x x x =-++.(1)求不等式()13f x <的解集;(2)若()f x 的最小值为k ,且211(0)k mn m n+=>,证明:16m n +≥. 试卷答案一、选择题1-5: CBABD 6-10: DCCAA 11、12:BC1.C ∵{|2}A x x =>,∴{|2}R C A x x =≤,又{|16}B x x =<≤,∴(){|12}R C A B x x =<≤I .2.B 因为1811582iz i i+==+-,所以z 的实部为5. 3.A 依题意可知,这个同学第1天,第2天,…,跑的路程依次成首项为5000,公差为200的等差数列,则这个同学7天一共将跑7650007200392002m ⨯⨯+⨯=. 4.B 71()n x x -的展开式的通项为8171()(1)r n r r r r n rr n n T C x C x x--+=-=-(0,1,,)r n =L ,令80n r -=,得8n r =,则整正数n 的最小值为8.5.D ∵()f x 是奇函数,∴2()(6)0f x f x +--<2()(6)(6)f x f x f x ⇔<---=+.又()f x 是减函数,∴22()(6)6f x f x x x <+⇔>+,故不等式2()(6)0f x f x +--<的解集为(,2)(3,)-∞-+∞U .6.D 该几何体是由12个棱长为1的正方体组合而成的,所以121224S =+=前后,336S =+=左右,6612S =+=上下,从而2461242S =++=表面.7.C 作出区域N (阴影部分),由图可知,当直线2z x y =+经过点(4,1)-时,z 取得最小值-7.8.C 设一大二小与一大四小的灯球数分别为,x y ,则360241200x y x y +=⎧⎨+=⎩,解得120240x y =⎧⎨=⎩,若随机选取两个灯球,则至少有一个灯球是一大四小的概率为2120236095811077C C -=.9.A 22(1)x y -+(,)M x y 到点(1,0)F 的距离,即点(,)M x y 到抛物线24y x =的准线1x =-22(2)(1)x y -+-(,)M x y 到点(2,1)A 的距离,所以2222(2)(1)(1)x y x y -+--+(2,1)A 到抛物线24y x =的准线1x =-的距离3,即2222min ((2)(1)(1)3x y x y -+--+=.10.A ∵22222()(sin cos )2sin cos f x x x x x =+-1cos 21cos 21222x x -+=-⨯⨯31cos 444x =+, ∴3131()()cos(4)sin 4844244g x f x x x ππ=+=++=-.11.B ∵327lg 64log 4log 64lg 27==,525lg 64log 8log 64lg 25==,∴35log 4log 8<, ∵2385<,∴3285<,∴32553log 8log 52<=. 又2443log 3log 9log 82=>=,∴253log 3log 8log 4>>,即a c b >>. 12.C 当0x >时,1()x e f x x -=,12(1)'()x e x f x x--=, 当01x <<时,'()0f x <,()f x 单调递减; 当1x >时,'()0f x >,()f x 单调递增,故min ()(1)1f x f ==.当0x ≤时,()3f x ax =+的图像恒过点(0,3),当0,0a x ≤≤时,()(0)3f x f ≥=;当0,0a x >≤时,()(0)3f x f ≤=.()(())2g x f f x =-有5个零点,即方程(())2f f x =有5个解,设()t f x =,则()2f t =. 结合图像可知,当0a >时,方程()2f t =有三个根1(,0)t ∈-∞,2(0,1)t ∈,3(1,3)t ∈(∵2(3)23e f =>,∴313t <<),于是1()f x t =有1个解,2()f x t =有1个解,3()f x t =有3个解,共有5个解.由32ax +=,得1x a =-,再由13ax a +=-,得2314x a a =--<-,∵0a >,∴01a <<.而当0a ≤时,结合图像可知,方程(())2f f x =不可能有5个解.二、填空题 13.5∵ 222()()9||4a b a b a b b +-=-=-=r r r r r r r g ,∴||5b =r14. 4由224x y =+得2244(0)x y x =+>,即221(0)4y x x -=>,故P 为双曲线221(0)4y x x -=>右 支上一点,且,A B 分别为该双曲线的左、右焦点,则||||22PA PB a -==,||224PA =+=.15. 12n n-∵1(1)(1)n n n a n S ++=-,∴11n n n na S nS +++=,∴11()n n n n n S S S nS ++-+=,∴1(1)2n nn S nS ++=,∴{}n nS 是首项为1,公比为2的等比数列,则12n n nS -=,∴12n n S n-=.16.3∵AB BC ⊥,∴ABC ∆的外心'O 为AC 的中点,∴'OO ⊥平面ABC ,易证//'PA OO ,∴PA ⊥平面ABC ,从而球O 的半径R OA =,又34863R ππ=,∴6R =,∵222425AC =+=,∴'5AO =,'1OO =,∴2PA AB ==.设PB 与AC 所成角为θ,则10cos cos cos 10225PBA BAC θ=∠∠=⨯=g . 故tan 3θ=.三、解答题17.解:(1)∵4sin ()(sin sin )c C b a B A =+-, ∴2224sin sin sin C B A =-, ∴2224c b a =-.假设,,a b c 依次成等差数列,则2a cb +=, 则2224()2a c c a ++=,即221532c a ac +=, 又22153652c a ac ac +≥>, ∴221532c a ac +≠,从而假设不成立,故,,a b c 不可能依次成等差数列. (2)∵2224c b a =-,3b c =,∴225a c =,则5a c =, 则(45)45a b c c ++=+=+,即1c =.从而223155 cos2136 A+-==⨯⨯,则11sin6A=.故ABC∆的面积111sin24S bc A==.18.(1)证明:因为AB AC=,BD DC=u u u r u u u r,所以AD BC⊥,又PA⊥平面ABC,则PA BC⊥,因为AD PA A=I,所以BC⊥平面PAD.又BC⊂平面PBC,所以平面PBC⊥平面PAD.(2)因为1119333224P ABDV PA-=⨯⨯⨯⨯⨯=,所以3PA=.以A为坐标原点,建立如图所示的空间直角坐标系A xyz-,则(0,0,0)A,(3,0,0)B,(0,3,0)C,(0,1,0)E,33(,,0)22D,(0,0,3)P,L 则31(,,0)22ED=u u u r,(0,1,3)PE=-u u u r.设平面PDE的法向量为(,,)n x y z=r,则n EDn PE⎧=⎪⎨=⎪⎩r u u u rgr u u u rg,即312230x yy z⎧+=⎪⎨⎪-=⎩,令1z=,得(1,3,1)n=-r,平面PAB的一个法向量为(0,1,0)m=u r,则311cos ,1111m n <>==u r r , 故平面PAB 与平面PDE 所成锐二面角的余弦值为31111. 19.(1)21x =,6y =,^2222(1521)(106)(1821)(86)(2421)(36)(2721)(26)630.7(1521)(1821)(2421)(2721)90b --+--+--+--==-=--+-+-+-, ^^6210.720.7a y b x =-=+⨯=,故y 关于x 的线性回归方程为^0.720.7y x =-+.(2)(ⅰ)若日需求量为15个,则15(104)(2415)(24)72X =⨯-+-⨯-=元 (ⅱ)若日需求量为18个,则18(104)(2418)(24)96X =⨯-+-⨯-=元 若日需求量为21个,则21(104)(2421)(24)120X =⨯-+-⨯-=元 若日需求量为24个或27个,则24(104)144X =⨯-=元 故分布列为1087530487296120144101.63030303030EX =⨯+⨯+⨯+⨯== 20.(1)由题意可知,12||=2c=2F F ,则1c =, 又2ABF ∆的周长为8,所以48a =,即2a =, 则12c e a ==, 2223b a c =-=.故C 的方程为22143x y +=. (2)假设存在点P ,使得PM PB u u u u r u u u rg 为定值.若直线BM 的斜率不存在,直线BM 的方程为1x =,3(1,)2B ,3(1,)2M -,则209(1)4PM PB x =--u u u u r u u u r g .若直线BM 的斜率存在,设BM 的方程为(1)y k x =-,设点11(,)B x y ,22(,)M x y ,联立22143(1)x y y k x ⎧+=⎪⎨⎪=-⎩,得2222(43)84120k x k x k +-+-=, 根据韦达定理可得:2122843k x x k +=+,212241243k x x k -=+,由于202(,)PM x x y =-u u u u r ,101(,)PB x x y =-u u u r,则212120012()PM PB x x x x x x y y •=-+++u u u u r u u u r 2222120120(1)()()k x x x k x x k x =+-++++2220002(485)31243x x k x k --+-=+因为PM PB u u u u r u u u r g 为定值,所以2200048531243x x x ---=, 解得0118x =,故存在点P ,且0118x =.21.解:(1)函数()f x 的定义域为(0,)+∞,1(1)()a a a a x f x ax x x --=-=,当0a <时,(0,1)x ∈,'()0f x <,所以()f x 在(0,1)上单调递减; (1,)x ∈+∞,'()0f x >,所以()f x 在(1,)+∞上单调递增. 当0a >时,(0,1)x ∈,'()0f x <,所以()f x 在(0,1)上单调递减; (1,)x ∈+∞,'()0f x >,所以()f x 在(1,)+∞上单调递增.(2)因为12max min |()()|()()f x f x f x f x -≤-,所以max min ()()2f x f x e -≤-, 由(1)知,()f x 在1[,1)e 上单调递减,在(1,]e 上单调递增,所以min ()(1)1f x f a ==-. 因为1()a f e e -=与()2a f e e a =-,所以max 1()max{(),()}f x f f e e =. 设1()()()2(0)a a g a f e f e e a a e -=-=-->,则'()220a a g a e e -=-->=,所以()g a 在(0,)+∞上单调递增,故()(0)0g a g >=,所以1()()f e f e >,从而max ()()2a f x f e e a ==-,所以2(1)2a e a a e ---≤-,即10a e a e --+≤. 设()1(0)a a e a e a ϕ=--+>,则'()1a a e ϕ=-, 当0a >时,'()0a ϕ>,所以()a ϕ在(0,)+∞上单调递增, 又(1)0ϕ=,所以10a e a e --+≤等价于()(1)a ϕϕ≤,则1a ≤. 因为0a >,所以a 的取值范围为(0,1].22.解:(1)直线l 的普通方程为:10x y +-=. 由2cos sin ρθθ=,得22cos sin ρθρθ=, 则2y x =,故曲线C 的直角坐标方程为2y x =.(2)将1222x ty t⎧=--⎪⎪⎨⎪=+⎪⎩代入2y x =,得220t -=,则122t t =-,故12||||||2PA PB t t ==g .23.(1)由()13f x <,得|1||2|13x x -++<, 则12113x x >⎧⎨+<⎩或21313x-≤≤⎧⎨<⎩或22113x x <-⎧⎨--<⎩,解得:76x -<<,故不等式()13f x <的解集为(7,6)-.(2)证明:因为()|1||2|f x x x =-++|1(2)|3x x ≥--+=, 所以3k =, 因为21191(0)k mn m n m n +=+=>,所以0,0m n >>,199()()(10)1016nmm n m n m n m n +=++=++≥+= 当且仅当9nmm n =,即4,12m n ==时取等号,故16m n +≥.。
