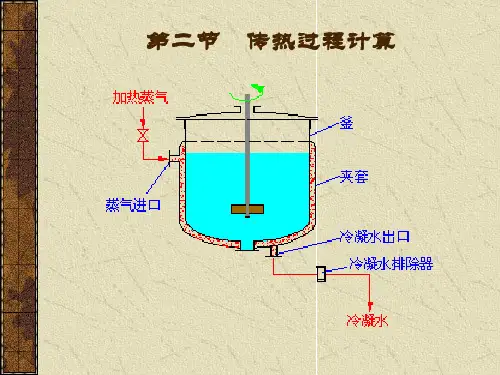
传热过程的计算
传热过程计算
7
二.总传热系数
T 冷 流 体
T Tw dQ1 i dSi (T Tw ) 1 i dSi
Q dQ2 dSm (Tw t w ) Tw t w b b dSm
15
4.4.3 总传热速率方程和平均温度差法 一.总传热速率方程
m1，t1
dQ KdS(T t )
Q
m2，T1 dS t2
T2
dQ Ktm dS
0 0
S
——总传热速率方程 传热计算的出发点和核心：
Q KStm
K—— 平均总传热系数 tm—— 平均温度差
Q KStm W1c p1 (T1 T2 ) W2c p 2 (t2 t1 )
①总传热系数Ko；
②管外对流传热系数αo增加一倍，总传热系 数有何变化？ ③管内对流传热系数αi增加一倍，总传热系 数有何变化？
13
①总传热系数Ko 解：
1 1 Ko 1 16 0.0015 16 1 1 do b do 1 40 14.5 90 i d i d m o 100013 1 80.8W/ m 2 C 0.00123 0.00004 0.01111
Tw 热 体
tw
对流
导热
t w－t dQ3 o dSo (t w－t ) t 1 o dSo 对流
对于稳定传热
dQ dQ1 dQ2 dQ3
T Tw Tw t w tw t T t dQ 1 b 1 1 b 1 8 i dSi dSm o dSo i dSi dSm o dSo
传热过程的计算
[
]
Q = KA∆tm = qm1c p1 (T1 −T2 ) = G2c p2 (t2 − t1 )
3.4.2 平均温度差的计算
一、恒温差传热
∆t m = T − t
二、变温差传热 分单侧变温和双侧变温， 与流体流向有关。 分单侧变温和双侧变温，∆tm还与流体流向有关。
逆流
并流
错流
折流
1. 逆、并流时的∆tm 并流时的∆
（1） α1不变 α2提高到 4W/(m2·K) ） 不变, 提高到10 （2） α2不变 α1提高到 ） 不变, 提高到80W/(m2·K) （3） α2不变 α1提高到 ） 不变, 提高到500W/(m2·K) 计算上面各种情况下的K值 计算上面各种情况下的 值？ 强化传热——应提高α小一侧流体的α 应提高 强化传热
Q = qm 1 r + cp1 (Ts − T2 ) = qm 2 cp2 (t 2 − t1 )
• 热负荷 由生产任务决定，对设备换热能力的要求 热负荷—由生产任务决定 由生产任务决定， • 传热速率 设备在一定操作条件下的换热能力 传热速率—设备在一定操作条件下的换热能力 传热过程计算的基础式： 传热过程计算的基础式：
3.4.4 壁温的计算
定态传热
Q = KA∆t m T − TW TW − t W t W − t = = = 1 b 1 α 1 A1 λ Am α 2 A2
t W = TW
bQ − λ Am
TW
Q =T − α 1 A1
tW
Q =t+ α 2 A2
（1）一般情况下 λ大，(b/λAm）小,可认为 tW≈TW ）一般情况下, 可认为
K (T − t )dA = −qm 1c p1dT = −qm 2 c p 2dt
传热过程计算公式
传热过程计算公式传热啊，就像是一场热的接力赛。
你知道传热过程计算公式吗？那可真是个神奇的东西。
想象一下，热量就像一群调皮的小恶魔，总是到处乱窜。
热传导就像是小恶魔们在固体里一个传一个地挤着走。
傅立叶定律这个计算公式呢，就像是给小恶魔们规定了行走路线的魔法规则。
如果把热量比作水流，那热传导就像是在细细的管道里慢慢流淌的涓涓细流，而这个公式就是控制水流速度和方向的阀门。
再说说对流传热吧。
这就好比是热小恶魔们搭上了风的便车或者水流的小船。
牛顿冷却定律这个计算公式，就像是给小恶魔们的乘车规则。
就像你在大风天里，热量从你身上被风快速带走，那速度就像小偷在夜色中溜走一样快。
对流传热里的热量传递速度，按照这个公式计算起来，有时候就像火箭发射一样迅速，一下子就把热从一个地方带到另一个地方。
辐射传热更是神奇，就像是热小恶魔们变身成了看不见的小超人，直接发射自己的热量能量。
斯蒂芬 - 玻尔兹曼定律这个计算公式，那就是小超人的超能力使用手册。
热辐射的热量传递，感觉就像是来自外太空的神秘力量，在黑暗中默默地传递着能量，而且速度之快，就像闪电在天空中划过一样让人惊叹。
要是把这三种传热方式放到一起，就像一场热的大杂烩派对。
计算总的传热过程的公式就像是派对的组织者，要把每个小恶魔在不同活动（热传导、对流传热、辐射传热）中的表现综合起来。
这个综合的公式看起来复杂，其实就是把热的小恶魔们在各种不同路径传递热量的情况都算个清楚明白。
有时候看着这些传热过程计算公式，就像在看一场魔术表演。
你以为热量的传递是无章可循的，但是这些公式就像魔术师的魔法棒，一挥之下，所有的奥秘都展现在眼前。
它们就像是打开热传递这个神秘大门的钥匙，让我们能够精确地知道热到底是怎么在不同的物体和环境中跑来跑去的。
要是没有这些公式，我们就像是在黑暗中摸索热传递的盲人。
有了它们，我们就能像超级侦探一样，追踪热量的每一个踪迹，不管它是偷偷摸摸地传导，还是大张旗鼓地辐射，都逃不过我们的计算大法。
2.2 传热过程计算
Δt
m
Δt 2 Δt ln Δt 2
1
Δt 1
第二节 传热过程计算
二、平均温度差 错流和折流
tm tm'
f (P, R)
R T1 T2 t2 t1
P t2 t1 T1 t1
பைடு நூலகம்
第二节 传热过程计算
三、传热计算的题型
(qmcp)hT
KS tm Q
(qmcp)ct qmhrh
1. 设计型
对于平壁或薄壁： 1 1 b 1 K αi λ αo
第二节 传热过程计算
一、总传热速率 Q KSt
对于平壁或薄壁： 1 1 b 1 K αi λ αo
二、平均温度差
Q KStm
tm： 平均温度差
第二节 传热过程计算
二、平均温度差 流体的流向
逆流
并流
错流
折流
第二节 传热过程计算
二、平均温度差 逆流和并流
Ｑ１＝Ｑ２＝Ｑ３ ＝．．． 一、传导传热
Q λ dt S dn 热通量（密度） 温度梯度 （Ｗ／ｍ２） （Ｋ／ｍ） 例：求平面壁定态热传导速率的表达式
Q λ t1 t2S
b
第一节 传热基本规律
二、对流传热 膜模型 湍流核心处温度一致 层流膜内符合热传导规律
牛顿冷却定律
S
Q t
,
t
Q St
第二节 传热过程计算
第二节 传热过程计算
第二节 传热过程计算
一、总传热速率 1b 1
R总 , T T t α iSi λ S m α oSo
Q t
Sot
R总 So bS o 1
α iSi λ Sm α o
令： 1 So bS o 1 K α iSi λ S m α o
传热过程的计算
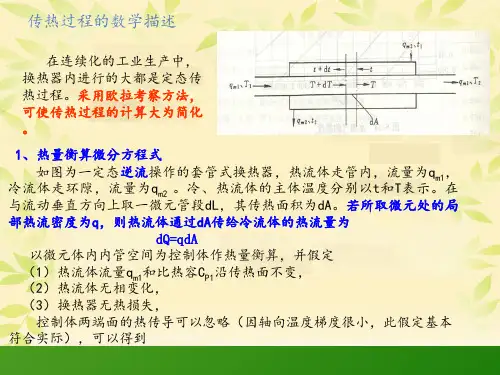
必须着力减少控制步骤的热阻，才更易以达到强化传热的目的。 。
实际计算换热管热流量，可依据管壁内表面积或外表面积写出两个方程 内表面： 外表面： Ql=KlA1 (T-t) Q2=K2A2 (T-t) (6-116)
式中，K1、K2分别为以内、外表面积为基准的传热系数，明显两者是不相等的。 但有 K1A1=K2A2 如圆管的内、外直径分别用d1、d2表示，结合式子： K 可导出： K 1
即
Q KAt m
称为传热过程基本方程式
式中
t m
T t 1 T t 2 T t 1 ln T t 2
称为对数平均温差或对数平均推动力。
对数平均推动力
对数平均推动力恒小于算术平均推动力，特别是当换热器两端推动力相差悬 殊时，对数平均值要比算术平均值小得多。 当换热器一端两流体温差接近于零时，对数平均推动力将急剧减小。 对数平均推动力这一特性，对换热器的操作有着深刻的影响。 例如，当换热器两端温差有一个为零时，对数平均温差必为零。 这意味着传递相应的热流量，需要无限大的传热面。 但是，当两端温差相差不大时，如0.5<(T-t)1/(T-t)2<2时，对数平均推动 力可用算术平均推动力代替。
qm1CP1dT=q1dA1=dQ （热流体在微元体内放出的热量） 同样，对冷流体作类似假定，并以微元体内环隙空 间为控制体作热量衡算，可得到 qm2CP2dt=q2dA2=dQ （冷流体在微元体内吸收的热量）
2、传热速率方程式 热流密度q是反映具体传热过程速率 大小的特征量。从理论上讲，根据前面 导热或对流给热规律，热流密度q已可以 计算。但是，这种做法必须引入壁面温 度；而在实际计算时，壁温往往是未知 的。为实用方便，希望能够避开壁温， 直接根据冷、热流体的温度进行传热速 率的计算。 如图所示的套管换热器中，热量序 贯地由热流体传给管壁内侧、再由管壁 内侧传至外侧，最后由管壁外侧传给冷 流体（参见 P201 图 6-35 ）。在定态条 件下，并忽略管壁内外表面积的差异， 则各环节的热流量相等，即
传热过程和换热器热计算基础
(m2·℃) / W
多层平壁的传热：
q=
n δi 1 1 +∑ + h1 i =1 λi h2
tf1－ tf2
二、圆筒壁的传热 每米长圆筒壁的总传热热阻热阻：
只有管道外径 d 2 超过某一值后包上热绝缘层才能 起到减少单位管长热损失的作用，把此直径称为临界 热绝缘直径，用 d c 表示。
d c 可由求 q1 对热绝缘层外径的一阶导数并令之 等于零而得到，即 d = 2λins c h2 （ d 2 > d c 加绝热层才能减少热损）
式中： 2 ——管道热绝缘层外表面对环境的表面传 h 热系数[W/(m2·K)]； λins ——保温材料的导热系数[W/(m·K)]。
' 肋面平均温度 t w2 (< tw2 )
肋片实际散热量：
h A (t
2
2
'
w2
− tf2
)
2
肋处于肋基温度下的理想散热量： h 肋片效率：
A2 (t w 2 − tf2 )
t w 2 − tf2 实际散热量 h2 A2 t w 2 − tf2 = = η= 理想散热量 h2 A2 (t w 2 − tf2 ) t w 2 − tf2
Φ = Ah2 (t w2 − tf2 )
λ Φ = A (t w1 − t W2 ) δ
Φ tf1 − t W1 = Ah Φ t w1 − t W2 = Aλ / δ Φ t w2 − t f2 = Ah2
传热方程：
A(t f1 − t f2 ) Φ= = KA ∆ t 1 / h1 + λ / δ + 1 / h2
传热过程的计算
第四节 传热过程计算化工原理中所涉及的传热过程计算主要有两类：一类是设计计算，即根据生产要求的热负荷，确定换热器的传热面积；另一类是校核计算，即计算给定换热器的传热量、流体的流量或温度等。
两者都是以换热器的热量衡算和传热速率方程为计算的基础。
应用前述的热传导速率方程和对流传热速率方程时，需要知道壁面的温度。
而实际上壁温常常是未知的，为了避开壁温，故引出间壁两侧流体间的总传热速率方程。
4—4—1 能量衡算对间壁式换热器做能量衡算，以小时为基准，因系统中无外功加入，且一般位能和动能项均可忽略，故实质上为焓衡算。
假设换热器绝热良好，热损失可以忽略时，则在单位时间内换热器中热流体放出的热量等于冷流体吸收的热量，即 ， .、)()(1221c c c h h h H H W H H W Q -=-= (4—30)式中 Q —换热器的热负荷，kj/h 或W ；W －流体的质量流量，kg ／h ；H －单位质量流体的焓，kJ ／kg 。
下标c 、h 分别表示冷流体和热流体，下标1和2表示换热器的进口和出口。
式4-30即为换热器的热量衡算式，它是传热计算的基本方程式，通常可由该式计算换热器的传热量(又称热负荷)。
.若换热器中两流体无相变化，且流体的比热容不随温度而变或可取平均温度下的比热容时，式4-30可表示为Q )()(1221t t c W T T c W pc c ph h -=-= （4-31）式中 c p －流体的平均比热容，kJ ／(kg ·℃)；t —冷流体的温度，℃；T －热流体的温度，℃。
若换热器中的热流体有相变化，例如饱和蒸气冷凝时，式4-30可表示为Q )(12t t c W r W pc c h -== (4-32)式中 W h —饱和蒸气(即热流体)的冷凝速率，k 2／h ；r —饱和蒸气的冷凝潜热，kJ ／kg 。
式4-32的应用条件是冷凝液在饱和温度下离开换热器。
若冷凝液的温度低于饱和温度时，则式4-32变为Q )()]([1221t t c W T T c r W pc c ph h -=-+= （4-33）式中 C ph －冷凝液的比热容，kJ ／(kg ·℃)；T s —冷凝液的饱和温度，℃。
化工原理.传热过程的计算
三、总传热系数
QKAtm
如何确定K值，是传热过程计算中的重要问题。
17
T
Tw
热 流 体
对流 导 热
冷 流 体
Q tw
t
•热流体
Q1 对流
固体壁面一侧
•固体壁面一侧
Q2 热传导
另一侧
•固体壁面另一侧
Q3 对流
冷流体
对流
dQ Kd(TA t)
18
管外对流：
d1 Q 1d1( A TT w )
液体－气体
K 700～1800
300～800 200～500 50～300
100～350 50～250 10～60
25
两流体 气体－气体 蒸气冷凝－气体 液体沸腾－液体 液体沸腾－气体 水蒸气冷凝－水 有机物冷凝－有机物 水蒸气冷凝－水沸腾 水蒸气冷凝－有机物沸腾
K 10～40 20～250 100～800 10～60 1500～4700 40～350 1500～4700 500～1200
21
K1——以换热管的外表面为基准的总传热系数；
dm——换热管的对数平均直径。
dm(d1d2)/lndd12
（3）以内表面为基准：
1 1 d2bd2 1
K2 1 d1 dm 2
（4）以壁表面为基准：
1 1 dmb1 dm
Km 1 d1 2 d2
d 1 2 近似用平壁计算
d2
22
（5）污垢热阻
27
四、壁温的计算
稳态传热 QK AtmT1TWTw btWtw1t
1A1 Am 2A2
bQ
tW TW Am ,
Q
TW
T
1A1
,
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
6
例1:总传热系数 K 的计算
管外，热空气对管壁的给热系数为90W/(m2.oC)。管内，冷却水与 管壁之间的给热系数为1000W/(m2.oC)。管外径16mm ，壁厚1.5mm 导热系数为40W/(m.oC) ,试求：1、传热系数K ;
2、管外给热系数 2 增加一倍，K有何变化？
3、管内给热系数 1增加一倍，K有何变化？
K'
1
1
1
d2 d1
1
2
'
1
0.00123 1
2 90
W 147.4 m 2 K
K’ 比K增加了83%
3、忽略管壁热阻， 1' 2 1
K"
1
1
85.3 W
1 d2 1 0.00123 1
m2 .K
21 d1 2
2 90
K”比K增加仅6%
为多少？
Q KAt m
T2 t1
t2 T1
2019/6/17
第 6 章 传热
22
qm1C p1(T1 T2 ) qm2C p2 (t2 t1 )
qm1C p1(T1 T2' ) 2qm2C p2(t2' t1 )
2019/6/17
第 6 章 传热
23
2019/6/17
t2
)
T t2
qm2C p2 (t2
t1 )
KA
(t2 t1 ) ln T t1
T t2
ln T t1 KA T t2 qm2C p2
T1 T2
T2
T1
t2
t1
T2
T1
t2
t1
2019/6/17
第 6 章 传热
21
传热基本方程式的应用
例1：在传热面积为10m2的管壳式换热器中，用工业水冷却各车间
解得：T' 123.8o C
T '80
T '80
2019/6/17
第 6 章 传热
25
第6章 传热（12学时）
第5讲：
6.6.3换热器的设计型计算 6.6.4 换热器的操作型问题
消元法 传热单元法 综合例题
2019/6/17
第 6 章 传热
26
6.6.3换热器的设计型计算
设计型命题方式：以热流体被冷却为例 计算条件：T1 T2 qm1 Cp1 K 计算目的：A（传热面积）
ro ri ln ro
ri
故面积比就等于直径比、半径比。
注意： K与A相对应
1 1 ro r0 1 K i ri rm 0
若内壁污垢热阻为 Ri ;外壁污垢热阻为Ro , 热阻单位
1 K
1
i
ro ri
Ri
ro ri
ro rm
Ro
1
o
m2 o C W
利用热传导式求δ2
Q
Tt
l
1
i 2ri
1
21
ln ri
1
ri
1
2 2
ln ri
1 2 ri 1
o
1
2ri 1
2
或者 Q K 2 r1 1 2 L T t
2019/6/17
第 6 章 传热
dQ o dAo (tw t)
定常态传热过程
dQ K dA (T t)
若、 以管外侧面积为基准
分析是否可以将dA扩展到整个传热面积A 上？
i o
都是总面积上的平均值，我们希望得到在总面积上为不变值的总传热系数K 。
1 1 Ao A0 1
K
i Ai
解：忽略管壁热阻 Tw tw
Байду номын сангаас
T
i
Tw tw o
t
q
T
Tw 1
Tw t w
tw t 1
1
解得Tw=56.7oC
2
11
90 Tw 1 1160 0.00086
Tw 50 1
1 0.00017
2 5800
2019/6/17
第 6 章 传热
9
解： （1） Q qmC p 2(t2 t1) 6106 KJ / h
110 110 20 80
tm
90 30 ln 90
54.6o C
30
A 15m2
Q KAt m
K
Q Atm
7.33103
KJ h m2 o C
2036
m
W 2 o
13
传热平均温度差：
在换热器的某截面：
2019/6/17
将 dT , dt 用 d(T-t) 代替。
第 6 章 传热
14
T1
T1 t2
t2
T2
t1
t2 t
换热过程的操作线
2019/6/17
第 6 章 传热
15
dT
T1
T1
t2
T2
T2
t1
d T
t
T1 T2 t2 t1
（2）t2.或qm2 t1确定后， t2或qm2只须选一个，受热量衡算限制。 t2过高，工业用水中所含盐类析出，易结垢 （3）冷流体入口t1选择 夏季与冬季水温t不同，计算时应该按夏天选定t1更为安全可靠 （4）流速选择
兼顾传热系数与压降
2019/6/17
第 6 章 传热
28
设计型问题中，冷却介质出口温度的选择： Q一定，t1一定，t2取得高，qm2最少，回收能量的价值高，输送 流体的动力消耗即操作费用少。但是， t2高，传热过程的平均推 动力 △tm小，完成传热任务Q所需的传热面积A大，设备投资费 用大。故，冷却介质出口温度的选择是一个经济上的权衡问题。
Q A
Kt m
A dol n
2019/6/17
第 6 章 传热
27
可供选择的条件：
（1）流向（逆流、并流等）
（2）冷流体t2或qm2
（3）冷流体t1
（4）流速
可以出现t2>T2
选择依据：
（1）流向——逆流优于并流
理由之一：在换热器四个端值T1,T2,t1,t2 相同的情况下，△tm逆＞ △tm并 理由之二：逆流操作可以在更宽的范围内完成传热任务
2019/6/17
第 6 章 传热
4
注意：
1 K
1 i
ro ri
Ri
ro ri
ro rm
Ro
1 o
即从热阻值大的一侧入手。
q
T
Tw 1
Tw t w
tw t 1
1
2
2019/6/17
壁温判断
因为是稳定连续的传热过程。
第 6 章 传热
5
例:保温层厚度的计算
第 6 章 传热
10
6.6.2 传热平均温度差与传热基本方程式
我们已经分析得到了在整个传热面积范围内是常数的总传热系数 K ,我们希望得到在整个传热面积范围内适用的传热速率的表达式， 传热温度差采用一平均值。
Q KAT t m KA tm
根据间壁两侧流体温度沿传热面是否有变化，可将传热分为恒温传热和变温传热。
T2
T1
T1
t2
t1
t1
T1
T2
T2
t2
t2
t1
2019/6/17
第 6 章 传热
11
在换热器内，热流体温度不断降低，冷流体温度不断升高，因此， 换热器内不同的部位，传热的温度差是不同的。 但是，因为是定 常态传热，换热器内，热流体的温度分布一定，冷流体的温度分布 也一定。故一定存在着一个与时间、位置无关的平均温度差。
t1
,
t
分
2
别
为
换
热
器两端
的
冷、热流体温度差。
2019/6/17
第 6 章 传热
20
Q KAtm
若传热过程中，某一种流体为恒温（例如水蒸气冷凝），另一 种流体变温，传热基本方程式的形式可以变化，并且此时无需 分辨是逆流还是并流。
qm2C
p2 (t2
t1 )
KA
(T
t1 ) (T ln T t1
dt
T1
t2
t2
t1
T2
t1
d T
t
2019/6/17
第 6 章 传热
16
dT
T1
T1 T2
t2 T2
t1 d T
t
dt
T1
t2
t2
t1
T2
t1 d T
t
qm1C p1(T1 T2 ) Q
qm2C p2(t2 t1 ) Q
见P308
19
Q KAtm
传热基本方程式是传热问题的一个“纲”
qm1C p1(T1 T2 ) Q
qm2C p2(t2 t1 ) Q
A dol n
1 K
1