第四章轴测图
合集下载
第4章轴测图

2.作图:
(1)在正投影图上选定坐标轴,将具有大小不等的端面选为 正面,即使其平行于XOY坐标面。 (2)画斜二测的轴测轴,根据坐标分别定出每个端面的圆心 位置。 (3)按圆心位置,依次画出圆柱、圆锥及各圆孔。 (4)擦去多余线条,加深后完成全图。
第4章 轴测投影图
4-1 轴测投影图的基本知识 4-2 正等轴测图 4-3 斜二等轴测图
4.1 轴测投影图的基本知识
1. 轴测投影图的形成
将物体连同确定其空间 位置的直角坐标系沿不平行 于任一坐标平面的方向S, 用平行投影法向单一投影面 P进行投影得到的投影图, 简称ຫໍສະໝຸດ 测图。2. 轴测投影基本概念
作组合体的正等轴测图,首先要进行形体分析,弄清形体 的基本组成情况,然后选定坐标轴,再按坐标关系将各个基本 体的正等轴测图逐一作出;最后擦去各形体间不该有的交线和 被遮挡图线,完成作图。
曲面立体正等轴测图的画法 图例1
Z X
O Y
曲面立体正等轴测图的画法 图例2
步骤一
步骤二
步骤三
步骤四
完成
4.2 正等轴测图
一. 轴间角和轴向伸缩系数
三个轴间角均为120°
轴向伸缩系数p1 = q1 = r1 ≈0.82
轴向简化系数:p=q=r=1
凡与轴测轴平行的线 段,作图时按实际长 度直接量取。
二、平面立体正等轴测图的画法
1.坐标法 2.切割法 3.叠加法
三、圆的正等轴测图的画法
1.坐标法 2.四圆心法
四、曲面立体正等轴测图的画法
1.圆柱的画法 (1)竖直圆柱的画法(2)不同方向的圆柱 2.圆角的画法 3.曲面立体的画法 (1)图例1(2)图例2
二、平面立体正等轴测图的画法 1.坐标法
(1)在正投影图上选定坐标轴,将具有大小不等的端面选为 正面,即使其平行于XOY坐标面。 (2)画斜二测的轴测轴,根据坐标分别定出每个端面的圆心 位置。 (3)按圆心位置,依次画出圆柱、圆锥及各圆孔。 (4)擦去多余线条,加深后完成全图。
第4章 轴测投影图
4-1 轴测投影图的基本知识 4-2 正等轴测图 4-3 斜二等轴测图
4.1 轴测投影图的基本知识
1. 轴测投影图的形成
将物体连同确定其空间 位置的直角坐标系沿不平行 于任一坐标平面的方向S, 用平行投影法向单一投影面 P进行投影得到的投影图, 简称ຫໍສະໝຸດ 测图。2. 轴测投影基本概念
作组合体的正等轴测图,首先要进行形体分析,弄清形体 的基本组成情况,然后选定坐标轴,再按坐标关系将各个基本 体的正等轴测图逐一作出;最后擦去各形体间不该有的交线和 被遮挡图线,完成作图。
曲面立体正等轴测图的画法 图例1
Z X
O Y
曲面立体正等轴测图的画法 图例2
步骤一
步骤二
步骤三
步骤四
完成
4.2 正等轴测图
一. 轴间角和轴向伸缩系数
三个轴间角均为120°
轴向伸缩系数p1 = q1 = r1 ≈0.82
轴向简化系数:p=q=r=1
凡与轴测轴平行的线 段,作图时按实际长 度直接量取。
二、平面立体正等轴测图的画法
1.坐标法 2.切割法 3.叠加法
三、圆的正等轴测图的画法
1.坐标法 2.四圆心法
四、曲面立体正等轴测图的画法
1.圆柱的画法 (1)竖直圆柱的画法(2)不同方向的圆柱 2.圆角的画法 3.曲面立体的画法 (1)图例1(2)图例2
二、平面立体正等轴测图的画法 1.坐标法
工程制图第4章 轴测图
20 /54 Wang chenggang
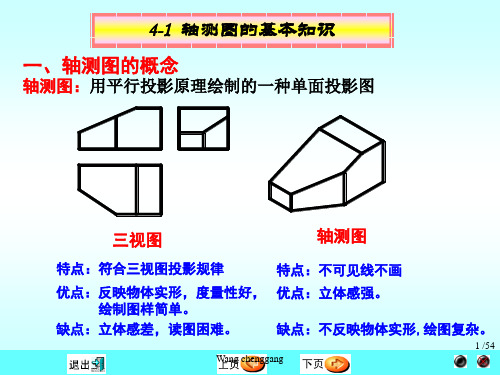
四、曲面立体的正等轴测图画法 1、平行于各个坐标面的圆的形状
Z1
平行于W 平行于W面的椭 圆长轴⊥ 圆长轴⊥O1X1轴 平行于H 平行于H面的椭 圆长轴⊥ 圆长轴⊥O1Z1轴
平行于V 平行于V面 的椭圆长轴 ⊥O1Y1轴
X1
Y1
注意:圆的正等测图是椭圆, 注意:圆的正等测图是椭圆,三个坐标面或其平行面上的圆的正 等测图是大小相等、形状相同的椭圆,只是长短轴方向不同。 等测图是大小相等、形状相同的椭圆,只是长短轴方向不同。
C1
5、正等轴测图综合举例
例:已知物体的三视图,画出其轴测图。 已知物体的三视图,画出其轴测图。
26 /54 Wang chenggang
4-3 斜二等轴测图的画法 二等轴测图 一、斜二等轴测图
坐标面与轴测投影面的平行 当XOZ坐标面与轴测投影面的平行时,用斜投影 坐标面与轴测投影面的平行时 法得到的投影图称为斜轴测图。 法得到的投影图称为斜轴测图。 斜轴测图 指采用斜投影的方法, 二等” “斜”指采用斜投影的方法,“二等”指X、Z二 、 二 变形系数相等 个轴向的变形系数相等。 个轴向的变形系数相等。 常用的轴间角和轴向变形系数: 常用的轴间角和轴向变形系数:
X1 Z O X Y
Z
Z1
X O Y
Z1
投影面
O1
Y1
O1 X1 Y1
轴间角
物体上: 物体上: OX, OY, OZ , , 投影面上: 投影面上: O1X1,O1Y1,O1Z1 ∠X1O1Y1, ∠ X1O1Z1, ∠ Y1O1Z1
Wang chenggang
坐标轴 轴测轴
5 /54
2、轴向伸缩系数 物体上平行于坐标轴的线段在轴测图上的长度 物体上平行于坐标轴的线段在轴测图上的长度 平行于坐标轴的线段在 实际长度之比叫做 长度之比叫做轴向伸缩系数 与实际长度之比叫做轴向伸缩系数。
第四章 轴测图
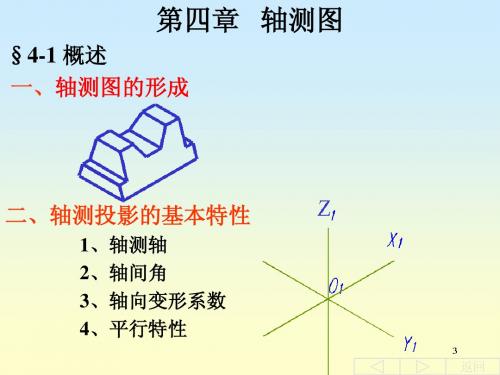
6)画立板圆孔。作出前表面上的 圆心,画出椭圆。再画出后表面 上的椭圆。为此,将圆心O5、O6 和切点e均沿Y向后移板厚距离得 中心O7、O8和切点eˊ,即可画出 椭圆的可见部分
7)画立板上部的半圆柱 8)完成轴测图
4.3 斜二轴测图
一、轴向伸缩系数和轴间角
1:1 Z1 X1 1:1 1:1 Y1 45° O1 Z1
正等轴测图
四、 轴测投影的基本性质
(1)物体上相互平行的线段的轴测投影仍相互平行 (2)物体上平行于坐标轴的直线段的轴测投影仍与 相应的轴测轴平行 (3)物体上两平行线段或同一直线上的两线段长度 之比,其轴测投影保持不变 凡是与坐标轴平行的直线,就可以在轴测图 上沿轴向进行度量和作图。
4.2 正等测轴测图
X1 1:1
O1 45°
Y1
轴向伸缩系数:p = r = 1 ,q = 0.5 轴间角: X1O1Z1 = 90° X1O1Y1 = Y1O1Z1 = 135°
二、平行于各坐标面的圆的画法
1 平行于V面的圆仍为圆,反映 实形。 2 平行于H面的圆为椭圆,长轴 对O1X1轴偏转7°, 长轴≈1.06d, 短轴≈0.33d。 3 平行于W面的圆与平行于H 面的圆的椭圆形状相同,长 轴对O1Z1轴偏转7°。 由于两个椭圆的作图相当繁,所以当物体这 两个方向上有圆时,一般不用斜二轴测图,而采 用正等轴测图。 斜二轴测图的最大优点: 物体上凡平行于V面的平面都反映实形。
平行于坐标面的圆的正等测图的画法
1. 坐标法
4 4
X
2
1 5 7 8
2 6 3
Y X1
6 8
5 7 3 Y
2. 四心法 Z
o4
o2
o5
机械制图之第四章 轴测图

是否相同又分为: ⑴正(斜)等轴测图,p1=q1=r1; ⑵正(斜)二轴测图,p1=q1≠r1或 q 1 = r 1 ≠ p 1 或 r 1 = p 1 ≠ q 1; ⑶正(或斜)三轴测图,p1≠q1≠r1。
X
V
X′ X A
Z′ Z
O′ C
O B A1 Y
Z1 C1
O1
B1
X1
Y1
O
Y
四、轴测图的投影特性 平行性:
o′ x′ O1 z′ X1 Z1 x o Y1
圆 弧 公 切 线
y
[例4-5] 作如图所示带圆角的长方体的正等轴测图。
x′
o′
z′ o
X1
O1
x
Y1
Z1
y
圆 弧 公 切 线
[例4-6] 作出如图所示支架的正等轴测图。
z′
Z1
圆弧公切线
a
x′
o′
1 2
A1
41 31
x
o
4 3
X1
o 11 21
图4–10 斜二轴测图的形成
二、斜二轴测图的画图参数
Z1
90°
X1 O1
135°
135°
Y1
∠X1O1Z1=90°
∠X1O1Y1=∠Y1O1Z1=135°
p1=r1=1,q1=0.5
形体上与轴测投影面平行的平面,其轴测投影为实形。
图4–11 斜二轴测图的画图参数
三、斜二轴测图的画法 平行于坐标面的斜二轴测图 平行X1O1Z1面,为圆; 平行X1O1Y1面,为椭圆,长 轴与O1X1轴倾斜约7°; 平行Y1O1Z1面,为椭圆,长 轴与O1Z1轴倾斜约7°; 短轴与长轴垂直。
o′ C
O A X1
X
V
X′ X A
Z′ Z
O′ C
O B A1 Y
Z1 C1
O1
B1
X1
Y1
O
Y
四、轴测图的投影特性 平行性:
o′ x′ O1 z′ X1 Z1 x o Y1
圆 弧 公 切 线
y
[例4-5] 作如图所示带圆角的长方体的正等轴测图。
x′
o′
z′ o
X1
O1
x
Y1
Z1
y
圆 弧 公 切 线
[例4-6] 作出如图所示支架的正等轴测图。
z′
Z1
圆弧公切线
a
x′
o′
1 2
A1
41 31
x
o
4 3
X1
o 11 21
图4–10 斜二轴测图的形成
二、斜二轴测图的画图参数
Z1
90°
X1 O1
135°
135°
Y1
∠X1O1Z1=90°
∠X1O1Y1=∠Y1O1Z1=135°
p1=r1=1,q1=0.5
形体上与轴测投影面平行的平面,其轴测投影为实形。
图4–11 斜二轴测图的画图参数
三、斜二轴测图的画法 平行于坐标面的斜二轴测图 平行X1O1Z1面,为圆; 平行X1O1Y1面,为椭圆,长 轴与O1X1轴倾斜约7°; 平行Y1O1Z1面,为椭圆,长 轴与O1Z1轴倾斜约7°; 短轴与长轴垂直。
o′ C
O A X1
第四章-机械制图轴测图课件

图4-10圆的斜二轴测图——椭圆的近似画法
例4-8 画出如图4-11a所示支架的斜二轴测图。
4-3作支座的斜二轴测图.swf
图4-11支架的斜二轴测图画法
例4-8 穿孔圆锥台的 斜二轴测图
4-3作圆台的斜二轴测图.swf
(a) 已知
穿孔圆锥台的斜二轴测图
z'
x'
o'
O
y
(c)画出轴测轴 x o
本章小结
在工程上常采用富有立体感的轴测图作为辅助图样来帮助说明零、部 件形状。在某些场合(如绘制产品包装图等)则直接用轴测图表示设计要求, 并依此作为加工和检验的依据。常用的轴测图有正等轴测图和斜二轴测图 两种。 1轴测投影的特性 (1) 空间互相平行的线段,在同一轴测投影中一定互相平行。与直角坐标 轴平行的线段,其轴测投影必与相应的轴测轴平行。 (2) 与轴测轴平行的线段,按该轴的轴向伸缩系数进行度量。与轴测轴倾 斜的线段,不能按该轴的轴向伸缩系数进行度量。 2轴测图的选用原则 在选用轴测图时,既要考虑立体感强,又要考虑作图方便。 (1) 正等轴测图的轴间角以及各轴的轴向伸缩系数均相同,用30°的三角 板和丁字尺作图较简便,它适用于绘制各坐标面上都带有圆的物体。 (2) 当物体上一个方向上的圆及孔较多时,采用斜二轴测图比较简便。 究竟选用哪种轴测图,应根据各种轴测图的特点及物体的具体形状进行综 合分析,然后作出决定。
(f)擦去多余图线
穿孔圆锥台的斜二轴测图
(g)描深,完成作图
第四节 轴测草图的画法
在绘制轴测草图时应注意:同方向的图线要平行;由于不 同方向的圆的轴测投影一般为椭圆,故要明确椭圆长短轴的方 向;要基本把握各部分间的比例关系。 画轴测草图的一般步骤为: 1从图样、模型或有关资料分析出物体的形状及各部分 间的比例关系。 2选择轴测图的种类,例如是画正等轴测草图,还是画 斜二轴测草图。 3确定合适的轴测投射方向,以便尽可能反映物体的形 状、结构。 4进行具体画图。
第4章 轴测图

正面斜二测的作图步骤与方法与正等轴测基本相同
第一步:正面平行于投影面,物体上凡平行于投影面 的图形均反映真实形状和大小,先做实形的V面投影 第二步:按OY方向画45º 平行线,长度为0.5y 第三步:完善轮廓,加深
例1:已知两面视图,画斜二测图。
0.5y
R2 0.5y
第一步:画正面形状 第二步:按OY方向画45º 平行线,长度为0.5y 第三步:圆心沿OY向后移0.5y,画出后表面的圆弧 第四步:作前后圆的切线 第五步:完善轮廓,加深
z' x'
2
z" Z1 o' o" o
4
y"
x
3
O1
●
y
X1
2
●
4
Y1
例2:画三棱锥的正等测图
s
Z
Z
s
S ●
Z1
X a
b s b
a
cO a b Y cO c
O
●
X
O1 C
Y
A● X1
Y1
●
B
例3:画六棱柱正等测图
2)切割法
对于能从基本体切割而成的形体,可先画基本体,然后进 行切割,得出该形体的轴测图。
1
O1
30
Y1
120
轴向伸缩系数:p = q = r = 0.82 简化轴向变化率:p = q = r = 1 简化后的正等测图比实际等测图放大了1.22倍
实际中,为作图简便,将轴向伸缩系数简化,p=q=r=1。
平行于坐标轴的线段可以按实际尺寸直接作图(按此
原则简化得到的正等测轴测图比实际正等测投影图放大 了1.22倍。
C)正三轴测
轴测轴间角
第一步:正面平行于投影面,物体上凡平行于投影面 的图形均反映真实形状和大小,先做实形的V面投影 第二步:按OY方向画45º 平行线,长度为0.5y 第三步:完善轮廓,加深
例1:已知两面视图,画斜二测图。
0.5y
R2 0.5y
第一步:画正面形状 第二步:按OY方向画45º 平行线,长度为0.5y 第三步:圆心沿OY向后移0.5y,画出后表面的圆弧 第四步:作前后圆的切线 第五步:完善轮廓,加深
z' x'
2
z" Z1 o' o" o
4
y"
x
3
O1
●
y
X1
2
●
4
Y1
例2:画三棱锥的正等测图
s
Z
Z
s
S ●
Z1
X a
b s b
a
cO a b Y cO c
O
●
X
O1 C
Y
A● X1
Y1
●
B
例3:画六棱柱正等测图
2)切割法
对于能从基本体切割而成的形体,可先画基本体,然后进 行切割,得出该形体的轴测图。
1
O1
30
Y1
120
轴向伸缩系数:p = q = r = 0.82 简化轴向变化率:p = q = r = 1 简化后的正等测图比实际等测图放大了1.22倍
实际中,为作图简便,将轴向伸缩系数简化,p=q=r=1。
平行于坐标轴的线段可以按实际尺寸直接作图(按此
原则简化得到的正等测轴测图比实际正等测投影图放大 了1.22倍。
C)正三轴测
轴测轴间角
第四章 轴测图

在斜二轴测图中,由于物体上的坐标平面XOZ与轴测投影面平行,因此物体上 平行于XOZ坐标平面的直线和图形在轴测投影面上均反映实长和实形。斜二轴测图 常用于绘制有较多圆或圆弧的物体。
(a)斜二轴测图
(b)轴间角
图4-11 斜二轴测图
(c)轴向伸缩系数
谢谢!
(f)
2.3 圆角的正等轴测图的画法
① 画轴测图的坐标轴和长方形板的正 等轴测图,接着在顶面上截得圆角的 四个切点1,2,3,4,如图4-10(b) 所示。
② 分别过各切点作其所在棱边的垂线, 其交点分别为O1,O2,如图2-41 (c)所示,然后以O1点为圆心,以 O11为半径连接切点1,2,接着以 O2点为切点,以O23为半径连接切点 3,4,即可得到顶面的圆角,如图410(d)所示。
图4-7 三个不同坐标平面的圆的正等轴测图
2.3 圆角的正等轴测图的画法
对于一些具有圆角(1/4圆柱面)结构的正等轴测图,可通过作各切点的垂直线来绘制。 例如,要画出图4-10(a)所示长方形板的正等轴测图,具体的作图步骤如下。
(a)
(b)
(c)
(d)
(e)
图4-7 三个不同坐标平面的圆的正等轴测图
1.2 轴测图的种类
根据投射方向与轴测投影面是否垂直,轴测图可分为正轴测图和斜轴测图两类。
图4-2 正轴测图
图4-3 斜轴测图
02
正等轴测图的画法
前言
正等轴测图简称为正等测,其轴测图、轴间角和轴向伸缩系数如图4-4所示。 正等测轴测图中的三个轴间角相等,均为120°。其中,OX轴表示长度,OY轴表示 宽度,OZ轴表示高度,且规定OZ轴画成铅垂线。三个轴的轴向伸缩系数相等,即 为p = q = r = 0.82,如图4-4(c)所示。实际作图时,为使作图方便,通常采用 简化的轴向伸缩系数,即p = q = r = 1。
(a)斜二轴测图
(b)轴间角
图4-11 斜二轴测图
(c)轴向伸缩系数
谢谢!
(f)
2.3 圆角的正等轴测图的画法
① 画轴测图的坐标轴和长方形板的正 等轴测图,接着在顶面上截得圆角的 四个切点1,2,3,4,如图4-10(b) 所示。
② 分别过各切点作其所在棱边的垂线, 其交点分别为O1,O2,如图2-41 (c)所示,然后以O1点为圆心,以 O11为半径连接切点1,2,接着以 O2点为切点,以O23为半径连接切点 3,4,即可得到顶面的圆角,如图410(d)所示。
图4-7 三个不同坐标平面的圆的正等轴测图
2.3 圆角的正等轴测图的画法
对于一些具有圆角(1/4圆柱面)结构的正等轴测图,可通过作各切点的垂直线来绘制。 例如,要画出图4-10(a)所示长方形板的正等轴测图,具体的作图步骤如下。
(a)
(b)
(c)
(d)
(e)
图4-7 三个不同坐标平面的圆的正等轴测图
1.2 轴测图的种类
根据投射方向与轴测投影面是否垂直,轴测图可分为正轴测图和斜轴测图两类。
图4-2 正轴测图
图4-3 斜轴测图
02
正等轴测图的画法
前言
正等轴测图简称为正等测,其轴测图、轴间角和轴向伸缩系数如图4-4所示。 正等测轴测图中的三个轴间角相等,均为120°。其中,OX轴表示长度,OY轴表示 宽度,OZ轴表示高度,且规定OZ轴画成铅垂线。三个轴的轴向伸缩系数相等,即 为p = q = r = 0.82,如图4-4(c)所示。实际作图时,为使作图方便,通常采用 简化的轴向伸缩系数,即p = q = r = 1。
第四章 轴测图
27
常用轴间角和轴向伸缩系数
28
【例】 画出如图所示建筑形体的水平斜二测
29
【例】绘制一个区域建筑群的总平面图,如下图所示。
30
三、平行于坐标面的圆的斜二测图的画法
正平圆在斜二测图中反映实形,水平圆和侧平圆的斜二测图都是椭 圆,其椭圆可用坐标法画出。
八点法
31
“八点法”作圆的斜二测图
32
【例】:带切口圆柱的斜二测图
5
• 四、轴测投影图的分类
按投影方向与轴测投影面之间的关 系,轴测投影可分为正轴测投影和斜轴 测投影两类。
(1)正轴测投影 当轴测投影的投射方向
S与轴测投影面P垂直时所形成的轴测投影 称为“正轴测投影”,如右图所示。 (2)斜轴测投影 当投影方向S与轴测 投影面P倾斜时所形成的轴测投影称为 “斜轴测投影”,如右图所示。
深,即完成斜垫块的正等测 图。
11
【例】:已知台阶正投影图,画出其正等测图
12
【例】作图示正六棱柱的正等测图。
13
叠加法 【例】 作图示柱脚的正等测图。
14
切割法 【例】 作图示物体的正等测图。
Z
O
8
16 25 Y
15
X
2、平行于坐标面圆的正等测图画法
Z
四心扁圆法”画圆的正等测图 平行于XOY坐标面的圆的正等测图画法
解:(1)分析 (2)作图
10
1、在斜垫块上选定直角坐标系;
2、画出正等轴测轴,按尺寸a、b, 画出斜垫块底面的轴测投影,见左图; 3、过底面的各顶点,沿O1Z1方向,
向上作直线,并分别在其上截取高
度h1和h2,得斜垫块顶面的各顶点, 见下图; 4、连接各顶点,画出斜垫块顶面;
常用轴间角和轴向伸缩系数
28
【例】 画出如图所示建筑形体的水平斜二测
29
【例】绘制一个区域建筑群的总平面图,如下图所示。
30
三、平行于坐标面的圆的斜二测图的画法
正平圆在斜二测图中反映实形,水平圆和侧平圆的斜二测图都是椭 圆,其椭圆可用坐标法画出。
八点法
31
“八点法”作圆的斜二测图
32
【例】:带切口圆柱的斜二测图
5
• 四、轴测投影图的分类
按投影方向与轴测投影面之间的关 系,轴测投影可分为正轴测投影和斜轴 测投影两类。
(1)正轴测投影 当轴测投影的投射方向
S与轴测投影面P垂直时所形成的轴测投影 称为“正轴测投影”,如右图所示。 (2)斜轴测投影 当投影方向S与轴测 投影面P倾斜时所形成的轴测投影称为 “斜轴测投影”,如右图所示。
深,即完成斜垫块的正等测 图。
11
【例】:已知台阶正投影图,画出其正等测图
12
【例】作图示正六棱柱的正等测图。
13
叠加法 【例】 作图示柱脚的正等测图。
14
切割法 【例】 作图示物体的正等测图。
Z
O
8
16 25 Y
15
X
2、平行于坐标面圆的正等测图画法
Z
四心扁圆法”画圆的正等测图 平行于XOY坐标面的圆的正等测图画法
解:(1)分析 (2)作图
10
1、在斜垫块上选定直角坐标系;
2、画出正等轴测轴,按尺寸a、b, 画出斜垫块底面的轴测投影,见左图; 3、过底面的各顶点,沿O1Z1方向,
向上作直线,并分别在其上截取高
度h1和h2,得斜垫块顶面的各顶点, 见下图; 4、连接各顶点,画出斜垫块顶面;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
得到轴测投影的面叫做轴测投影面。
用正投影法形成的轴测图叫正轴测图。 用斜投影法形成的轴测图叫斜轴测图。
轴测轴、轴间角和轴向伸缩系数
1. 轴测轴和轴间角 建立在物体上的坐标轴在投影面上的投影
叫做轴测轴,轴测轴间的夹角叫做轴间角。
投影面
X1 Z
Z1
O1
Y1
Z
X
O
Y
Z1 投影面
O1 X1
Y1
O
正轴测
斜轴测
例4-1已知长方体的三视图(图4-3a),画出它的正等轴测图。
图4-3 长方体的正等轴测图
解 分析:图4-3a为长方体的三视图。长方体共有八个顶点, 用坐标确定各顶点在其轴测图中的位置,然后连接各顶点 间的棱线即为所求。作图步骤如图:
图4-3 长方体的正等轴测图
巩固提高、布置作业
• 习题集P38 • 绘制正等轴测图
物体上与坐标轴平行的 直线,其轴测投影有何 特性?
平行于相应的 轴测轴
凡是与坐标轴平行的线段,就可以在轴测图上 沿轴向进行度量和作图。 轴测含义
注意:与坐标轴不平行的线段其伸缩系数与之不同, 不能直接度量与绘制,只能根据端点坐标,作 出两端点后连线绘制。
正等轴测图
一、轴间角与轴向伸缩系数
Z1
O1
X1
YB
XA11
O1 C1 B1
Y1
斜轴测
XA
B Y O1A1 OA
=p
X轴轴向伸缩系数
O1B1 OB
=q
Y轴轴向伸缩系数
O1C1 OC
=r
Z轴轴向伸缩系数
基本投影特性
在原物体与轴测投影间保持以下关系:
★ 空间互相平行的线段,在同一轴测投影中一定互相平行。
★ 与轴测轴平行的线段,按该轴的轴向伸缩系数进 行度量。
Y1
轴向伸缩系数:p = q = r = 0.82
简化轴向伸缩系数:p = q = r = 1
轴间角: X1O1Y1 = X1O1Z1 = Y1O1Z1 = 120°
合作讨论、共同探究
• 已知长方体三视图,能否画出正等轴测图?
学生展示、教师点拨
二、正等轴测图的画法 1.平面立体正等轴测图的画法
导入新课、展示目标
1、知识与技能
• 了解轴测投影的基本概念、特性和常用轴测图的 种类
• 了解正等轴测图的轴测轴、轴间角、轴向伸缩系 数
• 能画出简单形体的正等轴测图(重点) 2、教学过程与方法 • 学生带问题自学,教师点拨、强调 3、情感态度与价值观 • 培养学生的观察图形的能力与动手能力
设疑激探、自主学习
X
Y
物体上 OX, OY, OZ
坐标轴
轴间角
投影面上 O1X1,O1Y1,O1Z1 X1O1Y1, X1O1Z1, Y1O1Z1
轴测轴
2. 轴向伸缩系数
物体上平行于坐标轴的线段在轴测图上 的长度与实际长度之比叫做轴向伸缩系数。
投影面
C1 Z1
Z
X1 A1
C
O1 B1 Y1
O
正轴测
ZC XAO
Z1 投影面
• 认真阅读课本P63-64,思考下列问题 • 1、轴测图是怎么形成的? • 2、什么是轴测轴、轴间角、轴向伸缩系数? • 3、轴测投影的基本特性是什么?
轴测图的形成
将物体连同确定其空间位置的直角坐 标系,沿不平行于任一坐标面的方向,用 平行投影法将其投射在单一投影面上所得 的具有立体感的图形叫做轴测图。
