第二章:前向网络(2)
智能控制

1、智能控制: 即设计一个控制器(或系统),使之具有学习、抽象、推理、决策等功能,并能根据环境(包括被控对象或被控过程)信息的变化做出适应性反应,可以有各种人工智能的水平,从而实现由人来完成的任务。
2、智能控制由哪几部分组成?各自的特点是什么?①模糊控制(通过模拟人脑的思维方法设计控制器,可实现复杂系统的控制)②神经网络控制(从机理上对人脑生理系统进行简单结构的模拟,具有并行机制、模式识别、记忆和自学习能力的特点,能充分逼近任意复杂的非线性系统,能够学习与适应不确定系统的动态特性,有很强的鲁棒性和容错性)③遗传算法(可用于模糊控制规则的优化及神经网络参数及权值的学习)3、比较智能控制和传统控制的特点传统控制和智能控制的主要区别:①传统控制方法在处理复杂化和不确定性问题方面能力很低;智能控制在处理复杂性、不确定性方面能力较高。
智能控制系统的核心任务是控制具有复杂性和不确定性的系统,而控制的最有效途径就是采用仿人智能控制决策。
②传统控制是基于被控对象精确模型的控制方式;智能控制的核心是基于知识进行智能决策,采用灵活机动的决策方式迫使控制朝着期望的目标逼近。
传统控制和智能控制的统一:智能控制擅长解决非线性、时变等复杂控制问题,而传统控制适于解决线性、时不变等相对简单的控制问题。
智能控制的许多解决方案是在传统控制方案基础上的改进,因此,智能控制是对传统控制的扩充和发展,传统控制是智能控制的一个组成部分。
在这个意义上,传统控制和智能控制可以统一在智能控制的框架下,而不是被智能控制所取代。
智能控制研究对象的特点:(1)不确定性的模型 (2)高度的非线性 (3)复杂的任务要求智能控制的特点:(1)分层递阶的组织结构 (2)自学习能力 (3)自适应能力 (4)自组织能力(5)优化能力4、专家系统:是一类包含着知识和推理的智能计算机程序,其内部含有大量的某个领域的专家水平的知识和经验,具有解决专门问题的能力。
专家控制:是将专家系统的理论和技术同控制理论、方法与技术相结合,在未知环境下,仿效专家的经验,实现对系统的控制。
2.第二章方框图及简化(new)

多个输入同时作用于线性系统时,分别考虑 每个输入的影响
• 如考虑扰动的反馈控制系统:
• 只考虑给定输入时:
• 只考虑干扰输入时:
• 如考虑扰动的反馈控制系统:
• 只考虑给定输入时:
• 只考虑干扰输入时:
• 系统总的输出量
扰动的影响将被抑制!!!
若 G1 ( s )G2 ( s ) H ( s ) >> 1 且 G1 ( s) H ( s ) >> 1 ,则:
X o ( s) ≈ 1 X i ( s) H ( s)
• 上式表明,采用反馈控制的系统,适当选 上式表明,采用反馈控制的系统, 择元部件的结构参数, 择元部件的结构参数,可以增强系统抑制 干扰的能力。 干扰的能力。
• 结论 • 闭环系统具有抑制干扰的能力; • 闭环系统输入、输出的取法不同时,其传 递函数不同,但传递函数的分母不变,而 开环系统则不然。
反馈连接及其等效原则前向通道传递函数反馈回路传递函开环传递函数闭环传递函数前向通道反馈通道开环传递函数都只只是闭环系统部分环节或环节组合的传递函数而闭环传递函数才是系统的传递函数
第二章 系统的数学模型
2.3 系统的传递函数方框图及其简化
• 将组成系统的各个环节用传递函数方框表示,并将相应的变 量按信息流向连接起来,就构成系统的传递函数方框图
• 例2-10
• 一定要注意梅逊公式的两个条件; • 若系统不满足两个条件,可先将其方框图 化成满足使用条件的形式,然后再利用梅 逊公式。
多个输入同时作用于线性系统时,分别考虑 每个输入的影响
• 如考虑扰动的反馈控制系统:
• 只考虑给定输入时:ຫໍສະໝຸດ • 只考虑干扰输入时:• 如考虑扰动的反馈控制系统:
《人工智能》(答案)

I N 22 { P, Q} , 使子句 P Q 为假
I N 23 { P ,Q} , 使子句 P Q 为假
I N 21 { P, Q} , 使子句 P Q 为假
B ( y ) D (x, f ( x))
即该语义树是封闭的,由海伯伦定理知该子句集不可满足。证毕。 8. 证:此问题既是证明公式 (( H ( x) M ( x)) H ( a) M ( a)) 为恒假
1978
19. 分层前向网络 20. 槽 侧面 21. 综合数据库 22. 叙述性表示
反馈层向网络
规则库 控制系统 过程性表示
互连前向网络
二、选择题
1.B 2.C 3.C 4.C 5.A 6.B 7.A 8.B 9.C 10.D 11.D 12.B 13.C 14.A 15.D 16.B 17.A 18.B 19.B 20.A 三、判断题
(3)设 Input(x) :表示 x 是输入算法; Unification(y) :表示 y 是不能合一算法; Output(x) : 表示 x 是输出算法; mug(y) :y 是最小合一; Fall(x) :表示 x 失败,那么我们可以用一 阶谓词逻辑表示为:
( x)Input ( x) Unificatio n(x ) ( y)Output ( y ) Mug ( y);
xQ (x))
=
x ( P( x)
yQ ( y))
= x ( P (x)
yQ ( y))
= x(P ( x)
yQ ( y ))
= x(P ( x)
y Q ( y))
= x y ( P( x)
Q ( y))
12. 解: 1) ((x) P(x)
∨ (x) Q(x)) → (x) ( P(x) ∨ Q(x) )
第二章习题解题过程和参考答案

第二章习题解题过程和参考答案第二章习题解题过程和参考答案2-1 试建立题2-1图所示各系统的微分方程 [其中外力)(t f ,位移)(t x 和电压)(t u r为输入量;位移)(t y 和电压)(t u c为输出量;k (弹性系数),μ(阻尼系数),R (电阻),C (电容)和m (质量)均为常数]。
解:2-1(a) 取质量m 为受力对象,如图,取向下为力和位移的正方向。
作用在质量块m 上的力有外力f(t),重力mg ,这两个力向下,为正。
有弹簧恢复力[]0)(y t y k +和阻尼力()dy t dtμ,这两个力向上,为负。
其中,0y 为0)(=t f 、物体处于静平衡位置时弹簧的预伸长量。
根据牛顿第二定理F ma ∑=,有[]22()()()()dy t d y t f t mg k y t y m dt dtμ+-+-= 其中:0ky mg =代入上式得22)()()()(dt t y d mdt t dy t ky t f =--μ整理成标准式:22()()()()d y t dy t m ky t f t dt dtμ++=μμ()f t[()k y t +()dy t dt或也可写成:22()()1()()d y t dy t k y t f t dt m dt m mμ++=它是一个二阶线性定常微分方程。
2-1(b) 如图,取A 点为辅助质点,设该点位移为()Ax t ,方向如图。
再取B 点也为辅助质点,则该点位移即为输出量()y t ,方向如图A 点力平衡方程:1()()[()()][]AAdx t dy t k x t x t dt dtμ-=- ① B 点力平衡方程:2()()()[]Adx t dy t k y t dt dtμ=- ②由①和②:12[()()]()A k x t x t k y t -= 得:21()()()Akx t x t y t k=-二边微分:21()()()Adx t k dx t dy t dt dt k dt=-③将③代入②:221()()()()[]k dx t dy t dy t k y t dt k dt dtμ=--整理成标准式:1221()()()k k k dy t dx t y t k dt dtμ++=或也可写成:()A t AB1211212()()()()k k k dy t dx t y t dt k k k k dtμ+=++它是一个一阶线性定常微分方程。
自动控制原理课后习题答案第二章

第 二 章2-3试证明图2-5(a)的电网络与(b)的机械系统有相同的数学模型。
分析 首先需要对两个不同的系统分别求解各自的微分表达式,然后两者进行对比,找出两者之间系数的对应关系。
对于电网络,在求微分方程时,关键就是将元件利用复阻抗表示,然后利用电压、电阻和电流之间的关系推导系统的传递函数,然后变换成微分方程的形式,对于机械系统,关键就是系统的力学分析,然后利用牛顿定律列出系统的方程,最后联立求微分方程。
证明:(a)根据复阻抗概念可得:2221212112212211212112212122111()1()111oiR u C s R R C C s R C R C R C s R u R R C C s R C R C R C C sR C s R C s+++++==+++++++即220012121122121212112222()()i i o id u du d u duR R C C R C R C R C u R R C C R C R C u dt dt dt dt++++=+++取A 、B 两点进行受力分析,可得:o 112()()()i o i o dx dx dx dx f K x x f dt dt dt dt -+-=- o 22()dx dxf K x dt dt -= 整理可得:2212111221121212211222()()o o i i o id x dx d x dx f f f K f K f K K K x f f f K f K K K x dt dt dt dt ++++=+++经比较可以看出,电网络(a )和机械系统(b )两者参数的相似关系为1112221211,,,K f R K f R C C2-5 设初始条件均为零,试用拉氏变换法求解下列微分方程式,并概略绘制x(t)曲线,指出各方程式的模态。
(1) ;)()(2t t x t x =+(2))。
第二章 传递函数-梅逊公式
2.3 传递函数与系统动态结构图
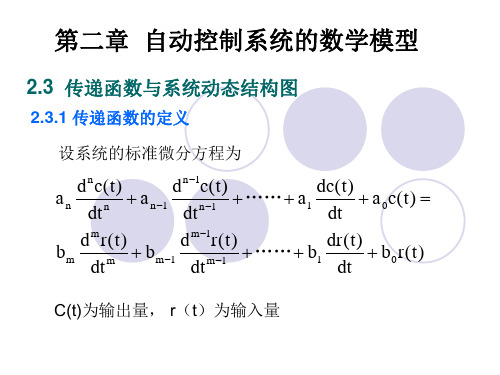
2.3.1 传递函数的定义
设系统的标准微分方程为
an
dnc(t) dt n
a n1
dn1c(t) dt n 1
……
a1
dc(t) dt
a0c(t)
bm
dmr(t) dt m
bm1
d m 1r ( t ) dt m1
……
b1
dr(t) dt
点
上图所示的是
G(s)
(s
(s 1)(s 2) 3)(s 2 2s
2)
的零、极点分布图。
2.2 传递函数
比
比例环节(无惯性环节): c(t)=kr(t)
例
传递函数:G(S)=C(S)/R(S)=k
c(t)
环
阶跃响应:R(S)=1/S
r(t)
节
C(S)=kR(S)=k/S C(t)=k
0
方框图: R(S) k/s C(S)
3
传
递
积分调节器:
C
在A点列方程可得:
函 数
Ur(t)
R
i2
i1
A
Uc(t) i2=i1, i1=Uc(t)/R Uc(t)=1/C∫i2(t)dt=1/(RC)∫Uc(t)dt
设RC=T(积分时间常数),则有:Uc(t)=1/T∫Uc(t)dt
拉氏变换后为:Uc(S)=1/(TS)Uc(S)
5)传递函数具有正、负号(输入量和输出量的变化方向)。
6)传递函数的单位是输出量的单位与输入量的单位之比。
m
(s z j )
7)传递函数可以写成
G(s)
Kg
j1 n
(完整版)自动控制原理试题答案
(完整版)⾃动控制原理试题答案∑??=i i i s s Q s H )()(1)(zidpngkongzhi1 闭环系统(或反馈系统)的特征:采⽤负反馈,系统的被控变量对控制作⽤有直接影响,即被控变量对⾃⼰有控制作⽤。
2 典型闭环系统的功能框图。
⾃动控制在没有⼈直接参与的情况下,通过控制器使被控对象或过程按照预定的规律运⾏。
⾃动控制系统由控制器和被控对象组成,能够实现⾃动控制任务的系统。
被控制量在控制系统中.按规定的任务需要加以控制的物理量。
控制量作为被控制量的控制指令⽽加给系统的输⼊星.也称控制输⼊。
扰动量⼲扰或破坏系统按预定规律运⾏的输⼊量,也称扰动输⼊或⼲扰掐⼊。
反馈通过测量变换装置将系统或元件的输出量反送到输⼊端,与输⼊信号相⽐较。
反送到输⼊端的信号称为反馈信号。
负反馈反馈信号与输⼈信号相减,其差为偏差信号。
负反馈控制原理检测偏差⽤以消除偏差。
将系统的输出信号引回插⼊端,与输⼊信号相减,形成偏差信号。
然后根据偏差信号产⽣相应的控制作⽤,⼒图消除或减少偏差的过程。
开环控制系统系统的输⼊和输出之间不存在反馈回路,输出量对系统的控制作⽤没有影响,这样的系统称为开环控制系统。
开环控制⼜分为⽆扰动补偿和有扰动补偿两种。
闭环控制系统凡是系统输出端与输⼊端存在反馈回路,即输出量对控制作⽤有直接影响的系统,叫作闭环控制系统。
⾃动控制原理课程中所讨论的主要是闭环负反馈控制系统。
复合控制系统复合控制系统是⼀种将开环控制和闭环控制结合在⼀起的控制系统。
它在闭环控制的基础上,⽤开环⽅式提供⼀个控制输⼊信号或扰动输⼊信号的顺馈通道,⽤以提⾼系统的精度。
⾃动控制系统组成闭环负反馈控制系统的典型结构如图1.2所⽰。
组成⼀个⾃动控制系统通常包括以下基本元件.给定元件给出与被控制量希望位相对应的控制输⼊信号(给定信号),这个控制输⼊信号的量纲要与主反馈信号的量纲相同。
给定元件通常不在闭环回路中。
2.测量元件测量元件也叫传感器,⽤于测量被控制量,产⽣与被控制量有⼀定函数关系的信号。
第二章 控制系统的数学模型习题及答案
第二章 控制系统的数学模型习题及答案2-1 试建立下图所示各系统的微分方程。
其中电压)(t u r 和位移)(t x 为输入量;电压)(t u c 和位移)(t y 为输出量;R (电阻),C (电容),k (弹性系数),和f (阻尼系数),均为常数。
解:(a )应用复数阻抗概念可写出)()(11)(11s U s I csR cs R s U c r ++= (1) 2)()(R s Uc s I =(2) 联立式(1)、(2),可解得:CsR R R R Cs R R s U s U r c 212112)1()()(+++=微分方程为:r r c c u CR dt du u R CR R R dt du 121211+=++ (b )如图解2-1(b)所示,取A,B 两点分别进行受力分析。
对A 点有 )()(111dtdydt dx f x x k -=- (1) 对B 点有 y k dtdydt dx f 21)(=- (2) 联立式(1)、(2)可得:dtdx k k k y k k f k k dt dy2112121)(+=++ 2-2 试证明下图所示的力学系统(a)和电路系统(b)是相似系统(即有相同形式的数学模型)。
解:(a) 取A 、B 两点分别进行受力分析,如图解所示。
对A 点有)()()(1122y y f y xf y x k -=-+- (1) 对B 点有1111)(y k y yf =- (2) 对式(1)、(2)分别取拉氏变换,消去中间变量1y ,整理后得)()(s X s Y = 21212121221212212121()1()1f f f fs s k k k k f f f f f s s k k k k k +++++++21221221221211221221k k s )k f k f k f (s f f k k s )k f k f (s f f +++++++= (b) 由图可写出sC R s U c 221)(+= sC R s C R sC R s U r 111112111)(+⋅++整理得)()(s U s U r c = 1)(1)(21221122121221122121+++++++s C R C R C R s C C R R s C R C R s C C R R 比较两系统的传递函数,如果设112211221,1,,,R k R k C f C f ====则两系统的传递函数相同,所以两系统是相似的。
移动通信复习资料
移动通信复习资料移动通信原理与系统复习资料第⼀章:1.在4G系统中,⽹元间的协议是基于IP的,每⼀个MT(移动终端)都有各⾃的IP地址。
2.IP核⼼⽹:它不是专门⽤作移动通信,⽽是作为⼀种统⼀的⽹络,⽀持有线和⽆线接⼊。
主要功能是:完成位置管理和控制、呼叫控制和业务控制。
3.4G⽹络应该是⼀个⽆缝连接的⽹络,也就是说各种有线和⽆线⽹都能以IP协议为基础连接到IP核⼼⽹。
当然为了与传统的⽹络互联则需要⽤⽹关建⽴⽹络的互联,所以将来的4G⽹络将是⼀个复杂的多协议的⽹络。
4.移动通信的定义:指通信双⽅或⾄少有⼀⽅处于运动中进⾏信息交换的通信⽅式。
5.移动通信系统包括:⽆绳电话、⽆线寻呼、陆地蜂窝移动通信、卫星移动通信等。
6.⽆线通信是移动通信的基础。
7.移动通信所受⼲扰种类:(1):互调⼲扰:指两个或多个信号作⽤在通信设备的⾮线性器件上,产⽣与有⽤信号频率相近的组合频率。
从⽽对通信系统构成⼲扰的现象。
(2):邻道⼲扰:指相邻或邻近的信道之间的⼲扰,是由于⼀个强信号串扰弱信号⽽造成的⼲扰。
(3):同频⼲扰:指相同频率电台之间的⼲扰。
8.移动通信的⼯作⽅式:(1):单⼯通信:指通信双⽅电台交替地进⾏收信和发信。
它常⽤于点到点通信。
(2)双⼯通信:指通信双⽅。
收发信机均同时⼯作。
即任⼀⽅讲话时都可以听到对⽅的话⾳,没有“按-讲”开关。
(3)半双⼯通信第⼆章:1. 移动通信的信道:指基站天线、移动⽤户天线和两幅天线之间的传播路径。
2. 从某种意义上来说,对移动⽆线电波传播特性的研究就是对移动信道的研究。
(判断)3. 移动信道的基本特性就是衰落特性。
4. ⽆线电波的传播⽅式:直射、反射、绕射和散射以及它们的合成。
5. 移动信道是⼀种时变信道。
在这种信道中传播表现出来的衰落⼀般为:随信号传播距离变化⽽导致的传播损耗和弥散。
6. (1)阴影衰落:由于传播环境中的地形起伏、建筑物及其它障碍物对电磁波的遮蔽所引起的衰落。
自动控制原理课后习题答案第二章
解:由图可得
联立上式消去中间变量U1与U2,可得:
2-8某位置随动系统原理方块图如图2-7所示。已知电位器最大工作角度,功率放大级放大系数为K3,要求:
(1) 分别求出电位器传递系数K0、第一级与第二级放大器得比例系数K1与K2;
(2) 画出系统结构图;
(3) 简化结构图,求系统传递函数。
证明:(a)根据复阻抗概念可得:
即 取A、B两点进行受力分析,可得:
整理可得:
经比较可以瞧出,电网络(a)与机械系统(b)两者参数得相似关系为
2-5 设初始条件均为零,试用拉氏变换法求解下列微分方程式,并概略绘制x(t)曲线,指出各方程式得模态。
(1)
(2)
2-7由运算放大器组成得控制系统模拟电路如图2-6所示,试求闭环传递函数Uc(s)/Ur(s)。
2-10试简化图2-9中得系统结构图,并求传递函数C(s)/R(s )与C(s)/N(s)。
图2-9 题2-10系统结构图
分析:分别假定R(s)=0与N(s)=0,画出各自得结构图,然后对系统结构图进行等效ቤተ መጻሕፍቲ ባይዱ换,将其化成最简单得形式,从而求解系统得传递函数。
解:(a)令N(s)=0,简化结构图如图所示:
可求出:
令R(s)=0,简化结构图如图所示:
所以:
(b)令N(s)=0,简化结构图如下图所示:
所以:
令R(s)=0,简化结构图如下图所示:
2-12 试用梅逊增益公式求图2-8中各系统信号流图得传递函 数C(s)/R(s)。
图2-11 题2-12系统信号流图
解:
(a)存在三个回路:
存在两条前向通路:
所以:
(3)简化后可得系统得传递函数为
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
= ∑dm-1(i)xm2 (i) r j
i=1
2.5.2 BP算法的数学表达 算法的数学表达
其中
m m dm-1(i) = d1 (i)w1,r1f ′ r (i)) (um-1 r
2.5.1 BP算法的原理 算法的原理
B. 反向传播 把误差信号按 原来正向传播 的路径反向传 回到每个神经 元,并对每个 隐层的各神经 元的权系数进 行修改,以使 误差信号趋向 最小.
Activation Flows
Hidden Output Units Output Units Input Units
w ∝ -gradwk
k r,j
r,j
e e 显然,根据BP算法原则,求 最关键.下面讨论求 ,有 k k wr,j wr,j
n e (xim oi ) n m xim = ∑(xim oi ) = ∑(xi oi ) k k k wr,j i=1 wr,j wr,j i=1
e e =- k wr,j
BP网络及BP算法 网络及BP 2.5 BP网络及BP算法
BP网络是将LMS(梯度下降算法) BP网络是将LMS(梯度下降算法)学习规则一般 网络是将LMS(梯度下降算法 对非线性, 化,对非线性,可微分的函数进行权值训练的多层网 络。 BP网络是一种多层前向反馈神经网络 网络是一种多层前向反馈神经网络, BP网络是一种多层前向反馈神经网络,其神经元 的变换函数是S型函数或其他处处可导的函数。 的变换函数是S型函数或其他处处可导的函数。由于激 活函数必须是处处可微的, 活函数必须是处处可微的,所以它就不能采用二值型 的阈值函数{0,1}或符号函数{-1,1},BP网络经常 的阈值函数{0,1}或符号函数{ 1},BP网络经常 {0 或符号函数 使用的是S型的对数或正切激活函数和线性函数( 使用的是S型的对数或正切激活函数和线性函数(一般 在输出时使用,是满足网络的输出不受限制)。 在输出时使用,是满足网络的输出不受限制)。
1 net 2 ′(net) = f (e ) = o o = o(1o) net 2 (1+ e )
xik = f(uik )
k-1 uik = ∑wi,j xk1 j j=1 nk1
其中nk-1为第k-1隐单元层的神经元个数.
2.2.1 BP算法的原理 算法的原理
BP算法分二步进行,即 NN输出计算的正向传播 正向传播和 正向传播 NN学习过程的反向传播 反向传播. 反向传播 这两个过程的工作简述如下. A. 正向传播 输入的样本从输入层经过隐单元一层一层进行处理,则传 向输出层,即在所给定的输入样本下,计算NN的输出. 在逐层处理的过程中,每一层神经元的状态只对下一 层神经元的状态产生影响. 在输出层把现行输出和期望输出进行比较,如果现行 输出不等于期望输出,则进入反向传播过程.
BP网络及BP算法 网络及BP 2.5 BP网络及BP算法
感知器学习算法是一种单层网络的学习算法. 感知器学习算法是一种单层网络的学习算法.不能用于多层 NN的学习 的学习. NN的学习. 1986年,Rumelhart提出了BP算法 提出了BP算法. 1986年,Rumelhart提出了BP算法.由于适用于多层网络的学 因此是目前应用最广泛的NN学习算法之一, NN学习算法之一 习,因此是目前应用最广泛的NN学习算法之一,在 学习系统、 学习系统、 拟合和逼近、 拟合和逼近、 自动控制 中应用较广. 中应用较广.
2.5.2 BP算法的数学表达 算法的数学表达
k 若k=m-1,即所讨论的 wr, j为输出层与倒数第二层间的权重,则 由上式,有 nm1 m1 m1 f ∑w1,s xs (i) n e s=1 = ∑(xim oi ) m-1 m-1 w1,j w1,j i=1
= ∑(xim oi )f ′ 1 (i))xm1(i) (um j
BP网络及BP算法 网络及BP 2.5 BP网络及BP算法
反向传播算法也称BP算法 反向传播算法也称BP算法 BP
由于这种算法在本质上是一种NN学习的数学模 由于这种算法在本质上是一种NN学习的数学模 NN 所以,有时也称为BP模型。 BP模型 型,所以,有时也称为BP模型。 BP算法是为了解决多层前向NN的权系数优化而 BP算法是为了解决多层前向NN的权系数优化而 算法是为了解决多层前向NN 提出来的,所以,BP算法也通常暗示着NN ,BP算法也通常暗示着NN的拓扑结 提出来的,所以,BP算法也通常暗示着NN的拓扑结 构是一种无反馈的多层前向网络。故而, 构是一种无反馈的多层前向网络。故而,有时也 称无反馈多层前向网络为BP模型。 称无反馈多层前向网络为BP模型。 BP模型2源自5.1 BP算法的原理 算法的原理
图2.6 网络学习结构
2.5.1 BP算法的原理 算法的原理
设有一个m层的NN,并在输入层加有样本x; 设第k层的i神经元的输入总和表示为uik,输出为xik; 从第k-1层的第j个神经元到第k层的第i个神经元的权系数 为wijk-1 各个神经元的激发函数为f(), 则各个变量的关系可用下面有关数学式表示:
BP网络及BP算法 网络及BP 2.5 BP网络及BP算法
结合二者的长处。 结合二者的长处。 将感知器网络结构扩展到多层, 将感知器网络结构扩展到多层,其作用 函数采用一种可微分的非线性函数, 函数采用一种可微分的非线性函数,这就 形成了功能比较强大的多层前向网络。 形成了功能比较强大的多层前向网络。 由于多层前向网络的权值调整是采用反 向传播学习算法( Propagation), 向传播学习算法(Back Propagation), 通常人们将其称为BP网络。 BP网络 通常人们将其称为BP网络。
从上述过程可知: 正向计算过程. 正向计算过程 多层网络的训练方法是把一个样本加到 输入层,并根据向前传播的规则不断一层一层向输出层传 递,最终在输出层可以得到输出xim. 反向学习过程. 反向学习过程 把xim和期望输出oi进行比较,如果两者不 等,则产生误差信号e,接着则按权系数的修正公式反向传 , e, 播修改权系数. 上面公式中,求取本层dik时,要用到高一层的dik+1. 可见,误差函数的求取是从输出层开始,到输入层的反向 传播过程.在这个过程中不断进行递归求误差. 通过多个样本的反复训练,同时向误差渐渐减小的方向对 权系数进行修正,以达最终消除误差.
BP网络及BP算法 网络及BP 2.5 BP网络及BP算法
Hornik等人证明了: Hornik等人证明了: 等人证明了 仅有一个非线性隐层的前馈网络就能以任意精 度逼近任意复杂度的函数. 度逼近任意复杂度的函数. 下面,将深入讨论反向传播学习的BP算法,主要内容有: 下面,将深入讨论反向传播学习的BP算法,主要内容有: BP算法 BP算法的原理 BP算法的原理 BP算法的数学表达 BP算法的数学表达 BP算法的执行步骤 BP算法的执行步骤
k = m1,...,1
k 其中s是指权系数wr, 的修正迭代次数,η是权重变化率,它视情况 j 不同而取值不同,一般取0~1之间的小数.
BP算法解释:隐含层误差dm-1可以认为是由输出层误差 m加 算法解释:隐含层误差 可以认为是由输出层误差d 算法解释 权组合形成的。 权组合形成的。
2.5.2 BP算法的数学表达 算法的数学表达
这里引入drm(i)的意义如前。
e 类似上述推导过程,有如下 计算式 k wr,j n e = ∑dk+1(i)xk (i) k = m3,...,2,1 r j wk i=1 r,j
其中
nk+1 k+1 k k dr (i) = ∑ds (i)ws,r f ′ r (i)) (uk s=1
2.5.2 BP算法的数学表达 算法的数学表达
BP网络的神经元的非线性激发函数为 函数, 网络的神经元的非线性激发函数为S 若BP网络的神经元的非线性激发函数为S函数, 由于神经元的输出: 由于神经元的输出:
1 o = f ( net ) = 1 + e net 其中net 其中 i=x1w1i+x2w2i+…+xnwni
2.5.1 BP算法的原理 算法的原理
BP算法的原理 1. BP算法的原理
BP算法是用于前馈多层网络的学习算法,前馈多层网络的结 BP算法是用于前馈多层网络的学习算法, 算法是用于前馈多层网络的学习算法 构一般如图2.6所示. 2.6所示 构一般如图2.6所示. 它含有输入层、输出层以及处于输入输出层间的中间层. 它含有输入层、输出层以及处于输入输出层间的中间层. 中间层有单层或多层, 中间层有单层或多层,由于它们和外界没有直接的联 故也称为隐层. 系,故也称为隐层. 在隐层中的神经元也称隐单元. 在隐层中的神经元也称隐单元. 隐层虽然和外界不连接, 隐层虽然和外界不连接,但是它们的状态影响输入输 出之间的关系. 出之间的关系. 这也是说,改变隐层的权系数,可以改变整个多 这也是说,改变隐层的权系数, NN的性能 的性能. 层NN的性能.
第二章: 第二章:前馈网络
BP网络及BP算法 网络及BP 2.5 BP网络及BP算法
感知器网络和线性激活函数,都存在一定缺点。 感知器网络和线性激活函数,都存在一定缺点。 单层感知器:硬限幅函数为作用函数, 单层感知器:硬限幅函数为作用函数,只能解 决简单的分类问题。 决简单的分类问题。 硬限幅函数的不可微分特性, 硬限幅函数的不可微分特性,使其扩展到多层 感知器时带来权值修正的困难。 感知器时带来权值修正的困难。 线性函数网络采用线性作用函数, 线性函数网络采用线性作用函数,处理复杂非 线性问题的能力相对较弱。 线性问题的能力相对较弱。 采用线性作用函数的多层网络等效为一个单层 线性网络,因此,简单地从结构上扩展Adaline 线性网络,因此,简单地从结构上扩展Adaline 并 不能加强它处理非线性问题的能力。 不能加强它处理非线性问题的能力。
