机器人学-欧拉角与RPY角
工业机器人学第三章习题

A3-1.写出齐次变换矩阵 T,它表示相对固定坐标系{A}作以下变换。
B1) 绕Z 퐴轴旋转 90°; 2) 再绕X 퐴轴转-90°;푇3) 最后做移动【3 7 9 】;A3-2.写出齐次变换矩阵 T,它表示相对坐标系{B}做以下变换。
B 푇1) 移动【3 7 9 】;2) 绕X 퐵轴旋转-90°; 3) 绕Z 퐵轴转 90°。
3-3.求下面齐次变换的逆变换푇−1 0 1 0 −10 0 −1 2 −1 0 0 0 T = []13-4.已知 0.25 0.43 0.86 5.0A B T 0.87 −0.50 0 −4.0= [ ] 0.43 0.75 −0.50 3.0 0 0 0 1A求 T的第(2,4)元素.B3-5 已知矩阵? 0 −1 0 ? 0 0 1 ? −10 2 ?1] [代表齐次坐标变换,求其中的未知元素值(第一列元素)。
푈3-6 设工件相对于参考系{U}的描述为T,机器人基座相对于参考系푃푈的描述为T,已知B010−1100100−12−1000푈=[푇푃0105푈]푃=[]퐵001900010001要求机器人手爪坐标系{H}与工件坐标系{P}重合,试求变换퐻퐵푇3-7. 已知坐标变换矩阵푈퐴푇,퐵퐴푇,푈퐶푇.0.866−0.50001110000.5000.8660−100.866−0.50010푈=[]퐵퐴푇=[푇] 퐴001800.5000.866−200001000 10.866−0.5000−30.4330.750−0.5−3퐶=[푇]푈0.2500.4330.86630001画出空间尺寸链图,并求퐵퐶푇.3-8.如图3-17 所示的多面体顶点坐标系,试求4x4 的齐次变换矩阵푖−1푖푇和0푖푇(i=1,2,3,4,5).3-9. 如图3-18 所示的多面体各顶点坐标系,试求4x4 的齐次变换矩阵푖−1푖푇和0푖푇(i=1,2,3,4).3-10. 如图3-19 所正方体的顶点和中心坐标系,试求4x4 的齐次变换矩阵푖−1푖푇和0푖푇(i=1,2,3)。
欧拉角名词解释

欧拉角名词解释欧拉角(EulerAngles)是旋转空间中最常见的表示姿态变换的数学方法,用它可以表示物体以某种方式从一个姿态旋转到另一个姿态的变换。
它是由普林斯顿大学的数学家兼物理学家Leonhard Euler 发明的一种角度表示法,因此也叫做“尤拉角”。
欧拉角一般被用来描述复杂的三维旋转,可以准确地表示一个空间中的物体的姿态。
【定义】欧拉角定义为三个独立的角度,如α,β,γ,分别表示绕某个坐标轴的顺时针或逆时针旋转角度。
它可以用来指定一个坐标系在另一个坐标系中的方位,以及实现两个坐标系相对旋转的偏转量。
【类型】欧拉角可以分为两种:绕Z-Y-X(顺时针)和绕Z-X-Y(逆时针)。
绕Z-Y-X欧拉角,第一个角度α表示绕Z轴旋转,第二个角度β表示绕Y轴旋转,第三个角度γ表示绕X轴旋转。
而绕Z-X-Y欧拉角中,第一个角度α表示绕Z轴旋转,第二个角度β表示绕X轴旋转,第三个角度γ表示绕Y轴旋转。
【应用】欧拉角在机器人、航空航天、计算机视觉等领域有着广泛的使用。
欧拉角可以用来精确描述物体的旋转变换,进而可以更加精确的描述物体的位置和姿态。
在用欧拉角表示旋转时,需要进行一定的换算,以解决旋转变换的问题,以确保得到的旋转变换的准确性。
另外,欧拉角还可以用来解决其他空间变换问题,例如多维空间的缩放问题,可以用旋转矩阵来进行求解。
由此可见,欧拉角在多维空间变换领域有着广泛的应用。
【特点】欧拉角的一个优点在于它不会受到四元数(Quaternion)的混乱,也不会受到旋转矩阵的低效问题的困扰,它具有较高的准确度和计算效率,从而使得欧拉角成为空间绝对变换的理想表示方法。
此外,欧拉角有着很好的迭代特性,可以容易地模拟空间物体的仿射变换。
当然,欧拉角也有一些缺点,例如它不容易用来表示方位不同,但同时仍未实现旋转差异的情况,这就要求其时刻保持七个自由度,以免发生死区现象。
【总结】从上面可以看出,欧拉角是旋转空间中最常见的表示姿态变换的数学方法,它可以准确地表示一个空间中的物体的姿态。
智慧树答案机器人学基础知到课后答案章节测试2022年

第一章1.为什么要发展机器人技术()。
答案:精神需求;生产需求;生活需求;探索需求2.下列哪个不是国内的机器人公司()。
答案:柯马3.沃康松发明的机械鸭,能够做扇动翅膀,吃谷物和排便的动作。
()答案:对4.按照机器人的几何结构来分,可分为:()答案:球面坐标;笛卡尔坐标;关节球面坐标;柱面坐标5.按照机器人的控制方式来分,可分为:()答案:非伺服机器人;伺服机器人6.机器人系统中的计算机就相当于人体的什么?()答案:大脑7.机器人的传感器分为内部传感器和外部传感器。
()答案:对8.机器人的精度是指机械零件抵抗变形的能力。
()答案:错9.机器人的控制系统包括()答案:作业控制器;驱动控制器;运动控制器10.搬运机器人属于下列那类机器人()答案:工业机器人第二章1.刚体的位姿表示刚体的位置和姿态,位置用p矩阵表示,姿态用R矩阵表示。
()答案:对2.刚体的位姿一般用什么样的矩阵来表示()。
答案:3×43.以下哪个矩阵表示坐标轴x轴()。
答案:[1 0 0 0]4.旋转变换与变换次序有关。
()答案:对5.以下哪个坐标系表示机器人的基坐标系()。
答案:{B}6.先沿着基坐标系的x轴平移r,再绕基坐标系的z轴旋转α,最后延基坐标系的z轴平移z,形成球面坐标。
()答案:错7.RPY角是绕着当前轴旋转的序列。
()答案:错8.如果已知一个任意的旋转矩阵,可以直接通过公式求得这个旋转变换的等效转角和等效转轴。
()答案:对9.旋转矩阵不是正交矩阵。
()答案:错10.欧拉角是绕着固定轴旋转的序列。
()答案:错第三章1.一个六自由度工业机器人,决定了其末端姿态()。
答案:手腕部分的后三个自由度2.沿着关节的运动轴方向,能确定连杆坐标系的()。
答案:z轴3.D-H参数中ai-1表示()。
答案:zi-1沿着xi-1到zi的距离4.一旦机器人的结构确定了,那么机器人的连杆参数就不变了,只有关节参数会发生变化。
()答案:对5.机器人运动学方程的求解步骤包括()。
机器人学第3章 机器人运动学

(3.46)
如果已知一个表示任意旋转的齐次变换,那么就能够 确定其等价欧拉角。
3.2 机械手运动方程的求解
21
3.2.2 滚、仰、偏变换解
直接从显式方程来求解用滚动、俯仰和偏转表示的变 换方程。 RPY变换各角如下:
atan2(n y , n x ) 180 atan2(n z , cn x sn y ) atan2( sa x ca y , so x co y )
0
T6 0T1 (1 )1T2 (2 )2T3 (3 )3T4 (4 )4T5 (5 )5T6 (6 )
3.1 机器人运动方向的表示
5
3.1.1 运动姿态和方向角
用横滚、俯仰和偏转角表示运动姿态 另一种常用的旋转集合是横滚(roll)、俯仰(pitch) 和偏转(yaw)。
图3.3 用横滚、俯仰和偏转表示机械手运动姿态
3.1 机器人运动方向的表示 6
3.1.1 运动姿态和方向角
对于旋转次序,规定:
1
(3.16)
3.1 机器人运动方向的表示
15
3.1.3 连杆变换矩阵及其乘积
如果机械手与参考坐标系的相对关系是由变换 Z 来 表示的,而且机械手与其端部工具的关系由变换 E 表示,那么此工具端部对参考坐标系的位置和方向 可由变换 X 表示如下:
可求得:
X ZT6 E
T6 Z 1 XE 1
(3.52)
3.2 机械手运动方程的求解
22
3.2.3 球面变换解
把求解滚、仰和偏变换方程的技术用于球面坐标表示 的运动方程。 球面变换的解为:
atan2( p y , p x ), 180 atan2(cp x sp y , p z )
姿态的欧拉角表示

姿态的欧拉角表示题目:比较分析,找出一种适合乒乓球机器人的末端姿态的欧拉角方法姿态的欧拉角表示任何旋转矩阵都可以通过三个欧拉角进行参数化,一般来说,绕三个坐标轴的顺次旋转可以达到任意的姿态,由于旋转矩阵的乘法是非交换的,因此旋转的次序是很重要的。
按照旋转所绕轴的次序的不同,共有12 种不同的欧拉角。
六种非对称型欧拉角: XYZ,XZY,YXZ,YZX,ZXY 和ZYX;六种对称型欧拉角: XYX,XZX,YXY,YZY,ZXZ 和ZYZ。
记绕三个坐标轴的基本旋转矩阵为:1、非对称型欧拉角表示当三个旋转所绕的坐标轴相互不同时,称为非对称型欧拉角表示。
以XYZ 欧拉角为例,假定起始时物体坐标系与惯性坐标系重合,首先刚体绕物体坐标系的x-轴旋转α角,接着绕y-轴旋转β角,最后绕z-轴旋转角,则刚体最终的姿态矩阵为:上式给出了XYZ 欧拉角参数的正运动学方程,反解该式可求得其逆运动学方程,给定姿态矩阵R=【r ij】3×3时,可求得其逆运动学方程为:从上式可以看出,当β = π2时,逆运动学存在奇异。
其他五种非对称型欧拉角表示的姿态矩阵计算结果列于表1。
这些表示均在β = π2时存在奇异。
对称型欧拉角表示当三个旋转所绕的坐标轴第一个和第三个相同时,称为对称型欧拉角表示,以ZYZ欧拉角为例,首先绕物体坐标系的z-轴旋转α角,接着绕y-轴旋转β角,最后绕x-轴旋转γ角,则刚体最终的姿态矩阵为:另外还有五种对称型欧拉角表示的姿态矩阵列于表2。
这些表示均在β = 0 时存在奇异。
欧拉角表示与RPY 角表示的对偶性姿态的三参数描述还有一种称为RPY 角参数的方法。
1 和 2 中所描述的欧拉角参数的运动过程都是在物体坐标系中进行的,因此其姿态矩阵是按照矩阵的右乘规则得到的。
而RPY 角参数的运动过程则是在惯性坐标系中完成的,其姿态矩阵是按照矩阵的左乘规则得到。
这样,与12 种欧拉角参数相对应的就有12 种RPY 角参数。
机器人运动学

58
斯坦福机器人反向运动学方程求解
• 已知斯坦福机器人的运动学方程为T6=A1A2A3A4A5A6, 以及T6 矩阵与各杆参数a、α、d,求关节变量θ1~θ6 , 其中θ3= d3。
• 求θ1:
59
斯坦福机器人反向运动学方程求解
• 求θ1:
• “+”号对应右肩位姿,“-”号对应左肩位姿。60
斯坦福机器人反向运动学方程求解
2 机器人运动学
• • • • 齐次坐标及动坐标系、对象物位姿的描述 齐次变换 机器人连杆坐标系及其齐次变换矩阵 机器人运动学方程及其求解
1
齐次坐标及动坐标系、对象物位姿的描述 • • • • • 点的直角坐标描述 点的齐次坐标描述 坐标轴方向的齐次坐标描述 动坐标系位姿的齐次坐标描述 对象物位姿的齐次坐标描述
n cos30 cos60 cos90 0 T 0.866 0.500 0.000 0
P 2 1 cos90 0 T 0.500 0.866 0.000 0 a 0.000 0.000 1.000 0
2
点的直角坐标描述
式中:Px、Py、Pz是点P在坐标 系{A}中的三个位置坐标分量。
点的直角坐标描述
3
点的齐次坐标描述
• 齐次坐标的表示不是惟一的,将其各元素同 乘一非零因子ω后,仍然代表同一点P,即
4
坐标轴方向的齐次坐标描述
坐标轴方向的描述
5
• 4 1列阵[a b c w]T中第四个元素不为零,则表示空 间某点的位置; • 4 1列阵[a b c w]T 中第四个元素为零,且满足 a2 + b2 + c2 = 1,则表示某轴(矢量)的方向。
44
正向运动学方程求解
3机器人的位姿描述与坐标变换
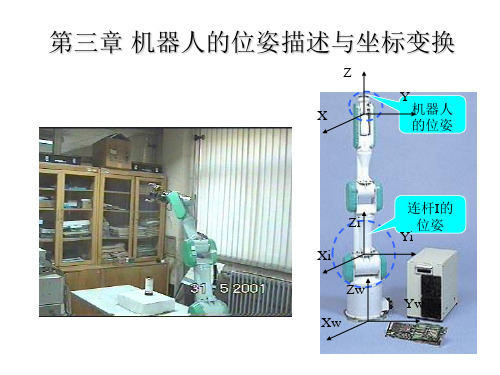
假设:
整理得:
旋转变换通式
讨论:
(1)
(2)
(3)
例:坐标系B原来与A重合,将坐标系B绕过原点O的轴线
转动
,求旋转矩阵
解答:
1)
2)
3)带入旋转通式得:
2、等效转轴与等效转角
转轴和转角
旋转矩阵
1
2?
1)将方程两边矩阵的主对角线元素分别相加,则
2)将方程两边矩阵的非对角线元素成对相减得:
►绕多个坐标轴旋转的转动矩阵
1)、绕固定坐标系旋转
2)、绕运动坐标系旋转
ZYZ欧拉角
注意:多个旋转矩阵连乘时,次序不同则含义不同。1)绕新的动坐标轴依次转动时,每个旋转矩阵要从左往右乘,即旋转矩阵的相乘顺序与转动次序相同;2)绕旧的固定坐标轴依次转动时,每个旋转矩阵要从右往左乘,即旋转矩阵的相乘顺序与转动次序相反。
解:
1)
2)
Z
i
X
i
Y
i
P
坐标系j由坐标系i旋转而成
求点P在i坐标系的坐标:
已知点P在j坐标系的坐标:
P
☺
►姿态矢量矩阵
坐标系j相对于i的方位
旋转矩阵的性质:
旋转矩阵
►绕一个坐标轴旋转的转动矩阵
1)RX
2)RY
3)RZ
转动矩阵的特点:(1) 主对角线上有一个元素为1,其余均为转角的余弦/正弦;(2) 绕轴转动的次序与元素1所在的行、列号对应;(3) 元素1所在的行、列,其它元素均为0;(4) 从元素1所在行起,自上而下,先出现的正弦为负,后出现的为正,反之依然。
2、变换矩阵T的相乘 ★矩阵相乘的顺序一般不可换,特殊可换的情况为变换都是同参考系下的平移或绕同一坐标轴的旋转。
机器人运动学

R3
Z
三个平移自由度 T1, T2, T3
三个旋转自由度 R1, R2, R3
T3
T1
T2
Y R2
X
2019/3/31
R1
2.2 刚体位姿描述
方位描述
第三章
机器人运动学
利用固定于物体的坐标系描述方位 (orientation)。方位又称为姿 态 (pose)。
在刚体 B上设置直角坐标系 {B} ,利用与 {B} 的坐标轴平行 的三个单位矢量表示B的姿态。
A
p R ( x , ) p
B
zB
zA
Bp
P
yB
{A}
1 0 R ( x , ) 0 c 0 s
c R ( y , ) 0 s 0 s 1 0 , 0 c
0 s c
s c 0 0 0 1
2019/3/31
i A iB A jB r11 r12
第三章
机器人运动学
2.2 刚体位姿描述
位置与姿态的表示 相对于参考坐标系{A},坐标系{B}的原点位置和坐标轴的 方位可以由位置矢量和旋转矩阵描述。刚体B在参考坐标 系{A}中的位姿利用坐标系{B}描述。
{ B}
当表示位置时 当表示方位时
zA
iB
jB
A
kA 坐标系{B}的三个单位主矢量在坐标系{A}中的描述:
pBo
kB
yA
{ A iB , A jB , A k B }
坐标系{B}相对于坐标系{A}的姿态描述:
A B
O
R { iB , jB , k B }
A A A
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0
1 0 0 0 c s 0
0 0 1 0 s 0 c 0 0 s c 0
0
0
0
1
0
0 0 1 0 0
0 1
将矩阵相乘得:
cc c s s sc c s c s s 0
Euler( , , ) sc s s s cc s s c c s 0
(3)
s
c s
c c
0
0
0
0
1
这一结果与绕固定轴X-Y-Z旋转的结果完全相同。
这种现象称为万向节锁死(gimbal lock)
机器人学院
二者对应关系
RPY角 (α、β、γ)
一对一 一对多
齐次变换矩阵 T
一对多有什么问题?
机器人学院
3.欧拉角
1、z-y-x欧拉角 这种坐标系运动的描述如下:
初始:运动坐标系的初始方位与参考坐标系相同。 运动:首先使运动系绕参考系的Z轴转α角,然后绕运动系的Y轴转 β角,最后绕运动系的X轴转γ角。
机器人学院
nx ox ax 0 cc c s s sc c s c s s 0
ny oy ay 0 = sc s s s cc s s c c s 0
nz 0
oz 0
az 0
0 1
s
0
c s
0
c c
0
0
1
如果β=±90°,cosβ=0,如何求解?
上述反解退化,这是只能解出α与γ的和或差
动画中的万向节锁死
❖ 这里也可以看出,欧拉角的万向节死锁并不是一 个真正的物理意义上的锁,只是由于我们选取的 空间姿态表示方式不够好,而遇到的一个数学意 义上的“锁”。
❖ 欧拉角的这个麻烦之处,是所有采用三个维度来 描述空间姿态的方法都无法避免的。所幸,数学 家发明出了四元数(Quaternion)的概念,用 四维向量来描述物体在三维空间的姿态以及姿态 变化,就这样完美地解决了万向节锁死的问题, 用起来也极其方便。
三次变换均相对于动系而言,故变换算子右乘,可得:
机器人学院
Euler( , , ) Rot(z, )Rot( y, )Rot(z, )
c s 0 0 c 0 s 0 c s 0 0
s
c
0
0
0
1 0 0 s
c
0 0
0 0 1 0 s 0 c 0 0 0 1 0
0
0
0
1
0
0
0
1
0
机器人学基础
——RPY角与欧拉角
LOGO
nx ox ax px
T ny
oy
ay
p
y
nz 0
oz 0
az 0
pz 1
分析该矩阵,可得:
(1)该矩阵由16个元素组成; (2)第四列表示位置; (3)前三行前三列表示姿态,为旋转矩阵。
oo 1 aa 1 aa 1 oa 0 an 0 n0 0
nx ox ax 0
令: RPY ( , , ) ny oy ay 0
nz 0
oz 0
az 0
0 1
(2)
式(1)与(2)相等,利用对应元素相等,可得到9个方程。共有 3个未知数,9个方程中有6个方程不独立。
因此,可以利用其中的3个方程解出3个未知数。
机器人学院
Atan2(y,x)是双变量反正切函数: 可根据x、y的符号判别求得的角所在的象限。例如:
Atan2(-2.0,-2.0)=-135° Atan2(2.0,2.0)=45° 一般的反正切函数的解可能丢失。 而我们经常在360°的范围内计算角度,因此一般用Atan2函数。 注意:当x=0,y=0时,Atan2为不定的。
机器人学院
nx ox ax 0 cc c s s sc c s c s s 0 ny oy ay 0 = sc s s s cc s s c c s 0
操作臂手爪姿态的规定方法类似,习惯上称为RPY角方法。
机器人学院
2.绕固定轴x-y-z旋转(RPY角)
RPY角描述飞机的姿态
机器人学院
这种描述坐标系{B}的姿态的法则如下: {B}的初始方位与参考系{A}重合。首先将{B}绕xA转γ角,再绕 yA转β角,最后绕zA转α角。如图所示。 因为三次都是相对于固定坐标系{A} 而言,按照“左乘”原则,的相应的 旋转矩阵:
机器人学院
万向节锁死
(xyz)表示固定不变 的外在坐标系,而附着 在end effector上的(xi, yi, zi)则表示其固有坐 标系。
这个机械臂从下往上三 个关节的转角 (θ1, θ2, θ3),不正代表了按照 (Z,X', Y'')顺序的欧 拉角描述的末端执行器 的姿态。
机器人学院
❖ 这个机械臂在θ2=90°(或-90°)处, 这是一个什么情形呢?
❖ 在第二个关节转了90度之后,第三个关节 不管怎么转,其实和第一个关节的转轴是 一样的!这个end effector在此刻失去了 绕外在坐标的y轴旋转的能力。图上只画了 θ1为0°的情况,但很容易想象,不管θ1 是多少,只要θ2=+/- 90°,这样的情况 都必然发生。
❖ 欧拉角的万向节死锁,正是在第二个关节 为90度(或-90度)时出现的。此时,物 体固有坐标系上的欧拉角最后一个旋转轴 ,与欧拉角第一个旋转轴正好重合;原本 可以表示三个自由度的欧拉角变成了只有 两个自由度。
能否用3个参数来表示姿态呢?
RPY角
欧拉角
机器人学院
2.绕固定轴x-y-z旋转(RPY角)
RPY角是描述船舶在海中航行时姿态的一种方法。
(Roll):将船的行驶方向取为Z轴,则绕Z轴的旋转(α角)称为滚动; (Pitch):把绕Y轴的旋转(β角)称为俯仰; (Yaw):而把垂直方向取为X轴,将绕X轴的旋转(γ角)称为偏转。
这种描述法中的各次转动都是相对于 运动坐标系的某轴进行的,而不是相 对于固定的参考系。 这样的三次转动角称为欧拉角。
欧拉角有多少种变换?
机器人学院
欧拉变换矩阵:
Euler(, , ) Rot(z, )Rot( y, )Rot(x, )
c s 0 0 c 0 s 0 1 0 0 0
s
c
0
0
A tan 2( nz2 oz2 , az ) A tan 2(ay , ax ) A tan 2(oz ,nz )
如果sinβ≠0,通常取[0,180°]。当β=0或180时,解是退化的。此时只能得到α和 γ的和或差。
这种现象称为万向节锁死。
机器人学院
RPY角的设定是相对固定坐标系旋转的,欧拉角是相对于运动 坐标系旋转的,都是以一定顺序绕坐标主轴旋转三次得到 方位的描述。他们都存在万向节锁死的现象。
0 0 1
cc c s s cc s sc c s 0
sc c c s sc s cc s s 0
s c
s s
c 0
0
0
0 1
同理,由相应矩阵可求解等价的z-y-z欧拉角。
机器人学院
绕Z-Y-Z转动的欧拉角的反解
nx ox ax 0 ny oy ay 0n0zoz 0az 00 1
如果sinβ≠0,则
机器人学院
这是因为绕固定轴旋转的顺序与绕运动轴旋转的顺序相反, 且旋转的角度也对应相等时,所得到的变换矩阵是相同的。
因此,用Z-Y-X欧拉角与固定轴X-Y-Z转角描述运动坐标系 是完全等价的。
2.绕Z-Y-Z转动的欧拉角
这种坐标系运动的描述如下:
初始:坐标系与参考坐标系重合。
运动:首先使运动系绕ZB轴转动α 角,然后绕运动系的YB轴转β角, 最后绕运动系的ZB轴转γ角。
RPY ( , , ) Rot(zA, )Rot( yA, )Rot(xA, )
机器人学院
c s 0 0 c 0 s 01 0 0 0
RPY( , , ) s c 0 0 0 1 0 00 c s 0 0 0 1 0 s 0 c 00 s c 0
0
0 0 1 0 0 0 10 0 0 1
nz 0
oz 0
az 0
0 1
s
0
c s
0
c c
0
0
1
可得出,cos
nx2
n
2 y
通常取-90°<β<90°中的一个解。
如果cosβ≠0,则得到各个角的反正切表达式:
A tan 2(nz ,
nx2
n
2 y
)
A tan 2(ny , nx )
A tan 2(oz , az )
式中,Atan2(y,x)是双变量反正切函数。
cc c s s sc c s c s s 0
sc s s s cc s sc c s 0
(1)
s
c s
c c
0
0
0
0
1
它表示绕固定坐标系的三个轴依次旋转得到的旋转矩阵, 因此称为绕固定轴X-Y-Z旋转的RPY角法。
机器人学院
现在来讨论它的逆问题:从给定的旋转矩阵求出等价的 绕固定轴X-Y-Z的转角γ、β、α。
