浙江省杭州市2019年中考数学一轮复习第一章数与式第六节数的开方与二次根式同步测试(含答案)
中考数学复习专题6数的开方和二次根式试题(A卷,含解析)

专题6 数的开方和二次根式一、选择题1. (浙江杭州,1,3分)9=( )A .2B .3C .4D .5 【答案】B .【逐步提示】本题考查了二次根式的性质,解题的关键是能利用a a =2(a >0)进行解答,首先应将被开方数9写成32,再利用“a a =2(a >0)”即可锁定答案.【解析】因为9=23=3,故选择B .【解后反思】本题亦可以理解为求9的算术平方根,根据算术平方根的定义进行切入思考与计算:看什么正数的平方等于9,这个正数就是9的算术平方根.另外,二次根式实质上就是非负数的算术平方根,熟练地掌握二次根式的性质:(1)2)(a =a (a ≥0);(2)2a =a =⎩⎨⎧<-≥)0()0(a a a a ,是进行二次根式化简求值的基础.【关键词】二次根式;二次根式的求值;算术平方根2.(浙江杭州,5,3分)下列各式的变形中,正确的是( ) A .x 2·x 3=x 6B .x x =2C .(x 2-x 1)÷x =x -1 D .x 2-x +1=(x -21)2+41 【答案】B .【逐步提示】本题考查了代数式的恒等变形,解题的关键是掌握整式的乘除法法则、二次根式的性质、及完全平方公式的特点.解题时,先按同底数幂乘法法则、整式乘除法法则计算A .C 选项的式子,判断这两个选项的变形的正确性;再根据完全平方式的特点,对D 选项的式子进行变形,从而判断选项D 的正确性;最后根据二次根式性质判断B 选项的正确性,从而轻松解题. 【解析】∵x 2·x 3=x 2+3=x 5,x x =2,(x 2-x 1)÷x =(x 2-x 1)·x 1=x -21x,x 2-x +1=x 2-x +41+43=(x -21)2+43,∴只有选项B 正确,故选择B . 【解后反思】本题是代数式的有关运算,涉及到整式的运算、二次根式的性质,分式的运算.只要熟练地掌握相关的运算法则与性质,对各个选项的变形逐一判断,即可得到正确答案.四个选项的变形,分别考查了代数式的四个领域:同底数幂相乘,底数不变,指数相加,即:a m ×a n =a m +n(m 、n 都是正整数);整式除法,转化为乘法,然后利用分式乘法法则进行计算;配方法得掌握完全平方公式的结构特征:前平方、后平方、积的2倍在中间,就不难进行代数式的配方变形.【关键词】代数式的恒等变形;同底数的乘除法;二次根式的性质;配方法;整式的除法3.(浙江宁波,4,4分)使二次根式1x -有意义的x 的取值范围是( )A. x ≠1B. x > 1C. x ≤1D. x ≥1 【答案】D【逐步提示】本题考查了二次根式的概念,解题的关键是正确理解二次根式有意义的条件. 先根据二次根式有意义的条件建立关于x 的不等式,再解这个不等式确定x 的取值范围. 【解析】根据题意,得10x -≥,解得x ≥1,故选择D .【解后反思】形式)0(≥a a 的式子是二次根式,因此二次根式的被开方数a 应满足条件a ≥0. 解答与二次根式概念有关的问题通常是根据这个条件建立不等式来求解. 【关键词】二次根式 4.(重庆B ,7,4分)若二次根式2a -有意义,则a 的取值范围是( ) A .a ≥2 B .a ≤2 C .a >2 D .a ≠2 【答案】A【逐步提示】a 所在的代数式为二次根式,必须使被开方数为非负数.【解析】由题意可知a -2≥0,解得a ≥2. 故选A .【解后反思】求代数式中字母的取值范围,要看给出的代数式是整式、分式、二次根式,还是有关代数式的组合,然后结合整式、分式及二次根式成立的条件判断即可. 【关键词】二次根式 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30. 31. 32. 33. 34. 35.36.37.38.39.二、填空题1.(山东聊城,13,3分)计算:278132⋅÷ =【答案】12【逐步提示】第一步直接利用二次根式乘除法法则把二次根式乘除法转化为被开方数的乘除法, 第二步计算二次根式乘除法, 第三步化简二次根式.278132⋅81827=272=916=34=12323⨯÷⨯⨯⨯⨯.故填12 .【解后反思】考查了二次根式的乘法,解题的关键是正确运用二次根式的乘法法则及二次根式的化简.二次根式相乘,把被开方数相乘,根指数不变;二次根式相乘,把被开方数相乘,根指数不变.【关键词】二次根式;二次根式乘法;二次根式除法;;2.(山东青岛,9,33282= .【答案】2【逐步提示】先计算分子中的减法,再进行除法运算.【详细解答】解:原式42222222,故答案为2.【解后反思】1.二次根式混合运算顺序:先乘方,再乘除,最后加减;2.二次根式运算的结果一般要化为最简二次根式;3.每个根式都可看成“单项式”,多项式的乘法法则及乘法公式仍然适用.【关键词】二次根式的混合运算3. (山东威海,14,3)188_____________.2【逐步提示】首先化简二次根式使其成为最简二次根式,然后合并同类二次根式.18832222=2 .【解后反思】一个二次根式,满足以下几个条件就被称为最简二次根式:(1) 被开放数不含有开得尽的因数或因式;(2)被开方数中不含分母;(3)分母中不含根号.同类二次根式:化简成最简二次根式之后,被开方数相同的二次根式称为同类二次根式.二次根式的加减步骤是先化简二次根式,然后再合并同类二次根式,法则类似于合并同类项.【关键词】二次根式;最简二次根式;同类二次根式,二次根式的加减4. (天津,14,3分)计算5353+)(-)的结果等于 .【答案】2【逐步提示】本题考查了二次根式的运算.利用乘法公式中的平方差公式(a+b)(a-b)=a2-b2,进行运算,合并化简即可.【解析】(53)(53)+-=22(5)(3)-=5-3=2,故答案为2.【解后反思】本题考查了二次根式的混合运算以及平方差公式,能根据算式的特点利用平方差公式简化运算是解题的关键.【关键词】二次根式的运算;平方差公式5. ( 四川省巴中市,9,3分)下列二次根式中,与3是同类二次根式的是( )A. 18B.13C.24D.0.3 【答案】B.【逐步提示】本题考查了二次根式的化简,以及同类二次根式的概念,解题的关键是应用二次根式的性质,将二次根式进行化简.先将各二次根式化简成最简二次根式,再根据同类二次根式的定义进行选择. 【详细解答】解:18=32,13=133,24=26,0.3=13010,其中只有133 与3是同类二次根式,故选择B.【解后反思】一个二次根式是否为最简二次根式,必须满足两个条件(1)根号内不含有开方开得尽的因数或因式,(2)二次根式的根号内不含有分母;而同类二次根式是指把二次根式化为最简二次根式后,被开方数相同的就是同类二次根式,被开方数不同的就不是同类二次根式, 【关键词】最简二次根式;同类二次根式;6. ( 四川南充,2,3分)下列计算正确的是( )A .1223=B .3322= C .3x x x -=- D .2x x = 【答案】A【逐步提示】本题考查了二次根式的化简、商的算术平方根,解题的关键是熟练掌握上述运算法则.根据对应的运算法则逐个计算再作出判断. 【详细解答】解:124323=⨯=,选项A 正确;336222==,选项B 错误; 因为3x -≥0,则x ≤032x x x x x -=-=--,选项C 2x x =,选项D 错误;故选择A .【解后反思】此题主要考查了二次根式的化简,正确掌握二次根式的性质是解题关键.【关键词】二次根式的化简;二次根式的乘法;二次根式的除法7(四川省自贡市,3,4分)下列根式中,不是最简二次根式的是 A .10 B .8 C .6 D .2【答案】B【逐步提示】看被开方数是否含有能开方的因式,若含有,则不是最简二次根式,若不含有则是最简二次根式. 【详细解答】解:B 选项中被开方数8可以分解为4×2,4可以开平方,所以B 不是最简二次根式,故选择B. 【解后反思】二次根式的化简主要运用二次根式的乘除法法则及二次根式的性质进行运算:1. 乘法法则:(a 0,b 0)a b ab •=≥≥.2.除法法则:(a 0,b 0)aa b b÷=≥>. 3.a a =2.【关键词】二次根式的化简8.(浙江金华,12,4分)能够说明“2x x =不成立...”的x 的值是 (写出一个即可). 【答案】如-1等(只要填一个负数即可)【逐步提示】认真审题,根据2x x =成立的条件,确定不成立的x 的值.【解析】因为2x x =成立的条件为x ≥0,所以“2x x =不成立...”的x 的值是所有负数,答案不唯一,故答案可以为如-1等(只要填一个负数即可) .【解后反思】根据公式成立的条件确定出公式不成立的条件. 【关键词】二次根式9.(浙江宁波,13,4分)实数-27 的立方根是 . 【答案】-3【逐步提示】本题考查了立方根的概念,解题的关键是掌握利用逆运算求立方根的方法.利用立方和开立方运算是互逆运算进行求解.【解析】由于(-3)3=-27,所以-27 的立方根是-3,故答案为-3 .【解后反思】任何实数的立方根只有一个;正数的立方根是正数,负数的立方根是负数,零的立方根是零.求一些特殊实数的立方根也是利用数的立方的逆运算来求的. 【关键词】 立方根的概念及求法10.(浙江衢州,12,4分)二次根式3x -中字母x 的取值范围是___.【答案】x ≥3.【逐步提示】由二次根式的被开方式是非负数,列出不等式求解. 【解析】依题意,得x -3≥0,解得x ≥3,故答案为x ≥3.【解后反思】正确理解二次根式的被开方式是非负数,是顺利求解此类问题的关键. 【关键词】二次根式的意义,不等式.11.(浙江舟山,12,4分)二次根式x -1中,字母x 的取值范围是 . 【答案】x ≥1【逐步提示】本题考查了二次根式的概念,解题的关键是根据二次根式有意义的条件建立关于x 的不等式求解. 二次根式有意义,必须满足被开方数是非负数.【解析】由题意,得x -1≥0,∴x ≥1,故答案为 x ≥1 .【解后反思】在一般的函数关系中自变量的取值范围主要考虑以下四种情况:⑴函数关系式为整式形式:自变量取值范围为任意实数;⑵函数关系式为分式形式:分母≠0;⑶函数关系式含算术平方根:被开方数≥0;⑷函数关系式含指数为0的幂的形式:底数≠0.【关键词】函数定义及其取值范围;解一元一次不等式12.. ( 四川乐山,14,3分)在数轴上表示实数a 的点如图7所示,化简2(5)2a a -+-的结果为___ _.图7a 52【答案】3.【逐步提示】观察数轴易得2<a <5,再将2(5)2a a -+-化简获解.【详细解答】解:由数轴得2<a <5,∴ 2(5)2a a -+-=5-a+a-2=5-2=3,故答案为3.【解后反思】(1)绝对值:正数的绝对值是它本身,负数的绝对值等于它的相反数,0的绝对值是0.(2) 二次根式有意义的条件是:被开方数必须是非负数.否则二次根式无意义. 【关键词】数轴;绝对值;二次根式 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30. 31. 32. 33. 34. 35. 36. 37. 38. 39.三、解答题1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.21.22.23.24.25.26.27.28.29.30.31.32.33.34.35.36.37.38.39.。
(浙江专用)2019年中考数学总复习第一章数与式1.3分式与二次根式(讲解部分)素材(pdf)

根式ꎬ并且分母中不含二次根式.
在二次根式的运算中ꎬ一般要把最后结果化为������ ������㊀ 最简 ㊀ 二次 ������
14
方法一㊀ 分式的化简求值
代入计算.
㊀ ㊀ 分式的化简求值是代数式求值常见题型之一ꎬ 也是中考中 的固定题型ꎬ其解法是先化简ꎬ再把字母的值或条件中所含关系 例 1㊀ 先化简 x -4x +4 4 ː x- x x 2 -2x
a+ b ( aȡ0ꎬbȡ0ꎬaʂb) . a-b
再相加减.
(3) 异分母分式相加减ꎬ先⑧㊀ 通分 ㊀ ꎬ 变为同分母分式ꎬ 然后
3. 分式的乘除运算 (1) 约分的关键是确定分子㊁分母的⑨㊀ 公因式㊀ .
{
积的分母.
(2) 分式乘分式ꎬ用分子的积作为积的分子ꎬ 分母的积作为
ab = a ������ b ( aȡ0ꎬbȡ0) . a a = ������ ������㊀ ㊀ ( aȡ0ꎬb >0) . ������ b b
考点二㊀ 分式的基本性质与分式运算
㊀ ㊀ 1. 分式的基本性质 2. 分式的加减运算
分式的分子与分母都③㊀ 乘( 除以) ㊀ 同一个不等于零的④㊀ 整 式㊀ ꎬ分式的值不变. (1) 通分的关键是确定几个分式的最简⑤㊀ 公分母㊀ . (2) 同分母分式相加减ꎬ⑥㊀ 分母㊀ 不变ꎬ把⑦㊀ 分子㊀ 相加减.
㊀ ㊀ 变式训练㊀ 若( m -1) 2 + A.-1 C.1 答案㊀ A
答案㊀ B
2x -1 = 0ꎬy -1 = 0ꎬ所以 x =
3 2 5 C.2 D. 2 解析㊀ 由完全平方式和二次根式的非负性及已知可知ꎬ 1 3 ꎬy = 1ꎬ所以 x + y = . 故选 B. 2 2
������������������������������������������������������������������������
中考第一轮复习--第一章数与式
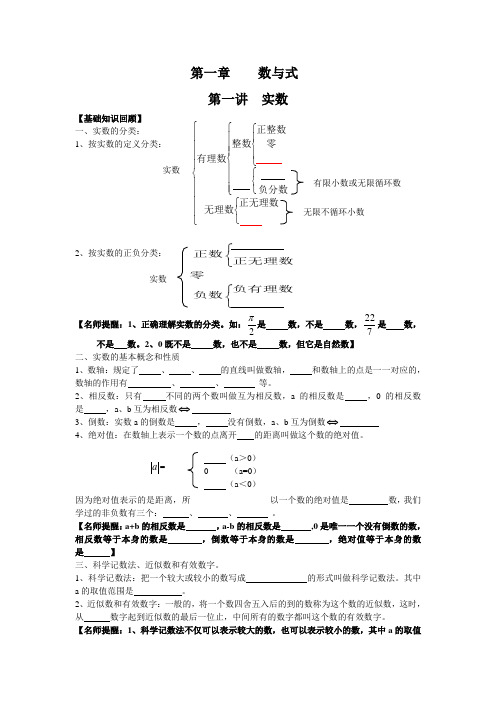
第一章 数与式第一讲 实数【基础知识回顾】 一、实数的分类: 1、按实数的定义分类: 实数 有限小数或无限循环数2、按实数的正负分类:实数【名师提醒:1、正确理解实数的分类。
如:2π是 数,不是 数,722是 数,不是 数。
2、0既不是 数,也不是 数,但它是自然数】二、实数的基本概念和性质1、数轴:规定了 、 、 的直线叫做数轴, 和数轴上的点是一一对应的,数轴的作用有 、 、 等。
2、相反数:只有 不同的两个数叫做互为相反数,a 的相反数是 ,0的相反数是 ,a 、b 互为相反数⇔3、倒数:实数a 的倒数是 , 没有倒数,a 、b 互为倒数⇔4、绝对值:在数轴上表示一个数的点离开 的距离叫做这个数的绝对值。
a =因为绝对值表示的是距离,所以一个数的绝对值是 数,我们学过的非负数有三个: 、 、 。
【名师提醒:a+b 的相反数是 ,a-b 的相反数是 ,0是唯一一个没有倒数的数,相反数等于本身的数是 ,倒数等于本身的数是 ,绝对值等于本身的数是 】三、科学记数法、近似数和有效数字。
1、科学记数法:把一个较大或较小的数写成 的形式叫做科学记数法。
其中a 的取值范围是 。
2、近似数和有效数字:一般的,将一个数四舍五入后的到的数称为这个数的近似数,这时,从 数字起到近似数的最后一位止,中间所有的数字都叫这个数的有效数字。
【名师提醒:1、科学记数法不仅可以表示较大的数,也可以表示较小的数,其中a 的取值⎪ ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎪ ⎨ ⎧ ⎩ ⎨ ⎧ ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎨ ⎧ ⎩ ⎨ ⎧ ⎪ ⎩ ⎪ ⎨ ⎧ 正无理数 无理数 负分数 零 正整数 整数 有理数 无限不循环小数 ⎧⎨⎩⎧⎨⎩正数正无理数零 负有理数负数 (a >0) (a <0) 0 (a=0)范围一样,n 的取值不同,当表示较大数时,n 的值是原整数数位减一,表示较小的数时,n 是负整数,它的绝对值等于原数中左起第一个非零数字前零的个数(含整数数位上的零)。
中考数学第一轮总复习数的开方与二次根式

数的开方与二次根式主备人 刘敖川 审核人 张丽丽【考点链接】1.式子)0(≥a a 叫做二次根式.注意被开方数a 只能是 .2. 的二次根式,叫做最简二次根式.3.化成最简二次根式后,被开方数 几个二次根式,叫做同类二次根式.4.二次根式的性质 :⑴ ; ⑵ ()=2a (a ≥0); ⑶=2a ; (4)=ab (0,0≥≥b a ); (5)=b a (0,0>≥b a ). 【典例精析】例1 (1x 取值范围是________.(2)已知a例2: )A B C例3:若a ,b 分别表示10的整数部分与小数部分,求41++b a 的值【中考演练】1_______, -164的立方根为_______.2x 的取值范围是 ( )A .13x >B .13x >- C . 13x ≥ D .13x ≥-3.(10上海)计算:2=__________.4. 若无理数a 满足不等式14<<a ,请写出两个符合条件的无理数_____________.5.(10长春)计算:(1)54-= _____________.(2+2)=_________.6.下列叙述中正确的是( )A .正数的平方根不可能是负数B .无限小数都是无理数C .实数和实数上的点一一对应D .带根号的数是无理数7.(10年福州市)下列各式中属于最简二次根式的是( )A B C8.(10年恩施自治州)若m 的值为( ) A .20511315 (32688)B C D9.(10海淀)合并的二次根式为( )A B C D 10.估算31-2的值( )A .在1和2之间B .在2和3之间C .在3和4之间D .在4和5之间11.若ab<0,化简二次根式321b a a-的结果是:( ). A.b b B.-b b C. b b - D. -b b -【课后作业】1.函数y=11+x 的自变量的取值范围是 . A.x≥-1 B. x>-1 C. x≠1 D. x≠-12.函数2-=x y 中,自变量x 的取值范围是 .3.(2010·绵阳)要使1213-+-x x 有意义,则x 应满足( ). A .21≤x ≤3 B .x ≤3且x ≠21 C .21<x <3 D .21<x ≤34.(2010,安徽芜湖)要使式子a 有意义,a 的取值范围是( ) A .a≠0 B .a>-2且a≠0C .a>-2或a≠0D .a≥-2且a≠0 5.(2010年常州)下列运算错误的是( ).A = B. = = D.2(2=6.下列各组中的两个根式是同类二次根式的是( )A .52x 和3xB .12ab 和13abC .x 2y 和xy 2D . a 和1a 27.下列二次根式中,是最简二次根式的是( )A .8xB .x 2-3C .x -y x D .3a 2b 8.在27 .112 .112中与 3 是同类二次根式的个数是( ) A .0 B .1 C .2 D .39.(2010年安徽)计算:=-⨯263_____:;=+312______10=___ __.11.(2010的的算术平方根是 .13.(10年永州) 下列判断正确的是( )A . 23<3<2B . 2<2+3<3C . 1<5-3<2D . 4<3·5<514.(2007===请你将发现的规律用含自然数n (n ≥1)的等式表示出来__________________________. 在实数范围内因式分解:x x 53-= ;15.计算(1)8132182+- (2)2543122÷⨯(3))92913(25523x x x x +- (4))622554(83--⨯(5)301007)6t a n 30)3-⎛⎫-- ⎪⎝⎭o(6)计算:|345tan |32)31()21(10-︒-⨯+--。
中考数学一轮复习第一部分教材同步复习第一章数与式第2讲数的开方与二次根式实用课件

编后语
常常可见到这样的同学,他们在下课前几分钟就开始看表、收拾课本文具,下课铃一响,就迫不及待地“逃离”教室。实际上,每节课刚下课时的几分 钟是我们对上课内容查漏补缺的好时机。善于学习的同学往往懂得抓好课后的“黄金两分钟”。那么,课后的“黄金时间”可以用来做什么呢?
一、释疑难
对课堂上老师讲到的内容自己想不通卡壳的问题,应该在课堂上标出来,下课时,在老师还未离开教室的时候,要主动请老师讲解清楚。如果老师已 经离开教室,也可以向同学请教,及时消除疑难问题。做到当堂知识,当堂解决。
二、补笔记
上课时,如果有些东西没有记下来,不要因为惦记着漏了的笔记而影响记下面的内容,可以在笔记本上留下一定的空间。下课后,再从头到尾阅读一 遍自己写的笔记,既可以起到复习的作用,又可以检查笔记中的遗漏和错误。遗漏之处要补全,错别字要纠正,过于潦草的字要写清楚。同时,将自己 对讲课内容的理解、自己的收获和感想,用自己的话写在笔记本的空白处。这样,可以使笔记变的更加完整、充实。
4
知识点二 二次根式的概念与性质
1.概念:形如 a(a≥0)的式子叫做二次根式,“
”称为二次根号.
2.使二次根式有意义的条件 (1)被开方数①__大__于__或__等__于__0_(_或__≥__0_)___;
(2)若根式在分母中出现,则被开方数大于②____0______(利用分式有意义的条
件,分母不为 0).
数 m,n 之间,即 m< a<n,从而得 a的整数部分为 m. 【注意】 对于一些常见的二次根式,记住其近似值,在解决估值问题时会更
方便,如 2≈1.414, 3≈1.732, 5≈2.236.
10
重难点 ·突破
重难点 二次根式的运算 难点 例 计算: 48÷ 3- 12× 12+ 24. 【答题规范】 解:原式= 16- 6+2 6 =4+ 6.
2019年中考数学总复习第一单元数与式课时05数的开方与二次根式课件

A. 在 1. 1 和 1. 2 之间
B. 在 1. 2 和 1. 3 之间
C. 在 1. 3 和 1. 4 之间
D. 在 1. 4 和 1. 5 之间
拓展 2【答案】B 【解析】∵2< 5<3,2.22=4.84,2.32=5.29, ∴2.2< 5<2.3, ∴2.2-1< 5-1<2.3-1,即 1.2< 5-1<1.3, 故选 B.
算术平方根的双重非负性: ������≥0(其中
������ a≥0)
若 b3=a,则 b 是 a 的立方根. 容 立方根
易得出(3 ������)3=⑤ a
正数有一个⑥ 正的 立方根,0 的立方根
Байду номын сангаас
3 ������
是⑦ 0
,负数有一个⑧ 负的 立方根
课前考点过关
考点三 二次根式的性质
两个重要
的性质
A. 2 ���2���= ������
B. 18- 8= 2 C. 6 15÷2 3=3 45 D. -3 3= 27
【答案】B
【解析】因为 2 ������=2× ������= 2������,所以 A 错误;
2
2
因为 18- 8=3 2-2 2= 2,所以 B 正确; 因为 6 15÷2 3=62 135=3 5,所以 C 错误; 因为-3 3=- 9 × 3=- 27,所以 D 错误.
D.
������ = 1, ������ = 1
[方法模型] 二次根式的性质:(1) ������2= ������ ;(2)( ������)2=a;(3) ������≥0;(4) 若 ������+ ������ =0,则 a=0,b=0.
中考数学第一轮复习(第4讲--数的开方与二次根式)

【例题1】 (2012·浙江宁波)下列计算正确的是( ). A.a6÷a2=a3 B.(a3)2=a5
解析 根据同底数幂的除法,幂的乘方,算术平方根,立方根运算
法则逐一计算作出判断:
A.a6÷a2=a6-2=a4≠a3,故本选项错误; B.(a3)2=a3×2=a6≠a5,故本选项错误;
第三十五 ,共44 。
【预测1】 下列计算:
答案 C
第三十六 ,共44 。
【预测2】 下列运算正确的是
( ).
答案 C
第三十七 ,共44 。
易 错防 范
第三十八 ,共44 。
数的开方、二次根式常见错误
第三十九 ,共44 。
【典型例题】
第四十 ,共44 。
第四十一 ,共44 。
第二十八 ,共44 。
A.a≠0
C.a>-2或a≠0
B.a>-2且a≠0 D.a≥-2且a≠0
答案 D
第二十九 ,共44 。
【预测3】 下列二次根式中,最简二次根式是( ).
答案 B
第三十 ,共44 。
答案 C
第三十一 ,共44 。
解析 考查二次根式和绝对值等非负数的性质,由已知得,x= -3,y=2 013,所以x+y=-3+2 013=2 010.
(3)混合运算:与实数的混合运算顺序相同.
状元笔记 (1)加减运算:需先化简,再合并;
(2)乘除运算:可先乘除,后化简.
第十四 ,共44 。
对 接中 考
第十五 ,共44 。
对接点一:平方根、立方根及算数平方根
常考角度
1. 平方根、算术平方根与立方根的概念; 2. 求一个数的平方根、算术平方根与立方根.
杭州市2019年中考数学一轮复习 第一章 数与式 第六节 数的开方与二次根式同步测试

亲爱的同学:这份试卷将再次记录你的自信、沉着、智慧和收获,我们一直投给你信任的目光……第六节 数的开方与二次根式姓名:________ 班级:________ 用时:______分钟1. (2018·辽宁抚顺中考)二次根式1-x 在实数范围内有意义,则x 的取值范围是( ) A .x≥1B .x≤1C .x >1D .x <12.(2018·浙江杭州中考)下列计算正确的是( ) A.22=2 B.22=±2 C.42=2D.42=±23.(2018·云南曲靖中考)下列二次根式中能与23合并的是( ) A.8 B.13C.18D.94.(2018·江苏泰州中考)下列运算正确的是( ) A.2+3= 5 B.18=2 3 C.2·3= 5D.2÷12=2 5.(2018·重庆中考A 卷)估计(230-24)·16的值应在( ) A .1和2之间 B .2和3之间 C .3和4之间D .4和5之间6.式子x -2x -3有意义的条件是__________________.7.(2018·山东潍坊中考)用教材中的计算器进行计算,开机后依次按下,把显示结果输入右侧的程序中,则输出的结果是______.8.(2018·广东广州中考)如图,数轴上点A 表示的数为a ,化简:a +a 2-4a +4=______.9.(2017·四川德阳中考)计算:(25-2)0+|2-5|+(-1)2 017-13×45.10.(2018·浙江台州模拟)已知x =2-1,求x 2+3x -1的值.11.已知y =2x -5+5-2x -3,则2xy 的值为( ) A .-15B .15C .-152D.15212.如果一个三角形的三边长分别为1,k ,4,那么化简|2k -5|-k 2-12k +36的结果是( ) A .3k -11 B .k +1 C .1D .11-3k13.已知a ,b 分别是6-13的整数部分和小数部分,那么2a -b 的值是( ) A .3-13 B .4-13 C.13D .2+1314.若关于x 的方程-2x +m 2 017-x +4 020=0存在整数解,则正整数m 的所有取值的和为________. 15.已知|a -2 017|+a -2 018=a ,则a -2 0172的值是______________. 16.已知a =1-3,b =1+3,求2a 2+2b 2-3ab -a +b 的值.17.请在方格内画△ABC,使它的顶点都在格点上,且三边长分别为2,25,412. (1)求△ABC 的面积; (2)求出最长边上的高.18.(2019·创新题)小明在学习《二次根式》后,发现一些含根号的式子可以写成另一个式子的平方,如3+22=(1+2)2.善于思考的小明进行了以下探索:设a+b2=(m+n2)2(其中a,b,m,n均为整数),则有a+b2=m2+2n2+2mn 2.∴a=m2+2n2,b=2mn.这样小明就找到了一种把类似a+2b的式子化为平方式的方法.请你仿照小明的方法探索并解决下列问题:(1)当a,b,m,n均为正整数时,若a+b3=(m+n3)2,用含m,n的式子分别表示a,b,得a=________,b=________;(2)利用所探索的结论,找一组正整数a,b,m,n填空:________+________3=(________+________3)2;(3)若a+43=(m+n3)2,且a,m,n均为正整数,求a的值.19.阅读下列材料,回答有关问题:在实数这章中,遇到过2,3,9,12,a这样的式子,我们把这样的式子叫做二次根式,根号下的数叫做被开方数.如果一个二次根式的被开方数中有的因数能开得尽方,可以利用a·b=a·b(a≥0,b≥0);a b =ab(a≥0,b>0)将这些因数开出来,从而将二次根式化简.当一个二次根式的被开方数中不含开得尽方的因数或者被开方数中不含有分母时,这样的二次根式叫做最简二次根式,例如,13化成最简二次根式是33,27化成最简二次根式是33,几个二次根式化成最简二次根式以后,如果被开方数相同,这几个二次根式叫做同类二次根式,如上面的例子中的13和27就是同类二次根式.(1)请判断下列各式中,哪些是同类二次根式? 2,75,18,150,127, 3. (2)二次根式中的同类二次根式可以像整式中的同类项一样合并,请计算: 2+75-18-150+127- 3.20.在进行二次根式化简时,我们有时会碰上如53,23,23+1一样的式子,其实我们还可以将其进一步化简:53=5×33×3=533,23=2×33×3=63,23+1=2×(3-1)(3+1)=2(3-1)(3)2-12=3-1,23+1还可以用以下方法化简:23+1=3-13+1=(3)2-123+1=(3+1)(3-1)3+1=3-1.以上这种化简的方法叫做分母有理化. (1)请化简25+3=________;(2)若a 是2的小数部分则3a=________;(3)矩形的面积为35+1,一边长为5-2,则它的周长为________;(4)化简21+5+25+9+29+13+…+24n-3+4n+1.参考答案【基础训练】1.B 2.A 3.B 4.D 5.B6.x≥2且x≠37.7 8.29.解:原式=1+5-2-1-5=-2. 10.解:∵x=2-1,∴x+1=2,∴(x+1)2=(2)2=2,即x2+2x+1=2,∴x2+2x=1,∴x2+3x-1=x2+2x+x-1=1+x-1=2-1. 【拔高训练】11.A 12.A 13.C 14.15 15.2 018 16.解:∵a=1-3,b=1+3,∴a-b=(1-3)-(1+3)=-23,ab=(1-3)(1+3)=-2,∴2a2+2b2-3ab-a+b=2(a-b)2-(a-b)+ab =2(-23)2-(-23)+(-2)=22+2 3.17.解:画图如图所示.(1)S △ABC =2.(2)最长边上的高为255.18.解:(1)∵a+b 3=(m +n 3)2, ∴a+b 3=m 2+3n 2+2mn 3, ∴a=m 2+3n 2,b =2mn.(2)答案不唯一,如:设m =1,n =1, ∴a=m 2+3n 2=4,b =2mn =2. (3)由题意,得: a =m 2+3n 2,b =2mn∵4=2mn ,且m ,n 为正整数, ∴m=2,n =1或m =1,n =2,∴a=22+3×12=7或a =12+3×22=13. 19.解:(1)75=53,18=32,150=210,127=39, ∴2,18,150是同类二次根式;75,127,3是同类二次根式. (2)原式=2+53-32-210+39-3=-21210+3739. 【培优训练】 20.解:(1)5- 3 (2)32+3 (3)30+16 5(4)原式=2(5-1)5-1+2(9-5)9-5+2(13-9)13-9+…+2(4n +1-4n -3)(4n +1)-(4n -3)=5-1+9-5+13-9+…+4n +1-4n -32=4n +1-12.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六节 数的开方与二次根式
姓名:________ 班级:________ 用时:______分钟
1. (2018·辽宁抚顺中考)二次根式1-x 在实数范围内有意义,则x 的取值范围是( ) A .x≥1
B .x≤1
C .x >1
D .x <1
2.(2018·浙江杭州中考)下列计算正确的是( ) A.22
=2 B.22
=±2 C.42=2
D.42
=±2
3.(2018·云南曲靖中考)下列二次根式中能与23合并的是( ) A.8 B.
1
3
C.18
D.9
4.(2018·江苏泰州中考)下列运算正确的是( ) A.2+3= 5 B.18=2 3 C.2·3= 5
D.2÷
1
2
=2 5.(2018·重庆中考A 卷)估计(230-24)·1
6
的值应在( ) A .1和2之间 B .2和3之间 C .3和4之间
D .4和5之间
6.式子
x -2
x -3
有意义的条件是__________________. 7.(2018·山东潍坊中考)用教材中的计算器进行计算,开机后依次按下,把显示结果输入右侧的程序中,
则输出的结果是______.
8.(2018·广东广州中考)如图,数轴上点A 表示的数为a ,化简:a +a 2
-4a +4=______.
9.(2017·四川德阳中考)计算:(25-2)0+|2-5|+(-1)2 017
-13×45.
10.(2018·浙江台州模拟)已知x =2-1,求x 2
+3x -1的值.
11.已知y =2x -5+5-2x -3,则2xy 的值为( ) A .-15
B .15
C .-15
2
D
.152
12.如果一个三角形的三边长分别为1,k ,4,那么化简|2k -5|-k 2
-12k +36的结果是( ) A .3k -11 B .k +1 C .1
D .11-3k
13.已知a ,b 分别是6-13的整数部分和小数部分,那么2a -b 的值是( ) A .3-13 B .4-13 C.13
D .2+13
14.若关于x 的方程-2x +m 2 017-x +4 020=0存在整数解,则正整数m 的所有取值的和为________. 15.已知|a -2 017|+a -2 018=a ,则a -2 0172
的值是______________. 16.已知a =1-3,b =1+3,求2a 2
+2b 2
-3ab -a +b 的值.
17.请在方格内画△ABC,使它的顶点都在格点上,且三边长分别为2,25,41
2
. (1)求△ABC 的面积; (2)求出最长边上的高.
18.(2019·创新题)小明在学习《二次根式》后,发现一些含根号的式子可以写成另一个式子的平方,如3+22=(1+2)2.善于思考的小明进行了以下探索:
设a+b2=(m+n2)2(其中a,b,m,n均为整数),则有a+b2=m2+2n2+2mn 2.
∴a=m2+2n2,b=2mn.这样小明就找到了一种把类似a+2b的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当a,b,m,n均为正整数时,若a+b3=(m+n3)2,用含m,n的式子分别表示a,b,得a=________,b=________;
(2)利用所探索的结论,找一组正整数a,b,m,n填空:
________+________3=(________+________3)2;
(3)若a+43=(m+n3)2,且a,m,n均为正整数,求a的值.
19.阅读下列材料,回答有关问题:
在实数这章中,遇到过2,3,9,12,a这样的式子,我们把这样的式子叫做二次根式,根号下的数叫做被
开方数.如果一个二次根式的被开方数中有的因数能开得尽方,可以利用a·b=a·b(a≥0,b≥0);a
b
=
a
b
(a≥0,b>0)将这些因数开出来,从而将二次根式化简.当一个二次根式的被开方数中不含开得尽方的因数或者被开方数中不含有分母时,这样的二次根式叫做最简二次根式,例如,
1
3
化成最简二次根式是3
3,27化成最简二次根
式是33,几个二次根式化成最简二次根式以后,如果被开方数相同,这几个二次根式叫做同类二次根式,如上面的例子中的
1
3
和27就是同类二次根式.
(1)请判断下列各式中,哪些是同类二次根式? 2,75,18,
150
,1
27
, 3. (2)二次根式中的同类二次根式可以像整式中的同类项一样合并,请计算: 2+75-18-1
50
+1
27
- 3.
20.在进行二次根式化简时,我们有时会碰上如
53,
23,23+1一样的式子,其实我们还可以将其进一步化简:53
=
5×33×3
=
5
3
3,23
=2×33×3=63,23+1=2×(3-1)(3+1)=2(3-1)(3)2-12
=3-1,2
3+1
还可以用以下方法化简:2
3+1=3-1
3+1=(3)2
-12
3+1=(3+1)(3-1)
3+1=3-1.
以上这种化简的方法叫做分母有理化. (1)请化简
25+3
=________;
(2)若a 是2的小数部分则3
a
=________;
(3)矩形的面积为35+1,一边长为5-2,则它的周长为________;
(4)化简2
1+5+
2
5+9
+
2
9+13
+…+
2
4n-3+4n+1
.
参考答案
【基础训练】
1.B 2.A 3.B 4.D 5.B
6.x≥2且x≠37.7 8.2
9.解:原式=1+5-2-1-5=-2. 10.解:∵x=2-1,∴x+1=2,
∴(x+1)2=(2)2=2,
即x2+2x+1=2,
∴x2+2x=1,
∴x2+3x-1=x2+2x+x-1=1+x-1=2-1. 【拔高训练】
11.A 12.A 13.C 14.15 15.2 018 16.解:∵a=1-3,b=1+3,
∴a-b=(1-3)-(1+3)=-23,
ab=(1-3)(1+3)=-2,
∴2a2+2b2-3ab-a+b=2(a-b)2-(a-b)+ab =2(-23)2-(-23)+(-2)
=22+2 3.
17.解:画图如图所示.
(1)S △ABC =2.
(2)最长边上的高为2
5
5.
18.解:(1)∵a+b 3=(m +n 3)2
, ∴a+b 3=m 2
+3n 2
+2mn 3, ∴a=m 2
+3n 2,b =2mn.
(2)答案不唯一,如:设m =1,n =1, ∴a=m 2
+3n 2
=4,b =2mn =2. (3)由题意,得: a =m 2
+3n 2,b =2mn
∵4=2mn ,且m ,n 为正整数, ∴m=2,n =1或m =1,n =2,
∴a=22
+3×12
=7或a =12
+3×22
=13. 19.解:(1)75=53,18=32,
150=210,127=39
, ∴2,18,
1
50
是同类二次根式;75,1
27
,3是同类二次根式. (2)原式=2+53-32-210+39-3=-21210+3739
. 【培优训练】 20.解:(1)5- 3 (2)32+3 (3)30+16 5
(4)原式=2(5-1)5-1+2(9-5)
9-5+
2(13-9)
13-9+…+
2(4n +1-4n -3)
(4n +1)-(4n -3)
=5-1+9-5+13-9+…+4n+1-4n-3
2
=4n+1-1
2
.。
