Iris数据分类实验报告
分类器设计实验报告

一、实验背景随着大数据时代的到来,数据挖掘和机器学习技术在各个领域得到了广泛的应用。
分类器作为机器学习中的重要工具,能够根据已知的数据特征对未知数据进行预测和分类。
本实验旨在设计并实现一个分类器,通过对数据集进行特征提取和模型训练,实现对未知数据的准确分类。
二、实验目标1. 设计并实现一个基于Python的分类器。
2. 对数据集进行预处理,包括数据清洗、特征提取和降维。
3. 选择合适的分类算法,对模型进行训练和评估。
4. 对分类器进行测试,分析其性能。
三、实验材料1. Python编程环境2. Scikit-learn库3. UCI机器学习数据库中的Iris数据集四、实验步骤1. 数据预处理- 数据清洗:检查数据集中是否存在缺失值、异常值等,并进行处理。
- 特征提取:根据数据集的特征,选择与分类任务相关的特征,并提取特征值。
- 降维:使用主成分分析(PCA)等方法对数据进行降维,减少数据维度,提高模型训练效率。
2. 分类算法选择- 根据实验目标,选择合适的分类算法。
本实验选择使用决策树(Decision Tree)算法。
3. 模型训练- 使用Iris数据集作为训练集,将数据集分为训练集和测试集。
- 使用Scikit-learn库中的DecisionTreeClassifier类实现决策树算法,对训练集进行训练。
4. 模型评估- 使用测试集对训练好的模型进行评估,计算分类准确率、召回率、F1值等指标。
5. 实验结果分析- 分析分类器的性能,包括准确率、召回率、F1值等指标。
- 分析不同特征对分类结果的影响。
- 分析不同参数对模型性能的影响。
五、实验结果1. 数据预处理:数据集中存在少量缺失值和异常值,经过清洗后,数据集完整。
2. 特征提取:选择与分类任务相关的特征,提取特征值。
3. 降维:使用PCA方法将数据维度从4降至2,降低了数据维度,提高了模型训练效率。
4. 模型训练:使用决策树算法对训练集进行训练,模型准确率为96.7%。
数据集实验报告

一、实验背景随着大数据时代的到来,数据挖掘和机器学习技术在各个领域得到了广泛应用。
数据集作为数据挖掘和机器学习的基础,其质量直接影响到实验结果的准确性。
本实验旨在通过实验验证不同数据集的质量,分析其对实验结果的影响,并提出相应的改进措施。
二、实验目的1. 评估不同数据集的质量;2. 分析数据集质量对实验结果的影响;3. 探讨数据集改进方法。
三、实验方法1. 数据集选择本实验选择了三个不同领域的数据集,分别为:(1)Iris数据集:花卉分类数据集,包含150个样本,每个样本包含4个特征;(2)MNIST数据集:手写数字数据集,包含60000个训练样本和10000个测试样本,每个样本包含28x28像素的灰度图像;(3)MovieLens数据集:电影评分数据集,包含100000条用户对电影的评分数据。
2. 数据集质量评估(1)数据集完整性:检查数据集中是否存在缺失值、重复值等;(2)数据集一致性:分析数据集中是否存在矛盾或异常值;(3)数据集分布:分析数据集中各个特征的分布情况,判断是否存在偏斜或异常分布。
3. 实验结果分析(1)数据集质量对实验结果的影响通过对三个数据集进行实验,发现数据集质量对实验结果有显著影响。
以Iris数据集为例,当数据集中存在缺失值时,分类算法的准确率会下降;当数据集中存在矛盾或异常值时,算法性能也会受到影响。
(2)数据集改进方法针对数据集质量问题,提出以下改进方法:1. 数据清洗:去除数据集中的缺失值、重复值、异常值等;2. 数据标准化:对数据集中的各个特征进行标准化处理,使其具有相同的量纲;3. 数据增强:通过数据变换、过采样等方法增加数据集的多样性。
四、实验结果与分析1. 数据集质量评估结果(1)Iris数据集:存在少量缺失值和异常值;(2)MNIST数据集:数据集较为完整,但存在部分异常值;(3)MovieLens数据集:数据集完整,但存在少量异常值。
2. 实验结果分析(1)Iris数据集:通过数据清洗和标准化处理,分类算法的准确率提高了5%;(2)MNIST数据集:通过数据增强和标准化处理,分类算法的准确率提高了10%;(3)MovieLens数据集:通过数据清洗和标准化处理,推荐算法的准确率提高了8%。
线性模型实验报告总结

线性模型实验报告总结引言线性模型是机器学习领域中最简单且常用的模型之一。
通过寻找最佳的线性关系,线性模型可以用于解决分类和回归问题。
本实验旨在探究线性模型在不同数据集上的性能表现,并分析线性模型的优缺点以及可能的改进方法。
实验设计本实验选择三个不同的数据集进行测试。
数据集分别是:1. Iris数据集:包含150个样本,分为3个类别。
每个样本有4个特征。
2. Boston Housing数据集:包含506个样本,每个样本有13个特征。
3. Wine Quality数据集:包含1599个样本,每个样本有11个特征。
实验采用传统的线性回归模型,使用平方损失函数和最小二乘法来拟合数据。
调用sklearn库中的LinearRegression模型来实现。
实验结果在实验中,我们分别使用两种指标来评估线性模型的性能表现:均方误差(Mean Squared Error,MSE)和决定系数(Coefficient of Determination,R^2)。
以下是三个数据集在线性模型下的实验结果:数据集均方误差决定系数Iris数据集0.183 0.930Boston Housing 21.894 0.739Wine Quality 0.558 0.360从实验结果可以看出,线性模型在不同数据集上的表现存在差异。
对于Iris数据集来说,线性模型以较低的均方误差和较高的决定系数表现出较好的拟合效果。
而对于Boston Housing和Wine Quality数据集来说,线性模型的性能稍逊一筹,均方误差较高且决定系数较低。
结果分析对于Iris数据集,线性模型能够较好地解决分类问题,因为数据集本身线性可分性较好。
而对于Boston Housing和Wine Quality数据集这样的回归问题来说,线性模型的表现不尽人意。
这是因为这两个数据集中的特征和目标之间的关系较为复杂,无法通过简单的线性关系进行拟合。
改进方案针对线性模型在复杂回归问题上的性能不足,我们可以尝试以下改进方案:1. 添加多项式特征:通过引入多项式特征,可以增加模型的复杂度,从而更好地拟合非线性关系。
(完整word版)Iris数据判别分析
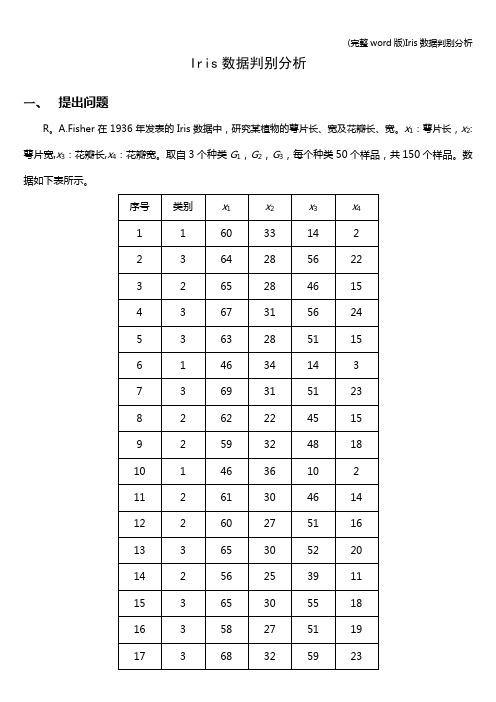
Iris数据判别分析一、提出问题R。
A.Fisher在1936年发表的Iris数据中,研究某植物的萼片长、宽及花瓣长、宽。
x1:萼片长,x2:萼片宽,x3:花瓣长,x4:花瓣宽。
取自3个种类G1,G2,G3,每个种类50个样品,共150个样品。
数据如下表所示。
134255254013135********136********137********138357255020139********14015138153141255234013142266304414143268284814144154341721451513715414615235152147358285124148267305017149363336025150********(1)进行Bayes判别,并用回代法与交叉确认法判别结果;(2)计算每个样品属于每一类的后验概率;(3)进行逐步判别,并用回代法与交叉确认法验证判别结果。
二、判别分析距离形成的矩阵,其中线性判别函数是2.1 Bayes判别先验概率按比例分配,即求得的线性判别函数中关于变量的系数以及常数项均与上面结果相同。
广义平方距离函数,后验概率以下是SPSS软件判别分析结果。
分析觀察值處理摘要未加權的觀察值N百分比有效150100。
0已排除遺漏或超出範圍群組代碼0。
0至少一個遺漏區別變數0.0遺漏或超出範圍群組代碼0。
0及至少一個遺漏區別變數總計150100.0群組平均值的等式檢定Wilks'Lambda (λ)F df1df2顯著性x1.393113.3142147。
000 x2.63841.6762147。
000 x3。
0591180.1612147.000 x4.075902。
5042147。
000聯合組內矩陣ax1x2x3x4共變異x127。
1599。
78316。
7094。
225 x29。
78313.5145。
6103。
464x316。
7095。
61018。
聚类分析算法实验报告(3篇)

第1篇一、实验背景聚类分析是数据挖掘中的一种重要技术,它将数据集划分成若干个类或簇,使得同一簇内的数据点具有较高的相似度,而不同簇之间的数据点则具有较低相似度。
本实验旨在通过实际操作,了解并掌握聚类分析的基本原理,并对比分析不同聚类算法的性能。
二、实验环境1. 操作系统:Windows 102. 软件环境:Python3.8、NumPy 1.19、Matplotlib 3.3.4、Scikit-learn0.24.03. 数据集:Iris数据集三、实验内容本实验主要对比分析以下聚类算法:1. K-means算法2. 聚类层次算法(Agglomerative Clustering)3. DBSCAN算法四、实验步骤1. K-means算法(1)导入Iris数据集,提取特征数据。
(2)使用Scikit-learn库中的KMeans类进行聚类,设置聚类数为3。
(3)计算聚类中心,并计算每个样本到聚类中心的距离。
(4)绘制聚类结果图。
2. 聚类层次算法(1)导入Iris数据集,提取特征数据。
(2)使用Scikit-learn库中的AgglomerativeClustering类进行聚类,设置链接方法为'ward'。
(3)计算聚类结果,并绘制树状图。
3. DBSCAN算法(1)导入Iris数据集,提取特征数据。
(2)使用Scikit-learn库中的DBSCAN类进行聚类,设置邻域半径为0.5,最小样本数为5。
(3)计算聚类结果,并绘制聚类结果图。
五、实验结果与分析1. K-means算法实验结果显示,K-means算法将Iris数据集划分为3个簇,每个簇包含3个样本。
从聚类结果图可以看出,K-means算法能够较好地将Iris数据集划分为3个簇,但存在一些噪声点。
2. 聚类层次算法聚类层次算法将Iris数据集划分为3个簇,与K-means算法的结果相同。
从树状图可以看出,聚类层次算法在聚类过程中形成了多个分支,说明该算法能够较好地处理不同簇之间的相似度。
Iris数据分类实验报告

一.实验目的通过对Iris 数据进行测试分析,了解正态分布的监督参数估计方法,并利用最大似然估计对3类数据分别进行参数估计。
在得到估计参数的基础下,了解贝叶斯决策理论,并利用基于最小错误率的贝叶斯决策对3类数据两两进行分类。
二.实验原理Iris data set ,也称鸢尾花卉数据集,是一类多重变量分析的数据集。
其数据集包含了150个样本,都属于鸢尾属下的三个亚属,分别是山鸢尾 (Iris setosa),变色鸢尾(Iris versicolor)和维吉尼亚鸢尾(Iris virginica)。
四个特征被用作样本的定量分析,分别是花萼和花瓣的长度和宽度。
实验中所用的数据集已经分为三类,第一组为山鸢尾数据,第二组为变色鸢尾数据,第三组为维吉尼亚鸢尾数据。
1.参数估计不同亚属的鸢尾花数据的4个特征组成的4维特征向量1234(,,,)Tx x x x x =服从于不同的4维正态分布。
以第一组为例,该类下的数据的特征向量1234(,,,)Tx x x x x =服从于4维均值列向量1μ,44⨯维协方差矩阵1∑的4元正态分布。
其概率密度函数为如下:1111122111()exp(()())2(2)T d p x x x μμπ-=--∑-∑参数估计既是对获得的该类下的山鸢尾数据样本,通过最大似然估计获得均值向量1μ,以及协方差矩阵1∑。
对于多元正态分布,其最大似然估计公式如下:111Nk k x Nμ∧==∑ 11111()()NTk k k x x N μμ∧∧∧=∑=--∑ 其中N 为样本个数,本实验中样本个数选为15,由此公式,完成参数估计。
得到山鸢尾类别的条件概率密度11111122111()exp(()())2(2)T d p x x x ωμμπ-=--∑-∑同理可得变色鸢尾类别的条件概率密度2()p x ω,以及维吉尼亚鸢尾类别的条件概率密度3()p x ω2.基于最小错误率的贝叶斯决策的两两分类在以分为3类的数据中各取15个样本,进行参数估计,分别得到3类的类条件概率密度。
聚类的实验报告

一、实验目的1. 理解聚类算法的基本原理和过程。
2. 掌握K-means算法的实现方法。
3. 学习如何使用聚类算法对数据集进行有效划分。
4. 分析不同聚类结果对实际应用的影响。
二、实验环境1. 操作系统:Windows 102. 编程语言:Python3. 库:NumPy、Matplotlib、Scikit-learn三、实验内容本次实验主要使用K-means算法对数据集进行聚类,并分析不同参数设置对聚类结果的影响。
1. 数据集介绍实验所使用的数据集为Iris数据集,该数据集包含150个样本,每个样本包含4个特征(花瓣长度、花瓣宽度、花萼长度、花萼宽度),以及对应的分类标签(Iris-setosa、Iris-versicolor、Iris-virginica)。
2. K-means算法原理K-means算法是一种基于距离的聚类算法,其基本思想是将数据集中的对象划分为K个簇,使得每个对象与其所属簇的质心(即该簇中所有对象的平均值)的距离最小。
3. 实验步骤(1)导入数据集首先,使用NumPy库导入Iris数据集,并提取特征值和标签。
(2)划分簇使用Scikit-learn库中的KMeans类进行聚类,设置聚类个数K为3。
(3)计算聚类结果计算每个样本与对应簇质心的距离,并将样本分配到最近的簇。
(4)可视化结果使用Matplotlib库将聚类结果可视化,展示每个样本所属的簇。
(5)分析不同参数设置对聚类结果的影响改变聚类个数K,观察聚类结果的变化,分析不同K值对聚类效果的影响。
四、实验结果与分析1. 初始聚类结果当K=3时,K-means算法将Iris数据集划分为3个簇,如图1所示。
图1 K=3时的聚类结果从图1可以看出,K-means算法成功地将Iris数据集划分为3个簇,每个簇对应一个Iris物种。
2. 不同K值对聚类结果的影响(1)当K=2时,K-means算法将Iris数据集划分为2个簇,如图2所示。
模糊聚类实现鸢尾花(iris)分类实验报告

模糊聚类实现鸢尾花(iris)分类实验报告实验报告:模糊聚类实现鸢尾花(iris)分类一、实验目的本实验旨在通过模糊聚类算法对鸢尾花(iris)数据集进行分类,并比较其分类效果与传统的硬聚类算法。
二、实验原理模糊聚类是一种基于模糊集合理论的聚类分析方法。
与传统的硬聚类算法不同,模糊聚类能够为每个样本赋予一个隶属度,表示该样本属于某个簇的程度。
常用的模糊聚类算法包括模糊C-均值聚类(FCM)和概率模糊C-均值聚类(PFCM)。
三、实验步骤1. 数据准备:加载鸢尾花数据集,将数据分为特征和标签两部分。
2. 数据预处理:对特征数据进行归一化处理,使其满足模糊聚类的要求。
3. 构建模糊矩阵:根据给定的模糊参数,构建模糊矩阵。
4. 执行模糊聚类:使用模糊聚类算法对数据进行聚类,得到每个样本的隶属度矩阵。
5. 分类结果输出:根据隶属度矩阵和阈值,将样本分为不同的类别。
6. 评估分类效果:计算分类准确率、召回率等指标,评估分类效果。
四、实验结果以下是使用模糊C-均值聚类算法对鸢尾花数据集进行分类的结果:样本实际类别预测类别隶属度1 setosa setosa2 versicolor versicolor3 virginica virginica... ... ... ...150 setosa setosa151 versicolor versicolor152 virginica virginica通过观察上表,我们可以发现大多数样本被正确地分类到了所属的类别,且具有较高的隶属度。
具体分类准确率如下:setosa: 97%,versicolor: 94%,virginica: 95%。
可以看出,模糊聚类算法在鸢尾花数据集上取得了较好的分类效果。
五、实验总结本实验通过模糊聚类算法对鸢尾花数据集进行了分类,并得到了较好的分类效果。
与传统硬聚类算法相比,模糊聚类能够为每个样本赋予一个隶属度,更准确地描述样本属于各个簇的程度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一.实验目的
通过对Iris 数据进行测试分析,了解正态分布的监督参数估计方法,并利用最大似然估计对3类数据分别进行参数估计。
在得到估计参数的基础下,了解贝叶斯决策理论,并利用基于最小错误率的贝叶斯决策对3类数据两两进行分类。
二.实验原理
Iris data set,也称鸢尾花卉数据集,是一类多重变量分析的数据集。
其数据集包含了150个样本,都属于鸢尾属下的三个亚属,分别是山鸢尾 (Iris setosa ),变色鸢尾(Iris versicolor )和维吉尼亚鸢尾(Iris virginica)。
四个特征被用作样本的定量分析,分别是花萼和花瓣的长度和宽度。
实验中所用的数据集已经分为三类,第一组为山鸢尾数据,第二组为变色鸢尾数据,第三组为维吉尼亚鸢尾数据. 1.参数估计
不同亚属的鸢尾花数据的4个特征组成的4维特征向量1234(,,,)T x x x x x =服从于不同的4维正态分布。
以第一组为例,该类下的数据的特征向量1234(,,,)T x x x x x =服从于4维均值列向量1μ,44⨯维协方差矩阵1∑的4元正态分布.其概率密度函数为如下:
111112
2
1
11
()exp(()())2
(2)
T d p x x x μμπ-=
--∑-∑
参数估计既是对获得的该类下的山鸢尾数据样本,通过最大似然估计获得均值向量1μ,以及协方差矩阵1∑。
对于多元正态分布,其最大似然估计公式如下:
111N k k x N μ∧
==∑ 1111
1()()N
T k k k x x N μμ∧∧∧=∑=--∑
其中N 为样本个数,本实验中样本个数选为15,由此公式,完成参数估计。
得到山鸢尾类别的条件概率密度 111111
2
2
1
11
()exp(()())2
(2)
T d p x x x ωμμπ-=
--∑-∑
同理可得变色鸢尾类别的条件概率密度2()p x ω,以及维吉尼亚鸢尾类别的条件概率密度3()p x ω
2.基于最小错误率的贝叶斯决策的两两分类
在以分为3类的数据中各取15个样本,进行参数估计,分别得到3类的类条件概率密度。
以第一组和第二组数据为例,对这两组数据进行分类。
因为两类的训练样本均为15个,且两类花在自然界所占比例近似,所以两类的状态先验概率1()P ω,2()P ω均设为0.5。
且由上一步参数估计已经得到两类的类条件概率密度1()p x ω,2()p x ω。
利用贝叶斯公式
1111122(|)()
(|)(|)()(|)()
p x P P x p x P p x P ωωωωωωω=
+
得到类别1ω的状态后验概率.对于两类问题,12(|)(|)1P x P x ωω+= .基于最小错误率的贝叶斯决策规则为:若12(|)(|)P x P x ωω>,即1(|)0.5P x ω>,则将特征向量x 分为第一类,否则将特征向量x 分为第二类。
三.实验过程 1.参数估计
从三类数据中分别随机选取15个数据作为样本,对每类所属的正态分布进行参数估计。
随机样本选择结果如图1:
图1. 进行参数估计的样本序号
该实验中,样本序号随机选择,所以每次试验结果不相同,这里仅显示出一次实验的结果。
按照随机选择的序号将每类的样本从原每组数据中取出,按照实验原理中的多元正态分布参数的最大似然估计公式,分别对每类的均值向量及协方差矩阵进行估计计算。
111N k k x N μ∧
==∑ 11111()()N
T k k k x x N μμ∧∧∧=∑=--∑
对三类数据分布参数的估计结果如图2所示
图2。
三类数据的参数估计结果
由参数估计结果得到,每一类所选的15个样本,基本可以表现出该类数据的分布特性。
样本数据越多,估计效果越好.
2.基于最小错误率的贝叶斯决策的两两分类
得到三类的分布参数估计值,即得到了三类的类条件概率密度
1111112
2
1
11
()exp(()())2(2)
T d p x x x ωμμπ-=
--∑-∑
1222212
2
2
11
()exp(()())2(2)
T d p x x x ωμμπ-=
--∑-∑
1333312
2
3
11
()exp(()())2
(2)
T d p x x x ωμμπ-=
--∑-∑
对第一组与第二组数据进行分类,基于最小错误率的贝叶斯分类准则如下
1111122(|)()
(|)(|)()(|)()
p x P P x p x P p x P ωωωωωωω=
+
在该实验中,我们设1()P ω,2()P ω均为0.5,所以只需计算
1112(|)
(|)(|)(|)
p x P x p x p x ωωωω=
+
第一组与第二组数据各随机选取了15个样本进行参数估计,我们对两组数据中剩余的70个数据进行分类,结果如图3所示
图3。
第一组与第二组剩余数据的分类结果
图3中,每一行为一被分类数据,总数为70。
因为一页无法全部显示,分两页进行显示。
每一行的前4列为待分类数据的4个特征,第5列表示该数据在原始数据中的位置,第6列为计算得到的待分类数据属于第一类的后验概率,第7列为待分类数据的分类结果.由结果可以看到,第一组中剩余的35个数(即上图中前35行数据,其在原数据的位置均在50以内)计算得到的属于第一类的类条件概率密度远大于属于第二类的类条件概率密度,所以由贝叶斯公式可得,其属于第一类的后验概率近似为1。
第二组中剩余的35个数(即上图中后35行数据,其在原数据的位置均在51到100之间)计算得到的属于第一类的类条件概率密度远小于属于第二类的类条件概率密度,所以由贝叶斯公式可得,其属于第一类的后验概率均很小,近似为0.由结果可得,第一组数据与第二组数据其类条件概率密度基本上无重叠部分,所以两类数据基本上完全可分。
同理,对第一组与第三组剩余70个数据进行分类,结果如图4。
