(完整版)平方根和立方根经典讲义
(完整版)平方根、算术平方根、立方根重点例题讲解
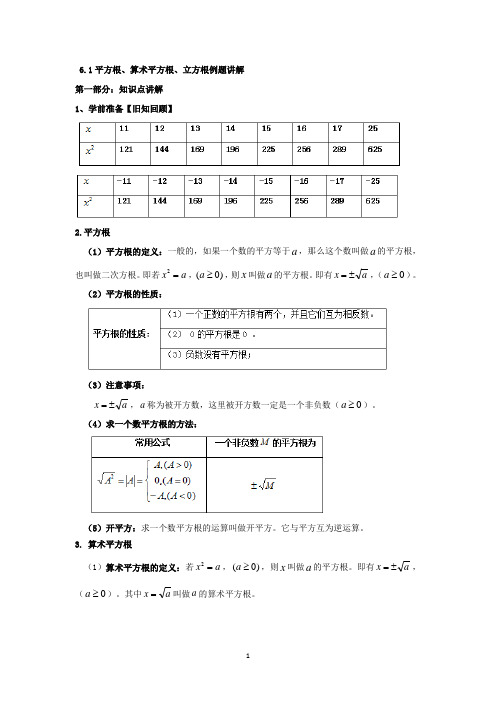
6.1平方根、算术平方根、立方根例题讲解 第一部分:知识点讲解 1、学前准备【旧知回顾】2.平方根(1)平方根的定义:一般的,如果一个数的平方等于a ,那么这个数叫做a 的平方根,也叫做二次方根。
即若a x =2,)0(≥a ,则x 叫做a 的平方根。
即有a x ±=,(0≥a )。
(2)平方根的性质:(3)注意事项:a x ±=,a 称为被开方数,这里被开方数一定是一个非负数(0≥a )。
(4)求一个数平方根的方法:(5)开平方:求一个数平方根的运算叫做开平方。
它与平方互为逆运算。
3. 算术平方根(1)算术平方根的定义:若a x =2,)0(≥a ,则x 叫做a 的平方根。
即有a x ±=,(0≥a )。
其中a x =叫做a 的算术平方根。
(2)算术平方根的性质:(3)注意点:在以后的计算题中,像22-52)(++,其中,25分别指的是2和5的算术平方根。
4.几种重要的运算: ① b a ab •=()0,0>>b a , ab b a =•()0,0>>b a②b a b a =)0,0(>≥b a , b aba =)0,0(>≥b a ③ a a =2)()0(≥a , a a =2 , a a =2-)(★★★ 若0<+b a ,则()ba b a b a b a --=+-=+=+2)(5.立方根(1)立方根的定义:一般地,如果一个数的立方等于a ,那么这个数叫做a 的立方根,也叫做三次方根。
即若a x =3,则x 叫做a 的立方根。
即有3a x =。
(2)立方根的性质:(3)开立方求一个数的立方根的运算叫做开立方,它与立方互为逆运算。
6.几个重要公式: ③ 333b a ab •=, 333ab b a =•333b a b a = )0(≠b , 333b a ba = )0(≠b④ a a =33)(可以为任何数)a (, a a =33 ,a a --33=)(第二部分:例题讲解题型1:求一个数的平方根、算术平方根、立方根。
初中数学课件 实数(平方根与立方根)

方根就是算术平方根,0的平方根是0,负数没有平方根.
(2)符号 a 只有当 a≥0 时有意,a<0 时无意义.
(3)当 a≥0 时, a 是一个非负数,它与a2 、a 统称为实数的“三大非负性”
(二)、立方根
(C)242
(D)88
,,
中,无理数的个数是
(A)1 个
(B)2 个
(C)3 个
(D)4 个
9.下列四个结论:(1)绝对值等于它本身的实数只有零;(2)相反数等于它本身的实数只
有零;(3)倒数等于它本身的实数只有 1;(4)算术平方根等于它本身的实数只有 1。其中
正确结论的个数是
(A)0 个 (B)1 个
(3) 3 1 35 3 8 2
27
27 3
例 6 若数m 的平方根 5 a 是 1
和a 1 9 ,求m 的值
解:由题意,知本题分两种情况来求解,
当m 0 时,其平方根为一对互为相反数,
则有: 5 a 1 a 1 9 0 故a , 3
则,5a 1 16 ,a 19 16,故m 162 256 当m 0 时,其方根是 0,
16
(A)3 是 9 的算术平方 9 根,3 即 =
(B)4 和-4 都是 16 的平方根,1 6即
= 4
(C)-3 是 9 的平方根,即 (2) 2
3.
x 的1 算术平方根是
=-3
2
(A)2
(B) 22
(C)
(D)4 是 16 的负的平方根,即
2
(D)
=-4
4.如果 (A)81
=3,则(x+1) 等于
平方根和立方根讲义

平方根与立方根知识梳理1、 平方根:(1)若x 2=a (a >0),那么x 叫做a 的 ,我们把 称为算术平方根,记为 。
规定,0的算术平方根为 。
(2)一个 的平方根有2个,它们互为 ; 只有1个平方根,它是0本身; 没有平方根。
(3)两个公式:()=2a ( );=2a2、立方根:(1)若x 3=a ,那么x 叫做a 的 ,记为 。
(2)一个正数的立方根有 个,0的立方根是 ,负数有 个立方根。
(3)立方根的性质:(3a )3 = ;33a =注意1:算术平方根与平方根的关系:算术平方根是平方根中正的一个值,它与它的相反数共同构成了平方根。
因此,算术平方根只有一个值,并且是非负数,它只表示为:a ;而平方根具有两个互为相反数的值,表示为:a ±。
注意2:平方根与立方根:每个数都有立方根,并且一个数只有一个立方根;但是,并不是每个数都有平方根,只有非负数才能有平方根。
典型例题一、弄清概念例1、9的平方根是 ,16的算术平方根是 ;327-的立方根是 。
例2、一个数的平方根是2m-4和3m-1,则这个数是 。
例3、已知23211a a -=-,求a 的值举一反三:1) 的平方是64,所以64的平方根是 ;(2) 的平方根是它本身。
(3)若x 的平方根是±2,则x= ;16的平方根是(4)当x 时,x 23-有意义。
(5)一个正数的平方根分别是m 和m-4,则m 的值是多少?这个正数是多少?二、利用算术平方根的双非负性解题例4、已知0262=-++b a ,解关于x 的方程 (a+2)x+b 2=a+1例5、若12)1(212-+-+-=x x x y ,求代数式2004)(y x +的值三、运用性质化简例6、a 、b 在数轴上的位置如图所示,化简:222)()1()1(b a b a ---++四、估算算术平方根的范围例7、已知79+与79-的小数部分分别为x 、y ,求3x+2y 的值[随堂练习]1、当_______m 时,5-m 有意义;当_______x 时,x -11有意义。
数的开方讲义

数的开方【教学内容】第十六章数的开方16.1 平方根16.2 立方根【知识点精析】一、平方根1.平方根如果一个数的平方等于a,那么这个数叫做a的平方根,即如果x2=a,则x叫做a的平方根,记作x=a±,其中a叫被开方数。
2.平方根的性质(1)任何一个正数的平方根有两个,它们互为相反数。
如正数a 的平方根是a+与-a恰是一对相反数;±,其中a(2)零的平方根是零,即00=;(3)负数没有平方根。
3.算术平方根正数a的正的平方根,叫做a的算术平方根。
4.开平方求一个非负数的平方根的运算,叫做开平方。
开平方与平方互为逆运算。
5.求一个正数的平方根的基本方法和基本步骤(1)明确(或易求出)所要求的正数是哪一个数的平方的。
①先写出是哪个数的平方等于已知的数;②再求出这个正数的算术平方根;③最后求出这个正数的平方根。
(2)不易求出所要求的正数是哪个数的平方的。
方法1:利用数学用表的平方根表查。
方法2:利用计算器计算。
6.注意的问题(1)负数没有平方根;(2)a的非负性,即当a≥0时,a≥0,非负数的算术平方根一定是非负数;(3)用计算器求一个正数的平方根应注意精确度,或根据精确度取近似数。
二、立方根1.立方根如果一个数的立方等于a,那么这个数叫做a的立方根,即如果x3=a,则x叫做a的立方根,记作:x=3a,其中a叫做被开方数,3叫做根指数。
2.立方根的性质任何一个正数的立方根是一个正数,即a>0时,3a>0;任何一个负数的立方根是一个负数,即a<0时,3a<0;零的立方根仍是零,即a=0时,3a=0。
3.开立方求一个数的立方根的运算叫做开立方。
开立方与立方互为逆运算。
4.求一个数的立方根的基本方法和基本步聚(1)明确(或易求出)所要求的数是哪一个数的立方的;①先指出所要求立方根的那个数是哪个数的立方;②根据立方根的定义,求出这个数的立方根。
(2)不易求出所要求的那个数是哪个数的立方的:①利用数学用表中的立方根表查;②利用计算器计算。
无理数、平方根与立方根讲义

一般地,如果一个数x 的立方等于a ,即x 3=a ,那么这个数x 就叫做a 的立方根(cube root, 也叫做三次方根).如:2是8的立方根,的立方根是--273,0是0的立方根。
注:正数的立方根是正数,负数的立方根是负数,0的立方根是0。
二、同步题型分析1、说说谁“有理”,谁“无理” 以下各数:-1,23,3.14,-π,3.⋅3,0,2,27,24,-0.2020020002……(相邻两个2之间0的个数逐次加1)其中,是有理数的是_____________,是无理数的是_______________. 在上面的有理数中,分数有______________,整数有______________. 答案:有理数:-1,23,3.14,3.3,0,2,27,24. 无理数:-π,-0.2020020002…… 分数:23,3.3,27整数:-1,0,2,242、在“()05,3.14 ,-π,()23,0.123334, 0.212212221…”这6个数中,无理数的个数是( )A .2个B .3个C .4个D .5个3、下列语句正确的是( ) A.3.78788788878888是无理数B.无理数分正无理数、零、负无理数C.无限小数不能化成分数D.无限不循环小数是无理数4、在直角△ABC 中,△C =90°,AC =23,BC =2,则AB 为( )A.整数B.分数C.无理数D.不能确定答案:B5、面积为3的正方形的边长______有理数;面积为4的正方形的边长______有理数.(填“是”或“不是”) 答案:不是,是)解:解:()28=±64±=即()2711=±)解:解:解:利用平方根来解下列方程.(2x-1)2-169=0变式训练:、下列计算正确的是(=±2 B ()0.02±0.0004±即()225=±11的平方根是(2)∵(x ﹣1)3=8, ∴x ﹣1=2, ∴x=3. 点评: 本题考查了学生开平方、立方的能力,也考查了解方程的方法,比较容易解答.变式训练1.求下列各式中的x :(1)4x 2=9; (2)1﹣(x+1)3=1001. 解答:解:(1)∵x 2=, ∴;(2)∵1﹣(x+1)3=1001,∴(x+1)3=﹣1000,∴x+1=﹣10,∴=﹣11.1、判断题(1)-0.01是0.1的平方根.………………………………………………………… …( )(2)-52的平方根为-5.……………………………………………………………… ( ) (3)0和负数没有平方根.……………………………………………………………… ( )(4)因为161的平方根是±41,所以161=±41.……………………………………… ( )(5)正数的平方根有两个,它们是互为相反数.…………………………………… ( ) 2、选择题(1)下列各数中没有平方根的数是( )A.-(-2)3B.3-3C.aD.-(a 2+1)(2)2a 等于( )A.aB.-aC.±aD.以上答案都不对(3)如果a (a >0)的平方根是±m ,那么( )A.a 2=±mB.a =±m2C.a =±mD.±a =±m(4)若正方形的边长是a ,面积为S ,那么( )A.S 的平方根是aB.a 是S 的算术平方根C.a =±SD.S =a3、填空题(1)若9x 2-49=0,则x =________.(2)若12 x 有意义,则x 范围是________.(3)已知|x -4|+y x +2=0,那么x =________,y =________.(4)如果a <0,那么2a =________,(a -)2=________.4、已知一个正方形ABCD 的面积是4a 2 cm 2,点E 、F 、G 、H 分别为正方形ABCD 各边的中点,依次连结E 、F 、G 、H 得一个正方形.(1)求这个正方形的边长.(2)求当a =2 cm 时,正方形EFGH 的边长大约是多少厘米?(精确到0.1cm )图1参考答案1.(1)× (2)× (3)× (4)× (5)√2.(1)D (2)D (3)D (4)B3.(1)±37 (2)x ≥-21(3)x =4,y =-8 (4)-a ,-a 4.(1)2a cm (2)2.8 cm【巩固练习】1、算术平方根等于它本身的数是( )A 、 1和0B 、0C 、1D 、 1±和0 2、2)6(-的平方根是( )A 、-6B 、36C 、±6D 、±6 3、满足53<<-x 的整数x 是( ) A 、3,2,1,0,1,2-- B 、3,2,1,0,1- C 、3,2,1,0,1,2-- D 、2,1,0,1-4、下列说法错误的是( )A. 1的平方根是1B. –1的立方根是-1C.2是2的平方根 D. –3是2)3(-的平方根5、已知x ,y 是实数,且34x ++(y-3)2=0,则xy 的值是( ) A .4 B .-4 C .94 D .-946、下列说法中正确的是( )A .9的平方根是3B .16的算术平方根是±2 C. 16的算术平方根是4 D. 16的平方根是±27、下列说法中,正确的是( )[来源:学&科&网Z&X&X&K]A.一个有理数的平方根有两个,它们互为相反数B.一个有理数的立方根,不是正数就是负数C.负数没有立方根D.如果一个数的立方根是这个数本身,那么这个数一定是-1,0,18、已知第一个正方体纸盒的棱长为6 cm ,第二个正方体纸盒的体积比第一个纸盒的体积大127 cm 3,求第二个纸盒的棱长. 答案:7cm。
讲解详细讲解平方根和立方根的概念运算规则和注意事项解答学生提出的疑问

讲解详细讲解平方根和立方根的概念运算规则和注意事项解答学生提出的疑问平方根和立方根是数学中重要的概念,它们在各个学科领域都有广泛的应用。
在本文中,我们将详细讲解平方根和立方根的概念、运算规则以及需要注意的事项,以解答学生们提出的疑问。
一、平方根的概念和运算规则平方根是指一个数的平方等于该数的非负根。
即,对于任意非负数x和非负数a,若a的平方等于x,那么我们称a是x的平方根。
用符号表示,可以写作√x=a。
平方根的运算规则如下:1. 非负数的平方根是唯一的。
即,一个非负数x只有一个非负平方根。
2. 负数没有实数平方根。
平方根的定义要求平方根是非负的,因此负数没有实数平方根。
3. 平方根运算具有交换律和结合律。
即,对于任意非负数x和y,有√(x*y)=√x*√y和√(x/y)=√x/√y。
4. 平方根运算满足开方运算法则。
即,对于任意正数x和正整数n,平方根运算和幂运算可以互相转换,即√(x^n)=(√x)^n。
二、立方根的概念和运算规则立方根是指一个数的立方等于该数的非负根。
即,对于任意数值x 和非负数a,若a的立方等于x,那么我们称a是x的立方根。
用符号表示,可以写作³√x=a。
立方根的运算规则如下:1. 实数的立方根是唯一的。
即,一个实数x只有一个实立方根。
2. 负数的立方根是存在的。
与平方根不同,负数是存在实数立方根的,例如-8的立方根是-2,因为(-2)^3=-8。
3. 立方根运算具有交换律和结合律。
即,对于任意数值x和y,有³√(x*y)=³√x*³√y和³√(x/y)=³√x/³√y。
4. 立方根运算也满足开方运算法则。
即,对于任意正数x和正整数n,立方根运算和幂运算可以互相转换,即³√(x^n)=(³√x)^n。
三、注意事项在计算平方根和立方根时,需要注意以下几点:1. 平方根和立方根的符号。
平方根是指非负根,因此其结果为正数或零。
平方根与立方根及解析

平方根与立方根及解析一、平方根的概念与运算性质平方根是数学中常见的运算,表示一个数的平方根。
如果一个数a的平方等于b(即a²=b),那么a就是b的平方根。
平方根通常用符号√表示。
平方根的运算性质如下:1. 非负数的平方根都是有意义的,即对于非负数b,b的平方根√b一定存在。
2. 负数的平方根在实数范围内没有实数解。
例如,-1的平方根不存在于实数范围内。
3. 如果a>0,那么a的平方根有两个解:一个是正的,一个是负的。
例如,4的平方根有±2两个解。
4. 平方根具有乘法性质,即√(ab)=√a * √b。
这个性质有助于进行平方根的计算。
二、立方根的概念与运算性质立方根是指一个数的立方等于另一个数的根。
如果一个数a的立方等于b(即a³=b),那么a就是b的立方根。
立方根通常用符号³√或者∛表示。
立方根的运算性质如下:1. 任意实数都有唯一的立方根。
即对于任意实数b,b的立方根³√b存在且唯一。
2. 正数的立方根只有一个解,即正数本身。
例如,8的立方根为2。
3. 负数的立方根在实数范围内没有实数解。
例如,-1的立方根不存在于实数范围内。
4. 立方根具有乘法性质,即³√(ab)=³√a *³√b。
这个性质有助于进行立方根的计算。
三、平方根与立方根的解析方法1. 平方根的解析方法求一个数的平方根可以使用不同的解析方法,其中最常见的方法有以下几种:(1)因数分解法:将一个数分解成若干个因数的乘积形式,然后对每个因数求平方根。
(2)二分法:首先确定一个范围,然后将范围内的数逐次求平方,直到找到与目标数接近的解。
(3)牛顿迭代法:利用泰勒级数来逼近目标数的平方根,通过迭代计算最终得到解。
2. 立方根的解析方法求一个数的立方根可以使用类似的解析方法,其中常见的方法包括:(1)因数分解法:将一个数分解成若干个因数的乘积形式,然后对每个因数求立方根。
平方根与算术平方根立方根无理数PPT课件

(2)个数不同:一个正数有两个平方根,而一个
正数的算术平方根只有一个。
(3)表示方法不同:正数a的算术平方根表示
第9页/共32页
立方根:
1. 定义:
一般地,如果一个数x的立方等于a,即x3=a, 那么这个数x就叫做a的立方根.(也叫做三次方 根) 。
2.表示方法:
第10页/共32页
什么叫做开平方?那开立方呢?
无理数: 无限不循环小数
含有 ~ 的数
有规律但不循环的数
第25页/共32页
按性质分类: 实数
正实数
0
负实数
正有理数
正无理数
负有理数
负无理数
负实数
正实数
0
第26页/共32页
你能在数轴上找到表示 的点吗?
2
小结:
有理数可以用数轴上的点表示,无理数也可以用数轴上的点 表示.
每一个无理数都能在数轴上表示出来. 数轴上的点有些表示有理数,有些表示无理数. 每一个实数都可以用数轴上的一个点来表示;反过来, 数轴上的每一点都表示一个实数。即实数和数轴上的 点是一一对应的。
第21页/共32页
思考:
2 介于哪两个整数之间?你是根据什么考虑的?
A
1
2
B 4D
1
2
2C
1.42 __<__( 2)2 __<__1.52
1.4 ___<_ 2 __<__1.5
1.412 _<___( 2)2 __<__1.42 2
1.41 ___<_ 2 __<__1.42
1.414 2 _<___( 2)2 _<___1.415 2
第28页/共32页
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
内容
基本要求
略高要求
较高要求
平方根、算术平方根
了解平方根及算术平方根的概念,
会用根号表示非负数的平方根及算术平方根 会用平方运算求某些非负数的平方根
立方根 了解立方根的概念,会用根号表示数的立方根
会用立方根运算求某些数的立方根 实数
了解实数的概念
会进行简单的实数运算
实数可按下图进行详细分类:
0⎧⎧⎫⎧⎪⎪⎪⎪⎨⎪
⎪
⎪
⎪
⎪⎪
⎪
⎨
⎬
⎩
⎪
⎪
⎪⎪
⎧⎨
⎪
⎪
⎨
⎪
⎪
⎪⎩
⎭
⎩⎪
⎪
⎫
⎧⎪⎪⎨⎬
⎪⎪⎩⎭⎩
正整数整数负整数有理数
有限小数或无限循环小数正分数实数分数负分数正无理数无理数无限不循环小数负无理数
实数与数轴上的点一一对应
.
(以下概念均在实数域范围内讨论
) 平方根的定义及表示方法:
如果一个数的平方等于a
,那么这个数叫做a 的平方根. 也就是说,若
2x a
=,则x
就叫做a 的平方根.
一个非负数
a 的平方根可用符号表示为
“
a
”.
算术平方根:
一个正数a
有两个互为相反数的平方根,其中正的平方根叫做a 的算术平方根,可用符号表示为
a ;
有一个平方根,就是0,
0的算术平方根也是0
,负数没有平方根,当然也没有算术平方根
.
知识点睛
中考要求
平方根和立方根
一个非负数的平方根不一定是非负数,但它的算术平方根一定是非负数,即若0a ≥0a .
平方根的计算:
求一个非负数的平方根的运算,叫做开平方.
开平方与平方是互逆运算,可以通过平方运算来求一个数的平方根或算术平方根,以及检验一个数是不是另一个数的平方根或算术平方根.
通过验算我们可以知道:
⑴ 当被开方数扩大(或缩小)2n 倍,它的算术平方根相应地扩大(或缩小)n 倍(0n ≥). ⑵ 平方根和算术平方根与被开方数之间的关系:
①若0a ≥,则2()a a =;②不管a 2(0)
||(0)a a a a a a ≥⎧==⎨-<⎩
注意二者之间的区别及联系.
⑶若一个非负数a 介于另外两个非负数1a 、2a 之间,即120a a a ≤<<1a 2a 之间,即:120a a a ≤<范围.
立方根的定义及表示方法:
如果一个数的立方等于a ,那么这个数叫做a 的立方根,也就是说,若3,x a =则x 就叫做a 的立方根, 一个数a 的立方根可用符号表3a ,其中“3”叫做根指数,不能省略. 前面学习的a 其实省略了根指数“2”2a a 3
a “三次根号a ”2a “二次根号a ”a “根号a ”.
任何一个数都有立方根,且只有一个立方根,
正数的立方根为正数,负数的立方根为负数,0的立方根为0.
立方根的计算:
求一个数的立方根的运算,叫做开立方,开立方与立方是互逆运算,可以通过立方运算来求一个数的立方根,以及检验一个数是不是另一个数的立方根.
通过归纳我们可以知道:
⑴当被开方数(大于0)扩大(或缩小)3n 倍,它的立方根相应地扩大(或缩小)n 倍. 33a a =,33()a a =
⑶若一个数a 介于另外两个数1a 、2a 之间,即12a a a <<, 31a 32a 33312a a a < 利用这个结论我们可以来估算一个数的立方根的大致范围.
重、难点
难点:平方根的性质
【例1】 判断下列各题,并说明理由
819±. ( ) a ( ) ⑶2a 的算术平方根是a . ( ) ⑷ 2()5a -,则5a =-. ( ) 93=±. ( ) ⑹ 6-是2(6)-的平方根. ( ) ⑺ 2(6)-的平方根是6-.
( )
⑻ 若236x =,则366x =±=±. ( ) ⑼ 若两个数平方后相等,则这两个数也一定相等. ( ) ⑽ 如果两个非负数相等,那么这两个数各自的算术平方根也一定相等. ( ) ⑾ 算术平方根一定是正数. ( ) ⑿ 2a -没有算术平方根. ( ) ⒀ 64的立方根是4±. ( )
⒁ 1-是1
6-的立方根. ( )
⒂ 33x x . ( ) ⒃ 互为相反数的两个数的立方根互为相反数. ( ) ⒄ 正数有两个互为相反数的偶数次方根,任何数都有唯一的奇数次方根. ( )
【例2】 ⑴ 若22(2)a =-,则a = ;若22()(3)x -=-,则x = .
⑵ 22x +,则(25)x +的平方根是 ;若25x =,则x = .
⑶ 2
1a =-,则a ;若20a a =,则a . ⑷ 当0m <,2m 的算术平方根是 .
⑸ 2()a b -算术平方根是a b -,则a b .
⑹ 若一个自然数的一个平方根是m ,那么比它大1的自然数的平方根是 .
⑺ 平方根等于本身的数是 ,算术平方根等于它本身的数是
,立方根等于它本身
的数是 ;平方根与立方根相等的数是 .
例题精讲
⑴21
(51)30x --=; ⑵3(100.2)0.027x -=-
3312573511164168
---
33321600010.125-
【例4】 已知某正数的两个平方根是35a -与1a +,求这个正数.
【例5】 已知3(2)27a b +=-235a b -=,求21(3)n a b ++的值(n 为正整数).
【例6】 求22221995199519961996+⋅+的平方根.
【例7】 (人大附单元测试)已知a 为实数,且满足200201a a a --=,求2200a -的值.
【练习1】若22(3)x =-,33(2)y =-,求x y +所有可能值.
【练习2】一个数的平方根是22a b +和4613a b -+,求这个数.
【练习3】(101数学实验班单元练习)
已知2a -的平方根是2±,27a b ++的立方根是3,求22a b +的平方根.
【练习4】(2007年成都)22(5)0a b -+=,那么a b +的值为 .
【练习5
】22111
a a
b -+-+=,求a ,b 的值.
课堂作业
【练习6】若a 、b 为实数,且|1|20a ab --,
求1111(1)(1)(2)(2)(1993)(1993)ab a b a b a b +++++++++的值.
1. ⑴ (安顺市中考题)
16的平方根是 ;2( 2.5)-的平方根是 ;2(2)-的平方根是 .
⑵ (威海中考题3
8的相反数是 ;64的立方根是 .
⑶ 平方根等于本身的数是 ,算术平方根等于它本身的数是 ,立方根 等于它本身的数是 ;平方根与立方根相等的数是 . ⑷ (江西省中考题)20n n 为( )
A .2
B .3
C .4
D .5 ⑸ (上海市中考题)12x -=的根是 . 31.815848 1.2231815848- _____. 2. 若一正数的平方根是36a +与29a +,求这个正数.
3. 已知x y +的负的平方根是3-,x y -的立方根是3,求25x y -的平方根. 4. 243a b x a -+=+3a +的算术平方根,323b a y b -+=-3b -的立方根,求y x -的立方根.
5.
已知:|1|2340a b a b -+--.求:24a b +的立方根. 家庭作业。
