第七讲 空间计量经济学模型的matlab估计
MATLAB中的统计推断与参数估计方法解析

MATLAB中的统计推断与参数估计方法解析MATLAB(Matrix Laboratory)是一种基于数值计算和编程语言的工具,广泛应用于科学、工程和金融等领域。
在统计学中,MATLAB提供了丰富的函数和工具箱,可以进行统计推断和参数估计等分析。
本文将针对MATLAB中的统计推断和参数估计方法进行解析,包括假设检验、置信区间估计和最大似然估计等。
一、假设检验假设检验是统计学中常用的一种方法,用于验证关于总体参数的假设。
在MATLAB中,可以利用t检验和χ²检验等函数进行假设检验分析。
1. t检验t检验主要用于比较两个样本均值是否存在显著差异。
在MATLAB中,可以使用ttest2函数进行双样本t检验,使用ttest函数进行单样本t检验。
例如,我们有两组数据x和y,想要判断它们的均值是否显著不同。
可以使用以下代码进行双样本t检验:```[h,p,ci,stats] = ttest2(x,y);```其中,h表示假设检验的结果,为0表示接受原假设,为1表示拒绝原假设;p 表示假设检验的p值;ci表示置信区间;stats包含了相关统计信息。
2. χ²检验χ²检验主要用于比较观察频数和期望频数之间是否存在显著差异。
在MATLAB 中,可以使用chi2gof函数进行χ²检验分析。
例如,我们有一组观察频数obs和一组对应的期望频数exp,可以使用以下代码进行χ²检验:```[h,p,stats] = chi2gof(obs,'Expected',exp);```其中,h表示假设检验的结果,为0表示接受原假设,为1表示拒绝原假设;p 表示假设检验的p值;stats包含了相关统计信息。
二、置信区间估计置信区间估计是用于估计总体参数范围的方法,可以帮助我们对总体参数进行合理的推断。
在MATLAB中,可以利用confint函数进行置信区间估计分析。
例如,我们有一组数据x,想要对它的均值进行置信区间估计。
经济预测与决策技术及MATLAB实现第7章 时间序列预测法

预测图
7.2 指数平滑预测法
7.2.1 一次指数平滑法
(1)一次指数平滑法的基本模型
S (1) t
Xt
(1
)
S (1) t 1
S (1) t
Xt
(1 ) X t1
L
(1
)t
1
X1
(1
)t
S (1) 0
Xˆ t1
S (1) t
其中,X0, X1,L , X n 为时间序列观测值,
首页
7.2.2 二次指数平滑法
(1)二次指数平滑法的线性模型为
XˆtT at btT
at
2
S (1) t
S (2) t
bt
1
(St(1)
St(2) )
S (1) t
Xt
(1 )St(11)
S (2) t
S (1) t
(1 )St(21)
【例7-4】 (续例7-1) 用二次指数平滑法预测2016年投 资额(=0.9)。
当时间序列既有季节性变动又有趋势性变动时,先建 立趋势预测模型,在此基础上求得季节指数,再建立 预测模型。其过程如下:
(1)计算历年同季平均数r;
(2)建立趋势预测模型,求趋势值
(3)计算出趋势值后,再计算出历年同季的平均数R; (4)计算趋势季节指数(k);用同季平均数与趋势值同 季平均数之比来计算。 (5)对趋势季节指数进行修正;
88773.6 109998.2 137323.9 172828.4...
224598.8 251683.77 311485.13 374694.74
MATLAB-空间计量模型详细步骤
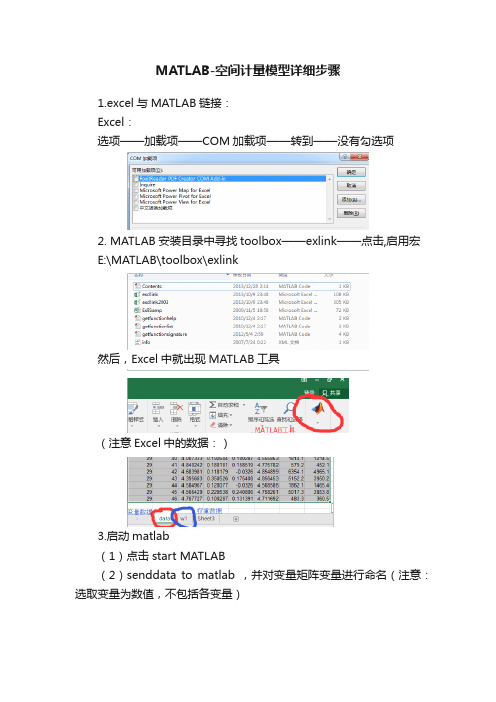
MATLAB-空间计量模型详细步骤1.excel与MATLAB链接:Excel:选项——加载项——COM加载项——转到——没有勾选项2. MATLAB安装目录中寻找toolbox——exlink——点击,启用宏E:\MATLAB\toolbox\exlink然后,Excel中就出现MATLAB工具(注意Excel中的数据:)3.启动matlab(1)点击start MATLAB(2)senddata to matlab ,并对变量矩阵变量进行命名(注意:选取变量为数值,不包括各变量)(data表中数据进行命名)(空间权重进行命名)(3)导入MATLAB中的两个矩阵变量就可以看见4.将elhorst和jplv7两个程序文件夹复制到MATLAB安装目录的toolbox文件夹5.设置路径:6.输入程序,得出结果T=30;N=46;W=norm(W1);y=A(:,3);x=A(:,[4,6]);xconstant=ones(N*T,1); [nobs K]=size(x);results=ols(y,[xconstant x]);vnames=strvcat('logcit','intercept','logp','logy');prt_reg(results,vnames,1);sige=results.sige*((nobs-K)/nobs);loglikols=-nobs/2*log(2*pi*sige)-1/(2*sige)*results.resid'*results.resid % The (robust)LM tests developed by ElhorstLMsarsem_panel(results,W,y,[xconstant x]); % (Robust) LM tests 解释附录:静态面板空间计量经济学一、OLS静态面板编程1、普通面板编程T=30;N=46;W=normw(W1);y=A(:,3);x=A(:,[4,6]);xconstant=ones(N*T,1);[nobs K]=size(x);results=ols(y,[xconstant x]);vnames=strvcat('logcit','intercept','logp','logy');prt_reg(results,vnames,1);sige=results.sige*((nobs-K)/nobs);loglikols=-nobs/2*log(2*pi*sige)-1/(2*sige)*results.resid'*results.resid % The (robust)LM tests developed by ElhorstLMsarsem_panel(results,W,y,[xconstant x]); % (Robust) LM tests2、空间固定OLS (spatial-fixed effects)T=30;N=46;W=normw(W1);y=A(:,3);x=A(:,[4,6]);xconstant=ones(N*T,1);[nobs K]=size(x);model=1;[ywith,xwith,meanny,meannx,meanty,meantx]=demean(y,x, N,T,model );results=ols(ywith,xwith);vnames=strvcat('logcit','logp','logy'); % should be changed if x is changedprt_reg(results,vnames);sfe=meanny-meannx*results.beta; % including the constant term yme = y - mean(y);et=ones(T,1);error=y-kron(et,sfe)-x*results.beta;rsqr1 = error'*error;rsqr2 = yme'*yme;FE_rsqr2 = 1.0 - rsqr1/rsqr2 % r-squared including fixed effectssige=results.sige*((nobs-K)/nobs);logliksfe=-nobs/2*log(2*pi*sige)-1/(2*sige)*results.resid'*results.residLMsarsem_panel(results,W,ywith,xwith); % (Robust) LM tests3、时期固定OLS(time-period fixed effects)T=30;N=46;W=normw(W1);y=A(:,3);x=A(:,[4,6]);xconstant=ones(N*T,1);[nobs K]=size(x);model=2;[ywith,xwith,meanny,meannx,meanty,meantx]=demean(y,x, N,T,model );results=ols(ywith,xwith);vnames=strvcat('logcit','logp','logy'); % should be changed if x is changedprt_reg(results,vnames);tfe=meanty-meantx*results.beta; % including the constant termyme = y - mean(y);en=ones(N,1);error=y-kron(tfe,en)-x*results.beta;rsqr1 = error'*error;rsqr2 = yme'*yme;FE_rsqr2 = 1.0 - rsqr1/rsqr2 % r-squared including fixed effectssige=results.sige*((nobs-K)/nobs);logliktfe=-nobs/2*log(2*pi*sige)-1/(2*sige)*results.resid'*results.residLMsarsem_panel(results,W,ywith,xwith); % (Robust) LM tests4、空间与时间双固定模型T=30;N=46;W=normw(W1);y=A(:,3);x=A(:,[4,6]);xconstant=ones(N*T,1);[nobs K]=size(x);model=3;[ywith,xwith,meanny,meannx,meanty,meantx]=demean(y,x, N,T,model );results=ols(ywith,xwith);vnames=strvcat('logcit','logp','logy'); % should be changed if x is changedprt_reg(results,vnames)en=ones(N,1);et=ones(T,1);intercept=mean(y)-mean(x)*results.beta;sfe=meanny-meannx*results.beta-kron(en,intercept);tfe=meanty-meantx*results.beta-kron(et,intercept);yme = y - mean(y);ent=ones(N*T,1);error=y-kron(tfe,en)-kron(et,sfe)-x*results.beta-kron(ent,intercept); rsqr1 = error'*error;rsqr2 = yme'*yme;FE_rsqr2 = 1.0 - rsqr1/rsqr2 % r-squared including fixed effects sige=results.sige*((nobs-K)/nobs);loglikstfe=-nobs/2*log(2*pi*sige)-1/(2*sige)*results.resid'*results.residLMsarsem_panel(results,W,ywith,xwith); % (Robust) LM tests二、静态面板SAR模型1、无固定效应(No fixed effects)T=30;N=46;W=normw(W1);y=A(:,[3]);x=A(:,[4,6]);for t=1:Tt1=(t-1)*N+1;t2=t*N;wx(t1:t2,:)=W*x(t1:t2,:);endxconstant=ones(N*T,1);[nobs K]=size(x);info.lflag=0;info.model=0;info.fe=0;results=sar_panel_FE(y,[xconstant x],W,T,info); vnames=strvcat('logcit','intercept','logp','logy');prt_spnew(results,vnames,1)% Print out effects estimatesspat_model=0;direct_indirect_effects_estimates(results,W,spat_model); panel_effects_sar(results,vnames,W);2、空间固定效应(Spatial fixed effects)T=30;N=46;W=normw(W1);y=A(:,[3]);x=A(:,[4,6]);for t=1:Tt1=(t-1)*N+1;t2=t*N;wx(t1:t2,:)=W*x(t1:t2,:);endxconstant=ones(N*T,1);[nobs K]=size(x);info.lflag=0;info.model=1;info.fe=0;results=sar_panel_FE(y,x,W,T,info);vnames=strvcat('logcit','logp','logy');prt_spnew(results,vnames,1)% Print out effects estimatesspat_model=0;direct_indirect_effects_estimates(results,W,spat_model);panel_effects_sar(results,vnames,W);3、时点固定效应(Time period fixed effects)T=30;N=46;W=normw(W1);y=A(:,[3]);x=A(:,[4,6]);for t=1:Tt1=(t-1)*N+1;t2=t*N;wx(t1:t2,:)=W*x(t1:t2,:);endxconstant=ones(N*T,1);[nobs K]=size(x);info.lflag=0; % required for exact resultsinfo.model=2;info.fe=0; % Do not print intercept and fixed effects; use info.fe=1 to turn onresults=sar_panel_FE(y,x,W,T,info);vnames=strvcat('logcit','logp','logy');prt_spnew(results,vnames,1)% Print out effects estimatesspat_model=0;direct_indirect_effects_estimates(results,W,spat_model);panel_effects_sar(results,vnames,W);4、双固定效应(Spatial and time period fixed effects)T=30;N=46;W=normw(W1);y=A(:,[3]);x=A(:,[4,6]);for t=1:Tt1=(t-1)*N+1;t2=t*N;wx(t1:t2,:)=W*x(t1:t2,:);endxconstant=ones(N*T,1);[nobs K]=size(x);info.lflag=0; % required for exact resultsinfo.model=3;info.fe=0; % Do not print intercept and fixed effects; use info.fe=1 to turn onresults=sar_panel_FE(y,x,W,T,info);vnames=strvcat('logcit','logp','logy');prt_spnew(results,vnames,1)% Print out effects estimatesspat_model=0;direct_indirect_effects_estimates(results,W,spat_model);panel_effects_sar(results,vnames,W);三、静态面板SDM模型1、无固定效应(No fixed effects)T=30;N=46;W=normw(W1);y=A(:,[3]);x=A(:,[4,6]);for t=1:Tt1=(t-1)*N+1;t2=t*N;wx(t1:t2,:)=W*x(t1:t2,:);endxconstant=ones(N*T,1);[nobs K]=size(x);info.lflag=0;info.model=0;info.fe=0;results=sar_panel_FE(y,[xconstant x wx],W,T,info);vnames=strvcat('logcit','intercept','logp','logy','W*logp','W*l ogy');prt_spnew(results,vnames,1)% Print out effects estimatesspat_model=1;direct_indirect_effects_estimates(results,W,spat_model);panel_effects_sdm(results,vnames,W);2、空间固定效应(Spatial fixed effects)T=30;N=46;W=normw(W1);y=A(:,[3]);x=A(:,[4,6]);for t=1:Tt1=(t-1)*N+1;t2=t*N;wx(t1:t2,:)=W*x(t1:t2,:);endxconstant=ones(N*T,1);[nobs K]=size(x);info.lflag=0; % required for exact resultsinfo.model=1;info.fe=0; % Do not print intercept and fixed effects; use info.fe=1 to turn onresults=sar_panel_FE(y,[x wx],W,T,info);vnames=strvcat('logcit','logp','logy','W*logp','W*logy');prt_spnew(results,vnames,1)% Print out effects estimatesspat_model=1;direct_indirect_effects_estimates(results,W,spat_model);panel_effects_sdm(results,vnames,W);3、时点固定效应(Time period fixed effects)T=30;N=46;W=norm(W1);y=A(:,[3]);x=A(:,[4,6]);for t=1:Tt1=(t-1)*N+1;t2=t*N;wx(t1:t2,:)=W*x(t1:t2,:);endxconstant=ones(N*T,1);[nobs K]=size(x);info.lflag=0; % required for exact resultsinfo.model=2;info.fe=0; % Do not print intercept and fixed effects; use info.fe=1 to turn on% New routines to calculate effects estimatesresults=sar_panel_FE(y,[x wx],W,T,info);vnames=strvcat('logcit','logp','logy','W*logp','W*logy');% Print out coefficient estimatesprt_spnew(results,vnames,1)% Print out effects estimatesspat_model=1;direct_indirect_effects_estimates(results,W,spat_model);panel_effects_sdm(results,vnames,W)4、双固定效应(Spatial and time period fixed effects)T=30;N=46;W=normw(W1);y=A(:,[3]);x=A(:,[4,6]);for t=1:Tt1=(t-1)*N+1;t2=t*N;wx(t1:t2,:)=W*x(t1:t2,:);endxconstant=ones(N*T,1);[nobs K]=size(x);info.bc=0;info.lflag=0; % required for exact resultsinfo.model=3;info.fe=0; % Do not print intercept and fixed effects; use info.fe=1 to turn onresults=sar_panel_FE(y,[x wx],W,T,info);vnames=strvcat('logcit','logp','logy','W*logp','W*logy');prt_spnew(results,vnames,1)% Print out effects estimatesspat_model=1;direct_indirect_effects_estimates(results,W,spat_model);panel_effects_sdm(results,vnames,W)wald test spatial lag% Wald test for spatial Durbin model against spatial lagmodelbtemp=results.parm;varcov=results.cov;Rafg=zeros(K,2*K+2);for k=1:KRafg(k,K+k)=1; % R(1,3)=0 and R(2,4)=0;endWald_spatial_lag=(Rafg*btemp)'*inv(Rafg*varcov*Rafg')*Raf g*btemp prob_spatial_lag=1-chis_cdf (Wald_spatial_lag, K) wald test spatial error% Wald test spatial Durbin model against spatial error model R=zeros(K,1);for k=1:KR(k)=btemp(2*K+1)*btemp(k)+btemp(K+k); % k changed in 1,7/12/2010% R(1)=btemp(5)*btemp(1)+btemp(3);% R(2)=btemp(5)*btemp(2)+btemp(4);endRafg=zeros(K,2*K+2);for k=1:KRafg(k,k) =btemp(2*K+1); % k changed in 1, 7/12/2010Rafg(k,K+k) =1;Rafg(k,2*K+1)=btemp(k);% Rafg(1,1)=btemp(5);Rafg(1,3)=1;Rafg(1,5)=btemp(1);% Rafg(2,2)=btemp(5);Rafg(2,4)=1;Rafg(2,5)=btemp(2);endWald_spatial_error=R'*inv(Rafg*varcov*Rafg')*Rprob_spatial_error=1-chis_cdf (Wald_spatial_error,K)LR test spatial lagresultssar=sar_panel_FE(y,x,W,T,info);LR_spatial_lag=-2*(resultssar.lik-results.lik)prob_spatial_lag=1-chis_cdf (LR_spatial_lag,K)LR test spatial errorresultssem=sem_panel_FE(y,x,W,T,info);LR_spatial_error=-2*(resultssem.lik-results.lik)prob_spatial_error=1-chis_cdf (LR_spatial_error,K)5、空间随机效应与时点固定效应模型T=30;N=46;W=normw(W1);y=A(:,[3]);x=A(:,[4,6]);for t=1:Tt1=(t-1)*N+1;t2=t*N;wx(t1:t2,:)=W*x(t1:t2,:);endxconstant=ones(N*T,1);[nobs K]=size(x);[ywith,xwith,meanny,meannx,meanty,meantx]=demean(y,[x wx],N,T,2); % 2=time dummiesinfo.model=1;results=sar_panel_RE(ywith,xwith,W,T,info);prt_spnew(results,vnames,1)spat_model=1;direct_indirect_effects_estimates(results,W,spat_model);panel_effects_sdm(results,vnames,W)wald test spatial lagbtemp=results.parm(1:2*K+2);varcov=results.cov(1:2*K+2,1:2*K+2);Rafg=zeros(K,2*K+2);for k=1:KRafg(k,K+k)=1; % R(1,3)=0 and R(2,4)=0;endWald_spatial_lag=(Rafg*btemp)'*inv(Rafg*varcov*Rafg')*Raf g*btempprob_spatial_lag= 1-chis_cdf (Wald_spatial_lag, K)wald test spatial errorR=zeros(K,1);for k=1:KR(k)=btemp(2*K+1)*btemp(k)+btemp(K+k); % k changed in 1,7/12/2010% R(1)=btemp(5)*btemp(1)+btemp(3);% R(2)=btemp(5)*btemp(2)+btemp(4);endRafg=zeros(K,2*K+2);for k=1:KRafg(k,k) =btemp(2*K+1); % k changed in 1, 7/12/2010 Rafg(k,K+k) =1;Rafg(k,2*K+1)=btemp(k);% Rafg(1,1)=btemp(5);Rafg(1,3)=1;Rafg(1,5)=btemp(1);% Rafg(2,2)=btemp(5);Rafg(2,4)=1;Rafg(2,5)=btemp(2);endWald_spatial_error=R'*inv(Rafg*varcov*Rafg')*Rprob_spatial_error= 1-chis_cdf (Wald_spatial_error,K)LR test spatial lagresultssar=sar_panel_RE(ywith,xwith(:,1:K),W,T,info);LR_spatial_lag=-2*(resultssar.lik-results.lik)prob_spatial_lag=1-chis_cdf (LR_spatial_lag,K)LR test spatial errorresultssem=sem_panel_RE(ywith,xwith(:,1:K),W,T,info);LR_spatial_error=-2*(resultssem.lik-results.lik)prob_spatial_error=1-chis_cdf (LR_spatial_error,K)四、静态面板SEM模型1、无固定效应(No fixed effects)T=30;N=46;W=normw(W1);y=A(:,[3]);x=A(:,[4,6]);for t=1:Tt1=(t-1)*N+1;t2=t*N;wx(t1:t2,:)=W*x(t1:t2,:);endxconstant=ones(N*T,1);[nobs K]=size(x);info.lflag=0;info.model=0;info.fe=0;results=sem_panel_FE(y,[xconstant x],W,T,info);vnames=strvcat('logcit','intercept','logp','logy');prt_spnew(results,vnames,1)% Print out effects estimatesspat_model=0;direct_indirect_effects_estimates(results,W,spat_model); panel_effects_sar(results,vnames,W);2、空间固定效应(Spatial fixed effects)T=30;N=46;W=normw(W1);y=A(:,[3]);x=A(:,[4,6]);for t=1:Tt1=(t-1)*N+1;t2=t*N;wx(t1:t2,:)=W*x(t1:t2,:);endxconstant=ones(N*T,1);[nobs K]=size(x);info.lflag=0;info.model=1;info.fe=0;results=sem_panel_FE(y,x,W,T,info);vnames=strvcat('logcit','logp','logy');prt_spnew(results,vnames,1)% Print out effects estimatesspat_model=0;direct_indirect_effects_estimates(results,W,spat_model); panel_effects_sar(results,vnames,W);3、时点固定效应(Time period fixed effects)T=30;N=46;W=normw(W1);y=A(:,[3]);x=A(:,[4,6]);for t=1:Tt1=(t-1)*N+1;t2=t*N;wx(t1:t2,:)=W*x(t1:t2,:);endxconstant=ones(N*T,1);[nobs K]=size(x);info.lflag=0; % required for exact resultsinfo.model=2;info.fe=0; % Do not print intercept and fixed effects; use info.fe=1 to turn onresults=sem_panel_FE(y,x,W,T,info);vnames=strvcat('logcit','logp','logy');prt_spnew(results,vnames,1)% Print out effects estimatesspat_model=0;direct_indirect_effects_estimates(results,W,spat_model);panel_effects_sar(results,vnames,W);4、双固定效应(Spatial and time period fixed effects)T=30;N=46;W=normw(W1);y=A(:,[3]);x=A(:,[4,6]);for t=1:Tt1=(t-1)*N+1;t2=t*N;wx(t1:t2,:)=W*x(t1:t2,:);endxconstant=ones(N*T,1);[nobs K]=size(x);info.lflag=0; % required for exact resultsinfo.model=3;info.fe=0; % Do not print intercept and fixed effects; use info.fe=1 to turn onresults=sem_panel_FE(y,x,W,T,info);vnames=strvcat('logcit','logp','logy');prt_spnew(results,vnames,1)% Print out effects estimatesspat_model=0;direct_indirect_effects_estimates(results,W,spat_model); panel_effects_sar(results,vnames,W);五、静态面板SDEM模型1、无固定效应(No fixed effects)T=30;N=46;W=normw(W1);y=A(:,[3]);x=A(:,[4,6]);。
空间经济计量学模型

Moran’s I = (n Σxy - ΣxΣy) / (n Σx² Σx²)
应用场景
注意事项
适用于检验空间分布的集聚程度,常用于 分析地理信息系统(GIS)中的空间数据。
Moran’s I检验假设数据符合正态分布, 因此在使用前应对数据进行正态性检验。
LM检验
定义
LM检验是空间滞后模型 (Spatial Lag Model)的简称, 用于检验空间滞后变量对被解
03
空间计量经济学模型
空间滞后模型
空间滞后变量
空间滞后模型中包含一个反映空间距 离影响的空间滞后变量。
模型估计方法
空间滞后模型的估计方法包括最小二 乘法、广义最小二乘法等。
适用范围
空间滞后模型适用于研究空间依赖性 较强的数据,例如地区间经济增长的 相互影响等。
模型参数解释
空间滞后模型的参数可以解释为空间 权重矩阵中的权重系数,反映了不同 地区之间的空间关系。
运用空间计量经济学模型,研究国际贸易的 空间效应,揭示贸易对周边地区经济发展的 影响机制。
详细描述
通过构建空间计量经济学模型,分析国际贸 易对周边地区经济发展的影响,探讨贸易对 不同地区经济发展的作用机制和程度差异, 为制定区域经济发展政策提供参考。
案例四:人口流动的空间影响因素研究
总结词
应用空间计量经济学模型,研究人口流动的 空间影响因素,为政府制定人口政策提供科 学依据。
空间自相关系数 = Σw_ij * y_j / Σw_ij * Σy_j
应用场景
注意事项
适用于分析空间分布的 集聚程度,常用于地理 信息系统(GIS)中的空间 数据分析。
空间自相关检验假设数 据符合正态分布,因此 在使用前应对数据进行 正态性检验。同时,空 间权重矩阵的选择对检 验结果有很大影响,需 要根据具体问题选择合 适的空间权重矩阵。
Matlab技术经济学应用

Matlab技术经济学应用引言:技术经济学是一门研究科技创新与经济发展之间相互关系的学科,而Matlab作为一种强大的数值计算和科学编程语言,被广泛应用于技术经济学领域。
本文将重点探讨Matlab在技术经济学中的应用,着重介绍其在经济评估、金融模型、企业决策等方面的应用。
一、经济评估1.1 投资成本分析在进行经济评估时,投资成本分析是一个重要的步骤。
Matlab可以帮助分析人员通过数学模型计算出投资成本,并进行灵活的调整和优化。
例如,可以使用Matlab编写一个程序,基于现金流量贴现法(NPV)来计算投资项目的净现值。
通过调整输入参数,可以模拟不同情况下的投资成本,并找到最优方案。
1.2 效益评估Matlab也可以用于效益评估,即对投资项目的经济效益进行分析。
例如,可以使用Matlab编写一个程序来计算投资项目的内部收益率(IRR),并评估其可行性和盈利能力。
通过在程序中引入不同的输入变量,可以进行灵活的模拟和分析,帮助决策者做出科学的投资决策。
二、金融模型2.1 期权定价模型期权定价是金融领域中的一个重要问题,Matlab提供了强大的数学计算功能,可以用于构建和求解各种期权定价模型。
例如,可以使用Matlab编写程序,基于布莱克-斯科尔斯(Black-Scholes)模型来估计欧式期权的价格。
通过调整输入参数,可以对不同情况下的期权价格进行计算和分析。
2.2 风险管理模型金融市场中存在着各种风险,如市场风险、信用风险等。
Matlab可以用于构建和求解各种风险管理模型,以帮助投资者进行风险评估和管理。
例如,可以使用Matlab编写程序,基于Value at Risk(VaR)模型来评估投资组合的风险水平,并制定相应的风险管理策略。
三、企业决策3.1 供应链优化供应链管理是现代企业中的一个重要问题,而Matlab可以帮助企业进行供应链优化。
例如,可以使用Matlab编写程序,基于线性规划模型来优化供应链网络的布局和物流运输方案。
Matlab 参数估计与假设检验ppt课件

H0 : ,
H1 :
2018/11/20
©
谢中华, 天津科技大学数学系.
2018/11/20
©
谢中华, 天津科技大学数学系.
参数估计假设检验
【例 5.2-2】化肥厂用自动包装机包装化肥,某日测得 9 包化肥 的质量(单位:kg)如下: 49.4 50.5 50.7 51.7 49.8 47.9 49.2 51.4 48.9 设每包化肥的质量服从正态分布,是否可以认为每包化肥的平 均质量为 50kg?取显著性水平 0.05 .
[...] = mle(data,'pdf',pdf,'cdf',cdf,'start',start,...)
[...] = mle(data,'logpdf',logpdf,'logsf',logsf,'start',start,...) [...] = mle(data,'nloglf',nloglf,'start',start,...)
% 定义样本观测值向量
>> x = [15.14 14.81 15.11 15.26 15.08 15.17 15.12 14.95 15.05 14.87];
% 调用normfit函数求正态总体参数的最大似然估计和置信区间 % 返回总体均值的最大似然估计muhat和90%置信区间muci, % 还返回总体标准差的最大似然估计sigmahat和90%置信区间sigmaci
分布的参数估计
二项分布的参数估计 分布拟合工具 极值分布的参数估计 指数分布的参数估计 分布的拟合
对数正态分布的参数估计 最大似然估计(MLE) 最大似然估计的渐进协方差矩阵 负二项分布的参数估计 正态(高斯)分布的参数估计 泊松分布的参数估计 瑞利(Rayleigh)分布的参数估计 均匀分布的参数估计 威布尔(Weibull)分布的参数估计
第六讲空间计量经济学基本模型的matlab估计

二、空间计量基本模型的Matlab估计 函数
一阶空间滞后模型
模型:y=ρwy+e 函数:far 使用方法:res=far(y,w) 例子:p57,example3.1
2020/7/28
空间滞后模型
模型:y=ρwy+xβ+e 函数:sar 使用方法:res=sar(y,x,w) 例子:p66,example3.4
2020/7/28
数据导入madat格式文件;.ford格式文件 例子:load anselin.dat;load anselin.ford
命令:xlsread
文件:anselin.xls 例子:A=xlsread(anselin.xls)
2020/7/28
2020/7/28
广义空间模型
模型:y=ρw1y+xβ+u, u=λw2u+e 函数:sac 使用方法:res=sac(y,x,w1,w2) 例子:p92,example3.11
2020/7/28
第六讲 空间计量经济学 模型的MatLab估计
一、Matlab使用前的准备
matlab工作流程
第一步:载入数据 第二步:调用函数,函数包含在各专业
工具箱(toolbox)内。 第三步:运行函数,输出结果。
2020/7/28
将专业函数包装入工具箱
第一步:下载专业函数包jplv7,解压。 第二步:装入工具箱(file-setpath)
矩阵的操作
A是一个n×m矩阵。 A(a:b,c:d),逗号之前a:b表示第a行到
第b行,逗号之后的c:d表示第c列到第d 列。A(a:b,c:d)表示位于第a行到第b 行,同时位于第c列到第d列的一个子矩 阵 A(:,1)表示第1列 A(:,1:3)表示第1至第3列 A(1,:)表示第1行 A(1:3,:)表示第1至第3行
07经济学模型DSGE模型讨论之七——最简单的DSGE模型的Dynare模拟和MLEBayesian估计

这个notes纯粹是扫盲用的。
我用了一个最简单的线性DSGE,只有两个方程。
先是我用手算的方法找到saddle-path 的policy function,然后手算出impulse response function。
这些我都用Dynare做了计算,程序和结果都写在note里面。
上面是我note的截图,这个DSGE模型实际上就是一个linear rational expecation model (LREM),但DSGE的线性化后的本质也就是个LRE。
虽然这个note提供的模型非常简单,但是思路在于如何用Dynare来深入学习这个动态系统。
有几个事情需要大家自己来做:1. beta和rho的大小,大家从换很多次calibration,看能对IRF带来什么影响?2. beta和rho都大于1的时候,你应该怎么修改模型,为了维持模型的稳定性?3. 看修改shock的stardard deviation能对模型带了什么影响?4. 如果你再加一个方程进去呢?什么样子的方程?以上内容我都试验过了。
这个东西没法帮大家试验,所以大家必须自己试着做。
这样你可以学到很多关于动态系统的感性认识。
之后,我用最大似然估计对参数估计,然后我故意制造under-identification的问题,让大家看一下结果是什么样子。
最后就是Bayesian estimation,我只估计了1个参数,用了2条平行马尔科夫链,做了超超短程模拟(只有500次,正常情况都是100000),为了省时间(我电脑只用50秒左右),所以我并没有让电脑跑很长的马尔科夫链和多个平行链条。
所以结果非常差,但是这不是的目的。
目的还是在于让从来没见过整个估计过程的同学看到一个全貌。
所以我没有提及理论内容,或者是一带而过。
对于Bayesian estimation,有个地方要注意的就是shock的个数必须大于等observable的个数,这是启动Kalman filter模拟likelihood function的充分条件。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
空间计量经济学基本模型的matlab估计一、空间滞后模型sar ()==================================================== ➢ 函数功能估计空间滞后模型(空间自回归-回归模型)),0(~2n I N x Wy y σεεβρ++=中的未知参数ρ、β和σ2。
==================================================== ➢ 使用方法res=sar(y ,x ,W ,info )*********************************************************** res : 存储结果的变量;y : 被解释变量;x : 解释变量;w : 空间权重矩阵;info :结构化参数,具体可使用help sar语句查看====================================================➢注意事项1)WW为权重矩阵,因为是稀疏矩阵,原始数据通常以n×3的数组形式存储,需要用sparse函数转换为矩阵形式。
***********************************************************2)ydev(不再需要)sar函数求解的标准模型可以包含常数项,被解释变量(因变量)y,不再需要转换为离差形式(ydev)。
***********************************************************3)x需要注意x的生成方式,应将常数项包括在内。
***********************************************************4)infoinfo为结构化参数,事前赋值;通常调整info.lflag(标准n?1000)、info.rmin和info.rmax。
***********************************************************5)vnames在输出结果中说明被解释变量。
使用方法:vnames=strvcat(‘variable name1’,’variable name2’……);***********************************************************6)Asymptotic t-stat(渐进t统计量)rho的检验:渐进t分布,估计值的显著性使用相应的Z 概率表示。
====================================================➢应用实例估计地区投票率受周边地区投票率的影响程度✓案例素材1997年,Pace等人研究了美国3107个县的选举投票率影响因素,运用的是美国1980年大选的公开投票数据,形成了一个包含3107个样本数据的截面数据集elect.dat。
可以通过matlab软件打开elect.dat查看,并打开elect.txt查看各列数据的含义。
✓计量模型认为各县的投票率受到相邻地区投票率的影响,同时,还受到选民教育水平、选民住房情况、选民收入水平的影响,据此得到如下计量模型:y=β0+ρWy+xβ+εε~N(0,σ2I n)转换为:y=ρWy+[1 x][β0β]’+εε~N(0,σ2I n)✓程序语句●1)近似估计缺省设置:info.lflag=1注意取对数值,得到y,x。
●2)精确估计info.lflag=0✓运行结果====================================================xy2cont()❖函数功能:使用地区x坐标和y坐标,生成空间邻接矩阵。
❖使用方法:[W1 W2 W3]=xy2cont(x,y)其中,W2是行标准化后的空间邻接矩阵。
❖一个例子:使用anselin数据,生成w,并与wmat比较其差异。
====================================================二、空间误差模型sem ()==================================================== ➢ 函数功能估计空间误差模型),0(~2n I N Wu u ux y σεελβ+=+=中的未知参数β、λ和σ2。
==================================================== ➢ 使用方法res=sem(y ,x ,W ,info )*********************************************************** res : 存储结果的变量;y : 被解释变量;x : 解释变量;w : 空间权重矩阵;info :结构化参数,具体可使用help sem语句查看====================================================➢注意事项1)xx应将常数项包括在内。
***********************************************************2)infoinfo为结构化参数,事前赋值;通常调整info.lflag(标准n?1000)、info.rmin和info.rmax。
***********************************************************3)vnames在输出结果中说明被解释变量。
使用方法:vnames=strvcat(‘variable name1’,’variable name2’……);*********************************************************** ====================================================➢应用实例估计地区投票率受周边地区投票率的影响程度✓案例素材1997年,Pace等人研究了美国3107个县的选举投票率影响因素,运用的是美国1980年大选的公开投票数据,形成了一个包含3107个样本数据的截面数据集elect.dat。
可以通过matlab软件打开elect.dat查看,并打开elect.txt查看各列数据的含义。
✓计量模型认为各县的投票率受到相邻地区投票率的影响,同时,还受到选民教育水平、选民住房情况、选民收入水平的影响,据此得到如下计量模型:y=β0+xβ+uu=λWu+εε~N(0,σ2I n)转换为:y=[1 x][β0β]’+uu=λWu+εε~N(0,σ2I n)✓程序语句●1)近似估计缺省设置:info.lflag=1注意取对数值,得到y,x。
●2)精确估计info.lflag=0✓运行结果====================================================➢误差项空间依赖性的检验***********************************************************1)Moran I统计量检验❖使用方法:res=moran(y,x,W);prt(res);***********************************************************2)似然比检验(lratios)❖使用方法:res=lratios(y,x,W);prt(res);***********************************************************3)拉格朗日乘子(LM)检验❖使用方法:res=lmerror(y,x,W);prt(res);***********************************************************4)沃德(Walds)检验❖使用方法:res=walds(y,x,W);prt(res);***********************************************************5)基于sar残差的检验❖使用方法:res=lmsar(y,x,W1,W2);prt(res);====================================================三、空间杜宾模型sdm ()==================================================== ➢ 函数功能估计空间杜宾模型),0(~W 221n I N WX X y y σεεββρ+++=中的未知参数ρ、β1、β2和σ2。
==================================================== ➢ 使用方法res=sdm(y ,X ,W ,info )*********************************************************** info :结构化参数,具体可使用help sdm语句查看==================================================== ➢ 注意事项1) X模型中,第一个X 包括常数项,第二个未包括常数项。
但程序中的X 应将常数项包括在内,程序会自动处理。
***********************************************************2)infoinfo为结构化参数,事前赋值;通常调整info.lflag(标准n?1000)、info.rmin和info.rmax。
*********************************************************** ====================================================➢应用实例1)估计地区犯罪率受周边地区犯罪率的影响程度✓案例素材Anselin在1980年研究了美国俄亥俄州(Ohio)哥伦布市(Columbus)49个县的犯罪率影响因素,形成了一个包含49个样本数据的截面数据集anselin.dat。
可以通过matlab软件打开anselin.dat查看,并打开anselin.txt查看各列数据的含义。
✓计量模型y=β0+ρWy+xβ1+Wxβ2+εε~N(0,σ2I n)✓程序语句●1)近似估计缺省设置info.lflag=1;或者info.lflag=2。
