微电子器件(3-1)资料精
电子科技大学《微电子器件》课件PPT微电子器件(3-10)
CTE↓
① ②
AE↓ ( NB↓(
l↓, s↓ ) 但会使
rbb’↑,VA↓)
要使 b↓,应: (1) WB↓( 但会使 rbb’↑,VA↓,且受工艺限制)
(2) η↑ ( 采用平面工艺 )
要使 d↓,应:xdc↓ →NC↑( 但会使 BVCBO↓, CTC↑)
要使 c↓,应:
(1) rcs↓
① ② ③
fT
rbb fT Le
2
CTC
3.10.3 高频晶体管的结构
由
M
fT
8 rbbCTC
可知,要提高 M ,应提高 fT ,降低 rbb’
和 CTC,因此应该采用由平面工艺制成的硅 NPN 管,并采用细
线条的多基极条和多发射极条结构。
l B E B E B ….…
S
提高 M 的各项具体措施及其副作用
除以上主要矛盾外,还存在一些相对次要的其它矛盾,在 进行高频晶体管的设计时需权衡利弊后做折衷考虑。
3.11 双极晶体管的开关特性
(自学)
3.12 SPICE 中的双极晶体管模型
(自学)
3.10 功率增益和最高振荡频率
3.10.1 高频功率增益与高频优值
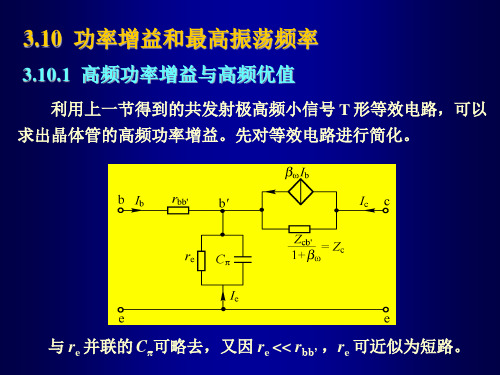
利用上一节得到的共发射极高频小信号 T 形等效电路,可以 求出晶体管的高频功率增益。先对等效电路进行简化。
与 re 并联的 Cπ可略去,又因 re << rbb’ ,re 可近似为短路。
再来简化
Zc
Zcb
1 ω
,
1 Zcb
1 rμ
(3) 对 NC 的要求
减小 d 及 rcs 与减小 CTC及提高 BVCBO 对 NC 有矛盾的要求。
这可通过在重掺杂 N+ 衬底上生长一层轻掺杂 N- 外延层来缓解。 外延层厚度与衬底厚度的典型值分别为 10 m 与 200 m 。
微电子器件基础PPT全套课件

电子管的发明
1883年,美国发明家爱迪生 (T· A· Edison,1847—1931)发现了 热的灯丝发射电荷的现象,并被称之为 “爱迪生效应”。 1897年,英国物理学家汤姆逊 (J· J· Thomson1856~1940 )解释了 这种现象,并把带电的粒子称为“电 子”。 1904英国伦敦大学电工学教授弗莱明 (S· J· A· Fleming1849~1945)研制出检测 电波用的第一只真空二极管,从而宣告 人类第一个电子二极管的诞生。
SW uP
MPEG ROM
PCB
ROM ATM ASIC
SW
FPGA
SW
SW
SRAM ROM
uP Core
MPEG ROM
FPGA A/D Block
ATM Glue Logic
SOC
SoC Example
R O M
D R A M
CPU
DSP
FPGA
SRAM
Flash
Switch
Fabric
Al V Rc Rb in out n SiO2 E n+ p n n+ B
300 Cu Strained Si high-K metal
300 ? Strained Si high-K metal
SiO2 poly Si
SiO2 poly Si
SiO2 poly Si
The limit for oxide -0.8 nm Dielectrics with high k= HfO2, ZrO2… Polysilicon metal
2009 0.045 64G 520 620 2500 8-9 0.6-0.9 300
电子学中的微电子器件和纳电子学

电子学中的微电子器件和纳电子学在当今电子技术飞速发展的时代,微电子器件和纳电子学是电子学领域中备受瞩目的研究方向。
它们不仅具有广泛的应用前景,而且可以为我们提供更灵活、更高效、更小巧的电子设备和系统。
本文将从微电子器件和纳电子学两个方面来介绍它们的基本概念、研究进展及应用前景。
微电子器件是指尺寸在微米级别的电子器件。
它主要应用于集成电路、传感器、激光器、光纤通信等领域,具有体积小、速度快、功耗低等优点。
其中最具代表性的就是集成电路。
作为计算机、手机等电子产品核心的集成电路,其重要性可想而知。
随着电子技术的不断进步,集成电路的制造工艺也在不断更新。
现在常用的工艺是CMOS工艺(互补金属-氧化物半导体),它能够制造出集成度更高、功耗更低的芯片。
此外,随着信息时代的来临,传感器在民用、工业、医疗等领域的应用也越来越广泛,这也使得微电子器件在未来的发展中将有更为广泛的应用前景。
而纳电子学则是指研究纳米级别下材料的电子性质和应用的学科。
与微电子器件相比,纳电子学的尺寸更小,结构更复杂,涉及到的物理和化学现象也更为微妙。
其中的纳米材料,如纳米线、纳米管、纳米颗粒等,可以在光电、磁电、荧光、热学等多个领域中发挥独特的性能。
以染料敏化太阳能电池为例,其关键组件就是纳米级的二氧化钛薄膜,它能够吸收太阳光,并将其转换为电能,使得太阳能电池具有更高的转换效率。
在生物医学领域,纳米材料也受到了广泛的关注,例如通过包覆纳米颗粒的方式,可以改善药物的生物分布和毒副作用,实现精准治疗。
在微电子器件和纳电子学的研究中,材料的制备是非常重要的一环。
传统材料制备工艺大多采用物理或化学手段,但在微型尺度下,这些工艺已经不再适用。
因此,研究人员就开始尝试新的制备方法。
近年来,利用生物、化学、物理等交叉学科的知识,在微电子器件和纳电子学领域出现了一些新的材料制备技术,如DNA自组装、容量耦合、微流控等。
这些技术使得微电子器件和纳电子学的研究更加多样化和创新性。
微电子器件课后答案(第三版)

Hale Waihona Puke 得:VBE 0.55V WB2 1 WB 已知: 1 1 , 将 n 106 s 及 WB 、DB 2 LB 2 DB n
q
s
N D xn , 由此得:xn
q
s
N A xp , 由此得:xp
s Emax
qN A
(2) 对于无 I 型区的 PN 结: q xi1 0, xi2 0, E1 N D ( x xn ), s
在 x 0 处,电场达到最大, Emax q
E3 N D xn
0
AE q 2 DE ni2 1 QEO
1
再根据注入效率的定义,可得:
J pE QBO DE J nE J nE 1 1 J E J nE J pE J nE QBE DB
9、
I C AE J nC AE J nE
1 2
39、
qV I F I 0 exp kT dI F qI F gD dV kT kT 当 T 300K 时, 0.026 V, 对于 I F 10 mA 0.01 A, q 10 1 gD 0.385s, rD 2.6 26 gD kT 373 在 100C 时, 0.026 0.0323V, q 300 10 1 gD 0.309s, rD 3.23 32.3 gD
微电子器件(2-1)
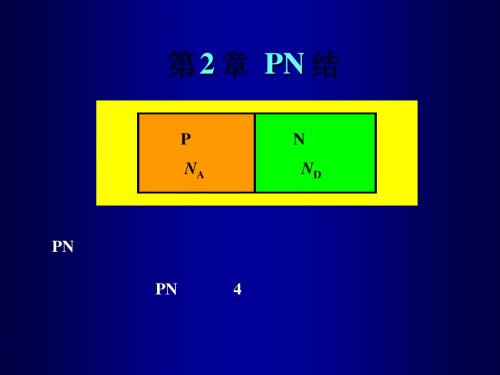
C =−
E(x) = q
q
εs
NDxn
(0 ≤ x ≤ xn )
(2-5a) )
εs
( x−xn ) ND
同理, 耗尽区中求解泊松方程, 同理,在 P 区耗尽区中求解泊松方程,得
E(x) =−
( x+ x ) N ε
q
s p
A
(−xp ≤ x ≤0)
(2-5b) )
P
N
E Emax
−xp
0
xn
x
内建电场。 以上求得的 E(x) 就是 PN 结的 内建电场。
ND >> NA
N0 ≈ NA
以上各式又可简化为
1 2
P
N+
E ax m
2qNA ≈ V εs bi
−xp
0
E
xn ≈ 0
2 s ε xp ≈ xd ≈ V bi qNA
1 2
− xp
0
x
可见,耗尽区主要分布在低掺杂的一侧, m 可见,耗尽区主要分布在低掺杂的一侧, E ax 与 x 也 d 主要取决于低掺杂一侧的杂质浓度。 主要取决于低掺杂一侧的杂质浓度。
2.1.3 能带图
已知突变结耗尽区内的电场分布 E(x) 后 ,对 E(x) 作一次 积分就可以求出耗尽区内的 电位分布 ψ(x)以及 电子的电位能 分布 [ −q (x)] 。 ψ 在平衡状态下, 在平衡状态下, PN 结能带图中的费米能级 EF 是水平的 , 而导带底 EC、价带顶 EV 与本征费米能级 Ei 则均与 [ −q (x)] 有 ψ 相同的形状, 结的能带图如下图所示。 相同的形状,由此可画出平衡 PN 结的能带图如下图所示。
电子科技大学《微电子器件》课程重点与难点.

重点与难点第1章半导体器件基本方程一般来说要从原始形式的半导体器件基本方程出发来求解析解是极其困难的,通常需要先对方程在一定的具体条件下采用某些假设来加以简化,然后再来求其近似解。
随着半导体器件的尺寸不断缩小,建立新解析模型的工作也越来越困难,一些假设受到了更大的限制并变得更为复杂。
简化的原则是既要使计算变得容易,又要能保证达到足够的精确度。
如果把计算的容易度与精确度的乘积作为优值的话,那么从某种意义上来说,对半导体器件的分析问题,就是不断地寻找具有更高优值的简化方法。
要向学生反复解释,任何方法都是近似的,关键是看其精确程度和难易程度。
此外,有些近似方法在某些条件下能够采用,但在另外的条件下就不能采用,这会在后面的内容中具体体现出来。
第2章PN结第2.1节PN结的平衡状态本节的重点是PN结空间电荷区的形成、内建电势的推导与计算、耗尽区宽度的推导与计算。
本节的难点是对耗尽近似的理解。
要向学生强调多子浓度与少子浓度相差极其巨大,从而有助于理解耗尽近似的概念,即所谓耗尽,是指“耗尽区”中的载流子浓度与平衡多子浓度或掺杂浓度相比可以忽略。
第2.2节PN结的直流电流电压方程本节的重点是对PN结扩散电流的推导。
讲课时应该先作定性介绍,让学生先在大脑中建立起物理图象,然后再作定量的数学推导。
当PN结上无外加电压时,多子的扩散趋势正好被高度为qV bi的势垒所阻挡,电流为零。
外加正向电压时,降低了的势垒无法阻止载流子的扩散,于是构成了流过PN结的正向电流。
正向电流的电荷来源是P区空穴和N区电子,它们都是多子,所以正向电流很大。
外加反向电压时,由于势垒增高,多子的扩散变得更困难。
应当注意,“势垒增高”是对多子而言的,对各区的少子来说,情况恰好相反,它们遇到了更深的势阱,因此反而更容易被拉到对方区域去,从而构成流过PN结的反向电流。
反向电流的电荷来源是少子,所以反向电流很小。
本节的难点是对有外加电压时势垒区两旁载流子的运动方式的理解、以及电子(空穴电流向空穴(电子电流的转化。
微电子器件(2-1)

Emax
s
qN0
Emax
(2-8)
式中,N0
NA ND NA ND
称为 约化浓度。
4、内建电势
对内建电场作积分可得 内建电势(也称为 扩散电势)Vbi
Vbi
xn E(x) dx
xp
1 2
xn xp
Emax
s
2qN0
E2 max
1
或
Emax
2qN0
2
1
xn
s
qND
Emax
2
q
s
ND
NA (NA
ND )
Vbi
2
1
xp
s
qNA
Emax
2s
q
NA
ND (NA
ND
)
Vbi
2
1
xd xn xp
2Vbi Emax
2 s
qN0
Vbi
2
5、单边突变结的情形 对于 P+N 单边突变结,
3、耗尽区宽度
在 x = 0 处,内建电场达到最大值,
q
q
E(0)
Emax
s
xn ND s
xp NA
由上式可求出 N 区与 P 区的耗尽区宽度 及 总的耗尽区宽度,
xn
s
qND
Emax
xp
s
qNA
Emax
(2-6) (2-7)
xd
xn
电子元器件基础知识大全

电子元器件基础知识大全篇一:电子元器件基础知识第一讲电子元器件基础知识课程大纲:第一章电子元器件分类第二章集成电路的基础知识第三章集成电路的发展及分类第四章集成电路的命名第五章集成电路的封装第六章集成电路的品牌第七章集成电路的品牌分销商第一章电子元器件分类第一节电子元器件分类●概念:电子元器件是电子工业发展的基础。
它们是组成电子设备的基本单元,属电子工业的中间产品。
●电子元器件分为两类:半导体、电子元件第二节行业概念●被动组件是电子产品中不可缺少的基本组件。
电子电路有主动与被动两种装置,所谓被动组件是不必接电就可以动作,而产生调节电流电压,储蓄静电、防治电磁波不干扰、过滤电流杂质等的功能。
相对应主动组件,被动足是在电压改变的时候,电阻和阻抗都不会随之改变。
被动组件可以涵盖三大类产品:电阻器、电感器和电容器。
●半导体分立器件主要包括半导体二极管、三极管、三极管阵列、MOS场效应管、结型场效应管、光电耦合器、可控硅等各种两端和三端器件。
●有源器件和无源器件简单地讲就是需能(电)源的器件叫有源器件,无需能(电)源的器件就是无源器件。
有源器件一般用来信号放大、变换等,无源器件用来进行信号传输,或者通过方向性进行“信号放大”。
电容、电阻、电感都是无源器件,IC、模块等都是有源器件。
●摩尔定律INTEL公司创建人之一戈登·摩尔的经验法则,他曾经这样描述:“随着芯片上的电路复杂度提高,元件数目必将增加,然而每个元件的成本却每年下降一半。
”摩尔定律看似非常简单,实则对于半导体工业的发展的指导意义深远。
一些分析家预测摩尔定律终将实效——一种自我激励的机制,只要半导体技术和经济的发展还能满足市场需要,摩尔定律还将继续生存下去,只不过是速度上的减缓。
第二章集成电路的基础知识第一节集成电路的基础介绍我们通常说的“芯片”是指集成电路,它是微电子技术的主要产品。
所谓微电子是相对“强电”、“弱电”等概念而言,指它处理的电子信号极其微小,它是现代信息技术的基础,我们通常所接触的电子产品,包括通讯、电脑、智能化系统、自动控制、空间技术、电台、电视等等都是在微电子技术的基础上发展起来的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
微电子器件分析的典型过程
平衡态
DC响应
AC响应
瞬态响应
1. 分区、近似求解 泊松方程得到平 衡态的参数
2. 平衡态载流子电 流密度等于零出 发推导出内建电 场的大小
1. 在边界条件下求 解中性区少子连 续性方程(扩散 方程)得到少子 浓度分布
2. 由电流密度方程 得到各电流密度 成分
求少子电荷 控制方程
P区
np0
N区
pn0 x
反偏二极管的反向电流有哪些可能的产生机制?
反偏二极管可以得到大电流输出吗? 怎样得到大电流输出?
P区
np0
N区
pn0 x
法1:使耗尽区产生电子-空穴对
P区
np0
N区
pn0 x
典型器件:光电二极管
光电二极管是将光信号转换为电信号的半 导体器件,器件核心是反向偏置的pn结
在没有光照时,由于pn结处于反向偏 置,只有微弱的反向电流流过
当有光照时,反向电流急剧增加(携带能 量的光子进入PN结后,把能量传给共价键 上的束缚电子,使部分电子挣脱共价键, 从而产生电子---空穴对,称为光生载流 子 )。
为了增加光照,pn结面积较大。
法2:使靠近耗尽区边界的中性区有更多的少子
P区
np0
N区
pn0 x
时间维度上,可以采用从开态(正偏)瞬时变为关态(反偏)实现
E E1
0
t
-E2
I
E1
ts
tf
RL
t
− E2
I0
RL
空间维度上,可以将正偏与反偏pn结背靠背放在一起来实现 利用正偏pn结提供载流子
P
NN P
两个近距离地背靠背PN结构成的一种新的器件——双极 结型晶体管(bipolar junction transistor, BJT)
• 双极含义是电子与空穴两种极性不同的载流子均参与了器件 的导通过程
• BJT是电压控制的电流源 • BJT与其它器件连接可实现放大电流、放大电压和放大功率 • Transistor 是 Transfer resistor的缩写 • /transistor/
William Shockley
John Bardeen
1947
Wakter Brattain
npn 和pnp 晶体管
=+++=CE BC EB C
B E V V V I I I 1、BJT 类型与工艺
制备工艺与特性
均匀基区BJT (扩散晶体管)
特点:
1.三个区内杂质均匀分布
2.发射结、集电结为突变结
3.载流子在基区中以扩散运动为主
合金工艺
缓变基区或双扩散
BJT
(漂移晶体管)
特点:1.
基区为缓变杂质分布,发射区杂质分布也缓变。
2. 载流子在基区中以漂移为主
平面工艺
电路用法
放大状态,用于模拟电路
3. 能带图与少子分布
a.耗尽区
b.能带图
c.电势
d.电场
e.电荷密度
注:
假设晶体管的各个
区域是均匀掺杂
的,并且
N
AE >>N
DB
>N
AC
平衡pnp BJT 平衡pn结
课堂练习
画出平衡条件下npn晶体管的能带图
PN 结能带图P
N
qV
E E Fp Fn =−
均匀基区pnp 晶体管能带图放大状态:
饱和状态:
截止状态:
倒向放大状态:
平衡态
qV
E E Fp Fn =−
NPN 晶体管在 4 种工作状态下的能带图: 放大状态: 饱和状态: 截止状态:
倒向放大状态:
课堂练习 写出小注入pn结非平衡态时的势垒区边界的少子分布
pn (xn ) =
pno
exp⎜⎛ ⎝
qV kT
⎟⎞, ⎠
( ) np − xp
=
n po
exp⎜⎛ ⎝
qV kT
⎟⎞, ⎠
pn x→∞ = pno n p x→−∞ = n po
Δpn (xn ) =
pno ⎢⎣⎡exp⎜⎝⎛
qV kT
⎟⎞ ⎠
− 1⎥⎦⎤,
( ) Δnp − xp
=
n po
⎢⎣⎡exp⎜⎝⎛
qV kT
⎟⎞ ⎠
−
1⎥⎦⎤,
Δpn x→∞ = 0 Δnp x→−∞ = 0
均匀基区pnp晶体管的各边界上少子浓度
E
nE = nE0
pB
=
pB0
exp
⎛ ⎜⎝
qVEB kT
⎞ ⎟⎠
Base Emitter
P
N
nE
=
nE 0
exp
⎛ ⎜⎝
qVEB kT
⎞ ⎟⎠
Collector P
nC
=
nC0
exp
⎛ ⎜⎝
qVCB kT
⎞ ⎟⎠
C
nC = nC0
B
pB
=
pB0
exp
⎛ ⎜⎝
qVCB kT
⎞ ⎟⎠
均匀基区pnp晶体管的少子分布图: 放大状态: 饱和状态:
截止状态:
倒向放大状态:
4、放大作用
处于放大模式偏置下的 pnpBJT中载流子的输运 BJT中载流子的输运过程: 1. 在正偏E-B结附近载流子的运动表现为多数载流子扩散过发射 结注入到另一边的准中性区(中性基区)
2. 由于基区宽度比少子扩散长度小得多,大多数的注入空穴通过 扩散穿越准中性基区并且进入C-B耗尽区,然后C-B耗尽区内的加 速电场(漂移)迅速把这些载流子扫进集电区。
课堂练习
画出PN结中的正向电流和反向电流的构成与载流子运动
情况
J= Jdp + Jdn + Jr
P区
Jdn
Jdp N 区
J= Jdp+Jdn+Jg
P区
Jdn
Jdp N
区
Jg
− xp 0 xn
Jr
−xp 0 xn
V
V
放大模式偏置下pnpBJT中的扩散电流(忽略耗尽区内的R-G电流)
I pE
I pC
I pr
Inc
In
I nE
I nr
I E = I pE + InE
NE>>NB,减少InE
I B = In E + Inr − Inc ≈ InE + Inr
Ic = Inc + I pc ≈ I pc = I pE − I pr = I E − InE − Inr
WB<<LB,减少Inr
电流放大系数的定义
共基极
定义1:发射结正偏,集电结零偏时的 IC 与 IE 之比,称为
共基极直流短路电流放大系数,记为α,即:
IC
α = VEB >0,VCB =0
IE
定义2:发射结正偏,集电结反偏时的 IC 与 IE 之比,称为 共基极静态电流放大系数,记为hFB,即:
IC
h = FB
VEB >0,VCB <0
IE
共发射极
定义3:发射结正偏,集电结零偏时的 IC 与 IB 之比,称为
共发射极直流短路电流放大系数,记为β,即:
IC
β = VEB>0,VCB=0
IB
定义4:发射结正偏,集电结反偏时的 IC 与 IB 之比,称为 共发射极静态电流放大系数,记为hFE,即:
IC
h = FE
VEB >0,VCB <0
IB
根据
IB
= IE − IC
,及
α
=
IC IE
的关系,可得β与α之间有
如下关系:
β
=
IC IB
=
IC IE
(IE − IC )
IE
=α 1−α
α= β 1+ β
对于一般的晶体管,α= 0.950~0.995,β = 20~200 。
。
