经典换面法及习题共19页
合集下载
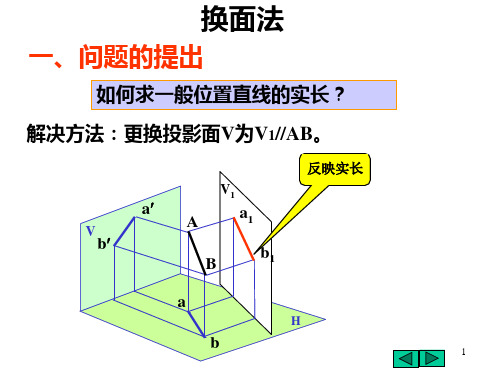
4换面法

a'
x
O x1
四、换面法的应用——举例
[例题2] 已知C与直线AB的投影,求点C到AB直线间的距离。
a1
a' k1 b1 k' c' H X V b' a k c b'2 a'2 k'2 c'2 c1
距离
b
空间分析
四、换面法的应用——举例
[例题3] 求交叉两直线AB和CD间的最短距离EF ,如图所示。
2.投影面保持不动,使空间几何要素绕某一轴线旋转到 平行或垂直于投影面的特殊位置,然后找出其旋转后的新投 影。这种方法称为——旋转法。
这里仅讲换面法
二、点的换面规律
V c' C b1' A X1 bB c a' b' X
c1 ' V1 a1'
a H
V/H 体系变为V1/H 体系
新投影面必须满足下列两条原则:
b a
H
a
作图特点:
① 新的投影轴必须平行于直线的一个投影,且可求出直线的实长和倾角 ②求直线对某投影面的倾角,新投影轴必须平行于该投影面直线的投影
三、换面法的基本作图
将一般位置直线变换成投影面平行线,并求出角? a'
b' V X H a b
a1
b1
三、换面法的基本作图
2、将平行线变换成垂直线 V a H1 a1 b1 V X H b
3、将一般位置平面变换成垂直面
V
a
b d c A b a d C c B D b1 d1 c1 H1 a b
a1
X
c b d
V X H a
H
c
画法几何换面法ppt课件

例:求出上一例题中的 △ABC平面的实形。
前一例的作图已将平面变 换为投影面垂直面,现只需 接着作后一次变换。
3、将一般位置平面变换为投影面平行面
作图步骤如下: 前一例的作图已将 平面变换为投影面 垂直面,现只需接 着作后一次变换。
此课件下载可自行编辑修改,供参考! 感谢您的支持,我们努力做得更好!
的原则和变换的规律与一次变换方法完全相同。 不过在作二次变换时要正确判断出不变投影、被替换的
投影、新轴和旧轴,准确定出点的新投影的位置。
图中先变换的是V1面,接着作第 二次变换。此时的H1面与V1面垂直, 被 替 换 是 H 面 , 而 V1 面 为 不 变 投 影 面。O2X2为新的投影轴,O1X1则成 了旧投影轴。
作图分析:由于△ABC平面为一 铅垂面 ,则O1X1轴应平行于平面的 积聚性投影。
作 图 过 程 如 图 所 示:
2、将一般位置平面变换为投影面垂直面 作图分析:
在作图时首先要考虑的是如何确定新投影面的位置。
将一般位置平面变换为投影面垂直面的作图步骤如下:
在空间平面内作一投影面平行线(下图中作了一条水
作图步骤:
1、点的一次变换 例:已知A点的两面投影a'、a,试作出给定位置的A点新 投影。又:作出A点在H1面上的投影。 作图分析: 变换H1面与变换V1面的作图分析和作图步骤相同。
本题的投影变换作图为 点A的两个一次变换。
2、点的二次变换 在用投影变换的方法求解一些实际问题时,需要变换两
次投影面,这样的变换方法称为二次变换。 二次变换实际上就是连续作出的两个一次变换。其变换
1、将一般位置直线变换为投影面平行线 通过一次变换可将一般位置直线变换为投影面平行线, 求得直线的实际长度以及直线对投影面的夹角。 为求得AB线的实长,所设置的新投影面V1应与AB平行。 从直观图上可看出,体现新面位置的新轴就应平行于AB 线的水平投影 ab。
前一例的作图已将平面变 换为投影面垂直面,现只需 接着作后一次变换。
3、将一般位置平面变换为投影面平行面
作图步骤如下: 前一例的作图已将 平面变换为投影面 垂直面,现只需接 着作后一次变换。
此课件下载可自行编辑修改,供参考! 感谢您的支持,我们努力做得更好!
的原则和变换的规律与一次变换方法完全相同。 不过在作二次变换时要正确判断出不变投影、被替换的
投影、新轴和旧轴,准确定出点的新投影的位置。
图中先变换的是V1面,接着作第 二次变换。此时的H1面与V1面垂直, 被 替 换 是 H 面 , 而 V1 面 为 不 变 投 影 面。O2X2为新的投影轴,O1X1则成 了旧投影轴。
作图分析:由于△ABC平面为一 铅垂面 ,则O1X1轴应平行于平面的 积聚性投影。
作 图 过 程 如 图 所 示:
2、将一般位置平面变换为投影面垂直面 作图分析:
在作图时首先要考虑的是如何确定新投影面的位置。
将一般位置平面变换为投影面垂直面的作图步骤如下:
在空间平面内作一投影面平行线(下图中作了一条水
作图步骤:
1、点的一次变换 例:已知A点的两面投影a'、a,试作出给定位置的A点新 投影。又:作出A点在H1面上的投影。 作图分析: 变换H1面与变换V1面的作图分析和作图步骤相同。
本题的投影变换作图为 点A的两个一次变换。
2、点的二次变换 在用投影变换的方法求解一些实际问题时,需要变换两
次投影面,这样的变换方法称为二次变换。 二次变换实际上就是连续作出的两个一次变换。其变换
1、将一般位置直线变换为投影面平行线 通过一次变换可将一般位置直线变换为投影面平行线, 求得直线的实际长度以及直线对投影面的夹角。 为求得AB线的实长,所设置的新投影面V1应与AB平行。 从直观图上可看出,体现新面位置的新轴就应平行于AB 线的水平投影 ab。
第5章 换面法
c● a
V XH
●
d
n●
●
由直角投影定理,把AB变为投影面 垂直线时,公垂线MN平行于V1 , 它的投影反映实长,且m1n1⊥c1d1。
A C N M
m
b
a c
●m ●
n
d b
B
D
d1
.
●
′
c1
a1(b1m1)
n1 d1
a′1(b ′1m ′1)
● ●
V1
.
n′ 1
H V 1
#
X1
c′ 1
(5)两交叉直线之间 →将一直线变换成投影面垂直线。
29
距离:
1.点到直线的距离; 4.线、面平行间的距离; 2.平行两直线的距离; 5.点到平面的距离; 3.两直线的公垂线; 6.平行两平面的距离。
30
5 、求夹角
(1)两直线之间 →将两直线组成的平面变换成投影面平行 面。 (2) 两平面之间 →将两平面变换成投影面的垂直面,即应将 两平面的交线变换成投影面的垂直线。
b
a b a
.
B A
a1
X
a H
H1 ● X1 V1 a1
//
●
X1
b1 a 2(b2)
X2轴的位置?
与a1b1垂直
14
例3:求两平行直线的距离.
作图: c● a
V H
●
d b
分析:转换为点到点 的距离问题。把AB、 CD换成投影面垂直线, 两点的距离即为所求。 (逆推法)
a1
V
A
X
V
ax
H
a
ax1 H V1 X1
X
ax1
V XH
●
d
n●
●
由直角投影定理,把AB变为投影面 垂直线时,公垂线MN平行于V1 , 它的投影反映实长,且m1n1⊥c1d1。
A C N M
m
b
a c
●m ●
n
d b
B
D
d1
.
●
′
c1
a1(b1m1)
n1 d1
a′1(b ′1m ′1)
● ●
V1
.
n′ 1
H V 1
#
X1
c′ 1
(5)两交叉直线之间 →将一直线变换成投影面垂直线。
29
距离:
1.点到直线的距离; 4.线、面平行间的距离; 2.平行两直线的距离; 5.点到平面的距离; 3.两直线的公垂线; 6.平行两平面的距离。
30
5 、求夹角
(1)两直线之间 →将两直线组成的平面变换成投影面平行 面。 (2) 两平面之间 →将两平面变换成投影面的垂直面,即应将 两平面的交线变换成投影面的垂直线。
b
a b a
.
B A
a1
X
a H
H1 ● X1 V1 a1
//
●
X1
b1 a 2(b2)
X2轴的位置?
与a1b1垂直
14
例3:求两平行直线的距离.
作图: c● a
V H
●
d b
分析:转换为点到点 的距离问题。把AB、 CD换成投影面垂直线, 两点的距离即为所求。 (逆推法)
a1
V
A
X
V
ax
H
a
ax1 H V1 X1
X
ax1
第五章 换面法

第 五 章
投 影 变 换 习 题 答 案
第 五 章
投 影 变 换 习 题 答 案
第 五 章
投 影 变 换 习 题 答 案
第 五 章
投 影 变 换 习 题 答 案
第 五 章
投 影 变 换 习 题 答 案
第 五 章
投 影 变 换 习 题 答 案
5-14:二平行直线相距20毫 米,补全直线ab的水平投影。
m l
X1
b'1
e'1
l'1
f'1
X2
f2
m2 k2(l2) n2
e2
第 五 章
投 影 变 换 习 题 答 案
第 五 章
投 影 变 换 习 题 答 案
X2 V2 H1 a2' (b2') d1
b1 c1
c2'(d2') a2' (b2') H1 X 1 V d'
a1
b'
b1 c'
a'
有二解 X a a1
c b d
V H
第 五 章
投 影 变 换 习 题 答 案
第 五 章
投 影 变 换 习 题 答 案
5-16 作直线KL与三角形ABC垂直,并与EF、MN两直线相交。 f' 方法一: 综合法: (1)过点F作直线 e' FD⊥平面ABC (2)求平面EFD 与MN直线交点K。 (3)过点K作 KL∥FD l' m' k' n'
d'
b'
a'
b m
c'
kቤተ መጻሕፍቲ ባይዱ
n
a d
投 影 变 换 习 题 答 案
第 五 章
投 影 变 换 习 题 答 案
第 五 章
投 影 变 换 习 题 答 案
第 五 章
投 影 变 换 习 题 答 案
第 五 章
投 影 变 换 习 题 答 案
第 五 章
投 影 变 换 习 题 答 案
5-14:二平行直线相距20毫 米,补全直线ab的水平投影。
m l
X1
b'1
e'1
l'1
f'1
X2
f2
m2 k2(l2) n2
e2
第 五 章
投 影 变 换 习 题 答 案
第 五 章
投 影 变 换 习 题 答 案
X2 V2 H1 a2' (b2') d1
b1 c1
c2'(d2') a2' (b2') H1 X 1 V d'
a1
b'
b1 c'
a'
有二解 X a a1
c b d
V H
第 五 章
投 影 变 换 习 题 答 案
第 五 章
投 影 变 换 习 题 答 案
5-16 作直线KL与三角形ABC垂直,并与EF、MN两直线相交。 f' 方法一: 综合法: (1)过点F作直线 e' FD⊥平面ABC (2)求平面EFD 与MN直线交点K。 (3)过点K作 KL∥FD l' m' k' n'
d'
b'
a'
b m
c'
kቤተ መጻሕፍቲ ባይዱ
n
a d
例题-换面法

例题-换面法
换面法是一种数学解决方案的常见思维模式。
它通过改变问题的角度来解决问题,从而使得问题更加清晰、易于理解。
换面法在数学中有着广泛的应用,其中包括几何、代数、概率和统计学等等。
换面法的主要思想就是将原有的问题和解决方案转化为新的问题和解决方案,从而更加容易理解和解决。
例如,在几何学中,我们可以利用换面法来证明两个多边形的相似性,即将多边形的任意一边拉伸成另一边的长度,然后证明多边形的其他边也是相等的,这样就可以证明两个多边形的相似性。
在代数学中,我们可以利用换面法来解决一些复杂的方程。
例如,对于一个多项式的方程,我们可以利用换面法来将其转化为一个更容易求解的形式,如分解因式或者求积分等。
此外,在概率和统计学中,也可以利用换面法来解决一些复杂的问题。
例如,当我们想要求解一个复杂的概率问题时,我们可以利用换面法来将其转换为更容易求解的形式,比如求解概率的期望值或者求解一个统计指标的分布概率等。
总而言之,换面法是一种很有用的解决数学问题的思维模式,它可以帮助我们从不同的角度来思考问题,更加清晰地理解问题,从而更加容易地解决问题。
第5章 投影变换——换面法

5.2 换面法
图5-17 求两条交叉直线间的距离
5.2 换面法
【例5-4】
求两平面ABC和ABDE之间的夹角,如图5-18(a)所示。 【解】分析:当两个平面的交线垂直于投影面时,则这两个平面 在该投影面上的投影为两条相交直线,它们之间的夹角即反映两 个平面间的夹角。 作图步骤如图5-18(b)所示。 (1)将平面ABC和ABDE的交线AB经二次变换成为垂直于H2面的 直线。(2)平面ABC和ABDE在H2面上的投影分别积聚为直线 c2a2(b2)和a2e2(b2d2)。 (3)∠c2a2e2即反映两个平面间的夹角θ。
第5章 投影变换——换面法
知识目标
掌握换面法的一般概念及特点。 能够使用换面法解决有关点、直线与平面等 几何元素之间的定位和度量问题。
5.1 投影变换概述
在图5-1所示的直线与平面中,图(a)和图(b) 投影反映实长、倾角和实形,图(c)投影反映点到 直线的距离,图(d)投影反映直线与平面的交点, 这时称这些几何元素处于有利于解题的位置。当 直线或平面处于不利于解题的位置时,通常可采 用下列方法进行解题:
5.2 换面法
图5-10 一般位置平面变换成垂直面(求α角)
5.2 换面法
5.将垂直面变换成平行面
如图5-13所示,△ABC是一个铅垂面,要求将其变换
成平行面。根据平行面的投影特性,积聚为一条直线的投
影必定为不变投影,因此必须变换V面,使新投影面V1平
行于△ABC。作图时取X1轴∥abc
ABC在V1面上的
5.2 换面法
图5-18 求两平面间的夹角
思考题
(1)投影变换的目的是什么?一般有几种方法? (2)什么叫换面法?新投影面如何选择?换面后 的新两面体系和原来的两面体系有什么关系? (3)试述用换面法把一般位置直线变为投影面平 行线和投影面垂直线的步骤。
换面法

● ●
b′ ′ a1 d1
● ●
θ c1
.
●
b1
.
d
a2≡ b2
●
θ
●
d2
.
a1
X
a H
H1 ● X1 P1 a1 X1
●
b1 a2≡b2
X2轴的位置? 轴的位置?
与a1b1垂直
3. 把一般位置平面变换成投影面垂直面
空间分析: 空间分析: 两平面垂直需满足什么条件? 两平面垂直需满足什么条件? 如果把平面内的一条直线变换成新投影面的垂 直线,那么该平面则变换成新投影面的垂直面。 直线,那么该平面则变换成新投影面的垂直面。 作图方法: 作图方法:
●
a′ ′ XV H a c
m′ ′
b′ ′
● ●
m
n
d b
d1
.
●
a1≡b1≡m1
●
c1
n1
d1
.
n1
请注意各点的投 H P 1 影如何返回? 影如何返回? X1 求m点是难点。 点是难点。 点是难点
c1
●
圆半径=MN 圆半径
点作直线CD与 相交成 相交成60º角 例3: 过C点作直线 与AB相交成 角。 点作直线
⑵
新旧投影之间的关系
a′ ′ ax a1
V X H
a′ ′ a1
.
V
A
P1
ax ax1
P1 H X1
ax1 a
H X1
a
X
一般规律: 一般规律: 点的新投影和与它有关的原投影的连线, 点的新投影和与它有关的原投影的连线,必垂直 于新投影轴。 于新投影轴。 点的新投影到新投影轴的距离等于被代替的投影 到原投影轴的距离。 到原投影轴的距离。
b′ ′ a1 d1
● ●
θ c1
.
●
b1
.
d
a2≡ b2
●
θ
●
d2
.
a1
X
a H
H1 ● X1 P1 a1 X1
●
b1 a2≡b2
X2轴的位置? 轴的位置?
与a1b1垂直
3. 把一般位置平面变换成投影面垂直面
空间分析: 空间分析: 两平面垂直需满足什么条件? 两平面垂直需满足什么条件? 如果把平面内的一条直线变换成新投影面的垂 直线,那么该平面则变换成新投影面的垂直面。 直线,那么该平面则变换成新投影面的垂直面。 作图方法: 作图方法:
●
a′ ′ XV H a c
m′ ′
b′ ′
● ●
m
n
d b
d1
.
●
a1≡b1≡m1
●
c1
n1
d1
.
n1
请注意各点的投 H P 1 影如何返回? 影如何返回? X1 求m点是难点。 点是难点。 点是难点
c1
●
圆半径=MN 圆半径
点作直线CD与 相交成 相交成60º角 例3: 过C点作直线 与AB相交成 角。 点作直线
⑵
新旧投影之间的关系
a′ ′ ax a1
V X H
a′ ′ a1
.
V
A
P1
ax ax1
P1 H X1
ax1 a
H X1
a
X
一般规律: 一般规律: 点的新投影和与它有关的原投影的连线, 点的新投影和与它有关的原投影的连线,必垂直 于新投影轴。 于新投影轴。 点的新投影到新投影轴的距离等于被代替的投影 到原投影轴的距离。 到原投影轴的距离。
换面法-直角三角形法PPT文档共29页

换面法-直角三角形法
36、如果我们国家的法律中只有某种 神灵, 而不是 殚精竭 虑将神 灵揉进 宪法, 总体上 来说, 法律就 会更好 。—— 马克·吐 温 37、纲纪废弃之日,便是暴政兴起之 时。— —威·皮 物特
38、若是没有公众舆论的支持,法律 是丝毫 没有力 量的。 ——菲 力普斯 39、一个判例造出另一个判例,它 迅速累 聚,进 而变成 法律。 ——朱 尼厄斯
40、人类法律,事物有规律,这是不 容忽视 的。— —爱献 生
31、只有永远躺在泥坑里的人,才不会再掉进坑里。——黑格尔 32、希望的灯一旦熄灭,生活刹那间变成了一片黑暗。——普列姆昌德 33、希望是人生的乳母。——科策布 34、形成天才的决定因素应该是勤奋。——郭沫若 35、学到很多东西的诀窍,就是一下子不要学很多。——洛克
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
换面法—空间几何元素的位置保持不动,用新的投影面 来代替旧的投影面,使对新投影面的相对位置变成有利 解题的位置,然后找出其在新投影面上的投影。
返回
二、点的换面及规律
1. 点的一次变换
V1
a1 '
X1
返回
2. 点的两次变换
a2
X2
a' 旧
水平书写好
不变 X2
新V1 H2 a2
旧
新 不变
新与旧是相对的
作 图: c●
几个解?
a
d b
两个解!
●a2
X
V H
a
●
c
d ●
b
.
b2●d●2 60°
.
a'1●b'1
D点的投影 如何返回? ● c2
如何解?
思考:
HX1V1
●
c1'
H2 V1 X2
解法相同!
已知点C是等边三角形的顶点,另两个顶点在直线AB上,
求等边三角形的投影。(用基本法和换面法分别求解)
例4 已知E点在平面ABC上,距离A、B为15,求点E的投影。
c1'
V1 H2
c2
X2
过c1作线平行于x2轴。
例2. 求两直线AB与CD的公垂线 。
b' 1'
2'
1
X2
V1 H2 c2
2
22
12
d2
c1'
21' d1'
b1'
a2b2
a1'
11'
返回
例3: 过C点作直线CD与AB相交成60º角。
空间及投影分析:AB与CD都平行于投影面时,其投影
的夹角才反映实大(60°),因此需将AB与C点所确定的 平面变换成投影面平行面。
a
V
b
A
P1a1
b1
B
作图:
a
XV H
b b
a
Hb
换H面行吗? 不行!
a
.
H
X1 P1
a●1
b●1
新投影轴的位置?
与ab平行。
2. 把一般位置直线变换成投影面垂直线
空间分析: 一次换面把直线变成投影面平行线;
二次换面把投影面平行线变成投影面垂直线。
V X
X2
a2b2 b P2
ax2
P1
a
b1
B A
三、点的变换规律是换面法的作图基础,四个基本 问题是解题的基本作图方法,必需熟练掌握。
换面法的四个基本问题:
1. 把一般位置直线变成投影面平行线 变换一次投影面
2. 把一般位置直线变成投影面垂直线 变换两次投影面
3. 把一般位置平面变成投影面垂直面 变换一次投影面 需先在面内作一条投影面平行线
4. 把一般位置平面变成投影面平行面 变换两次投影面
例1:求点C到直线AB的距离,并求垂足D。
空间及投影分析:
作图:
求C点到直线AB的距离, c
b
就是求垂线CD的实长。
如下图:当直线AB 垂直于投影面时,CD平
XV H
行于投影面,其投影反映 c
a d
b
距离
实长。
AD
C
B
abd
P
c
ad
.
H X1 V1
a1' d. 1'
b1'. a2b2d2
如何确定d1 点的位置?
垂直面。
思考:
X
若变换H面,需在面
内取什么位置直线?
正平线!
d b
A
a
c
D B
d b H
P1 C c1
a1 d1
c
b1
X1
例:把三角形ABC变换成投影面垂直面。
b
a
d
作 图 过 程:
★ 在平面内取一条水平
c
XV H
线AD。
a
b
★ 将AD变换成新投影
d.
面的垂直线。
c
H
●α
●
●
反映平面对哪
X1 P1 c1 a1 d1 b1 个投影面的夹角?
4. 涉及直线与平面垂直、两平面垂直问题,不要求掌握,可
以自学。
看书:P41~P47 作业:3-4、8、9、10、11、12
四、解题时一般要注意下面几个问题:
⒈ 分析已给条件的空间情况,弄清原始条件中物体 与原投影面的相对位置,并把这些条件抽象成几 何元素(点、线、面等)。
⒉ 根据要求得到的结果,确定出有关几何元素对新 投影面应处于什么样的特殊位置(垂直或平行), 据此选择正确的解题思路与方法。
⒊ 在具体作图过程中,要注意新投影与原投影在变 换前后的关系, 既要在新投影体系中正确无误地 求得结果,又能将结果返回到原投影体系中去。
4. 把一般位置平面变换成投影面平行面
空间分析:
一次换面, 把一般位置平面需变经换几成次新变投换影?面的垂直面;
二次换面,再变换成新投影面的平行面。
作 图: c
AB是水平 线
a
b
●a2
XV
Ha
b2● b . a1 b1.
●
c
●
c2 平面的实形
HX1P1
c●1
X2轴的位置? 与其平行
四、换面法的应用
返回
三、换面法的四个基本作图 1. 把一般位置直线变为投影面平行线 2. 把一般位置直线变为投影面垂直线 3. 把一般位置平面变为投影面垂直面 4. 把一般位置平面变为投影面平行面
返回
1. 把一般位置直线变换成投影面平行线
例:求直线AB的实长及与H面的夹角。
空间分析:用P1面代替V面,在P1/H投影体系中,AB//P1。
a1
作图:
b
a
XV
H
b
a
b
H1
a
X1 P1a1●
●.
b1a2b2ຫໍສະໝຸດ HX1 X2轴的位置?
与a1 b1 垂直
3. 把一般位置平面变换成投影面垂直面
空间分析: 如果把平两面平内面的垂一直条需直满足线什变么换条成件新?投影面的垂
直线,那么该平面则变换成新投影面的垂直面。
作图方法:
在平面内取一条 投影一面般平位行置线直,线经变一换 V 成次投换影面面后垂变直换线成,新需投经 几影平能次面面否变的变只换垂成进?直新行线投一,影次则面变该的换? a
求解距离、夹角、实形、交点的最佳投影分析
b’ a’
a
b
两点之间距离
c’ b’
a’
a
c
b
三角形实形
c’ a’
d’ dc a
两平面夹角
c’
d’ b’ a’
b’
a
cd
b
b
直线 与平面的交点
返回
一. 换面法的基本概念
旧面
新面 c1'
V1
c1 ' b1'
新轴 a1'
b1'
旧轴a1'
不变面
X1
X1
V/H 体系变为V1/H 体系
15 b2
a2 e2
e1
d2
c2
e d
ed
小结
本章主要介绍了投影变换的一种常用方法 ——换面法。
一、 换面法就是改变投影面的位置,使它与所给物 体或其几何元素处于解题所需的特殊位置。
二、 换面法的关键是要注意新投影面的选择条件, 即必须使新投影面与某一原投面保持垂直关系, 同时又有利于解题需要,这样才能使正投影规 律继续有效。
