北林水保考研数学大纲
北林水保大纲

硕士研究生入学《水土保持学》考试大纲一、考试大纲的性质水土保持学是水土保持与荒漠化防治学科综合专业课程,是其它相关专业的选修课或必修课。
它是报考水土保持学科硕士研究生的考试科目之一。
为帮助考生明确考试复习范围和有关要求,特制定本考试大纲。
适用于报考北京林业大学硕士研究生的考生。
二、考试内容(一)水土保持与荒漠化防治的理论基础1.土壤侵蚀、水土流失、水力侵蚀、风力侵蚀、重力侵蚀、混合侵蚀、荒漠、荒漠化、沙漠化、荒漠化防治工程、封沙育草育林、风沙流、风沙流结构、输沙率、起沙风速、机械沙障等基本概念。
2.我国土壤侵蚀的分类;土壤侵蚀形式的特点;水土流失类型划分。
3.土壤侵蚀动力与分类。
4.土壤侵蚀规律:雨滴击溅;水蚀过程;风蚀过程;重力侵蚀过程。
5.土壤侵蚀影响因素。
6.水循环与水量平衡。
7.泥沙的分类;流域产流产沙规律;泥沙运动过程。
8.森林植被的水文作用。
(二)水土保持规划与工程技术1.水土保持坡面治理工程的类型及特点。
2.水土保持沟道治理工程的类型及特点。
3.水土保持综合调查的内容及方法。
4.水土保持规划的分区;水土保持规划步骤;水土保持规划方法。
5.水土保持效益分类;水土保持效益监测的内容;水土保持效益的评价方法。
(三)水土保持生物技术1.水土保持林的概念;水土保持林体系组成及空间配置。
2.水土保持林的防护目的、特点及配置技术。
3.防护林带的防护目的、特点及配置技术。
4.水库、河岸防护林的特点及配置技术。
5.水土保持生态修复的概念;水土流失区植被恢复技术。
6.水土保持耕作措施的概念;水土保持耕作措施的种类。
7.水土保持造林技术。
(四)沙漠化综合防治技术1.风沙区分类。
2.荒漠化成因;荒漠化危害。
3.沙漠化监测的内容;沙漠化评价的指标体系。
4.植物对风沙环境的适应和作用原理。
5.沙地造林的树种选择;沙地人工植被配置技术要点;风沙区防护林体系建设技术。
6.封沙育草育林的具体措施;飞播造林的关键技术。
北京林业大学硕士研究生(水保、林学)入学考试数学考试大纲

《730数学(自)》考试大纲考试科目:高等数学、数理统计考试形式和试卷结构一、试卷满分及考试时间:试卷满分为150分,考试时间为180分钟.二、答题方式:闭卷,笔试,考生要求携带计算器.三、试卷内容结构:高等教学约50%数理统计约50%四、试卷题型结构:单项选择题 8小题,每小题4分,共32分填空题 6小题,每小题4分,共24分解答题(包括证明题)9小题,共94分(一)高等数学1、函数、极限、连续考试内容:函数的概念及表示法, 函数的有界性、单调性、周期性和奇偶性复合函数,反函数, 分段函数和隐函数, 基本初等函数的性质及其图形, 初等函数, 函数关系的建立, 数列极限与函数极限的定义及其性质, 函数的左极限和右极限, 无穷小量和无穷大量的概念及其关系, 无穷小量的性质及无穷小量的比较, 极限的四则运算, 极限存在的两个准则:单调有界准则和夹逼准则, 两个重要极限, 函数连续的概念, 函数间断点的类型, 初等函数的连续性闭区间上连续函数的性质.考试要求:理解函数的概念,掌握函数的表示法,会建立应用问题中的函数关系.了解函数的有界性、单调性、周期性和奇偶性.理解复合函数及分段函数的概念,了解反函数及隐函数的概念.掌握基本初等函数的性质及其图形,了解初等函数的概念.了解数列极限和函数极限(包括左极限和右极限)的概念.了解极限的性质与极限存在的两个准则,掌握极限的四则运算法则,掌握利用两个重要极限求极限的方法.理解无穷小量的概念和基本性质,掌握无穷小量的比较方法,会用等价无穷小量求极限,了解无穷大量的概念及其与无穷小量的关系.理解函数连续性的概念(含左连续与右连续),会判断函数间断点的类型.了解连续函数的性质和初等函数的连续性,理解闭区间上连续函数的性质(有界性、最大值和最小值定理、介值定理),并会应用这些性质.2、一元函数微分学考试内容:导数和微分的概念, 导数的几何意义, 函数的可导性与连续性之间的关系, 平面曲线的切线和法线, 导数和微分的四则运算, 基本初等函数的导数, 复合函数和隐函数的微分法, 高阶导数, 微分中值定理, 洛必达(L’Hospital)法则, 函数单调性的判别, 函数的极值, 函数图形的凹凸性、拐点及渐近线, 函数的最大值与最小值.考试要求:理解导数的概念及可导性与连续性之间的关系,了解导数的几何意义,会求平面曲线的切线方程和法线方程.掌握基本初等函数的导数公式、导数的四则运算法则及复合函数的求导法则,会求分段函数的导数,会求隐函数的导数.了解高阶导数的概念,掌握二阶导数的求法.了解微分的概念以及导数与微分之间的关系,会求函数的微分.理解罗尔(Rolle)定理和拉格朗日(Lagrange)中值定理,掌握这两个定理的简单应用.会用洛必达法则求极限.掌握函数单调性的判别方法,了解函数极值的概念,掌握函数极值、最大值和最小值的求法及应用.会判断函数图形的凹凸性,会求函数图形的拐点和渐近线(水平、铅直渐近线).3、一元函数积分学考试内容:原函数和不定积分的概念, 不定积分的基本性质, 基本积分公式, 定积分的概念和基本性质, 定积分中值定理, 积分上限的函数与其导数, 牛顿-莱布尼茨(Newton-Leibniz)公式, 不定积分和定积分的换元积分方法与分部积分法, 反常(广义)积分, 定积分的应用.考试要求:理解原函数与不定积分的概念,掌握不定积分的基本性质与基本积分公式,掌握不定积分的换元积分法与分部积分法.了解定积分的概念和基本性质,了解定积分中值定理,理解积分上限的函数并会求它的导数,掌握牛顿-莱布尼茨公式以及定积分的换元积分法与分部积分法.会利用定积分计算平面图形的面积和旋转体的体积.了解无穷区间上的反常积分的概念,会计算无穷区间上的反常积分.4、多元函数微积分学考试内容:多元函数的概念, 二元函数的几何意义, 二元函数的极限与连续的概念, 多元函数偏导数的概念与计算, 多元复合函数的求导法与隐函数求导法, 二阶偏导数, 全微分, 多元函数的极值和条件极值, 二重积分的概念、基本性质和计算.考试要求:了解多元函数的概念,了解二元函数的几何意义.了解二元函数的极限与连续的概念.了解多元函数偏导数与全微分的概念,会求多元复合函数一阶、二阶偏导数,会求全微分,会求多元隐函数的偏导数.了解多元函数极值和条件极值的概念,掌握多元函数极值存在的必要条件,了解二元函数极值存在的充分条件.了解二重积分的概念与基本性质,掌握二重积分的计算方法(直角坐标、极坐标).5、常微分方程考试内容:常微分方程的基本概念, 变量可分离的微分方程, 一阶线性微分方程.考试要求:了解微分方程及其阶、解、通解、初始条件和特解等概念.掌握变量可分离的微分方程和一阶线性微分方程的求解方法.(二)数理统计1、数理统计的基本概念分布,t分布,F分布.考试内容:总体和样本,随机抽样方法,统计量,2考试要求:理解总体、样本、统计量的概念.掌握样本平均数、样本方差、标准差、极差、分布,t分布,F分布、几个重要正态样变异系数、样本原点矩、中心矩的计算.掌握2本统计量的分布.2、参数估计考试内容:点估计法(矩法、极大似然法),估计量的评选标准(无偏性、有效性、相合性),总体均值、总体频率的大样本估计,正态总体均值的小样本估计,正态总体方差的估计.考试要求:掌握用矩估计法和极大似然估计法确定常用分布的参数估计量.理解点估计和区间估计的概念.掌握总体均值、总体频率的大样本估计.掌握正态总体均值的估计;掌握正态总体方差的估计.3、假设检验考试内容:假设检验的概念、基本原理和基本步骤,总体平均数的假设检验(包括正态总体和大样本两种情况),总体频率的假设检验(大样本情况),两个总体均值的差异显著性检验(包括正态总体和大样本两种情况),两个总体频率的差异显著性检验(大样本情况),正态总体方差齐性检验,总体分布的假设检验.考试要求:了解假设检验的统计思想,掌握假设检验的一般步骤.掌握总体平均数的假设检验;掌握总体频率的假设检验.掌握两个总体均值的差异显著性检验.掌握两个总体频率的差异显著性检验.掌握正态总体方差齐性检验.掌握总体分布的假设检验.4、方差分析考试内容:单因素方差分析,多重比较,双因素方差分析.考试要求:理解方差分析的逻辑基础,熟练进行单因素方差分析、多重比较的计算、掌握双因素方差分析.5、回归分析考试内容:一元线性回归,常用线性回归的方法,多元线性回归.考试要求:理解回归分析的基本思想.掌握一元线性回归方程的求法和相关性检验的方法.了解常用线性回归的方法.了解多元线性回归.(三)主要参考书[1] 同济大学数学系. 高等数学(上、下册)(第六版),高等教育出版社.[2] 高孟宁,徐梅. 高等数学,中国农业大学出版社.[3] 贾乃光,张青,李永慈. 数理统计(第四版),中国林业出版社.[4] 盛骤,谢式千,潘承毅. 概率论与数理统计(第四版),高等教育出版社.。
华北水利水电大学2023年硕士研究生入学考试初试专业基础课考试大纲 704-数学(自命题)

华北水利水电大学
2023年硕士研究生入学考试初试科目考试大纲
科目代码:704科目名称:数学(自命题)
考试形式和试卷结构
一、试卷分值及考试时间
考试时间180分钟(3个小时),满分150分。
二、考试基本要求
本考试大纲适用于报考华北水利水电大学地理学(070500)专业的学术型硕士研究生入学考试。
704数学(自命题)包括三部分内容:(1)高等数学;(2)线性代数;(3)概率论与数理统计。
主要考察学生是否掌握了大学数学类课程的基本概念、基本理论和基本方法以及是否具备运用基本理论和基本方法对实际问题分析建立简单数学模型的能力。
三、试卷内容及结构
1.高等数学(约56%)
1.1函数、极限、连续
1.2一元函数微分学
1.3一元函数积分学
1.4多元函数微积分学
1.5常微分方程
2.线性代数(约22%)
2.1行列式
2.2矩阵
2.3向量
2.4线性方程组
2.5矩阵的特征值与对角化
3.概率论与数理统计(约22%)
3.1随机事件和概率
3.2随机变量及其分布
3.3多维随机变量及其分布
3.4随机变量的数字特征
3.5大数定律和中心极限定理
3.6数理统计的基本概念
四、试卷题型结构
主要题型有:
1.单项选择题:8小题,每小题4分,共32分;
2.填空题;6小题,每小题4分,共24分;
3.解答题(包括证明题):9小题,共94分。
2018北京林业大学水保学院考研复试通知复试时间复试分数线复试经验
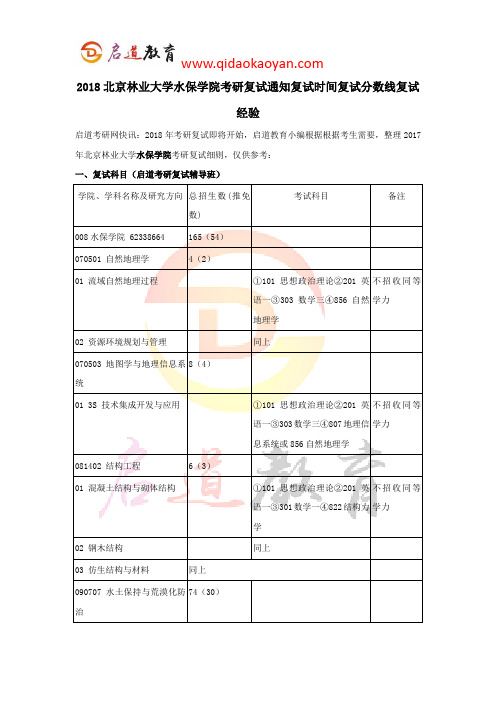
2018北京林业大学水保学院考研复试通知复试时间复试分数线复试经验启道考研网快讯:2018年考研复试即将开始,启道教育小编根据根据考生需要,整理2017年北京林业大学水保学院考研复试细则,仅供参考:一、复试科目(启道考研复试辅导班)二、复试通知(启道考研复试辅导班)依据《北京林业大学2017年招收硕士研究生复试、录取工作实施细则》,坚持“德智体全面衡量、择优录取、宁缺毋滥”的原则,加强推进信息公开,不断加强监督管理,切实严明招生纪律,确保研究生招生录取工作“公平、公正、公开”。
结合我院情况,制定学院复试工作方案,通知如下:一、复试资格审核、体检、考生学院双向沟通活动要求1.复试考生资格审查的工作程序和办法时间与地点:3月26日下午14:00—下午17:00主楼608、613(自然地理、地图学与地理信息系统、结构工程、林业硕士);3月22日下午14:00—下午17:00(水土保持与荒漠化防治学术型硕士不同研究方向审查地点详见该学科复试办法)。
操作方式:各学科秘书审查复试学生证件材料,经审查符合条件者,持体检表(详见体检要求)、复试登记表(个人信息及导师意向信息齐全)及100元复试费缴费截图(缴费网址:/web/main.action?meetingId=319,请提前操作缴费)至学院研究生秘书处登记盖章。
各类考生需查验审核的材料及要求如下。
(1)统考考生(应届本科毕业、往届本科毕业生):①准考证;②毕业证书原件及复印件(应届生应交学生证复印件,本科阶段成绩单原件或复印件,英语四级成绩单复印件,入学时交验毕业证);③有效身份证原件及复印件;4发表的论文原件及复印件(附加分考核依据,如有请提供)。
学院留取②③4复印件。
(2)少数民族骨干计划考生:按(1)审查,同时须提交“报考2017 年少数民族高层次骨干人才计划硕士研究生考生登记表”原件。
2. 体检要求我校校医院于2017年3月23日及3月27日提供两次集中体检服务,如在此时间段不能参加体检的可以到二级甲等以上医院自行体检(体检表上加盖学院公章方为有效),并于4月6日前将体检结果邮寄招生处。
东北林业大学2023自命题科目考研复试大纲:概率论与数理统计及常微分方程

东北林业大学2023自命题科目考研复试大纲:概率论与数理统计及常微分方程1500字东北林业大学2023自命题科目考研复试大纲:概率论与数理统计及常微分方程一、概率论与数理统计概率论与数理统计是现代科学与工程领域必不可少的基础知识,它们在林业学科中也有着广泛的应用。
本科目旨在考察考生对概率论与数理统计的理解与掌握程度,以及能够运用相关知识解决实际问题的能力。
1. 概率论1.1 基本概念- 随机事件与样本空间- 概率的定义与性质- 条件概率与乘法公式- 全概率公式与贝叶斯公式1.2 随机变量与概率分布- 随机变量的概念与分类- 离散型随机变量与概率分布- 连续型随机变量与概率密度函数- 期望、方差和协方差的计算1.3 多维随机变量与联合分布- 多维随机变量的概念与性质- 联合分布函数与边缘分布函数- 条件分布与独立性- 两个随机变量的协方差和相关系数的计算2. 数理统计2.1 参数估计- 点估计与区间估计的概念与性质- 极大似然估计- 矩估计- 最小二乘估计2.2 假设检验- 假设检验的基本思想与步骤- 单侧检验与双侧检验- 正态总体的假设检验- 两个总体均值的假设检验2.3 方差分析- 单因素方差分析的基本思想与步骤- 多因素方差分析的基本思想与步骤- 方差齐性的检验- 非参数统计方法的应用二、常微分方程常微分方程是数学的重要分支之一,广泛应用于物理、生物、工程等领域。
本科目旨在考察考生对常微分方程的基本概念与解法的掌握情况,以及能够运用常微分方程解决实际问题的能力。
1. 常微分方程的基本概念- 常微分方程的定义与分类- 阶数与线性性质- 初始值问题与边值问题的概念2. 一阶常微分方程- 可分离变量的一阶常微分方程- 齐次方程和非齐次方程的解法- 线性方程的解法- 变量可分离的高阶方程的解法3. 高阶常微分方程- 齐次线性方程与非齐次线性方程的解法- 常系数线性方程的解法- 变系数线性方程的解法- 线性方程的特解与齐次方程的通解4. 系数待定法与常系数线性方程组- 常系数线性方程的系数待定法- 非齐次线性方程组的特解与齐次方程组的通解5. 变类系数与常微分方程的应用- 变类系数线性方程与非线性方程的解法- 常微分方程的应用实例分析以上为东北林业大学2023自命题科目考研复试大纲:概率论与数理统计及常微分方程的内容,希望对考生的复试准备有所帮助。
华北水利水电大学 2024年硕士大纲 701-数学分析

华北水利水电大学2024年硕士研究生入学考试初试科目考试大纲科目代码:701科目名称:数学分析考试形式和试卷结构一、试卷分值及考试时间考试时间180分钟(3个小时),满分150分。
二、考试基本要求要求考生比较系统地理解数学分析的基本概念和基本理论,掌握数学分析的基本思想和方法。
要求考生具有抽象思维能力、逻辑推理能力、运算能力和综合运用所学的知识分析问题和解决问题的能力。
三、试卷题型计算题(7小题,105分)和证明题(3小题,45分)。
四、试卷内容及结构1.数列极限,占约10%(1)实数概念、确界(2)数列极限2.一元函数微积分,占约30%(1)导数概念及几何意义(2)求导公式求导法则(3)高阶导数(4)微分(5)微分中值定理(6)L’Hospital法则(7)Taylor公式(8)应用导数研究函数(9)不定积分法与可积函数类(10)定积分的概念、性质与计算(11)定积分的应用(12)广义积分3.级数,占约20%(1)数项级数的敛散判别与性质(2)函数项级数与一致收敛性(3)幂级数(4)Fourier级数4.多元函数微积分,占约40%(1)欧氏空间(2)多元函数的极限(3)多元连续函数(4)偏导数与微分(5)隐函数定理(6)Taylor公式(7)多元微分学的几何应用(8)多元函数的极值(9)重积分的概念与性质(10)重积分的计算(11)二重、三重广义积分(12)含参变量的正常积分和广义积分(13)曲线积分与Green公式(14)曲面积分(15)Gauss公式、Stokes公式及线积分与路径无关五、参考书目《数学分析》(第四版),华东师范大学数学系,高等教育出版社,2011;。
水保基础课大纲‘

附件1勘探设计注册土木工程师(水利水电工程)资格考试基础考试大纲一、高等数学空间解析几何向量代数直线平面柱面旋转曲面二次曲面空间曲线微分学极限持续导数微分偏导数全微分导数与微分的应用积分学不定积分定积分广义积分二重积分三重积分平面曲线积分积分应用无穷级数数项级数幂级数泰勒级数傅里叶级数常微分方程可分离变量方程一阶线性方程可降阶方程常系数线性方程概率与数理统计随机事件与概率古典概型一维随机变量的散布和数字特点数理统计参数估量假设查验方差分析一元回归分析向量分析线性代数行列式矩阵n维向量线性方程组矩阵的特点值与特点向量二次型二、一般物理热学气体状态参量平稳态理想气体状态方程理想气体的压力和温度的统计说明能量按自由度均分原理理想气体内能平均碰撞次数和平均自由程麦克斯韦速度散布律功热量内能热力学第必然律及其对理想气体等值进程和绝热进程的应用气体的摩尔热容循环进程热机效率热力学第二定律及其统计意义可逆进程和不可逆进程熵波动学机械波的产生和传播简谐波表达式波的能量驻波声速超声波次声波多普勒效应光学相干光的取得杨氏双缝干与光程薄膜干与迈克尔干与仪惠更斯一菲涅耳原理单缝衍射光学仪器分辨本领x射线衍射自然光和偏振光布儒斯特定律马吕斯定律双折射现象偏振光的干与人工双折射及应用三、一般化学物质结构与物质状态原子核外电子散布原子、离子的电子结构式原子轨道和电子云离子键特点共价键特点及类型分子结构式杂化轨道及分子空间构型极性分子与非极性分子分子间力与氢键分压定律及计算液体蒸气压沸点汽化热晶体类型与物质性质的关系溶液溶液的浓度及计算非电解质稀溶液通性及计算渗透压电解质溶液的电离平稳电离常数及计算同离子效应缓和冲溶液水的离子积及pH值盐类水解平稳及溶液的酸碱性多相离子平稳溶度积常数溶解度计算周期表周期表结构周期族原子结构与周期表关系元素性质氧化物及其水化物的酸碱性递变规律化学反映方程式化学反映速度与化学平稳化学反映方程式写法及计算反映热热化学反映方程式写法化学反映速度表示方式浓度、温度对反映速度的阻碍速度常数与反映级数活化能及催化剂化学平稳特点及平稳常数表达式化学平稳移动原理及计算压力熵与化学反映方向判定氧化还原与电化学氧化剂与还原剂氧化还原反映方程式写法及配平原电池组成及符号电极反映与电池反映标准电极电势能斯特方程及电极电势的应用电解与金属侵蚀有机化学有机物特点、分类及命名官能团及分子结构式有机物的重要化学反映:加成取代消去氧化加聚与缩聚典型有机物的分子式、性质及用途:甲烷乙炔苯甲苯乙醇酚乙醛乙酸乙酯乙胺苯胺聚氯乙烯聚乙烯聚丙烯酸酯类工程塑料(ABS) 橡胶尼龙66四、理论力学静力学平稳刚体力约束静力学公理受力分析力对点之矩力对轴之矩力偶理论力系的简化主矢主矩力系的平稳物体系统(含平面静定桁架)的平稳滑动摩擦摩擦角自锁考虑滑动摩擦时物体系统的平稳重心运动学点的运动方程轨迹速度和加速度刚体的平动刚体的定轴转动转动方程角速度和角加速度刚体内任一点的速度和加速度动力学动力学大体定律质点运动微分方程动量冲量动量定理动量守恒的条件质心质心运动定理质心运动守恒的条件动量矩动量矩定理动量矩守恒的条件刚体的定轴转动微分方程转动惯量回转半径转动惯量的平行轴定理功动能势能动能定理机械能守恒惯性力刚体惯性力系的简化达朗伯原理单自由度系统线性振动的微分方程振动周期频率和振幅约束自由度广义坐标虚位移理想约束虚位移原理五、材料力学轴力和轴力图拉、压杆横截面和斜截面上的应力强度条件虎克定律和位移计算应变能计算剪切和挤压的有效计算剪切虎克定律切(剪)应力互等定理外力偶矩的计算扭矩和扭矩图圆轴扭转切(剪)应力及强度条件扭转角计算及刚度条件扭转应变能计算静矩和形心惯性矩和惯性积平行移轴公式形心主惯性矩梁的内力方程切(剪)力图和弯矩图散布载荷、剪力、弯矩之间的微分关系正应力强度条件切(剪)应力强度条件梁的合理截面弯曲中心概念求梁变形的积分法叠加法和卡氏第二定理平面应力状态分析的数值解法和图解法一点应力状态的主应力和最大切(剪)应力广义虎克定律四个经常使用的强度理论斜弯曲偏心紧缩(或拉伸) 拉—弯或压—弯组合扭—弯组合细长压杆的临界力公式欧拉公式的适用范围临界应力总图和体会公式压杆的稳固校核六、流体力学流体的要紧物理性质流体静力学流体静压强重力作用下静水压强的散布规律总压力的计算流体动力学基础以流场为对象描述流动流体运动的总流分析恒定总流持续性方程、能量方程和动量方程流动阻力和水头损失实际流体的两种流态—层流和紊流圆管中层流运动、紊流运动的特点沿程水头损失和局部水头损失边界层附面层大体概念和绕流阻力孔口、管嘴出流有压管道恒定流明渠恒定均匀流渗流定律井和集水廊道相似原理和量纲分析流体运动参数(流速、流量、压强)的测量七、运算机应用技术运算机应用技术硬件的组成及功能软件的组成及功能数制转换Windows操作系统大体知识、系统启动有关目录、文件、磁盘及其它操作网络功能注:以Windows 98为基础运算机程序设计语言程序结构与大体规定数据变量数组指针赋值语句输入输出的语句转移语句条件语句选择语句循环语句函数子程序(或称进程) 顺序文件随机文件注:鉴于目前情形,暂采纳FORTRAN语言八、电工电子技术电场与磁场库仑定律高斯定理环路定律电磁感应定律直流电路电路大体元件欧姆定律基尔霍夫定律叠加原理戴维南定理正弦交流电路正弦量三要素有效值复阻抗单相和三相电路计算功率及功率因数串联与并联谐振平安用电常识RC和RL电路暂态进程三要素分析法变压器与电动机变压器的电压、电流和阻抗变换三相异步电动机的利用经常使用继电—接触器操纵电路二极管及整流、滤波、稳压电路三极管及单管放大电路运算放大器理想运放组成的比例加、减和积分运算电路门电路和触发器大体门电路RS、D、JK触发器九、工程经济现金流量组成与资金等值计算现金流量投资资产固定资产折旧本钱经营本钱销售收入利润工程项目投资涉及的要紧税种资金等值计算的经常使用公式及应用复利系数表的用法投资经济成效评判方式和参数净现值内部收益率净年值费用现值费用年值差额内部收益率投资回收期基准折现率备选方案的类型寿命相等方案与寿命不等方案的比选不确信性分析盈亏平稳分析盈亏平稳点固定本钱变更本钱单因素灵敏性分析灵敏因素投资项目的财务评判工业投资项目可行性研究的大体内容投资项目财务评判的目标与工作内容获利能力分析资金筹措的要紧方式资金本钱债务归还的要紧方式基础财务报表全投资经济成效与自有资金经济成效全投资现金流量表与自有资金现金流量表财务成效计算偿债能力分析改扩建和技术改造投资项目财务评判的特点(相对新建项目)价值工程价值工程的内容与实施步骤功能分析十、水力学水静力学静水压强绝对压强相对压强真空及真空度作用于物体上的静水总压力液体运动的一元流分析法恒定流与非恒定流迹线与流线流管过水断面流量断面平均流速恒定一元流持续性方程能量方程式渐变流急变流层流、紊流及其水头损失湿周水力半径均匀流非均匀流沿程水头损失达西公式层流紊流雷诺数谢才公式局部水头损失有压管中恒定均匀流计算大体公式串联管道并联管道分叉管道沿程均匀泄流管道明渠恒定均匀流计算大体公式明渠均匀流粗糙度不同的明渠复式断面明渠明渠恒定非均匀流缓流临界流急流弗汝德数临界水深临界底坡棱柱体明渠渐变流水面曲线分析及计算水跃水跃方程共轭水深及水跃长度计算堰流及闸孔出流的水力计算计算公式薄壁堰有效堰宽顶堰闸孔出流泄水建筑物下游的水力衔接与消能底流式消能挑流式消能面流式消能消力戽式消能隧洞的水力计算水流状态及判定有压隧洞无压隧洞渗流达西定律渗透系数恒定均匀渗流与非均匀渗流恒定渐变渗流的浸润曲线形式及计算高速水流脉动压力气蚀掺气冲击波水工模型实验基础力学相似:几何相似运动相似动力相似相似准则:重力相似准则阻力相似准则动水压力相似准则十一、岩土力学土的组成和物理性质三项指标土的三项组成和三项指标土的矿物组成和颗粒级配土的结构黏性土的界限含水量塑性指数液性指数砂土的相对密实度土的最佳含水量和最大干密度土的工程分类土中应力散布及计算土的自重应力基础地面压力基底附加压力土中附加应力土的紧缩性与地基沉降紧缩实验紧缩曲线紧缩系数紧缩指数回弹指数紧缩模量载荷实验变形模量高压固结试验土的应力历史先期固结压力超固结比正常固结土超固结土欠固结土沉降计算的弹性理论法分层总合法有效应力原理一维固结理论固结系数固结度土的抗剪强度土中一点的应力状态库仑定律土的极限平稳条件内摩擦角黏聚力直剪试验及其适用条件三轴试验总应力法有效应力法特殊性土软土黄土膨胀土红粘土盐渍土冻土填土可液化土土压力静止土压力主动土压力被动土压力朗肯土压力理论库仑土压力理论边坡稳固分析土坡滑动失稳的机理均质土坡的稳固分析土坡稳固分析的条分法地基承载力地基破坏的进程地基破坏型式临塑荷载和临界荷载地基极限承载力斯肯普敦公式太沙基公式汉森公式岩石的物理性质岩石的破坏机理与强度岩石的变形岩体的工程分类围岩稳固性岩坡稳固性分析十二、结构力学平面体系的几何组成几何不变体系的组成规律及其应用静定结构受力分析与特性静定结构受力分析方式反力内力的计算与内力图的绘制静定结构特性及其应用静定结构位移广义力与广义位移虚功原理单位荷载法荷载下静定结构的位移计算图乘法支座位移和温度转变引发的位移互等定理及其应用超静定结构受力分析及特点超静定次数力法大体体系力法方程及其意义等截面直杆刚度方程位移法大体未知量、大体体系、大体方程及其意义等截面直杆的转动刚度力矩分派系数与传递系数单结点的力矩分派对称性利用超静定结构位移超静定结构特性阻碍线极为应用静力法做阻碍线机动法做阻碍线持续梁的阻碍线阻碍线的应用结构动力特性与动力反映单自由度体系自振周期频率振幅与最大动内力阻尼对振动的阻碍十三、钢筋混凝土结构材料性能钢筋混凝土设计原那么结构功能极限状态及其设计表达式靠得住度承载能力极限状态计算受弯构件受扭构件受压构件受拉构件冲切局压疲劳正常利用极限状态验算抗裂裂痕挠度预应力混凝土轴拉构件受弯构件肋形结构及刚架结构整体式单向板肋形结构双向板肋形结构刚架结构牛腿柱下基础抗震设计一样规定构造要求十四、工程测量测量工作特点形状和大小地面点位的确信测量工作大体概念水准测量水准测量原理水准仪的构造利用和查验校正水准测量方式及功效整理角度测量经纬仪的构造利用和查验校正水平角观测垂直角观测距离测量卷尺量距视距测量光电测距测量误差测量误差分类与特性评定精度的标准观测值的精度评定误差传播定律操纵测量平面操纵网的定位与定向导线测量交会定点高程操纵测量地形图测绘地形图大体知识地物平面图测绘等高线地形图测绘地形图应用地形图应用的大体技术工程设计中的地形图应用计划设计中的地形图应用工程测量工程操纵测量施工放样测量安装测量建筑物变形观测3S技术RS的大体技术及数字图象 GIS 的大体要求 GPS的大体要求及定位技术 3S 技术在水利工程中的应用十五、建筑材料材料科学与物质结构材料的组成:化学组成矿物组成及其对材料性质的阻碍材料的微观机构及其对材料性质的影响:原子结构离子键金属键共价键晶体与无定型体(玻璃体)材料的宏观机构及其对材料性质的影响建筑材料的性质密度表观密度与堆积密度孔隙与孔隙率建筑材料的工程特点材料的力学性能亲水性与憎水性吸水性与吸湿性耐水性抗水性抗冻性导热性与变形性脆性与韧性无机胶凝材料气硬性胶凝材料石膏和石灰技术性质与应用水硬性胶凝材料水泥的组成水化与凝结硬化机理性能与应用混凝土原材料技术要求拌合物的和易性及阻碍因素强度性能与变形性能耐久性抗渗性抗冻性碱-骨料反映混凝土外加计与配合比设计建筑钢材组成、组织与性能的关系加工处置及其对钢材性能的阻碍建筑钢材和种类与选用土工合成材料常见土工合成材料的特性及工程应用十六、工程水文学基础水文循环与径流形成水文循环与水量平稳河流与流域降水土壤水、下渗与地下水径流水文考试水位观测流量考试泥沙考试与计算水文调查水文数据处置流域产、汇流降雨径流要素产流计算汇流计算设计洪水水文频率分析样本分析相关分析设计洪水计算设计年径流频率分析时程分派勘探设计注册土木工程师(水利水电工程)资格考试基础考试分科题量、时刻、分数分派说明上午段:高等数学24题流体力学12题普通物理12题计算机应用技术10题普通化学12题电工电子技术12题理论力学13题工程经济10题材料力学15题合计120题,每题1分。
含线性代数)考试大纲 - 北京林业大学

6.关于定积分及其应用:定积分的定义与性质:变上限积分函数的定义、性质及其导数;牛顿一莱布尼兹公式及证明:定积分的计算(换元积分法、分部积分法); I型、Ⅱ型广义积分的定义及计算;求定积分在几何中的应用(在平面直角坐标系下求曲线所围图形的面积,旋转体的体积):定积分在物理学中的应用(功、水压力)。
(二)线性代数部分
1.关于行列式:行列式的性质:计算行列式,
2.关于矩阵:矩阵的定义;各种矩阵(零矩阵,单位矩阵、转置矩阵、上三角矩阵等)的性质:矩阵运算(加法、数乘、乘法);矩阵运算的性质:分块矩阵的运算:逆矩阵的定义及存在的充要条件;矩阵的秩;用初等变换求矩阵的逆矩阵和秩;关于矩阵及其运算的证明题。
微积分约占总分的70%,线性代数约占总分的30%。
(二)试卷的结构
1、填空、选择题:占总分的25%左右,内容为概念和基本计算,主要覆盖本门课程的各部分知识点。
2、计算或解答题:占总分的60%左右,主要为各部分的重要计算题、应用题
3、证明题:占总分的15%左右。
六、主要参考节
7.关于二元函数:空间直角坐标系的概念;平面、柱面及球面方程;二元函数的定义;二元函数的极限与连续:求二元函数的偏导数:计算二重积分。
8.关于微分方程:常微分方程的定义(阶、解、通解、特解、初始条件等概念);用分离变量法、常数变易法求一阶微分方程的解;求可降阶的二阶微分方程和二阶线性常系数齐次微分方程的解,一阶微分方程的应用。
3.关于线性方程组:线性方程组无解、有唯一解,有无穷解的充要条什;求线性方程组的全部解:向量的线性组合、线性表示、线性相关与线性无关的定义和定理:向量组的秩;判断、证明向量组的线性相关、线性无关。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《730数学(自)》考试大纲
考试科目:高等数学、数理统计
考试形式和试卷结构
一、试卷满分及考试时间:试卷满分为150分,考试时间为180分钟.
二、答题方式:闭卷,笔试,考生要求携带计算器.
三、试卷内容结构:
高等教学约50%
数理统计约50%
四、试卷题型结构:
单项选择题8小题,每小题4分,共32分
填空题6小题,每小题4分,共24分
解答题(包括证明题)9小题,共94分
(一)高等数学
1、函数、极限、连续
考试内容:函数的概念及表示法,函数的有界性、单调性、周期性和奇偶性复合函数,反函数,分段函数和隐函数,基本初等函数的性质及其图形,初等函数,函数关系的建立,数列极限与函数极限的定义及其性质,函数的左极限和右极限,无穷小量和无穷大量的概念及其关系,无穷小量的性质及无穷小量的比较,极限的四则运算,极限存在的两个准则:单调有界准则和夹逼准则,两个重要极限,函数连续的概念,函数间断点的类型,初等函数的连续性闭区间上连续函数的性质.
考试要求:理解函数的概念,掌握函数的表示法,会建立应用问题中的函数关系.了解函数的有界性、单调性、周期性和奇偶性.理解复合函数及分段函数的概念,了解反函数及隐函数的概念.掌握基本初等函数的性质及其图形,了解初等函数的概念.了解数列极限和函数极限(包括左极限和右极限)的概念.了解极限的性质与极限存在的两个准则,掌握极限的四则运算法则,掌握利用两个重要极限求极限的方法.理解无穷小量的概念和基本性质,掌握无穷小量的比较方法,会用等价无穷小量求极限,了解无穷大量的概念及其与无穷小量的关系.理解函数连续性的概念(含左连续与右连续),会判断函数间断点的类型.了解连续函数的性质和初等函数的连续性,理解闭区间上连续函数的性质(有界性、最大值和最小值定理、介值定理),并会应用这些性质.
2、一元函数微分学
考试内容:导数和微分的概念,导数的几何意义,函数的可导性与连续性之间的关系,平面曲线的切线和法线,导数和微分的四则运算,基本初等函数的导数,复合函数和隐函数的微分法,高阶导数,微分中值定理,洛必达(L’Hospital)法则,函数单调性的判别,函数的极值,函数图形的凹凸性、拐点及渐近线,函数的最大值与最小值.
考试要求:理解导数的概念及可导性与连续性之间的关系,了解导数的几何意义,会求平面曲线的切线方程和法线方程.掌握基本初等函数的导数公式、导数的四则运算法则及复合函数的求导法则,会求分段函数的导数,会求隐函数的导数.了解高阶导数的概念,掌握二阶导数的求法.了解微分的概念以及导数与微分之间的关系,会求函数的微分.理解罗尔(Rolle)定理和拉格朗日(Lagrange)中值定理,掌握这两个定理的简单应用.会用洛必达法则求极限.掌握函数单调性的判别方法,了解函数极值的概念,掌握函数极值、最大值和最小值的求法及应用.会判断函数图形的凹凸性,会求函数图形的拐点和渐近线(水平、铅直渐近线).
3、一元函数积分学
考试内容:原函数和不定积分的概念,不定积分的基本性质,基本积分公式,定积分的概念
和基本性质,定积分中值定理,积分上限的函数与其导数,牛顿-莱布尼茨(Newton-Leibniz)公式,不定积分和定积分的换元积分方法与分部积分法,反常(广义)积分,定积分的应用.
考试要求:理解原函数与不定积分的概念,掌握不定积分的基本性质与基本积分公式,掌握不定积分的换元积分法与分部积分法.了解定积分的概念和基本性质,了解定积分中值定理,理解积分上限的函数并会求它的导数,掌握牛顿-莱布尼茨公式以及定积分的换元积分法与分部积分法.会利用定积分计算平面图形的面积和旋转体的体积.了解无穷区间上的反常积分的概念,会计算无穷区间上的反常积分.
4、多元函数微积分学
考试内容:多元函数的概念,二元函数的几何意义,二元函数的极限与连续的概念,多元函数偏导数的概念与计算,多元复合函数的求导法与隐函数求导法,二阶偏导数,全微分,多元函数的极值和条件极值,二重积分的概念、基本性质和计算.
考试要求:了解多元函数的概念,了解二元函数的几何意义.了解二元函数的极限与连续的概念.了解多元函数偏导数与全微分的概念,会求多元复合函数一阶、二阶偏导数,会求全微分,会求多元隐函数的偏导数.了解多元函数极值和条件极值的概念,掌握多元函数极值存在的必要条件,了解二元函数极值存在的充分条件.了解二重积分的概念与基本性质,掌握二重积分的计算方法(直角坐标、极坐标).
5、常微分方程
考试内容:常微分方程的基本概念,变量可分离的微分方程,一阶线性微分方程.
考试要求:了解微分方程及其阶、解、通解、初始条件和特解等概念.掌握变量可分离的微分方程和一阶线性微分方程的求解方法.
(二)数理统计
1、数理统计的基本概念
考试内容:总体和样本,随机抽样方法,统计量,分布,t分布,F分布.
考试要求:理解总体、样本、统计量的概念.掌握样本平均数、样本方差、标准差、极差、变异系数、样本原点矩、中心矩的计算.掌握分布,t分布,F分布、几个重要正态样本统计量的分布.
2、参数估计
考试内容:点估计法(矩法、极大似然法),估计量的评选标准(无偏性、有效性、相合性),总体均值、总体频率的大样本估计,正态总体均值的小样本估计,正态总体方差的估计.
考试要求:掌握用矩估计法和极大似然估计法确定常用分布的参数估计量.理解点估计和区间估计的概念.掌握总体均值、总体频率的大样本估计.掌握正态总体均值的估计;掌握正态总体方差的估计.
3、假设检验
考试内容:假设检验的概念、基本原理和基本步骤,总体平均数的假设检验(包括正态总体和大样本两种情况),总体频率的假设检验(大样本情况),两个总体均值的差异显著性检验(包括正态总体和大样本两种情况),两个总体频率的差异显著性检验(大样本情况),正态总体方差齐性检验,总体分布的假设检验.
考试要求:了解假设检验的统计思想,掌握假设检验的一般步骤.掌握总体平均数的假设检验;掌握总体频率的假设检验.掌握两个总体均值的差异显著性检验.掌握两个总体频率的差异显著性检验.掌握正态总体方差齐性检验.掌握总体分布的假设检验.
4、方差分析
考试内容:单因素方差分析,多重比较,双因素方差分析.
考试要求:理解方差分析的逻辑基础,熟练进行单因素方差分析、多重比较的计算、掌
握双因素方差分析.
5、回归分析
考试内容:一元线性回归,常用线性回归的方法,多元线性回归.
考试要求:理解回归分析的基本思想.掌握一元线性回归方程的求法和相关性检验的方法.了解常用线性回归的方法.了解多元线性回归.
(三)主要参考书
[1]同济大学数学系.高等数学(上、下册)(第六版),高等教育出版社.
[2]高孟宁,徐梅.高等数学,中国农业大学出版社.
[3]贾乃光,张青,李永慈.数理统计(第四版),中国林业出版社.
[4]盛骤,谢式千,潘承毅.概率论与数理统计(第四版),高等教育出版社.。
